п.1. От ускорения к скорости и координате
Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac{at^2}{2}+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac{at^2}{2}+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).
п.2. Физические величины как интегралы других величин
Если (v(t)) – скорость некоторого физического процесса, уравнение этого процесса можно найти интегрированием: $$ f(t)=int v(t)dt $$ Такие величины часто встречаются в различных разделах физики и техники.
Исходная величина (скорость)
Уравнение процесса (интеграл по времени)
Ускорение (a(t))
Скорость (v(t)=int a(t)dt)
Скорость (v(t))
Координата (x(t)=int v(t)dt)
Угловое ускорение (beta(t))
Угловая скорость (omega(t)=int beta(t) dt)
Угловая скорость (omega(t))
Угол поворота (varphi(t)=intomega(t)dt)
Скорость расходования горючего (u(t))
Масса горючего ракеты (m(t)=int u(t)dt)
Сила тока (I(t))
Заряд (q(t)=int I(t)dt)
Мощность (N(t))
Работа (A(t)=int N(t)dt)
ЭДС индукции (varepsilon(t))
Магнитный поток (Ф(t)=-intvarepsilon(t)dt)
Скорость радиоактивного распада (I(t))
Число атомов радиоактивного вещества (N(t)=int I(t)dt)
Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_{x_1}^{x_2}F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.
В современной физике интеграл по времени берётся также и от самого уравнение движения. Полученная скалярная величина называется действием и носит фундаментальный характер. В простейшем случае: $$ S_0=int overrightarrow{p}cdot overrightarrow{v}dt $$ где (overrightarrow{p}cdot overrightarrow{v}) – скалярное произведение векторов импульса и скорости.
п.3. Примеры
Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin{gather*} s(t)=int_{t_1}^{t_2}v(t)dt\ s=int_{0}^{6}(3t+2t^2)dt=left(frac{3t^2}{2}+frac{2t^3}{3}right)|_{0}^{6}=frac{3cdot 36}{2}+frac{2cdot 36cdot 6}{3}-0=\ =3cdot 18+4cdot 36=54+144=198 text{(м)} end{gather*}
б) (v(t)=2(t+2)^{5/2}, t_1=0, t_2=7) begin{gather*} s=int_{0}^{7}2(t+2)^{5/2}dt =2cdotfrac{(t+2)^{frac52+1}}{frac72}|_{0}^{7}=frac47cdot 9^{frac72}-0=frac47cdot 3^7approx 1250 text{(м)} end{gather*}
Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^{-t}+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin{gather*} Q(t)=int_{t_1}^{t_2}I(t)dt end{gather*} По условию: begin{gather*} Q=int_{2}^{6}(e^{-t}+2t)dt=(-e^{-t}+t^2)|_{2}^{6}=-e^{-6}+6^2+e^{-2}-2^2=frac{1}{e^2}-frac{1}{e^6}+32=\ =frac{e^4-1}{e^6}+32approx 32,1 text{(Кл)} end{gather*}
Пример 3*. Найдите путь, который пройдет тело от начала движения до возвращения в исходную точку, если его скорость (v(t)=18t-9t^2) (время в секундах, скорость в м/с). Движение тела прямолинейное.
Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin{array}{l} t=0\ t=2 end{array} right. $$ (t=0) – начало движения, (t=2) – разворот.
 |
Уравнение движения: $$ x(t)=int(18t-9t^2)dt=9t^2-3t^3+C $$ В начальный момент времени (x_0=0Rightarrow C=0) $$ x(t)=9t^2-3t^3 $$ В точке C(2;12) кривая (x(t)) имеет максимум. Тело двигалось в течение 2 с в одну сторону и прошло 12 м, а затем за 1 с вернулось обратно. Общий путь: 12+12 = 24 м. |
Ответ: 24 м
Пример 4*. Найдите работу, которую необходимо совершить, чтобы выкачать воду из полусферического котла радиуса R м.
Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) – по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin{gather*} A=int_{0}^{R}dA=int_{0}^{R}pirho gH(R^2-H^2)dH=pirho gint_{0}^{R}(HR^2-H^3)dH=\ =pirho gleft(frac{H^2}{2}R^2-frac{H^4}{4}right)|_{0}^{R}=pirho gleft(frac{R^4}{2}-frac{R^4}{4}-0right)=fracpi 4=rho gR^4 end{gather*} Ответ: (A=fracpi 4=rho gR^4)
Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с2, радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с2 (R_E=6371) км.
Ускорение свободного падения на поверхности планеты: (g_0=Gfrac{M}{R^2})
Ускорение свободного падения при подъеме на высоту x: begin{gather*} g(x)=Gfrac{M}{(R+x)^2} end{gather*} Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin{gather*} A=int_{0}^{h}mg(x)dx=mint_{0}^{h}Gfrac{M}{(R+x)^2}dx=GmMint_{0}^{h}frac{dx}{(R+x^2)}=\ =GmMcdotleft(-frac{1}{R+x}right)|_{0}^{h}=GmMcdotleft(-frac{1}{R+h}+frac1Rright)=GmMleft(frac1R-frac{1}{R+g}right)=\ =GmMfrac{R+h-R}{R(R+h)}=GmMfrac{h}{R(R+h)} end{gather*} Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=frac{GM}{R^2}frac{mhR^2}{R(R+h)}=mg_0frac{hR}{R+h} $$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac{R^2}{2R}=frac{mg_0R}{2} $$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac{A_E(R_E)}{A_M(R_M)}=frac{mg_ER_E}{mg_MR_M}=frac{g_ER_E}{g_MR_M}, frac{A_E(R_E)}{A_M(R_M)}=frac{9,81cdot 6371}{1,62cdot 1737}approx 22,2 $$ На Земле работа в 22,2 раза больше.
Ответ: (A=GmMfrac{h}{R(R+h)}; frac{A_E(R_E)}{A_M(R_M)}approx 22,2)
В одной из статей, мы с Вами уже рассматривали производную функции. Сегодня задача ознакомиться с интегралом функции и понять его физический смысл. Прежде всего отмечу. что это интегрирование – процесс обратный извлечению производной. То есть, если Вы взяли производную от функции X, то взяв полученный результат – проинтегрируете его, снова получить Х. Есть, конечно, определенные детали, но сейчас их не берем во внимание. Так если Вы интегрируете скорость, то получите пройденное расстояние, Если интегрируете мощность, то получите работу, и так далее. А теперь ближе к физическому смыслу.
Пример:Вы едете на велосипеде и у Вас постоянная скорость, 20 км/ч, то за два часа Вы пройдете расстояние в 40 км. Вы просто умножили скорость на время и получили значение. Тут все очевидно, а теперь предположим, что вы едете, по разнородной местности, где есть подъемы, спуски, есть места, где нужно идти пешком. Тогда на всем участке у Вас скорость будет разная, значит формула S=V*t уже не работает. Как в этом случае быть, да очень просто.
Если посмотреть, на второй график, то видим, что подсчитать в данном случае площадь фигуры намного сложнее, но тоже возможно. Когда скорость постоянна, мы можем легко этот вопрос решить, а когда скорость переменная, то необходимо применять разные варианты.
На третьем рисунке, мы разбили функцию всей скорости, на разные участки, приближенные к прямой. Если рассмотреть самый первый участок, то скорость там постоянна, значит площадь ограниченной сверху этим участком подсчитать мы можем. Далее наклонная прямая вверх, при желании тоже легко позволяет найти площадь. и так далее.На тех участках, где у нас гладкие функции, например, парабола или экспонента, мы дробим на большее количество участков.
Небольшое замечание, если взять первый постоянный отрезок скорости и разбить его на 100 других отрезков, и подсчитать площадь каждого, а после суммировать, то общая площадь и сумма площадей каждого из них будут равны. То есть в данном случае под интегрированием понимается процесс дробления на участки и суммирования их площадей. А теперь если взять например 6 участок и разбить его на 100 частей, то вместо общей гладкой функции мы получим 100 маленьких отрезков, каждый из которых будет ограничен сверху по сути прямой. Далее подсчитать площадь такого участка проще и мы считаем, площадь каждого участка и суммируем их вместе, получив достаточно точный результат. Чем больше точность нужна, тем больше делаем число разбиений на участки.
Таким образом, глядя на рисунки, видим, что увеличивая число отрезков, мы снижаем погрешность, и независимо от функции приближаемся к точному значению пройденного расстояния. Если число отрезков устремить к бесконечному, то получим точную функцию интегрирования, по которой можем точно подсчитать значение площади. При этом помним, что поиск производной функции – это обратный процесс интегрированию функции. А теперь еще раз к смыслу интегрирования. Если у нас есть сложная функция, то мы берем интеграл от этой функции (дробим на бесконечное число отрезков) и находим площадь каждого отрезка, и после этого суммируем все площади. Возникает вопрос, а как нам найти конкретные значения в данной точке, а очень просто, у нас же есть функция по времени, например V=7t*t+24t+7. В каждый момент времени мы находим значение V и считаем площадь, в итоге получается найти площади всех маленьких участков..
Отмечу сразу, что данная методика дробления или преобразования в удобные функции часто используется, когда мы не знаем точную входную функцию, мы описываем её в виде подходящей функции с заданной точностью и оперируем с ней. Опять же в виде матрицы или полинома. А после интегрируем полином или производную.
Итак, подводим итог не простой темы. Процесс интегрирования – это процесс дробления функции через который мы можем найти точную площадь каждого участка, а значит и всей функции на данном участке. Если мы будем интегрировать функцию скорости по времени, то получим пройденное расстояние, если будем интегрировать ускорение по времени, то площадью будет текущая скорость. Если будем интегрировать скорость слива воды с емкости, то проинтегрировав – получим вылитый объем в единица времени. Если будем интегрировать мощность затраченную за время. получим совершенную работу.
Отмечу, тема не простая, если есть вопросы – пишите. Без таких тем в регулирование даже не стоит суваться, даже простое.
Если Вам понравилась публикация, подписывайтесь на канал, за Ваши лайки чаще показывают Наши публикации.
Для поиска публикаций через поисковые системы, просто вводите слово Вивитроника.
Свои комментарии можете предлагать в группе вконтакте,
Если есть вопросы или по желания, то пишите, через Обратную связь.
Канал телеграм.
Цель урока:
- обобщить и закрепить ключевые задачи по теме;
- научиться работать с теоретическими вопросами
темы; - научиться применять интеграл к решению
физических задач.
План урока:
1. Схема решения задач на приложения
определенного интеграла
2. Нахождение пути, пройденного телом при
прямолинейном движении
3. Вычисление работы силы, произведенной при
прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение
или сжатие пружины
5. Определение силы давления жидкости на
вертикально расположенную пластинку
Тип урока: интегрированный.
Воспитательная работа: расширение
кругозора и познавательной деятельности
учащихся, развитие логического мышления и умения
применять свои знания.
Техническое обеспечение:
интерактивная доска. Компьютер и диск.
Приложение: «Рапсодия
природы».
ХОД УРОКА
I. Организационный момент
II. Постановка цели урока
– Урок хотелось бы провести под девизом
Готфрида Вильгельма Лейбница – немецкого философа,
логика,
математика,
физика:
«Общее искусство знаков представляет чудесное
пособие, так как оно разгружает воображение…
Следует заботиться о том, чтобы обозначения были
удобны для открытий. Обозначения коротко
выражают и отображают сущность вещей. Тогда
поразительным образом сокращается работа
мысли».
III. Повторим основные понятия и
ответим на вопросы:
– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с
применением интеграла?
IV. Объяснение нового материала
(рассмотрение теории):
1. Схема решения задач на приложения
определенного интеграла
С помощью определенного интеграла можно решать
различные задачи физики, механики и т. д., которые
трудно или невозможно решить методами
элементарной математики.
Так, понятие определенного интеграла
применяется при решении задач на вычисление
работы переменной силы, давления жидкости на
вертикальную поверхность, пути, пройденного
телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они
объединяются одной и той же схемой рассуждений
при их решении. Искомая величина (путь, работа,
давление и т. д.) соответствует некоторому
промежутку изменения переменной величины,
которая является переменной интегрирования. Эту
переменную величину обозначают через Х, а
промежуток ее изменения – через [а, b].
Отрезок [a, b] разбивают на n равных частей, в
каждой из которых можно пренебречь изменением
переменной величины. Этого можно добиться при
увеличении числа разбиений отрезка. На каждой
такой части задачу решают по формулам для
постоянных величин.
Далее составляют сумму (интегральную сумму),
выражающую приближенное значение искомой
величины. Переходя к пределу при , находят искомую величину
I в виде интеграла
I = , где f(x)
– данная по условиям задачи функция (сила,
скорость и т. д.).
2. Нахождение пути, пройденного телом при
прямолинейном движении
Как известно, путь, пройденный телом при
равномерном движении за время t, вычисляется по
формуле S = vt.
Если тело движется неравномерно в одном
направлении и скорость его меняется в
зависимости от времени t, т. е. v = f(t), то для
нахождения пути, пройденного телом за время от до
, разделим этот
промежуток времени на n равных частей Δt. В каждой
из таких частей скорость можно считать
постоянной и равной значению скорости в конце
этого промежутка. Тогда пройденный телом путь
будет приблизительно равен сумме , т.е.

Если функция v(t) непрерывна, то
Итак,
3. Вычисление работы силы, произведенной
при прямолинейном движении тела
Пусть тело под действием силы F движется по
прямой s, а направление силы совпадает с
направлением движения. Необходимо найти работу,
произведенную силой F при перемещении тела из
положения a в положение b.
Если сила F постоянна, то работа находится по
формуле
(произведение силы на длину пути).
Пусть на тело, движущееся по прямой Ох,
действует сила F, которая изменяется в
зависимости от пройденного пути, т. е. . Для того чтобы найти
работу, совершаемую силой F на отрезке пути от а
до b, разделим этот отрезок на n равных частей
. Предположим,
что на каждой части сила сохраняет постоянное значение
Составим интегральную сумму, которая
приближенно равна значению произведенной
работы:
т.е. работа, совершенная этой силой на участке
от а до b, приближенно мала сумме:
Итак, работа переменной силы вычисляется по
формуле: 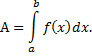
4. Вычисление работы, затраченной на
растяжение или сжатие пружины
Согласно закону Гука, сила F, необходимая для
растяжения или сжатия пружины, пропорциональна
величине растяжения или сжатия.
Пусть х – величина растяжения или сжатия
пружины. Тогда ,
где k – коэффициент пропорциональности,
зависящий от свойства пружины.
Работа на участке выразится формулой
, а вся затраченная работа
или
. Если
то погрешность величины
работы стремится к нулю.
Для нахождения истинной величины работы
следует перейти к пределу
Итак,
5. Определение силы давления жидкости на
вертикально расположенную пластинку
Из физики известно, что сила Р давления
жидкости на горизонтально расположенную
площадку S, глубина погружения которой равна h,
определяется по формуле:
, где
– плотность жидкости.
Выведем формулу для вычисления силы давления
жидкости на вертикально расположенную пластинку
произвольной формы, если ее верхний край
погружен на глубину a, а нижний – на глубину b.
Так как различные части вертикальной пластинки
находятся на разной глубине, то сила давления
жидкости на них неодинаковa. Для вывода формулы
нужно разделить пластинку на горизонтальных
полос одинаковой высоты . Каждую полосу приближенно
можно считать прямоугольником (рис.199).
По закону Паскаля сила давления жидкости на
такую полосу равна силе движения жидкости на
горизонтально расположенную пластинку той же
площади, погруженной на ту же глубину.
Тогда согласно формуле (4) сила давления на
полосу, находящуюся на расстоянии х от
поверхности, составит , где
– площадь полосы.
Составим интегральную сумму и найдем ее предел,
равный силе давления жидкости на всю пластинку:
т.е.
Если верхний край пластинки совпадает с
поверхностью жидкости, то а=0 и формула (5) примет
вид
Ширина каждой полосы зависит от формы
пластинки и является функцией глубины х
погружения данной полосы.
Для пластинки постоянной ширины формула (5)
упрощается, т.к. эту постоянную можно вынести за
знак интеграла:
V. Разбор задач по теме
1) Скорость движения материальной точки
задается формулой = (4
м/с.
Найти путь, пройденный точкой за первые 4с от
начала движения.
Решение:
2) Скорость движения изменяется по закону м/с . Найти длину
пути, пройденного телом за 3-ю секунду его
движения.
Решение:
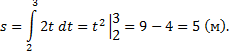
3) Скорость движения тела задана уравнением м/с. Определить
путь, пройденный телом от начала движения до
остановки.
Решение:
Скорость движение тела равна нулю в момент
начала его движения и остановки. Найдем момент
остановки тела, для чего приравняем скорость
нулю и решим уравнение относительно t; получим
Следовательно,
4) Тело брошено вертикально вверх со скоростью,
которая изменяется по закону м/с. Найти наибольшую высоту
подъема.
Решение:
Найдем время, в течении которого тело
поднималось вверх: 29,4–9,8t=0 (в момент наибольшего
подъема скорость равна нулю); t = 3 с. Поэтому
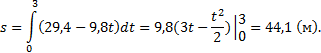
5) Какую работу совершает сила в 10Н при
растяжении пружины на 2 см?
Решение:
По закону Гука сила F, растягивающая пружину,
пропорциональна растяжению пружины , т.е. F = kx.
Используя условие, находим (Н/м), т.е. F = 500x. Получаем
6) Сила в 60Н растягивает пружину на 2 см.
Первоначальная длина пружины равна 14 см. Какую
работу нужно совершить, чтобы растянуть ее до 20
см?
Решение:
Имеем (H/м) и,
следовательно, F=3000x. Так как пружину требуется
растянуть на 0,06 (м), то
7) Определить силу давления воды на стенку
шлюза, длина которого 20 м, а высота 5 м (считая шлюз
доверху заполненным водой).
Здесь y = f(x) = 20, a = 0, b = 5 м, кг/
.
Находим
8) В воду опущена прямоугольная пластинка,
расположенная вертикально. Ее горизонтальная
сторона равна 1 м, вертикальная 2 м. Верхняя
сторона находится на глубине 0,5 м. Определить
силу давления воды на пластинку.
Решение:
Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), = 1000 кг/
. Следовательно,
9) Скорость прямолинейного движения точки
задана уравнением . Найти уравнение движения точки.
Решение:
Известно, что скорость прямолинейного движения
тела равна производной пути s по времени t, т.е. , откуда ds = v dt.
Тогда имеем
Это искомое уравнение.
10) Скорость тела задана уравнением . Найти уравнение
движения, если за время тело прошло путь
.
Решение:
Имеем ds = v dt = (6+ 1) dt; тогда
Подставив в найденное уравнение начальные
условия s = 60 м, t = 3 c, получим
откуда С = 3.
Искомое уравнение примет вид
11) Тело движется со скоростью м/с. Найти закон движения s(t),
если в начальный момент тело находилось на
расстоянии 5 см от начала отсчета.
Решение:
Так как ds = v dt = (, то
Из условия следует, что если t = 0, то s = 5 см = 0,05 м.
подставив эти данные в полученное уравнение,
имеем откуда
0,05 = С.
Тогда искомое уравнение примет вид
12) Вычислить силу давления воды на плотину,
имеющую форму трапеции, у которой верхнее
основание, совпадающее с поверхностью воды,
имеет длину 10 м, нижнее основание 20 м, а высота 3 м.
Решение:
13) Цилиндрический стакан наполнен ртутью.
Вычислить силу давления ртути на боковую
поверхность стакана, если его высота 0,1 м, а
радиус основания 0,04 м. Плотность ртути равна 13600
кг/.
Решение:
Вычислим площадь круглой полоски
Элементарная сила давления составляет
Следовательно
VI. Самостоятельное решение задач на доске,
коллективный разбор решений задач:
- Скорость движения тела задана уравнением
. Найти уравнение
движения, если в начальный момент времени - Найти уравнение движения точки, если к моменту
начала отсчета она прошла путь, а его скорость задана
уравнением - Скорость движения тела пропорциональна
квадрату времени. Найти уравнение движения тела,
если известно, что за 3 с оно прошло 18 м. - Тело движется прямолинейно со скоростью
м/с. Найти путь,
пройденный телом за 5 с от начала движения. - Скорость движения тела изменяется по закону
м/с. Найти путь,
пройденный телом за 4 с от начала движения. - Найти путь пройденный телом за 10-ю секунду, зная,
что что скорость его прямолинейного движения
выражается формулойм/с.
- Найти путь, пройденный точкой от начала
движения до ее остановки, если скорость ее
прямолинейного движения изменяется по законум/с.
- Какую работу совершает сила в 8 Н при растяжении
пружины на 6 см? - Сила в 40 Н растягивает пружину на 0,04 м. Какую
работу надо совершить, чтобы растянуть пружину
на 0,02 м? - Вычислить силу давления воды на вертикальную
прямоугольную пластинку, основание которой 30 м, а
высота 10 м, причем верхний конец пластинки
совпадает с уровнем воды. - Вычислить силу давления воды на одну из стенок
аквариума, имеющего длину 30 см и высоту 20 см.
VII. Минутка релаксации
Запуск приложения «Минутка
релаксации»
VIII. Подведение итогов урока:
– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее
сложными? Почему?
Список литературы:
- Журнал «Потенциал»
- «Алгебра и начала анализа» 11 класс С.М.
Никольский, М.К. Потапов и др. - «Алгебра и математический анализ» Н.Я. Виленкин
и др. - «Учебник по математическому анализу» Град О.Г.,
Змеев О.А. - «Высшая математика: Учебник для вузов». В 3
томах. Бугров Я.С. Никольский С.М. - «Математический анализ». Е.Б. Боронина
Главная >> Фейнмановские лекции по физике >> Том 1 >> Глава 8. Движение
Расстояние как интеграл
Обсудим теперь обратную проблему. Пусть вместо таблицы расстояний нам дана таблица скоростей в различные моменты времени, начиная с нуля.
В табл. 8.4 представлена зависимость скорости падающего шара от времени. Аналогичную таблицу можно составить и для машины, если записывать показания спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины в любой момент времени, вычислить расстояние, которое ею было пройдено? Эта задача обратна той, которую мы только что рассмотрели. Как же решить ее, если скорость машины непостоянна, если она то ускоряется до 90 км/час, то замедляется, затем где-то останавливается у светофора и т.д.? Сделать это нетрудно. Нужно использовать ту же идею и выражать полное расстояние через бесконечно малые его части. Пусть в первую секунду скорость будет vi, тогда по формуле Δs= v1Δt можно вычислить расстояние, пройденное за эту секунду. В следующую секунду скорость будет несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние, пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца пути. В результате мы получим много маленьких отрезков, которые в сумме дадут весь путь. Таким образом, путь является суммой скоростей, умноженных на отдельные интервалы времени, или s — ∑vΔt, где греческая буква ∑ (сигма) означает суммирование. Точнее, это будет сумма скоростей в некоторые моменты времени, скажем ti, умноженные на Δt:
причем каждый последующий момент ti+1 находится по правилу ti+1=t + Δt. Но расстояние, полученное этим методом, не будет точным, поскольку скорость за время Δt все же изменяется. Выход из этого положения заключается в том, чтобы брать все меньшие и меньшие интервалы Δt, т. е. разбивать время движения на все большее число все меньших отрезков. В конце концов мы придем к следующему, теперь уже точному выражению для пройденного пути:
Математики придумали для этого предела, как и для дифференциала, специальный символ. Значок Δ превращается в d, напоминая о том, что интервал времени сколь угодно мал, а
знак суммирования превращается в ∫ – искаженное большое S, первая буква латинского слова «Sumrna». Этот значок назван интегралом. Таким образом, мы пишем
где v(t) — скорость в момент t. Сама же операция суммирования этих членов называется интегрированием. Она противоположна операции дифференцирования в том смысле, что производная этого интеграла равна v(t), так что один оператор (d/dt) «уничтожает» другой ( ∫ ). Это дает возможность получать формулы для интегралов путем обращения формул для дифференциалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет равен функции, стоящей в левой колонке. Дифференцируя все виды функций, вы сами можете составить таблицу интегралов.
Любая функция, заданная в аналитическом виде, т. е. выражающаяся через комбинацию известных нам функций, дифференцируется очень просто — вся операция выполняется чисто алгебраически, и в результате мы всегда получаем какую-то известную функцию. Однако интеграл не от всякой функции можно записать в аналитическом виде. Разумеется, для каждого частного интеграла всегда сначала пытаются найти такую функцию, которая, будучи продифференцирована, давала бы функцию, стоящую после знака интеграла (она называется подынтегральной). Однако это не всегда удается сделать. В таких случаях интеграл вычисляют просто суммированием, т. е. вычисляют суммы типа (8.6) со все меньшими и меньшими интервалами, пока не получат результат с достаточной точностью.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 ноября 2022 года; проверки требует 1 правка.
В механике функция 





Интегралы движения, обладающие аддитивностью или асимптотической аддитивностью, называются законами сохранения.
Интегралы движения в классической механике[править | править код]
В классической механике для замкнутой системы из 

Применение[править | править код]
Интегралы движения полезны потому, что некоторые свойства этого движения можно узнать даже без интегрирования уравнений движения. В наиболее успешных случаях траектории движения представляют собой пересечение изоповерхностей соответствующих интегралов движения. Например, построение Пуансо показывает, что без крутящего момента вращение твердого тела представляет собой пересечение сферы (сохранение полного углового момента) и эллипсоида (сохранение энергии) — траекторию, которую трудно вывести и визуализировать. Поэтому нахождение интегралов движения — важная цель в механике.
Методы нахождения интегралов движения[править | править код]
Существует несколько методов нахождения интегралов движения:
- Наиболее простой, но и наименее строгий метод заключается в интуитивном подходе, часто основанном на экспериментальных данных и последующего математического доказательства сохранения величины.
- Уравнение Гамильтона — Якоби предлагает строгий и прямой метод нахождения интегралов движения, особенно если гамильтониан принимает знакомую функциональную форму в ортогональных координатах.
- Другой подход заключается в сопоставлении сохраняющейся величины и какой-либо симметрии Лагранжиана. Теорема Нётер даёт систематический способ вывода таких величин из симметрий. Например, закон сохранения энергии является результатом того, что лагранжиан не изменяется относительно сдвига по времени, закон сохранения импульса эквивалентен инвариантности лагранжиана относительно сдвига начала координат в пространстве (трансляционная симметрия) и закон сохранения момента импульса следует из изотропности пространства (лагранжиан не меняется при поворотах системы координат). Обратное тоже верно: каждая симметрия лагранжиана соответствует интегралу движения.
- Величина
сохраняется, если она не зависит явным образом от времени и её скобки Пуассона с гамильтонианом системы равны нулю:
.
Другой полезный результат известен как теорема Пуассона, в которой утверждается, что если есть два интеграла движения 

![[A, B]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1993067bb075f2ebfa02e78959b7c5bed68e06f4)
Система с 

В гидродинамике[править | править код]
При свободном (без внешних сил) движении идеальной (нет диссипации, вязкость отсутствует) несжимаемой (объём любой части сохраняется) жидкости сохраняются следующие величины:
Если движение двумерно, то сохраняется также энстрофия 
В идеальной магнитной гидродинамике первый интеграл (полная энергия как сумма кинетической энергии жидкости и энергии магнитного поля) сохраняется, второй (гидродинамическая спиральность) пропадает, но появляется два других интеграла движения:
В квантовой механике[править | править код]
Наблюдаемая величина Q сохраняется, если она коммутирует с гамильтонианом H, который не зависит явным образом от времени. Поэтому
-
,
где используется коммутационное соотношение
.
Вывод[править | править код]
Пусть имеется некоторая наблюдаемая 
-
,
а также имеется волновая функция, которая является решением соответствующего уравнения Шрёдингера
-
.
Для вычисления производной по времени от среднего значения наблюдаемой 
В итоге получим
![{displaystyle {frac {d}{dt}}{hat {Q}}={frac {i}{hbar }}left[{hat {mathcal {H}}},{hat {Q}}right]+{frac {partial {hat {Q}}}{partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50cd821b07cb9d068659529b4c2c0326989e9fca)
Отношение к квантовому хаосу и квантовой интегрируемости[править | править код]
В классической механике имеется теорема Лиувилля, согласно которой система, в которой число интегралов движения в инволюции совпадает с числом степеней свободы 




Квантовый аналог теоремы Лиувилля неизвестен, однако и в квантовом случае системы можно разделить на интегрируемые и неинтегрируемые. Под интегрируемыми в этом случае подразумевают системы, которые допускают точное решение в смысле возможности найти все собственные значения и собственные функции гамильтониана в разумном виде. Известен квантовый аналог метода разделения переменных, однако его применение не столь универсально в классических случаях. Известные примеры показывают, что в квантовых интегрируемых системах, также как и в классических, имеется 

Все остальные квантовые системы проявляют в той или иной степени признаки квантового хаоса. Классические хаотические системы допускают квантование в том смысле, что может быть корректно определено их пространство состояний и гамильтониан, однако как и классические хаотические системы, так и квантовые, по-видимому, не допускают точного решения. Их можно исследовать приближёнными методами, такими как теория возмущений и вариационный метод, а также исследованы численно методами молекулярной динамики в классическом случае или численной диагонализации гамильтониана в квантовом случае.
См. также[править | править код]
- Поле Киллинга
- Суперинтегрируемая гамильтонова система
Примечания[править | править код]
- ↑ Савельев, 1987, с. 74.
Литература[править | править код]
- Griffiths, David J. (англ.) (рус.. Introduction to Quantum Mechanics (2nd ed.) (англ.). — Prentice Hall, 2004.
- Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
- Арнольд В. И. Математические методы классической механики. — 5-е изд. — М.: Едиториал УРСС, 2003. — ISBN 5-354-00341-5.
- Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — 432 с.

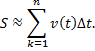
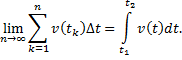
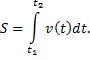
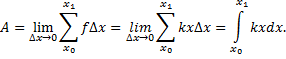
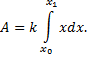
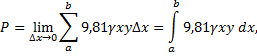
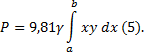
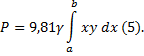
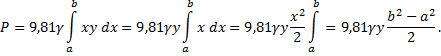
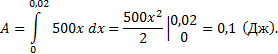
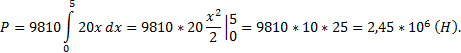

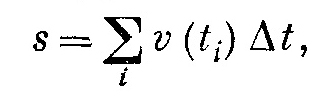
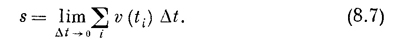

![{displaystyle {frac {dA}{dt}}={frac {partial A}{partial t}}+[A,H]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/496ae8717bce23db0e39110fc8ce8db953b96bba)
![{displaystyle {frac {d}{dt}}langle psi |{hat {Q}}|psi rangle ={frac {i}{hbar }}langle psi |left[{hat {mathcal {H}}},{hat {Q}}right]|psi rangle +langle psi |{frac {partial {hat {Q}}}{partial t}}|psi rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/44876f575616d738d747fbc3dfea8fd69b6f17f2)
![[hat{mathcal H},hat{Q}] = hat{mathcal H} hat{Q} - hat{Q} hat{mathcal H}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3513fecb3fdb11f73e2b17ee2bdd186e4fe4011)


