Как найти скорость сближения двух автомобилей

В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.

Ситуация 1

Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить. 

Задача

Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа? 

1) 90 + 70 = 160 (км/ч) – скорость удаления. 

2) 160 × 4 = 640 (км) 

Ответ: 640 км будет расстояние между автомобилями через 4 часа.

Ситуация 2

Представь, что вы с мамой идете навстречу друг другу. 

В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.

Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить. 

Задача

Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся? 

1) 90 + 70 = 160 (км/ч) – скорость сближения

2) 640 : 160 = 4 (ч)

Ответ: автомобили встретятся через 4 часа.

Ситуация 3

Представь, что ты идешь по улице и видишь, что впереди  идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость  сближения. 

Задача

Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?

1) 90 – 70 = 20 (км/ч) – скорость сближения

2) 120 : 20 = 6 ( ч)

Ответ: второй автомобиль догонит первый через 6 часов.

Ситуация 4

Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую. 

Задача

Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа? 

1) 90 – 70 = 20 (км/ч) – скорость удаления

2) 20 × 4 = 80 (км)

Ответ: 80 км будет расстояние между автомобилями через 4 часа.

Делитесь своим мнением в комментариях, подписывайтесь на мой канал

Для решения задач на движение по прямой используется одна основная формула:

где:

• Скорость (V) — расстояние, пройденное за единицу времени.
• Время (t) — время в пути.
• Расстояние (S) — пройденный путь, или расстояние.

Зная эту формулу (для расстояния), вы можете легко  вывести из неё формулу для скорости, или времени.

Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.

Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.

Все задачи на движение делятся на следующие типы:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решение простых задач на движение: скорость, время и расстояние

В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:

Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние. 
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.

Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.

Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь? 
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.

В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах,  то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.

Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.

Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)

При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:

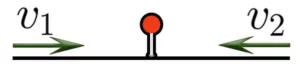
При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле: 

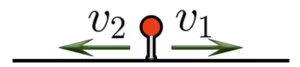
При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.

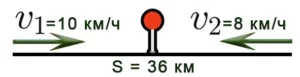
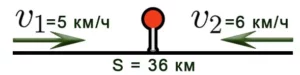
Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся? 
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.

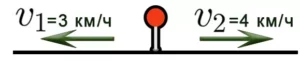
Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.

Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.

Решение задач на движение в одном направлении: сближение и удаление

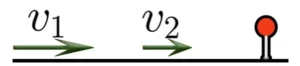
Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:

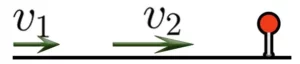
Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:

Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.

Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.

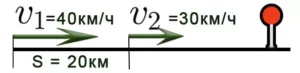
Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.

2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.

Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.

Решение задач на движение по реке

Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:

• по течению реки → скорость увеличивается;
• против течения реки → скорость уменьшается.

Таким образом, в задачах рассматривают 2 скорости: 

• Скорость собственная — Vs;
• Скорость течения реки — Vt.

Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается. 
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.

Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится. 
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.

Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок? 
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.

Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt  – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt  – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону:  t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону:  t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.

Больше задач на движение Ваш ребёнок может решить, скачав программы:

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Полезные советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
• При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

Задачи на движение в одном направлении

Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.

Задачи на скорость сближения

Скорость сближения — это скорость, с которой объекты сближаются друг с другом.

Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) — расстояние между автомобилями,

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

Решение задачи по действиям можно записать так:

Ответ: Через 5 часов второй пешеход догонит первого.

Задача на скорость удаления

Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.

Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.

1) Чему равна скорость удаления между автомобилями?

2) Какое расстояние будет между автомобилями через 3 часа?

3) Через сколько часов расстояние между ними будет 200 км?

Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

1) Скорость удаления между автомобилями равна 40 км/ч.

2) Через 3 часа между автомобилями будет 120 км.

3) Через 5 часов между автомобилями будет расстояние в 200 км.

Источник

Движение навстречу друг другу

Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.

Если два объекта движутся навстречу друг другу, то они сближаются:

Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:

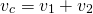
Скорость сближения больше, чем скорость каждого из них.

Скорость, время и расстояние связаны между собой формулой пути:

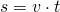
Рассмотрим некоторые задачи на встречное движение.

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Условие задач на движение удобно оформлять в виде таблицы:

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.

1) 20:2=10 (км/ч) скорость сближения пешеходов

2) 10-6=4 (км/ч) скорость другого пешехода.

73 Comments

Саетлана Михайловна, будьте добры, помогите с решением, пожалуйста. Два велосипедиста одновременно выехали навстречу друг другу из пункта А в пункт В, скорость первого 12 км/ч, второго 15 вм/ч, расстояние между пунктами равно 71 км, через какое время после (!) встречи, расстояние между велосипедистами будет 8 км?

1)12+15=27 (км/ч) скорость сближения велосипедистов
Когда велосипедисты встретятся, вместе они преодолеют все расстояние от пункта А до пункта В, что равно 71 км. Когда расстояние после их встречи станет равным 8 км, они проедут ещё дополнительно 8 км.
2)71+8=79 (км) расстояние, которое проехали 2 велосипедиста вместе с момента старта
3) 79:27=79/27=2 25/27 (часа) время, через которое расстояние между велосипедистами станет равным 8 км.

Насколько я поняла, требуется, чтобы все три объекта встретились в одной точке одновременно.
Примем расстояние между объектами 2 и 3 за s. Так как скорость объекта 3 в 3 раза больше скорости объекта 2, то за время до встречи объект пройдёт (3/4)s, а объект 2 — (1/4)s.
Так как в начальный момент движения расстояние от объекта 1 до объекта 3 в два раза меньше, чем до объекта 2, то расстояние от объекта 1 до объекта 3 составляет (1/3)s, а до объекта 2 — (2/3)s. Следовательно, объекту 1 следует двигаться в сторону объекта 2, чтобы попасть в точку в точку встречи.
Расстояние, которое нужно пройти объекту 1, можно найти как разность расстояний между объектами 1 и 2 в начальный момент времени и в момент встречи: (2/3)s — (1/4)s=(5/12)s.
Время в пути до встречи каждого из трёх объектов одинаково. Чтобы найти время, надо расстояние разделить на скорость. Время в пути объекта 2 равно ((1/4)s)/2, время в пути объекта 1 — ((5/12)s)/x, где x – скорость объекта 1. Из уравнения ((1/4)s)/2=((5/12)s)/x находим x=(10/3) км/ч.

Расстояние между поселком и городом 80 км. Из поселка в город выехал велосипедист со скоростью 15 км/ч. Одновременно из города в поселок выехал второй велосипедист со скоростью 12 км/ч. Какое расстояние будет между ними через 2 часа?

1) 15+12=27(км/ч) скорость сближения велосипедистов
2) 27∙2=54 (км) проехали велосипедисты вместе за 2 часа
3) 80-54=26 (км) такое расстояние будет между велосипедистами через 2 часа.

Пожалуйста помогите с задачей:расстояние между двумя пристанями равно 330 км. От этих пристаней одновременно навстречу друг другу отправились два катера. Скорость одного из них равна 24 км / ч что составляет 6 седьмых скорости второго. Какой будет расстояние между катерами через 4,5 часа после начала движения?

1) 26:(6/7)=24∙(7/6)=28 (км/ч) скорость первого катера
2) 28+24=52 (км/ч) скорость сближения катеров
3) 52∙4,5=234 (км) расстояние, которое прошли два катера навстречу друг другу за 4,5 часа
4) 330-234=96 (км) расстояние между катерами через 4,5 часа после начала движения.

Уважаемая Светлана! Прошу Вас пояснить, почему в задаче на сближение (прислала Карина 5 декабря 2018 г.)Вы, приняв расстояние между объектами 2 и 3 за единицу определили пути объектов как 14S и 34S пропорционально из скоростям (почему четверти. А расстояние между объектами 1, 2 и 3 Вы определяете как 1/3S и 2/3S (почему трети)и почему расстояние между объектами 1, 2 и 3 тоже приняли за S.
Большое спасибо. Жду с нетерпением Ваш комментарий!

С ДВУХ ПЕЩЕР,ЧТО НАХОДЯТСЯ НА РАССТОЯНИИ 12КМ, В ОДНОМ НАПРАВЛЕНИИ ВЫБЕЖАЛИ ДВА ТИГРА.СКОРОСТЬ ОДНОГО 12КМ/ЧАС, А ВТОРОГО — 22КМ/ЧАС. Через сколько времени первый тигр догонит второго?

1) 22-12=10(км/ч) скорость сближения тигров
2)12:10=1,2(ч) время, через которое второй тигр догонит первого.

Не указано в задаче, что тигры бегут навстречу друг другу. А если они бегут параллельно? Ведь это тоже в одном направлении!
Вы пересказали задачу или она так в учебнике сформулирована?

Я разобралась — бегут параллельно, но сближаются!

Татьяна, большие буквы в интернете означают крик.

Зачем же удалять мой вопрос к решению задачи? Модератор не понял логику. Прошу вернуть мой вопрос. Спасибо.

Наталья, Ваш вопрос не удаляла. Но для ответа просто не хватает времени.

как Это? навстречу друг другу параллельно?

Движение навстречу друг другу не на одной прямой, а по параллельным прямым.

Два поезда, расстояние между которыми 420 км, идут на встречу друг другу, один со скоростью 65 км/ч, другой — 75 км/ч. Какое расстояние будет между ними через 2 ч?

1)65+75=140 (км/ч) скорость сближения поездов
2)140∙2=280(км) столько прошли два поезда навстречу друг другу за 2 часа
3) 420-280=140(км) будет между поездами через 2 часа.

Примем весь путь за 1. Тогда второй пешеход в минуту проходит 1:45=1/45 пути, а вместе — 1:18=1/18 пути. Следовательно первый пешеход в минуту проходит 1/18-1/45=3/90=1/30 пути. 1:(1/30)=30 минут — время, за которое пройдёт расстояние между пунктами первый пешеход.

Большое спасибо за помощь! Я голову ломал целый день (((

Алексей, каждый раз, обдумывая задачу, мы шаг за шагом продвигаемся вперёд. И следующая задача может быть решена быстрее :).

Может Вы сможете помочь с уровнением.
4 1/2*16/45*(х:1 1/3)=1 1/2:4
просмотрел ни одно видео похожего уровнения не нашел. Ломаю голову второй день,удалёнка это кашмар для родителей.

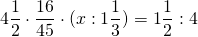
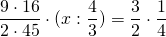
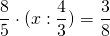
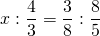
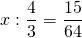
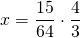
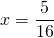
Успехов Вам, Алексей!

Светлана Михайловна, здравствуйте, помогите с задачей. Из двух пунктов на встречу друг другу, выехали два велосипедиста. Первый отправился со скоростью 15 км/ч. Через 4 часа выехал второй, со скоростью 17 км/ч. Через 7 часов они встретились. Определите расстояние между пунктами.

1) 15∙4=60(км) проехал первый велосипедист за 4 часа
2) 15+17=32(км/ч) скорость сближения велосипедистов
3) 32∙7=224 (км) проехали велосипедисты вместе до встречи
4) 60+224=284 (км) расстояние между пунктами

Светлана Михайловна, добрый день! Уже какой день голову ломаем. Нужно решить в двух действиях. Помогите, пожалуйста! Расстояние между городами 18 км. Из двух городов одновременно вышли два пешехода в одном направлении. Скорость первого 12 км/ч. Какая Скорость второго, если первый догнал его через 3 часа

Это задача на движение вдогонку.
1) 18:3=6(км/ч) скорость сближения пешеходов
2) 12-6=6(км/ч) скорость 2-го пешехода

Светлана МИхайловна, спасибо огромное!

Два велосипедиста из пунктов A и B отправились на встречу друг к другу. Скорость первого велосипедиста составляет 6 км/ч, что на 1,2 км/ч меньше скорости второго. Найдите расстояние между пунктами, если они встретились через 5 часов.помогите пожалуйста

6+1,2=7,2 (км/ч) скорость 2-го велосипедиста
6+7,2=13,2 (км/ч) скорость сближения
13,2∙5=66 (км) расстояние между пунктами.

Светлана Михайловна,пож-та,помогите решить задачу:
Расстояние между сёлами 90км.Навстречу друг другу выехали велосипедист и пешеход.Через 3 часа встретились.Если бы велосипедист выехал на 1ч15мин раньше пешехода, они встретились бы через 2ч.Какова скорость движения велосипедиста и пешехода?

Так как за 3 часа, двигаясь навстречу друг другу, велосипедист и пешеход преодолели 90 км, то их скорость сближения равна 90:3=30 км/ч. Пусть скорость пешехода равна x км/ч, тогда скорость велосипедиста — (30-x) км/ч. Известно, что если бы велосипедист выехал на 1ч15мин раньше пешехода, они встретились бы через 2ч. В этом случае время в пути велосипедиста рано 3 ч15 мин=3 ¼ ч= 13/4 ч, а пешехода — 2ч.
За это время велосипедист проехал 13/4 ∙ (30-x) км, пешеход — 2∙x км, а вместе — 90 км.
13/4 ∙ (30-x)+ 2x =90
x=6

Скорость пешехода 6 км/ч, велосипедиста — 30-6=24 км/ч.

Здравствуйте помогите пожалуйста. Расстояние между точками А и Б 180км. Это расстояние легковой автомобиль проезжает за 2часа (90км/час), а грузовой автомобиль за 3 часа (60 км/час). Из точки А в точку Б выехало грузовое авто, в это же время из точки Б в точку А выехал легковой автомобиль. Найдите расстояние до точки А когда эти два авто встретятся

90+60=150(км/ч) скорость сближения автомобилей
180:150=1,2(ч) через такое время автомобили встретятся
60∙1,2=72(км) расстояние, которое прошел до места встречи грузовой автомобиль, а значит, это расстояние от А до места встречи.

Два поезда одновременно выходят навстречу друг другу из пунктов А и В, расстояние между которыми равно 300 км. Поезд, вышедший из пункта А, может пройти это расстояние за 5 ч, другой — за 7,5 ч. Сколько времени пройдет до встречи поездов?

300:5=60(км/ч) скорость 1-го поезда
300:7,5=40(км/ч) скорость 2-го поезда
60+40=100(км/ч) скорость сближения
300:100=3(ч) — время, через которое поезда встретятся.

Помогите решить задачу.
2 велосипедиста выехали одновременно навстречу друг другу и через 3 ч встретились. Найди скорость каждого, если известно,что скорость первого на 4 км/ч больше скорсти второго,а вместе они проехали 108 км.

Из двух городов навстречу друг другу одновременно вышли два автомобиля. Скорость одного автомобиля 60,5 км/ч второго на 4 км/ч больше. Какое расстояние будет между автомобилями через 4 часа, если расстояние между городами 400 км?

60,5+4=64,5 км/ч скорость 2-го автомобиля
64,5+60,5=125 км/ч скорость сближения автомобилей
125∙4=500 км проехали автомобили за 4 часа.
500-400=100 км — такое расстояние между автомобилями через 4 часа после начала движения.

Здравствуйте! Помогите уже целый день не можем решить. Расстояние между точками А и В 280км. Две машины одновременно из этих точек вышли друг к другу и встретились через 2 часа. А пришла к пункту В на 1ч.10м. позже чем В на пункт А. Какова их скорость?

Пусть скорость одной машины x км/ч, другой — y км/ч. Так как за 2 часа они проехали вместе 280 км, то 2x+2y=280.
1й автомобиль на весь путь затратил на 1 час 10 мин= 1 1/6 ч=7/6 ч больше, чем другой, то 280/x-280/y=7/6. Остается решить систему уравнений.
x=60,y=80.

Светлана Михайловна помогите пожалуйста с решением задачи.
Два велосипедиста выехали одновременно из А и В навстречу друг другу.Скорость первого V1,а второго V2. При встрече оказалось,что второй проехал на а км больше первого. Найти длину пути.

Пусть 1-й велосипедист проехал до встречи x км, тогда 2-й — (x+a)км. Время в пути 1-го велосипедиста равно

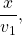
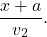
Так как они затратили на путь одинаковое время, то

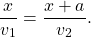
Отсюда xv2=xv1+av1, x(v2-v1)=av1,

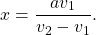
Весь путь равен x+(x+a)=2x+a=

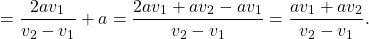
Здравствуйте.Помогите пожалуйста решить задачу.Расстояние между точками А и Б пешеход, вышедший из точки А проходит за 2 часа 24 минут, а пешеход, вышедший из точки Б, проходит за 3 часа. Если они начнут движение одновременно, через сколько минут они встретятся?

Примем весь путь за 1. Один пешеход проходит этот путь за 2 часа 24 минуты=144 минуты. Значит, за 1 минуту он проходит 1/144 часть пути. Второй пешеход проходит путь за 3 часа = 180 минут. За 1 минуту он преодолевает 1/180 пути. Поскольку пешеходы движутся навстречу друг другу, скорость их сближения равна

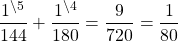
пути в минуту. Значит, до встречи они пройдут

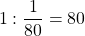
Одновременно на встречу друг к другу отправились из города Душанбе — автомобилист со скоростью 20 м/с, и из города Худжанд — велосипедист со скоростью 20 км/ч. Расстояние между городами 346 км. Какое расстояние будет между автомобилем и велосипедом через 2 часа?

1)20 м/с=20∙3,6=72 км/ч — скорость автомобиля
2)72+20=92(км/ч) скорость сближения автомобилиста и велосипедиста
2)92∙2=184 (км) — расстояние, которое проехали автомобилист и велосипедист вместе за 2 часа
3) 346-184=162 (км) таким будет расстояние между автомобилистом и велосипедистом через 2 часа после начала движения.

Пусть скорость первого автомобиля равна x км/ч, скорость второго — y км/ч.Если они начнут двигаться друг другу навстречу одновременно, то встретятся через 4 часа. Отсюда 4(x+y)=420.
Если первый автомобиль начнет движение на 4 часа и 12 минут раньше, то встретятся они через 2 часа после выезда другого.
4часа 12 минут=4 12/60 часа=4,2 ч. Отсюда 6,2x+2y=420.
Составляем и решаем систему из двух уравнений с двумя неизвестными.
x=50, y=55.
Ответ: 50 км/ч и 55 км/ч.
Но это уже алгебра 7 класса :).

Светлана Михайловна, помогите пожалуйста решить задачу:пешеход и велосипедист начали движение навстречу друг другу в 10 часов из двух пунктов между которыми 4 км. их встреча произошла в 10 ч 20 мин. на следующий день велосипедист выехал в 10 ч, а пешеход вышел в 10 ч.16 мин. поэтому в этот день они встретились в 10 ч 24 мин. найдите скорость пешехода

В первый день пешеход и велосипедист вместе преодолели 4 км за 20 минут =20/60=1/3 часа. Значит, скорость их сближения равна 4:1/3=12 км/ч.
Во второй день пешеход и велосипедист вместе ехали всего 10 ч 24 мин-10 ч 16 мин = 8 минут=8/60 часа. За это время они преодолели 12∙8/60=8/5=1,6 км.
Следовательно, велосипедист до начала движения пешехода проехал 4-1,6=2,4 км. Это расстояние он проехал за 10 ч 16 мин-10 ч = 16 минут = 16/60 часа. Отсюда, скорость велосипедиста
2,4:16/60=9 км/ч.
Скорость сближения пешехода и велосипедиста равна 12 км/ч, значит, скорость пешехода равна 12-9 = 3 км/ч.
Можно решить с помощью системы уравнений, но системы уравнений проходят в конце 7 класса.

Спасибо огромное. Все очень понятно!

Два пешехода одновременно отправились навстречу друг другу из пунктов, расположенных на расстоянии 36 км друг от друга. Скорость первого пешехода 5 км/ч, скорость второго пешехода 7 км/ч. Сколько километров прошел до встречи второй пешеход?

1)5+7=12(км/ч) скорость сближения пешеходов
2)36:12=3(ч) время с момента начала движения и до встречи
3)7∙3=21(км) прошёл до встречи второй пешеход.

Здравствуйте, Светлана Михайловна! Подскажите пожалуйста, как решить задачу, где из 2 городов выехали в одно время грузовик и легковой авто. Скорость авто v км/ч, а грузовика u км/ч. Найти надо расстояние между городами, если авто и грузовик вмтретились через t ч. Если v=70, u=40, t=2

Грузовик и авто едут навстречу друг другу, поэтому скорость сближения равна сумме их скоростей:v+u км/ч.
Они выехали одновременно и ехали до встречи t часов. Чтобы найти расстояние, надо скорость умножить на время: s=(v+u)t.
Если v=70, u=40, t=2, то s=(70+40)∙2=220 км.

По прямой дороге навстречу друг другу едут велосипедист и мопедист. Велосипидиста скорость 12 км/ч, мопедиста – 18 км/ч. Через сколько времени расстояние между ними будет 400метров, если в начале наблюдения расстояние между ними 2 км

12+18=30 км/ч — скорость сближения
400 м= 0,4 км
2-0,4=1,6 км — расстояние, на которое должно уменьшится данное расстояние
1,6:30=1,6/30=16/300=4/75 часа=(4/75)∙ 60 минут = 16/5 минуты= 3,2 минуты — через это время расстояние между объектами станет равным 400 метрам первый раз.

Можно сначала перевести километры в час в метры в минуту
30 км/ч = 30 ∙ 1000/60 м/мин=500 м/мин
2 км=2000 м
2000-400=1600 м
1600:500=3,2 минуты.

Добрый день! Помогите пожалуйста решить задачу! От двух пристаней, находящихся друг от друга на расстоянии 343км,вышли одновременно навстречу друг другу два парохода. Один пароход шёл со скоростью 26 км/ч. С какой скоростью шёл второй пароход, если они встретились через 8 часов?

343:8 = 42 7/8 (км/ч) скорость сближения пароходов.
42 7/8 — 26 = 16 7/8 = 16,875 (км/ч) скорость второго парохода.

Здравствуйте, Светлана, помоги пожалуйста срочно! Из пункта А в пункт В, расстояние между которыми 40 км, вышел пешеход со скоростью 6 км/ч. Через 15 минут из В в А выехал велосипедист со скоростью 16 км/ч. Через какое время после выхода пешехода они встретятся? На каком расстоянии от В произойдет встреча?

Фируза, срочно не получилось.
Пусть велосипедист и пешеход встретятся через t часов после выхода пешехода из пункта А. За это время пешеход пройдёт 6t км.
Так как велосипедист выехал через 15 минут=15/60=1/4 часа после пешехода, то он проехал 16(t-1/4) км.
Вместе до встречи пешеход и велосипедист преодолели расстояние 40 км.
6t+16(t-1/4)=40
6t+16t-4=40
22t=44
t=2
Таким образом, велосипедист и пешеход встретятся через 2 часа после выхода пешехода. Пешеход за это время пройдёт 6∙2=12 км. Значит, от В место встречи находится на расстоянии 40-12=28 км.

Помогите пожалуйста разобраться с задачей.
Из двух поселков, между которыми 45 км, одновременно друг навстречу другу отправились два туриста, скорость одного была 4км/ч, второго 5км/ч. На каком расстоянии от каждого поселка будет их пункт встречи?

1)4+5=9(км/ч) скорость сближения туристов.
2)45:9=5(ч) через такое время после начала движения туристы встретятся
3)4∙5=20(км) пройдёт до места встречи один турист
4)5∙5=25(км) пройдёт другой турист.

Источник

Фізика – легко!

Вивчаємо фізику та не тільки

Задачи на сближение и удаление

Для начала вспомним формулы, которые используют при решении подобных задач: S = υ·t, υ = S : t, t = S : υ
где S – расстояние, υ – скорость движения, t – время движения.

Когда два объекта движутся равномерно с разными скоростями, то расстояние между ними за каждую единицу времени или увеличивается, или уменьшается.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.

Трудность для некоторых учеников заключается в том, чтобы правильно поставить «+» или «–» между скоростями при нахождении скорости сближения объектов или скорости удаления.

Примеры решения задач.

Задача №1. Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
υ₁ = 60 км/ч
υ₂ = 80 км/ч
Найти υ_сб
Решение.
υ_сб = υ₁ + υ₂ – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_сб = 60 + 80 = 140 (км/ч)
Ответ: скорость сближения 140 км/ч.

Задача №2. Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
υ₁ = 60 км/ч
υ₂ = 80 км/ч
Найти υ_уд
Решение.
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_уд = 80 + 60 = 140 (км/ч)
Ответ: скорость удаления 140 км/ч.

Задача №3. Из одного пункта в одном направлении выехали сначала автомобиль со скоростью 60 км/ч, а затем мотоцикл со скоростью 80 км/ч. Определите скорость сближения машин.
(Видим, что здесь случай движения вдогонку, поэтому находим скорость сближения)
υ_ав = 60 км/ч
υ_мот = 80 км/ч
Найти υ_сб
Решение.
υ_сб = υ₁ – υ₂ – скорость сближения (знак «–» так как из условия понятно, что машины движутся в одном направлении)
υ_сб = 80 – 60 = 20 (км/ч)
Ответ: скорость сближения 20 км/ч.

То есть название скорости – сближения или удаления – не влияют на знак между скоростями. Имеет значение только направление движения.

Рассмотрим другие задачи.

Задача № 4. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3 ч?
υ₁ = 5 км/ч
υ₂ = 4 км/ч
t = 3 ч
Найти S
Решение.
υ_уд = υ₁ + υ₂ – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υ_уд = 5 + 4 = 9 (км/ч)
(Пройденное расстояние находим по формуле)
S = υ_уд·t
S = 9·3 = 27 (км)
Ответ: через 3 ч расстояние будет 27 км.

Задача № 5. Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
S = 36 км
υ₁ = 10 км/ч
υ₂ = 8 км/ч
Найти t
Решение.
υ_сб = υ₁ + υ₂ – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υ_сб = 10 + 8 = 18 (км/ч)
(время встречи можно рассчитать по формуле)
t = S : υ_сб
t = 36 : 18 = 2 (ч)
Ответ: встретятся через 2 ч.

1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся? (2 ч)
2. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 10 км/ч и 20 км/ч. Через сколько часов расстояние между ними будет 60 км? (2 ч)
3. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа? (9 км, 27 км)
4. Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие? (140 км, есть)
5. Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км? (28 км/ч, 2 ч)
6. Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость первого 40 км/ч, второго 50 км/ч. Через сколько часов второй догонит первого?
7. Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов они встретятся?
8. Из села вышел пешеход со скоростью 4 км/ч. Через 3 часа вслед за ним выехал велосипедист со скоростью 10 км/ч. За сколько часов велосипедист догонит пешехода?
9. Расстояние от города до села 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?
10. Старинная задача. Некий юноша пошел из Москвы к Вологде. Он проходил в день 40 верст. Через день вслед за ним был послан другой юноша, проходивший в день 45 верст. Через сколько дней второй догонит первого?
11. Старинная задача. Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака за 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?
12. Старинная задача. Из Москвы в Тверь вышли одновременно 2 поезда. Первый проходил в час 39 верст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 верст. Сколько верст от Москвы до Твери?

Залишити відповідь Скасувати відповідь

Щоб відправити коментар вам необхідно авторизуватись.

Источник

Для решения задач на движение стоит прояснить объекты сближаются или удаляются, ответ зависит от вида движения.  Когда объекты двигаются навстречу друг другу из разных пунтков, то они сближаются:

(v_1+v_2=20+30=50) км/час скорость сближения

(v_1+v_2=20+30=50) км/час скорость удаления

Скорость время расстояние

Онлайн калькулятор поможет Вам рассчитать время пути из пункта А в пункт Б и среднюю скорость движения.

Смотрите также

в описании к калькулятору добавьте, что из-за особенностей Javascript он не принимает «,» даже не представляю сколько людей погорело у вас тут.

Спасибо.
Поддержку «,» добавили.

Два пешехода вышли навстречу друг другу. Скорость первого составляет 3 м/мин, а второго — 4 м/мин. Через
сколько минут они встретятся, если расстояние между ними 1680 метров?​

Медвежат отвезли за 600 км от населенного пункта. Через 18 дней (432часа) они вернулись в посёлок. Вопрос: Это реально? И с какой скоростью они могли передвигаться в сутки?

За какое время пройдёт машина расстояние 10 метров со скоростью 170км/ч

задача.1 трактор ехал со скоростью 36 км.в час .2 трактор _32 км в час между ними .растояние 136км.нужно найти время когда встретятся.

От города A до города B расстояние 40 км. Два велосипедиста выехали из A и B навстречу друг другу, один со скоростью 10 км/ч, а другой — 15 км/ч. Муха вылетела с первым из A со скоростью 100 км/ч, долетела до второго, села ему на лоб и полетела обратно к первому, села ему на лоб, вернулась ко второму и так далее, пока они не столкнулись лбами и не раздавили ими муху. Сколько километров пролетела муха?

машина едет со скоростью 85 км в час ,за сколько минут проедет машина 78 км

Если пешеход вышел в деревню со скоростью 4.8 км/ч,возвращался со скоростью 6 км/ч и вернулся на час раньше. Какое расстояние от села до деревни?

Задачи на движение в одном направлении

Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.

Задачи на скорость сближения

Скорость сближения — это скорость, с которой объекты сближаются друг с другом.

Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) — расстояние между автомобилями,

2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

Решение задачи по действиям можно записать так:

1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,

Ответ: Через 5 часов второй пешеход догонит первого.

Задача на скорость удаления

Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.

Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.

1) Чему равна скорость удаления между автомобилями?

2) Какое расстояние будет между автомобилями через 3 часа?

3) Через сколько часов расстояние между ними будет 200 км?

Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

Формула нахождения значений скорости, времени и расстояния

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+. +vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+. +Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.