Движение является способом существования всего, что человек видит вокруг себя. Поэтому задачи на перемещение разных объектов в пространстве являются типичными проблемами, которые предлагается разрешить школьникам. В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.
Что такое движение?
Перед тем, как переходить к рассмотрению формул движения вдогонку, необходимо разобраться с этим понятием подробнее.
Под движением подразумевают изменение пространственных координат объекта за определенный промежуток времени. Например, автомобиль, который движется по дороге, самолет, который летит в небесах, или кошка, бегущая по траве, – все это примеры движения.
Важно отметить, что рассматриваемый движущийся объект (автомобиль, самолет, кошка) считают безмерным, то есть его размеры не имеют совершенно никакого значения для решения проблемы, поэтому ими пренебрегают. Это своего рода математическая идеализация, или модель. Для подобного объекта существует название: материальная точка.
Движение вдогонку и его особенности
Теперь перейдем к рассмотрению популярных школьных задач на движение вдогонку и формул для него. Под этим видом движения понимают перемещение двух или более объектов в одном направлении, которые отправляются в свой путь из разных пунктов (материальные точки имеют разные начальные координаты) или/и в разное время, но из одного и того же пункта. То есть создается ситуация, при которой одна материальная точка пытается догнать другую (другие), поэтому эти задачи получили такое название.
Согласно определению, особенностями движения вдогонку являются следующие:
- Наличие двух и более движущихся объектов. Если двигаться будет только одна материальная точка, то ей “некого” будет догонять.
- Прямолинейное перемещение в одном направлении. То есть объекты осуществляют движение вдоль одной и той же траектории и в одном направлении. Движение навстречу друг другу не входит в число рассматриваемых задач.
- Пункт отправления играет важную роль. Идея заключается в том, чтобы в момент начала движения объекты были разделены в пространстве. Такое разделение будет иметь место, если они стартуют в одинаковое время, но из разных пунктов или же из одного пункта, но в разное время. Старт двух материальных точек из одного пункта и в одинаковое время к задачам вдогонку не относится, поскольку в этом случае один объект будет постоянно удаляться от другого.
Формулы движения вдогонку
В 4 классе общеобразовательной школы обычно рассматриваются подобные задачи. Это означает, что формулы, которые необходимы для решения, должны быть максимально простыми. Такому случаю удовлетворяет равномерное прямолинейное движение, в котором фигурируют три физических величины: скорость, пройденный путь и время движения:
- Скорость – величина, показывающая расстояние, которое проходит тело за единицу времени, то есть она характеризует быстроту изменения координат материальной точки. Обозначается скорость латинской буквой V и измеряется, как правило, в метрах в секунду (м/с) или в километрах в час (км/ч).
- Путь – это расстояние, которое проходит тело за время своего движения. Он обозначается буквой S (D) и выражается обычно в метрах или километрах.
- Время – период движения материальной точки, который обозначается буквой T и приводится в секундах, минутах или часах.
Описав основные величины, приведем формулы движения вдогонку:
- s = v*t;
- v = s/t;
- t = s/v.
Решение любой задачи рассматриваемого типа базируется на применении этих трех выражений, которые необходимо запомнить каждому школьнику.
Пример решения задачи №1
Приведем пример задачи движения вдогонку и решения (формулы, необходимые для него, приведены выше). Проблема формулируется следующим образом: “Грузовик и легковой автомобиль одновременно выезжают из пунктов A и B со скоростями 60 км/ч и 80 км/ч соответственно. Оба транспортных средства движутся в одном направлении так, что автомобиль приближается к пункту A, а грузовик удаляется от обоих пунктов. Через какое время автомобиль догонит грузовик, если расстояние между A и B составляет 40 км?”.
Перед тем как решать задачу, необходимо научить ребят определять суть проблемы. В данном случае она заключается в неизвестном времени, которое проведут оба транспортных средства в пути. Предположим, что это время равно t часам. То есть через время t автомобиль догонит грузовик. Найдем это время.
Рассчитаем расстояние, которое пройдет каждый из движущихся объектов за время t, имеем: s1 = v1*t и s2 = v2*t, здесь s1, v1 = 60 км/ч и s2, v2 = 80 км/ч – пройденные пути и скорости движения грузовика и автомобиля до того момента, когда второй догонит первого. Поскольку расстояние между пунктами A и B равно 40 км, то автомобиль, догнав грузовик, пройдет путь на 40 км больше, то есть s2 – s1 = 40. Подставляя в последнее выражение формулы для путей s1 и s2, получим: v2*t – v1*t = 40 или 80*t – 60*t = 40, откуда t = 40/20 = 2 ч.
Отметим, что данный ответ можно получить, если использовать понятие скорости сближения между движущимися объектами. В задаче она равна 20 км/ч (80-60). То есть при этом подходе возникает ситуация, когда один объект движется (автомобиль), а второй относительно него стоит на месте (грузовик). Поэтому достаточно поделить расстояние между пунктами A и B на скорость сближения, чтобы решить задачу.
Пример решения задачи №2
Приведем еще один пример задач на движение вдогонку (формулы для решения используются те же): “Из одного пункта выезжает велосипедист, а через 3 часа в ту же сторону выезжает автомобиль. Через какое время после начала своего движения автомобиль догонит велосипедиста, если известно, что он движется в 4 раза быстрее?”.
Решать эту задачу следует так же, как и предыдущую, то есть необходимо определить, какой путь пройдет каждый участник движения до момента, когда один догонит другого. Предположим, что автомобиль догнал велосипедиста через время t, тогда получаем следующие пройденные пути: s1 = v1*(t+3) и s2 = v2*t, здесь s1, v1 и s2, v2 – пути и скорости велосипедиста и автомобиля соответственно. Заметим, что до того, как автомобиль догнал велосипедиста, последний находился в пути t + 3 часа, так как он выехал на 3 часа раньше.
Зная, что оба участника отправились из одного пункта, и пройденные ими пути будут равны, получаем: s2 = s1 или v1*(t+3) = v2*t. Скорости v1 и v2 нам не известны, однако в условии задачи сказано, что v2 = 4*v1. Подставляя это выражение в формулу для равенства путей, получим: v1*(t+3) = 4*v1*t или t+3 = 4*t. Решая последнее, приходим к ответу: t = 3/3 = 1 ч.
Некоторые советы
Формулы движения вдогонку являются простыми, тем не менее школьников в 4 классе важно научить мыслить логически, понимать значение величин, с которыми они имеют дело, и осознавать проблему, которая перед ними стоит. Ребят рекомендуется призывать к рассуждениям вслух, а также к командной работе. Кроме того, для наглядности задач можно использовать компьютер и проектор. Все это способствует развитию у них абстрактного мышления, коммуникативных навыков, а также математических способностей.
Рассмотрим задачи на движение вдогонку, в которых объекты движутся в одном направлении, но выезжают из разных пунктов, находящихся на некотором расстоянии друг от друга.
При движении вдогонку объекты могут как сближаться, так и удаляться.
Если скорость объекта, который идет впереди, меньше скорости идущего вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
![[{v_c} = {v_1} - {v_2}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f23d77f1fd5e9c02b0f414481cd8ee72_l3.png "Rendered by QuickLaTeX.com")
![[({v_1} > {v_2}).]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-424d4c0082e799c7e82ae5375315b76c_l3.png "Rendered by QuickLaTeX.com")
Если скорость идущего впереди объекта больше скорости объекта, который движется следом, то второй не сможет догнать первого и они удаляются друг от друга.
Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
![[{v_y} = {v_2} - {v_1}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-0e282bde92844a03b48bb0e0c274d7b0_l3.png "Rendered by QuickLaTeX.com")
![[({v_2} > {v_1}).]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-4dc4ed6d265c61d12a97445225919b6c_l3.png "Rendered by QuickLaTeX.com")
Скорость, время и расстояние связаны между собой формулой пути:
![[s = v cdot t]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-115885a6d144cc69d9c8e04b83841a1c_l3.png "Rendered by QuickLaTeX.com")
Задача 1.
Расстояние между двумя пунктами 20 км. Из этих пунктов в одном направлении одновременно выехали автомобиль и мотоциклист, причем автомобиль двигался впереди. Через 5 часов расстояние между ними стало 170 км. Найти скорость мотоциклиста, если скорость автомобиля 70 км/ч.
Решение:
|
v, км/ч |
t, ч |
s, км |
|
|
Автомобиль |
70 |
5 |
? |
|
Мотоциклист |
? |
5 |
? |
1) 170-20=150 (км) на столько увеличилось расстояние между автомобилем и мотоциклистом за 5 часов
2) 150:5=30 (км/ч) скорость удаления автомобиля от мотоциклиста
3) 70-30=40 (км/ч) скорость мотоциклиста.
Ответ: 40 км/ч.
Задача 2.
Расстояние между двумя станциями 40 км. Из этих станций одновременно в одном направлении вышли скорый и товарный поезда, причем товарный поезд едет впереди. Через сколько часов скорый поезд догонит товарный, если его скорость равна 80 км/ч, а скорость товарного поезда — 60 км/ч?
Решение:
|
v, км/ч |
t, ч |
s, км |
|
|
Пассажирский |
80 |
? |
? на 40 км больше |
|
Товарный |
60 |
? |
? |
1) 80-60=20 (км/ч) скорость сближения поездов
2) 40:20=2 (ч) через такое время скорый поезд догонит товарный.
Ответ: через 2 ч.
Задача 3.
Расстояние между пунктами равно 50 км. Из этих пунктов одновременно в одном направлении выезжают велосипедист и мотоциклист, причем велосипедист едет впереди. Скорость велосипедиста равна 13 км/ч, скорость мотоциклиста — 38 км/ч. На каком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста?
Решение:
|
v, км/ч |
t, ч |
s, км |
|
|
Мотоциклист |
38 |
? |
? на 50 км больше |
|
Велосипедист |
13 |
? |
? |
1) 38-13=25 (км/ч) скорость сближения мотоциклиста и велосипедиста
2) 50:25=2 (ч) через столько часов после своего выезда мотоциклист догонит велосипедиста
3) 38∙2=76 (км) на таком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста.
Ответ: 76 км.
Содержание материала
- Задачи на скорость сближения
- Видео
- Скорость сближения
- Задачи на течение реки
- Скорость
- Задача на движение объектов в одном направлении
- Движение в противоположных направлениях
- Относительное движение
- Примеры решения задач
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.
Видео
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Задачи на течение реки
Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.
Особенность этих задач в том, что к скорости, с которой движется тело по воде добавляется (или вычитается) скорость течения реки.
Давай разберемся.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:
Скорость удаления больше скорости любого из них.
Задача 1
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Решение:
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1. (км/ч)
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2. (ч)
Ответ: Через три часа расстояние между переходами будет 27 км.
Задача 2
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?
Решение:
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1. (км)
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2. (км)
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3. (км/ч)
Ответ: Скорость второго пешехода – 4 км/ч.
Задача 3
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?
Решение:
1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
Задача 4
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?
Решение:
1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Относительное движение
Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:
- сумме скоростей, если тела движутся навстречу друг другу;
- разности скоростей, если тела движутся в одном направлении.
Примеры решения задач
Два туриста на велосипедах отправились в одно и то же время из разных пунктов в точку назначения. Время в пути первого велосипедиста составило 2 ч. Для того чтобы прибыть в точку назначения одновременно с первым туристом, второму велосипедисту потребовалось проехать каждый последующий км пути на 1 мин быстрее по сравнению с предыдущим. Расстояние, которое преодолел второй турист на велосипеде больше на 6 км, чем путь первого туриста. Требуется определить скорости первого и второго велосипедистов.
Решение
Предположим, что первый турист на велосипеде преодолевал каждый км пути за х мин. Тогда его скорость равна 60/х км/ч. В таком случае, скорость второго велосипедиста составит 60/(х-1) км/ч. Составим уравнение:
60/(х–1)*2–(60/х)*2=6
х1=5
х2=–4
Второй корень является посторонним.
Ответ: скорость первого велосипедиста 12 км/ч, второй велосипедист двигался со скоростью 15 км/ч.
Теги
1. Когда два объекта движутся навстречу друг другу или вдогонку, то до встречи расстояние между ними уменьшается.
За единицу времени объекты вместе проходят расстояние, равное скорости сближения
v сбл.
, а за время
tвстр.
движения до встречи они проходят расстояние (s), которое было между ними в момент начала движения.
Начальное расстояние между объектами при движении навстречу друг другу или движении вдогонку равно произведению скорости сближения и времени движения до встречи:
s=vсбл.⋅tвстр.
Эти виды движения отличаются только нахождением скорости сближения.
При движении навстречу друг другу скорость сближения равна
vсбл.=v1+v2
.
При движении вдогонку скорость сближения равна
vсбл.=v1−v2
(
v1>v2
).
2. При движении в противоположных направлениях и с отставанием расстояние между объектами увеличивается, поэтому встреча не может произойти.
При движении в противоположных направлениях скорость удаления равна
vуд.=v1+v2
.
За (t) единиц времени начальное расстояние между объектами увеличивается на
s=vуд.⋅t
.
При движении с отставанием скорость удаления равна
vуд.=v1−v2
(
v1>v2
).
За (t) единиц времени начальное расстояние между объектами увеличивается на
s=vуд.⋅t
.
Источники:
Изображения: схемы движения. © ЯКласс.
§ 1 Скорость сближения и скорость удаления
В этом уроке познакомимся с такими понятиями, как «скорость сближения» и «скорость удаления».
Для ознакомления с понятиями «скорость сближения» и «скорость удаления» рассмотрим 4 реальные ситуации.
Из двух городов навстречу друг другу одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается ли расстояние между автомобилями? Если да, то с какой скоростью?
Изобразим движение данных автомобилей на координатном луче.
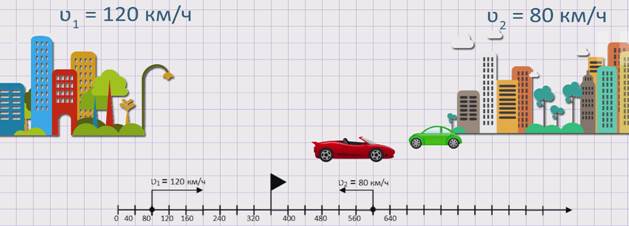
Из рисунка видно, что два автомобиля, двигаясь навстречу друг другу, приближаются. Значит, расстояние между ними сокращается. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо к скорости первого автомобиля прибавить скорость второго. А именно, скорость сближения равна сумме скоростей первого и второго автомобилей: ʋсбл. = ʋ1 +ʋ2.
Найдем скорость сближения данных автомобилей:
Значит, расстояние между автомобилями сокращается со скоростью 200 км/ч. Рассмотрим вторую ситуацию.
Из двух городов одновременно в одном направлении, вдогонку, выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается или увеличивается расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
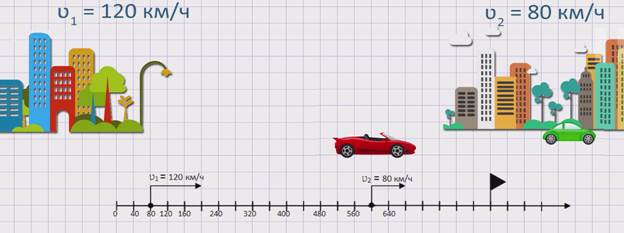
Из рисунка видно, что первый автомобиль движется быстрее второго автомобиля или же движется вдогонку второму автомобилю. Значит, расстояние между автомобилями будет сокращаться. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость сближения равна разности скоростей двух автомобилей: ʋсбл. = ʋ1 – ʋ2 .
Найдем скорость сближения данных автомобилей: ʋсбл. = ʋ1 – ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями сокращается со скоростью 40 км/ч.
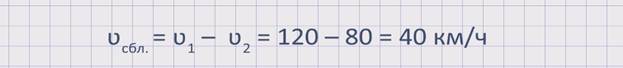
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Рассмотрим следующую третью ситуацию.
Из двух городов в противоположных направлениях одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Будет ли увеличиваться расстояние между автомобилями? Если да, то на сколько?
Изобразим движение данных автомобилей на координатном луче.
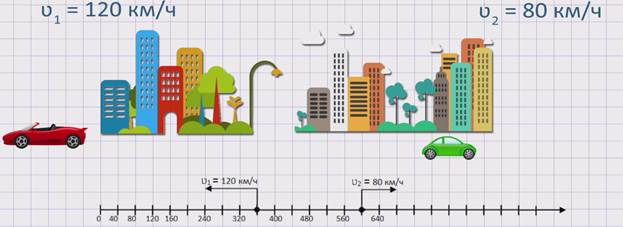
Из рисунка видно, что два автомобиля, двигаясь в противоположных направлениях, удаляются друг от друга. Значит, расстояние между ними увеличивается. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо к скорости первого автомобиля прибавить скорость второго автомобиля. А именно, скорость удаления равна сумме скоростей двух автомобилей: ʋуд. = ʋ1 + ʋ2 .
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 + ʋ2 = 120 + 80 = 200 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 200 км/ч.
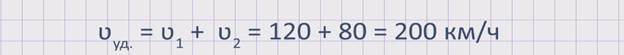
Рассмотрим последнюю четвертую ситуацию.
Из двух городов водном направление одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Причем второй автомобиль движется с отставанием. Будет увеличиваться или уменьшаться расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
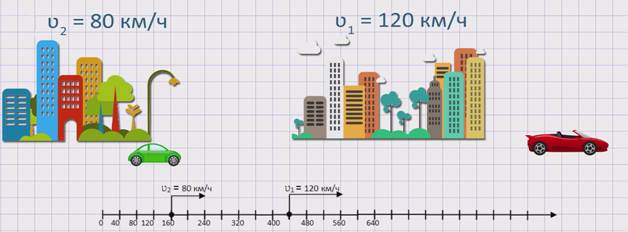
Из рисунка видно, что второй автомобиль движется медленнее первого автомобиля или же движется с отставанием от первого автомобиля. Значит, расстояние между автомобилями будет увеличиваться. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость удаления равна разности скоростей двух автомобилей: ʋуд. = ʋ1 – ʋ2 .
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 – ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 40 км/ч.
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость удаления». Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
§ 2 Краткие итоги по теме урока
1.Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
2.При движении двух объектов навстречу друг другу скорость сближения равна сумме скоростей этих объектов. ʋсбл. = ʋ1 + ʋ2
3.При движении вдогонку скорость сближения равна разности скоростей объектов движения. ʋсбл. = ʋ1 – ʋ2
4.Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
5.При движении двух объектов в противоположных направлениях скорость удаления равна сумме скоростей этих объектов. ʋуд. = ʋ1 + ʋ2
6.При движении с отставанием скорость удаления равна разности скоростей объектов движения. ʋуд. = ʋ1 – ʋ2
