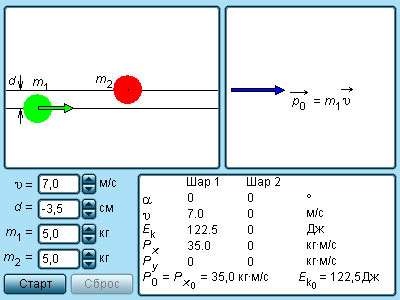
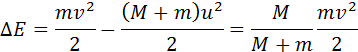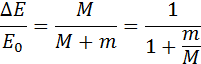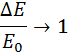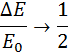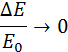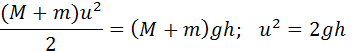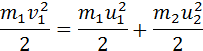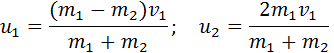Определение скоростей шаров
При
абсолютно упругом столкновении шара
массой m1
(m
= (111,67 ±0,04)·10-3
кг), который движется со скоростью V1,
с шаром массой m2
(m=(111,506±0,009)·10-3
кг), который движется со скоростью V2
(V2<V1,рис.2),
поверхности
их
деформируются, но этот процесс обратим,
так как форма шаров мгновенно
восстанавливается, а энергия деформации
без потерь превращается в кинетическую
энергию движения шаров.
П
удара шары будут двигаться с измененными
скоростямиU1
и U2,
определить которые можно с помощью
законов сохранения кинетической энергии
и сохранения
импульса (количества движения)
m1V1+m2V2=m1U1+m2U2,
(2)
После несложных
преобразований находят скорости шаров
после удара
Если происходит
встречный центральный абсолютно упругий
удар (скорости шаров до удара имеют
противоположные знаки), то необходимо
учитывать знак скорости при вычислении
соответствующих величин в выражениях
(3), (4). При равенстве масс шаров (т1
= т2
= т) из (3) и
(4) следует
U1=V2,
U2=V1,
(5)
т.е. первый шар
приобрел после удара скорость, равную
скорости второго шара, и наоборот. Если
до столкновения один из шаров (например,
второй) покоился (V2
= 0), то U1
= 0; U2
= V1).
После абсолютно
неупругого удара тела совершают
совместное движение (рис. 3), а кинетическая
энергия соударяющихся тел частично
переходит в другие виды энергии, и тела
приобретают остаточную деформацию. При
этом закон сохранения механической
энергии системы не выполняется. Скорость
U1
после удара, как известно, можно
определить, используя закон сохранения
импульса и считая, что внешние силы
отсутствуют, а масса системы после удара
– т1+
т2:
Е
первоначально тело было поднято на
высотуh1,
то в момент удара его кинетическая
энергия равна исходной потенциальной
энергии (рис. 4):
.
Скорости шаров
после взаимодействия можно определить
из условий
где
h2
и h3
–
высота подъемов второго и первого шара
после взаимодействия.
Из
этих соотношений следует
1) По измеренному
значению угла a
начального отклонения правого шара
вычислить по формулам (7) и (9) его скорость
U1
при прохождении им положения равновесия.
2) Определить
теоретические значения скоростей шаров
после взаимодействия для случаев
абсолютно упругого удара (формулы (3),
(4) и абсолютно неупругого удара (формула
(6)).
3) По измеренным
углам отклонения шаров после их
взаимодействия (β
и γ)
вычислить по формулам (8), (9) действительные
значения скоростей шаров.
4) Сравнить
теоретические и экспериментальные
значения
скоростей, дать объяснение полученным
результатам.
Определение работы деформации при ударе шаров
При неупругом
ударе часть механической энергии тел
переходит в другие формы энергии
(например, тепловую) и затрачивается на
работу остаточной, деформации поверхности
шаров. В этом случае полная энергия
системы не изменяется, кинетическая
энергия шаров после удара будет меньше,
чем до удара.
Уменьшение
механической энергии системы ∆W
с достаточной степенью точности можно
считать равным работе сил, создающих
остаточную деформацию.
По закону сохранения
энергии при столкновении реальных тел
следует учесть работу деформации тел
A,
т.е. ту часть общей энергии, которая
необратимо расходуется на совершение
невосстанавливающейся деформации и
преобразуется в энергию теплового
движения молекул вещества:
Это уравнение
позволяет определить работу деформации
шаров равных
масс (m1
= m2
= m),
закрепленных на нерастяжимых нитях
длины R.
Если второй шар покоится (V2
= 0), а первый
– отклонен на
угол α
от вертикального положения (рис. 4), то
(10) преобразуется к виду:
A=∆W=mg(h1-h2-h3),
(11)
где
h2
и h3
– высота подъема второго и первого шара
после удара. С учетом (9)
A=mgR(cosβ+cosγ-cosα-1),
(12)
1) Вычислить
кинетическую энергию шара в момент
удара по измеренному значению угла a
первоначального отклонения первого
шара.
2) По измеренным
значениям углов a,
β
и γ
и длины подвеса шаров R
вычислить по формуле (12) изменение
механической энергии системы – работу
деформации.
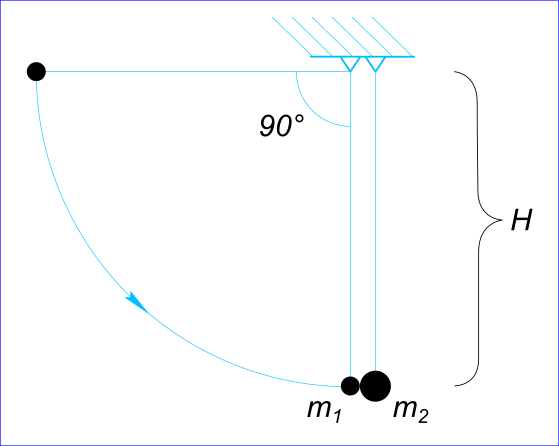
Два шара массами 0,2 кг и 0,8 кг, подвешенные на двух параллельных нитях длиной l = 2 м, касаются друг друга. Меньший шар отводится на α=90° от первоначального положения и отпускается. Найти скорости шаров после столкновения, считая удар абсолютно упругим. Какова скорость шаров после столкновения, если удар абсолютно неупругий? Какая часть энергии пойдет на нагревание шаров?
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Решения задачи
Данные задачи: Два шара подвешены на двух параллельных нитях
| Масса шара №1 | $m_{1}$ | 0,2 | кг |
|---|---|---|---|
| Масса шара №2 | $m_{2}$ | 0,8 | кг |
| Длина нити | H | 2 | м |
| Скорость шара №1 (до соударения) | $v_{1}$ | ||
| Скорость шара №2(до соударения) | $v_{2}$ | 0 | |
| и | |||
| Скорость шара №1 и №2 (Удар неупругий) | ? |
Изобразим на рисунке условия задачи
Абсолютно упругим ударом называется такой удар, при котором механическая энергия соударяющихся тел не преобразуется в другие виды энергии.
По закону сохранения механической энергии
$ m_{1}gH = frac{1}{2}m_{1}(v_{1})^{2} $
Откуда находим
$ v_{1}=sqrt{2gH}=sqrt{2×9,81×2}=6.264frac{м}{с} $
Согласно закону сохранения импульса:
$ m_{1}v_{1}+m_{2}v_{2} = m_{1}u_{1}+m_{2}u_{2} $
или
$ m_{1}(v_{1}-u_{1}) = m_{2}(u_{2}-v_{2}) $
Согласно закону сохранения механической энергии:
$ frac{m_{1}(v_{1})^{2}}{2}+frac{m_{2}(v_{2})^{2}}{2}=frac{m_{1}(u_{1})^{2}}{2}+frac{m_{2}(u_{2})^{2}}{2} $
или
$ m_{1}((v_{1})^{2})-(u_{1})^{2}) = m_{2}((u_{2})^{2})-(v_{2})^{2}) $
Подставив в формулу «разность квадратов» получим
$ m_{1}(v_{1}-u_{1})(v_{1}+u_{1}) = m_{2}(u_{2}-v_{2})(u_{2}+v_{2}) $
Воспользовавшись законом сохранения импульса, находим
$ v_{1}+u_{1} = u_{2}+v_{2} $
Откуда
$ u_{2} = u_{1}+v_{1}-v_{2} $
и
$ u_{1} = u_{2}+v_{2}-v_{1} $
Подставляем в закон сохранения импульса
$ m_{1}(v_{1}-u_{1}) = m_{2}((v_{1}+v_{1}-v_{2})-v_{2}) $
и
$ m_{1}(v_{1}-v_{2}-u_{2}+v_{1}) = m_{2}(u_{2}-v_{2}) $
Раскрываем скобки
$ m_{1}v_{1}-m_{1}u_{1}=m_{2}u_{1}+m_{2}v_{1}-2m_{2}v_{2} $
Откуда
$u_{1}=frac{2m_{2}v_{2}+(m_{1}-m_{2})v_{1}}{m_{1}+m_{2}}=frac{(0,2-0,8)×6.26}{0,2+0,8}=-3,76frac{м}{с}$
Раскрываем скобки
$ m_{1}v_{1}-m_{1}v_{2}-m_{1}u_{2}+m_{1}v_{1}=m_{2}u_{2}-m_{2}v_{2} $
Откуда
$u_{2}=frac{2m_{1}v_{1}+(m_{2}-m_{1})v_{2}}{m_{2}+m_{1}}=frac{2×0,2×6,26}{0,8+0,2}=2.51frac{м}{с}$
Абсолютно неупругий удар характеризуется тем, что кинетическая энергия тел превращается во внутреннюю энергию и после соударения тела либо покоятся, либо движутся с одинаковой скоростью:
$ u = frac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}=frac{0,2v_{1}+0,8×0}{0,2+0,8}=0,2×6,26=1.25frac{м}{с} $
Ответ: Скорость шаров
$ №1 после упругого соударения u_{1}=-3.76frac{м}{с} $
$ №2 после упругого соударения u_{2}=2.51frac{м}{с} $
$ после неупругого соударения u=1.25frac{м}{с} $
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь
Применим закон сохранения механической энергии для расчета скорости тел при абсолютно упругом ударе – ударе, при котором не происходит превращения механической энергии в другие виды энергии.
На рисунке 5.8 изображены два шара m1 и m2.
Обозначим и как скорость шаров после их столкновения.
В данном случае можно воспользоваться законом сохранения механической энергии и законом сохранения импульса (в проекциях на ось x):
Решив эту систему уравнений относительно и , получим
Таким образом, скорости шаров после абсолютно упругого удара не могут быть одинаковыми по величине и по направлению.
Рассмотрим теперь абсолютно упругий удар шара о неподвижную массивную стенку. Стенку можно рассматривать как неподвижный шар с υ2 = 0, массой .
Разделим числитель и знаменатель на m2 и пренебрежем m1/m2 , тогда
,
.
Так, шар m1 изменит направление скорости на противоположное.
§ 6.10. Столкновение упругих шаров
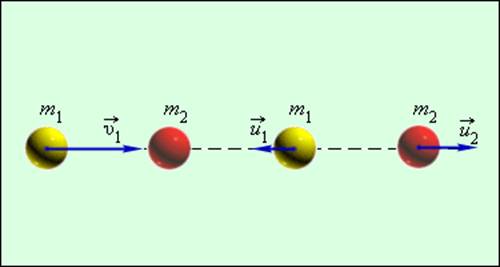
Под абсолютно упругим ударом понимают такой удар, при котором механическая энергия сохраняется(1). Если начальные скорости шаров направлены по линии, соединяющей их центры (рис. 6.22), то удар называют центральным.
Для абсолютно неупругого удара скорости шаров после удара можно найти с помощью закона сохранения импульса (см. гл. 5). При упругом ударе этого закона недостаточно, так как шары после удара будут иметь различные скорости. Значит, нужно еще одно уравнение, которое дает закон сохранения энергии.
Обозначим массы шаров через m1 и m2, их скорости до удара через 



Закон сохранения энергии запишется так:
Нами получена система двух уравнений с двумя неизвестными u1х и u2х. Для решения этой системы ее удобно переписать так:
Разделив почленно второе уравнение на первое, получим:
Умножив обе части этого уравнения на m2 и сложив полученный результат почленно с уравнением (6.10.3), приходим к выражению:
Применив аналогичный прием, получим выражение для проекции скорости 
Применим эти формулы для двух частных случаев.
1. Второй шар до удара покоился (v2x = 0), тогда
При m1 > m2 первый шар продолжает двигаться в том же направлении, что и до удара, но с меньшей скоростью. Если m1
2. Оба шара имеют одинаковую массу, тогда
Шары при соударении обмениваются скоростями. Проверьте на опыте справедливость этих выводов.
Рассмотрено центральное столкновение абсолютно упругих шаров. Полученные формулы справедливы не только для столкновения макроскопических тел, но и в широких пределах для атомов и элементарных час тиц.
(1) Для этого необходимо, чтобы силы взаимодействия между телами зависели только от деформаций, но не от скоростей их движения друг относительно друга.
Упругие и неупругие соударения
Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.
Применение такого вида задач используется в технике и физике элементарных частиц.
Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.
При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.
Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.
Абсолютно неупругий удар. Скорость
Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.
Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.
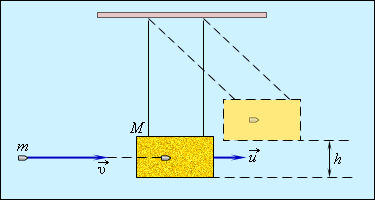
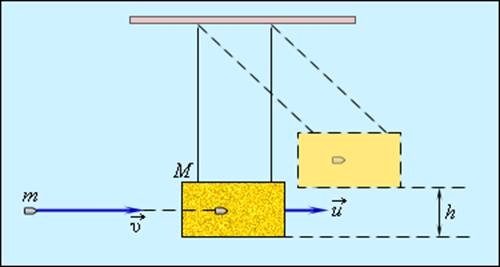
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1 . 21 . 1 , m – горизонтально летящая пуля с v → скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.
Если скорость ящика с пулей обозначить как u → , тогда, используя формулу сохранения импульса, получаем:
m v = ( M + m ) u ; u = m M + m v .
Когда пуля застревает в песке, то механическая энергия теряется:
∆ E = m v 2 2 – ( M + m ) u 2 2 = M M + m · m v 2 2 .
M ( M + m ) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда
∆ E E 0 = M M + m = 1 1 + m M .
Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.
Когда m М ∆ E E 0 → 1 2 , тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆ E E 0 → 0 , только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим ( m > > М ) , отношение принимает вид ∆ E E 0 → 0 .
Расчет движения маятника производится по закону сохранения механической энергии. Получаем
( M + m ) u 2 2 = ( M + m ) g h ; u 2 = 2 g h .
В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что
v = M + m m 2 g h .
При известной высоте h возможно определение скорости пули v .
Рисунок 1 . 21 . 1 . Баллистический маятник.
Абсолютно упругий удар
Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1 . 21 . 2 .
Центральный удар – это соударение, когда скорости шаров направлены по линии центра.
Рисунок 1 . 21 . 2 . Абсолютно упругий центральный удар шаров.
Встречаются случаи, когда массы m 1 и m 2 не равны. Тогда, используя закон сохранения механической энергии, получаем
m 1 v 1 2 2 = m 1 v 1 2 2 + m 2 v 2 2 2 .
За v 1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v 2 = 0 скорость второго шара, u 1 и u 2 – скорости после столкновения.
Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:
m 1 v 1 = m 1 u 1 + m 2 u 2 .
Полученная система из двух уравнений позволяет найти неизвестные скорости u 1 и u 2 шаров после столкновения.
u 1 = m 1 – m 2 v 1 m 1 + m 2 ; u 2 = 2 m 1 v 1 m 1 + m 2 .
Если массы равны, то есть, тогда происходит остановка первого шара ( u 1 = 0 ) , а второй продолжает движение u 2 = v 1 . происходит обмен скоростями и импульсами.
При наличии нулевой скорости второго шара ( v 2 ≠ 0 ) , задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v 2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v 1 ‘ = v 1 – v 2 . После определения скорости шаров v 1 и v 2 производится переход к «неподвижной» системе.
С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.
Рисунок 1 . 21 . 3 . Модель упругие и неупругие соударения.
При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1 . 21 . 4 .
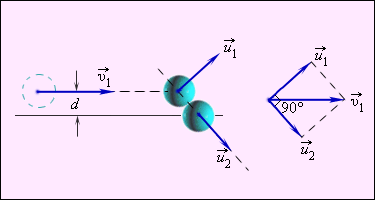
Рисунок 1 . 21 . 4 . Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.
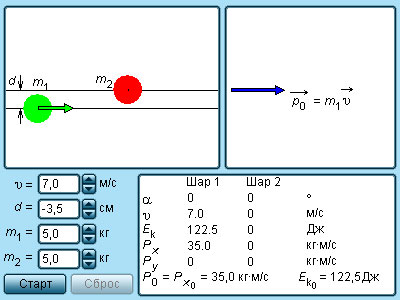
Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v 1 и v 2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d , изображенное на рисунке 1 . 21 . 4 .
Предельное расстояние
Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v 1 → летящего шара.
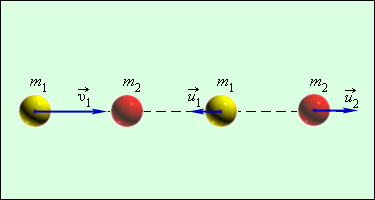
При одинаковых массах шаров векторы v 1 → и v 2 → имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m 1 = m 2 = m , тогда определение примет вид
v 1 → = u 1 → + u 2 → ; v 1 2 = u 1 2 + u 2 2 .
Первое равенство значит, что векторы v 1 → , u 1 → , u 2 → образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u 1 → и u 2 → , равняется 90 градусов.
Рисунок 1 . 21 . 5 . Модель соударения упругих шаров
[spoiler title=”источники:”]
http://tepka.ru/fizika_10/92.html
http://zaochnik.com/spravochnik/fizika/zakony-sohranenija-v-mehanike/uprugie-i-neuprugie-soudarenija/
[/spoiler]
Задание
KiS me
Профи
(975),
на голосовании
12 лет назад
5. Два шара массой 200 г и 600 г движутся навстречу друг другу со скоростью 2 м/с. Определите скорость шаров после неупругого взаимодействия.
Голосование за лучший ответ
Guzelina
Мастер
(2272)
12 лет назад
Задача на закон сохранения импульса. По условию задачи произошел абсолютно неупругий удар, т. е. шары после столкновения стали двигаться вместе:
м1*и1+м2*и2 = (м1+м2)*И
где м1,м2 – массы тел, и1,и2 – скорости тел до столкновения, И – искомая скорость.
Выражаем И, подставляем, считаем (помним о том, что шары летят навстречу, значит одна скорость будет со знаком -):
И = (м1*и1-м2*и2)/(м1+м2) =(0.6кг*2м/с-0.2кг*2м/с) /(0.2кг+0.6кг) = 1м/с
(да, верно, забыла про знак, спасибо)
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m << M
почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M
во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
|
|
|
Рисунок 1.21.1. Баллистический маятник |
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
|
|
|
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров |
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
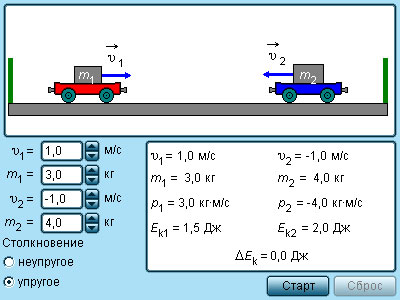 |
|
Модель. Упругие и неупругие соударения. |
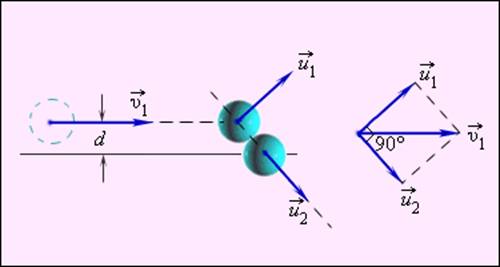
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
|
|
|
Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние |
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
налетающего шара. Если массы шаров одинаковы, то векторы скоростей
и
шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:
Первое из этих равенств означает, что векторы скоростей ,
и
образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами
и
равен 90°.
 |
|
Модель. Соударения упругих шаров. |