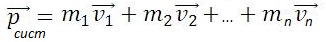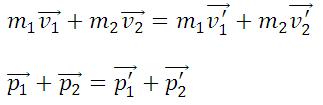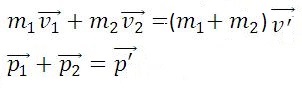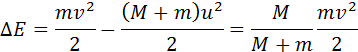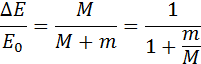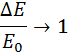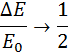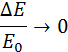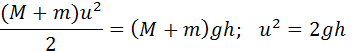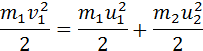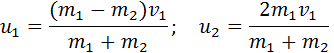Как найти скорость шара после взаимодействия

другом (первый за вторым) со скоростями v1= 9 м/с и v2= 4 м/с соответственно. После столкновения шаров происходит упругий удар, в результате которого скорость первого шара уменьшается на Δv= 5 м/с, и шарики раскатываются в разные стороны. Определи скорость второго шарика после столкновения. (Ответ округли до десятых.) Шаг 1. Найди импульс первого шарика до взаимодействия: p1= кг·м/с. Шаг 2. Найди импульс второго шарика до взаимодействия: p2= кг·м/с. Шаг 3. Найди суммарный импульс двух шариков до взаимодействия, учитывая, что шарики движутся друг за другом (первый за вторым): p= кг·м/с. Шаг 4. Найди скорость первого шарика после взаимодействия: V1= м/с. Шаг 5. Найди импульс первого шарика после взаимодействия: P1= кг·м/с. Шаг 6. Обозначив скорость второго шарика после взаимодействия как V, запиши импульс P второго шарика после взаимодействия: = ⋅. Шаг 7. Обрати внимание, что в результате упругого столкновения шарики будут двигаться в разные стороны. Запиши суммарный импульс шариков после взаимодействия: p′=∣∣ − ⋅ ∣∣.

Шаг 8. Поскольку два шарика являются замкнутой системой, то для них выполняется закон сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия. Составь уравнение согласно закону сохранения импульса: =∣∣ − ⋅ ∣∣ — и реши его относительно V с точностью до десятых: V = м/с.

Определение скоростей шаров

При
абсолютно упругом столкновении шара
массой m₁
(m
= (111,67 ±0,04)·10^-3
кг), который движется со скоростью V₁,
с шаром массой m₂
(m=(111,506±0,009)·10^-3
кг), который движется со скоростью V₂
(V₂<V₁,рис.2),
поверхности
их
деформируются, но этот процесс обратим,
так как форма шаров мгновенно
восстанавливается, а энергия деформации
без потерь превращается в кинетическую
энергию движения шаров.

После
удара шары будут двигаться с измененными
скоростямиU₁
и U₂,
определить которые можно с помощью
законов сохранения кинетической энергии

и сохранения
импульса (количества движения)

m₁V₁+m₂V₂=m₁U₁+m₂U₂,
(2)

После несложных
преобразований находят скорости шаров
после удара

Если происходит
встречный центральный абсолютно упругий
удар (скорости шаров до удара имеют
противоположные знаки), то необходимо
учитывать знак скорости при вычислении
соответствующих величин в выражениях
(3), (4). При равенстве масс шаров (т₁
= т₂
= т) из (3) и
(4) следует

U₁=V₂,
U₂=V₁,
(5)

т.е. первый шар
приобрел после удара скорость, равную
скорости второго шара, и наоборот. Если
до столкновения один из шаров (например,
второй) покоился (V₂
= 0), то U₁
= 0; U₂
= V₁).

После абсолютно
неупругого удара тела совершают
совместное движение (рис. 3), а кинетическая
энергия соударяющихся тел частично
переходит в другие виды энергии, и тела
приобретают остаточную деформацию. При
этом закон сохранения механической
энергии системы не выполняется. Скорость
U₁
после удара, как известно, можно
определить, используя закон сохранения
импульса и считая, что внешние силы
отсутствуют, а масса системы после удара
– т₁+
т₂:

Если
первоначально тело было поднято на
высотуh₁,
то в момент удара его кинетическая
энергия равна исходной потенциальной
энергии (рис. 4):
.

Скорости шаров
после взаимодействия можно определить
из условий

где
h₂
и h₃
–
высота подъемов второго и первого шара
после взаимодействия.

Из
этих соотношений следует

1) По измеренному
значению угла a
начального отклонения правого шара
вычислить по формулам (7) и (9) его скорость
U₁
при прохождении им положения равновесия.

2) Определить
теоретические значения скоростей шаров
после взаимодействия для случаев
абсолютно упругого удара (формулы (3),
(4) и абсолютно неупругого удара (формула
(6)).

3) По измеренным
углам отклонения шаров после их
взаимодействия (β
и γ)
вычислить по формулам (8), (9) действительные
значения скоростей шаров.

4) Сравнить
теоретические и экспериментальные
значения
скоростей, дать объяснение полученным
результатам.

Определение работы деформации при ударе шаров

При неупругом
ударе часть механической энергии тел
переходит в другие формы энергии
(например, тепловую) и затрачивается на
работу остаточной, деформации поверхности
шаров. В этом случае полная энергия
системы не изменяется, кинетическая
энергия шаров после удара будет меньше,
чем до удара.

Уменьшение
механической энергии системы ∆W
с достаточной степенью точности можно
считать равным работе сил, создающих
остаточную деформацию.

По закону сохранения
энергии при столкновении реальных тел
следует учесть работу деформации тел
A,
т.е. ту часть общей энергии, которая
необратимо расходуется на совершение
невосстанавливающейся деформации и
преобразуется в энергию теплового
движения молекул вещества:

Это уравнение
позволяет определить работу деформации
шаров равных
масс (m₁
= m₂
= m),
закрепленных на нерастяжимых нитях
длины R.
Если второй шар покоится (V₂
= 0), а первый
– отклонен на
угол α
от вертикального положения (рис. 4), то
(10) преобразуется к виду:

A=∆W=mg(h₁-h₂-h₃),
(11)

где
h₂
и h₃
– высота подъема второго и первого шара
после удара. С учетом (9)

A=mgR(cosβ+cosγ-cosα-1),

(12)

1) Вычислить
кинетическую энергию шара в момент
удара по измеренному значению угла a
первоначального отклонения первого
шара.

2) По измеренным
значениям углов a,
β
и γ
и длины подвеса шаров R
вычислить по формуле (12) изменение
механической энергии системы – работу
деформации.

Лабораторная работа № 2

Тема: Изучение закона сохранения импульса

Цель: экспериментально проверить справедливость закона сохранения импульса тел при прямом упругом соударении

Оборудование: 1. Два металлических шарика разной массы.

                        2. Рама для подвеса шариков.

                        3. Измерительная линейка.

Теория

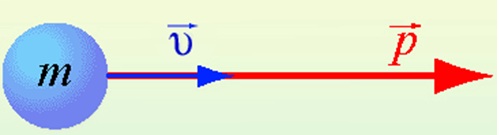
   Величина, равная произведению массы материальной точки на ее скорость, называется импульсом.

p=mυ  

p — импульс тела

m — масса тела

υ — скорость тела   

   Импульс тела направлен в ту же сторону, что и скорость тела.

   Единицей измерения импульса в СИ является 1 кг·м/с.

   Изменение импульса тела происходит при взаимодействии тел, например, при ударах.

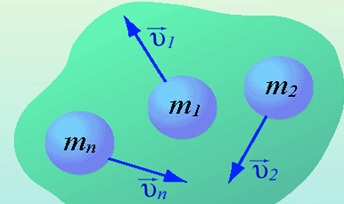
   Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма.

   Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. Замкнутая система – это система тел, которые взаимодействуют только друг с другом.

   Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

m₁, m₂ — массы взаимодействующих тел, кг

υ₁, υ₂ — скорости тел до столкновения, м/с

υ’₁, υ’₂ — скорости тел после столкновения, м/с

   Закон сохранения импульса можно сформулировать и так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления.

   Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближенно выполняется для этих процессов даже при наличии внешних сил, действующих на тела системы со стороны тел, не входящих в нее, т.к. за малое время внешние силы не успевают значительно изменить импульс системы.

   Под ударом в механике понимается кратковременное взаимодейс­твие двух или более тел,  возникающее в результате их соприкосно­вения (соударение шаров, удар молота о наковальню и др.). Самым простым является прямой (центральный) удар, то есть такой удар, при котором скорости соударяющихся тел до удара направлены по линии, соединя­ющей центры тел. При соударении взаимодействие  длится такой короткий промежуток времени (иногда измеряемый тысячными долями секунды) и возни­кают столь большие внутренние силы взаимодействия, что внешними силами можно пренебречь и систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.

   В зависимости от упругих свойств тел соударения могут проте­кать весьма различно. Принято выделять два крайних случая: абсо­лютно упругий и абсолютно неупругий удары.

   Абсолютно упругим называется удар, при котором после взаимодействия тела полностью восстанавливают свою форму. Таких ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел. Однако для некоторых  тел, например стальных закаленных шаров, потерями механической энергии при столкновении можно пренебречь и считать удар абсолютно упру­гим. В случае центрального абсолютно упругого удара двух тел с массами m₁, m₂  и скоростями υ₁, υ₂  до удара и υ′₁, υ′₂ после удара можно записать закон сохранения импульса тел:

   Абсолютно неупругим называется удар, при котором после соп­рикосновения тел они не восстанавливают полностью свою форму, со­единяются вместе и движутся как единое целое с одной скоростью. При этом ударе часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). Столкновение двух шаров из пластилина, когда после столкновения шары слипаются и движутся вместе, является примером абсолютно неупругого удара. В случае центрального абсолютно неупругого удара двух тел с массами m₁, m₂  движущихся со скоростями υ₁, υ₂  до удара и υ′ после удара можно записать законы сохранения импульса тел:

   Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:

1. Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.
2. Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике – при забивании свай, ковке металлов и т.д

Описание работы

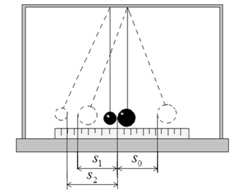
Установка состоит из двух стальных шаров, на длинных подвесах и измерительной линейки под шарами. Центры масс соприкасающихся шарв лежат на одном уровне от точки подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно произвести прямой (центральный) удар шаров.

Если до столкновения один из шаров покоился υ₂=0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:

m₁∙υ₁= m₁∙υ′₁ + m₂∙υ′₂ 

   

   рис. 2

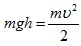
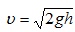
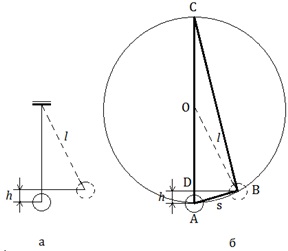
   Для определения скорости первого шара υ₁ до удара  и скоростей шаров υ′₁ и υ′₂ после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его кинетической энергии при ударе , отсюда .

   Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис.3,а).

рис. 3

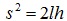
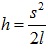
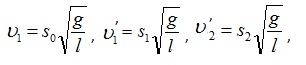
Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2l и своей проекцией на гипотенузу АD  (рис.3,б):  АВ²=АС·AD то есть , откуда . Следовательно, величины скоростей можно выразить так: где S₀,  S₁ – максимальные отклонения первого шара до и после удара; S₂ – максимальное отклонение второго шара после удара.

Запишем уравнение закона сохранения через выражения скоростей:

  или  m₁∙S₀= m₁∙S₁ + m₂∙S₂.

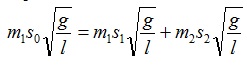
Таким образом, проверка закона сохранения импульса в данной работе сводится к проверке справедливости последнего уравнения.

 При малых углах отклонения шара от положения равновесия S₀,  S₁ и S₂ можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.

Выполнение работы.

1. Перенесите рисунок 2 в отчет по работе.

2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1
2
3

3. Определите массы шаров m₁ и m₂. Запишите их результат в таблицу.

4. Отрегулируйте подвеску шаров так, чтобы их центры и точка касания находились на одной горизонтальной линии.

5. Отклоните шар большей массы на 3 см от положения расновесия (S₀) и затем отпустите его. Заметьте максимальное отклонение шара большей массы после удара (S₁). Повторите опыт 5 раз и найдите среднее значение отклонения S_1ср. Запишите его в таблицу (S₁).

6. Повторите опыт, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S₂). Повторите опыт 5 раз, и найдите среднее значение отклонения S_2ср. Запишите его в таблицу (S₂).

7. Повторите опыт, отклоняя шар большей массы на 4 см и 5 см. Результаты измерений запишите в таблицу.

8. Используя значения S₀, S₁ и S₂, вычислите импульс шара до удара m₁∙S₀ и сумму импульсов шаров после удара  m₁∙S₁ + m₂∙S₂ и внесите в таблицу их результаты.

9. Сравните импульс шара до удара с суммой импульсов шаров после удара. Запишите вывод по полученным результатам работы.

10. Ответьте на контрольные вопросы.

Контрольные вопросы

1. Что называется импульсом материальной точки? По какой формуле он находится? В каких единицах он измеряется?

2. Импульс – величина векторная или скалярная?

3. Запишите формулу и формулировку закона сохранения импульса.

4. При каких условиях выполняется закон сохранения импульса?

5. Какое соударение называется абсолютно упругим?

6. Для каких видов соударений выполняется закон сохранения импульса?

Вариант выполнения измерений.

1. Определяем массы шариков m₁ и m₂  при помощи динамометра (или весов) и записываем в таблицу:

m₁=62 г

m₂=27,5 г

2. Отклоняем большой шар от положения расновесия на 3 см и отпускаем его. 

S₀=3 см=30 мм

Замечаем его максимальное отклонение после удара. Повторяем опыт 5 раз, находим среднее значение отклонения и записываем в таблицу S_1ср.

S₁=13мм   S₁=15мм   S₁=18мм    S₁=14мм   S₁=16мм

S_1ср=(13мм+15мм+18мм+14мм+16мм)/5=15,2 мм

3. Повторяем этот же опыт, но теперь замечаем после удара отклонение шара меньшей массы. Повторяем опыт 5 раз, находим среднее значение и записываем в таблицу S_2ср.

S₂=31мм   S₂=34мм   S₂=36мм    S₂=35мм   S₂=32мм

S_2ср=(31мм+34мм+36мм+35мм+32мм)/5=34мм

4. Повторяем опыт, отклоняя шар большей массы на 4 см и 5 см. 

S₀=4 см=40 мм

S₁=18 мм   S₁=19 мм   S₁=23 мм    S₁=22 мм   S₁=18 мм

S_1ср=(18 мм+19 мм+23 мм+22 мм+18 мм)/5=20 мм

S₂=43 мм   S₂=44 мм   S₂=46 мм    S₂=47 мм   S₂=45 мм

S_2ср=(43 мм + 44 мм + 46 мм + 47 мм + 45 мм)/5=45 мм

S₀=5 см=50 мм

Результаты измерений записываем в таблицу.

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1	62,0	27,5	30	15	34
2	62,0	27,5	40	20	45
3	62,0	27,5	50	25	56

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

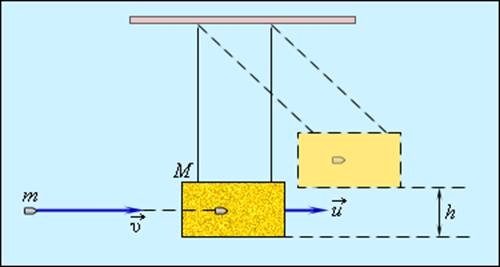
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью  попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.

Обозначим скорость ящика с застрявшей в нем пулей через  Тогда по закону сохранения импульса

При застревании пули в песке произошла потеря механической энергии:

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:

Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

При m << M

почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M

во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:

где h – максимальная высота подъема маятника. Из этих соотношений следует:

Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.

Рисунок 1.21.1. Баллистический маятник

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

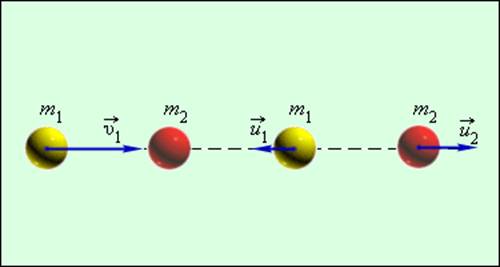
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

Рисунок 1.21.2. Абсолютно упругий центральный удар шаров

В общем случае массы m₁ и m₂ соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии

Здесь υ₁ – скорость первого шара до столкновения, скорость второго шара υ₂ = 0, u₁ и u₂ – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u₁ и u₂ шаров после столкновения:

В частном случае, когда оба шара имеют одинаковые массы (m₁ = m₂), первый шар после соударения останавливается (u₁ = 0), а второй движется со скоростью u₂ = υ₁, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ₂ ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ₂ относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ₁‘ = υ₁ – υ₂. Определив по приведенным выше формулам скорости u₁ и u₂ шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

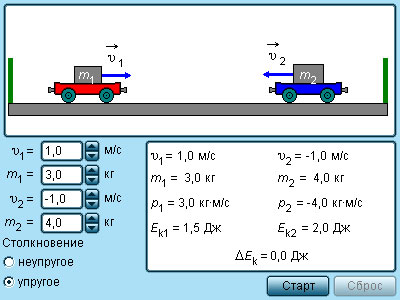Модель. Упругие и неупругие соударения.

Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).

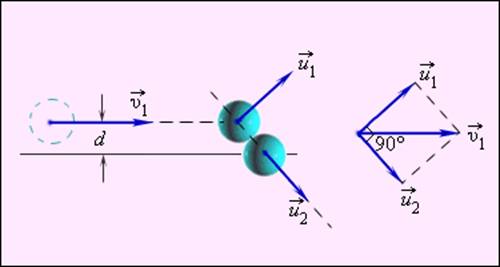
Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние

После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей  и  после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости  налетающего шара. Если массы шаров одинаковы, то векторы скоростей  и  шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m₁ = m₂ = m эти законы принимают вид:

Первое из этих равенств означает, что векторы скоростей ,  и  образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами  и  равен 90°.

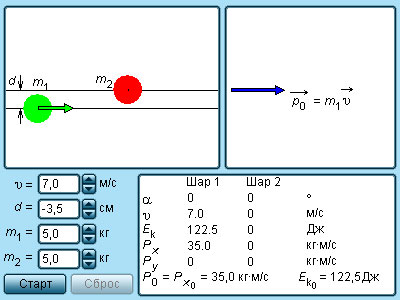Модель. Соударения упругих шаров.