Как найти скорость системы тел

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

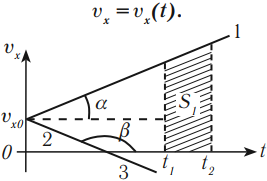
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

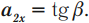
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

Импульс

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.

Импульс тела — это векторная величина, равная произведению массы тела на его скорость:

.

Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:

.

Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.

к оглавлению ▴

Второй закон Ньютона в импульсной форме

Пусть — равнодействующая сил, приложенных к телу массы . Начинаем с обычной записи второго закона Ньютона:

.

С учётом того, что ускорение тела равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:

.

Вносим константу под знак производной:

.

Как видим, в левой части получилась производная импульса:

. ( 1)

Соотношение ( 1) и есть новая форма записи второго закона Ньютона.

Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.

Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.

Производную в формуле ( 1) можно заменить на отношение конечных приращений:

. ( 2)

В этом случае есть средняя сила, действующая на тело в течение интервала времени . Чем меньше величина , тем ближе отношение к производной , и тем ближе средняя сила к своему мгновенному значению в данный момент времени.

В задачах, как правило, интервал времени достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда — средняя сила, действующая на мяч со стороны стенки во время удара.

Вектор в левой части соотношения ( 2) называется изменением импульса за время . Изменение импульса — это разность конечного и начального векторов импульса. А именно, если — импульс тела в некоторый начальный момент времени, — импульс тела спустя промежуток времени , то изменение импульса есть разность:

.

Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1):

Рис. 1. Изменение импульса

Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен ) и отскакивает назад без потери скорости (импульс после удара равен ). Несмотря на то, что импульс по модулю не изменился (), изменение импульса имеется:

.

Геометрически эта ситуация показана на рис. 2:

Рис. 2. Изменение импульса при отскоке назад

Модуль изменения импульса, как видим, равен удвоенному модулю начального импульса мяча: .

Перепишем формулу ( 2) следующим образом:

, ( 3)

или, расписывая изменение импульса, как и выше:

.

Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:

.

(Обратите внимание, что оказывается ещё одной возможной единицей измерения импульса тела.)

Словесная формулировка равенства ( 3) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.

к оглавлению ▴

Пример вычисления силы

В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.

Задача. Шарик массы г, летящий горизонтально со скоростью м/с, ударяется о гладкую вертикальную стену и отскакивает от неё без потери скорости. Угол падения шарика (то есть угол между направлением движения шарика и перпендикуляром к стене) равен . Удар длится с. Найти среднюю силу,
действующую на шарик во время удара.

Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом (рис. 3).

Рис. 3. К задаче (вид сверху)

Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила — сила упругости, направленная перпендикулярно стене (рис. 4).

Рис. 4. К задаче

Согласно ( 3) имеем: . Отсюда следует, что вектор изменения импульса сонаправлен с вектором , то есть направлен перпендикулярно стене в сторону отскока шарика (рис. 5).

Рис. 5. К задаче

Векторы и
равны по модулю
(так как скорость шарика не изменилась). Поэтому треугольник, составленный из векторов , и , является равнобедренным. Значит, угол между векторами и равен , то есть угол отражения действительно равен углу падения.

Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:

.

И тогда искомая средняя сила, действующая на шарик:

.

к оглавлению ▴

Импульс системы тел

Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами и соответственно. Импульс системы данных тел — это векторная сумма импульсов каждого тела:

.

Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1). Давайте выведем эту формулу.

Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть — результирующая внешняя сила, действующая на тело 1. Аналогично — результирующая внешняя сила, действующая на тело 2 (рис. 6).

Рис. 6. Система двух тел

Кроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой . Тогда тело 1 действует на тело 2 с силой . По третьему закону Ньютона силы и равны по модулю и противоположны по направлению: . Силы и — это внутренние силы, действующие в системе.

Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1):

, ( 4)

. ( 5)

Сложим равенства ( 4) и ( 5):

.

В левой части полученного равенства стоит сумма производных, равная производной суммы векторов и . В правой части имеем в силу третьего закона Ньютона:

.

Но — это импульс системы тел 1 и 2. Обозначим также — это результирующая внешних сил, действующих на систему. Получаем:

. ( 6)

Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.

Формула ( 6) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.

Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:

.

Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4) и ( 5), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6) останется справедливым и в общем случае.

к оглавлению ▴

Закон сохранения импульса

Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.

Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: . В этом случае из ( 6) получаем:

.

Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:

.

Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.

Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.

Задача. Тело массы г движется со скоростью м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы г со скоростью м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение. Ситуация изображена на рис. 7. Ось направим в сторону движения первого тела.

Рис. 7. К задаче

Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:

,
.

Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:

. ( 7)

Импульс системы до удара — это сумма импульсов тел:

.

После неупругого удара получилось одно тело массы , которое движется с искомой скоростью :

.

Из закона сохранения импульса ( 7) имеем:

.

Отсюда находим скорость тела, образовавшегося после удара:

.

Переходим к проекциям на ось :

.

По условию имеем: м/с, м/с, так что

.

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси . Искомая скорость: м/с.

к оглавлению ▴

Закон сохранения проекции импульса

Часто в задачах встречается следующая ситуация. Система тел не является замкнутой (векторная сумма внешних сил, действующих на систему, не равна нулю), но существует такая ось , сумма проекций внешних сил на ось равна нулю в любой момент времени. Тогда можно сказать, что вдоль данной оси наша система тел ведёт себя как замкнутая, и проекция импульса системы на ось сохраняется.

Покажем это более строго. Спроектируем равенство ( 6) на ось :

.

Если проекция равнодействующей внешних сил обращается в нуль, , то

.

Следовательно, проекция есть константа:

.

Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция импульса системы не меняется с течением времени.

Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.

Задача. Мальчик массы , стоящий на коньках на гладком льду, бросает камень массы со скоростью под углом к горизонту. Найти скорость , с которой мальчик откатывается назад после броска.

Решение. Ситуация схематически показана на рис. 8. Мальчик изображён прямогольником.

Рис. 8. К задаче

Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.

Стало быть, система, которую образуют мальчик и камень, не замкнута. Почему? Дело в том, что векторная сумма внешних сил не равна нулю во время броска. Величина больше, чем сумма , и за счёт этого превышения как раз и появляется вертикальная компонента импульса системы.

Однако внешние силы действуют только по вертикали (трения нет). Стало быть, сохраняется проекция импульса на горизонтальную ось . До броска эта проекция была равна нулю. Направляя ось в сторону броска (так что мальчик поехал в направлении отрицательной полуоси), получим:

,

откуда

.

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:

s′ = s₁ + s₂

s′ — перемещение МТ относительно НСО, s₁— перемещение МТ относительно ПСО, s₂ — перемещение ПСО относительно НСО.

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ + s₂

• Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ – s₂

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = √(s₁² + s₂²)

• Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s₁=0, перемещение s′ = s₂
• Если тело движется относительно двух НСО, то его перемещение относительно НСО₁ равно перемещению движения относительно НСО₂. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s₂=0, перемещение s′ = s₁

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

s′=|s₁ – s₂|=|10 – 2|=8 (м).

Относительность скорости в ПСО и НСО

Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:

v′ = v + u

v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v + u

• Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v – u

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = √(v² + u²)

• Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
• Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u

Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

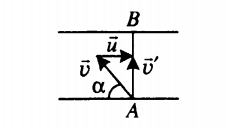
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v_отн = v₁– v₂

v_отн — относительная скорость, или скорость первого тела относительно второго, v₁ и v₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

• v₁₂ — скорость первого тела относительно второго. Ее проекция равна:

v_12x = v_1x – v_2x

• v₂₁ — скорость второго тела относительно первого. Ее проекция равна v_21x = v_2x – v_1x

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Полезные факты

• Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:

v_отн = |v₁ – v₂|

• Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:

v_отн = |v₁ + v₂|

• Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:

v_отн = √(v₁² + v₂²)

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .

Сложение двух сонаправленных векторов
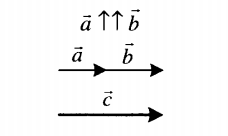	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
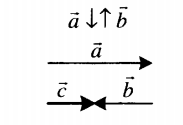	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
Сложение двух векторов, расположенных друг к другу под углом
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
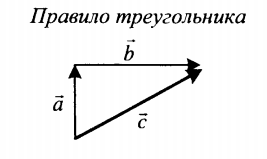	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .
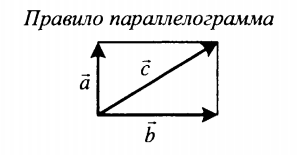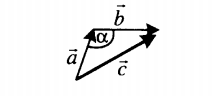	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .
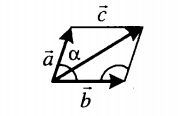	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .

Правила вычитания векторов

Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Вычитание двух сонаправленных векторов
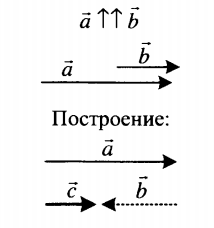	Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|.
Вычитание двух противоположно направленных векторов
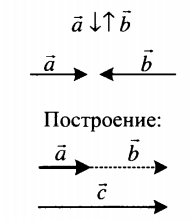	Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b.
Вычитание двух векторов, расположенных друг к другу под углом
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
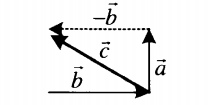	Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: .
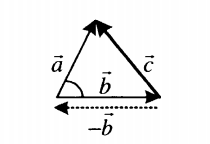	Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: .

Алиса Никитина | Просмотров: 7.3k

Динамика: движения системы связанных тел. 

Проецирование сил нескольких объектов.

Действие второго закона Ньютона на тела, которые скреплены нитью 

---

Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.

А для тех, кто все помнит, поехали!

Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?

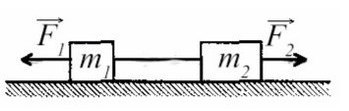
Движение происходит только на оси X. 

Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.

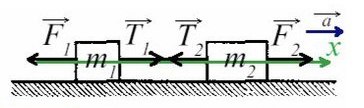
По II з. Ньютона спроецируем силы обоих тел на Ох:

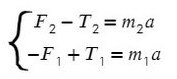
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T₁ и Т₂.

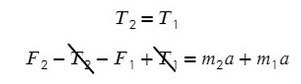
Выразим ускорение:

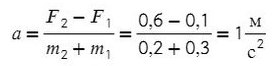
Ответ: 1 м/с²

Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.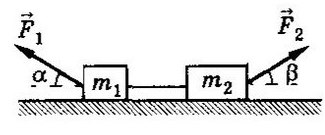

Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).

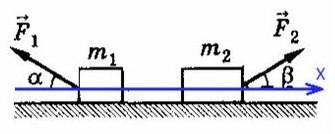
По II з. Ньютона спроецируем силы обоих тел на Ох:

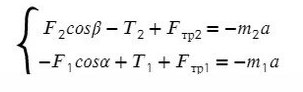
Сложим уравнения и выразим ускорение:

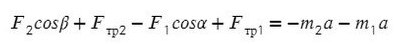
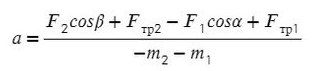
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:

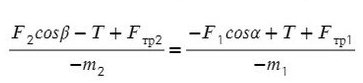
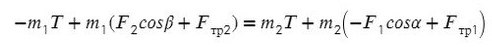
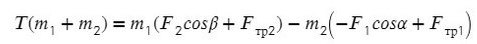
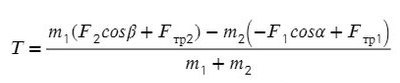
Задача 3. Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения? 

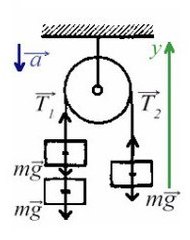
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.

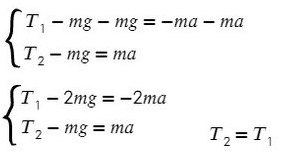
Вычтем из первого уравнения второе:

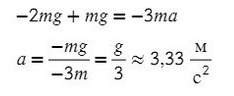
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:

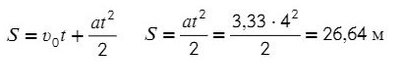
Ответ: 26,64 м

Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.

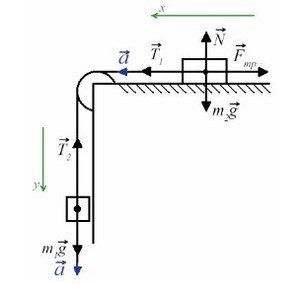
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):

(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)

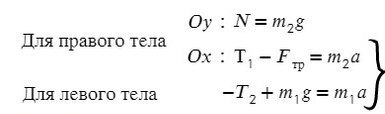
Сложим два нижних уравнения для того, чтобы T сократилось:

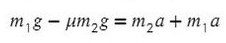
Выразим ускорение:

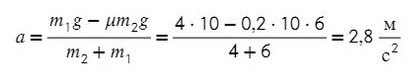
Ответ: 2,8 м/с²

Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?

Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.

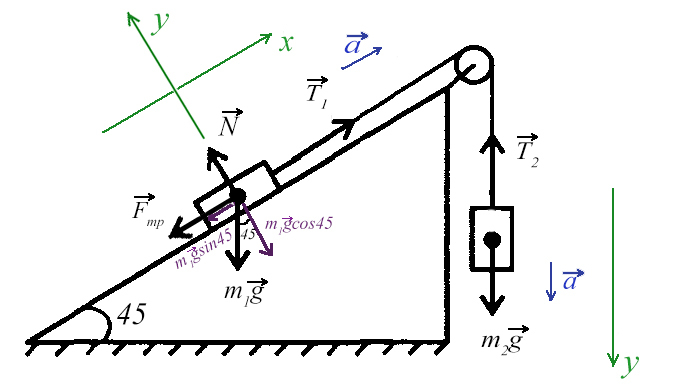
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):

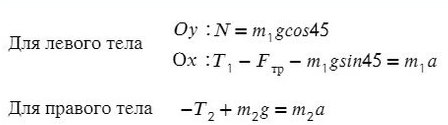
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:

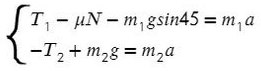
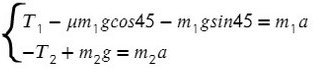
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:

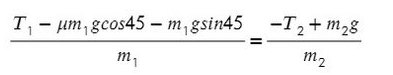
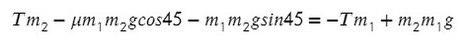
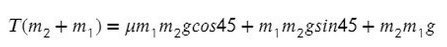
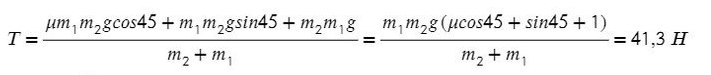
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:

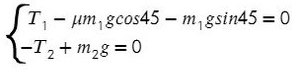
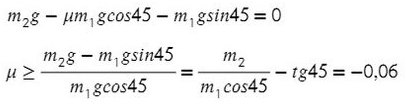
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.

Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.

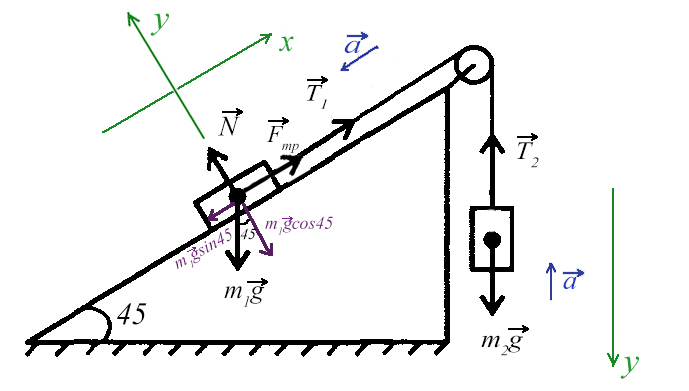
Ответ: 0,06

Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1.  Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.

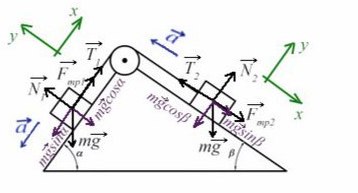
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:

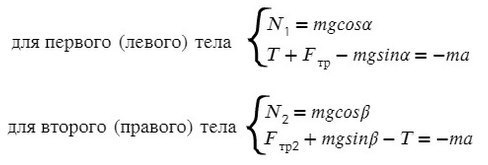
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:

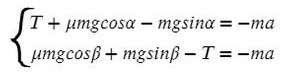
Сложим уравнения и сократим на массу:

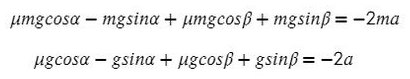
Выразим ускорение:

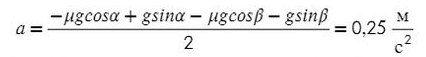
Подставив в любое уравнение найденное ускорение, найдем Т:

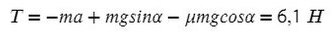А теперь одолеем последний пункт и разберемся с соотношением масс. Сумма всех сил, действующих на любое из тел, равна нулю для того, чтобы система находилась в равновесии:

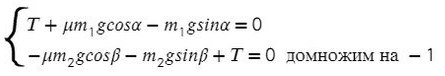
Сложим уравнения

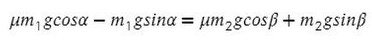
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:

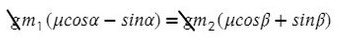
Получили, что отношение масс должно быть таким:

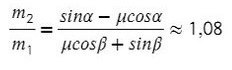
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:

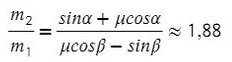
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.

У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.

В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.

Ответ: от 1,08 до 1,88

Задачи для закрепления.
Система связанных тел.

Будь в курсе новых статеек, видео и легкого технического юмора.