Как найти скорость скатывающегося цилиндра - Сайт, где вы сможете решить свои вопросы

Рассмотрим задачу на динамику твердого тела, которую будет удобно решать с помощью законов сохранения энергии.

Скорость цилиндра при скатывании с наклонной плоскости

Задача:

В задаче есть опечатка! Скорость у склона горки забыли добавить.

Решение:

Сделаем схематический рисунок.

Запишем закон изменения энергии в самом общем виде-изменение механической энергии равно работе неконсервативных сил.

Закон изменения энергии, который часто упускают в школьной программе

Что такое “работа” мы все знаем-это скалярное произведение векторов силы и перемещения. Но возникает вопрос какие силы называются неконсервативными?

Неконсервативными мы называем силы, работа которых не зависит от траектории.

Какие же это силы? А это все силы, кроме тяжести, электрической силы и силы упругости. Если будет интересно, почему, пишите в комментарии, я сделаю об этом отдельный пост.

Рассмотрим работу каждой из действующих сил, а именно работу силы тяжести, силы трения и силы реакции опоры.

Работа силы реакции опоры.

Распишем работы силы по определению. Мы видим, что угол между этими векторами равен 90 градусов, а значит работа зануляется.

Как мы видим работа силы реакции опоры равна нулю!

Работа силы тяжести.

Сила тяжести является консервативной силой. То есть ее работа не зависит от траектории. А значит мы е просто не учитываем. Кстати, сможете доказать, что сила тяжести является консервативной силой?

Сила трения же в нашем случае является силой трения покоя (почему?) и ее работа равна нулю (почему?). Ваши предложения и ответы пишите в комментарии.

Таким образом, мы получили, что изменение полной механической энергии равно нулю.

Зануляем правую часть и получаем уже закон сохранения энергии

Учтем кинетическую энергию вращения:

Закон сохранения энергии с учетом вращения цилиндра

Момент инерции берем из таблицы.

Второе слагаемое записано для центра масс, а значит и момент инерции мы должны взять именно относительно центра масс!

Таким образом, получаем уравнение, сокращаем массу и находим ответ:

Вопросы по задаче пишите в комментариях или мне в сообщения. Также жду задач на разбор!

Источник

Динамика и кинематика – это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

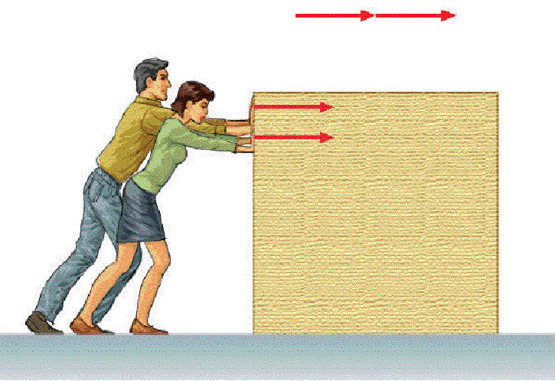
Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r – радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

тяжести;
реакции опоры;
трения качения и/или скольжения;
натяжение нити;
сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a

Здесь φ – это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) – F_r= m*a

Где F_r – сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

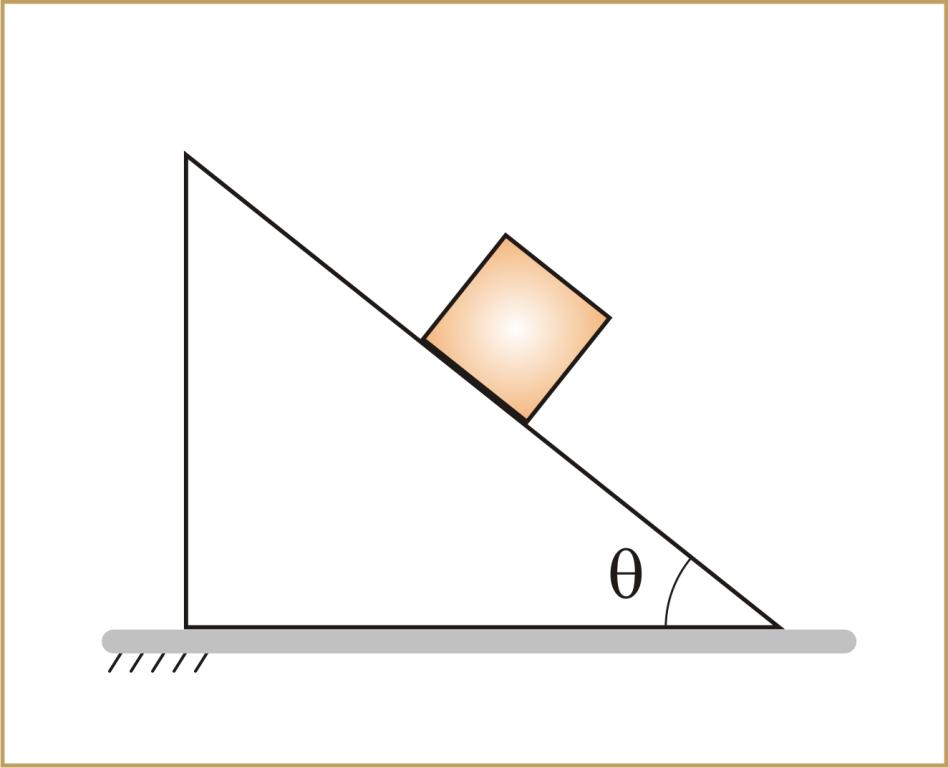
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) – µ*cos(φ)) = m*a =>

a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

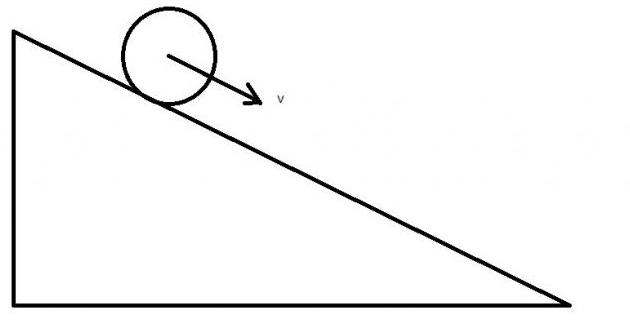
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) – F_r= m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) – 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Источник

Скатывание цилиндра с наклонной плоскости

Пусть
цилиндр радиуса

скатывается
без скольжения по наклонной плоскости.
Ось x
удобно выбрать вдоль наклонной плоскости.
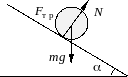
На цилиндр действуют сила тяжести

,
сила трения

и сила реакции опоры

.
Уравнения движения для цилиндра имеют
вид

Учитывая,
что

,
а

,
получим

или

,

.

Таким
образом, цилиндр скатывается с постоянным
ускорением, величина которого зависит
от угла наклона .

2.9. Движение твердого тела, закрепленого в точке

В
общем случае движения вектор угловой
скорости изменяет свое направление в
пространстве и свою ориентировку
относительно тела, то есть мгновенная
ось вращения меняет свою ориентировку.
Удобно рассматривать это движение в
системе координат, жестко связанной с
телом. Начало координат естественно
поместить в точку закрепления тела. Она
находится в покое. Получающиеся при
этом уравнения движения называются
уравнениями Эйлера.

Уравнение
движения центра масс тела имеет вид

, (2.16)

где

–
радиус-вектор центра масс тела, проведенный
из точки его закрепления

Оси
связанной с телом системы координат

удобно направить по главным осям инерции.
В этом случае тензор инерции сводится
к трем своим главным значениям

а момент импульса приобретает простой
вид:

,

,

,
причем

,

,

–
проекции угловой скорости на движущиеся
вместе с телом оси координат. В уравнении
моментов производная

вычисляется относительно инерциальной
системы координат. Необходимо определить
эту величину относительно движущейся
системы координат, жестко связанной с
телом.

Пусть
некоторый вектор

задан компонентами относительно системы
координат

:

где

–
единичные орты связанной с телом системы
координат. С течением времени изменяются
проекции

на движущиеся оси координат и ориентировка
осей координат относительно инерциальной
системы отсчета. Имеем

. (2.17)

Скорость
точки вращающегося тела, радиус-вектор
которой

,
равна

.
Аналогично, следя за концом вектора

,
проведенным из точки на оси вращения,
находим

.
Такой же вид имеют производные от

и

.
Следовательно,

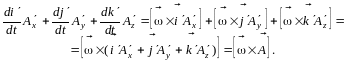
Поэтому
формула (2.17) может быть записана в виде

где

– производная от

,
вычисленная в предположении, что оси

неподвижны. Эта формула справедлива
для любых векторов

.
Применяя ее к вектору

в уравнении моментов, можно представить
уравнение моментов следующим образом:

. (2.18)

Принимая
во внимание, что

,

,

,
уравнение (2.18) перепишем в проекциях на
оси движущейся системы координат:

, (2.19)

Подчеркнем
еще раз, что все величины в этих уравнениях
отнесены к движущимся осям координат,
жестко связанных с телом, штрихи же не
проставлены лишь для упрощения написания
формул.

Эти
уравнения называют уравнениями Эйлера.
Они в принципе всегда позволяют
определить движение тела, закрепленного
в одной точке, хотя практически решение
может быть весьма сложным и трудно
выполнимым.

2.10. Свободные оси

Допустим,
что твердое тело вращается вокруг
закрепленной оси, например оси, проходящей
через неподвижные подшипники. Со стороны
подшипников на тело действуют силы
реакции. Их момент относительно оси
равен нулю. Предположим, что других сил
нет, поэтому моменты сил

равны нулю.

Примем
за начало системы координат центр масс,
а оси системы координат, жестко связанной
с телом, направим по центральным главным
осям. Моменты инерции

в этом случае являются центральными
главными моментами инерции тела. Уберем
подшипники и выясним, при каких условиях
движение тела не изменится, то есть
останется вращением вокруг выбранной
оси. Ось вращения, сохраняющая направление
в пространстве неизменным без воздействия
извне, называется свободной осью.

Из
(2.19) непосредственно следует, что
невозможно такое свободное вращение
тела, при котором угловая скорость
сохраняет свое абсолютное значение и
ориентировку относительно тела, но не
совпадает по направлению ни с одной из
центральных главных осей с разными
моментами инерции. Допустим, что это
возможно, то есть, что

,

,

.
Тогда из уравнений следует, что должно
быть

,

,

. (2.20)

Эти
соотношения можно одновременно
удовлетворить только в том случае, если
две проекции угловой скорости одновременно
равны нулю. А это означает, что угловая
скорость совпадает по направлению с
одной из центральных главных осей.
Пусть, например,

.
Тогда соотношения (2.20) будут удовлетворены.
Угловая скорость при этом направлена
вдоль оси X,
то есть вдоль центральной главной оси.

Таким
образом, свободное вращение твердого
тела возможно лишь вокруг центральных
главных осей. Эти оси и называются
свободными. Моменты инерции
относительно этих осей, вообще говоря,
различны. Можно доказать, что вращение
тела будет устойчивым только относительно
центральной главной оси с максимальным
или минимальным моментом инерции.
Вращение вокруг центральной главной
оси со средним моментом инерции
неустойчиво. При небольшом случайном
отклонении оси вращения от этого
направления возникают силы, увеличивающие
отклонение. Это обстоятельство можно
наглядно продемонстрировать на таком
опыте. У тела в виде прямоугольного
параллелепипеда центральными главными
осями являются три взаимно перпендикулярные
оси, проходящие через его геометрический
центр параллельно сторонам. Параллелепипед
имеет наибольшие и наименьшие моменты
инерции относительно осей, параллельных
его самой длинной и самой короткой
сторонам. Если его подбросить с
одновременным вращением вокруг одной
из этих осей, то движение происходит
устойчиво с сохранением направления
оси вращения. Если же его вращать вокруг
оси, параллельной средней стороне, то
устойчивого движения не получается и
тело начинает беспорядочно кувыркаться.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Отчёт по лабораторной работе №3-I. Расчёт и измерение скорости сплошного цилиндра, скатывающегося с наклонной плоскости

Главная > Отчет

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Отчёт по лабораторной работе № 3-I.

Расчёт и измерение скорости сплошного цилиндра, скатывающегося с наклонной плоскости.

Цель работы : рассчитать кинематические характеристики движения цилиндра v , a ,  , скатывающегося по наклонной плоскости. Результаты расчёта проверить экспериментально.

Оборудование: штатив, наклонная плоскость, линейки ученическая и демонстрационная, штангенциркуль, секундомер(0,2с), упор.

Устанавливаем доску в наклонном положении с минимальным углом наклона. Измеряем высоту наклонной плоскости h .

Рассчитываем теоретическую скорость скатывания цилиндра .

Измеряем длину наклонной плоскости l и время скатывания t .

Рассчитываем скорость цилиндра в конце наклонной плоскости . Проделываем пункты 1-4 не менее 4-х раз при разных высотах h .

Рассчитываем теоретически ускорение центра масс и угловое ускорение цилиндра .

Рассчитываем те же величины по экспериментальным данным.

Строим теоретический и экспериментальный график.

Рассчитываем погрешности, делаем вывод.

1. Цилиндр едет без проскальзывания.

2. Цилиндр геометрически правильной формы.

3. Поверхность ровная (на используемой нами доске был довольно большой сучок).

4. Нет трения качения.

5. На больших высотах (при больших скоростях) сложно точно измерить время.

Задача 24107 Запишите уравнение движения и уравнение.

Условие

Запишите уравнение движения и уравнение моментов для цилиндра, скатывающегося без проскальзывания с наклонной плоскости с углом альфа. Определите ускорение его центра масс.

Решение

Ответ: В решение

Момент силы (в векторном виде) по определению равен векторному произведению радиус-вектора на силу (М=[r,F], жирным шрифтом нередко в литературе обозначаются векторы) . Модуль этого векторного произведения равен r*F*sin(a), где а – угол между векторами r и F. Чему равны r, F И sin(a) для силы реакции опоры и силы тяжести? поиогите, пж.

Движение по наклонной плоскости тела: скорость, трение, время

Основная формула динамики

В случае движения вращения второй закон Ньютона записывается в виде:

Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.

Формулы кинематики

Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

Здесь r – радиус вращения.

Движение по наклонной плоскости: силы

тяжести;
реакции опоры;
трения качения и/или скольжения;
натяжение нити;
сила внешней тяги.

Методика решения

Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.

Здесь φ – это угол наклона плоскости к горизонту.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45 o . Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с 2

Откуда следует выразить время, и подставить известные значения:

Задача со скатывающимся по плоскости цилиндром

Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30 o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

Момент инерции I цилиндра вычисляется по формуле:

m*g*sin(φ) – 1/2*m*a = m*a =>

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

[spoiler title=”источники:”]

http://reshimvse.com/zadacha.php?id=24107

http://fb.ru/article/443466/dvijenie-po-naklonnoy-ploskosti-tela-skorost-trenie-vremya

[/spoiler]

Источник

Решение.
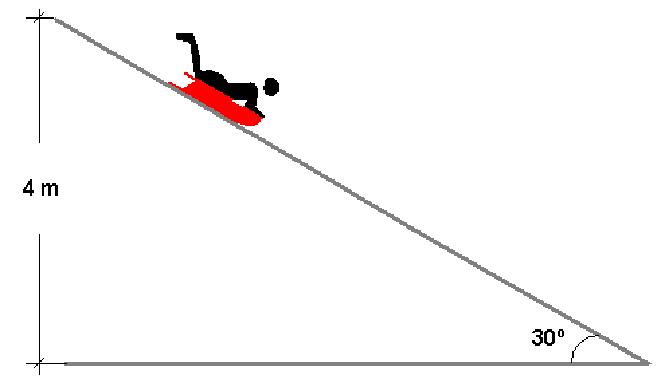
Для решения задачи используем закон сохранения энергии. Потенциальная энергия переходит в кинетическую энергию. Кинетическая энергия состоит из энергии поступательного движения и энергии вращательного движения.

[ mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{Jcdot {{omega }^{2}}}{2} (1). ]

m – масса сплошного цилиндра, h – высота с которой спускается тело (см. рис.), υ – линейная скорость тела в конце спуска, J – момент инерции сплошного цилиндра, ω – угловая скорость вращения тела.
В конце спуска угловая скорость связана с линейной скоростью:

[ omega =frac{upsilon }{R} (2). ]

Определим скорость центра масс поступательного движения сплошного цилиндра. Момент инерции сплошного цилиндра определяется как момент инерции диска по формуле:

[ J=frac{mcdot {{R}^{2}}}{2} (3). ]

Подставим (3) и (2) в (1):

[ begin{align}
& mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{mcdot {{R}^{2}}cdot {{upsilon }^{2}}}{4cdot {{R}^{2}}}, gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{mcdot {{upsilon }^{2}}}{4}, gcdot h=frac{3cdot mcdot {{upsilon }^{2}}}{4}, \
& {{upsilon }^{2}}=frac{4cdot gcdot h}{3}, upsilon =sqrt{frac{4cdot gcdot h}{3}} (4). \
end{align} ]

υ = 1,63 м/с.

Источник

Основная формула динамики

Формулы кинематики

Движение по наклонной плоскости: силы

Методика решения

Задача на движение бруска по наклонной плоскости

Задача со скатывающимся по плоскости цилиндром

Скатывание цилиндра с наклонной плоскости

2.9. Движение твердого тела, закрепленого в точке

2.10. Свободные оси

Отчёт по лабораторной работе №3-I. Расчёт и измерение скорости сплошного цилиндра, скатывающегося с наклонной плоскости

Главная > Отчет

Задача 24107 Запишите уравнение движения и уравнение.

Условие

Решение

Движение по наклонной плоскости тела: скорость, трение, время

Основная формула динамики

Формулы кинематики

Движение по наклонной плоскости: силы

Методика решения

Задача на движение бруска по наклонной плоскости

Задача со скатывающимся по плоскости цилиндром

Вам также может понравиться

Как найти родственников в таджикистане

Как найти технический результат

Площадь квадрата 36см как найти

Добавить комментарий Отменить ответ