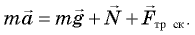Как найти скорость скольжения бруска

Цель этой
работы: с помощью экспериментальной установки определить среднюю
скорость скольжения бруска по наклонной плоскости.

Для выполнения этой работы мы будем использовать оборудование
из комплекта № 5 в составе: штатив с креплением для наклонной плоскости,
направляющая со шкалой, деревянный брусок с пусковым магнитом, электронный
секундомер с датчиками, три груза, массой по сто граммов каждый, линейка и
транспортир.

Прежде чем приступить к работе давайте с вами вспомним, что
механические явления являются одними из самых распространённых физических
явлений в мире. И чаще всего в повседневной жизни мы сталкиваемся с таким
явлением, как неравномерное движение.

Напомним, что неравномерное движение — это такое
движение, при котором тело, за любые равные промежутки времени совершает разные
перемещения.

Для описания быстроты изменения положения тела с течением
времени при неравномерном движении, вводится понятие средней скорости. Она
показывает, какое перемещение в среднем совершало тело за единицу времени:

Но пользоваться этой формулой для определения модуля средней
скорости можно лишь в том случае, если тело движется вдоль прямой в одну
сторону. Во всех остальных случаях эта формула не работает.

Поэтому на практике пользуются понятием средней путевой
скорости, с которым вы знакомы ещё с седьмого класса. Напомним, что средняя
путевая скорость определяется отношением пути к промежутку времени, за
который этот путь пройден:

Именно среднюю скорость движения тела нам и предстоит
определить в данной работе. Ну что ж, приступим.

Для начала
давайте соберём экспериментальную установку. Для этого на штативе закрепим
наклонную плоскость. После этого, используя транспортир, установим направляющую
под углом 30° к поверхности стола.

Далее
установим на направляющей датчики секундомера: первый расположим в точке 0, а
второй — в точке 40 см. При пуске бруска пусковой магнит мы установим на 0,5 см
выше первого датчика. Грузы закрепим на бруске.

Далее мы
сделаем рисунок нашей установки. Для этого схематически изобразим штатив с
прикреплённой к нему направляющей. На направляющей расположим брусок так, как
это показано на экране. Также на рисунке мы должны будем указать перемещение
тела и направление вектора ускорения. Не лишним будет показать и угол, под
которым установлена направляющая.

Запишем формулы, которыми будем пользоваться при выполнении
данной работы. Она у нас одна: средняя скорость равна отношению пути к
промежутку времени, за который этот путь пройден:

С формулой разобрались, теперь запишем результат измерения
пути, пройденного бруском, с учётом абсолютной погрешности измерения (путь нам
дан в условии задания):

Теперь приступим непосредственно к выполнению работы. Итак,
подключаем электронные датчики к секундомеру, а брусок устанавливаем так, чтобы
пусковой магнит находился на пол сантиметра выше первого датчика. Отпускаем
брусок.

Значение промежутка времени, за которое брусок преодолел
заданный отрезок пути, записываем в бланке ответов с учётом погрешности
измерения:

Опыт повторяем ещё два раза, каждый раз записывая результаты
измерений.

Прямы измерения мы с вами завершили. Теперь давайте определим
среднее значение промежутка времени. Для этого мы должны сложить результаты
наших экспериментов, а сумму разделить на количество экспериментов (в нашем
случае на 3):

Найденное среднее значение времени мы должны записать также с
учётом погрешности измерения:

И, наконец, мы определяем среднюю скорость скольжения бруска.
Для чего в расчётную формулу подставляем значения пути и среднего времени
движения бруска на этом отрезке пути:

Тогда в выводе можно написать: средняя скорость
движения бруска по наклонной плоскости составляет 0,27 м/с.

Динамика и кинематика – это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀ ± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀ ± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r – радиус вращения.

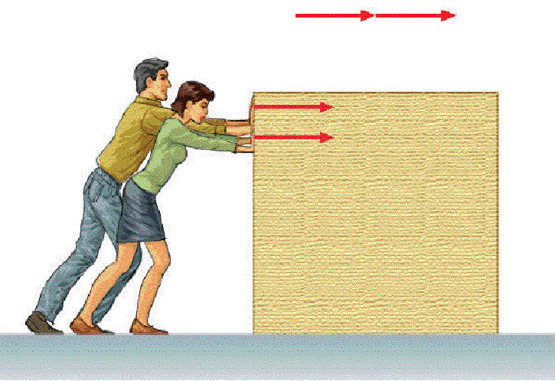
Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a

Здесь φ – это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) – F_r = m*a

Где F_r – сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

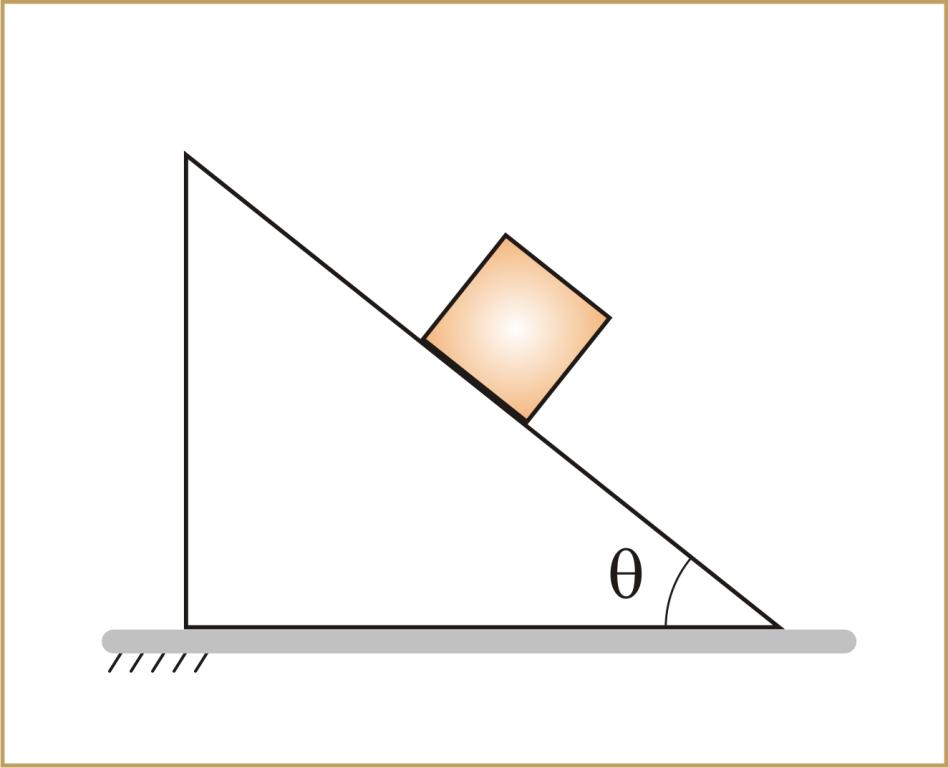
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) – µ*cos(φ)) = m*a =>

a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

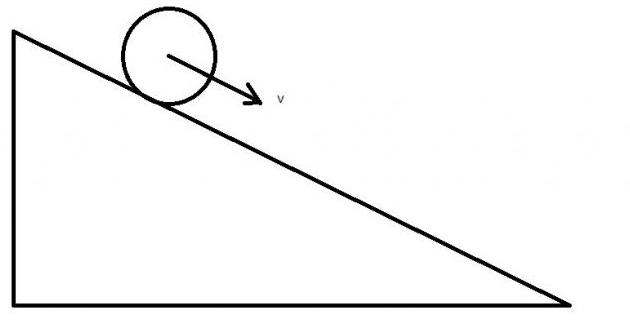
Задача со скатывающимся по плоскости цилиндром

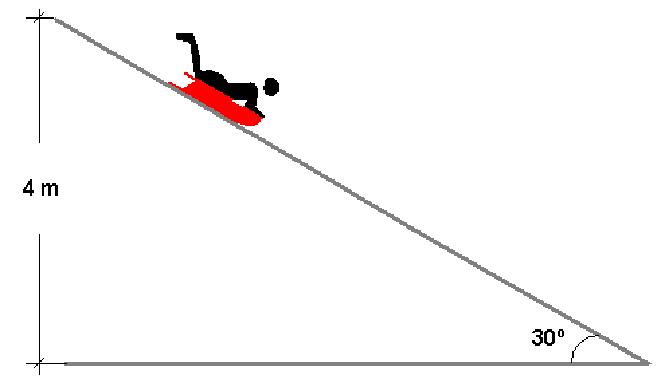
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) – F_r = m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) – 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com



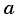
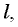
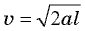
Чтобы ответить на поставленный вопрос, надо определить сначала, с каким ускорением будет двигаться брусок вдоль наклонной плоскости. Зная ускорение и пройденный путь можно будет найти скорость бруска в конце спуска, воспользовавшись уже выведенной нами формулой для равноускоренного движения (см. § 3. Ускорение. Прямолинейное равноускоренное движение).

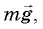
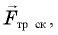
На брусок, скользящий по наклонной плоскости, действуют три силы: сила тяжести сила нормальной реакции и сила трения скольжения направленная вдоль наклонной плоскости вверх.

Чтобы найти ускорение тела, надо воспользоваться вторым законом Ньютона

Выбирая оси координат так же, как в рассмотренном выше примере, получаем:

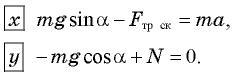
Кроме того, выполняется соотношение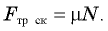

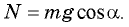
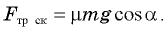
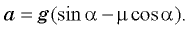
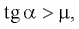
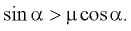
Из второго уравнения системы следует, что Обратите внимание: для тела, находящегося на наклонной плоскости, сила нормальной реакции меньше силы тяжести. Отсюда следует, что Подставляя это соотношение в первое уравнение системы, находим, что ускорение бруска Мы можем быть уверены в том, что это величина положительная, поскольку, согласно условию, брусок начал соскальзывать с наклонной плоскости — а это означает, в соответствии с предыдущим примером, что то есть

Подставляя найденное выражение для ускорения в формулу для скорости в конце спуска, получаем

Механика.
2014

 

Физика — наука экспериментальная. Любую физическую величину можно измерить.

Первым учёным, проводившим измерения физических величин для изучения механического движения, был Галилео Галилей (рубеж XVI и XVII веков). До Галилея изучение природы было чисто философским, никаких измерений не проводилось.

Механическое движение — это изменение положения тела с течением времени. Точных приборов для измерения времени во времена Галилея ещё не было. По часам в XVI веке можно было измерять собственно часы, но не минуты и не секунды. Поэтому Галилей для измерения времени использовал собственный пульс.

Простейшим видом механического движения является прямолинейное равномерное движение. Но встречается оно в природе чрезвычайно редко. Гораздо чаще можно встретить неравномерное движение. Но, даже доказав, что движение не является равномерным, можно найти его среднюю скорость, что мы и проделаем в данной лабораторной работе.