Когда объект запускается, он следует параболическому пути и движению, известному как движение снаряда. В этом посте мы рассмотрим параметры и способы их расчета. движение снаряда в подробном анализе.
Когда объект запускается и движется по симметричной параболической траектории, движение называется движением снаряда, а параболический путь объекта называется его траекторией. В этом случае объект перемещается одновременно по вертикали и горизонтали. В результате движение снаряда становится двумерным. При движении снаряда вам нужно только приложить силу в начале траектории; после этого на объект действует только сила тяжести.
Теперь давайте посмотрим, как рассчитать движение снаряда:
Предположим, вы стреляете пушечным ядром. Он начинает двигаться вверх и вперед, пока не достигнет максимальной высоты. С этого момента он будет продолжать двигаться вперед, но в нисходящем направлении. Он отслеживает этот изогнутый маршрут, известный как траектория, имеющая форму параболы. Любой объект, движущийся таким образом, называется движущимся снарядом. Поскольку траектория движения снаряда всегда параболическая, она представляется как:
у = ах + bx2
Прежде чем достичь Земли, пушечное ядро во время своего путешествия пойдет по параболическому маршруту. Компания скорость по оси X остается постоянной на протяжении всего движения, тогда как скорость по оси Y изменяется в зависимости от его положения. Только ускорение свободного падения 9.8 м / с2, управляет этим типом движения. Ускорение, направленное вниз, остается постоянным во время полета ядер.
Кинематические уравнения движения снаряда:
Формула начальной скорости:
Предположим, что начальная скорость равна u, а угол полета снаряда равен. У начальной скорости есть две составляющие: горизонтальная и вертикальная.
Горизонтальная составляющая начальной скорости ux и предоставлено:
ux = ты ᐧ потому что𝛳
Вертикальная составляющая начальной скорости равна uy и определяется выражением:
uy = и ᐧ грех

Время полета снаряда:
Время полета снаряда – это промежуток времени между запускаемым объектом и достижением земли. Величина стартовой скорости и угол полета снаряда определяют время полета, которое обозначается T.
Формула ускорения:
В горизонтальном направлении ускорение отсутствует, поскольку горизонтальная составляющая ускорения остается постоянной на протяжении всего движения. Единственное ускорение в вертикальном направлении происходит за счет силы тяжести.
ax = 0 и
ay = -г
Отрицательный знак означает ускорение вниз.
Формула скорости в момент времени t:
На протяжении всего движения горизонтальная составляющая скорости остается постоянной. Однако, поскольку вертикальное ускорение постоянно, вертикальная составляющая скорости изменяется линейно.
В результате скорость может быть рассчитана в любой момент времени t по следующей формуле:
vx = тыx = ты ᐧ потому что𝛳
vy = u ᐧ sin𝛳 – g ᐧ t
Используя теорему Пифагора, можно найти величину скорости.
Формула смещения в момент времени t:
В момент времени t смещение может быть определено как:
х = (и ᐧ cos𝛳) ᐧ т
y = (u ᐧ sin𝛳) ᐧ t – ½ (gt2)
Формула параболической траектории:
Мы можем использовать уравнения смещения в направлениях x и y, чтобы вывести уравнение для параболической формы движения снаряда:
Формула дальности снаряда:
Общее горизонтальное расстояние, пройденное объектом за время полета, определяется как его дальность. Если объект запускается с земли (начальная высота = 0), формула выглядит следующим образом:
Согласно приведенному выше уравнению, максимальная дальность полета по горизонтали может быть получена при угле полета снаряда 𝛳 = 45 °. Rm представляет собой максимальный диапазон.
Формула максимальной высоты:
Когда вертикаль составляющая скорости равна нулю, vy = 0, максимальная высота может быть достигнута. Поскольку время полета – это полное время снаряда, для достижения максимальной высоты потребуется половина этого времени. Таким образом, время для достижения максимальной высоты составляет:
Таким образом, из уравнения перемещения максимальная высота может быть определена как:
Формула движения снаряда по горизонтали:
Горизонтальный снаряд Движение – это тип движения снаряда, при котором объект запускается горизонтально с возвышенной плоскости, а не с земли.

Угол запуска указывать не нужно, поскольку он параллелен земле (т. Е. Угол равен 0 °). В результате у нас есть только одна начальная составляющая скорости: Vx = V, тогда как Vy = 0.
В этом случае уравнения движения следующие:
Скорость горизонтального движения снаряда:
Горизонтальная скорость: vx = V
И вертикальная скорость: vx = -g ᐧ т
Расстояние, пройденное объектом при горизонтальном движении снаряда:
В этом случае горизонтальное расстояние рассчитывается следующим образом:
х = v ᐧ т
А расстояние по вертикали можно определить как:
y = – (g ᐧ t2) / 2
Ускорение при горизонтальном движении снаряда:
Горизонтальное ускорение ax = 0, так как горизонтальная скорость постоянна..
Вертикальное ускорение аy = -г
Уравнение траектории горизонтального движения снаряда:
Уравнение траектории в этом случае может быть задано следующим образом:
Время полета при горизонтальном движении снаряда:
Время полета в этом случае может быть определено как:
Дальность полета снаряда при горизонтальном движении снаряда:
Дальность полета снаряда при горизонтальном движении снаряда составляет:
Поскольку мы запускаем объект с максимальной высоты, нам не нужно рассчитывать максимальную высоту в этом сценарии.
Давайте посмотрим на некоторые проблемы движения снаряда.
Проблема 1: Каким будет θmax, при котором расстояние от частицы до метателя всегда увеличивается до конца пути снова у земли?
Решение: Горизонтальное расстояние, пройденное объектом, называется его горизонтальным диапазоном и определяется по формуле:
Максимальная дальность полета может быть достигнута при угле выстрела 45 °.
Таким образом, для максимального угла Rm θmax = 45 °.
Задача 2: Если мяч брошен вертикально вверх со скоростью u, расстояние, пройденное за последние t секунд его всплытия, будет:
Решение: Поскольку мяч брошен вертикально, угол полета снаряда 𝛳 = 90 °.
Поскольку 𝛳 = 90 °
Где Tm – время, необходимое объекту для достижения максимальной высоты.
Предположим, что h представляет собой расстояние, пройденное объектом за последние t секунд его подъема. Затем скорость в этот момент рассчитывается следующим образом:
V = u – g ᐧ (T – t)
= u – g ᐧ (u / g – t)
= гт
Таким образом, расстояние, пройденное за последнюю t секунду, составляет:
h = vt – ½ gt2
= гт2 – ½ гт2
= ½ гт2
3 задачи: Частица проецируется под углом 60 ° над горизонтом со скоростью 10 м / с. Через некоторое время скорость составит угол 30 ° от горизонтали. Скорость частицы в этот момент составляет?
Решение: Горизонтальная составляющая скорости определяется как:
vx = ты ᐧ потому что𝛳
Здесь в первом случае угол проекции составляет 60 °, а начальная скорость u = 10 м / с. Таким образом,
vx = ты ᐧ cos60
= 10 x 0.5
= 5 м / с.
Теперь вертикальная составляющая скорости vy изменяется во время движения, но vx остается постоянным. Таким образом,
vx = v ᐧ cos𝛳2
Где 𝛳2 = 30 °, а v – скорость, когда объект составляет угол 𝛳 = 30 ° с горизонтом.
|
Как найти начальную скорость пули игрушечного пистолета, пользуясь только рулеткой? При выстреле 1) вертикально вверх и 2) горизонтально поверхности земли. Сопротивлением воздуха пренебречь, что допустимо при малых скоростях движения.
Если сопротивление воздуха не учитывать, то при стрельбе вверх скорость считтать по формуле равенства кинетической и потенциальной энергий V^2=2*g*H (V – начальная скорость, g – 9.8, H – высота верхней точки траектории пули). При горизонтальной V=S/sqrt(2h/g) (S – расстояние от ствола до места падения пули, h – высота ствола над поверхностью). автор вопроса выбрал этот ответ лучшим Михаил Белодедов 9 лет назад 1) sqrt(2gh), где g – ускорение свободного падения, h – высота подьема над точкой старта. 2) s*sqrt(g/(2h)), где g – ускорение свободного падения, h – высота старта, s – пройденный путь до приземления. Только это не на смекалку, это обычные школьные задачи. bezdelnik 9 лет назад Задача на смекалку проста. Кинетическая энергия пули в момент выстрела вверх Ек =(mV^2)/2 будет равна потенциальной энергии пули на высоте взлета Еп = mgH. Отсюда начальная скорость пули V = √2gH. Например при высоте взлета 10 м начальная скорость V = √(2*981*10)= 14 м/c. При выстреле горизонтально начальная скорость будет такой же – винтовка и пуля одинаковые. Знаете ответ? |
6
Лабораторная
работа № 106
Определение скорости
снаряда с помощью баллистического
маятника
Приборы
и принадлежности: прибор
FРМ
– 09, снаряды, вес, штангенциркуль.
Цель
работы: определение скорости пули.
Введение:
Использование баллистического маятника
для измерения скорости снаряда основано
на том, что баллистический отброс (первое
наибольшее отклонение маятника)
пропорционален импульсу снаряда, если
в момент удара снаряда о маятник последний
остается неподвижным. Характерной
особенностью баллистического маятника
является его большой момент инерции и,
следовательно, большой период собственных
колебаний. Если время соударения снаряда
с маятником мало по сравнению с периодом
Т колебаний маятника, то он не успевает
заметно отклониться от исходного
положения за время соударения. Это
значит, что во время удара не возникает
силы, стремящейся вернуть маятник в
исходное положение. В таком случае
систему снаряд-маятник можно рассматривать
как замкнутую и применять к ней закон
сохранения момента импульса
Основным
элементом лабораторной установки
является крутильный маятник (рис.1). При
попадании в него выпущенного стреляющим
устройством снаряда маятник начинает
вращаться вокруг вертикальной оси. Если
снаряд попал в мишень на расстоянии l
от оси
маятника, то на основании закона
сохранения момента импульса для замкнутой
системы снаряд – мишень можно написать
![]()
,


ℓ

φ










М
М


R


υ0



m
Рис.1.
Где
m
– масса снаряда, v
– ее скорость, J
– момент
инерции маятника , ![]()
– угловая скорость вращения маятника
сразу после удара, когда он находится
еще в положении равновесия. Закон
сохранения механической энергии маятника
после удара запишем в виде
![]()
![]()
Где
![]()
– модуль кручения проволоки,
![]()
– максимальное отклонение маятника.
Учитывая, что
![]()
из закона сохранения получим
![]() (1)
(1)![]()
В
это равенство входят неизвестные
![]()
и
![]()
,которые определяются с помощью
дополнительных опытов. Если не учитывать
момент сил трения, то уравнение свободного
движения крутильного маятника запишется
так:
![]() ,
,
Где
![]()
– угол отклонения маятника от положения
равновесия,
![]()
Это уравнение гармонических
колебаний с периодом
![]() (2)
(2)
Изменив
расположение грузов
![]()
![]()
М , мы получим колебания с другим
периодом, соответствующим моменту
инерции
![]()
,
![]()
![]() (3)
(3)
Пренебрегая
размерами грузов по сравнению с их
расстояниями
![]()
и
![]()
от оси вращения, запишем:
![]()
(4)
![]()
Здесь
![]()
– момент инерции маятника без грузов.
Исключив из системы (2) –(4)
![]()
,получим
![]() (5)
(5)
Модуль
кручения проволоки
![]()
найдем из равенства(2):
![]() (6)
(6)
После
подстановки (5) и (6) в (1) получим
![]()
![]() (7)
(7)
По
формуле (7) определяется скорость
снаряда, так как все величины в правой
части формулы могут быть непосредственно
измерены.
Описание
прибора.
Общий
вид баллистического маятника показан
на рис.2.Основание 1 оснащено регулируемыми
ножками 2 , которые позволяют выравнивать
прибор. В основании платформы закреплена
колонна 3 , на которой крепятся три
кронштейна 4 . К среднему кронштейну
прикреплено стреляющее устройство 5 ,
прозрачный цилиндр ( экран ) 6 с нанесенной
на нем угловой шкалой и фотоэлектрический
датчик 7. С помощью крайних кронштейнов
подвешен маятник, состоящий из двух
мисочек – мишеней 8., наполненных
пластилином , двух перемещаемых по
стержню 9 грузов 10. На основании 1
установлены электронные счетчик числа
колебаний и миллисекундомер.
Измерения.
-
Нажатием
клавиши «сеть» включить питающее
напряжение. При этом возникает свечение
цифровых индикаторов и лампочки
фотоэлектронного датчика. -
Поднять
цилиндр – экран 6 и повесить его на
верхний кронштейн. Установить грузы М
10 на
максимальное расстояние

от оси
маятника. Определить период колебаний
маятника. Для этого поворачивают маятник
на небольшой угол
 =
=
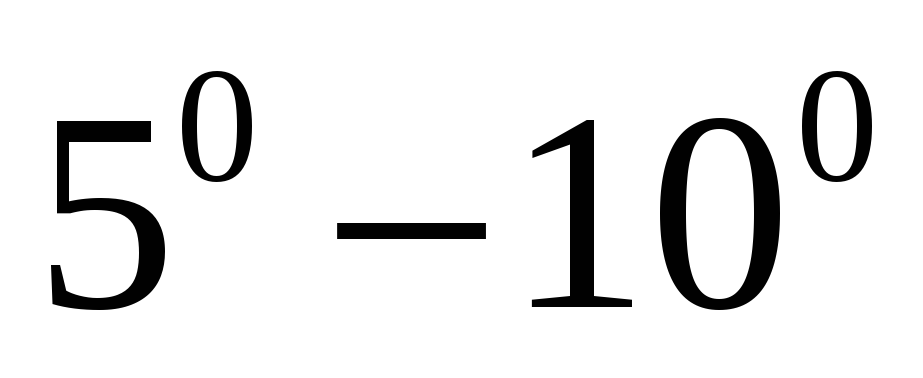
и отпускают. При помощи секундомера
измеряют время

10–20 полных колебаний маятника. Нажатием
клавиши «сброс» повторить измерения
5–10 раз. Определить величину периода

.Результаты
записать в таблицу №1. -
Установить
грузы М
на минимальное расстояние
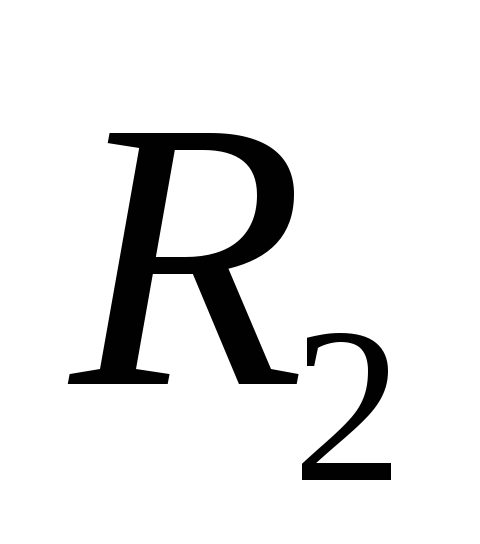
от оси маятника. Повторить п.2.Определить
величину
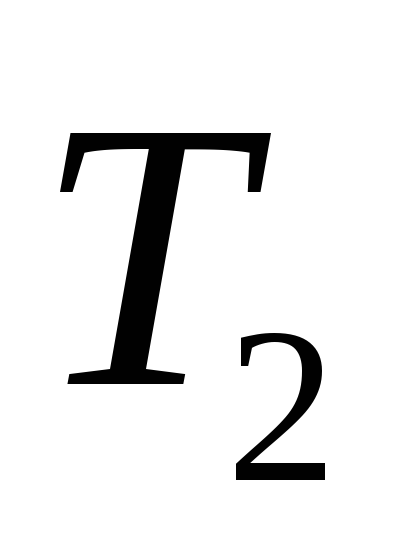
.Результаты записать в таблицу №1. -
Установить
маятник около нулевого деления шкалы
цилиндр – экрана 6.Определить массу
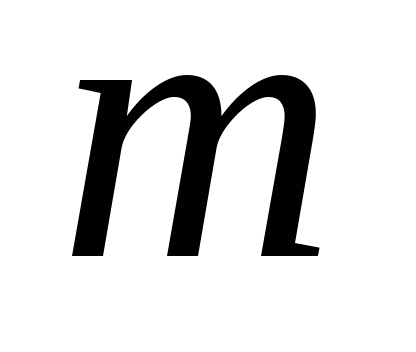
снаряда. Грузы М
располагают и закрепляют на равном
расстоянии как можно дальше от оси
вращения. С помощью рукояток стреляющего
устройства 5 сжать пружину 11 .Установить
снаряд 12 рис.2. Путем нажатия сверху
вниз правой рукоятки курка освободить
пружину, которая своим ударом выбросит
снаряд в сторону мисочки-мишени 8.
Отметить первое максимальное отклонение
маятника

и расстояние
от оси маятника до места попадания
снаряда .Опыт повторить 5-10 раз. Результаты
записать в таблицу № 2 -
Повторить
п. 4 для другого снаряда.
Таблица
№ 1
Материал
пули №1
|
№ |
|
|
|
|
|
|
|
|
Таблица №2
![]() =
=
М=
|
№ |
Рад. |
(м) |
(м/с) |
|
|
Обработка
результатов измерений.
1.Найти
среднее значения периодов
![]()
и
![]()
.
2.
По формуле (7) найти скорость снаряда
для каждого выстрела. Угол в радианах.
3.
Вычислить погрешность результата по
формуле.
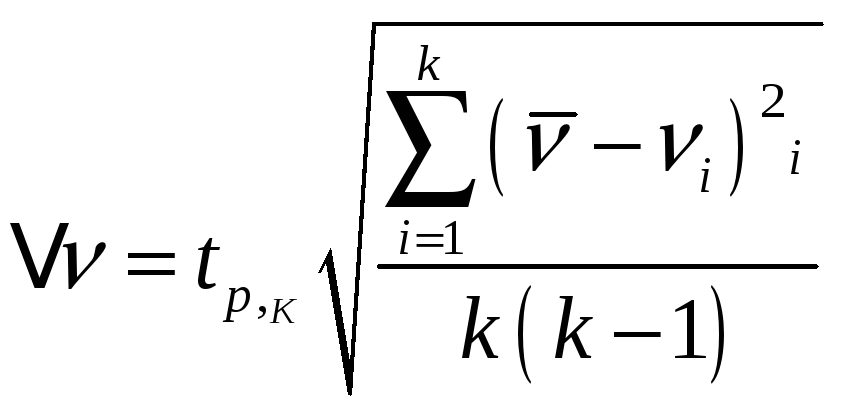
4.
Окончательный результат записывают в
виде
![]()
![]()
с
указанием коэффициента доверия р=0,95
5.
По экспериментальным результатам
оцените кинетическую энергию маятника
![]() .
.
6.
Оцените, какая часть кинетической
энергии снаряда при ударе переходит в
теплоту.
Контрольные
вопросы
-
В
чем особенность баллистического
маятника? -
Дайте
определение момента импульса и
сформулируйте закон сохранения этой
величины. -
Покажите,
что при прямолинейном движении снаряда
его момент импульса остается постоянным. -
Чему
равна кинетическая и потенциальная
энергия крутильного маятника?
Сформулируйте закон сохранения
механической энергии. Можно ли его
использовать при выводе рабочей формулы
в данной работе? -
Как
можно измерить модуль кручения проволоки? -
Увеличится
или уменьшится период колебаний
маятника, если грузы М удалить от оси
вращения? -
Какие
факторы ограничивают точность определения
скорости снаряда в данной работе? -
Вывод
формулы(2).
Библиографический
список.
1.
Стрелков С.П. Механика. -М.: Наука, 1975.
Гл.14.
2.
Сивухин Д.В. Механика. -М,: Наука, 1989. Т.6.
3. Савельев
И.В. Курс общей физики. -М.: Наука. 1989. Т.2
Г
Приложение.
Крутильный маятник
Интересным примером
гармонического осциллятора является
крутильный
маятник. Он
представляет собой массивное тело,
подвешенное на
тонкой упругой струне или кварцевой
нити. При повороте
маятника из положения равновесия на
некоторый угол рис 1. на него со
стороны нити действует «упругий» момент
![]()
(1)
пропорциональный углу поворота
![]() ;
;
D — постоянная,
характеризующая момент упругих сил
(аналогична жесткости k
пружины).
Если струна достаточно
тонкая и длинная, то, как показывает
опыт, зависимость (1) справедлива и
для довольно больших углов, например
> 2![]() .
.
Кроме того, затухание крутильного
маятника обычно
мало. Все это делает его удобным прибором
для измерения
различных физических величин.
Затухание маятника
определяется моментом сил трения,
пропорциональным угловой скорости
![]() :
:
![]()
(2)
Движение маятника описывается уравнением
моментов
![]()
(3)
которое с учетом (1) и (2) легко привести
к уравнению осциллятора
с вязким трением:
![]()
(4)
где I – момент инерции
маятника относительно оси вращения,
![]()
– постоянная затухания,
![]() .
.
Период слабозатухающих (![]() )
)
колебаний маятника
равен
![]()
Соседние файлы в папке Методички (мех)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
График выполнения работ физического практикума
10 А класса 1 цикл .
1.Определение
начальной скорости снаряда, дальности полета и высоты
подъема при
стрельбе под углом 450 .
2. Изучение
зависимости дальности полета от угла вылета снаряда.
3. Изучение второго
закона Ньютона.
4. Определение
коэффициента трения скольжения с помощью вращающегося
диска.
5. Измерение массы
тела методом гидростатического взвешивания.
6. Определение
скорости снаряда с помощью баллистического маятника.
Лабораторная работа
№1 по теме:
ОПРЕДЕЛЕНИЕ НАЧАЛЬНОЙ
СКОРОСТИ СНАРЯДА, ДАЛЬНОСТИ И ВЫСОТЫ ПОДЪЕМА ПРИ СТРЕЛЬБЕ ПОД УГЛОМ 45°.
В
работе ставится задача: рассчитать места для установки мишеней и кольца так,
чтобы при выстреле из пистолета под углом 45° к горизонту снаряд пролетел
сквозь кольцо и поразил мишень.
Очевидно,
мишень надо установить на расстоянии l,
которое можно вычислить по известной формуле дальности полета:
![]() ,
,
(1)
а кольцо закрепить на
штативе посередине между мишенью и пистолетом на высоте h,
которая определяется по формуле максимальной высоты поднятия снаряда при
стрельбе под углом к горизонту:
![]() , (2)
, (2)
Для вычисления
этих величин необходимо знать начальную скорость снаряда, ее следует определить
на опыте. Для этого надо направить пистолет вертикально вверх и, сделав
несколько выстрелов, измерить высоту подъема снаряда. Затем, зная Н и g,
вычислить начальную скорость снаряда:
![]()
ВЫПОЛНЕНИЕ РАБОТЫ.
Оборудование: баллистический пистолет, лента измерительная, штатив с
кольцом, небольшой листок бумаги.
1. Прикрепите баллистический пистолет к краю стола и
направьте его по угломеру строго вертикально.
2. Рядом с пистолетом натяните и держите вертикально
измерительную ленту так, чтобы начало отсчета совпадало с центром снаряда.
Сделайте несколько выстрелов и заметьте по делениям ленты высоту поднятия
снаряда.
3. Вычислите скорость полета снаряда, а затем дальность
полета снаряда 1 и максимальную высоту его поднятия hmax
4. Направьте пистолет вдоль стола под углом 45° к
горизонту. На вычисленном расстоянии положите небольшой листок бумаги, который
будет служить мишенью. Посередине между мишенью и пистолетом поставьте штатив и
закрепите на нем кольцо
в вертикальной плоскости на вычисленной высоте h.
Внимательно проследите за тем, чтобы снаряд, кольцо и мишень находились в
одной вертикальной плоскости.
5. Произвести выстрел. Если расчет сделан правильно, снаряд
должен пролететь сквозь кольцо и поразить мишень.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Отличается ли
максимальная высота поднятия снаряда при стрельбе под углом 45° и при зенитной
стрельбе?
2. Под каким углом надо
установить пистолет, чтобы максимальная высота поднятия снаряда оказалась в 4
раза меньше высоты при зенитной стрельбе?
3. Каким способом можно
поразить цель, если дальность при стрельбе под углом 30° соответствует
нахождению цели, но высота холма на пути снаряда немного превышает высоту
поднятия снаряда?
4. Выведите формулу (1) и
(2).
Лабораторная
работа №2
Изучение
зависимости дальности полета от угла вылета снаряда
При стрельбе на
горизонтальной поверхности под различными углами к горизонту дальности полета
снаряда выражается формулой:
![]()
![]() (1)
(1)
Из этой формулы
следует, что при изменении угла вылета снаряда от 90о до 0о![]() дальность его падения сначала
дальность его падения сначала
увеличивается от нуля до некоторого максимального значения, а затем снова
уменьшится до нуля. Дальность падения максимальна, когда sin2α принимает
наибольшее значение. Эту зависимость в данной работе следует проверить на опыте
с помощью баллистического пистолета.
Выполнение работы.
Оборудование:
баллистический пистолет, лента измерительная,2-3 листа писчей бумаги и 1 лист
копировальной бумаги, липкая лента.
1. Приготовьте в
тетради таблицу для записи результатов измерений и вычислений
|
Угол вылета шарика |
20о |
30о |
40о |
45о |
50о |
60о |
70о |
|
Средняя дальность |
2. На краю стола
закрепите струбцину с баллистическим пистолетом и установите пистолет с помощью
угломера под углом 45 градусов. Не накладывая бумаги, произведите пробный
выстрел и заметьте приблизительно место падения шарика. Закрепите на столе
полосу бумаги так, чтобы при стрельбе под углом 45 градусов шарик падал у ее
дальнего конца и наложите копировальную бумагу.
3.Устанавливая
пистолет под углами 20, 30, 40, 45 градусов, сделайте по 3-4 выстрела для
каждого угла.
4. Поверните пистолет
немного в сторону и, устанавливая его под углами 50, 60, 70 градусов, снова
сделайте 3-4 выстрела для каждого угла. Следы падения шарика обведите
карандашом и рядом отметьте углы бросания.
5. Измерьте среднюю
дальность падения шарика для каждого угла. Результаты запишите в таблицу.
Контрольные
вопросы.
1. При каком угле
вылета дальность полета шарика наибольшая?
2. При каких углах
вылета дальность полета приблизительно одинакова, и чему равна сумма этих
углов? Как это согласуется с формулой дальности?
3. Можно ли вычислить
начальную скорость вылета шарика по результатам опыта, например, для углов
30,50,70 градусов? Выполните эти расчеты.
4. Выведите формулу
для расчета дальности полета (1).
Лабораторная работа №3
Изучение второго закона ньютона
Оборудование:
динамометр учебный с укрепленной на планке динамометра трубкой, секундомер,
весы учебные со штативом, гири, пробки резиновые разной массы с отверстиями-2
шт., леска диаметром 0.3-0.4 мм или прочная нить
Задание
Рассчитайте
ускорение, с которым движется резиновая пробка по окружности под действием
постоянной по модулю силы. Результат расчета проверьте экспериментально.
Метод выполнения
работы
Второй закон ньютона
утверждает, что ускорение а тела прямо пропорционально действующей силы F и
обратно пропорционально массе тела m:
 (1)
(1)
В работе исследуется
движение резиновой пробки массой m по окружности под действием постоянной по
модулю силы упругости нитки F![]() ,
,
направленной к центру окружности. Зная эту силу и массу пробки, можно
рассчитать модуль ускорения пробки. Результат расчета можно α Модуль
центростремительного ускорения в этом случае равен
 (2)
(2)
Выразив
линейную скорость через период T обращения пробки (который можно измерить),
Формула для расчета
ускорения можно привести к виду:
 (3)
(3)
Итак, цель работы
заключается в сравнении значения ускорения, вычисленного по формуле (1), и
значения ускорения найденного по формуле(3), позволяющей измерить ускорение
тела движущегося по окружности.
 Порядок
Порядок
выполнения работы
Измерьте массу m1
пробки с помощью весов и гирь
Привяжите пробку к
одному концу нити длиной 30-40 см. Второй конец нити пропустите через трубку,
укрепленную на планке динамометра, и привяжите к крючку динамометра.
Приведите пробку во
вращательное движение в горизонтальной плоскости. Установите такую скорость
движения пробки по окружности, при которой сила упругости нити, являющаяся
причиной возникновения центростремительного ускорения была равна 2Н.
Измерьте время t, за
которое пробка совершает по окружности n=20 оборотов.
Рассчитайте период T
обращения пробки по окружности радиусом R:

Измерьте радиус R
окружности, по которой движется пробка :
![]()
Lо – длина нити от
пробки до трубки до начала опыта, х – удлинение пружины
Рассчитайте ускорение
пробки по формуле (1)и по результатам опыта:


Повторите опыт с той
же пробкой, но при такой скорости движения, при которой сила упругости нити
равна 4Н.
Результаты измерений
и расчетов занесите в отчетную таблицу
Рассчитайте
абсолютную и относительную погрешность измерений
|
№ опыта |
M1,кг |
Fy, H |
|
t,c |
n |
T,c |
R,м |
аЭ, м/с2 |
|
1 2 |
2 4 |
Сравните значение
ускорений, вычисленных по второму закону Ньютона, со значениями ускорений,
полученными из опыта с учетом погрешности измерения и сделайте вывод.
Контрольные
вопросы. Повторить §25 Физика
10 Г.Я. Мякишев.
1. Сформулируйте
второй закон Ньютона. Справедлив ли этот закон для произвольного тела или
только для материальной точки?
2. Измеряется
ускорение тела движущегося равномерно по окружности.
Какие условия
необходимы для того, что бы тело двигалось с постоянным ускорением?
3.Почему при
выполнении опытов осуществлялось вращение пробки в горизонтальной плоскости, а не
в вертикальной?
4. Почему
теоретическое и экспериментальное значения ускорений пробки отличаются друг от
друга?
Лабораторная работа №4
Определение коэффициента трения скольжения с помощью
вращающегося диска.
Оборудование: проигрыватель с вращающемся диском, деревянное и
металлическое тело небольших размеров, секундомер, линейка с миллиметровыми
делениями.
Метод выполнения работы:

Второй закон Ньютона утверждает,
что ускорение тела прямо пропорционально действующей силе и обратно
пропорционально массе тела.

Тело, находящееся на вращающемся диске удерживается от проскальзывания
силой трения покоя. Вращаясь по окружности оно испытывает центростремительное
ускорение![]() . Эту формулу можно привести к виду:
. Эту формулу можно привести к виду:  . Где n– число оборотов, t – время,
. Где n– число оборотов, t – время,
за которое диск сделал n оборотов, R – радиус окружности.
Видим, что ускорение прямо пропорционально радиусу окружности, а
следовательно и силе трения покоя. Если увеличить радиус окружности, то сила
трения покоя возрастает, но она может возрастать до определенного максимального
значения, после чего трение покоя заменяется трением скольжения, и тело
начинает скользить, улетая с диска. Таким образом, цель работы заключается в
том, чтобы найти положение тела на диске, при котором трение покоя принимает
максимально возможное значение и переходит в трение скольжения. Сила трения
скольжения равна ![]()
Подставим все полученные выражения во второй закон Ньютона. Получим
![]() . Учитывая, что по оси ОY тело
. Учитывая, что по оси ОY тело
покоится, согласно первому закону Ньютона реакция опоры N равна по
модулю силе тяжести mg, имеем
![]()
Порядок выполнения работы:
1. Включите проигрыватель на 78 об/мин и измерьте время t 15-20
оборотов диска.
2. Положите тело на покоящийся диск и включите проигрыватель.
3. Проделайте это несколько раз, изменяя радиус вращения тела R.
Найдите минимальное значение радиуса окружности, при котором начинается
скольжение тела по диску.
4. Результаты измерений и расчетов занесите в таблицу.
|
тело |
R,м |
ΔR,м |
n |
t,с |
Δt,с |
μ |
Δ μ |
ε μ |
|
дерево |
||||||||
|
металл |
5. Оцените границы погрешности измерения коэффициента трения
скольжения.
Границу относительной погрешности коэффициента трения можно вычислить
по формуле:
ε μ= ε R+2 ε t+
ε g , но погрешностью ε g можно пренебречь, если считать g=9,8 м/с2
. Следовательно ![]() .
.
Граница абсолютной погрешности измерения коэффициента трения равна
![]()
6. Запишите результат в виде
![]()
Контрольные вопросы. ( §§25,37 Учебник Г.Я. Мякишев)
1. Сформулируйте второй закон Ньютона. Справедлив ли этот закон для
произвольного тела или только для материальной точки?
2.Какие условия необходимы для того, чтобы тело двигалось с постоянным
ускорением?
3.Дайте определение массы.
4.Когда возникает сила трения покоя? От чего зависят ее модуль и
направление? В каких пределах может изменяться сила трения покоя?
5.Может ли сила трения скольжения увеличить скорость тела?
6. Какая сила сообщает ускорение автомобилю?
7. От чего зависит коэффициент трения скольжения?
Лабораторная работа№5 по теме:
ИЗМЕРЕНИЕ МАССЫ ТЕЛА МЕТОДОМ ГИДРОСТАТИЧЕСКОГО
ВЗВЕШИВАНИЯ
Повторить § 34, 35 «Фнзика-10»
Г.Я.Мякишев
Оборудование: динамометр
школьный с заклеенной шкалой; измерительный цилиндр; тело неизвестной массы;
штатив; сосуд с водой; линейка измерительная.
Задание:
Отградуируйте
пружину и измерьте массу тела с помощью полученных пружинных весов.
Метод выполнения работы
Трудность работы
заключается в том, что для градуировки пружины (определения ее жесткости) нет
грузов известной массы. Эту трудность можно преодолеть, измерив удлинение x1 пружины при
подвешивании к ней груза неизвестной массы т в воздухе, а затем
удлинение x2 этой же пружины при
погружении груза в воду.
Запишем уравнение, равновесия груза на пружине
в воздухе:
mg = kx1 (1)
(k — жесткость
пружины) и уравнение равновесия этого же груза, опущенного в сосуд с водой:
mg – FA=kx2, (2)
где FA — архимедова сила,
действующая на груз. Она равна
FA = ρ0Vg, (3)
где ρ0 — плотность воды, V — объем тела.
Измерив объем тела
с помощью измерительного цилиндра, можно из выражений (1), (2) и (3)
рассчитать жесткость пружины:
![]() (4)
(4)
и искомую массу груза:


![]() (5)
(5)
Порядок выполнения работы:
1. Укрепите
динамометр с заклеенной шкалой в штативе. Проведите линию, фиксирующую
положение конца ненагруженной пружины.
2. Подвесьте
к пружине груз неизвестной массы и отметьте положение конца пружины. Измерьте
линейкой удлинение x1 пружины.
3. Опустите
груз в сосуд с водой (рис. 1) и
измерьте новое удлинение х2 пружины.
4. Налейте
в измерительный цилиндр определенный объем воды. Опустите в цилиндр груз и измерьте увеличение объема
воды в измерительном цилиндре, равное объему V груза.
5. Вычислите
жесткость k пружины по формуле (4) и массу груза по формуле (5).
6. Рассчитайте границы абсолютной и относительной погрешностей
измерения массы груза.
В
качестве границы абсолютной погрешности измерения объема ![]() можно принять цену деления измерительного
можно принять цену деления измерительного
цилиндра, для границ абсолютных погрешностей измерения удлинений ![]() и
и ![]() – цену деления
– цену деления
измерительной линейки.
7. Результаты
измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
|
x1, м |
x2, м |
x1–x2, м |
V, м3 |
k, Н/м |
m, |
|
Контрольные вопросы
1.
Как
можно измерить жесткость пружины, используя
груз неизвестной массы?
2.
Каким образом можно уменьшить
погрешности измерений при выполнении работы описанным
методом?
3.
Сформулируйте закон Гука. При каких условиях он выполняется?
4.
Сформулируйте закон Архимеда.
Лабораторная работа
№6 по теме:
ОПРЕДЕЛЕНИЕ СКОРОСТИ СНАРЯДА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО
МАЯТНИКА
Повторить § 40, 50 «Фнзика-10». Г.Я. Мякишев
В настоящей работе требуется определить методом
баллистического маятника скорость снаряда, выпущенного «ракетной установкой».
Для этого собирают установку, показанную на рисунке 1.
С помощью лапки штатива «ракетную установку»
укрепляют в горизонтальном положении точно против отверстия в коробке,
подвешенной на длинных нитях, как маятник. Снаряд перед проведением опыта
надевают на стержень со спиральной пружиной. При этом пружина сжимается и
снаряд закрепляется специальным захватом.
Затем производят выстрел. Снаряд застревает в
коробке, сообщая ей импульс.

По закону сохранения импульса можно записать:
mv = (M+m)u,
где m — масса снаряда; v — его скорость; М — масса коробки; и — скорость коробки с застрявшим в ней снарядом.
Если массы снаряда и коробки известны (их измеряют путем взвешивания), то для
определения скорости снаряда v необходимо
знать скорость и движения коробки после попадания в нее снаряда:
![]()
Применяя закон сохранения энергии, можно скорость
коробки выразить через максимальную высоту ее подъема h по отношению к
начальному уровню (рис. 2):
![]()
откуда
![]()
Высоту подъема h можно
определить, измерив длину подвеса l и хорду АВ (рис. 3):
BD2 = BC2 – CD2=l2
– (l – h)2 = 2lh – h2,
BD2 = AB2 – AD2 = s2 – h2,
следовательно,
2lh – h2 = s2 –
h2
или
![]()


Рис.
2 Рис.
3
Выполнение работы:
Оборудование: 1) баллистический маятник
(коробка, подвешенная на штативе); 2) игрушка «ракетная установка»; 3) штатив
лабораторный; 4) измерительная линейка; 5) измерительная лента; 6) весы с
разновесом.
1. Подготовьте в тетради таблицу
для записи результатов измерений и вычислений.
|
№ опыта |
т, г |
М, г |
s, |
h , м |
l, м |
u, м/с |
V, м/с |
|
1 |
|||||||
|
2 |
|||||||
|
3 |
2. С помощью весов определите массы снаряда и
коробки (т, М), а измерительной
лентой – длину нити подвеса l.
3.
Произведите 3—5
выстрелов, измеряя каждый раз величину отклонения баллистического маятника s. Определите среднее
значение отклонения scp.
4.
Вычислите высоту h подъема
маятника, скорость u и скорость
снаряда v.
5. Полученные результаты внесите в таблицу.
6. Рассчитайте абсолютную и относительную
погрешность измерений скорости снаряда.
Контрольные вопросы:
1. Поясните принцип действия данной установки по
определению скорости снаряда.
2.Почему для нахождения скорости снаряда баллистического маятника
не используется следующий способ вычислений:
![]() ,
, ![]() ?
?
3.Сформулируйте закон сохранения импульса. В каких случаях его
можно применять?
4. Что называется полной механической энергией системы? Может ли
сохраняться механическая энергия системы, на которую действуют внешние силы?
Глава 6
![]()
Главная > Раздел “Военное дело” > Полная версия

Глава шестая
ПОЛЕТ СНАРЯДА
«
СКОРОСТЬ ПОЛЕТА СНАРЯДА
Во времена Петра I скорость полета ядра доходила до 200 метров в секунду.
Современные же артиллерийские снаряды летят значительно быстрее. Скорость полета современного снаряда в первую секунду равна обычно 600–800 метрам, а некоторые снаряды летят еще быстрее, — со скоростью 1000 и более метров в секунду. Эта скорость так велика, что снаряд, когда он летит, даже не виден: глаз не успевает его уловить.
Следовательно, современный снаряд летит со скоростью, в 40 раз превышающей скорость курьерского поезда и в 8 раз превышающей скорость самолета.
Впрочем, здесь речь идет об обыкновенных пассажирских самолетах и об артиллерийских снарядах, летящих со средней скоростью.
Если же взять для сравнения, с одной стороны, самый «медленный» снаряд, а с другой, — современный реактивный самолет, тогда разница будет уже не так велика, и притом — не в пользу снаряда: реактивные самолеты делают в наше время около 900 километров в час, то-есть около 250 метров в секунду, а очень «медленный» снаряд, например снаряд 152-миллиметровой гаубицы, при наименьшем заряде пролетает в первую секунду всего лишь 238 метров.
Получается, что реактивный самолет не только не отстанет от такого снаряда, но и перегонит его. Летя на таком самолете, можно было бы ясно увидеть попутный снаряд.
А если взять для сравнения мину современного 120-миллиметрового миномета, то она пролетит при самом маленьком заряде всего лишь 119 метров в секунду. Реактивный самолет летит в два с лишним раза быстрее этой мины!
ЧТО ТЯНЕТ СНАРЯД ВНИЗ?
Пассажирский самолет пролетает за час около 500 километров. Сколько же пролетит за час снаряд, летящий в 8 раз быстрее самолета?
Казалось бы, снаряд должен пролететь за час около 4000 километров.
На самом деле, однако, весь полет артиллерийского снаряда продолжается обычно меньше минуты, снаряд пролетает 15–20 километров и лишь у некоторых орудий — больше.
В чем же тут дело? Что мешает снаряду лететь так же долго и так же далеко, как летит самолет?
Самолет летит долго потому, что воздушный винт тянет или реактивный двигатель толкает его все время вперед. Двигатель работает несколько часов подряд, — пока хватит горючего. Поэтому и самолет может лететь непрерывно несколько часов подряд.
Снаряд же получил толчок в канале орудия, а дальше летит уже сам по себе, никакая сила больше не толкает его вперед. С точки зрения механики, летящий снаряд будет телом, движущимся по инерции. Такое тело, — учит механика, — должно подчиняться очень простому закону: оно должно двигаться прямолинейно и равномерно, если только к нему не приложена больше никакая сила.
Подчиняется ли снаряд этому закону, движется ли он прямолинейно?
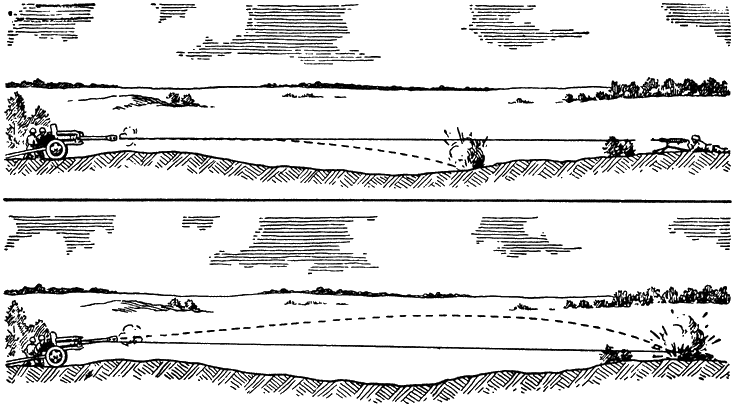
Представьте себе, что за километр от вас находится какая-либо цель, например неприятельский пулемет. Попробуйте навести орудие так, чтобы ствол его был направлен прямо в пулемет (рис. 130), потом произведите выстрел.
 |
|
Рис. 130. Как летел бы снаряд при выстреле из орудия, ствол которого направлен прямо в цель, и как надо направить ствол, чтобы снаряд попал в цель |
 |
 |
|
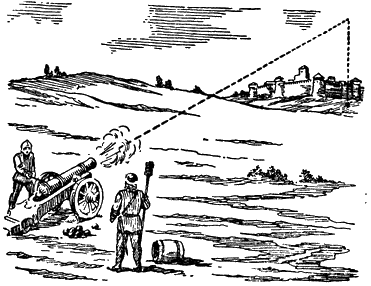
Рис. 131. Так представляли себе полет снаряда артиллеристы XVI века |
Рис. 132. Брошенный камень летит по кривой |
Сколько бы раз вы так ни стреляли, в цель вы не попадете никогда: всякий раз снаряд будет падать на землю и разрываться, пролетев всего лишь метров 200–300. Если вы будете продолжать опыты, то скоро придете к такому выводу: чтобы попасть, надо направить ствол не в цель, а несколько выше ее (см. рис. 130).
Выходит, что снаряд летит вперед не по прямой линии: в полете он опускается. В чем дело? Почему снаряд летит не прямолинейно? Какая сила тянет снаряд вниз?
Ученые-артиллеристы конца XVI и начала XVII веков давали этому явлению такое объяснение: снаряд, летящий наклонно вверх, теряет силу, подобно человеку, взбирающемуся на крутую гору. И когда снаряд окончательно потеряет силу, он на миг остановится в воздухе, а затем «камнем» упадет вниз. Путь снаряда в воздухе казался артиллеристам XVI века таким, как изображено на рис. 131.
В наши дни каждый школьник, зная законы, открытые Галилеем и Ньютоном, даст более верный ответ: на летящий снаряд действует сила тяжести и заставляет его опускаться во время полета. Ведь всякий знает, что брошенный камень летит не прямо, а описывает кривую и, пролетев небольшое расстояние, падает на землю (рис. 132). При прочих равных условиях камень летит тем дальше, чем сильнее он брошен, чем большую скорость он получил в момент броска.
Поставьте на место человека, бросающего камень, орудие, а камень замените снарядом; как и всякое летящее тело, снаряд будет притянут при полете к земле и, следовательно, отойдет от той линии, по которой он был брошен; эта линия так и называется в артиллерии линией бросания, а угол между этой линией и горизонтом орудия — углом бросания (рис. 133).
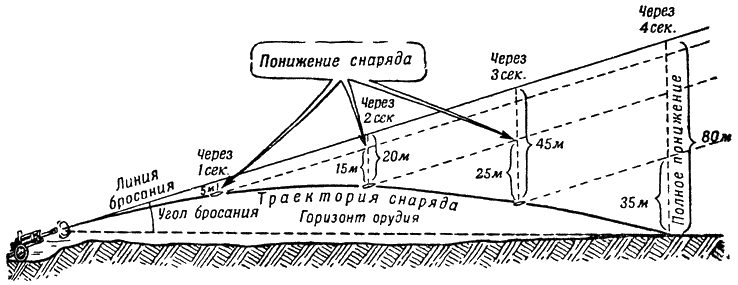
Если предположить, что на снаряд при его полете действует только сила тяжести, то под действием этой силы в первую секунду полета снаряд опустится приблизительно на 5 метров (точнее — на 4,9 метра), во вторую — почти на 15 метров (точнее — на 14,7 метра) и в каждую
 |
|
Рис. 133. Так понижался бы снаряд под линией бросания при стрельбе в безвоздушном пространстве |
следующую секунду скорость падения будет увеличиваться почти на 10 метров в секунду (точнее — на 9,8 метра в секунду). Таков закон свободного падения тел, открытый Галилеем.
Поэтому-то линия полета снаряда — траектория — получается не прямой, а точно такой же, как и для брошенного камня, похожей на дугу.
КАК ДАЛЕКО ЛЕТИТ СНАРЯД
Теперь попытайтесь ответить на такой вопрос: нет ли связи между углом бросания и расстоянием, которое пролетает снаряд?
Попробуйте выстрелить из орудия один раз при горизонтальном положении ствола, другой раз — придав стволу угол бросания 3 градуса, а в третий раз — при угле бросания 6 градусов.
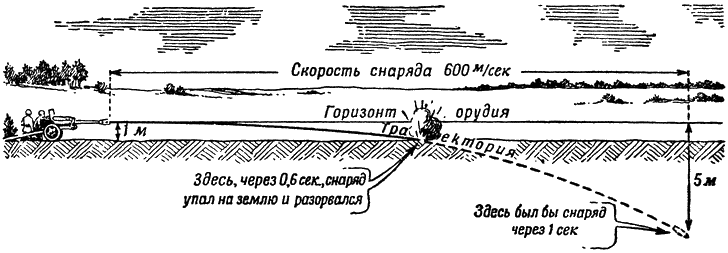
В первую же секунду полета снаряд, как мы уже знаем, должен отойти вниз от линии бросания на 5 метров. И значит, если ствол орудия лежит на станке высотой 1 метр от земли и направлен горизонтально, то снаряду некуда будет опускаться, он ударится о землю раньше, чем истечет первая секунда полета. Расчет показывает, что уже через 6 десятых секунды произойдет удар снаряда о землю (рис. 134).
 |
|
Рис. 134. Так летел бы снаряд, если бы стволу орудия придали горизонтальное положение |
Снаряд, брошенный со скоростью 600–700 метров в секунду, при горизонтальном положении ствола пролетит до падения на землю всего лишь метров 300.
Теперь произведите выстрел под углом бросания в 3 градуса. Линия бросания пойдет уже не горизонтально, а под углом в 3 градуса к горизонту (рис. 135).
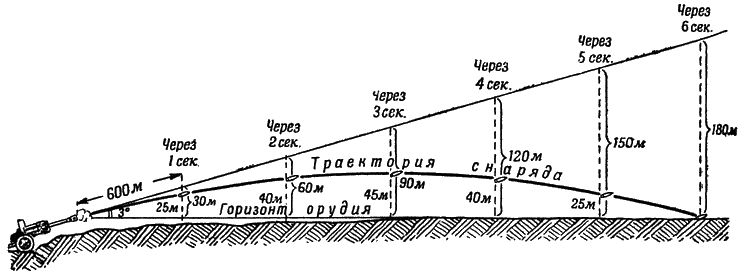
По нашим расчетам, снаряд, вылетевший со скоростью 600 метров в секунду, должен был бы через секунду подняться уже на высоту 30 метров, но сила тяжести отнимет у него 5 метров подъема, и на самом деле снаряд окажется на высоте 25 метров над землей. Через 2 секунды снаряд, не будь силы тяжести, поднялся бы уже на высоту 60 метров, на самом же деле сила тяжести отнимет на второй секунде полета еще 15 метров, а всего 20 метров. К концу второй секунды снаряд окажется на высоте 40 метров. Если продолжим расчеты, они покажут, что уже на четвертой секунде снаряд не только перестанет подниматься, но начнет опускаться все ниже и ниже. И к концу шестой секунды, пролетев 3600 метров, снаряд упадет на землю (см, рис. 135).
Расчеты для выстрела под углом бросания 6 градусов похожи на те, которые мы только что делали, но считать придется много дольше: снаряд будет лететь 12 секунд и пролетит 7200 метров.
 |
|
Рис. 135. Траектория снаряда в безвоздушном пространстве при угле бросания, равном 3 градусам |
Вы нашли правило: чем больше угол бросания, тем дальше летит снаряд.
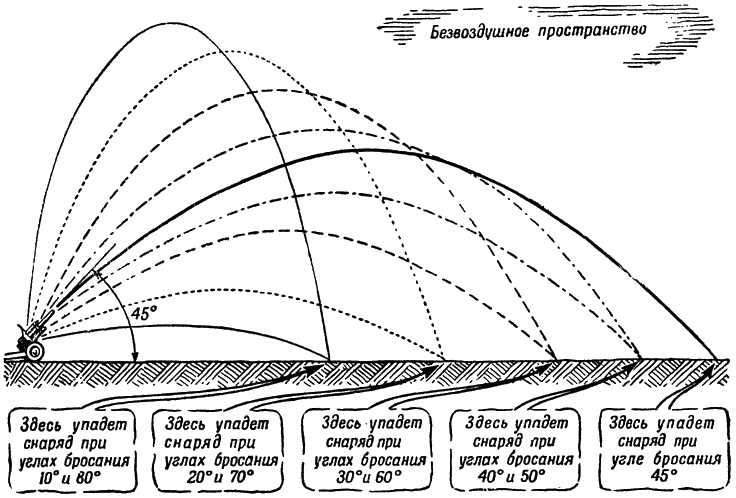
Но этому увеличению дальности есть предел: дальше всего снаряд летит, если его бросить под углом 45 градусов (рис. 136).
Если еще увеличивать угол бросания, снаряд будет забираться все выше, но зато падать он будет все ближе.
Само собою разумеется, что дальность полета будет зависеть не только от угла бросания, но и от скорости: чем больше начальная скорость снаряда, тем дальше он упадет при прочих равных условиях.
 |
|
Рис. 136. Угол наибольшей дальности и траектории при стрельбе под разными углами бросания |
Например, если бросить снаряд под углом 6 градусов со скоростью не 600, а 170 метров в секунду, то он пролетит не 7200 метров, а всего лишь 570.
Остается только проверить теперь эти вычисления на опыте.
ЧТО ТОРМОЗИТ ПОЛЕТ СНАРЯДА?
Итак, проделаем опыт. Зарядим орудие таким зарядом, который выбрасывает 152-миллиметровый снаряд с начальной скоростью 170 метров в секунду. При угле бросания 20 градусов снаряд по расчетам должен пролететь 1900 метров. Приблизительно столько пролетит он и на самом деле, — расчеты подтвердились.
Повторим теперь наш опыт с другим орудием. Зарядим 76-миллиметровую пушку, снаряд которой имеет скорость около 680 метров в секунду, и выстрелим так, чтобы угол бросания был равен тем же 20 градусам.
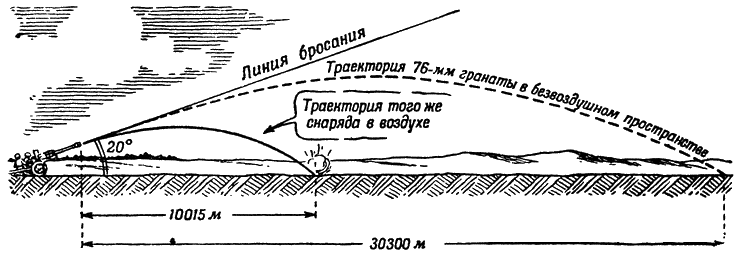
Мы ожидаем, что снаряд пролетит очень большое расстояние — 30 300 метров. А на самом деле снаряд упадет на расстоянии всего лишь 10 015 метров от орудия (рис. 137).
Вы недоумеваете. В чем дело? Неужели на этот раз мы ошиблись в расчетах?
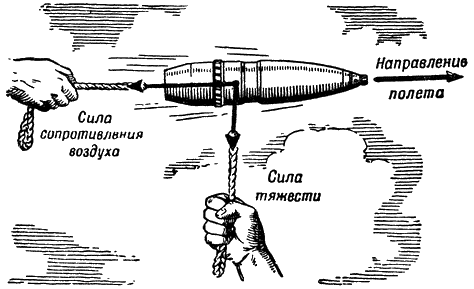
Нет, расчеты верны. Но они неполны: мы считали, что на летящий снаряд действует только сила тяжести. Это было бы верно, если бы мы стреляли в безвоздушном пространстве. А при полете снаряда в воздухе возникает еще одна сила, которую нельзя сбросить со счета: это — сила сопротивления воздуха (рис. 138). {181}
Сопротивление воздуха резко возрастает, когда увеличивается скорость движущегося тела.
Когда вы идете пешком, вы вовсе не чувствуете сопротивления воздуха. Но попробуйте сесть в открытый автомобиль и развить скорость хотя бы 60 километров в час, то-есть всего лишь около 17 метров в секунду, и вы почувствуете, как даже в самый тихий день сильный «ветер» начнет трепать ваши волосы, срывать фуражку с головы. А если
 |
|
Рис. 137. Как летел бы снаряд в безвоздушном пространстве и как он летит в воздухе |
вы высунетесь во время полета из кабины даже учебного самолета, летящего со скоростью всего лишь около 70 метров в секунду, то страшный «ураган» начнет так хлестать вам в лицо, что не даст и смотреть: придется надеть авиационные очки.
Так же обстоит дело и со снарядом. Если выстрелить из орудия, бросающего снаряд с небольшой скоростью, то сопротивление воздуха полету такого снаряда будет ничтожно, оно почти не отразится на его полете. Так и случилось со снарядом при первом опыте. Но положение резко изменится, если выстрелить снарядом, который летит со скоростью 680 метров в секунду — почти в 10 раз быстрее учебного самолета; представьте же себе,
 |
|
Рис. 138. Силы, действующие на снаряд во время |
как сопротивляется воздух полету этого снаряда! Именно из-за сопротивления воздуха наш снаряд и пролетел не 30 300 метров, а всего лишь 10 015. Очевидно, в этом случае нельзя уже не считаться с огромной силой, которая втрое уменьшила дальность полета снаряда.
Почему же воздух тормозит снаряд? {182} Потому что воздух, как и всякое другое вещество, обладает определенной плотностью. Он состоит из бесчисленного количества частиц. Снаряд расходует часть своей энергии на то, чтобы растолкать частицы воздуха, мешающие его полету.
 |
|
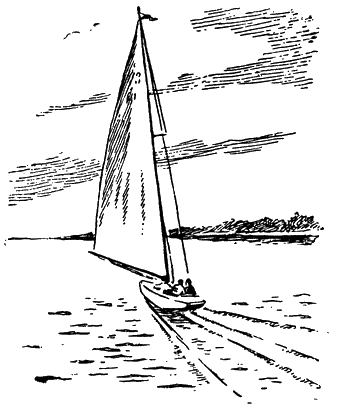
Рис. 139. Быстро идущая яхта создает две волны — носовую и кормовую |
Посмотрите с высокого берега на быстро идущую яхту (рис. 139). Впереди яхты образуется волна, которая, огибая носовую часть яхты, расходится вправо и влево от нее и долго держится на поверхности воды. Она тем выше, чем больше скорость яхты. За кормой вытесненная яхтой вода стремится занять место, освободившееся после того, как яхта прошла. И за кормой также тянутся длинные волны вправо и влево.
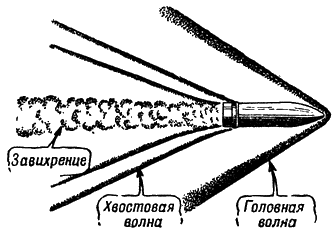
Нечто подобное происходит и в воздухе во время полета снаряда (рис. 140). Перед его головной частью образуется уплотнение воздуха. От этого уплотнения расходится во все стороны головная волна. Позади летящего снаряда образуется зона разреженного воздуха: пустота, которую оставил позади себя снаряд, вытолкнувший частицы воздуха, еще не успевает заполниться. Частицы воздуха несутся со всех сторон в эту пустоту, стремясь ее заполнить. Образуются завихрения. За дном снаряда тянется хвостовая волна.
Сгущение воздуха впереди головной части снаряда тормозит его полет. Разреженная зона позади снаряда засасывает снаряд и этим еще усиливает торможение. Кроме того, стенки снаряда испытывают трение о частицы воздуха.
 |
|
Рис. 140. Сопротивление воздуха летящему снаряду при быстром полете снаряда создает в воздухе головную и хвостовую волны и завихрения |
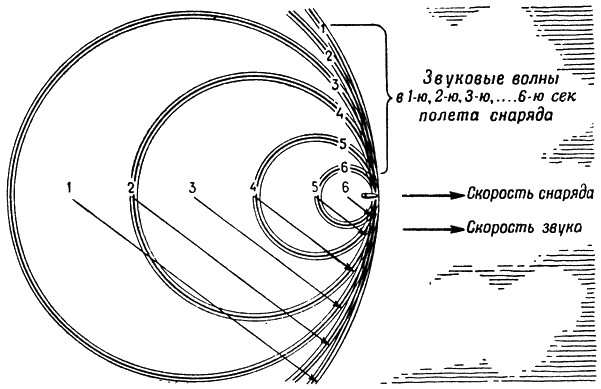
Головная волна, резко увеличивающая торможение снаряда, возникает в том случае, когда скорость снаряда равна или больше скорости звука. Скорость звука, как известно, приблизительно равна 340 метрам в секунду, а снаряды многих орудий летят вдвое и даже втрое быстрее звука.
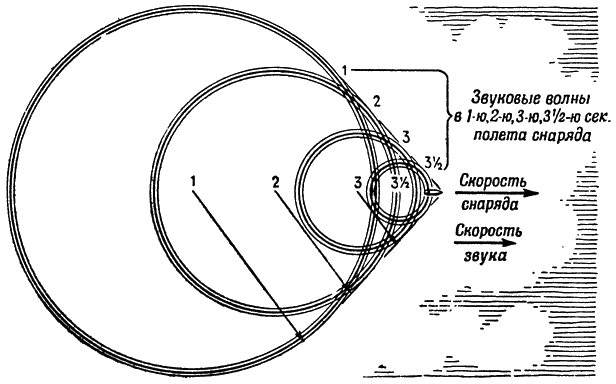
Если скорость снаряда равна скорости звука, то снаряд летит как бы на гребне звуковой волны (рис. 141). Если же скорость снаряда больше скорости звука, то в этом случае снаряд обгоняет все звуковые волны, образующиеся перед его головной частью
 |
|
Рис. 141. Распространение звуковых волн, порождаемых в воздухе снарядом, двигающимся со скоростью звука |
(рис. 142). И в том и в другом случае движение снаряда сильно тормозится, он быстро теряет свою скорость.
Опыты показывают, что даже при скоростях снаряда, меньших скорости звука, сопротивление воздуха растет не пропорционально скорости снаряда, а гораздо быстрее: если выбросить снаряд с удвоенной скоростью, то потеря им скорости из-за сопротивления воздуха возрастет примерно вчетверо. Утройте скорость снаряда,— замедление возрастет примерно в 9 раз.
 |
|
Рис. 142. Распространение звуковых волн, порожденных в воздухе снарядом, двигающимся быстрее звука |
Словом, при скоростях до 300 метров в секунду замедление полета снаряда возрастает приблизительно пропорционально квадрату скорости его полета, а при больших скоростях полета снаряда — и еще больше.
КАК УМЕНЬШИТЬ СОПРОТИВЛЕНИЕ ВОЗДУХА
Воздух тормозит летящий снаряд, замедляет его полет.
Можно ли бороться с этим замедлением?
Один способ мы уже знаем — уменьшить скорость самого снаряда. Но ведь снаряд, летящий медленнее, упадет ближе. Этот способ применим только в том случае, когда нам нет надобности бросать снаряд далеко.
А на войне важно иметь возможность забросить снаряд как можно дальше. Поэтому уменьшать его скорость не всегда выгодно.
Поищем, нет ли других, более подходящих способов бороться с замедлением полета снаряда из-за сопротивления воздуха.
Такие способы существуют.
Представьте себе, что вы хотите выбраться из трамвая, битком набитого пассажирами. Попробуйте итти прямо — грудью вперед; пожалуй, вы не доберётесь до выхода. Но если вы начнете пробираться боком, вам уже не так трудно будет протолкнуться.
Нечто подобное испытывает и снаряд в полете: не безразлично, как он будет пробираться между частицами воздуха.
Был в старину — во время первой севастопольской обороны — такой снаряд: светящее ядро к полупудовой медной мортире. Это ядро имело форму цилиндра.
В полете оно подставляло воздуху плоскую поверхность — круг и поэтому испытывало большое сопротивление воздуха. А сзади этого цилиндрического ядра получалась зона разреженного воздуха, сильно засасывавшая это ядро, отнимавшая у него скорость.
Такое ядро летело всего лишь метров на 500.
Обыкновенное шаровое ядро той же мортиры, хотя и встречало также большое сопротивление воздуха, но все же по форме было выгоднее цилиндра, и оно могло пролететь метров 800 — в полтора раза дальше светящего ядра.
Заострить головную часть снаряда еще выгоднее: как заостренный нос быстро идущей яхты легко рассекает воду, так и снаряд с заостренной головной частью продвигается в воздухе легче, чем цилиндрическое или шаровое ядро.
Вот почему головную часть снаряда начали заострять, едва лишь научились делать устойчивым в полете продолговатый снаряд,— еще в середине XIX века.
Донная часть такого снаряда оставалась, однако, еще цилиндрической, и позади снаряда получалась большая зона разреженного {185} воздуха, сильно засасывавшая снаряд, отнимавшая у него значительную часть скорости (см. рис. 140).
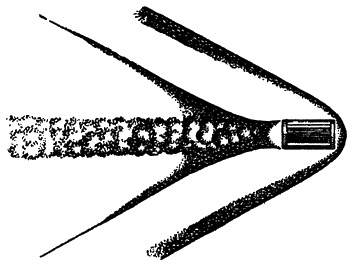 |
|
Рис. 143. Если бы снаряд с плоской поверхностью вылетел из ствола орудия со сверхзвуковой скоростью, он вызвал бы огромное сопротивление воздуха и через короткое время потерял бы свою скорость |
В XX веке резко возросли скорости транспорта всех видов, быстро развилась авиация. Ученые начали внимательно изучать действие сопротивления воздуха на быстро движущиеся предметы разной формы. Оказалось, что не только для самолета, но даже для быстроходного автомобиля или поезда важна такая форма, которая является удобообтекаемой. Если автомобилю придать такую форму, то при большой скорости движения он экономит 10–15 процентов горючего или при том же расходе горючего движется заметно быстрее.
Тем большее значение имеет форма снаряда: ведь снаряд движется во много раз быстрее автомобиля, он встречает огромное сопротивление воздуха.
Взгляните на рис. 140 и 143–145. Перед вами четыре снаряда разной формы. На рисунках изображены волны и завихрения воздуха, которые сопровождали бы полет каждого из этих снарядов, если бы скорость их всех была одна и та же, и притом больше, чем скорость звука. Давление на головную часть снаряда тем меньше, чем она острее. Разреженная зона за снарядам также тем меньше, чем больше скошена его донная часть; меньше в этом случае и завихрений позади летящего снаряда.
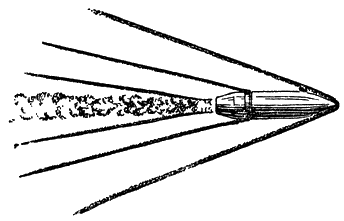
Очевидно, что наиболее выгодна форма снаряда, изображенная на рис. 145.
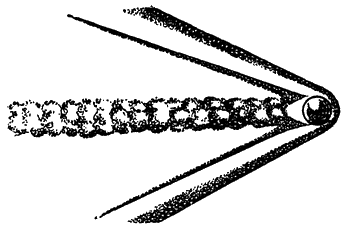 |
 |
|
Рис. 144. Велико было бы сопротивление воздуха шаровому ядру, летящему со сверхзвуковой скоростью |
Рис. 145. Наименьшее сопротивление воздуха вызывает современный дальнобойный снаряд обтекаемой формы |
Более подробное изучение этого вопроса показало, что каждой скорости полета соответствует своя наиболее выгодная форма снаряда.
Чем больше скорость снаряда, тем острее должна быть его головная часть.
Допустим, что воздух давит на головную часть снаряда с силой 4 атмосферы, а в разреженной зоне позади снаряда давление составляет всего лишь четверть атмосферы.
Давление на дно снаряда уменьшилось против нормального на три четверти атмосферы: это составляет примерно пятую часть того давления, которое испытывает головная часть снаряда.
 |
|
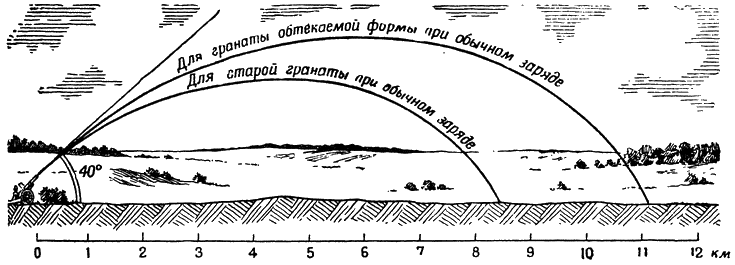
Рис. 146. При улучшении формы снаряда значительно увеличивается дальность его полета |
А вот другой снаряд: скорость его значительно больше, чем у первого, а потому он испытывает и большее сопротивление воздуха,— предположим, равное давлению 100 атмосфер. Пусть он летит так быстро, что за ним позади образуется почти полная пустота: частицы воздуха не успевают ее заполнить. Разница с нормальным давлением составляет целую атмосферу.
Но это всего лишь 1 процент — всего сотая часть — того давления, которое испытывает головная часть такого снаряда!
Вот почему снарядам, летящим с очень большой скоростью, придают теперь такую форму, при которой головная часть их очень сильно заострена. А снарядам, летящим сравнительно медленно, можно и не очень заострять головную часть, но зато нужно обязательно удлинить и сильно скосить их донную часть.
30 лет тому назад граната 76-миллиметровой пушки могла пролететь около 8,5 километра.
Но стоило только заострить ее головную часть, удлинить и скосить донную часть, как граната такого же веса стала лететь больше чем на 11 километров; простое изменение формы снаряда увеличило почти на одну треть дальность его полета (рис. 146).
КАКОЙ СНАРЯД ЛЕТИТ ДАЛЬШЕ — ЛЕГКИЙ ИЛИ ТЯЖЕЛЫЙ?
Секрет дальнобойности — не только в форме снаряда.
Выпустим снаряды одинаковой формы из трех разных орудий.
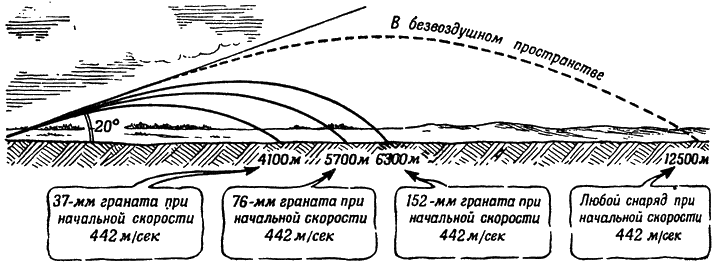
Орудия эти подобраны так, что начальная скорость их снарядов одна и та же — 442 метра в секунду. Снаряды почти совершенно одинаковы по форме. Пусть и угол бросания у всех трех орудий будет один и тот же — 20 градусов (рис. 147).
Снаряд 37-миллиметровой пушки при этих условиях пролетит 4100 метров.
Снаряд 76-миллиметровой пушки пролетит 5700 метров.
А снаряд 152-миллиметровой пушки залетит дальше всех — на 6300 метров.
В чем же дело? Ведь форма у всех трех снарядов одна и та же, и скорость одинакова, и угол бросания один и тот же.
Неодинаков только размер и вес этих снарядов: 37-миллиметровая граната весит 0,5 килограмма; 76-миллиметровая граната — побольше, она весит 6,5 килограмма, то-есть она в 13 раз тяжелее 37-миллиметровой гранаты; 152-миллиметровая граната — самая тяжелая, она весит около 41 килограмма.
Выходит так: чем тяжелее снаряд, тем меньше влияет на него сила сопротивления воздуха.
Чем же объяснить такое влияние веса снаряда?
Попробуйте проделать такой простой опыт. Подберите одинаковой величины и формы пробку и камешек. Бросьте их с высоты нескольких десятков метров от земли, например, из окна верхнего этажа высокого дома. Вы увидите, что камешек долетит до земли раньше, чем пробка. Закон свободного падения — один и тот же для всех тел. Форма и величина у камня и пробки одинаковы,— значит, в начале падения одинаково и сопротивление воздуха их движению.
Почему же его влияние на пробке сказалось сильнее, чем на камешке? Почему воздух больше затормозил полет пробки, чем полет камешка? Плотность пробки меньше плотности камешка. В пробке меньше
 |
|
Рис. 147. Вот как действует сопротивление воздуха на снаряды разного веса |
вещества. Стало быть, меньше и инерция пробки, то-есть ее способность сохранять состояние, в котором она находится. Пробку поэтому легко затормозить. Камень гораздо тяжелее пробки, вещества в нем во много раз больше. Значит, и инерция камня во столько же раз больше. Его движение затормозить гораздо труднее.
Каждый железнодорожник знает, что груженый поезд труднее затормозить, чем порожний.
Тяжелый снаряд испытывает при своем полете точно такое же сопротивление воздуха, как и легкий, если их размеры, скорость и форма одинаковы.
Но на полет тяжелого снаряда это сопротивление оказывает меньшее влияние. Поэтому-то замедление его полета меньше, поэтому-то и летит он дальше.
ПОПЕРЕЧНАЯ НАГРУЗКА
Однако в действительности дело обстоит еще сложнее.
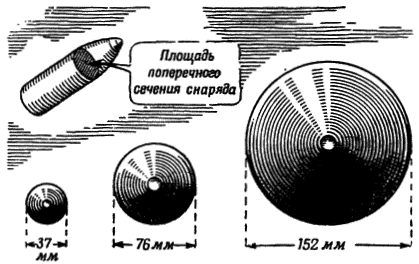
Вес, масса, инерция у более крупного снаряда больше. Но зато и поверхность, на которую действует сопротивление воздуха, у него тоже больше. А чем эта поверхность больше, тем, разумеется, больше и сопротивление воздуха полету такого снаряда: в этом случае воздух давит на большую площадь (рис. 148).
 |
|
Рис. 148. Площадь поперечного сечения снаряда |
Получается так: с одной стороны, большой снаряд тяжелее маленького, поэтому его инерция больше, он лучше сохраняет свою скорость; с другой же стороны, он подставляет действию воздуха большую поверхность и поэтому испытывает более сильное сопротивление воздуха.
Выходит, что способность снаряда сохранять свою скорость зависит не просто от его веса, а от отношения веса к площади, встречающей сопротивление воздуха,— иными словами, от той нагрузки, которая приходится на каждый квадратный сантиметр площади поперечного сечения снаряда.
Вес, приходящийся на квадратный сантиметр площади поперечного сечения снаряда, называют его «поперечной нагрузкой». При одинаковой форме, скорости и угле бросания дальше летит тот снаряд, у которого поперечная нагрузка больше: такой снаряд лучше сохраняет свою скорость во время полета, получает меньшее замедление.
Сравним теперь наши три снаряда.
37-миллиметровый снаряд весит почти 0,5 килограмма, а площадь его поперечного сечения {189}
 |
|
Рис. 149. Вот как «выросли» снаряды за последние 100 лет |
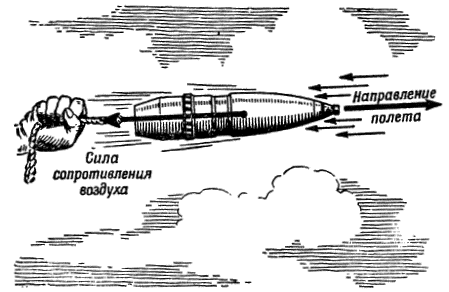 |
|
Риc. 150. Так сила сопротивления воздуха действует на снаряд в самом начале его полета |
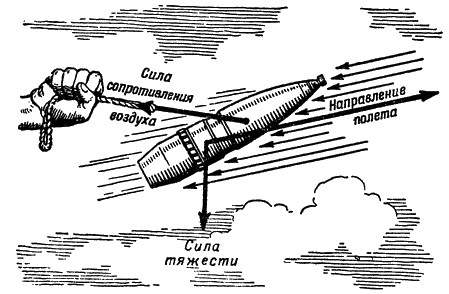 |
|
Рис. 151. Так сила сопротивления воздуха действует на снаряд во время его полета |
сечения — около 11 квадратных сантиметров. Значит, его поперечная нагрузка — 500 граммов, деленные на 11 квадратных сантиметров, или около 45 граммов на 1 квадратный сантиметр.
А поперечная нагрузка 76-миллиметрового снаряда — 142 грамма на 1 квадратный сантиметр, вчетверо больше.
152-миллиметровый снаряд имеет самую большую поперечную нагрузку — около 226 граммов на 1 квадратный сантиметр.
Вот почему он и летит дальше, чем остальные.
Выгоднее всего, значит, увеличить вес снаряда, не увеличивая в то же время площади его поперечного сечения, то-есть площади, на которую давит воздух.
Для этого достаточно сделать снаряд длиннее.
Так на деле и поступают: на смену шаровым снарядам пришли продолговатые; и эти продолговатые снаряды делаются, по мере своего совершенствования, все длиннее и длиннее.
В артиллерии принято измерять длину снаряда не только в обычных линейных мерах, но и в калибрах; если длина снаряда вдвое больше его диаметра, то говорят: снаряд имеет длину 2 калибра.
Так вот, круглая граната, длина которой, разумеется, один калибр, сменилась продолговатой, в два {190} калибра длиной. Это был снаряд начала шестидесятых годов XIX века. 10 лет спустя граната достигла длины 3 калибров. Ко времени первой мировой войны снаряд вытянулся еще больше и достиг 4 калибров в длину. А современная граната имеет в длину примерно уже 5 калибров (рис. 149).
Заметно «подросли» снаряды за последние 100 лет!
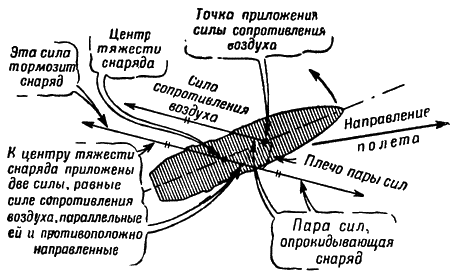 |
|
Рис. 152. Действие силы сопротивления воздуха на летящий снаряд: пара сил, опрокидывающая снаряд |
Однако, если это так выгодно, почему бы не сделать снаряд еще длиннее, например в 10 калибров длиной? Почему бы не создать очень длинный снаряд — снаряд-копье?
Оказывается, этому мешает все тот же воздух.
Вглядитесь в рис. 150,— снаряд выброшен из орудия головной, частью вперед: сила сопротивления воздуха только тормозит движение снаряда. Но под действием силы тяжести он стал опускаться все ниже под линией бросания (рис. 151). И чем больше он опускается, тем больше подставляет сопротивлению воздуха уже не только головную часть, но и боковую поверхность корпуса. Площадь, на которую давит воздух, становится, больше, и сила сопротивления воздуха стремится уже не только тормозить, но и опрокинуть снаряд головной частью назад (рис. 152), снаряд начнет кувыркаться (рис. 153).
Кувыркающийся снаряд подставляет воздуху то одну сторону, то другую, то дно; он быстро теряет скорость и падает на землю.
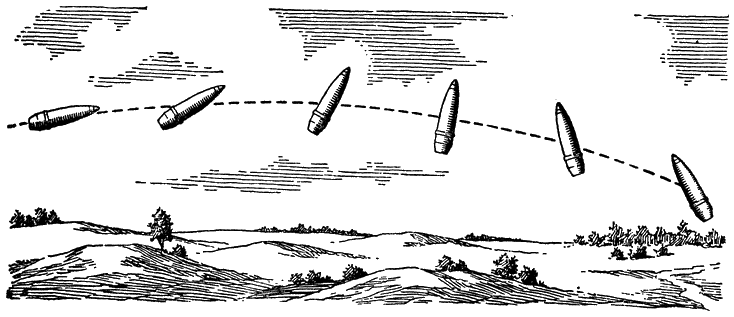 |
|
Рис. 153. Так летел бы в воздухе невращающийся продолговатый снаряд |
Мы старались сделать снаряд подлиннее для того, чтобы он лучше преодолевал сопротивление воздуха. А оказывается: чем длиннее снаряд, тем легче его опрокинуть. Кувыркаясь же, снаряд, конечно, будет испытывать большее сопротивление воздуха.
Неужели тут нет выхода?
КАК ДОБИТЬСЯ УСТОЙЧИВОСТИ СНАРЯДА НА ПОЛЕТЕ
Каждый видел детскую игрушку «волчок». Пока «волчок» быстро вертится, он стоит на своей острой ножке.
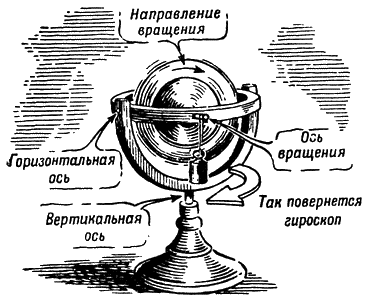
Еще интереснее прибор, называемый гироскопом (рис. 154 и 155). Он знаком всем из физики.
Гироскоп состоит из маховика, который может вращаться вокруг трех осей: во-первых, вокруг своей основной оси, на которую он посажен; во-вторых, вместе с кольцом, поддерживающим основную ось,— вокруг горизонтальной оси, перпендикулярной к первой, и, в-третьих, вместе с внешним полукольцом — вокруг вертикальной оси.
У гироскопа есть замечательное свойство: когда он быстро вращается, он не только сохраняет положение своей оси в пространстве, но и сопротивляется всяким попыткам изменить ее положение.
Этой замечательной способностью вращающегося тела сохранять свою устойчивость и воспользовались артиллеристы: они заставили снаряды быстро вращаться в полете. Достигается это, как мы уже знаем, благодаря нарезам в канале ствола.
Едва снаряд сдвинется с места, его медный поясок врезается в нарезы, а так как нарезы идут винтообразно, то снаряд, следуя по ходу нарезов, начинает быстро вращаться.
Вылетев из ствола, он сохраняет вращение и в воздухе. Вращается он в наших орудиях слева вверх направо, то-есть, если смотреть сзади, по направлению движения часовой стрелки.
 |
 |
|
Рис. 154. Гироскоп |
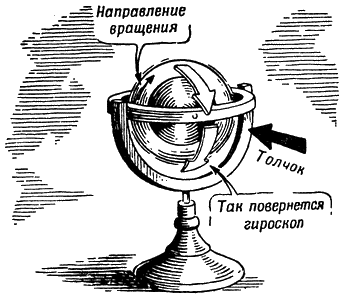
Рис. 155. Как изменится положение оси вращения гироскопа, получившего толчок |
Снаряды различных орудий делают от 200 до 500 оборотов в секунду.
Колесо автомобиля на полном ходу делает в секунду около 16 оборотов, винт самолета — от 35 до 75. Снаряд вращается в 30 раз быстрее автомобильного колеса и в 5–7 раз быстрее, чем воздушный винт самолета.
Эта огромная скорость достаточна, чтобы обеспечить устойчивость современного продолговатого снаряда во время полета.
Но вернемся к вопросу о вращении летящего снаряда.
ЛЕТЯЩИЙ ГИРОСКОП
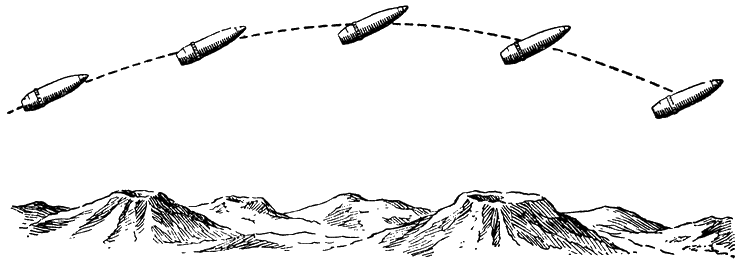
Если бы снаряд был в полете вполне устойчив, он летел бы, как изображено на рис. 156, и падал бы на землю не головой, а дном.
На самом же деле снаряд летит не так.
Еще один опыт с гироскопом поможет нам лучше понять особенности полета снаряда.
Навесим груз на один из концов оси вращения маховика, как изображено на рис. 154.
Вы думаете, вращающийся гироскоп наклонится вниз, в сторону груза? Ничуть не бывало: гироскоп повернется вокруг своей вертикальной оси слева направо, как показывает стрелка на рис. 154.
Попробуйте теперь толкнуть гироскоп, ударить по одному из концов горизонтальной оси (см. рис. 155). Казалось бы, гироскоп должен от такого толчка повернуться на своей вертикальной оси.
Не тут-то было: на самом деле гироскоп начнет поворачиваться вокруг горизонтальной оси так, как изображено на рис. 155.
В этом и заключается основное свойство гироскопа: он изменяет положение своей оси, двигаясь всегда под прямым углом к направлению действия внешней силы и в сторону своего вращения.
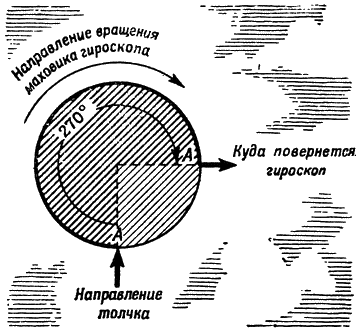
При этом он подчиняется такому правилу: если какая-то точка гироскопа получила толчок, направленный перпендикулярно (по нормали) к его оси, то от толчка гироскоп отклонится в ту сторону, куда должна прийти через три четверти оборота точка, получившая толчок (рис. 157).
 |
|
Рис. 156. Так летел бы вращающийся снаряд в безвоздушном пространстве |
 |
 |
|
Рис. 157. Как отражается на вращающемся снаряде полученный им толчок |
Рис. 158. Действие сопротивления воздуха на вращающийся снаряд |
Быстро вращающийся во время полета снаряд напоминает маховик гироскопа. Как и гироскоп, снаряд стремится сохранить положение своей оси в пространстве. Но при этом снаряд, конечно, опускается под линией бросания. Пока ось снаряда совпадала с касательной к траектории, сопротивление воздуха распределялось равномерно по всем точкам головной части снаряда и только замедляло его полет (см. рис. 150).
Но едва лишь ось снаряда начала отходить от касательной к траектории (это произошло в самом начале движения), как снаряд подставил сопротивлению воздуха боковую поверхность корпуса (см. рис. 151). Невращающийся снаряд опрокинулся бы при этом. Но снаряд вращается. Как и маховик гироскопа, он стремится сохранить устойчивость; на действие внешней силы он отвечает поворотом в направлении, перпендикулярном к тому, по которому действует сила.
Сопротивление воздуха толкает головную часть снаряда снизу вверх; снаряд отвечает на это тем, что поворачивает головную часть
 |
|
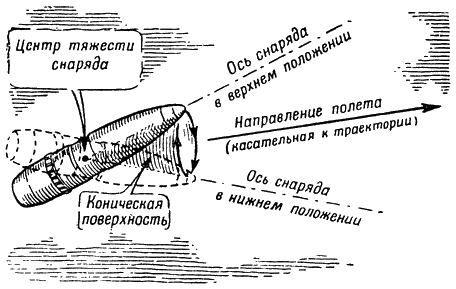
Рис. 159. Коническое вращение головной части снаряда |
вправо, под прямым углом к направлению действия внешней силы и в сторону своего вращения (рис. 158).
В этом новом положении воздух сильнее давит на снаряд слева, стремится отклонить его головную часть вправо. Упрямый снаряд-гироскоп повернет ее вниз. Тогда воздух, действуя на
 |
|
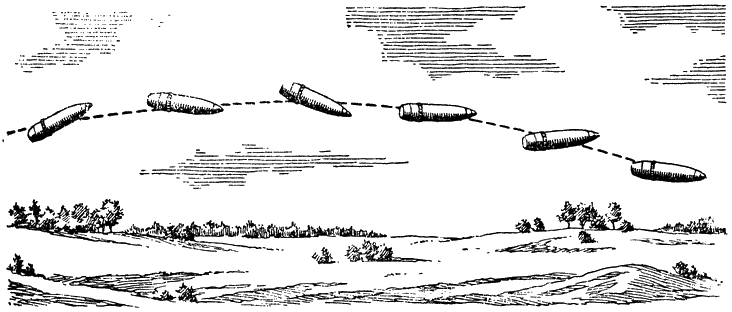
Рис. 160. Так на самом деле летит в воздухе вращающийся снаряд |
снаряд сверху, начнет отклонять его головную часть вниз. А снаряд-гироскоп сделает опять по-своему — повернет ее влево. Как только воздух попробует отклонить головную часть снаряда влево, снаряд поднимет ее вверх. И такая борьба снаряда-гироскопа с силой сопротивления воздуха продолжается на протяжении всего полета. Головная часть снаряда перемещается то вправо, то вниз, то влево, то вверх, то-есть описывает около траектории окружность, а ось снаряда образует коническую поверхность (рис. 159).
В результате вращающийся снаряд летит все время головной частью вперед и в таком же положении падает на землю (рис. 160).
И получается, что та же самая сила сопротивления воздуха, которая мешала, опрокидывала невращающийся снаряд, начинает помогать артиллеристам, как только снаряд приобретает вращательное движение: сила сопротивления воздуха теперь уже «привязывает» головную часть снаряда к траектории.
 |
|
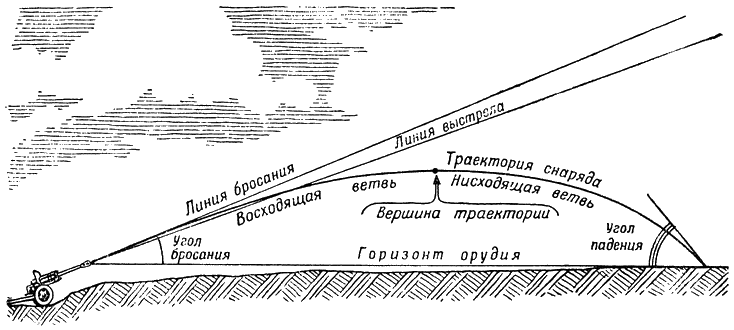
Рис. 161. Элементы траектории |
Теперь, когда мы узнали о всех силах, действующих на снаряд во время полета, мы должны понять разницу в очертаниях траекторий, показанных на рис. 137.
При полете в воздухе траектория снаряда всегда несимметрична: нисходящая ветвь у нее круче и короче восходящей, и угол падения снаряда всегда больше угла бросания. На рис. 161 показаны основные элементы траектории — линии и углы, связанные с нею.
ДЕРИВАЦИЯ
Уже в начале применения нарезных орудий артиллеристы столкнулись с непонятным на первых порах явлением: вращающийся снаряд падал не туда, куда наводили орудие, а в русской артиллерии — всегда правее цели, во французской — всегда левее цели.
У ненарезных орудий таких постоянных отклонений не наблюдалось, значит это явление связано с нарезами, — сделали вывод артиллеристы.
Но почему же при стрельбе из русских орудий снаряд отклоняется всегда вправо от того направления, по которому наведено орудие, а при стрельбе из французских орудий — влево? В чем тут дело? Отчего происходит такое различие в направлении отклонения снаряда?
Объяснить это явление удалось русскому ученому-артиллеристу Н. А. Забудскому. Он доказал, что постоянное отклонение снаряда в сторону от направления, по которому наведено орудие, зависит от того, как идут нарезы в канале ствола орудия: когда нарезы идут, как в русских орудиях, слева вверх направо, так что снаряд, вылетев из орудия, вращается по направлению движения часовой стрелки,— он отклоняется всегда вправо; если же нарезы идут, как во французских орудиях, справа вверх налево, так что направление вращения снаряда противоположно направлению движения часовой стрелки,— снаряд отклоняется влево.
Деривация — так стали называть это постоянное боковое отклонение снаряда, выпущенного из нарезного орудия.
В чем же заключается причина деривации?
Задайте себе такой вопрос: одинаковое ли сопротивление воздуха испытывают все части боковой поверхности летящего снаряда, или это сопротивление сильнее с какой-либо одной стороны? На первый взгляд может показаться, что — одинаковое: ведь снаряд последовательно поворачивает на полете свою головную часть вправо, вниз, влево и вверх. Но такой ответ будет слишком поспешным. Давая такой ответ, мы допустили бы ошибку, так как не учли бы, что снаряд непрерывно понижается под линией бросания из-за действия силы тяжести.
Вот что надо вспомнить для правильного ответа на этот вопрос.
Снаряд испытывает более сильное сопротивление воздуха попеременно слева, справа и сверху исключительно оттого, что во время полета он поворачивает головную часть в ту или другую сторону; снизу же {196} он испытывает более сильное сопротивление, чем с других сторон, еще и из-за того, что под действием силы тяжести он опускается под линией бросания по закону свободного падения тел. Вы уже знаете, что понижение снаряда под линией бросания происходит в течение всего времени его полета, и притом с нарастающей скоростью; 4,9 метра в первую секунду полета и еще на 9,8 метра больше в каждую последующую секунду (см. стр. 178). Вот это-то непрерывное понижение снаряда под линией бросания и приводит к тому, что снизу снаряд испытывает более сильное сопротивление воздуха, чем с любой другой стороны — слева, сверху или справа.
Теперь вам ясно, что действие силы сопротивления воздуха на боковую поверхность летящего снаряда значительно сильнее снизу, чем справа, слева или сверху.
Вспомните, что при «толчке» снизу гироскоп, вращающийся слева вверх направо (по ходу часовой стрелки), повернется вправо. Но ведь снаряд испытывает такие «толчки» непрерывно, один за другим в течение всего своего полета, так как понижение снаряда под линией бросания происходит непрерывно; значит так же непрерывно головная часть снаряда будет отклоняться вправо от первоначального направления — дополнительно к круговому коническому вращению. Следовательно, в течение всего времени полета снаряд будет забирать вправо и притом чем дальше, тем больше.
Таким образом, при более подробном изучении вопроса о полете снаряда, вращающегося слева вверх направо, мы должны будем сказать, что под действием силы сопротивления воздуха и силы тяжести такой снаряд описывает головной частью окружность вокруг траектории и непрерывно отклоняется вправо от направления, по которому был выпущен; поэтому он падает не в той точке, куда было наведено орудие, а правее.
В этом и заключается явление, называемое деривацией. Величина деривации тем больше, чем продолжительнее полет снаряда. Снаряд 76-миллиметровой пушки при стрельбе на 5 километров отклоняется вправо на 5 метров, а при стрельбе на 10 километров — уже на 50 метров. При стрельбе на 10 километров из 122-миллиметровой гаубицы деривация получается еще больше — 110 или даже 310 метров — в зависимости от того, будем ли мы стрелять при углах возвышения меньше 45 или больше 45 градусов.
Таким образом, вследствие деривации траектория снаряда представляет собой кривую не только в вертикальной плоскости, но и в горизонтальной (рис. 162).
Если снаряд вращается справа вверх налево, как у французских орудий, по тем же причинам он отклоняется влево от первоначального направления.
Невращающиеся снаряды (например мины современных минометов), понятно, не имеют деривации, так как деривация связана именно с вращением снаряда. {197}
 |
|
Рис. 162. Так выглядит траектория снаряда, летящего в воздухе, если на нее посмотреть сверху |
Часто задают такой вопрос: ну, а будет ли деривация у снаряда, выпущенного вертикально вверх? На этот вопрос надо ответить так: при стрельбе строго вверх деривация отсутствует, так как действие силы тяжести на снаряд, выпущенный вертикально, выразится только в том, что его поступательная скорость будет постепенно уменьшаться, давление же воздуха на корпус такого снаряда будет оставаться равномерным со всех сторон.
НАРЕЗНОЙ СНАРЯД
Вернемся теперь к вопросу — почему же не сделать очень длинный снаряд, так сказать, снаряд-копье?
Оказывается, такой снаряд был бы все же недостаточно устойчив в полете.
Чтобы обеспечить ему устойчивость, надо было бы вращать его еще раза в 2–3 быстрее, чем вращается современный снаряд.
Для этого и нарезы в орудии надо было бы сделать раза в 2–3 круче, чем их делают теперь.
Но тогда мягкий медный ведущий поясок снаряда не выдержал бы громадного давления, какое пришлось бы на его долю при такой крутой нарезке и при большом весе длинного снаряда,— он был бы сорван нарезами в канале ствола,
Нужны, значит, какие-то новые технические приемы, чтобы обеспечить такому длинному и тяжелому снаряду достаточно быстрое вращение.
Что можно сделать в этом направлении?
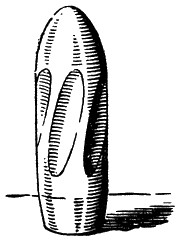
Еще в шестидесятых годах XIX века испытывался многоугольный (или, как говорят, полигональный) снаряд (рис. 163). Разумеется, и канал орудия, предназначенного для стрельбы этим снарядом, представлял собой в сечении многоугольную призму, несколько скрученную, чтобы придать вращение этому снаряду.
В свое время это предложение не нашло широкого применения, а вскоре и вовсе было забыто.
Были и другие предложения. Уже после первой мировой войны были изготовлены опытные снаряды с готовыми выступами, или, {198}
 |
|
Рис. 163. Полигональный (многоугольный) снаряд |
иначе, нарезные снаряды в 10 калибров длиной (рис. 164). Снаряд этот, казалось, имел большие преимущества перед старыми: поперечная нагрузка у нарезного снаряда была вдвое больше, чем у обычного, а поэтому и летел он заметно дальше. Объем внутренней каморы нарезного снаряда был примерно вдвое больше, чем у старого снаряда, а потому в нем помещалось значительно больше взрывчатого вещества, чем в старом.
Но изготовлять снаряды с готовыми нарезами трудно и дорого, а заряжать орудие таким снарядом долго и неудобно: уже во время заряжания снаряд должен двигаться своими выступами по нарезам орудия.
 |
|
Рис. 164. Нарезной снаряд |
Поэтому нарезные снаряды не нашли широкого применения, и в течение всей второй мировой войны никто не стрелял такими снарядами. В современных сражениях снаряды расходуются миллионами, промышленность должна изготовлять их в огромных количествах; поэтому снаряды должны быть просты в изготовлении и возможно более дешевы; а дорогие и сложные в производстве нарезные снаряды не удовлетворяют этим требованиям: вот почему они относятся к тем многочисленным остроумным предложениям, которые, однако, не находят применения на практике.
СНАРЯД С ОПЕРЕНИЕМ
Во второй мировой войне широкое применение получили снаряды с оперением — мины.
Вспомните древние стрелы, которыми в те времена, когда еще не было огнестрельного оружия, воины и охотники стреляли из лука; вы, несомненно, видели такую стрелу, если не в музее, то хотя бы на рисунке. Ее устойчивости на полете добивались тем, что снабжали ее оперением. Оперение оказывало во время полета стрелы такое же действие, как руль у лодки во время ее движения: если руль поставлен прямо, то и лодка идет прямо. Так же летела и стрела,— оперение играло роль руля, поставленного прямо.
Мысль изготовить снаряд с оперением появилась впервые у русских артиллеристов осажденной японцами крепости Порт-Артур в 1904 году. Изготовив мины, которые не помещались в ствол
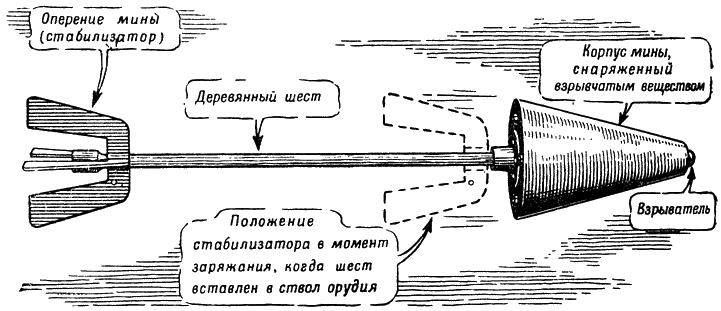 |
|
Рис. 165. Первый артиллерийский снаряд с хвостовым оперением — шестовая мина к миномету С. Н. Власьева и Л. Н. Гобято |
орудия, изобретатели С. Н. Власьев и Л. Н. Гобято должны были подумать и о том, как сделать эти мины устойчивыми на полете; они снабдили каждую мину стабилизатором из четырех железных перьев (рис. 165).
Эта идея русских артиллеристов была использована при создании минометов во время первой мировой войны (взгляните на рис. 180 на стр. 212), и с тех пор и до наших дней минометы стреляют оперенными снарядами-минами.
Но современная мина имеет уже не 2 пера, как древняя стрела, и не 4, как мина защитников Порт-Артура или времен первой мировой войны, а значительно больше: например, у мины 82-миллиметрового миномета 6 или чаще 10 перьев, а у мины 120-миллиметрового миномета — 12 перьев. Такое количество перьев хорошо обеспечивает устойчивость мины на полете: 12 перьев — это как бы 12 рулей, каждый из которых помогает мине быть устойчивой во время полета.
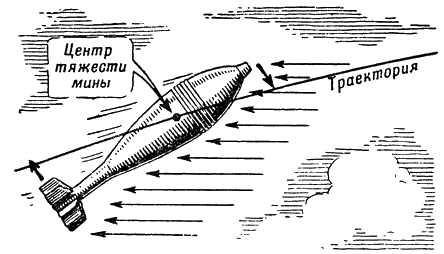 |
|
Рис. 166. Действие силы сопротивления воздуха на летящую мину: хвостовое оперение выравнивает мину на полете, заставляет ее головную часть „следить” за траекторией и этим обеспечивает полет мины головой вперед |
Оперенная мина так же «следит за траекторией», как и вращающийся снаряд: как только под действием силы тяжести мина начинает опускаться под линией бросания, давление воздуха на перья стабилизатора станет больше с одной стороны, чем с другой, а из-за этого хвост мины повернется, — ось мины снова совместится с касательной к траектории (рис. 166).
Таким образом, в наши дни наряду со снарядами, быстро вращающимися на полете, получили широкое распространение не вращающиеся во время полета оперенные снаряды — мины.
В СТРАТОСФЕРУ
Как видите, много хлопот причинило артиллеристам сопротивление воздуха. Кое с чем удалось справиться, и притом с успехом: заставив снаряд вращаться, добились того, что он стал устойчив на полете.
Но главное заключается в том, что сопротивление воздуха все же резко сокращает дальность полета снаряда.
Нельзя ли избавиться и от этого действия воздуха? Но для этого надо избавиться от сопротивления воздуха. А как же это сделать? Ведь воздух окружает Землю со всех сторон!
Да, вся Земля окружена воздухом. Но зато плотность его различна на разных высотах. На большой высоте, в стратосфере, воздух сильно разрежен, сопротивление его ничтожно. Пусть хотя бы часть пути снаряд пролетит без воздействия воздуха!
Незадолго до первой мировой империалистической войны известный русский артиллерист В. М. Трофимов пришел однажды в Главное артиллерийское управление царской армии со смелым проектом: построить такое орудие, которое забросит снаряд очень высоко — в стратосферу — и благодаря этому будет стрелять на сотню с лишним километров.
Это было в 1911 году.
А 7 лет спустя — в 1918 году — немцы начали обстрел столицы Франции — Парижа — с расстояния более 100 километров. Стал ли им известен проект В. М. Трофимова, как и многие другие тайны русского царского военного министерства, или они через несколько лет после В. М. Трофимова самостоятельно пришли к тем же выводам — этого мы не знаем.
Но в то время, как ученые-артиллеристы Франции, Англии и Америки были в полном недоумении и не могли объяснить, каким образом немцы сумели стрелять на такое расстояние, В. М. Трофимов пришел в Главное артиллерийское управление Красной Армии и сказал: «Я объясню, в чем дело. Не понимаю только, как они об этом узнали, но они осуществили мой проект 1911 года. Если хотите, я построю такое орудие для Красной Армии».
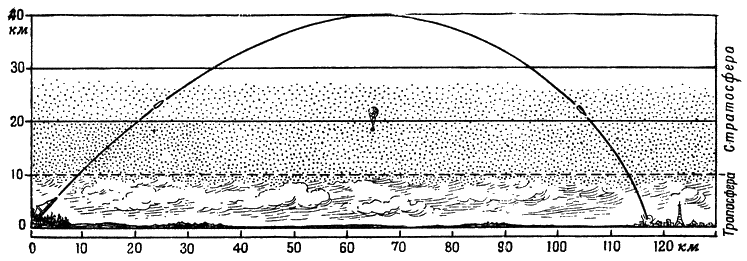 |
|
Рис. 167. Траектория сверхдальнобойного снаряда |
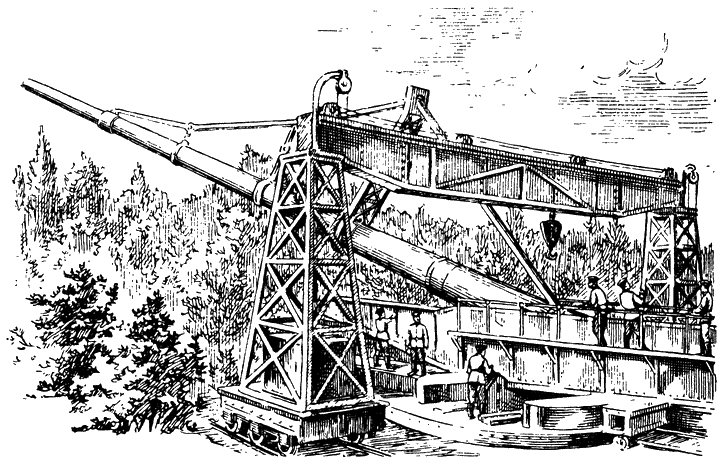 |
|
Рис. 168. Сверхдальнобойная пушка, стрелявшая по Парижу в 1918 году |
 |
|
Рис. 169. Снаряд и заряд сверхдальнобойной пушки по сравнению со снарядом и зарядом обыкновенной пушки того же калибра |
В чем же заключалась сущность «сверхдальней» стрельбы?
Снаряд сверхдальнобойного орудия, выпущенный с большой скоростью — около 2000 метров в секунду — под углом около 52 градусов, быстро пробивал нижний плотный слой воздуха и вырывался на простор стратосферы, входя в нее под углом 45 градусов, то-есть как раз под углом наибольшей дальности полета в безвоздушном пространстве (рис. 167). К этому времени снаряд сохранял еще скорость около 1000 метров в секунду. Такая скорость позволяла ему пролететь в стратосфере около 100 километров, после чего он опускался на землю с заоблачных высот, проделав в воздухе путь около 120 километров.
Немецкие сверхдальнобойные орудия имели огромную длину ствола, достигавшую 34 метров (рис. 168). Стволы были снабжены в середине стойками, связанными стальными тягами с {202} дульной и казенной частями орудий. Иначе при такой длине ствол мог прогнуться под действием собственного веса. Да и так после каждого выстрела ствол колебался в течение двух-трех минут.
Снаряды с готовыми выступами, калибром от 210 до 232 миллиметров, весили от 104 до 126 килограммов каждый.
А заряд весил почти вдвое больше — около 215 килограммов (рис. 169). Это особенно резко отличает сверхдальнобойную пушку от обычных орудий, в которых вес заряда в несколько раз меньше веса снаряда.
Необычной длине ствола и огромному весу заряда соответствовал и огромный вес орудия. Орудие с установкой весило 750 тонн.
Для перевозки такой пушки в разобранном виде вместе с установкой понадобился бы товарный поезд из 50 вагонов. Вот какой огромный вес влечет за собой большое увеличение длины ствола и веса заряда! Конечно, о подвижности такого орудия не может быть и речи. Да и точность стрельбы его оказалась очень плохой. Из всех снарядов, выпущенных по огромной площади Парижа, в город попала всего лишь небольшая часть.
Понятно, что массового распространения сверхдальнобойная артиллерия не получила. Слишком ничтожны оказались результаты ее стрельбы. И, кроме того, чем могущественнее орудие, чем оно дальнобойнее, тем короче его «жизнь». Ствол сверхдальнобойной пушки приходил в негодность после 50–70 выстрелов. И уже после первых двух десятков выстрелов значительно уменьшалась точность стрельбы, возрастало рассеивание. Вообще говоря, можно построить пушку, которая стреляла бы не только на 100 километров, а и гораздо дальше. Но такая пушка будет очень невыгодна: изготовление ее будет стоить, огромных денег, а выстрелит она всего лишь несколько раз.
В наши дни большая дальность полета снаряда достигается применением реактивного двигателя, находящегося в самом снаряде. Такие снаряды летят на расстояние более 300 километров.

| << |
|
{203} |
|
>> |
