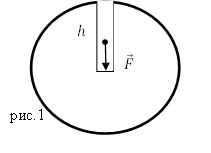
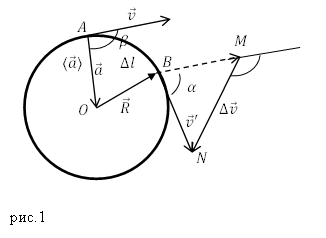
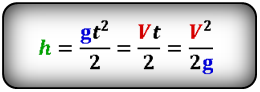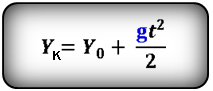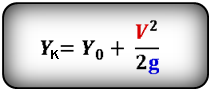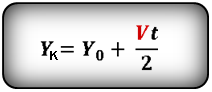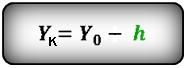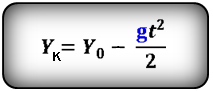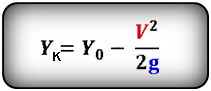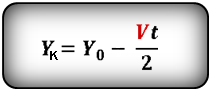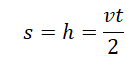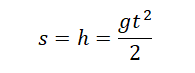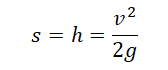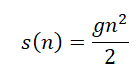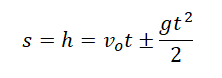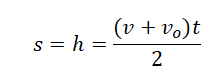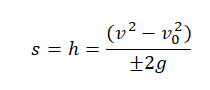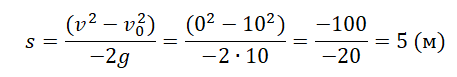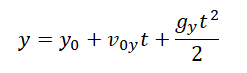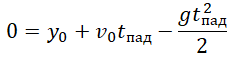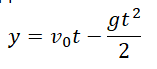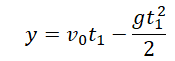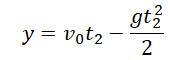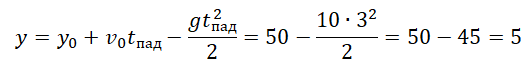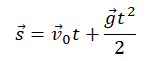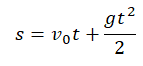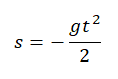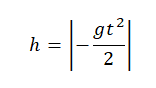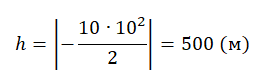Как найти скорость падения тела, но не имея времени падения?
ФизикаМеханикаРешение задач по физике
Артем Жиров
13 июля 2020 · 11,3 K
Углубляюсь в познание физики, на данный момент конкретно интересует квантовая гравитация. · 28 сент 2020
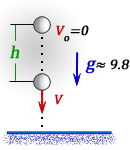
При свободном падении тела без начальной скорости, то есть Vo = 0. Тогда, имеем слдеующие формулы:
Vy = gt
y = (gt^2)/2
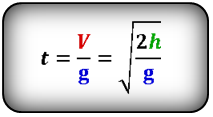
из последней можно найти время t = кв. корень (2h/g)
Из чего следует:
V = кв. корень (2gh)
где g – ускорение свобоного падения 9,81 м/с^2
h – высота
V – скорость
y – вертикальное направление, то есть взято из системы координат.
12,7 K
Комментировать ответ…Комментировать…
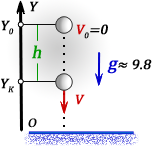
1. Формулы скорости, высоты, времени в условиях свободного падения при начальной скорости равной нулю
h – раcстояние пройденное телом за время t
V – скорость тела в момент времени t
t – время падения за которое тело пролетело расстояние или опустилось на высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в определенный момент времени или на определенной высоте (V):
Формула высоты, на которую опустилось тело или расстояния, которое пролетело тело при падении (h):
Формула времени свободного падения тела вертикально вниз (t):
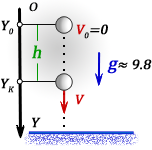
2. Формулы координаты тела, если направление оси OY совпадает с направлением скорости падующего тела V
h – раcстояние пройденное телом за время t
V – скорость тела в момент времени t
t – время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Yo , Yк – начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):
3. Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V
h – раcстояние пройденное телом за время t
V – скорость тела в момент времени t
t – время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Yo , Yк – начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):
- Подробности
-
Опубликовано: 20 июля 2015
-
Обновлено: 13 августа 2021
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g.
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скорость
v = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота падения
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
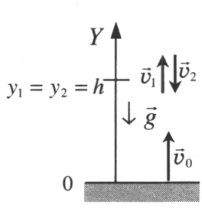
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (v↑↓g).
Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону (v↑↑g).
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело падает без начальной скорости (свободно) v0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
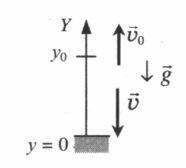
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
Свободное падение на землю с некоторой высоты
Чертеж:
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
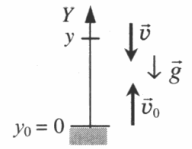
–v = v0 – gt
Уравнение координаты:
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
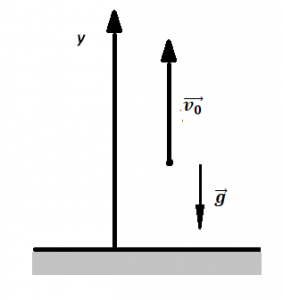
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.6k
Свободное падение тела — это его равнопеременное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист прыгает из самолета, первые несколько секунд после прыжка он падает в свободном состоянии. Этот короткий отрезок времени характеризуется ощущением невесомости, сходным с тедж.м, что испытывают космонавты на борту космического корабля.
История открытия явления
О свободном падении тела ученые узнали еще в Средневековье: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Например, они утверждали, что скорость падающего тяжелого предмета возрастает прямо пропорционально пройденному расстоянию. В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.
В 1590 г. итальянский физик Галилео Галилей сформулировал закон, который устанавливает четкую зависимость пройденного падающим предметом пути от времени. Также ученым было доказано, что при отсутствии воздушного сопротивления все предметы на Земле падают с одинаковым ускорением, хотя до его открытия было принято считать, что тяжелые предметы падают быстрее.
Была открыта новая величина — ускорение свободного падения, которое состоит из двух составляющих: гравитационного и центробежного ускорений. Обозначается ускорение свободного падения буквой g и имеет различное значение для разных точек земного шара: от 9,78 м/с2 (показатель для экватора) до 9,83 м/с2 (значение ускорения на полюсах). На точность показателей влияют долгота, широта, время суток и некоторые другие факторы.
Стандартное значение g принято считать равным 9,80665 м/с2. В физических расчетах, которые не требуют соблюдения высокой точности, значение ускорения принимают за 9,81 м/с2. Для облегчения расчетов допускается принимать значение g равным 10 м/с2.
Для того чтобы продемонстрировать, как предмет падает в соответствии с открытием Галилея, ученые устраивают такой опыт: в длинную стеклянную трубку помещают предметы с различной массой, из трубки выкачивают воздух. После этого трубку переворачивают, все предметы под действием силы тяжести падают одновременно на дно трубки, независимо от их массы.
Когда эти же предметы помещены в какую-либо среду, одновременно с силой тяжести на них действует сила сопротивления, поэтому предметы в зависимости от своей массы, формы и плотности будут падать в разное время.
Формулы для расчетов
Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с2).
Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.
Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2/2.
Формула для определения скорости падающего предмета в конце падения при известном времени падения: u = gt .
Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.
Интересные факты
Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.
В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.
В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.
В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.
Видео
Посмотрите интересное и познавательное видео, которое расскажет вам о скорости падения тел.
Формула скорости свободного падения в физике
Формула скорости свободного падения
Ускорение и скорость при свободном падении
Движение тела около поверхности Земли под воздействием силы тяжести называют свободным падением. При исследовании свободного падения тела, обычно силы сопротивления воздуха не учитывают.
Напомним, что величина ускорения свободного падения около поверхности Земли вычисляется как:
[g=gamma frac{M}{({R+h)}^2}left(1right),]
где $gamma =6,67cdot {10}^{-11}frac{Нcdot м^2}{{кг}^2}$- гравитационная постоянная; $M$ – масса Земли; $R$ – радиус Земли.
Если расстояние, с которого падает тело много меньше, чем радиус Земли ($ hll R$), то ускорение свободного падения считают постоянной величиной, равной:
[g=gamma frac{M}{R^2}approx 9,8 (frac{м}{с^2})left(2right).]
Кинематическое уравнение скорости при свободном падении
Свободное падение происходит с постоянным ускорением, что было установлено еще Галилеем, поэтому скорость в кинематике определяет уравнение для равнопеременного движения:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(3right).]
Уравнение (3) показывает изменение вектора скорости $overline{v}left(tright),$ где ${overline{v}}_0$ – начальная скорость движения тела.
Используя это уравнение, и зная начальные условия движения тела можно найти скорость тела относительно избранной системы отсчета для любого момента времени.
Скорость тела, брошенного под углом к горизонту
Допустим, что тело бросили под углом $alpha $ к горизонту. Ось X системы координат направим горизонтально, ось Y перпендикулярно горизонту вверх, тогда начальные условия движения для скорости данного тела запишем как:
[left{ begin{array}{c}
v_xleft(t=0 right)=v_0{cos alpha , } \
v_yleft(t=0 right)=v_0{sin alpha } end{array}
right.left(4right).]
Это означает, что тело бросили под углом $alpha $ к горизонту с начальной скоростью ${overline{v}}_0$. При этом проекции уравнения (3) дадут нам систему уравнений:
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha -gt } end{array}
right.left(5right).]
Формула скорости при свободном падении тела из состояния покоя
Начальные условия для скорости движения для тела, которое падает из состояния покоя, запишем так:
[left{ begin{array}{c}
v_xleft(t=0 right)=0, \
v_yleft(t=0 right)=0 end{array}
right.left(6right).]
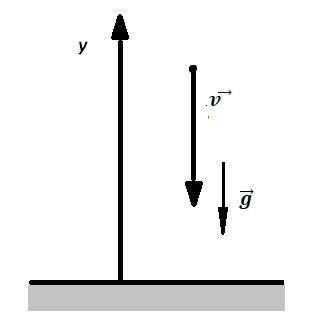
В таком случае выражение (3) в проекции на ось Y, которую выберем вдоль направления движения (рис.1), тела будет выглядеть как:
[left{ begin{array}{c}
v_y=-gt end{array}
right.left(7right).]
В момент падения скорость тела при свободном его падении с высоты $h$ равна:
[v_{pad}=-sqrt{2gh}left(8right).]
Знак минус в формуле (8) означает, что скорость падения направлена против нашей оси Y.
Отметим, что тело, брошенное вертикально вверх движется до максимальной высоты подъема столько же времени, сколько оно потом падает с этой высоты до точки бросания.
Примеры задач с решением
Пример 1
Задание. Тело бросили вертикально вверх. Оно вернулось в точку бросания через $t’$ секунд. Какова начальная скорость тела?textit{}
Решение. Сделаем рисунок.
Запишем уравнение для скорости движения тела в векторном виде:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(1.1right).]
Найдем проекцию этого уравнения на ось Y:
[v=v_0-gt left(1.2right).]
В точке максимального подъема скорость тела равна нулю, следовательно:
[0=v_0-g{t }_{pod}to v_0=g{t }_{pod}left(1.3right).]
Принимая во внимание, что время подъема равно времени спуска при отсутствии сил трения, имеем:
[{t }_{pod}=frac{t’}{2}left(1.4right).]
Подставим (1.4) в (1.3), имеем:
[v_0=gfrac{t’}{2}.]
Ответ. $v_0=gfrac{t’}{2}$
Пример 2
Задание. Одно тело бросили вертикально вверх с начальной скоростью равной $v_0.$ В этот же момент времени вертикально вниз с начальной скоростью $v_0$ бросили второе тело. Высота, с которой бросили это тело равно высоте максимального подъема первого тела. Какова скорость первого и второго тел в момент встречи этих двух тел? Тела считайте материальными точками, сопротивление воздуха не учитывать.
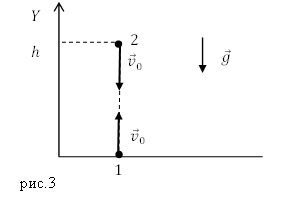
Решение. Сделаем рисунок.
За основу решения задачи примем уравнение для скорости движения тела в поле тяжести Земли:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(2.1right).]
Для первого тела уравнение (2.1) в проекции на ось Y будет иметь вид:
[v_1=v_0-gt left(2.2right).]
Уравнение скорости второго тела при его падении выглядит как:
[{-v}_2=-v_0-gt left(2.3right).]
Для решения задачи будем использовать кинематическое уравнение для перемещения тела с постоянным ускорением:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(2.4right).]
В проекции на ось Y это уравнение для первого тела, поднимающегося вверх, даст выражение:
[y_1=v_0t-frac{gt^2}{2}left(2.5right).]
Для второго тела при его падении в проекции на ось Y (2.4) запишется как:
[y_2=h-v_0t-frac{gt^2}{2}left(2.6right).]
Найдем время встречи тел ($t’$) из системы уравнений (2.5) и (2.6), учитывая, что при встрече тел $y_1=y_2$:
[v_0t’-frac{g{t’}^2}{2}=h-v_0t’-frac{g{t’}^2}{2}to 0=h-2v_0t’to t’=frac{h}{2v_0}left(2.7right).]
Подставим время $t’$ в уравнение (2.2) получим скорость первого тела в момент встречи:
[v_1=v_0-gfrac{h}{2v_0}left(2.8right).]
Найдем высоту $h$, на которую способно подняться первое тело. Для этого найдем время подъема тела, зная, что в точке максимального подъема скорость тела равна нулю:
[v_1=v_0-gt=0to t_{pod}=frac{v_0}{g}left(2.9right).]
Высота подъема, она же высота с которой бросили второе тело найдётся из уравнения (2.5), если в него подставить $t_{pod}$:
[y_1=h=v_0t-frac{g{t_{pod}}^2}{2}=v_0frac{v_0}{g}-frac{g}{2}frac{v^2_0}{g^2}=frac{v^2_0}{2g}left(2.10right).]
Подставляя вместо $h$ правую часть уравнения (2.10) в формулу (2.8) получим скорость движения первого тела в его момент встречи со вторым телом:
[v_1=v_0-gfrac{v^2_0}{2g}frac{1}{2v_0}=frac{3}{4}v_0.]
Используя уравнение (2.3), подставляя в нее время встречи тел ($t’$) из (2.7), учитывая (2.10) получим скорость движения второго тела в момент встречи:
[v_2=v_0+gt=v_0+gfrac{1}{2v_0}frac{v^2_0}{2g}=v_0+frac{v_0}{4}=frac{5}{4}v_0.]
Ответ. $v_1=frac{3}{4}v_0,$ $v_2=frac{5}{4}v_0$
Читать дальше: формула ускорения свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!