
Свободное падение яблока.
Свобо́дное падéние — равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы. На поверхности Земли (на уровне моря) ускорение свободного падения меняется от 9,832 м/с² на полюсах, до 9,78 м/с² на экваторе.
В частности, парашютист в течение нескольких первых секунд прыжка находится практически в свободном падении.
Свободное падение возможно на поверхность любого тела, обладающего достаточной массой (планеты и их спутники, звёзды, и т. п.).
Во время свободного падения какого-либо объекта этот объект находится в состоянии невесомости (как если бы он находился на борту космического аппарата, движущегося по околоземной орбите). Данное обстоятельство используется, например, при тренировке космонавтов: самолёт с космонавтами набирает большую высоту и пикирует, находясь в течение нескольких десятков секунд в состоянии свободного падения; космонавты и экипаж самолёта при этом испытывают состояние невесомости[1].
Комментарий к определению[править | править код]
Поскольку сила тяжести понимается как сила, действующая вблизи планеты, определению «свободного падения» строго соответствуют движения тела около поверхности Земли или другого крупного астрономического объекта. Важным условием является малость сопротивления среды (или её отсутствие[2]). Примером служит полёт камня, брошенного с поверхности или с некоторой высоты под любым углом (при небольших скоростях сопротивлением воздуха можно пренебречь), причём движение вверх тоже является свободным падением, вопреки интуитивному восприятию. Траектория может иметь форму участка параболы или отрезка прямой.
Очень часто, однако, под «свободным падением» подразумевается только движение тела вертикально вниз и без начальной скорости, у земной поверхности[3]. При этом, в бытовых рассуждениях, сила сопротивления атмосферы иногда трактуется не как искажающий фактор, а как полноценный атрибут такого движения, на равных с силой тяжести.
Изредка «свободное падение» трактуется шире официального определения, а именно допускается движение тела на значительном удалении от планеты. Тогда в определение вписываются, скажем, вращение Луны вокруг Земли или падение тел из космоса. Объект, свободно падающий из бесконечности на планету, достигает её поверхности или верхних слоёв атмосферы со скоростью не ниже второй космической, а траектория представляет собой кусок гиперболы, параболы или прямой; ускорение непостоянно, так как изменения гравитационной силы в пределах изучаемой области существенны.
История[править | править код]
Первые попытки построить количественную теорию свободного падения тяжёлого тела были предприняты учёными Средневековья; в первую очередь следует назвать имена Альберта Саксонского и Николая Орема. Однако они ошибочно утверждали[4][5], что скорость падающего тяжёлого тела растёт пропорционально пройденному пути. Эту ошибку впервые исправил Д. Сото (1545), который сделал правильный вывод о том, что скорость тела растёт пропорционально времени, прошедшему с момента начала падения, и нашёл[6][7] закон зависимости пути от времени при свободном падении (хотя эта зависимость была дана им в завуалированном виде). Чёткая же формулировка закона квадратичной зависимости пути, пройденного падающим телом, от времени принадлежит[8] Г. Галилею (1590) и изложена им в книге «Беседы и математические доказательства двух новых наук»[9]. Сначала Лейбниц, а затем, в 1892—1893 гг. профессор МГУ Н. А. Любимов поставили опыты, демонстрирующие возникновение невесомости при свободном падении[10].
Демонстрация явления[править | править код]

Свободное падение. Вектор силы тяжести направлен вертикально вниз.
При демонстрации явления свободного падения откачивают воздух из длинной трубки, в которую помещают несколько предметов разной массы. Если перевернуть трубку, то тела, независимо от их массы, упадут на дно трубки одновременно.
Если же эти предметы поместить в какую-либо среду, то к действию силы тяжести добавится сила сопротивления, и тогда времена падения данных предметов уже не обязательно будут совпадать, а будут в каждом случае зависеть от формы тела и его плотности.
Количественный анализ[править | править код]
Введём систему координат Oxyz с началом на поверхности Земли и направленной вертикально вверх осью y и рассмотрим свободное падение тела массы m с высоты y0[11], пренебрегая вращением Земли и сопротивлением воздуха. Дифференциальное уравнение движения тела в проекции на ось y имеет[12] вид:
где g — ускорение свободного падения, а точками над величиной обозначается её дифференцирование по времени.
Интегрируя данное дифференциальное уравнение при заданных начальных условиях y = y0 и v = v0 (здесь v — проекция скорости тела на вертикальную ось), находим[13] зависимость переменных y и v от времени t:
В частном случае, когда начальная скорость равна нулю (то есть тело начинает падение, не испытав толчка вверх или вниз), из этих формул видно, что текущая скорость тела пропорциональна времени, прошедшему с момента начала свободного падения, а пройденный телом путь — квадрату времени.
Подчеркнём, что результаты не зависят от значения массы m.
Рекорды свободного падения[править | править код]
В бытовом смысле под свободным падением нередко подразумевают движение в атмосфере Земли, когда на тело не действуют никакие сдерживающие или ускоряющие факторы, кроме силы тяжести и сопротивления воздуха.
Согласно Книге рекордов Гиннесса, мировой рекорд расстояния, преодолённого при свободном падении, составляющий 24 500 м, принадлежит Евгению Андрееву. Последний установил данный рекорд во время парашютного прыжка с высоты 25 457 м, совершённого 1 ноября 1962 года в районе Саратова; тормозной парашют при этом не применялся[14].
16 августа 1960 г. Джозеф Киттингер совершил рекордный прыжок с высоты 31 км с использованием тормозного парашюта.
В 2005 году Луиджи Кани установил мировой рекорд скорости (прыжок в тропосфере), достигнутой в свободном падении — 553 км/ч.
В 2012 году Феликс Баумгартнер установил новый мировой рекорд скорости в свободном падении, развив скорость 1342 километра в час[15].
30 июля 2016 года американский скайдайвер Люк Айкинс установил уникальный рекорд, совершив прыжок без парашюта с высоты 7600 метров на сеть размером 30×30 м с использованием наземных средств для ориентации[16].
См. также[править | править код]
- Перемещение
Примечания[править | править код]
- ↑ Бутенин, Лунц, Меркин, 1985, с. 132—136.
- ↑ Е. И. Бутиков, А. С. Кондратьев. Физика для углублённого изучения, разд. 1 «Механика», стр. 50. М.: Физматлит (2004). — «Свободным падением называют движение в вакууме, когда сопротивление воздуха отсутствует». Дата обращения: 13 февраля 2018. Архивировано 27 января 2018 года.
- ↑ Свободное падение. Справочный портал «Калькулятор». — «Падение тела, обусловленное притяжением Земли, при отсутствии начальной скорости и сопротивления воздуха считают свободным падением». Дата обращения: 13 февраля 2018. Архивировано 16 февраля 2018 года.
- ↑ Моисеев, 1961, с. 100–101.
- ↑ Тюлина, 1979, с. 51.
- ↑ Моисеев, 1961, с. 105.
- ↑ Тюлина, 1979, с. 53—54.
- ↑ Моисеев, 1961, с. 116.
- ↑ Галилео Галилей. День четвёртый. // Математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению. — М.—Л.: ГИТТЛ, 1934.
- ↑ Перельман Я. И. Межпланетные путешествия. Начальные основания звездоплавания. — 6-е изд. — Л.: Прибой. — С. 163. — 5000 экз.
- ↑ Считаем, что тело при своём движении не слишком удаляется от поверхности Земли, так что ускорение свободного падения можно считать постоянным.
- ↑ Бутенин, Лунц, Меркин, 1985, с. 22.
- ↑ Бутенин, Лунц, Меркин, 1985, с. 23, 32.
- ↑ Рекорд ФАИ № 1623 Архивировано 14 июля 2014 года. — на сайте Международной авиационной федерации (ФАИ).
- ↑ World Record Jump | Red Bull Stratos. Дата обращения: 12 сентября 2013. Архивировано 2 октября 2013 года.
- ↑ Бес страховки. Дата обращения: 2 августа 2016. Архивировано 20 августа 2016 года.
Литература[править | править код]
- Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики: Учебник. Т. II. 3-е изд. — М.: Наука, 1985. — 496 с.
- Моисеев Н. Д. Очерки истории развития механики. — М.: Изд-во Моск. ун-та, 1961. — 478 с.
- Тюлина И. А. История и методология механики. — М.: Изд-во Моск. ун-та, 1979. — 282 с.
Скорость, время и высота свободного падения
- Главная
- /
- Физика
- /
- Скорость, время и высота свободного падения
Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Скорость свободного падения
Если известно время падения
Ускорение свободного падения g =
Время падения
t =
Расстояние h =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Если известно расстояние (высота падения)
Ускорение свободного падения g =
Расстояние h =
Время падения
t =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Расстояние и время свободного падения
Ускорение свободного падения g =
Скорость свободного падения
V =/
Расстояние h =
0
Время падения
t =
0
Округление ответа:
Просто введите данные, и получите ответ.
Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.
Теория
Ускорение свободного падения
Ускорение свободного падения (g) – ускорение, которое придаёт падающему телу сила тяжести. У каждого небесного тела своё значение ускорения свободного падения, например, у планеты Земля оно составляет g = 9,80665 м/с².
Для небесных тел солнечной системы ускорение свободного падения имеет следующие значения:
- Земля – 9,80665 м/с²
- Луна – 1,62 м/с²
- Меркурий – 3,7 м/с²
- Венера – 8,87 м/с²
- Марс – 3,711 м/с²
- Сатурн – 10,44 м/с²
- Юпитер – 24,79 м/с²
- Нептун – 11,15 м/с²
- Уран – 8,87 м/с²
- Плутон – 0,617 м/с²
- Ио – 1,796 м/с²
- Европа – 1,315 м/с²
- Ганимед – 1,428 м/с²
- Каллисто – 1,235 м/с²
- Солнце – 274,0 м/с²
Как найти скорость свободного падения
Скорость свободного падения V можно рассчитать, зная расстояние (высоту) падения h или время падения t.
Зная время падения:
Формула
V = g⋅t
Пример
Для примера, рассчитаем с какой скоростью врежется в землю монета, брошенная из окна небоскрёба, если известно, что она упала за 5 секунд:
V = 9.8 ⋅ 5 = 49 м/с
Монетка ударилась об землю на скорости 49 м/с
Зная высоту падения:
Формула
V = √2⋅h⋅g
Пример
Для примера, определим скорость при ударе об землю ядра скинутого с 100 метровой вышки:
V = √2 ⋅ 100 ⋅ 9.8 = √1960 ≈ 44 м/с
Ядро ударится об землю на скорости 44 м/с
Время свободного падения
Время свободного падения – время, которое потребуется телу для того чтоб упасть на землю под действием силы тяжести. Чтобы рассчитать время свободного падения t необходимо знать высоту падения h или скорость в конце падения V.
Зная высоту падения:
Формула
t = √2h⁄g
Пример
Посчитаем чему будет равно время свободного падения t тела упавшего с высоты h = 100 метров:
t = √2⋅100⁄9.8 = √20.4 ≈ 4.5 с
Время свободного падения данного тела составит 4.5 секунды.
Зная скорость в конце падения:
Формула
t = V⁄g
Пример
Если тело после падения ударилось об землю со скоростью V = 50 м/с, то сколько секунд оно падало?
t = 50 ÷ 9.8 = 5.1 с
Время падения данного тела составило 5.1 секунды.
Высота свободного падения
Высота падения – высота с которой сбросили тело, численно равная расстоянию, которое пролетает тело за время падения. Чтобы рассчитать высоту падения h необходимо знать время падения t или скорость в конце падения V.
Зная время падения:
Формула
h = gt²⁄2
Пример
Для примера определим с какой высоты сбросили тело, если известно, что время его падения составило t = 5с:
h = 9.8 ⋅ 5² ÷ 2 = 122.5 м
Тело сбросили с высоты в 122.5 метров.
Зная скорость в конце падения:
Формула
h = V²⁄2g
Пример
Если тело после падения ударилось об землю со скоростью V = 60 м/с, то с какой высоты оно упало?
h = 60² ÷ 2⋅9.8 = 3600 ÷ 19.6 = 183.67 м
Тело упало с высоты в 183.67 метра.
См. также
Random converter
- Калькуляторы
- Механика
Калькулятор скорости, времени и расстояния при свободном падении

График зависимости скорости v (м/с) и расстояния h (м) от времени t (с) падения свободно падающего тела при нулевом сопротивлении воздуха
Этот калькулятор определяет скорость и время свободного вертикального падения тела на поверхность Земли или другой планеты, если известна высота, с которой сброшено тело. Сопротивление воздуха не учитывается. Калькулятор может также рассчитать высоту и время падения, если известна скорость, или скорость и высоту, если известно время.
Пример: Рассчитать скорость при ударе об землю тела, сброшенного с высоты 1000 м.
Ускорение свободного падения
g
или Планета
Высота
h
Время падения
t с
Скорость
v
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета введите ускорение свободного падения g или выберите планету и введите одну из трех величин h, t or v в соответствующие поля, выберите британские или метрические единицы и нажмите на кнопку Рассчитать. Будут рассчитаны две другие единицы.

Внутри спускаемого аппарата Союз ТМА-19М в экспозиции Музея науки в Лондоне
Определения и формулы
В классической механике состояние объекта, который свободно движется в гравитационном поле, называется свободным падением. Если объект падает в атмосфере, на него действует дополнительная сила сопротивления и его движение зависит не только от гравитационного ускорения, но и от его массы, поперечного сечения и других факторов. Однако на тело, падающее в вакууме, действует только одна сила, а именно сила тяжести.
Примерами свободного падения являются космические корабли и спутники на околоземной орбите, потому что на них действует единственная сила — земное притяжение. Планеты, вращающиеся вокруг Солнца, также находятся в свободном падении. Предметы, падающие на землю с небольшой скоростью, также могут считаться свободно падающими, так как в этом случае сопротивление воздуха незначительно и им можно пренебречь. Если единственной силой, действующей на предметы, является сила тяжести, а сопротивление воздуха отсутствует, ускорение одинаково для всех предметов и равно ускорению свободного падения на поверхности Земли 9,8 метров в секунду за секунду second (м/с²) или 32,2 фута в секунду за секунду (фут/ с²). На поверхности других астрономических тел ускорение свободного падения будет другим.

Командный модуль Аполлона-14 в Космическом центре им. Кеннеди, Флорида
Парашютисты, конечно, говорят, что перед раскрытием парашюта они в свободном падении, но на самом деле в свободном падении парашютист не может быть никогда, даже если парашют еще не раскрыт. Да, на парашютиста в «свободном падении» действует сила притяжения, но на него также действует противоположная сила — сопротивление воздуха, причем сила сопротивления воздуха лишь слегка меньше силы земного притяжения.
Если бы не было сопротивления воздуха, скорость тела, находящегося в свободном падении, каждую секунду увеличивалась бы на 9,8 м/с.
Скорость и расстояние свободно падающего тела вычисляется так:


где
v₀ — начальная скорость (м/с).
v — конечная вертикальная скорость (м/с).
h₀ — начальная высота (м).
h — высота падения (м).
t — время падения (с).
g — ускорение свободного падения (9,81 м/с² у поверхности Земли).
Если v₀=0 и h₀=0, имеем:

если известно время свободного падения:


если известно расстояние свободного падения:


если известна конечная скорость свободного падения:


Эти формулы и используются в данном калькуляторе свободного падения.
В свободном падении, когда нет силы для поддержания тела, возникает невесомость. Невесомость — это отсутствие внешних сил, действующих на тело со стороны пола, стула, стола и других окружающих предметов. Иными словами — сил реакции опоры. Обычно эти силы действуют в направлении, перпендикулярном поверхности соприкосновения с опорой, и чаще всего вертикально вверх. Невесомость можно сравнить с плаванием в воде, но так, что кожа воду не ощущает. Все знают это ощущение собственного веса, кода выходишь на берег после долгого купания в море. Именно поэтому для имитации невесомости при тренировках космонавтов и астронавтов используются бассейны с водой.
Само по себе гравитационное поле не может создать давление на ваше тело. Поэтому если вы находитесь в состоянии свободного падения в большом объекте (например, в самолете), который также находится в этом состоянии, на ваше тело не действуют никакие внешние силы взаимодействия тела с опорой и возникает ощущение невесомости, почти такое же, как и в воде.

Самолет для тренировок в условиях невесомости предназначен для создания кратковременной невесомости с целью тренировки космонавтов и астронавтов, а также для выполнения различных экспериментов. Такие самолеты использовались и в настоящее время эксплуатируются в нескольких странах. В течение коротких периодов времени, которые длятся около 25 секунд в течение каждой минуты полета самолет находится в состоянии невесомости, то есть для находящихся в нем людей отсутствует реакция опоры.
Для имитации невесомости использовались различные самолеты: в СССР и в Росси для этого с 1961 года использовались модифицированные серийные самолеты Ту-104АК, Ту-134ЛК, Ту-154МЛК и Ил-76МДК. В США астронавты тренировались с 1959 г. на модифицированных AJ-2, C-131, KC-135 и Boeing 727-200. В Европе Национальным центром космических исследований (CNES, Франция) для тренировок в невесомости используют самолет Airbus A310. Модификация заключается в доработке топливной, гидравлической и некоторых других систем с целью обеспечения их нормальной работы в условиях кратковременной невесомости, а также усиления крыльев для того чтобы самолет мог выдерживать повышенные ускорения (до 2G).
Несмотря на то, что иногда при описании условий свободного падения во время космического полета на орбите вокруг Земли говорят об отсутствии гравитации, конечно сила тяжести присутствует в любом космическом аппарате. Что отсутствует, так это вес, то есть сила реакции опоры на объекты, находящиеся в космическом корабле, которые движутся в пространстве с одинаковым ускорением свободного падения, которое только немного меньше, чем на Земле. Например, на околоземной орбите высотой 350 км, на которой Международная космическая станция (МКС) летает вокруг Земли, гравитационное ускорение составляет 8,8 м/с², что всего на 10% меньше, чем на поверхности Земли.

Для описания реального ускорения объекта (обычно летательного аппарата) относительно ускорения свободного падения на поверхности Земли обычно используют особый термин — перегрузка. Если вы лежите, сидите или стоите на земле, на ваше тело действует перегрузка в 1 g (то есть ее нет). Если же вы находитесь в самолете на взлете, вы испытываете перегрузку примерно в 1,5 g. Если тот же самолет выполняет координированный поворот с малым радиусом, то пассажиры, возможно, испытают перегрузку до 2 g, означающую, что их вес удвоился.

Манекен в костюме военного пилота и кислородной маске в Канадском музее авиации и космоса
Люди привыкли жить в условиях отсутствия перегрузок (1 g), поэтому любая перегрузка сильно влияет на человеческий организм. Как и в самолетах-лабораториях для создания невесомости, в которых все системы, работающие с жидкостями, должны быть модифицированы для того, чтобы они правильно работали в условиях нулевой (невесомость) и даже отрицательной перегрузки, люди также нуждаются в помощи и аналогичной «модификации», чтобы выжить в таких условиях. Нетренированный человек может потерять сознание при перегрузке 3–5 g (в зависимости от направления действия перегрузки), так как такая перегрузка достаточна для того, чтоб лишить мозг кислорода, потому что сердце не может подать в него достаточно крови. В связи с этим военные пилоты и космонавты тренируются на центрифугах в условиях высоких перегрузок, чтобы предотвратить потерю сознания при них. Для предотвращения кратковременной потери зрения и сознания, которые, по условиям работы, могут оказаться фатальными, пилоты, космонавты и астронавты надевают высотно-компенсирующие костюмы, который ограничивает отток крови от мозга во время перегрузок путем обеспечения равномерного давления на всю поверхность тела человека.
Механика
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Содержание
- Как рассчитать скорость свободного падения на планете
- Формула для расчета скорости свободного падения
- Пример расчета скорости свободного падения на Земле
- Расчет скорости свободного падения на других планетах
- Итог
- Как рассчитать скорость свободного падения на планете
- Определение гравитационной постоянной
- Рассчет радиуса планеты
- Рассчет массы планеты
- Формула для расчета скорости свободного падения
- Пример расчета скорости свободного падения на Земле
- Выводы
- Как рассчитать скорость свободного падения на планете?
- Формула расчета скорости свободного падения
- Пример расчета скорости свободного падения на Земле
- Расчет скорости свободного падения на других планетах
- Итог
Как рассчитать скорость свободного падения на планете
Скорость свободного падения — это скорость, с которой объект падает на поверхность планеты, когда на него не действует никаких сил. Каждая планета имеет свою уникальную скорость свободного падения, которая зависит от ее массы и радиуса. В этой статье мы расскажем, как рассчитать скорость свободного падения на различных планетах нашей солнечной системы.
Формула для расчета скорости свободного падения
Для расчета скорости свободного падения на планете используется следующая формула:
v = √(GM/r)
- v — скорость свободного падения (м/с)
- G — гравитационная постоянная (6,6743 × 10^-11 м^3/(кг * с^2))
- M — масса планеты (кг)
- r — радиус планеты (м)
Пример расчета скорости свободного падения на Земле
Для примера мы рассчитаем скорость свободного падения на Земле используя формулу выше.
- M (масса Земли) = 5,97 × 10^24 кг
- r (радиус Земли) = 6 371 км = 6 371 000 м
- G (гравитационная постоянная) = 6,6743 × 10^-11 м^3/(кг * с^2)
Подставляя значения в формулу, мы получаем:
v = √((6,6743 × 10^-11 м^3/(кг * с^2) × 5,97 × 10^24 кг) / (6 371 000 м)) = 9,81 м/с^2
Таким образом, скорость свободного падения на Земле равна 9,81 м/с^2.
Расчет скорости свободного падения на других планетах

Для расчета скорости свободного падения на других планетах необходимо знать их массу и радиус. В таблице ниже мы приводим значения массы и радиуса для всех планет солнечной системы, а также расчеты скорости свободного падения на каждой из них.
| Планета | Масса (кг) | Радиус (м) | Скорость свободного падения (м/с) |
|---|---|---|---|
| Меркурий | 3,30 × 10^23 | 2 440 000 | 3,70 |
| Венера | 4,87 × 10^24 | 6 052 000 | 8,87 |
| Земля | 5,97 × 10^24 | 6 371 000 | 9,81 |
| Марс | 6,42 × 10^23 | 3 397 000 | 3,71 |
| Юпитер | 1,90 × 10^27 | 71 492 000 | 24,79 |
| Сатурн | 5,68 × 10^26 | 60 268 000 | 10,44 |
| Уран | 8,68 × 10^25 | 25 559 000 | 8,87 |
| Нептун | 1,02 × 10^26 | 24 764 000 | 11,15 |
Итог

Скорость свободного падения — это важная физическая величина, которая зависит от массы и радиуса планеты. Расчет скорости свободного падения на различных планетах может быть полезен для многих научных и технических целей, от разработки космических аппаратов до изучения гравитации. Для расчета скорости свободного падения на планете необходимо знать ее массу и радиус и использовать соответствующую формулу. Надеемся, что наша статья была полезной и позволит вам лучше понять эту важную физическую величину.
Как рассчитать скорость свободного падения на планете
Скорость свободного падения — это скорость, с которой объект падает на поверхность планеты под воздействием силы тяжести. Эта скорость является фундаментальной физической константой и зависит от массы планеты и её радиуса.
Определение гравитационной постоянной
Первым шагом в рассчете скорости свободного падения является определение гравитационной постоянной. Гравитационная постоянная — это значение, которое связывает силу тяготения между двумя объектами в зависимости от их массы и расстояния между ними. Значение гравитационной постоянной равно 6,674 × 10^-11 Н * м^2/кг^2.
Рассчет радиуса планеты

Следующим шагом является определение радиуса планеты. Радиус планеты можно найти измерив диаметр планеты и разделив его на 2. Возьмем Землю в качестве примера. Диаметр Земли составляет примерно 12 742 километра. Разделив это число на 2, получим радиус Земли, равный примерно 6 371 километру.
Рассчет массы планеты
Для того, чтобы рассчитать скорость свободного падения на планете, необходимо также знать её массу. Массу планеты можно найти, изучая её гравитационное воздействие на объекты в её окрестности. Например, для определения массы Земли можно изучить астрономические данные о движении Луны вокруг Земли. Масса Земли составляет примерно 5,972 × 10^24 кг.
Формула для расчета скорости свободного падения
Теперь, когда мы знаем гравитационную постоянную, радиус и массу планеты, мы можем рассчитать скорость свободного падения на её поверхности с помощью следующей формулы:
v = √(G * M / r)
где:
- G — гравитационная постоянная
- M — масса планеты
- r — радиус планеты
Пример расчета скорости свободного падения на Земле

Вернемся к примеру Земли. Мы уже знаем, что масса Земли составляет 5,972 × 10^24 кг, а её радиус примерно равен 6 371 километру. Подставляем эти значения в формулу:
𝑣 = √(6.674 х 10^-11 * 5.972 × 10^24 / 6 371 000)
Выполняем простые математические вычисления и получаем, что скорость свободного падения на поверхности Земли составляет примерно 9,8 м/с^2.
Выводы
Скорость свободного падения на планете зависит от массы планеты и её радиуса. Рассчитать скорость свободного падения на планете можно, зная гравитационную постоянную, радиус и массу планеты. Учитывая, что скорость свободного падения на Земле составляет примерно 9,8 м/с^2, можно легко рассчитать скорость свободного падения на любой другой планете в нашей солнечной системе.
Как рассчитать скорость свободного падения на планете?
Скорость свободного падения — это скорость, с которой объект падает в гравитационном поле планеты под воздействием силы тяжести. Зная значение скорости свободного падения, мы можем рассчитать, как быстро объект будет двигаться при свободном падении на планете. Как рассчитать скорость свободного падения на планете?
Формула расчета скорости свободного падения
Скорость свободного падения — это функция массы и радиуса планеты, на которой объект падает. Формула для расчета скорости свободного падения на планете выглядит следующим образом:
g = GM/r^2
где:
- g — скорость свободного падения (м/с^2)
- G — гравитационная постоянная (6,67430 × 10^-11 м^3 / (кг * с^2))
- M — масса планеты (кг)
- r — радиус планеты (м)
Пример расчета скорости свободного падения на Земле

Давайте рассмотрим конкретный пример расчета скорости свободного падения на Земле. Значения для расчета возьмем из источников, чтобы избежать ошибок в данных.
Масса Земли: 5,972 × 10^24 кг
Радиус Земли: 6,3781 × 10^6 м

Мы можем подставить эти значения в формулу:
g = (6,67430 × 10^-11 м^3 / (кг * с^2)) × (5,972 × 10^24 кг) / (6,3781 × 10^6 м)^2 = 9,81 м/с^2
Таким образом, скорость свободного падения на Земле равна 9,81 м/c^2. Это означает, что если объект будет падать со свободного падения, он будет ускоряться со скоростью 9,81 метров в секунду каждую секунду.
Расчет скорости свободного падения на других планетах
Расчет скорости свободного падения на других планетах может отличаться от расчета на Земле. Это связано с изменением массы и радиуса планеты, на которой мы рассчитываем скорость свободного падения.
Например, скорость свободного падения на Луне составляет около 1,62 м/с^2, что на порядок ниже, чем на Земле. Это связано с тем, что Луна меньше Земли и имеет меньшую массу.
Вот еще несколько расчетов скорости свободного падения на других планетах и спутниках системы Солнечной системы:
- Марс: 3,71 м/с^2
- Юпитер: 24,79 м/с^2
- Сатурн: 10,44 м/с^2
- Уран: 8,87 м/с^2
- Нептун: 11,15 м/с^2
- Луна: 1,62 м/с^2
Итог
Как мы видим, расчет скорости свободного падения на планете может быть выполнен с использованием универсальной формулы, которая учитывает массу и радиус планеты. Расчеты показывают, что скорость свободного падения различается на разных планетах и спутниках. Знание скорости свободного падения может быть полезно во многих областях, таких как астрономия, космическая инженерия и другие науки.
Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
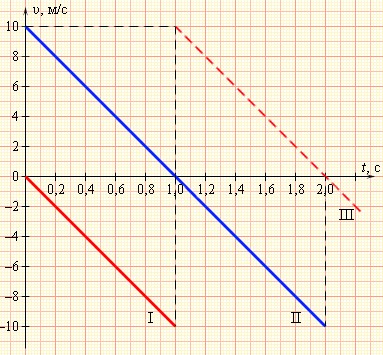
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
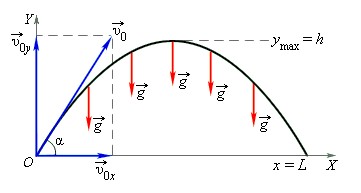
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.



