Через уравнение.
S – пройденный путь, растояние, которое прошла, например, лодка. (км)
t – время, за которое она прошла расстояние S. (часов, минут)
V – собственная её скорость (км/ч, м/ч)
Такие задачи решаются далее: если известны: (под формулы подставляем числа)
t и V, то перемножаем – t * V, получаем S.
t и S, то расстояние делим время – S : t, получаем V
S и V, также – S : V, получаем t
Также если в задаче указана V (её ищем)
по течению, то V собственная + V по течению
против течения, то V собств. – V прот. теч.
Тогда формулы звучат так: если известны:
t и V, то t * (V с. +/- V) = S
t и S, то S : t = V с. +/- V
V и S, то S : (V c. +/- V) = t
Теперь ещё раз:
V c. – собственная скорость
V c. + V – скорость + скорость по теч.
V c. – V – скорость + скорость прот. теч.
Ну так чтоли… Плохой из меня учитель(((
Содержание материала
- Скорость тела. Средняя скорость тела
- Видео
- Задача с рыбаком и лодкой
- Ширина русла и водоносность
- Задача с моторной лодкой
- Формулы, которые необходимо запомнить
- Движение по реке. Скорость течения реки
Скорость тела. Средняя скорость тела
Решение задач на движение опирается на хорошо известную из курса физики формулу

позволяющую найти путь S , пройденный за время t телом, движущимся с постоянной скоростью v .
Сразу же сделаем важное
Замечание 1. Единицы измерения величин S , t и v должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.
В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости, которая вычисляется по формуле
 |
(1) |
Например, если тело в течение времени t1 двигалось со скоростью v1 , в течение времени t2 двигалось со скоростью v2 , в течение времени t3 двигалось со скоростью v3 , то средняя скорость
 |
(2) |
Задача 1. По расписанию междугородный автобус должен проходить путь в 100 километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на 25 минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на 20 км/час. Какова скорость автобуса по расписанию?
Решение. Обозначим буквой v скорость автобуса по расписанию и будем считать, что скорость v измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.


Рис. 1
Тогда
 – время движения автобуса по расписанию (в часах);
– время движения автобуса по расписанию (в часах);
 – время, за которое автобус проехал первую половину пути (в часах);
– время, за которое автобус проехал первую половину пути (в часах);
v + 20 – скорость автобуса во второй половине пути (в км/час);
 – время, за которое автобус проехал вторую половину пути (в часах).
– время, за которое автобус проехал вторую половину пути (в часах).
В условии задачи дано время остановки автобуса – 25 минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:


Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

Решим это уравнение:


По смыслу задачи первый корень должен быть отброшен.
Ответ. 40 км/час.
Задача 2. (МИОО) Первый час автомобиль ехал со скоростью 120 км/час, следующие три часа – со скоростью 105 км/час, а затем три часа – со скоростью 65 км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение. Воспользовавшись формулой (2), получаем


Ответ. 90 км/час.
Задача 3. Первую половину пути поезд шел со скоростью 40 км/час, а вторую половину пути – со скоростью 60 км/час. Найдите среднюю скорость поезда на протяжении всего пути.
Решение. Обозначим буквой S длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.


Рис. 2
Тогда
 – время, за которое поезд прошел первую половину пути, выраженное в часах;
– время, за которое поезд прошел первую половину пути, выраженное в часах;
 – время, за которое поезд прошел вторую половину пути, выраженное в часах.
– время, за которое поезд прошел вторую половину пути, выраженное в часах.
Следовательно, время, за которое поезд прошел весь путь, равно


В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути

Ответ. 48 км/час.
Замечание 2. Средняя скорость поезда в задаче 3 равна 48 км/час, а не 50 км/час, как иногда ошибочно полагают, вычисляя среднее арифметическое чисел (скоростей) 40 км/час и 60 км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по формуле (1).
Видео
Задача с рыбаком и лодкой

Разобравшись, как найти скорость течения реки, решим следующую задачу. Известно, что рыбак на лодке должен проплыть по реке 10 км. Проведя необходимые измерения, он установил, что течение в реке составляет 1 м/с. Какое время рыбаку понадобиться для того, чтобы по течению проплыть указанное расстояние, не используя при этом дополнительные средства тяги (мотор, весла).
Переводим скорость из м/с в км/ч, получаем 3,6 км/ч. Тогда искомое время будет равно:
t = S/v = 10/3,6 ≈ 2,8 ч.
Ширина русла и водоносность
Для более глубокого понимания вопроса, как найти скорость течения реки, важно знать еще один момент. Дело в том, что одна и та же река в разных местах может течь с различной скоростью. Причиной является изменение площади сечения ее русла, которое внешне связано с изменение ширины. Справедливости ради отметим, что не только изменение ширины, но и колебания в глубине влияют на быстроту течения воды (чем глубже, тем медленнее).
В виду сказанного выше, о скорости перемещения воды в реке имеет смысл говорить, если на достаточно длительном участке (километры и более) параметры ее русла колеблется незначительно, и река не имеет на этом участке притоков.
Более надежной характеристикой для любой реки является ее водоносность. Под водоносностью понимают объем воды, проходящий через вертикальное сечение русла за единицу времени. Водоносность не зависит от параметров русла, однако, она так же, как и скорость, изменится, если на рассматриваемом участке реки имеется приток.
В данной статье мы ограничимся предоставленной информацией о водоносности и перейдем к вопросу, как найти скорость течения реки.
Задача с моторной лодкой

Моторная лодка совершает каждый день переходы по реке из пункта A в пункт B. Дистанция между A и B составляет 7 км. Известно, что скорость лодки по течению равна 8 км/ч. Чему равна скорость течения, если на путь вниз по реке лодка затрачивает на 10 минут больше времени, чем при движении вверх по ней.
В данном случае мы не знаем ни скорость моторной лодки, ни скорость воды в реке. Обозначим первую как y, а вторую как x. Тогда можно записать следующие четыре уравнения:
x + y = 8;
S/t1 = x + y;
S/t2 = y — x;
t2 — t1 = 1/6
Первое уравнение отражает скорость лодки по течению, второе и третье уравнения связывают время и скорость при движении вниз и вверх по реке соответственно. Четвертое уравнение следует из условия задачи о разности времен прямого и обратного пути между пунктами A и B.
Сначала найдем из этих уравнений время t1 и t2:
t1 = 7/8 = 0,875 ч;
t2 = 1/6 + 7/8 = 1,0417 ч
Для определения скорости x воды в реке вычтем из второго третье уравнение, получим:
S/t1 — S/t2 = 2*x =>
x = S/2*(1/t1 — 1/t2)
Подставляем в это равенство рассчитанные величины t1 и t2, а также расстояние между пунктами S, получаем, что вода в реке течет со скоростью 0,64 км/ч.
Формулы, которые необходимо запомнить
Помимо приведенной выше информации, для решения задач на скорость течения реки следует запомнить несколько формул. Перечислим их.
Скорость течения является величиной постоянной, а вот скорость тела (лодки, катера, пловца) в общем случае может меняться, как по величине, так и по направлению. Для равномерного прямолинейного движения справедливой будет формула:
S = v*t
Где S — пройденный путь, v — скорость перемещения тела. Если движение происходит с ускорением a, тогда следует применять формулу:
S = a*t2/2
Помимо этих формул, для успешного решения задач следует уметь пользоваться тригонометрическими функциями при разложении векторов скорости на составляющие.
Теперь перейдем к решению конкретных задач.
Движение по реке. Скорость течения реки
В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.
По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела (скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.
Задача 4. Моторная лодка прошла по течению реки 14 км, а затем 9 км против течения, затратив на весь путь 5 часов. Скорость лодки в стоячей воде 5 км/час. Найдите скорость течения реки.
Решение. Обозначим буквой v скорость течения реки и будем считать, что скорость v измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.


Рис. 3
Тогда
5 + v – скорость, с которой лодка шла по течению реки (в км/час);
 – время движения лодки по течению реки (в часах);
– время движения лодки по течению реки (в часах);
5 – v – скорость, с которой лодка шла против течения реки (в км/час);
 – время движения лодки против течения реки (в часах);
– время движения лодки против течения реки (в часах);
Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:

Решим это уравнение:


По смыслу задачи первый корень должен быть отброшен.
Ответ. 2 км/час.
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.
Решение. Обозначим vс (км/ч) скорость лодки в стоячей воде и обозначим vр (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.


Рис. 4


Рис. 5
Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:
 |
(3) |
Если ввести обозначение

то, воспользовавшись формулой
vс = xvр ,
перепишем уравнение (3) в виде
 |
(4) |
Умножая уравнение (4) на vр , получим


По смыслу задачи первый корень должен быть отброшен.
Ответ. 7,5 .
Теги
Как найти собственную скорость лодки
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение – самое главное в решении любого типа задач.

Инструкция
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать “на зубок” – формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. – 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. – Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:
Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
441-Х2=0
Х2=441
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Источники:
- решение задач на течение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Одними из увлекательных задач по математике и физике, которые предлагает учитель решить школьникам, являются задачи на определение скорости течения реки. В данной статье рассмотрим особенности решения этих задач и приведем несколько конкретных примеров.
О каких задачах пойдет речь?
Каждый знает, что вода в реке обладает некоторой скоростью течения. Равнинные реки (Дон, Волга) текут относительно медленно, небольшие же горные реки отличаются сильным течением и присутствием водяных воронок. Любой плавающий предмет, который брошен в реку, будет удаляться от наблюдателя со скоростью течения реки.

Люди, которые купались в реке, знают, что против ее течения плыть очень тяжело. Чтобы продвинуться на несколько метров, необходимо приложить намного больше усилий, чем при движении в стоячей воде озера. Наоборот, движение по течению осуществляется практически без каких-либо затрат энергии. Достаточно лишь поддерживать тело на плаву.
Все эти особенности позволяют сделать следующий важный вывод: если тело, имеющее в стоячей воде скорость v, будет двигаться в русле реки, то его скорость относительно берега будет равна:
- v + u для движения по течению;
- v – u для движения против течения.
Здесь u – скорость течения.
Если тело движется под некоторым углом к течению, то результирующий вектор его скорости будет равен сумме векторов v¯ и u¯.
Формулы, которые необходимо запомнить
Помимо приведенной выше информации, для решения задач на скорость течения реки следует запомнить несколько формул. Перечислим их.
Скорость течения является величиной постоянной, а вот скорость тела (лодки, катера, пловца) в общем случае может меняться, как по величине, так и по направлению. Для равномерного прямолинейного движения справедливой будет формула:
S = v*t
Где S – пройденный путь, v – скорость перемещения тела. Если движение происходит с ускорением a, тогда следует применять формулу:
S = a*t2/2
Помимо этих формул, для успешного решения задач следует уметь пользоваться тригонометрическими функциями при разложении векторов скорости на составляющие.
Теперь перейдем к решению конкретных задач.
Задача с лодкой и рыбаком

Один рыбак решил отправиться на своей лодке без мотора вверх против течения реки на расстояние 2 километра. В стоячей воде он бы преодолел это расстояние за 30 минут, но при движении по реке ему понадобился целый час. Необходимо найти, чему равна скорость течения реки.
Поскольку скорость воды в реке является величиной неизвестной, то обозначим ее буквой x. Скорость лодки также неизвестна, однако ее можно вычислить, используя значения из условия для движения в стоячей воде. Получаем для скорости v лодки:
v = S/t1 = 2/0,5 = 4 км/ч
Мы нашли скорость, с которой рыбак на лодке может перемещаться по спокойному озеру. Чтобы найти скорость лодки против течения, необходимо из найденной величины вычесть значение x. Тогда для движения вверх по реке можно записать следующее равенство:
S = (4 – x)*t2
Выражаем отсюда значение неизвестного параметра, имеем:
x = 4 – S/t2
Осталось подставить цифры из условия задачи и записать ответ:
x = 4 – S/t2 = 4 – 2/1 = 2 км/ч
Таким образом, скорость течения в реке в два раза меньше таковой для лодки.
Задача с моторной лодкой

Моторная лодка совершает каждый день переходы по реке из пункта A в пункт B. Дистанция между A и B составляет 7 км. Известно, что скорость лодки по течению равна 8 км/ч. Чему равна скорость течения, если на путь вниз по реке лодка затрачивает на 10 минут больше времени, чем при движении вверх по ней.
В данном случае мы не знаем ни скорость моторной лодки, ни скорость воды в реке. Обозначим первую как y, а вторую как x. Тогда можно записать следующие четыре уравнения:
x + y = 8;
S/t1 = x + y;
S/t2 = y – x;
t2 – t1 = 1/6
Первое уравнение отражает скорость лодки по течению, второе и третье уравнения связывают время и скорость при движении вниз и вверх по реке соответственно. Четвертое уравнение следует из условия задачи о разности времен прямого и обратного пути между пунктами A и B.
Сначала найдем из этих уравнений время t1 и t2:
t1 = 7/8 = 0,875 ч;
t2 = 1/6 + 7/8 = 1,0417 ч
Для определения скорости x воды в реке вычтем из второго третье уравнение, получим:
S/t1 – S/t2 = 2*x =>
x = S/2*(1/t1 – 1/t2)
Подставляем в это равенство рассчитанные величины t1 и t2, а также расстояние между пунктами S, получаем, что вода в реке течет со скоростью 0,64 км/ч.
Задача: движение катера под углом к течению

Теперь решим задачу, которая требует умения пользоваться тригонометрическими формулами.
Катер начал движение от одного берега реки к другому под углом 60o к течению. Скорость катера в стоячей воде равна 10 км/ч. Скорость течения составляет 2 км/ч. Необходимо определить, на какое расстояние катер сместится вдоль берега, прибыв на противоположную сторону реки. Ширина русла реки равна 500 метров.
Данную задачу следует решать, разбив путь катера на две составляющие: перпендикулярную и параллельную берегу. Используя данные задачи, для перпендикулярной составляющей пути можно записать выражение:
v*sin(60o)*t = S1
Где v – скорость катера, S1 – ширина реки. Подставляя данные, находим время, которое катер находился в пути:
t = S1/(v*sin(60o)) = 0,0577 ч
Для вычисления параллельного берегу пути S2 к горизонтальной проекции скорости катера следует добавить скорость течения, тогда соответствующее равенство будет иметь вид:
S2 = (v*cos(60o) + 2)*t
Подставляя известные величины, получаем ответ: катер вдоль берега пройдет путь 404 метра.
Содержание:
Движение жидкостей и газов:
Вы знаете, что в состоянии покоя жидкости и газы оказывают давление на стенки сосуда. В природе и в быту жидкость находится не только в состоянии покоя, но и в движении. Какие силы возникают в текущей по арыкам, каналам, рекам и водопроводным трубам воде?
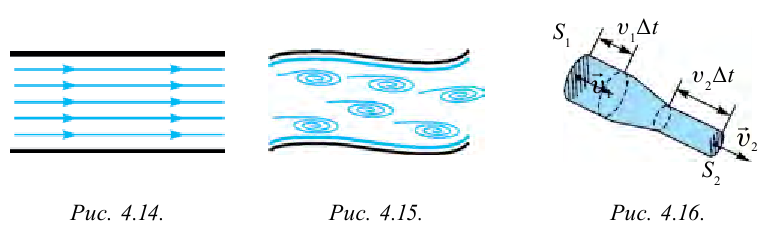
Для изучения этого явления рассмотрим поверхность воды, текущей в арыке. В середине широкого полноводного канала вода, в основном, течет равномерно по одной линии. В этом можно удостовериться, наблюдая за телами, плывущими в воде (рис. 4.14). Такое течение называется послойным или ламинарным. Вода в горной реке течет быстро. Если наблюдать за телами, плывущими по этой реке, то можно увидеть, что течение образовывает водовороты (рис. 4.15). Такое течение называется турбулентным. Значит, если жидкость течет по трубам, то за счет трения о стенки трубы слои жидкости текут с разной скоростью: в середине трубы – быстрее, у стенок – медленнее. Рассмотрим течение жидкости по трубке с изменяющим поперечным сечением, не учитывая трение (рис. 4.16).
Жидкость затекает в часть трубки с сечением 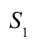
Обе стороны уравнения делим на 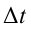 и получаем:
и получаем:

Полученный результат можно сформулировать следующим образом:
Модули скоростей несжимаемой жидкости, текущей по трубам с разными сечениями, обратно пропорциональны сечениям трубы.
Это называется уравнением непрерывности течения для несжимаемой жидкости.
Таким образом, в широком месте трубки скорость жидкости будет меньше, чем в узком месте. Например, когда нужно, чтобы вода из водопроводного шланга брызгала дальше, нужно сжать отверстие шланга.
Рассмотрим распределение давления в двигающихся жидкостях.
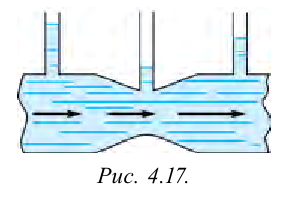
Пусть вода течет по трубе разного сечения, с тонкими измерительными трубками наверху (рис 4.17). При стационарном течении жидкость по измерительным трубкам поднимается вверх. По высоте подъема жидкости можно сделать вывод об оказываемом ею на стенки трубы давлении. Опыты показывают, что в широких местах трубы давление будет больше, чем в узких местах. Согласно уравнению непрерывности течения, скорость течения в широкой части будет меньшей, а в узкой части будет больше.
На основании вышеизложенного можно сделать следующий вывод:
- В потоке жидкости давление велико, если скорость течения мала, и давление мало, если скорость велика.
Математическое выражение зависимости давления жидкости от скорости течения определил в 1738 году Д. Бернулли.
Уравнение Бернулли можно вывести из закона сохранения механической энергии применительно к течению жидкости.
Установим трубку с изменяющимся сечением, по которой течет жидкость, под наклоном относительно горизонта. (рис. 4.18).
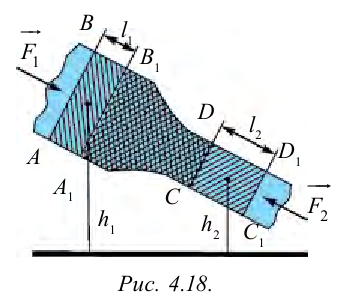
На широком отрезке трубки за время  через сечение
через сечение  протекает определенный объем жидкости. Поскольку жидкость считается несжимаемой, через сечение
протекает определенный объем жидкости. Поскольку жидкость считается несжимаемой, через сечение  за это время протекает такое же количество жидкости. Обозначим площадь сечения
за это время протекает такое же количество жидкости. Обозначим площадь сечения 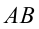 как
как 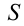 , скорость течения жидкости через это сечение
, скорость течения жидкости через это сечение 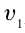 , соответственно площадь сечении
, соответственно площадь сечении 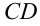 обозначим
обозначим 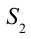 и скорость
и скорость 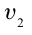 .
.
Сила давления 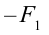 и
и 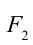 . Под действием силы тяжести выделенный объем жидкости в течение времени
. Под действием силы тяжести выделенный объем жидкости в течение времени 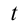 смещается в правую сторону.
смещается в правую сторону.
Выполненная при этом работа равна:
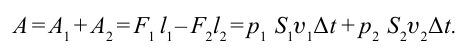
При стационарном течении энергия жидкости в части 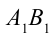 и
и 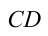 не меняется, т.е. жидкость, занимающая объем
не меняется, т.е. жидкость, занимающая объем 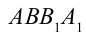 , переносится и занимает объем
, переносится и занимает объем 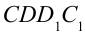 . Согласно закону сохранения энергии выполненная работа внешних сил равна изменению энергии:
. Согласно закону сохранения энергии выполненная работа внешних сил равна изменению энергии:
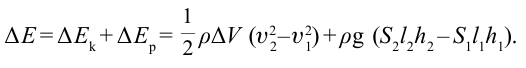
Учитывая, что 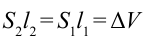 , сокращаем выражение на
, сокращаем выражение на 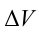 , получаем:
, получаем:
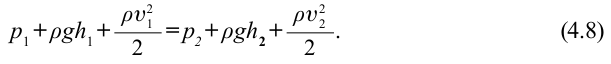
Это выражение называется уравнением Бернулли для течения идеальной жидкости или газа.
Если 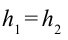 получаем
получаем
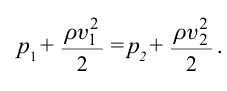
Образец решения задачи:
Емкость имеет на дне маленькое отверстие закрытое пробкой. В емкость залили воду высотой 1 м. На поверхности воды установили поршень массой 1 кг и площадью 100 см2 . Через стенки емкости и поршня вода не просачивается. С какой скоростью будет выливаться вода, если резко открыть пробку?
Дано:
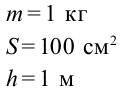
Найти:
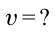
Решение:
Используем уравнение Бернулли. Давление потока воды равно давлению 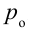 . Давление в нижней части на высоте
. Давление в нижней части на высоте 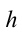 считая от отверстия равно:
считая от отверстия равно: 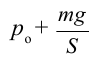 . По уравнению Бернулли
. По уравнению Бернулли
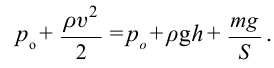
Отсюда: 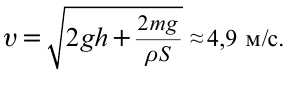
Ответ: 4,9 м/c.
Использование в технике зависимости давления от скорости двигающихся газов и жидкостей
Мы наблюдали, что при движении жидкости по сравнению с состоянием покоя давление изменяется. Это давление зависит от динамического давления. Для наблюдения зависимости динамического давления от скорости жидкости или газа проведем следующий опыт. Возьмем два листа бумаги и зафиксируем их в вертикальном положении. Затем подуем в промежуток между листами (рис. 4.19). Листы начнут приближаться друг к другу. Причиной этого явилось то, что воздух между листами пришел в движение, и давление между ними уменьшилось.
Давление с внешней стороны листа будет больше, чем с внутренней, и за счет этого появится сила, сдавливающая листы.
Иногда корабли, плывущие в одну сторону, сталкиваются без видимых причин. Это явление объясняется появлением разности давления в пространстве между ними.
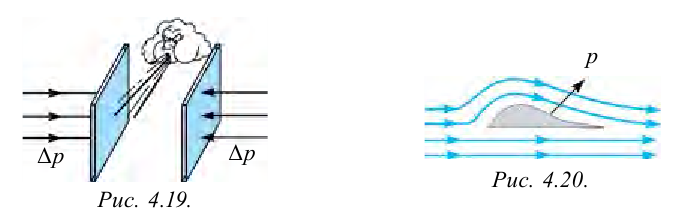
Сила, поднимающая крылья самолета
Полет самолетов тоже возможен благодаря этому явлению, на котором основано специальное устройство крыла (рис. 4.20). Крылья самолета имеют вогнутую форму для того, чтобы встречный поток воздуха обтекал крыло снизу и сверху. Путь, денный потоком снизу. Поэтому скорость потока воздуха над крылом больше, чем его скорость под крылом. Значит, давление 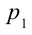 в том месте, где скорость потока выше, меньше давления
в том месте, где скорость потока выше, меньше давления 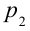 под крылом, где скорость потока меньше. В результате появляется разность давлений
под крылом, где скорость потока меньше. В результате появляется разность давлений 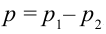 , направленная снизу вверх. Если поток будет турбулентным, разность давлений будет больше. В результате разницы этих давлений появляется сила, которая называется подъемной силой крыла.
, направленная снизу вверх. Если поток будет турбулентным, разность давлений будет больше. В результате разницы этих давлений появляется сила, которая называется подъемной силой крыла.
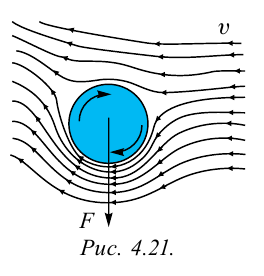
Эффект Магнуса
Многие видели, как футбольный мяч, отправленный с угла поля, по дуге попадает в ворота. Что заставляет мяч поворачиваться? Опытный футболист пинает мяч не по центру, как обычно делают все, а ударяет по его краю. В результате под воздействием такого удара мяч во время движения поворачивается. Кроме того, в результате такого удара меняется
скорость течения воздуха с левой и правой сторон мяча, что создает разницу давлений в воздухе, и мяч попадает в ворота. Такое явление называется эффектом Магнуса (рис. 4.21).
- Заказать решение задач по физике
Расчет скорости воды, вытекающей из отверстия сосуда
Используя уравнение Бернулли, можно вычислить скорость вытекания жидкости из отверстия, находящегося на глубине 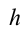 от поверхности жидкости (рис. 4.22).
от поверхности жидкости (рис. 4.22).
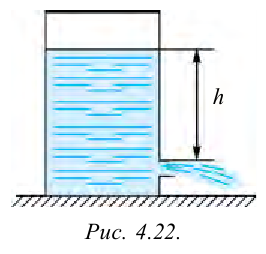
Давление на поверхности жидкости, которая находится в сосуде, равно давлению атмосферы 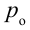 . Скорость жидкости
. Скорость жидкости 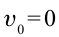 . Давление жидкости перед отверстием тоже равно
. Давление жидкости перед отверстием тоже равно 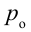 . Скорость
. Скорость
жидкости, вытекающей из отверстия, обозначим 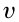 , и для этих двух случаев применим формулу:
, и для этих двух случаев применим формулу:
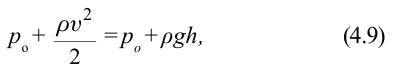
отсюда получим: 
Эта формула называется формулой Торричелли для идеальной жидкости.
Образец решения задачи:
В баке высотой 5 м, на высоте 50 см от земли установлен кран. С какой скоростью будет вытекать вода, если открыть кран?
Дано:
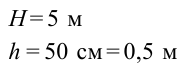
Найти:
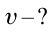
Формула:
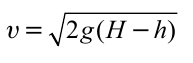
Решение:
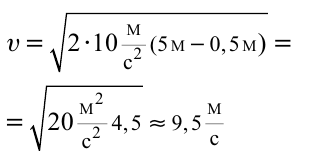
Ответ: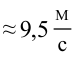
Основные понятия, правила и законы
| Устойчивое равновесие | При выведении тела из положения равновесия возникают силы, возвращающие тело в прежнее положение. Это явление называется устойчивым равновесием. |
| Неустойчивое равновесие | При выведении тела из положения равновесия возникают силы, удаляющие его от положения равновесия. Такое равновесие называется неустойчивым равновесием |
| Безразличное равновесие | Безразличным равновесием называется явление, при котором тело выводится из равновесного состояния и не появляется сила, изменяющая его состояние. |
| Момент силы | Произведение силы на плечо силы: 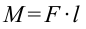 |
| Условие равновесия тела, которое имеет ось вращения |
Когда векторная сумма моментов сил, действующих на тело, равняется нулю, тело остается в равновесии: 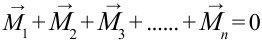 |
| Двухплечный рычаг | Опора находится между точками, к которым приложены силы. |
| Одноплечный рычаг | Опора расположена на одном конце рычага, а груз устанавливается на второй конец рычага |
| Степенной полиспаст | Комплекс подвижных и неподвижных блоков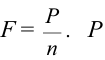 – вес груза; – вес груза; 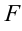 – сила тяги. – сила тяги. |
| Ламинарное течение | Течение жидкости отдельными слоями |
| Турбулентное течение | Движение жидкости в виде воронки |
| Уравнение непрерывности течения |
Модули скоростей несжимаемой жидкости, теку- щей по трубам разного сечения, обратно пропорциональны сечениям трубы: 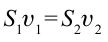 . . |
| Уравнение Бернулли | 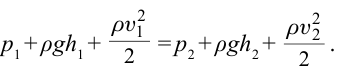 В потоке жидкости давление велико, если скорость течения мала, и давление мало, если скорость велика. |
| Динамическое давление | Давление, создаваемое в результате движения жидкости. |
| Эффект Магнуса | Изменение направления движения предмета в результате появления разницы давлений газа или жидкости по сторонам предмета, который совершает вращательное движение. |
| Формула Торричелли | 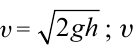 – скорость течение воды; – скорость течение воды; 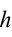 – высота. – высота. |
Движение жидкости и газа
Можно ли не очень опытному пловцу попробовать переплыть горную реку? Казалось бы, почему нет, особенно если река не очень широкая. Но этого не стоит делать ни в коем случае — это очень опасно! И дело не в ширине реки, а в том, что, как правило, в горных реках есть стремнины — участки с большой скоростью течения. Выплыть из стремнины очень трудно — она затягивает и «не отпускает» пловца.
Где жидкость движется быстрее
Возьмем горизонтальную трубку с разными поперечными сечениями, закрытую поршнем (можно взять шприц без иглы). Наполним трубку водой и будем перемещать поршень с некоторой постоянной скоростью (рис. 18.1). Увидим, что скорость воды в узкой части трубки будет больше, чем в широкой части. Результаты этого опыта можно было бы и спрогнозировать.
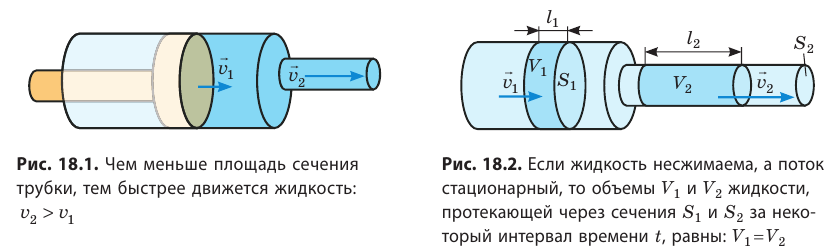
Рассмотрим стационарный поток идеальной несжимаемой жидкости, то есть поток, в каждой точке которого скорость движения жидкости не изменяется со временем, а силы трения пренебрежимо малы (рис. 18.2). Пусть 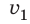 — скорость течения в широкой части трубы с площадью сечения
— скорость течения в широкой части трубы с площадью сечения  , а
, а  — скорость течения в узкой части трубы с площадью сечения
— скорость течения в узкой части трубы с площадью сечения 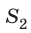 .
.
За некоторое время t через эти сечения протекают равные объемы жидкости: 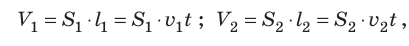 , где
, где 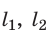 — расстояния, которые проходит жидкость за время t.
— расстояния, которые проходит жидкость за время t.
Поскольку 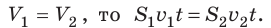 После сокращения на t получим уравнение неразрывности струи:
После сокращения на t получим уравнение неразрывности струи:
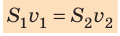
Таким образом, и эксперименты, и теоретические исследования подтверждают: чем меньше площадь сечения, тем быстрее движется жидкость. Подобное явление можно наблюдать, если спускаться или подниматься по реке: течение медленное и плавное там, где река глубокая и широкая, а на мелководье или в узкой части русла скорость течения заметно увеличивается.
Как давление внутри жидкости зависит от скорости ее движения
Вернемся к рис. 18.2. Скорость течения в месте перехода из широкой части трубы в узкую увеличивается, то есть жидкость ускоряет свое движение. Наличие ускорения означает, что в этом месте на жидкость действует некая сила. Труба расположена горизонтально, поэтому сила, придающая ускорение, не может быть следствием притяжения Земли. Эта сила возникает в результате разности давлений, то есть давление жидкости в широкой части трубы (где скорость течения меньше) больше давления жидкости в узкой части трубы (где скорость течения больше).
Первым к такому выводу пришел швейцарский физик и математик Даниил Бернулли (1700–1782), который установил закон, касающийся любого стационарного потока жидкости, — закон Бернулли:
При стационарном движении жидкости давление жидкости меньше там, где скорость течения больше, и наоборот, давление жидкости больше там, где скорость течения меньше.
Закон Бернулли является следствием закона сохранения механической энергии: жидкость получает кинетическую энергию (увеличивает скорость своего движения) благодаря тому, что потенциальная энергия упругого взаимодействия молекул жидкости уменьшается (и наоборот). Если поток жидкости не горизонтальный, изменение кинетической энергии жидкости происходит еще и за счет изменения ее потенциальной энергии гравитационного взаимодействия с Землей.
Почему летают самолеты
Садясь в самолет или наблюдая за его полетом, вы, вероятно, задумывались о том, почему самолет поднимается и какая сила удерживает его в воздухе. Кто-то скажет, что это архимедова сила (но это не так, ведь неподвижный самолет не поднимется). Некоторые предположат, что самолет держит сила реактивной тяги двигателей (и это тоже неправильно, ведь эта сила только разгоняет самолет и поддерживает скорость его движения). Самолет держится в воздухе благодаря силе давления, создающей подъемную силу.
Возникновение подъемной силы можно объяснить с помощью закона Бернулли, ведь при определенных условиях воздушный поток можно рассматривать как стационарный поток жидкости.
Во время полета на крылья самолета все время набегает встречный поток воздуха, и крылья как бы «разрезают» его на две части: одна часть обтекает верхнюю поверхность крыла, другая — нижнюю. Форма большинства крыльев такова, что поток, обтекающий верхнюю (выпуклую) часть крыла, преодолевает за то же время большее расстояние (движется с большей скоростью), чем поток, обтекающий крыло снизу (рис. 18.3). Согласно закону Бернулли там, где скорость потока больше, давление меньше. Следовательно, сила давления, действующая на крыло сверху, меньше силы давления, действующей на крыло снизу.
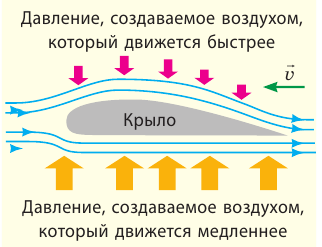
Рис. 18.3. Обычно крыло самолета имеет аэродинамическую форму: верхняя поверхность крыла более выпуклая, чем нижняя. Голубыми стрелками показано движение воздуха, набегающего на крыло, зеленой стрелкой — направление движения самолета
Однако самая важная причина образования подъемной силы — это наличие угла атаки — наклона крыльев самолета под определенным углом a к воздушному потоку (рис. 18.4). В таком случае подъемная сила возникает как за счет уменьшения давления над крылом, так и за счет увеличения давления под крылом. Благодаря наличию угла атаки в воздух поднимаются и самолеты с симметричным профилем крыла.
Разницу сил давлений называют полной аэродинамической силой (см. рис. 18.4).
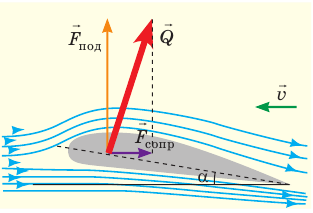
Рис. 18.4. Угол атаки α и полная аэродинамическая сила . Вертикальная составляющая силы
. Вертикальная составляющая силы 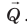 — подъемная сила
— подъемная сила 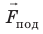 , горизонтальная составляющая — сила сопротивления
, горизонтальная составляющая — сила сопротивления 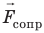
Выводы:
- Для стационарного потока жидкости или газа выполняется закон Бернулли: давление жидкости (газа) больше там, где скорость течения меньше, и наоборот.
- Закон Бернулли объясняет одну из причин возникновения подъемной силы крыла самолета: аэродинамическая форма крыла заставляет воздух над его верхней поверхностью двигаться с большей скоростью, поэтому давление над крылом меньше, чем давление под крылом.
- Гидравлические машины в физике
- Весовое давление жидкостей в физике
- Сообщающиеся ссуды в физике
- Атмосферное давление в физике и его измерение
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
