Механическое движение имеет множество характеристик. Вы уже узнали, что оно относительно и бывает разных видов: прямолинейное и криволинейное, равномерное и неравномерное.
Тела движутся по воображаемым линиям, которые называются траекториями, а длина траектории – это путь, который проходит тело.
В этом уроке мы рассмотрим новую физическую величину, характеризующую движение – скорость.
Скорость при равномерном движении
Взгляните на рисунок 1. Если мы предположим, что бегуны, велосипедисты и автомобили двигаются равномерно, то чем будет отличаться их движение?
В таких случаях обычно мы говорим, что машина будет двигаться быстрее, чем велосипедист, а велосипедист – быстрее, чем бегун. Здесь в физике появляется такая величина, как скорость.
Скорость – это физическая величина, характеризующая быстроту движения тел.
В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время – 60 км, то есть движутся с различными скоростями.
Что показывает скорость при равномерном движении?
Скорость при равномерном движении тела показывает, какой путь проходит тело в единицу времени.
Скорость при равномерном движении постоянна.
Как вычислить скорость
По какой формуле определяют скорость тела, если известен его путь и время, за которое он пройден?
Чтобы определить скорость при равномерном движении, нужно путь, пройденный телом за выбранный промежуток времени, разделить на этот промежуток времени:
$Скорость = frac{Путь}{Время}$
или
$upsilon = frac{S}{t}$.
Здесь $upsilon$ — скорость, $S$ – путь, $t$ — время.
Дадим определение.
Cкорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое пройден этот путь.
Соответственно, если автомобиль проезжает в течение 10 с путь, равный 20 метрам (рисунок 2), то его скорость будет равна $frac{20 space м}{10 space с} = 2 frac{м}{с}$ (2 метра в секунду).
Скорость при неравномерном движении
При неравномерном движении тело проходит разные пути за равные промежутки времени, т.е. скорость тела изменяется от одного участка пути к другому.
Как же определить скорость на всем пути? Здесь нам поможет понятие средней скорости.
Как определяют среднюю скорость при неравномерном движении?
Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:
$upsilon_{ср} = frac{S}{t}$.
Отметим, что средняя скорость описывает движение тела за весь промежуток времени. В это время тело можно замедляться, разгоняться, останавливаться.
Например, если вы выезжаете на автомобиле из Москвы в Санкт-Петербург (рисунок 3), то весь путь займет у вас 10 ч. В это время машина будет то набирать скорость, то тормозить, сделает остановку. Общий путь, который вы при этом проедите, будет равен 600 км.
Средняя скорость движения автомобиля будет равна:
$upsilon_{ср} = frac{S}{t} = frac{600 space км}{10 space ч} = 60 frac{км}{ч}$.
Взгляните на таблицу 1, где приведены различные средние скорости.
| Тело | Скорость, $frac{м}{с}$ | Тело | Скорость, $frac{м}{с}$ |
|---|---|---|---|
| Улитка | 0,0014 | Пассажирский самолет | 220 |
| Черепаха | 0,05-0,14 | Звук в воздухе при $0 degree C$ | 332 |
| Муха | 5 | Пуля автомата Калашникова | 760 |
| Пешеход | 1,5 | Луна вокруг Земли | 1000 |
| Конькобежец | 13 | Молекула водорода при $0 degree C$ | 1693 |
| Скворец | 20 | Молекула водорода при $25 degree C$ | 1770 |
| Страус | 22 | Земля вокруг Солнца | 30 000 |
| Автомобиль | 20 | Свет и радиоволны | 300 000 000 |
Единицы измерения скорости
Какова единица измерения скорости в СИ?
В Международной системе (СИ) скорость измеряется в метрах в секунду $frac{м}{с}$.
За единицу скорости принимают скорость такого равномерного движения, при котором за 1 секунду тело проходит путь длиной 1 метр.
Следственно, скорость в системе СИ — количество метров, которое тело пройдёт за 1 секунду.
В повседневной жизни мы чаще видим, что скорость измеряют в километрах в час $frac{км}{ч}$. Также можно использовать километры в секунду $frac{км}{с}$ и сантиметры в секунду $frac{см}{с}$.
Наиболее часто встречаемое ограничение скорости в городах – $ 60 frac{км}{ч}$. Переведем это значение в $frac{м}{с}$:
$60 frac{км}{ч} = 60 cdot frac{1 space км}{1 space ч} = 60 cdot frac{1000 space м}{3600 space с} = frac{60 cdot 1000}{3600} frac{м}{с} approx 17 frac{м}{с}$
Так мы увидели, что числовое значение скорости зависит от выбранной единицы измерения.
Скорость как вектор
Чем, кроме числового значения, характеризуется скорость тела?
Логично, что, кроме числового значения, скорость имеет и направление. Например, чтобы узнать, где будет находиться велосипедист через 1 час после того, как он выехал из дома, нам необходимо знать скорость движения и ее направление.
Физические величины делятся на те, которые имеют направление и те, которые его не имеют — на векторные и скалярные:
1. Векторные величины – это величины, которые, кроме числового значения (модуля), имеют еще и направление.
Скорость – это векторная физическая величина
Векторные величины обозначаются буквами со стрелочками. Скорость обозначается как $vec{upsilon}$, а модуль скорости — $upsilon$.
На рисунке 4 стрелкой показано направление скорости (направление движение тела).
2. Скалярные величины – это физические величины, которые не имеют направления и характеризуются только числовым значением. Это путь, объем, время, длина, масса и др.
Примеры задач на нахождение скорости
Задача №1
Равномерно двигаясь, поезд за 3 часа прошел путь длиной 152 км. Найдите скорость движения поезда в единицах СИ.
Дано:
$S = 152 space км$
$t = 3 space ч$
$upsilon -?$
Показать решение и ответ
Скрыть
Решение:
Скорость рассчитывается по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{152}{3} frac{км}{ч} approx 51 frac{км}{ч}$.
Выразим в единицах СИ:
$51 frac{км}{ч} = frac{51 000}{3600} frac{м}{c} approx 14 frac{м}{c}$.
Ответ: $upsilon = 14 frac{м}{с}$.
Задача №2
Скорость лыжника первую часть пути составляла $20 frac{км}{ч}$ в течение 15 мин. Следующие 45 мин его скорость была $10 frac{км}{ч}$. Найдите среднюю скорость лыжника.
Обозначим первую часть пути как $s_1$, вторую как $s_2$. Время, соответствующее движению на этих участках, $t_1$ и $t_2$ (рисунок 5). Скорости — $upsilon_1$ и $upsilon_2$.
Дано:
$upsilon_1 = 20 frac{км}{ч}$
$t_1 = 15 space мин$
$upsilon_2 = 10 frac{км}{ч}$
$t_2 = 45 space мин$
$upsilon_{ср} -?$
Показать решение и ответ
Скрыть
Решение:
Скорость лыжника на первой и второй частях пути:
$upsilon_1 = frac{S_1}{t_1}$; $upsilon_2 = frac{S_2}{t_2}$.
Выразим из этих уравнений неизвестные $s_1$ и $s_2$:
$s_1 = upsilon_1t_1$; $s_2 = upsilon_2t_2$.
Чтобы найти среднюю скорость лыжника, нужно его полный путь разделить на все время движения:
$upsilon_{ср} = frac{s_1+s_2}{t_1+t_2} = frac{upsilon_1t_1+upsilon_2t_2}{ t_1+t_2}$.
Выпишем отдельно часть выражения и переведем в часы:
$t_1+t_2 = 15 space мин + 45 space мин = 1space ч$.
Тогда:
$t_1 = frac{1}{4} space ч = 0.25 space ч$,
$t_2 = frac{3}{4} space ч = 0.75 space ч$.
$upsilon_{ср} = frac{20 frac{км}{ч} cdot 0.25 space ч+10 frac{км}{ч} cdot 0.75 space ч}{1 space ч} = frac{5 space км +7.5 space км}{1 space ч} = 12.5 frac{км}{ч}$.
Ответ: $upsilon_{ср} = 12,5 frac{км}{ч}$.
Упражнения
Упражнение №1
Выразите скорости тел: $90 frac{км}{ч}$ и $36 frac{км}{ч}$ в $frac{м}{с}$.
Показать решение
Скрыть
Решение:
$upsilon_1 = 90 frac{км}{ч} = 90 cdot frac{1000 space м}{3600 space с} = frac{1000}{40} frac{м}{с} = 25 frac{м}{с}$.
$upsilon_2 = 36 frac{км}{ч} = 36 cdot frac{1000 space м}{3600 space с} = frac{1000}{100} frac{м}{с} = 10 frac{м}{с}$.
Упражнение №2
Поезд идет со скоростью $72 frac{км}{ч}$. Выразите его скорость в $frac{м}{с}$.
Показать решение
Скрыть
Решение:
$upsilon = 72 frac{км}{ч} = 72 cdot frac{1000 space м}{3600 space с} = frac{1000}{50} frac{м}{с} = 20 frac{м}{с}$.
Упражнение №3
Гоночный автомобиль за $10 space мин$ проезжает путь, равный $50 space км$. Определите его среднюю скорость.
Дано:
$t = 10 space мин$
$S = 50 space км$
СИ:
$t = 600 space с$
$S = 50 space 000 space м$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Средняя скорость при неравномерном движении рассчитывается по формуле:
$upsilon_{ср} = frac{S}{t}$.
$upsilon_{ср} = frac{50 space 000 space м}{600 space с} approx 83.3 frac{м}{с}$.
Ответ: $upsilon_{ср} approx 83.3 frac{м}{с}$.
Упражнение №4
Лучшие конькобежцы дистанцию $1500 space м$ пробегают за $1 space мин$ и $52.5 space с$. С какой средней скоростью они проходят эту дистанцию?
Дано:
$t =1 space мин space 52.5 space с$
$S = 1500 space м$
СИ:
$t = 112.5 space с$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Средняя скорость при неравномерном движении рассчитывается по формуле:
$upsilon_{ср} = frac{S}{t}$.
$upsilon_{ср} = frac{1500 space м}{112.5 space с} approx 13.3 frac{м}{с}$.
Ответ: $upsilon_{ср} approx 13.3 frac{м}{с}$.
Упражнение №5
Лыжник, спускаясь с горы, проходит $50 space м$ за $5 space с$. Спустившись с горы и продолжая двигаться, он до полной остановки проходит еще $30 space м$ за $15 space с$. Найдите среднюю скорость лыжника за все время движения.
Дано:
$S_1 = 50 space м$
$t_1 = 5 space с$
$S_2 = 30 space м$
$t_2 = 15 space с$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Средняя скорость при неравномерном движении рассчитывается по формуле:
$upsilon_{ср} = frac{S}{t}$, где $S$ — весь путь, пройденный лыжником, $t$ — общее время движения.
Общий путь равен: $S = S_1 + S_2$.
Общее время движения: $t = t_1 + t_2$.
Подставим эти значения в формулу для средней скорости и рассчитаем ее:
$upsilon_{ср} = frac{S_1 + S_2}{t_1 + t_2}$,
$upsilon_{ср} = frac{50 space м + 30 space м}{5 space с + 15 space с} = frac{80 space м}{20 space с} = 4 frac{м}{с}$.
Ответ: $upsilon_{ср} = 4 frac{м}{с}$.
Задание
Найдите с помощью интернета фамилии советских летчиков, совершивших впервые в мире беспосадочный перелет Москва-Северный полюс-США. Известно, что расстояние в $8582 space км$ они пролетели за $63 space ч$ и $16 space мин$. Определите, с какой скоростью летел самолет.
Первый беспосадочный перелет Москва-Северный полюс-США совершили советские авиаторы 18-20 июня в 1937 году. Перелет был совершен на самолете АНТ-25. Состав: командир экипажа В. П. Чкалов, второй пилот Г. Ф. Байдуков и штурман А. В. Беляков.
Дано:
$S = 8582 space км$
$t = 63 space ч space 16 space мин$
СИ:
$S = 8 space 582 space 000 space м$
$t = 227 space 760 space с$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость:
$upsilon = frac{S}{t}$,
$upsilon = frac{8 space 582 space 000 space м}{227 space 760 space с} approx 37.7 frac{м}{с}$.
Ответ: $upsilon approx 37.7 frac{м}{с}$.
Одинаковое расстояние можно проехать за разное время.
Например, спортивная машина один километр может проехать быстрее, чем тяжело нагруженная грузовая машина. Одна и та же машина может ехать как быстрее, так и медленнее.

Обрати внимание!
Чтобы сравнить различные движения, необходимо знать скорость движения.
Скоростью движения называется величина, численно равная пути, проходимому телом в единицу времени.
Скорость вычисляется по формуле
v=st
, где
(s) — пройденный путь;
(t) — время.
Чем больше скорость, тем больший путь проходит тело за единицу времени. Если путь измеряется в метрах (м), а время движения в секундах (с), то скорость тела измеряется в (м/с).
Метр в секунду (м/с) — единица скорости в международной системе единиц.
Скорость можно выражать и в других единицах, например в км/с или в км/ч.
Различные примеры скорости:
1. скорость реактивного самолета — 3000 км/ч.
2. Скорость спринтера на дистанции — 37 км/ч.
3. Скорость звука в воздухе — 1224 км/ч.
4. Средняя скорость ходьбы — 6 км/ч.
5. Максимальная скорость гепарда — 114 км/ч.
6. Скорость улитки — 0,02 км/ч.
Расчёт
пути и времени движения
«Движение
– это жизнь»
Аристотель
В
данной теме будем применять приобретённые знания о механическом движении на
практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь
– это физическая величина, равная длине траектории, по которой двигалось тело,
в течение данного промежутка времени. Путь является скалярной величиной,
то есть, не имеет направления. Скорость при равномерном движении – это
величина, равная отношению пройденного пути к промежутку времени, за который
этот путь пройден.
Скорость
является векторной величиной, то есть, характеризуется как числовым значением,
так и направлением.
Средняя
скорость при неравномерном движении – это величина, равная отношению всего
пройденного пути к общему времени в пути.
Задача
1.
Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?
В
первую очередь, необходимо научиться правильно оформлять задачи по физике.
При решении любой задачи нужно писать «дано». То есть, в левой части
листа необходимо записать слово «дано», после которого ставится двоеточие, а
дальше в столбик перечисляете все исходные данные, которые указаны в условии
задачи. В нашем случае – это скорость и время в пути. После этого, нужно
очеркнуть данные и ниже (уже под линией) записать, что необходимо найти.
В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем
непосредственно к решению задачи.
А
теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть,
сколько километров автомобиль проходит за час. А время в условии дано в
минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в
часы.
В
общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами
измерения, можно (и даже нужно) переводить данные в систему СИ сразу после
того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в
км/ч необходимо
1 м/с = 3,6 км/ч
1 км/ч = 1/3,6 м/с
Время
в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому,
чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как
перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее
пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется
переводить данные в систему СИ.
Задача
2.
Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.
Получившееся
выражение, в котором остались, только те величины, которые были даны
изначально, называется расчетной формулой. Только в расчетную формулу необходимо
подставлять числовые значения, а до этого, все делается в буквенном виде.
Задача
3.
Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального
пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя
скорость?
Сразу
хочется обратить ваше внимание на распространенную ошибку. Среднюю
скорость нельзя находить как среднее арифметическое разных скоростей на разных
участках движения. В этом можно убедиться с помощью простых расчетов:
если подсчитать среднюю скорость, как среднее арифметическое скоростей, то
получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю
скорость как отношение всего пройденного пути к общему времени в пути. В
результате получим 214,3 м/с. Получается вроде небольшая разница. В
результате неверных расчётов за каждую секунду, пройденное расстояние
увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное
расстоянии будет больше на 8,6 км, а это существенно.
Задача
4.
Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть
своего пути велосипедист проехал за 3 минуты. За какое время велосипедист
проехал вторую часть, если общий путь составил 2 км?
Задача
5.
Определите по графику скорость равномерного движения тела.
Здесь,
конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не
нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика:
какие величины они обозначают и в каких единицах измеряются. Вертикальная ось –
обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах.
Значит, это график зависимости пройденного пути от времени. При равномерном
движении скорость постоянна, значит, можно путь, пройденный за определенный
промежуток времени, разделить на это время и, таким образом, найти скорость.
Для наибольшей точности желательно найти точку, на графике, наиболее близкую к
пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие
координаты, то есть, на значения пути и времени. Для этого из точки опускаем
перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.
Основные
выводы:
В
качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.
Конспект по физике для 7 класса «Скорость». ВЫ УЗНАЕТЕ: Что такое скорость. Как можно определить скорость движения тел. Каковы единицы скорости. Как вычислить скорость тела при равномерном движении. Как построить графики зависимости скорости от времени. Как построить графики зависимости пути от времени. ВСПОМНИТЕ: В каком случае тело движется равномерно? Что такое путь, единицы пути?
Конспекты по физике Учебник физики Тесты по физике
СКОРОСТЬ
За одно и то же время различные тела могут проходить разные расстояния. За 5 мин движения поезд прошёл большее расстояние, чем проехал велосипедист, а велосипедист большее расстояние, чем пролетела муха. Значит, одно и то же расстояние поезд проезжает быстрее, чем велосипедист, а велосипедист быстрее, чем пролетает муха.

ПОНЯТИЕ СКОРОСТИ
В физике быстроту перемещения тола характеризует такая величина, как скорость. Например, человек может за время 1 ч пройти путь 5 км, автомобиль за это же время может проехать 60 км, а самолёт пролетит 850 км. Тогда говорят, что человек движется со скоростью 5 километров в час, скорость автомобиля составляет 60 километров в час, а скорость самолёта — 850 километров в час.
В окружающем нас мире встречаются самые разные скорости. Так, черепаха может ползти со скоростью от 0,05 до 0,14 м/с. Идущий в среднем темпе человек движется со скоростью 1,4 м/с. Скорость гепарда может превышать 30 м/с. Скорость ветра во время урагана может превышать 32,6 м/с. Звук в воздухе распространяется со скоростью приблизительно 333 м/с. а Земля движется вокруг Солнца со скоростью около 30 000 м/с. Скорость света в вакууме — самая большая скорость во Вселенной равна 299 792 458 м/с.
СКОРОСТЬ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ
Скорость при равномерном движении тела показывает, какой путь проходит тело за единицу времени. Так как при равномерном движении тело за равные промежутки времени проходит равные пути, то скорость при таком движении оказывается постоянной.
Для того чтобы определить скорость тела при равномерном движении, необходимо путь, пройденный телом, разделить на время, за которое этот путь пройден.
Если обозначить величины: скорость ʋ, путь — s и время — t, то скорость рассчитывают по формуле ʋ = s / t.
ЕДИНИЦЫ СКОРОСТИ
В Международной системе единиц (СИ) за единицу скорости принимают скорость такого равномерного движения, при котором движущееся тело за 1 секунду проходит путь, равный 1 метру. Эту единицу называют 1 метр в секунду и обозначают 1 м/с.
Очень часто используются и другие единицы скорости: километр в час (км/ч), километр в секунду (км/с), сантиметр в секунду (см/с). При выборе разных единиц скорость тоже будет иметь разные численные значения.
НАПРАВЛЕНИЕ СКОРОСТИ
Величины, которые, кроме числового значения (модуля), имеют ещё и направление, называют векторными. Числовое значение векторной величины также называется модулем вектора.
Скорость, кроме числового значения, всегда имеет направление, следовательно, скорость — это векторная величина. Именно поэтому скорость обозначается как ![]() (со стрелочкой), а её модуль как ʋ (без стрелочки).
(со стрелочкой), а её модуль как ʋ (без стрелочки).
Говоря о модуле скорости, мы можем понять, насколько быстро или медленно движется физическое тело. Для решения большинства задач необходимо ещё знать, куда направлена скорость тела.
Кроме скорости, существуют и другие векторные физические величины, которые характеризуются числовым значением и направлением (с ними вы познакомитесь чуть позже). Вместе с тем существуют и другие физические величины, которые не имеют направления, а характеризуются только числовым значением. Такие физические величины называют скалярными. Примерами скалярных величин могут служить путь, объём, площадь и т. д.
ГРАФИКИ ЗАВИСИМОСТИ ПУТИ И СКОРОСТИ ОТ ВРЕМЕНИ
Путь, пройденный телом, и скорость его движения с течением времени могут изменяться. Для большей наглядности эти изменения часто изображают графически.
Для построения графиков на горизонтальной оси (абсцисс) откладывают время, а на вертикальной оси (ординат) — путь, пройденный телом, или его скорость.
График зависимости скорости от времени при равномерном движении — это прямая, параллельная оси абсцисс. Действительно, с течением времени скорость при таком движении остаётся постоянной.
График зависимости пути, пройденного телом, от времени при прямолинейном равномерном движении — это прямая, расположенная в первой четверти координатной плоскости и проведённая из начала координат. Действительно, при движении тела с постоянной скоростью с течением времени путь, пройденный телом, увеличивается. Причём эта зависимость прямая, так как она описывается уравнением s = ʋt.
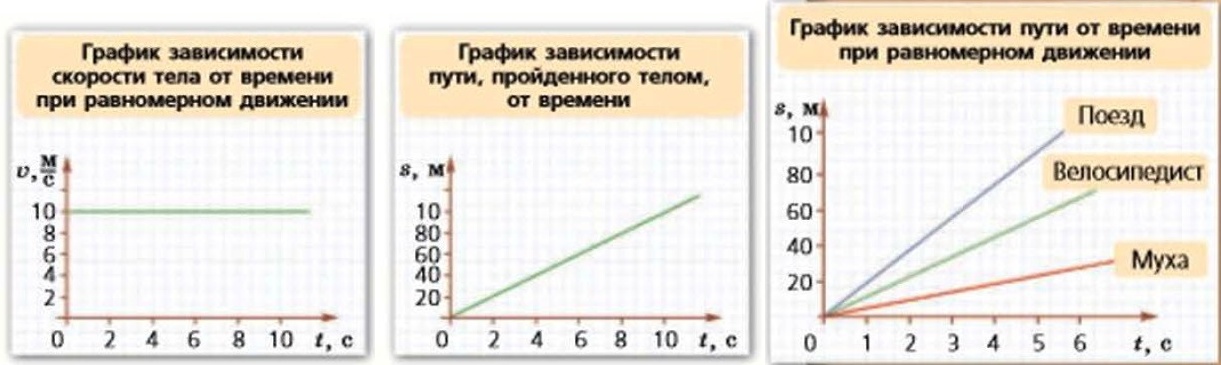
Вы смотрели Конспект по физике для 7 класса «Скорость»: Что такое скорость. Как можно определить скорость движения тел. Каковы единицы скорости. Как вычислить скорость тела при равномерном движении. Как построить графики зависимости скорости от времени. Как построить графики зависимости пути от времени.
Вернуться к Списку конспектов по физике (оглавление).
Пройти онлайн-тест «Скорость, путь и время»
Равномерное и неравномерное движение.
Рассмотрим движение автомобиля. Например, если автомобиль за каждую четверть часа (15 мин) проходит 15 км, за каждые полчаса (30 мин) – 30 км, а за каждый час – 60 км, считается, что он движется равномерно.

Если тело за любые равные промежутки времени проходит равные пути, его движение считается равномерным.
Равномерное движение встречается очень редко. Почти равномерно движется Земля вокруг Солнца, за год Земля делает один оборот вокруг Солнца.
Практически никогда водителю автомобиля не удается поддерживать равномерность движение – по разным причинам приходится то ускорять то замедлять езду. Движение стрелок часов (минутной и часовой) только кажется равномерным, в чем легко убедиться, наблюдая за движением секундной стрелки. Она то движется, то останавливается. Точно так же движутся и две остальные стрелки, только медленно, и поэтому их рывков не видно. Молекулы газов, ударяясь друг об друга, на какое-то время останавливаются, затем снова разгоняются. При следующих столкновениях, уже с другими молекулами, они снова замедляют свое движение в пространстве.
Все это примеры неравномерного движения. Так движется поезд, отходя от станции, проходя за одинаковые промежутки времени все бóльшие и бóльшие пути. Лыжник или конькобежец проходят на соревнованиях равные пути за различное время. Так движутся взлетающий самолет, открываемая дверь, падающая снежинка.
Если тело за равные промежутки времени проходит разные пути, то его движение называют неравномерным.
Неравномерное движение можно наблюдать на опыте. На рисунке изображена тележка с капельницей, из которой через одинаковые промежутки времени падают капли. При движении тележки под действием к ней груза мы видим, что расстояния между следами от капель неодинаковы. А это и означает, что за одинаковые промежутки времени тележка проходит разные пути.
Скорость. Единицы скорости.
Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Например, по шоссе шагает турист, мчится автомобиль, в воздухе летит самолет. Допустим, что все они движутся равномерно, тем не менее движение этих тел будет отличаться.
Автомобиль движется быстрее пешехода, а самолет быстрее автомобиля. В физике величиной, характеризующей быстроту движения, называется скорость.
Предположим, что турист за 1 час проходит 5 км, автомобиль 90 км, а скорость самолета 850 км в час.
Скорость при равномерном движении тела показывает, какой путь прошло тело в единицу времени.
Таким образом, используя понятие скорости, мы можем теперь сказать, что турист, автомобиль и самолет движутся с различными скоростями.
При равномерном движении скорость тела остается постоянной.
Если велосипедист проезжает в течение 5 с путь, равный, 25 м, то его скорость будет равна 25м/5с = 5м/с.
Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени:
скорость = путь/время.
Скорость обозначают буквой v, путь – s, время – t. Формула для нахождения скорости будет иметь такой вид:
v=s/t.
Скорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое этот путь пройден.
В Международной системе (СИ) Скорость измеряют в метрах в секунду (м/с).
Это значит, что за единицу скорости принимается скорость такого равномерного движения, при котором за одну секунду тело проходит путь, равный 1 метру.
Скорость тела можно измерять также в километрах в час (км/ч), километрах в секунду (км/с), сантиметрах в секунду (см/с).
Пример. Поезд, двигаясь равномерно, за 2 ч проходит путь, равный 108 км. Вычислите скорость движения поезда.
Итак, s = 108 км; t = 2 ч; v = ?
Решение. v = s/t, v = 108 км/2 ч = 54 км/ч. Легко и просто.
Теперь, выразим скорость поезда в единицах СИ, т.е километры переведем в метры, а часы в секунды:
54 км/ч = 54000 м/ 3600 с = 15м/с.
Ответ: v = 54 км/ч, или 15 м/с.
Таким образом, числовое значение скорости зависит от выбранной единицы.
Скорость, кроме числового значения, имеет направление.
Например, если требуется указать, где будет находиться через 2 ч самолет, вылетевший из Владивостока, то необходимо указать, не только значение его скорости, но и его пункт назначения, т.е. его направление. Величины, которые, кроме числового значения (модуля), имеют еще и направление, называются векторными.
Скорость – это векторная физическая величина.
Все векторные величины обозначают соответствующими буквами со стрелочкой. Например, скорость обозначается символом v со стрелочкой, а модуль скорости той же буквой, но без стрелочки v.
Некоторые физические величины не имеют направления. Они характеризуются только числовым значением. Это время, объем, длина и др. Они являются скалярными.
Если при движении тела его скорость изменяется от одного участка пути к другому, то такое движение является неравномерным. Для характеристики неравномерного движения тела, введено понятие средней скорости.
Например, поезд от Москвы до Санкт-Петербурга идет со скоростью 80 км/ч. Какую скорость имеют ввиду? Ведь скорость поезда на остановках равна нулю, после остановки – увеличивается, а перед остановкой – уменьшается.
В данном случае поезд движется неравномерно, а значит, скорость, равная 80 км/ч, – это средняя скорость движения поезда.
Она определяется почти так же, как и скорость при равномерном движении.
Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:
vср = s/t.
Следует напомнить, что только при равномерном движении отношение s/t за любой промежуток времени будет постоянно.
При неравномерном движении тела средняя скорость характеризует движение тела за весь промежуток времени. Она не поясняет, как двигалось тело в различные моменты времени этого промежутка.
В таблице 1 приводится средние скорости движения некоторых тел.
Таблица 1
Средние скорости движения некоторых тел, скорость звука, радиоволн и света.
| наименование | скорость, м/с | наименование | скорость, м/с |
|---|---|---|---|
| Улитка | 0,0014 | Самолет Ил-18 | 180 |
| Черепаха | 0,05-0,4 | Звук в воздухе при 0 °С | 332 |
| Муха комнатная | 5 | Пуля автомата Калашникова (при вылете из ствола) | 715 |
| Пешеход | 1,3 | Луна вокруг Земли | 1000 |
| Конькобежец | до 13 | Молекула водорода (при 0 °С) | 1693 |
| Скворец | 20 | Молекула водорода (при 25 °С) | 1770 |
| Страус | 22 | Искусственный спутник Земли | 8000 |
| Тепловоз ТЭ10Л | до 28 | Земля вокруг Солнца | 30 000 |
| Автомобиль “Жигули” | 40 | Свет и радиоволны | около 300 000 000 |
Расчет пути и времени движения.
Если известны скорость тела и время при равномерном движении, то можно найти пройденный им путь.
Поскольку v = s/t, то путь определяют по формуле
s = vt.
Чтобы определить путь, пройденный телом при равномерном движении, надо скорость тела умножить на время его движения.
Теперь, зная, что s = vt, можно найти время, в течение которого двигалось тело, т.е.
t = s/v.
Чтобы определить время при неравномерном движении, надо путь, пройденном телом, разделить на скорость его движения.
Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движение, находят путь:
s = vсрt.
Пользуясь этой формулой, можно определить время при неравномерном движении тела:
t = s/vср.
Инерция.
Наблюдения и опыты показывают, что скорость тела сама по себе измениться не может.

Футбольный мяч лежит на поле. Ударом ноги футболист приводит его в движение. Но сам мяч не изменит свою скорость и не начнет двигаться, пока на него не подействуют другие тела. Пуля, вложенная в ствол ружья, не вылетит до тех пор, пока ее не вытолкнут пороховые газы.
Таким образом, и мяч и пуля не имеют свою скорость, пока на них не подействуют другие тела.
Футбольный мяч, катящийся по земле, останавливается из-за трения о землю.
Тело уменьшает свою скорость и останавливается не само по себе, а под действием других тел. Под действием другого тела происходит также изменение направления скорости.
Теннисный мяч меняет направление движения после удара о ракетку. Шайба после удара о клюшку хоккеиста также изменяет направление движения. Направление движения молекулы газа меняется при ударении ее с другой молекулой или со стенками сосуда.
Значит, изменение скорости тела (величина и направления) происходит в результате действия на него другого тела.
Проделаем опыт. Установим наклонно на столе доску. Насыплем на стол, на небольшом расстоянии от конца доски, горку песка. Поместим на наклонную доску тележку. Тележка, скатившись с наклонной доски быстро останавливается, попав в песок. Скорость тележки уменьшается очень быстро. Ее движение неравномерно.
Выровняем песок и вновь отпустим тележку с прежней высоты. Теперь тележка пройдет большее расстояние по столу, прежде чем остановится. Ее скорость изменяется медленнее, а движение становится ближе к равномерному.
Если совсем убрать песок с пути тележки, то препятствием ее движению будет только трение о стол. Тележка до остановки еще медленнее, и проедет она больше,чем в первый, и во второй разы.
Итак, чем меньше действие другого тела на тележку, тем дольше сохраняется скорость ее движения и тем ближе оно к равномерному.
Как же будет двигаться тело, если не него совсем не будут действовать другие тела? Как это можно установить на опыте? Тщательные опыты по изучению движения тел были впервые проведены Г. Галилеем. Они позволили установить, что если на тело не действуют другие тела, то оно находится или в покое, или движется прямолинейно, и равномерно относительно Земли.
Явление сохранения скорости тела при отсутствии действия на него других тел, называется инерцией.
Инерция – от латинского инерциа – неподвижность, бездеятельность.
Таким образом, движения тела при отсутствии действия на него другого тела, называется движением по инерции.
Например, пуля вылетевшая из ружья, так и летела бы, сохраняя свою скорость, если бы на нее не действовало другое тело – воздух (а точнее, молекулы газов, которые в нем находятся.). Вследствие этого скорость пули уменьшается. Велосипедист, перестав крутит педали, продолжает двигаться. Он смог бы сохранить скорость своего движения, если бы на него не действовала бы сила трения.
Итак, если на тело не действуют другие тела, то оно движется с постоянной скоростью.
Взаимодействие тел.
Вам уже известно, что при неравномерном движении скорость тела меняется с течением времени. Изменение скорости тела происходит под действием другого тела.
![]()
Проделаем опыт. К тележке прикрепим упругую пластинку. Затем изогнем ее и свяжем нитью. Тележка относительно стола находится в покое. Станет ли двигаться тележка, если упругая пластинка выпрямится?
Для этого перережем нить. Пластинка выпрямится. Тележка же останется на прежнем месте.
Затем вплотную к согнутой пластинке поставим еще одну такую же тележку. Вновь пережжем нить. После этого обе тележки приходят в движение относительно стола. Они разъезжаются в разные стороны.
Чтобы изменить скорость тележки, понадобилось второе тело. Опыт показал, что скорость тела меняется только в результате действия на него другого тела (второй тележки). В нашем опыте мы наблюдали, что в движение пришла и вторая тележка. Обе стали двигаться относительно стола.

Тележки действуют друг на друга , т.е они взаимодействуют. Значит, действие одного тела на другое не может быть односторонним, оба тела действуют друг на друга, т. е. взаимодействуют.
Мы рассмотрели самый простой случай взаимодействия двух тел. Оба тела (тележки) до взаимодействия находились в покое относительно друг друга, и относительно стола.

Например, пуля также находилась в покое относительно ружья перед выстрелом. При взаимодействии (во время выстрела) пуля и ружье движутся в разные стороны. Получается явление – отдачи.
Если человек, сидящий в лодке, отталкивает от себя другую лодку, то происходит взаимодействие. Обе лодки приходят в движение.
Если же человек прыгает с лодки на берег, то лодка отходит в сторону, противоположную прыжку. Человек подействовал на лодку. В свою очередь, и лодка действует на человека. Он приобретает скорость, которая направлена к берегу.
Итак, в результате взаимодействия оба тела могут изменить свою скорость.
Масса тела. Единица массы.
При взаимодействии двух тел скорости первого и второго тела всегда меняются.
![]()
Одно тело после взаимодействия приобретает скорость, которая может значительно отличаться от скорости другого тела. Например, после выстрела из лука скорость стрелы гораздо больше скорости, которую приобретает тетива лука после взаимодействия.
Почему так происходит? Проведем опыт, описанный в параграфе 18. Только теперь, возьмем тележки разного размера. После того, как нить пережгли, тележки разъезжаются с разными скоростями. Тележка, которая после взаимодействия движется медленнее, называется более массивной. У нее больше масса. Тележка, которая после взаимодействия движется с большей скоростью, имеет меньшую массу. Значит, тележки имеют разную массу.
Скорости, которые приобрели тележки в результате взаимодействия, можно измерить. По этим скоростям сравнивают массы взаимодействующих тележек.
Пример. Скорости тележек до взаимодействия равны нулю. После взаимодействия скорость одной тележки стала равна 10 м/с, а скорость другой 20 м/с. Поскольку скорость, которую приобрела вторая тележка, в 2 раза больше скорости первой, то и ее масса в 2 раза меньше массы первой тележки.
В случае, если после взаимодействия скорости изначально покоившихся тележек одинаковы, то их массы одинаковы. Так, в опыте, изображенном на рисунке 42, после взаимодействия тележки разъезжаются с равными скоростями. Следовательно, их массы были одинаковы. Если после взаимодействия тела приобрели разные скорости, то их массы различны.

Во сколько раз скорость первого тела больше (меньше) скорости второго тела, во столько раз масса первого тела меньше (больше) массы второго.
Чем меньше меняется скорость тела при взаимодействии, тем большую массу оно имеет. Такое тело называется более инертным.
И наоборот, чем больше меняется скорость тела при взаимодействии, тем меньшую массу оно имеет, тем меньше оно инертно.
Значит, что для всех тел характерно свойство по-разному менять свою скорость при взаимодействии. Это свойство называется инертностью.
Масса тела – это физическая величина, которая характеризует его инертность.
Следует знать, что любое тело: Земля, человек, книга и т.д. – обладает массой.
Масса обозначается буквой m. За единицу массы в СИ принят килограмм (1 кг).
Килограмм – это масса эталона. Эталон изготовлен из сплава двух металлов: платины и иридия. Международный эталон килограмма хранится в г. Севре (близ Парижа). С международного эталона сделано более 40 точнейших копий, разосланных в разные страны. Одна из копий международного эталона находится в нашей стране, в институте метрологии им. Д. И. Менделеева в Санкт-Петербурге.
На практике используют и другие единицы массы: тонна (т), грамм (г), миллиграмм (мг).
| 1 т | = 1000 кг (103 кг) | 1 г | = 0,001 кг (10-3 кг) |
| 1 кг | = 1000 г (103 г) | 1 мг | = 0,001 г (10-3 г) |
| 1 кг | = 1 000 000 мг (106 мг) | 1 мг | = 0,000001 кг (10-6 кг) |
В дальнейшем при изучении физики понятие массы будет раскрыто глубже.
Измерение массы тела на весах.
Для того, чтобы измерить массу тела, можно использовать метод, описанный в параграфе 19.

Сравнивая скорости, приобретенные телами при взаимодействии, определяют, во сколько раз масса одного тела больше (или меньше) массы другого. Измерить массу тела этим способом можно, если масса одного из взаимодействующих тел известна. Таким способом определяют в науке массы небесных тел, а также молекул и атомов.
На практике массу тела можно узнать с помощью весов. Весы бывают различного типа: учебные, медицинские, аналитические, аптекарские, электронные и др.

Рассмотрим учебные весы. Главной частью таких весов, является коромысло. К середине коромысла прикреплена стрелка – указатель, которая движется вправо или влево. К концам коромысла подвешены чашки. При каком условии весы будут находиться в равновесии?
Поместим на чашки весов тележки, которые применялись в опыте (см. § 18). поскольку при взаимодействии тележки приобрели одинаковые скорости, то мы выяснили, что их массы одинаковы. Следовательно, весы будут находится в равновесии. Это значит, что массы тел, лежащих на чашках весов, равны друг другу.
Теперь на одну чашку весов, поместим тело, массу которого надо узнать. На другую будем ставить гирьки, массы которых известны, до тех пор, пока весы не окажутся в равновесии. Следовательно, масса взвешиваемого тела будет равна общей массе гирь.
При взвешивании используется специальный набор гирь.
Различные весы предназначены для взвешивания разных тел, как очень тяжелых, так и очень легких. Так, например, с помощью вагонных весов можно определить массу вагона от 50 т до 150 т. Массу комара, равную 1мг, можно узнать с помощью аналитических весов.
Плотность вещества.

Тела, окружающие нас, состоят из различных веществ: дерева, железа, резины и т.д.
Масса любого тела зависит не только от его размеров, но и оттого, из какого вещества оно состоит. Поэтому тела, имеющие одинаковые объемы, но состоящие из разных веществ, имеют разные массы.
Проведем такой опыт. Взвесим два цилиндра одинакового объема, но состоящие из разных веществ. Например, один из – алюминия, другой из – свинца. Опыт показывает, что масса алюминиевого меньше свинцового, то есть, алюминий легче свинца.
В то же время тела с одинаковыми массами, состоящие из разных веществ, имеют разные объемы.

Так, железный брус массой 1 т занимает объем 0,13 м3 , а лед с такой же массой в 1 т – объем 1,1 м3 . Объем льда почти в 9 раз больше объема железного бруса. Это объясняется тем, что разные вещества могут иметь разную плотность.
Отсюда следует, что тела объемом, например, 1 м3 каждое, состоящие из разных веществ, имеют разные массы. Приведем пример. Алюминий объемом 1 м3 имеет массу 2700 кг, свинец такого же объема имеет массу 11 300 кг. То есть, при одинаковом объеме (1 м3), свинец, имеет массу, превышающую массу алюминия, примерно в 4 раза.
Плотность показывает, чему равна масса вещества, взятого в определённом объёме.
Как же можно найти плотность какого-либо вещества?
Пример. Мраморная плита имеет объем 2м3 , а ее масса равна 5400 кг. Надо определить плотность мрамора.
Итак, нам известно, что мрамор объемом 2м3 имеет массу 5400 кг. Значит, 1 м3 мрамора будет иметь массу в 2 раза меньшую. В нашем случае – 2700 кг (5400 : 2 = 2700). Таким образом, плотность мрамора будет равна 2700 кг на 1 м3 .
Значит, если известна масса тела и его объем, можно определить плотность.
Чтобы найти плотность вещества, надо массу тела разделить на его объем.
Плотность это физическая величина, которая равна отношению массы тела к его объему:
плотность = масса/объем.
Обозначим величины, входящие в это выражение, буквами: плотность вещества – ρ (греч. буква “ро”), масса тела – m, его объем – V. Тогда получим формулу для вычисления плотности:
ρ = m/V.
Единицей плотности вещества в СИ является килограмм на кубический метр (1кг/м3).
Плотность вещества выражают очень часто и в граммах на кубический сантиметр (1г/см3 ).
Если плотность вещества выражена в кг/м3 , то ее можно перевести в г/см3 следующим образом.
Пример. Плотность серебра 10 500 кг/м3 . Выразите ее в г/см3 .
10 500 кг = 10 500 000 г (или 10,5 * 106 г),
1м3 = 1 000 000 см3 (или 106 см3 ).
Тогда ρ = 10 500 кг/м3 = 10,5 * 106 / 106 г/см3 = 10,5 г/см3 .
Следует помнить, что плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна. Так, плотность льда равна 900 кг/м3 , воды 1000 кг/м3 , а водяного пара – 0,590 кг/м3 . Хотя все это состояния того же вещества – воды.
Ниже приведены таблицы плотностей некоторых твердых тел, жидкостей и газов.
Таблица 2
Плотности некоторых твердых тел (при норм. атм. давл., t = 20 °C)
| Твердое тело | ρ, кг/м3 | ρ, г/см3 | Твердое тело | ρ, кг/м3 | ρ, г/см3 |
|---|---|---|---|---|---|
| Осмий | 22 600 | 22,6 | Мрамор | 2700 | 2,7 |
| Иридий | 22 400 | 22,4 | Стекло оконное | 2500 | 2,5 |
| Платина | 21 500 | 21,5 | Фарфор | 2300 | 2,3 |
| Золото | 19 300 | 19,3 | Бетон | 2300 | 2,3 |
| Свинец | 11 300 | 11,3 | Кирпич | 1800 | 1,8 |
| Серебро | 10 500 | 10,5 | Сахар-рафинад | 1600 | 1,6 |
| Медь | 8900 | 8,9 | Оргстекло | 1200 | 1,2 |
| Латунь | 8500 | 8,5 | Капрон | 1100 | 1,1 |
| Сталь, железо | 7800 | 7,8 | Полиэтилен | 920 | 0,92 |
| Олово | 7300 | 7,3 | Парафин | 900 | 0,90 |
| Цинк | 7100 | 7,2 | Лед | 900 | 0,90 |
| Чугун | 7000 | 7 | Дуб (сухой) | 700 | 0,70 |
| Корунд | 4000 | 4 | Сосна (сухая) | 400 | 0,40 |
| Алюминий | 2700 | 2,7 | Пробка | 240 | 0,24 |
Таблица 3
Плотности некоторых жидкостей (при норм. атм. давл. t=20 °C)
| Жидкость | ρ, кг/м3 | ρ, г/см 3 | Жидкость | ρ, кг/м3 | ρ, г/см3 |
|---|---|---|---|---|---|
| Ртуть | 13 600 | 13,60 | Керосин | 800 | 0,80 |
| Серная кислота | 1 800 | 1,80 | Спирт | 800 | 0,80 |
| Мед | 1 350 | 1,35 | Нефть | 800 | 0,80 |
| Вода морская | 1030 | 1,03 | Ацетон | 790 | 0,79 |
| Молоко цельное | 1030 | 1,03 | Эфир | 710 | 0,71 |
| Вода чистая | 1000 | 1,00 | Бензин | 710 | 0,71 |
| Масло подсолнечное | 930 | 0,93 | Жидкое олово (при t = 400 °C) | 6800 | 6,80 |
| Масло машинное | 900 | 0,90 | Жидкий воздух (при t = -194 °C) | 860 | 0,86 |
Таблица 4
Плотности некоторых газов (при норм. атм. давл. t=20 °C)
| Газ | ρ, кг/м3 | ρ, г/см3 | Газ | ρ, кг/м3 | ρ, г/см3 |
|---|---|---|---|---|---|
| Хлор | 3,210 | 0,00321 | Оксид углерода (2) (угарный газ) | 1,250 | 0,00125 |
| Оксид углерода (4) (углекислый газ) | 1,980 | 0,00198 | Природный газ | 0,800 | 0,0008 |
| Кислород | 1,430 | 0,00143 | Водяной пар (при t = 100 °C) | 0,590 | 0,00059 |
| Воздух (при 0 °C) | 1,290 | 0,00129 | Гелий | 0,180 | 0,00018 |
| Азот | 1,250 | 0,00125 | Водород | 0,090 | 0,00009 |
Расчет массы и объема по его плотности.
Знать плотность веществ очень важно для различных практических целей. Инженер, проектируя машину, заранее по плотности и объему материала может рассчитать массу будущей машины. Строитель может определить, какова будет масса строящегося здания.
Следовательно, зная плотность вещества и объем тела, всегда можно определить его массу.
Поскольку плотность вещества можно найти по формуле ρ = m/V, то отсюда можно найти массу т.е.
m = ρV.
Чтобы вычислить массу тела, если известны его объем и плотность, надо плотность умножить на объем.
Пример. Определите массу стальной детали объем 120 см3.
По таблице 2 находим, что плотность стали равна 7,8 г/см3 . Запишем условие задачи и решим ее.
Дано:
V = 120 см3;
ρ = 7,8 г/см3;
m – ?
Решение:
m = ρ · V ,
m = 120 см3 · 7,8 г/см3 = 936 г.
Ответ: m = 936 г.
Если известна масса тела и его плотность, то объем тела можно выразить из формулы m = ρV, т.е. объем тела будет равен:
V = m/ρ.
Чтобы вычислить объем тела, если известна его масса и плотность, надо массу разделить на плотность.
Пример. Масса подсолнечного масла, заполняющего бутылку, равна 930 г. Определите объем бутылки.
По таблице 3 находим, что плотность подсолнечного масла равна 0,93 г/см3 .
Запишем условие задачи и решим ее.
Дано:
ρ = 0,93 г/см3
m = 930 г
V – ?
Решение:
V = m/ρ,
V = 930/0.93 г/см3 = 1000 см3 = 1л.
Ответ: V = 1 л.
Для определения объема пользуются формулой, как правило, в тех случаях, когда объем сложно найти с помощью простых измерений.
Сила.
Каждый из нас постоянно встречается с различными случаями действия тел друг на друга. В результате взаимодействия скорость движения какого-либо тела меняется. Вам уже известно, что скорость тела меняется тем больше, чем меньше его масса. Рассмотрим некоторые примеры, подтверждающие это.
Толкая руками вагонетку, мы можем привести ее в движение. Скорость вагонетки меняется под действием руки человека.
Кусочек железа, лежащий на пробке, опущенной в воду, притягивается магнитом. Кусочек железа и пробка изменяют свою скорость под действием магнита.
Действуя на пружину рукой, можно ее сжать. Сначала в движение приходит конец пружины. Затем движение передается остальным ее частям. Сжатая пружина, распрямляясь, может, например, привести в движение шарик.
При сжатии пружины действующим телом была рука человека. Когда пружина распрямляется, действующим телом является сама пружина. Она приводит в движение шарик.
Ракеткой или рукой можно остановить или изменить направление движения летящего мячика.
Во всех приведенных примерах одно тело под действием другого тела приходит в движение, останавливается, или изменяет направление своего движения.
Таким образом, скорость тела меняется при взаимодействии его с другими телами.
Часто не указывается какое тело и как действовало на данное тело. Просто говорится, что на тело действует сила или к нему приложена сила. Значит, силу можно рассматривать как причину изменения скорости движения.
Сила, действующая на тело, может не только изменить скорость своего тела, но и отдельных его частей.

Например, если надавить пальцами на ластик или кусочек пластилина, он сожмется и изменит свою форму. Это называется деформацией.
Деформацией называется любое изменение формы и размера тела.
Приведем другой пример. Доска, лежащая на опорах, прогибается, если на нее садится человек, или любой другой груз. Середина доски перемещается на большее расстояние, чем края.
Под действием силы скорость различных тел за одно и то же время может измениться одинаково. Для этого необходимо к этим телам приложить разные силы.
Так, чтобы привести в движение грузовую машину, необходима большая сила, чем для легкового автомобиля. Значит, числовое значение силы может быть различным: большим или меньшим. Что же такое сила?
Сила является мерой взаимодействия тел.
Сила – физическая величина, значит, ее можно измерить.

Сила, как и скорость, является векторной величиной. Она характеризуется не только числовым значением, но и направлением. Сила обозначается буквой F со стрелочкой (как мы помним стрелочкой обозначается направление), а ее модуль тоже буквой F, но без стрелочки.
Когда говорят о силе, важно указывать, к какой точке тела приложена действующая сила.
На чертеже силу изображают в виде отрезка прямой со стрелкой на конце. Начало отрезка – точка А есть точка приложения силы. Длина отрезка условно обозначает в определенном масштабе модуль силы.
Итак, результат действия силы на тело зависит от ее модуля, направления и точки приложения.
Явление тяготения. Сила тяжести.

Если выпустить камень из рук – он упадет на землю. То же самое произойдет и с любым другим телом. Если мяч бросить в горизонтальном направлении, он не летит прямолинейно и равномерно. Его траекторией будет кривая линия.

Искусственный спутник Земли также не летит по прямой, он летит вокруг Земли.

В чем же причина наблюдаемых явлений? А вот в чем. На эти тела действует сила – сила притяжения к Земле. Из-за притяжения к Земле падают тела, поднятые над Землей, а потом опущенные. А также, из-за этого притяжения, мы ходим по Земле, а не улетаем в бесконечный Космос, где нет воздуха, чтоб дышать.
Листья деревьев опускаются на Землю, потому что Земля притягивает их. Благодаря притяжению к Земле течет вода в реках.
Земля притягивает к себе любые тела: дома, людей, Луну, Солнце, воду в морях и океанах и др. В свою очередь, и Земля притягивается ко всем этим телам.
Притяжение существует не только между Землей и перечисленными телами. Все тела притягиваются друг к другу. Притягиваются между собой Луна и Земля. Притяжение Земли к Луне вызывает приливы и отливы воды. Огромные массы воды поднимаются в океанах и морях дважды в сутки на много метров. Вам хорошо известно, что Земля и другие планеты движутся вокруг Солнца, притягиваясь к нему и друг к другу.
Притяжение всех тел Вселенной друг к другу называется всемирным тяготением.
Английский ученый Исаак Ньютон первым доказал и установил закон всемирного тяготения.
Согласно этому закону, силы притяжения между телами тем больше, чем больше массы этих тел. Силы притяжения между телами уменьшаются, если увеличивается расстояние между ними.
Для всех живущих на Земле одна из особенно важных значений имеет сила притяжения к Земле.
Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
Сила тяжести обозначается буквой F с индексом: Fтяж . Она всегда направлена вертикально вниз.
Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся у полюсов расположены немного ближе к центру Земли. Поэтому, сила тяжести на полюсе немного больше, чем на экваторе, или на других широтах. Сила тяжести на вершине горы несколько меньше, чем у ее подножия.
Сила тяжести прямо пропорциональна массе данного тела.
Если сравнивать два тела с разной массой, то тело с большей массой – тяжелее. Тело же с меньшей массой – легче.
Во сколько раз масса одного тела больше массы другого тела, во столько же раз и сила тяжести, действующая на первое тело, больше силы тяжести, действующей на второе. Когда массы тел одинаковы, то одинаковы и действующие на них силы тяжести.
Сила упругости. Закон Гука.
Вам уже известно, что на все тела, находящиеся на Земле, действует сила тяжести.
На книгу, лежащую на столе, также действует сила тяжести, но она не проваливается сквозь стол, а находится в покое. Повесим-ка тело на нити. Оно падать не будет.

Почему же покоятся тела, лежащие на опоре или подвешенные на нити? По-видимому, сила тяжести уравновешивается какой-то другой силой. Что же это за сила и откуда она берется?
Проведем опыт. На середину горизонтально расположенной доски, расположенную на опоры, поставим гирю. Под действием силы тяжести гиря начнет двигаться вниз и прогнет доску, т.е. доска деформируется. При этом возникает сила, с которой доска действует на тело, расположенное на ней. Из этого опыта можно сделать вывод, что на гирю, кроме силы тяжести направленной вертикально вниз, действует другая сила. Эта сила направлена вертикально вверх. Она и уравновесила силу тяжести. Эту силу называют силой упругости.
Итак, сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение, называется силой упругости.
Силу упругости обозначают буквой F с индексом Fупр.
Чем сильнее прогибается опора(доска), тем больше сила упругости. Если сила упругости становится равной силе тяжести, действующей на тело, то опора и тело останавливаются.
Теперь подвесим тело на нити. Нить (подвес) растягивается. В нити (подвесе), также как и в опоре, возникает сила упругости. При растяжении подвеса сила упругости будет равна силе тяжести, то растяжение прекращается. Сила упругости возникает только при деформации тел. Если исчезает деформация тела, то исчезает и сила упругости.

Деформации бывают разных видов: растяжения, сжатия, сдвига, изгиба и кручения.
С двумя видами деформации мы уже познакомились – сжатия и изгиба. Более подробно эти и другие виды деформации вы изучите в старших классах.
Теперь попытаемся выяснить, от чего зависит сила упругости.
Файл:Opyt s pezinovym shnurom i girey.jpg
Английский ученый Роберт Гук, современник Ньютона, установил, как зависит сила упругости от деформации.
Рассмотрим опыт. Возьмем резиновый шнур. Один его конец закрепим в штативе. Первоначальная длина шнура была l0. Если к свободному концу шнура подвесить чашку с гирькой, то шнур удлинится. Его длина станет равной l. Удлинение шнура можно найти так:
Δl = l – l0.
Если менять гирьки на чашке, то будет меняться и длина шнура, а значит, ее удлинение Δl .
Опыт показал, что модуль силы упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тела.
В этом и заключается закон Гука. Записывается закон Гука следующим образом:
Fупр = -kΔl,

где Δl – удлинение тела (изменение его длины), k – коэффициент пропорциональности, который называется жесткостью.
Жесткость тела зависит от формы и размеров, а также от материала, из которого оно изготовлено.
Закон Гука справедлив только для упругой деформации. Если после прекращения действий сил, деформирующих тело, оно возвращается в исходное положение, то деформация является упругой.
Более подробно закон Гука и виды деформаций вы изучите в старших классах.
Вес тела.
В повседневной жизни очень часто используется понятие “вес” . Попытаемся выяснить что же это за величина. В опытах, когда тело ставили на опору, сжималась не только опора, но и тело, притягиваемое Землей.
Деформированное, сжатое тело давит на опору с силой, которую называют весом тела. Если тело подвешено на нити, то растянута не только нить, но и само тело.
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Вес тела – это векторная физическая величина и обозначается она буквой P со стрелочкой над этой буквой, направленная вправо.
Однако следует помнить, что сила тяжести приложена к телу, а вес приложен к опоре или подвесу.
Если тело и опора неподвижны или движутся равномерно и прямолинейно, то вес тела по своему числовому значению равен силе тяжести, т.е.
P = Fтяж.
Следует помнить, что сила тяжести является результатом взаимодействия тела и Земли.
Итак, Вес тела – это результат взаимодействия тела и опоры (подвеса). Опора (подвес) и тело при этом деформируются, что приводит к появлению силы упругости.
Единицы силы. Связь между силой тяжести и массой тела.
Вам уже известно, что сила – это физическая величина. Она кроме числового значения (модуля) имеет направление, т. е. это векторная величина.
Силу, как и любую физическую величину, можно измерить, сравнить с силой, принятой за единицу.
Единицы физических величин всегда выбирают условно. Так, за единицу силы можно принять любую силу. Например, можно принять за единицы силы силу упругости какой-то пружины, растянутой до определенной длины. За единицу силы, можно принять и силу тяжести, действующей на тело.
Вы знаете, что сила является причиной изменения скорости тела. Именно поэтому за единицу силы, принята сила, которая за время 1с изменяет скорость тела массой 1 кг на 1 м/с.
В честь английского физика Ньютона эта единица названа ньютоном (1 Н). Часто применяют и другие единицы – килоньютоны (кН), миллиньютоны (мН):
1кН=1000 Н, 1Н = 0,001 кН.
Попытаемся определить величину силы в 1 Н. Установлено, что 1 Н приблизительно равен силе тяжести, которая действует на тело массой 1/10 кг, или более точно 1/9,8 кг (т. е. около 102 г).
Необходимо помнить, что сила тяжести, действующая на тело, зависит от географической широты, на которой находится тело. Сила тяжести меняется при изменении высоты над поверхностью Земли.
Если известно, что единицей силы является 1 Н, то как рассчитать силу тяжести, которая действует на тело любой массы?
Известно, что, во сколько раз масса одного тела, больше массы другого тела, во столько же раз сила тяжести, действующей на первое тело, больше силы тяжести, действующей на второе тело. Таким образом, если на тело массой 1/9,8 кг действует сила тяжести равная 1 Н, то на тело 2/9,8 кг будет действовать сила тяжести, равная 2 Н.
На тело массой 5/9,8 кг – сила тяжести равная – 5 Н, 5,5/9,8 кг – 5,5 Н, и т. д. На тело массой 9,8/9,8 кг – 9,8 Н.
Поскольку 9,8/9,8 кг = 1 кг, то на тело массой в 1 кг будет действовать сила тяжести, равная 9,8 Н. Значение силы тяжести, действующей на тело массой 1 кг, можно записать так: 9,8 Н/кг.
Значит, если на тело массой 1 кг действует сила, равная 9,8 Н, то на тело массой 2 кг будет действовать сила, в 2 раза большая. Она будет равна 19,6 Н, и так далее.
Таким образом, чтобы определить силу тяжести, действующую на тело любой массы, необходимо 9,8 Н/кг умножить на массу этого тела.
Масса тела выражается в килограммах. Тогда получим, что:
Fтяж = 9,8 Н/кг · m.
Величину 9,8 Н/кг обозначают буквой g, и формула для силы тяжести будет иметь вид:
Fтяж = gm,
где m – масса, g – называется ускорением свободного падения. (Понятие ускорения свободного падения будет дано в 9 классе.)
При решении задач где не требуется большой точности, g = 9,8 Н/кг округляют до 10 Н/кг.
Вам уже известно, что P = Fтяж , если тело и опора неподвижны или движутся равномерно и прямолинейно. Следовательно, вес тела можно определить по формуле:
P = gm,
Пример. На столе стоит чайник с водой массой 1,5 кг. Определите силу тяжести и вес чайника. Покажите эти силы на рисунке 68.
Дано:
m = 1,5 кг
g ≈ 10 Н/кг
Fтяж – ?
P – ?
Решение:
Fтяж = gm,
P = gm,
Fтяж = P ≈ 10 Н/кг · 1,5 кг = 15 Н.
Ответ: Fтяж = P = 15 Н.
Теперь изобразим силы графически. Выберем масштаб. Пусть 3 Н будет равен отрезку длиной 0,3 см. Тогда силу в 15 Н. необходимо начертить отрезком длиной 1,5 см.
Следует учитывать, что сила тяжести действует на тело, а значит, приложена к самому телу. Вес действует на опору или подвес, т. е. приложен к опоре, в нашем случае к столу.
Динамометр.

На практике часто приходится измерять силу, с которой одно тело действует на другое. Для измерения силы используется прибор, который называется динамометр (от греч. динамис – сила, метрео – измеряю).
Динамометры бывают различного устройства. Основная их часть – стальная пружина, которой придают разную форму в зависимости от назначения прибора. Устройство простейшего динамометра основывается на сравнении любой силы с силой упругости пружины.
Простейший динамометр можно изготовить из пружины с двумя крючками, укрепленной на дощечке. К нижнему концу пружины прикрепляется указатель, а на доску наклеивается полоска бумаги.
Отметим на бумаге черточкой положение указателя при не натянутой пружине. Эта отметка будет нулевым делением.

Затем к крючку будем подвешивать груз массой 1/9,8 кг, т. е. 102 г.На этот груз будет действовать сила тяжести 1 Н. Под действием этой силы (1 Н) пружина растянется, указатель опустится вниз. Его новое положение отмечаем на бумаге и ставим цифру 1. После чего, подвешиваем груз массой 204 г и ставим отметку 2. Это означает, что в таком положении сила упругости пружины равна 2 Н. Подвесив груз массой 306 г, наносим отметку 3, и т. д.
Для того, чтобы нанести десятые доли ньютона, надо нанести деления – 0,1; 0,2; 0,3; 0,4 и т. д. Для этого расстояния между каждыми целыми отметками делятся на десять равных частей. Так можно сделать, учитывая, что сила упругости пружины Fупр увеличивается во столько раз, во сколько увеличивается ее удлинение Δl . Это следует из закона Гука: Fупр = kΔl, т. е. сила упругости тела при растяжении прямо пропорциональна изменению длины тела.

Проградуированная пружина и будет простейшим динамометром.
С помощью динамометра измеряется не только сила тяжести, но и другие силы, такие как – сила упругости, сила трения и т. д.
Так, например, для измерения силы различных мышечных групп человека используется медицинские динамометры.
Для измерения мускульной силы руки при сжатии кисти в кулак применяется ручной динамометр – силомер.
Применяются также ртутные, гидравлические, электрические и другие динамометры.
В последнее время широко применяются электрические динамометры. У них имеется датчик, преобразующий деформацию в электрический сигнал.
Для измерения больших сил, таких, например, как тяговые усилия тракторов, тягачей, локомотивов, морских и речных буксиров, используют специальные тяговые динамометры. Ими можно измерить силы до нескольких десятков тысяч ньютонов.

Сложение двух сил, направленных по одной прямой. Равнодействующая сил.
В большинстве случаев, с которыми мы встречаемся в жизни, на тело действует не одна, а сразу несколько сил. Так, например, на парашютиста, спускающегося на Землю, действуют сила тяжести и сила сопротивления воздуха. На тело, висящее на пружине, действуют две силы: сила тяжести и сила упругости пружины.
В каждом подобном случае можно заменить несколько сил, в действительности приложенных к телу, одной силой, равноценной по своему действию этим силам.
Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.
Найдем равнодействующую этих двух сил, действующих на тело по одной прямой в одну сторону.
Обратимся к опыту. К пружине один под другим подвесим два груза массой 102 г и 204 г, т. е. весом 1 Н и 2 Н. Отметим длину, на которую растянулась пружина. Снимем эти грузы заменим одним грузом, который растягивает пружина на такую же длину. Вес этого груза оказывается равным 3 Н.
- Из опыта следует, что: равнодействующая сил, направленных по одной прямой в одну и ту же сторону, а ее модуль равен сумме модулей составляющих сил.
На рисунке равнодействующая сил, действующих на тело, обозначена буквой R, а слагаемые силы – буквами F1 и F2. В этом случае
R = F1 + F2.
Выясним теперь, как найти равнодействующую двух сил, действующих на тело по одной прямой в разные стороны. Тело – столик динамометра. Поставим на столик гирю весом 5 Н, т.е. подействуем на него силой 5 Н, направленной вниз. Привяжем к столику нить и подействуем на него с силой, равной 2 Н, направленной вверх. Тогда динамометр покажет силу 3 Н. Эта сила есть равнодействующая двух сил: 5 Н и 2Н.
- Итак, равнодействующая двух сил, направленных по одной прямой в противоположные стороны, направлена в сторону большей по модулю силы, а ее модуль равен разности модулей составляющих сил (рис.):
R = F1 – F2 .
Если к телу приложены две равные и направленные противоположно силы, то равнодействующая этих сил равна нулю. Например, если в нашем опыте за конец потянуть силой в 5 Н, то стрелка динамометра установится на нулевом делении. Равнодействующая двух сил в этом случае равна нулю:
R = 5 H – 5 H,
R = 0.
Тело под действием двух равных и противоположно направленных сил будет находится в покое или двигаться равномерно и прямолинейно.
Сила трения.

Сани, скатившись с горы, движутся по горизонтальному пути неравномерно, скорость их постепенно уменьшается, и через некоторое время они останавливаются. Человек, разбежавшись, скользит на конька по льду, но, как бы ни был гладок лед, человек все-таки останавливается. Останавливается и велосипед, когда велосипедист прекращает крутить педали. Мы знаем, что причиной таких явлений, является сила. В данном случае это сила трения.
При соприкосновении одного тела с другим получается взаимодействие, препятствующее их относительному движению, которое называется трением. А сила, характеризующая это взаимодействие называется силой трения.
Сила трения – это еще один вид силы, отличающийся от рассмотренных ранее силы тяжести и силы упругости.
Одна из причин возникновения силы трения, является шероховатость поверхностей соприкасающихся тел.

Даже гладкие на вид поверхности тел имеют неровности, бугорки и царапины. На рисунке 79, а неровности изображены в увеличенном виде. Когда одно тело скользит или катится по поверхности другого, эти неровности цепляются друг за друга, так, что получается некоторая сила, задерживающая движение.
Другая причина трения – взаимное притяжение молекул соприкасающихся тел.
Возникновение силы трения обусловлено главным образом первой причиной, когда поверхности тел шероховаты. Но если поверхности хорошо отполированы, то при соприкосновении часть их молекул располагается очень близко друг от друга. В этом случае начинает заметно проявляться притяжение между молекулами соприкасающихся тел.

Силу трения можно уменьшить во много раз, если ввести между трущимися поверхностями смазку. Слой смазки разъединяет поверхности трущихся тел. В этом случае соприкасаются не поверхности тел, а слои смазки. Смазка же в большинстве случаев жидкая, а трение слоев жидкости меньше, чем твердых поверхностей. Например, на коньках малое трение при скольжении по льду объясняется также действием смазки. Между коньками и льдом образуется тонкий слой воды. В технике в качестве смазки широко применяют различные масла.
При скольжении одного тела по поверхности другого возникнет трение, которое называют трением скольжения. Например, такое трение возникнет при движении саней и лыж по снегу.
Если же одно тело не скользит, а катится по поверхности другого, то трение, возникающее при этом, называют трением качения. Так, при движении колес вагона, автомобиля, при перекатывании бревен или бочек по земле проявляется трение качения.
Силу трения можно измерить. Например, чтобы измерить силу трения скольжения деревянного бруска по доске или по столу, надо прикрепить к нему динамометр. Затем равномерно двигать брусок по доске, держа динамометр горизонтально. Что при этом покажет динамометр? На брусок в горизонтальном направлении действуют две силы. Одна сила – сила упругости пружины динамометра, направленная в сторону движения. Вторая сила – это сила трения, направленная против движения. Так как брусок движется равномерно, то это значит, что равнодействующая этих двух сил равна нулю. Следовательно, эти силы равны по модулю, но противоположны по направлению. Динамометр показывает силу упругости (силу тяги), равную по модулю силе трения.
Таким образом, измеряя силу, с которой динамометр действует на тело при его равномерном движении, мы измеряем силу трения.
Если на брусок положить груз, например гирю, и измерить по описанному выше способу силу трения, то она окажется больше силы трения, измеренной без груза.
- Чем больше сила, прижимающая тело к поверхности, тем больше возникающая при этом сила трения.
Положив деревянный брусок на круглые палочки, можно измерить силу трения качения. Она оказывается меньше силы трения скольжения.
Таким образом, при равных нагрузках сила трения качения всегда меньше силы трения скольжения. Именно поэтому, люди еще в древности применяли катки для перетаскивания больших грузов, а позднее стали использовать колесо.
Трение покоя.

Мы познакомились с силой трения, возникающей при движении одного тело по поверхности другого. Но можно ли говорить о силе трения между соприкасающимися твердыми телами, если они находятся в покое?
Когда тело находится в покое на наклонной плоскости, оно удерживается на ней силой трения. Действительно, если бы не было трения, то тело под действием тяжести соскользнуло бы вниз по наклонной плоскости. Рассмотрим случай, когда тело находится в покое на горизонтальной плоскости. Например, на полу стоит шкаф. Попробуем его передвинуть. Если бы шкаф нажать слабо, то с места он не сдвинется. Почему? Действующая сила в этом случае уравновешивается силой трения между полом и ножками шкафа. Так как эта сила существует между покоящимися друг относительно друга телами, то эта сила называется силой трения покоя.
На рисунке изображен транспортер, с помощью которого поднимаются тюки с хлóпком. Тюки удерживаются на ленте транспортера силой трения покоя.
Сила трения покоя удерживает гвоздь, вбитый в доску, не дает развязаться банту на ленте, удерживает нитку, которой сшиты два куска ткани, и т. п.
Трение в природе и технике.

В природе и технике трение имеет большое значение. Трение может быть полезным и вредным. Когда оно полезно, его стараются увеличить, когда вредно – уменьшить.
Без трения покоя ни люди, ни животные не смогли бы ходить по земле, так как при ходьбе мы отталкиваемся от земли. Когда трение между подошвой обуви и земли (или льдом) малó, например, в гололедицу, то отталкиваться от земли очень трудно, ноги скользят. Чтобы ноги не скользили, тротуары посыпаются песком. Это увеличивает силу трения между подошвой обуви и льдом.
Не будь трения, предметы выскальзывали бы из рук.
Сила трения останавливает автомобиль при торможении, но без трения он не смог бы стоять на месте, буксовал. Что-бы увеличить трение, поверхность шин у автомобиля делаются с ребристыми выступами. Зимой, когда дорога бывает особенно скользкая, ее посыпают песком, очищают ото льда.
У многих растений и животных имеются различные органы, служащие для хватания (усики растений, хобот слона, цепкие хвосты лазающих животных). Все они имеют шероховатую поверхность для увеличения трения.

Вам уже известно, что в некоторых случаях трение вредно и с ним приходится бороться. Например, во всех машинах из-за трения нагреваются и изнашиваются движущиеся части. Для уменьшения трения соприкасающиеся поверхности делают гладкими, между ними вводят смазку. Что-бы уменьшить трение вращающихся валов машин и станков, их опирают на подшипники. Деталь подшипника, непосредственно соприкасающуюся с валом, называется вкладышем. Вкладыши делают из твердых металлов – бронзы, чугун или стали. Внутреннюю поверхность их покрывают особыми материалами, чаще всего баббитом (это сплав свинца или олова с другими металлами), и смазывают. Подшипники, в которых вал при вращении скользит по поверхности вкладыша, называют подшипниками скольжения.
Мы знаем, что сила трения качения при одинаковой нагрузке значительно меньше силы трения скольжения. На этом явлении основано применение шариковых и роликовых подшипников. В таких подшипниках вращающийся вал не скользит по неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах.
Устройство простейших шарикового и роликового подшипников изображено на рисунке. Внутреннее кольцо подшипника, изготовленное из твердой стали, насажено на вал. Наружное же кольцо закреплено в корпусе машины. При вращении вала внутреннее кольцо катится на шариках или роликах, находящихся между кольцами. Замена в машине подшипников скольжения шариковыми или роликовыми подшипниками позволяет уменьшить силу трения в 20-30 раз.
Шариковые и роликовые подшипники используются в разнообразных машинах: автомобилях, токарных станках, электрических двигателях, велосипедах, и т. д. Без подшипников (они используют силу трения), невозможно представить современную промышленность и транспорт.
Ссылки
- Уроки по физике за 7 класс по школьной программе
