Как найти скорость тела в момент времени - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Скорость — это быстрота перемещения объекта в заданном направлении. ^[1] В общих целях нахождение скорости объекта (v) — простая задача: нужно разделить перемещение (s) в течение определенного времени (s) на это время (t), то есть воспользоваться формулой v = s/t. Однако таким способом получают среднюю скорость тела. Используя некоторые вычисления, можно найти скорость тела в любой точке пути. Такая скорость называется мгновенной скоростью и вычисляется по формуле v = (ds)/(dt), то есть представляет собой производную от формулы для вычисления средней скорости тела.^[2]

1
Начните с уравнения. Для вычисления мгновенной скорости необходимо знать уравнение, описывающее перемещение тела (его позицию в определенный момент времени),^[3] то есть такое уравнение, на одной стороне которого находится s (перемещение тела), а на другой стороне — члены с переменной t (время).^[4] Например:

s = -1.5t² + 10t + 4
- В этом уравнении:
  
  Перемещение = s. Перемещение — пройденный объектом путь. Например, если тело переместилось на 10 м вперед и на 7 м назад, то общее перемещение тела равно 10 – 7 = 3 м (а на 10 + 7 = 17 м).
  
  Время = t. Обычно измеряется в секундах.
2
Вычислите производную уравнения. Чтобы найти мгновенную скорость тела, чьи перемещения описываются приведенным выше уравнением, нужно вычислить производную этого уравнения. Производная — это уравнение, позволяющее вычислить наклон графика в любой точке (в любой момент времени). Чтобы найти производную, продифференцируйте функцию следующим образом: если y = a*xⁿ, то производная = a*n*x^n-1. Это правило применяется к каждому члену многочлена.
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
  
  s = -1.5t² + 10t + 4
  (2)-1.5t^(2-1) + (1)10t^{1 – 1} + (0)4t⁰
  -3t¹ + 10t⁰
  -3t + 10
3
Замените “s” на “ds/dt”, чтобы показать, что новое уравнение — это производная от исходного уравнения (то есть производная s от t). Производная — это наклон графика в определенной точке (в определенный момент времени). Например, чтобы найти наклон линии, описываемой функцией s = -1.5t² + 10t + 4 при t = 5, просто подставьте 5 в уравнение производной.
- В нашем примере уравнение производной должно выглядеть следующим образом:
  
  ds/dt = -3t + 10
4
В уравнение производной подставьте соответствующее значение t, чтобы найти мгновенную скорость в определенный момент времени.^[5] Например, если вы хотите найти мгновенную скорость при t = 5, просто подставьте 5 (вместо t) в уравнение производной ds/dt = -3 + 10. Затем решите уравнение:

ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 м/с
- Обратите внимание на единицу измерения мгновенной скорости: м/с. Так как нам дано значение перемещения в метрах, а время — в секундах, и скорость равна отношению перемещения ко времени, то единица измерения м/с — правильная.
Реклама

1
Постройте график перемещения тела. В предыдущей главе вы вычисляли мгновенную скорость по формуле (уравнению производной, позволяющему найти наклон графика в определенной точке).^[6] Построив график перемещения тела, вы можете найти его наклон в любой точке, а следовательно определить мгновенную скорость в определенный момент времени.
- По оси Y откладывайте перемещение, а по оси X — время. Координаты точек (x,у) получите через подстановку различных значений t в исходное уравнение перемещение и вычисления соответствующих значений s.
- График может опускаться ниже оси X. Если график перемещения тела опускается ниже оси X, то это значит, что тело движется в обратном направлении от точки начала движения. Как правило, график не распространяется за ось Y (отрицательные значения x) — мы не измеряем скорости объектов, движущихся назад во времени!
2
Выберите на графике (кривой) точку P и близкую к ней точку Q. Чтобы найти наклон графика в точке P, используем понятие предела. Предел — состояние, при котором величина секущей, проведенной через 2 точки P и Q, лежащих на кривой, стремится к нулю.
- Например, рассмотрим точки P(1,3) и Q(4,7) и вычислим мгновенную скорость в точке P.
3

Найдите наклон отрезка PQ. Наклон отрезка PQ равен отношению разницы значений координат «у» точек P и Q к разнице значений координат «х» точек P и Q. Другими словами, H = (y_Q – y_P)/(x_Q – x_P), где H — наклон отрезка PQ. В нашем примере наклон отрезка PQ равен:

H = (y_Q – y_P)/(x_Q – x_P)
H = (7 – 3)/(4 – 1)
H = (4)/(3) = 1.33
4

Повторите процесс несколько раз, приближая точку Q к точке P. Чем меньше расстояние между двумя точками, тем ближе значение наклона полученных отрезков к наклону графика в точке P. В нашем примере проделаем вычисления для точки Q с координатами (2,4.8), (1.5,3.95) и (1.25,3.49) (координаты точки P остаются прежними):

Q = (2,4.8): H = (4.8 – 3)/(2 – 1)
H = (1.8)/(1) = 1.8

Q = (1.5,3.95): H = (3.95 – 3)/(1.5 – 1)
H = (.95)/(.5) = 1.9

Q = (1.25,3.49): H = (3.49 – 3)/(1.25 – 1)
H = (.49)/(.25) = 1.96
5
Чем меньше расстояние между точками P и Q, тем ближе значение H к наклону графика в точке P При предельно малом расстоянии между точками P и Q, значение H будет равно наклону графика в точке P Так как мы не можем измерить или вычислить предельно малое расстояние между двумя точками, графический способ дает оценочное значение наклона графика в точке Р.
- В нашем примере при приближении Q к P мы получили следующие значения H: 1.8; 1.9 и 1.96. Так как эти числа стремятся к 2, то можно сказать, что наклон графика в точке P равен 2.
- Помните, что наклон графика в данной точке равен производной функции (по которой построен этот график) в этой точке. График отображает перемещение тела с течением времени и, как отмечалось в предыдущем разделе, мгновенная скорость тела равна производной от уравнения перемещения этого тела. Таким образом, можно заявить, что при t = 2 мгновенная скорость равна 2 м/с (это оценочное значение).
Реклама

1
Вычислите мгновенную скорость при t = 4, если перемещение тела описывается уравнением s = 5t³ – 3t² + 2t + 9. Этот пример похож на задачу из первого раздела с той лишь разницей, что здесь дано уравнение третьего порядка (а не второго).
- Сначала вычислим производную этого уравнения:
  
  s = 5t³ – 3t² + 2t + 9
  s = (3)5t^{(3 – 1)} – (2)3t^{(2 – 1)} + (1)2t^{(1 – 1) + (0)9t^{0 – 1}
  15t⁽²⁾ – 6t⁽¹⁾ + 2t^{(0)
  15t⁽²⁾ – 6t + 2}}
- Теперь подставим в уравнение производной значение t = 4:
  
  s = 15t⁽²⁾ – 6t + 2
  15(4)⁽²⁾ – 6(4) + 2
  15(16) – 6(4) + 2
  240 – 24 + 2 = 22 м/с
2
Оценим значение мгновенной скорости в точке с координатами (1,3) на графике функции s = 4t² – t. В этом случае точка P имеет координаты (1,3) и необходимо найти несколько координат точки Q, лежащий близко к точке P. Затем вычислим H и найдем оценочные значения мгновенной скорости.
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
  
  s = 4t² – t
  
  t = 2: s = 4(2)² – (2)
  4(4) – 2 = 16 – 2 = 14, so Q = (2,14)
  
  t = 1.5: s = 4(1.5)² – (1.5)
  4(2.25) – 1.5 = 9 – 1.5 = 7.5, so Q = (1.5,7.5)
  
  t = 1.1: s = 4(1.1)² – (1.1)
  4(1.21) – 1.1 = 4.84 – 1.1 = 3.74, so Q = (1.1,3.74)
  
  t = 1.01: s = 4(1.01)² – (1.01)
  4(1.0201) – 1.01 = 4.0804 – 1.01 = 3.0704, so Q = (1.01,3.0704)
- Теперь вычислим H:
  
  Q = (2,14): H = (14 – 3)/(2 – 1)
  H = (11)/(1) = 11
  
  Q = (1.5,7.5): H = (7.5 – 3)/(1.5 – 1)
  H = (4.5)/(.5) = 9
  
  Q = (1.1,3.74): H = (3.74 – 3)/(1.1 – 1)
  H = (.74)/(.1) = 7.3
  
  Q = (1.01,3.0704): H = (3.0704 – 3)/(1.01 – 1)
  H = (.0704)/(.01) = 7.04
- Так как полученные значения H стремятся к 7, то можно сказать, что мгновенная скорость тела в точке (1,3) равна 7 м/с (оценочное значение).
Реклама

Советы

Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.

Об этой статье

Эту страницу просматривали 83 377 раз.

Была ли эта статья полезной?

Источник

Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.

Что такое мгновенная скорость? Мгновенная скорость — скорость тела в данный момент времени. Обозначается v_мгн. Далее, когда мы будем говорить о скорости, мы будем понимать под ней мгновенную скорость тела и обозначать ее просто — v.

Определение

Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t₀ и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:

v = v₀+ at

v — скорость тела в данный момент времени, v₀ —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось

Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.

Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.

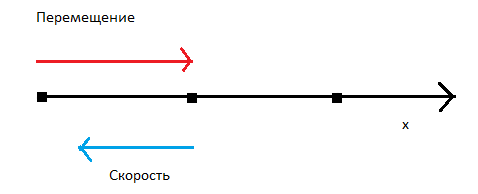
Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.

Скалярная формула скорости

В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:

v = v₀± at

Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.

Проекция скорости

Проекция скорости при равноускоренном прямолинейном движении имеет вид:

v_x= v_0x + a_xt

Знак проекции скорости зависит от того, в какую сторону движется тело:

Знак проекции скорости имеет знак «+», если тело движется в сторону направления оси ОХ.
Знак проекции скорости имеет знак «–», если тело движется противоположно направлению оси ОХ.

Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.

График скорости

График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.

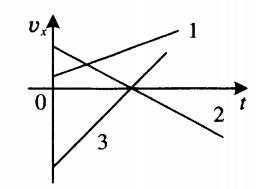
Определение направления движения тела относительно оси ОХ по графику скорости

Если график скорости лежит выше оси времени, то тело движется в направлении оси ОХ. На рисунке этому утверждению соответствует график 1.
Если график скорости пересекает ось времени, то модуль скорости тела сначала уменьшался, и тело тормозило. Но с момента пересечения оси времени оно меняло направление движения в противоположную сторону и двигалось ускоренно. На рисунке этому соответствуют графики скорости 2 и 3.
Если график скорости лежит ниже оси времени, тело движется в направлении, противоположном направлению оси ОХ. На рисунке тело 3 до пересечения с осью времени двигалось противоположно направлению ОХ. Но тело 2 двигалось противоположно оси только после пересечения с этой осью.

Сравнение модулей ускорения по графикам скоростей

Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.

Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.

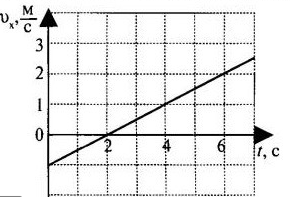
На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.

Полезные факты

Если тело начинало движение из состояния покоя, его начальная скорость равна 0, а его ускорение положительно: v₀= 0, a > 0.
Если тело заканчивает движение остановкой, то его мгновенная скорость в конечный момент времени равна 0, а его ускорение отрицательно: v = 0, a < 0.
Если тело покоится, его скорость и ускорение равны 0: v₀= 0, a = 0.

Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.

Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:

v = v₀– at

Выразим начальную скорость:

v₀ = v + at

Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

v₀ = 0 + 2 ∙ 5 = 10 (м/с)

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x(t)=x0+v0t+at22

Теперь мы можем выделить кинематические характеристики движения тела:

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

s=v0t+at22

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x(t)=v0t+at22=5t−3t2

Кинетическая энергия тела определяется формулой:

Ek=mv22

Скорость при прямолинейном равноускоренном движении равна:

v=v0+at=5−6t

Поэтому кинетическая энергия тела равна:

Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2

Следовательно, правильная последовательность цифр в ответе будет: 34.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18202

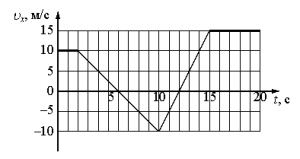
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18027

На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.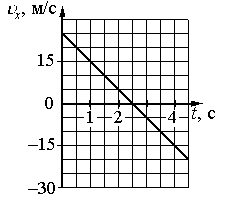

Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.1k

Источник

В данной статьи изложены мысли, которые возникали при решении задач с сайта “Решу ЕГЭ” в разделе – https://phys-ege.sdamgia.ru/test?theme=204. Рисунки взяты оттуда же.

1. Общий подход

Анализ и использование данного графика базируется на формуле перемещения тела S, м:

Формула 1

Как видно из формулы площадь под графиком равна перемещению тела. Например, тело с 1 по 2 секунду на графике, представленном на рис. 1 прошло S = V * t = 2м/с * (2с – 1с) = 2м/с *1с = 2м

Рис. 1. График зависимости скорости от времени

2. Чуть посложнее

Если мы захотим найти перемещение тела с начала движения t = 0c до 4-ой секунды движения тела согласно графику на рис. 2, то нам необходимо найти сумму площадей трех геометрических фигур: с 0с по 1с – треугольник, с 1с по 2с прямоугольник, со 2с по 4с – трапеция.

Рис. 2. Находим перемещение как сумму площадей геометрических фигур

S треугольника = (1/2) * длину высоты треугольника * длину сторону треугольника, к которой проведена высота =
=(1/2) * 2м/с * (1с – 0с) = 1/2 * 2м/с * 1с = 1м
S прямоугольника мы находили в начале статьи = 2м
S трапеции = (1/2) * сумму оснований трапеции * высоту трапеции =
=(1/2) * (2м/с + 6м/с) * (4с – 2с) = (1/2) * 8м/с * 2с = 8м
Итого S = 1м + 2м + 8м = 11м

3. А если скорость равна нулю?

Не стоит пугаться нулевых скоростей на каком-либо интервале времени. Например с 3с по 5с на графике, представленном на рис. 3 перемещение тела равно 0м, т. к. площадь фигуры с 3с по 5с равна 0.

Рис. 3. Нулевое перемещение

4. А если скорость ушла “в минус”?

Рис. 4. Отрицательная скорость

А вот отрицательная скорость может вызвать некоторые затруднения. Здесь надо очень внимательно читать задание и не перепутать очень похожие физические величины: путь и перемещение. Путь – величина скалярная и поэтому для ее нахождения с помощью графика на рис. 4 надо зеркально отобразить отрицательные участки скорости и сложить площади фигур (см. Рис. 5)

Рис. 5. Зеркальное отображение отрицательных участков

Перемещение – величина векторная и поэтому при определении этой величины необходимо учитывать знак площади. Например, если нужно найти перемещение тела с 0с по 10с (см. рис. 5), то нужно площадь треугольника с 0с по 4с сложить с площадью треугольника с 8с по 10с и из полученного результата вычесть площадь треугольника с 4с по 8с.

5. Когда можно и не считать!

Рис. 6. Анализ графиков

Иногда требуется визуальный анализ графиков. Например, необходимо определить какой автомобиль из 4-х с 0с до 15с проехал наибольшее расстояние?
Рассматривая площади геометрических фигур под графиками (см. рис. 6) видим, что площадь больше у графика (и машины) №3.

6. Переходим к ускорению

До сих пор мы на линейных графиках с координатами скорости и времени (см. рис. 7) видели скорость, время и перемещение (или путь).

Рис. 7. Ищем на графике ускорение

А тут ещё прячется ускорение. Давайте попробуем его найти. Вспоминаем формулу равноускоренного движения

Формула 2 . Формула равноускоренного движения

Рассматривая график на рис. 7 определим Vo при t = 0с => Vo = 2м/с.
А теперь возьмём на графике точку в момент времени t = 1c и определим по графику скорость в этот момент времени => V = 4м/с.
Подставляем найденные значения в формулу 2 =>
4м/с = 2м/с + a * 1c => а = (4м/с – 2м/с) / 1с = 2м/с2

Возвращаемся к графику (см. рис. 8)

Рис. 8. Находим уравнение графика

Теперь мы можем сказать, что на рис. 8 представлен график линейного уравнения V = Vo + a*t = 2 + 2*t. Эти знания расширяют область использования графика на рис. 8. Например мы можем сказать, что при
t = 10c скорость будет равна V = 2м/с + 2м/с2*10с = 22м/с

7. Ищем ускорение на произвольном прямолинейном участке графика

Нас могут попросить найти ускорение тела на произвольном прямолинейном участке графика. Например с 6с по 10с на графике, представленном на рис. 9.

Рис. 9. Находим ускорение на произвольном прямолинейном участке графика

Для этого получим формулу для ускорения, усложнив формулу 2 заменив t на (t – to):

Формула 3. Формула для определения ускорения

Возвращаемся к поиску ускорения:
а = (5м/с – (-5м/с))/(10с – 6с) = 10м/с / 4с = 2.5м/с2

8. Ищем координаты тела

Зная начальные координаты тела, начальную скорость, ускорение тела и время перемещения можем найти координаты тела в любой момент времен (формула 4)

Формула 4. Уравнение для координаты тела

9. Ищем скорость в пространстве

Рис. 10. Скорость в пространстве

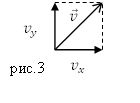
Мы можем знать значение проекций скорости на оси: х, y и z. Нас могут попросить найти модуль скорости. Ищем по формуле 5:

Формула 5. Формула для модуля скорости

Для понимания формулы 5 можно представить модуль скорости диагональю параллелепипеда, а проекции скорости сторонами параллелепипеда (см. рис. 11)

рис. 11 Расшифровка формулы 4

Заключение

Пока, это все мысли, которые появлялись во время решения задач в разделе сайта “Решу ЕГЭ” по адресу https://phys-ege.sdamgia.ru/test?theme=204. Пишите в комментариях, если что-то напрашивается добавить.

Автор с благодарностью примет любые пожертвования на развитие канала “От сложного к простому” https://money.yandex.ru/to/4100170126360.

Источник

Мгновенная скорость, теория и онлайн калькуляторы

Мгновенная скорость

Мгновенная скорость при прямолинейном движении материальной точки

При рассмотрении неравномерного движения часто интересует не средняя скорость движения тела, а скорость в определенный момент времени, или мгновенная скорость. Так, если тело стукнулось о препятствие, то сила воздействия тела на препятствие в момент удара, определено скоростью в момент соударения, а не средней скоростью движения тела. Форма траектории перемещения снаряда и его дальность полета зависит от скорости в момент запуска, а не от средней скорости.

Средняя скорость ($leftlangle vrightrangle $) движения материальной точки по оси X равна:

[leftlangle vrightrangle =frac{Delta x}{Delta t}left(1right),]

$Delta t$ – промежуток времени движения тела.

Определение

Мгновенную скорость определим как предел к которому стремится средняя скорость за бесконечно малый промежуток времени:

[v={mathop{lim }_{Delta tto 0} leftlangle vrightrangle }={mathop{lim }_{Delta tto 0} frac{Delta x}{Delta t}left(2right). }]

Такой предел в математике называют производной:

[v=frac{dx}{dt}=dot{x}left(3right).]

Выражение (3) обозначает, что мгновенная скорость (скорость в определенный момент времени) – производная от координаты. При прямолинейном движении материальной точки Мгновенную скорость можно определить как производную от пути ($s$) по времени:

[v=frac{ds}{dt}=dot{s}left(4right).]

Мгновенная скорость равномерного движения материальной точки

Средняя скорость равномерно движущейся точки величина постоянная, значит, мгновенная скорость равномерно перемещающейся точки является неизменной величиной.

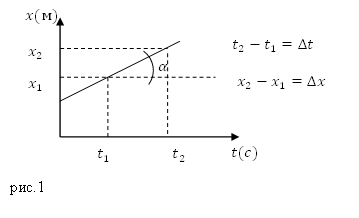
Скорость равномерного движения численно равна тангенсу угла наклона прямой к оси времени (рис.1):

[v=k tg alpha left(4right),]

где $k$ – безразмерный коэффициент, определяющий отношение масштаба единиц перемещения (ось ординат) и единиц времени (ось абсцисс).

При графическом изображении переменного движения материальной точки мгновенная скорость численно равна тангенсу угла наклона касательной к графику и осью абсцисс.

Мгновенная скорость при криволинейном движении

Положение материальной точки на траектории зададим радиус-вектором $overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:

[overline{v}=frac{doverline{r}}{dt}=dot{overline{r}}left(5right).]

скорость – это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.

Примеры задач с решением

Пример 1

Задание. Две материальные точки движутся согласно уравнениям:

[left{ begin{array}{c}
x_1=-3t+4t^2-t^3(м) \
x_2=t-2t^2-t^3(м) end{array}
right.left(1.1right),]

в какой момент времени скорости этих точек будут равны?

Решение. В задаче речь идет о нахождении времени, когда будут равны мгновенные скорости материальных точек. Величину мгновенной скорости будем находить как:

[v=frac{dx}{dt}left(1.2right).]

Тогда подставляя по очереди уравнения из системы (1.1) получим:

[left{ begin{array}{c}
v_1=frac{dx_1}{dt}=-3+8t-3t^2 \
v_2=frac{dx_2}{dt}=1-4t-3t^2 end{array}
right.left(1.3right).]

Приравняем правые части уравнений в системе (1.3), найдем момент времени в который скорости равны ($v_1=v_2$):

[-3+8t-3t^2=1-4t-3t^2to 8t+4t=1+3to 12t=4to t=frac{1}{3}left(cright).]

Ответ. $t=frac{1}{3}$ с

Пример 2

Задание. Материальная точка движется на плоскости XOY. Закон изменения координаты $x$ задан графиком рис.2 . Координата $y $задана аналитическим выражением: $y=At(1+Bt)$, где $A$ и $B$ постоянные величины. Запишите выражение, связывающее мгновенную скорость и время ($v(t)$).

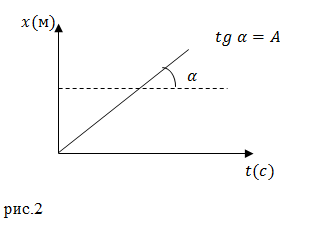
Решение. Из рис. 2 мы можем записать уравнение, которое определяет изменение координаты $x$ от времени:

[xleft(tright)=At left(2.1right).]

Получили, что движение материальной точки в плоскости XOY описывают при помощи системы уравнений:

[left{ begin{array}{c}
xleft(tright)=At;; \
y=Atleft(1+Btright) end{array}
left(2.2right).right.]

Найдем составляющие скорости движения материальной точки:

[v_x=frac{dx}{dt}=frac{d}{dt}left(Atright)=A;;]

[v_y=frac{dy}{dt}=frac{d}{dt}left(Atleft(1+Btright)right)=A+2ABt.]

Модуль скорости найдем как:

[v=sqrt{v^2_x+v^2_y}=sqrt{A^2+{(A+2ABt)}^2}=sqrt{A^2+A^2+2A^2Bt+4A^2B^2t^2}=]

[=Asqrt{2+2Bt+4B^2t^2.}]

Ответ. $v=Asqrt{2+2Bt+4B^2t^2}$

Читать дальше: механические волны.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

2.2.1 Как перевести из км/ч в м/с и т. д?

В задачах часто необходимо переводить из одних единиц измерения в другие:

1 км/ч = (1000 м)/(3600 с) = 5/18 м/с,

1 м/с = 18/5 км/ч,

1 км/с = 1000 м/с,

1 см/с = 0,01 м/с,

1 м/мин = 1/60 м/с.

Например, если то для того, чтобы перевести в м/с, нужно умножить на 5/18:

2.2.2 Как найти скорость тела, если известен закон движения?

Закон равномерного движения имеет вид:

Видим, что в этой формуле скорость стоит коэффициентом перед временем. Поэтому, если в условии задачи дан закон движения, необходимо посмотреть на коэффициент перед t — это и есть скорость.

Например, пусть закон движения имеет вид: В данном случае коэффициент перед t равен 5, следовательно,

2.2.3 Как определить скорость по графику координаты от времени?

Закон равномерного движения имеет вид:

Графиком этого закона является прямая линия. Так как nu_x — коэффициент перед t, то nu_x является угловым коэффициентом прямой.

Для графика 1:

То, что график 1 «поднимается вверх», означает — тело едет в положительном направлении оси Ox.

Для графика 2:

То, что график 2 «опускается вниз», означает — тело едет в отрицательном направлении оси Ox.

Для определения Delta x и Delta t выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

2.2.4 Как найти закон движения, если известны координаты тела в моменты времени и ?

Пусть в момент времени t_1 тело находилось в точке с координатой x_1, а в момент времени t_2 тело находилось в точке с координатой x_2.

Для времени t_1 имеем:

Для времени t_2 имеем:

Решая систему уравнений (2.19) и (2.20), получим

2.2.5 Как найти графически момент и координату встречи двух тел?

Пусть даны законы движения двух тел: и Согласно пункту 2.5 графиками обоих законов являются прямые линии. Необходимо на одном графике построить оба закона.

Графики пересекаются в одной точке. Координаты этой точки и являются временем и местом встречи.

2.2.6 Как аналитически найти координату и время встречи двух тел?

Пусть даны законы движения двух тел: и В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

Решение уравнения имеет вид:

Для нахождения координаты достаточно подставить вместо t найденное значение в любой из законов движения:

или

2.2.7 Как найти среднюю скорость, если тело половину пути проехало со скоростью а вторую половину пути

По определению (2.8):

В нашем случае, так как на каждой половине пути тело едет с постоянной скоростью, то

Получаем

В общем случае, если весь путь разбить на n равных участков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если весь путь разбит на равные участки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.8 Как найти среднюю скорость, если тело половину времени проехало со скоростью а вторую половину времени

По определению (2.8):

В нашем случае, так как каждую половину времени тело едет с постоянной скоростью, то

Получаем

В общем случае, если все время разбито на n равных промежутков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если все время разбито на равные промежутки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.9 Как найти скорость, с которой движется моторная лодка по течению реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета nu_0 (в нашем случае — собственная скорость лодки).

При движении по течению вектора и vecu направлены в одну сторону, следовательно, получаем сложение двух векторов, направленных в одну сторону — используем формулу (1.15):

Таким образом, при движении любого тела по течению его скорость определяется формулой

2.2.10 Как найти скорость, с которой движется моторная лодка против течения реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли) равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета nu_0 (в нашем случае — собственная скорость лодки).

Перепишем формулу в виде:

Вектора и направлены в одну сторону, следовательно, получаем вычитание двух векторов, направленных в одну сторону — используем формулу :

2.2.11 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена перпендикулярно течению реки?

В данном случае вектора и vecnu направлены перпендикулярно, следовательно, получаем задачу о сложении взаимно перпендикулярных векторов — используем формулу :

2.2.12 Как найти расстояние, на которое снесет лодку, если ее скорость направлена перпендикулярно скорости реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OD. В результате, когда тело окажется на противоположном берегу, оно попадет в точке D, и его снесет на длину CD=S.

Треугольник OAB подобен треугольнику OCD:

2.2.13 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена под углом φ к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OB. Как видим, получили треугольник, в котором известен один из углов — Тогда по теореме косинусов:

2.2.14 Как найти расстояние, на которое снесет лодку, если ее скорость направлена под углом к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OB. В результате, когда тело окажется на противоположном берегу, оно попадет в точке В, и его снесет на длину АВ=S.

В задачах, когда движение происходит в плоскости, то есть и вдоль оси Ox, и вдоль оси Oy, необходимо введение системы координат для того, чтобы упростить рассмотрение задачи.

Проекция nu_x:

Проекция nu_y:

Формулы и не просто результат математической операции нахождения проекции, nu_x и nu_y имеют физический смысл: со скоростью nu_x тело плывет вдоль оси Ox, то есть по течению; со скоростью nu_y тело переплывает реку. Например, время, за которое тело переплывет реку, можно найти просто поделив ширину реки на nu_y:

Тогда

2.2.15 Под каким углом α нужно направить собственную скорость лодки, чтобы за минимальное время переплыть реку?

Согласно формуле скорость, с которой лодка переплывает реку, равна:

Очевидно, что время будет минимальным, если nu_y будет максимальным, то есть

2.2.16 С какой скоростью машина обгоняет вторую машину, если они движутся в одну сторону?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина также движется вправо со скоростью Скорость обгона — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Так как и направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула :

Заметим, что при обгоне, естественно поэтому

2.2.17 За какое время проедут мимо друг друга два поезда, двигающиеся в одном направлении?

Пусть длина 1-го поезда L_1, а скорость 2-го поезда L_2. Скорость обгона определяется формулой Тогда

2.2.18 С какой скоростью машина едет навстречу вторую машину, если они движутся в противоположных направлениях?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется влево со скоростью Скорость движения навстречу — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Перепишем эту формулу в виде:

2.2.19 За какое время проедут мимо друг друга два поезда, двигающиеся в противоположных направлениях?

Пусть длина 1-го поезда L_1, а скорость 2-го поезда L_2. Скорость обгона определяется формулой Тогда

2.2.20 Как найти относительную скорость, если тела движутся по взаимно перпендикулярным направлениям?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется перпендикулярно первой со скоростью Относительная скорость определяется формулой :

Так как вектора и перпендикулярны, то воспользуемся формулой :

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Проекция скорости

График скорости

Сравнение модулей ускорения по графикам скоростей

1. Общий подход

2. Чуть посложнее

3. А если скорость равна нулю?

4. А если скорость ушла “в минус”?

5. Когда можно и не считать!

6. Переходим к ускорению

7. Ищем ускорение на произвольном прямолинейном участке графика

8. Ищем координаты тела

9. Ищем скорость в пространстве

Заключение

Мгновенная скорость

Мгновенная скорость при прямолинейном движении материальной точки

Мгновенная скорость равномерного движения материальной точки

Мгновенная скорость при криволинейном движении

Примеры задач с решением

Вам также может понравиться

Как найти периметр прямоугольника 2 класс решение

Как найти электронный диплом об образовании

Как найти калькулятор на ноутбуке

Добавить комментарий Отменить ответ