|
|
Скорость тени
|
|
27/03/14 |
Фонарь опускается по вертикали с высоты — 13.12.2014, 22:11 — Продолжу решение, кажется, я до чего- то додумался. Пусть фонарь переместился на
|
|
|
|
|
Ms-dos4 |
Re: Скорость тени
|
||
25/02/08 |
fronnya 1)Да
|
||
|
|
|||
|
fronnya |
Re: Скорость тени
|
|
27/03/14 |
Вообще говоря, что- то не так.
|
|
|
|
|
Ms-dos4 |
Re: Скорость тени
|
||
25/02/08 |
Так то зачем, вы же получили Ну и
|
||
|
|
|||
|
fronnya |
Re: Скорость тени
|
|
27/03/14 |
Аааа, ну да, производную.. Все получилось, в выражении для — 13.12.2014, 22:25 — Ms-dos4 , одновременно написали — 13.12.2014, 22:26 — Так то зачем, вы же получили Ну и Вы конечно же правы, но я сюда написал то, что первое в голову пришло
|
|
|
|
|
Ms-dos4 |
Re: Скорость тени
|
||
25/02/08 |
fronnya 1)Чисто физические соображения – пусть фонарь движется равномерно. За конечный интервал времени он достигнет такого положения, когда тень будет на бесконечности. А тень же сначала бежит с конечной скоростью, но движение равномерным быть не может, иначе она за конечный интервал времени в бесконечность не убежит (а убегает ведь!). Значит скорость у неё непостоянна — Сб дек 13, 2014 23:28:55 — P.S.Кстати, стоит заметить, что формула для скорости тени имеет смысл лишь для
|
||
|
|
|||
|
fronnya |
Re: Скорость тени
|
|
27/03/14 |
fronnya 1)Чисто физические соображения – пусть фонарь движется равномерно. За конечный интервал времени он достигнет такого положения, когда тень будет на бесконечности. А тень же сначала бежит с конечной скоростью, но движение равномерным быть не может, иначе она за конечный интервал времени в бесконечность не убежит (а убегает ведь!). Значит скорость у неё непостоянна — Сб дек 13, 2014 23:28:55 — P.S.Кстати, стоит заметить, что формула для скорости тени имеет смысл лишь для Да, смысл формулы я понимаю. Ms-dos4 писал(а): 2)Тупо глянуть в полученную вами формулу. Видите, скорость зависит от Прочитав задачу, я вообще не предвидел такого — 13.12.2014, 22:33 — Жизненная, прям, задачка. — 13.12.2014, 22:35 — Ну на уровне интуиции я все таки понимал, что тень не движется равномерно. Но я ведь не могу всегда верить своей интуиции. — 13.12.2014, 22:37 — Ms-dos4 , я так понял, что вы догадались, что задача из Матвеева
|
|
|
|
|
Ms-dos4 |
Re: Скорость тени
|
||
25/02/08 |
fronnya 1)Тут помогут несложные физические соображения. Интуиция в общем то не при чём
|
||
|
|
|||
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
 |
Поздним вечером молодой человек ростом h идет по краю горизонтального прямого тротуара с постоянной скоростью v. На расстоянии l от края тротуара стоит фонарный столб. Горящий фонарь закреплен на высоте H от поверхности земли. Постройте график зависимости скорости движения тени головы человека от координаты x. |
Решение:
Выберем систему отсчета с центром у основания фонаря. Пусть в некоторый момент проекция луча на землю образует угол α с линией тротуара (вид сверху). Учитывая прямолинейность распространения света, можем записать:
отсюда:
| lo = | l | • | h | . |
| sin α | H − h |
Тогда:
| yT = l + losin α = l • | H |
| H − h |
(yT
— координата конца тени) есть величина постоянная! Следовательно, тень от головы движется по прямой параллельной оси X со скоростью:
что легко получить, составив пропорцию:

График зависимости скорости тени от x есть прямая линия, параллельная оси абсцисс.
[тема: графическое решение задач по физике]
Теги:
- задачи с решениями
- кинематика
- механика
- формулы и графики
- неравномерное движение
Связанные проблемы ставок – это Ватерлоо для многих студентов исчисления. Лучший способ освоить их – проработать множество примеров, например, этот вопрос с движущейся тенью.
Практический вопрос
Человек ростом 6 футов, глядя через плечо, видит свою тень, отбрасываемую фонарным столбом высотой 15 футов перед ним. Тень пугает его, и он начинает убегать от нее – к фонарному столбу. К сожалению, это только усугубляет ситуацию, так как заставляет напугать его голову. Он начинает паниковать и бежит еще быстрее. За пять футов до того, как он врезается в фонарный столб, он бежит со скоростью 15 миль в час. На данный момент, как быстро движется кончик тени?
Ответ и объяснение
Он движется со скоростью 25 миль в час.
Начните с диаграммы:

Теперь перечислите известные и неизвестные тарифы.

Теперь вы можете написать формулу, которая соединяет переменные.
Это похожая ситуация с треугольником. Замечания: Для двух ваших одинаковых треугольников вы можете использовать любую из этих фигур, но не обе.

Дифференцировать по отношению к т .

Наконец, подставьте известные значения.

Таким образом, верхняя часть тени движется к фонарному столбу со скоростью 25 миль в час (и таким образом набирает обороты для человека со скоростью 25-15 = 10 миль / час).
Несколько необычный поворот в этой проблеме заключается в том, что вам никогда не приходилось подключаться на заданном расстоянии 5 футов. Это потому, что скорость тени не зависит от положения человека.
Мальчик, рост которого h идет с постоянной скоростью v по прямой дорожке, проходящей на расстоянии l от фонаря высотой H (см. рисунок). Найти скорость тени на земле от головы мальчика в тот момент времени, когда расстояние от мальчика до очки дорожки, находящейся на минимальном расстоянии от основания фонаря, равно
Спрятать решение
Решение.
Докажем, что тень от головы мальчика движется по прямой линии, параллельной дорожке. Для этого рассмотрим такое положение мальчика, когда расстояние от него до фонаря равно некоторой величине y (см. рис.; мальчик схематически показан жирным вертикальным отрезком с шариком (головой) наверху). Тогда из подобия треугольников АВЕ и ACD (см. рис.) имеем
где H — высота фонаря (сторона AD в треугольнике ACD), H – h — сторона AE в треугольнике ABE. Из этого соотношения находим
Теперь из подобия треугольников ODM и OCN находим расстояние от тени от головы мальчика
Из формулы (*) следует, что расстояние от тени от головы мальчика до дорожки не зависит от положения мальчика, и, следовательно, тень движется по прямой, параллельной дорожке. Поэтому чтобы найти скорость тени нужно следить только за ее координатой вдоль дорожки (а не поперек, поскольку последняя, как мы доказали, не меняется). Расстояние от тени до точки Q, ближайшей от траектории тени до основания фонаря CQ (см. рис.) также можно найти из подобия треугольников ОDM и OCN
Когда мальчик идет, расстояние OM уменьшается со скоростью υ, соответственно уменьшается и расстояние CQ — перемещается тень. Если мальчик пройдет малое расстояние Δx, отрезок OM уменьшится на величину Δx, расстояние CQ уменьшится на величину
которое и представляет собой перемещение тени. Отсюда находим скорость тени
Поскольку эта величина не зависит от положения мальчика, тень движется с постоянной скоростью.
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии по заданию | Баллы |
|---|---|
| Доказано, что граница тени от головы мальчика движется по прямой | 0,5 |
| Уравнение для вычисления мгновенной скорости границы тени в
рассматриваемый момент (не для средней скорости за какой-то интервал времени) |
0,5 |
| Правильная геометрическая связь перемещения мальчика и
перемещения границы тени |
0,5 |
| Правильный ответ с комментарием, что скорость границы тени
постоянна |
0,5 |
Классификатор: Оптика. Распространение света в однородной среде
You really need a picture here:

begin{align}
L:&text{ height of Lamp} \
H:&text{ height of man} \
x:&text{ distance from lamp to man}\
s:&text{ distance from lamp to tip of shadow}
end{align}
It’s helpful to introduce the part $s – x$ because you should recognize that you have similar triangles: $1$) the small one with $s – x$ and $H$ and $2$) the large one with $s$ and $L$. Those ratios must be equal:
$$
frac{L}{s} = frac{H}{s – x} text{ or } frac{s}{L} = frac{s – x}{H} \
frac{1}{L}s – frac{1}{H}s = -frac{1}{H}x \
s = -frac{HL}{(H – L)H}x = frac{L}{L – H}x \
frac{ds}{dt} = frac{L}{L – H}frac{dx}{dt}
$$
Note that the speed of the shadow depends only on $frac{dx}{dt}$ and not the distance from the lamp. Also note that the shadow tip always moves away from the person since $L > L – H$ which makes the coefficient in front of $frac{dx}{dt}$ strictly greater than $1$.
Or you could draw this picture:

Now the two similar triangles are the top, small one and, again, the large (full) one, giving:
$$
frac{x}{L – H} = frac{s}{L} rightarrow s = frac{L}{L – H}x
$$
…of course we get the same thing as before!
 с постоянной скоростью
с постоянной скоростью  На расстоянии
На расстоянии  расположен столб высотой
расположен столб высотой  . С какой скоростью
. С какой скоростью  будет двигаться конец тени, падающей от столба на землю через время
будет двигаться конец тени, падающей от столба на землю через время  после начала движения фонаря?
после начала движения фонаря? 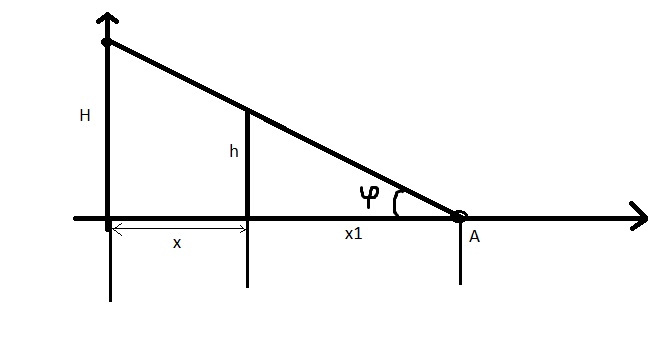
 – это и есть длина тени столба?
– это и есть длина тени столба? , точка A будет находиться на бесконечности? Ну или по крайней мере не на земле?
, точка A будет находиться на бесконечности? Ну или по крайней мере не на земле?  будет так же равномерно двигаться?
будет так же равномерно двигаться?  . Ну вообще, сначала стоит найти
. Ну вообще, сначала стоит найти  Откуда
Откуда  Ну а тогда
Ну а тогда 
 , то положение точки
, то положение точки  и теперь он находится на высоте
и теперь он находится на высоте  . Но тогда и точка A сместится на какое- то расстояние
. Но тогда и точка A сместится на какое- то расстояние  . Пусть новое положение точки
. Пусть новое положение точки  . Для него, по аналогии с
. Для него, по аналогии с  , можно записать:
, можно записать:  . С другой стороны
. С другой стороны  , тогда, учитывая выражения для
, тогда, учитывая выражения для  Правильно?
Правильно?![$[{frac{{d{x_1}}}{{dt}}}]$ $[{frac{{d{x_1}}}{{dt}}}]$](https://dxdy-01.korotkov.co.uk/f/0/f/6/0f66e055448a0bcb55d7893db41923bd82.png)
![$[{x_1} = frac{h}{{H - h}}x]$ $[{x_1} = frac{h}{{H - h}}x]$](https://dxdy-02.korotkov.co.uk/f/9/0/2/90286be611af28ca9fb574bd33bc37a582.png) , в условии сказано, что фонарь опускается равномерно, значит
, в условии сказано, что фонарь опускается равномерно, значит ![$[H(t) = {H_0} - vt]$ $[H(t) = {H_0} - vt]$](https://dxdy-01.korotkov.co.uk/f/c/d/d/cdd4886bb175481cf55af0748d581dd182.png) .
. ![$[frac{{d{x_1}}}{{dt}} = frac{{hvx}}{{{{({H_0} - h - vt)}^2}}}]$ $[frac{{d{x_1}}}{{dt}} = frac{{hvx}}{{{{({H_0} - h - vt)}^2}}}]$](https://dxdy-04.korotkov.co.uk/f/7/7/3/7737afcdda4267c37cca3fca17a38d4182.png)
 Отсюда ищем производную по времени и получаем ответ
Отсюда ищем производную по времени и получаем ответ 
![$[t]$ $[t]$](https://dxdy-04.korotkov.co.uk/f/f/e/c/fec13b062dacf4d206f3d8d64bd169c982.png) .
.![$[t < frac{{{H_0} - h}}{v}]$ $[t < frac{{{H_0} - h}}{v}]$](https://dxdy-02.korotkov.co.uk/f/9/c/9/9c94c12664173c4bc679aa849e3a9be082.png) (при равенстве тень на бесконечности, а далее просто бессмысленно).
(при равенстве тень на бесконечности, а далее просто бессмысленно).