Как найти скорость точечного заряда

Движение заряженных частиц в магнитном поле

Порешаем сегодня задачки про электроны, влетающие в магнитное поле. Начнем,  как всегда, с простого, потом возьмемся за более «продвинутые»  задачи.

Задача 1. Точечный заряд Кл влетает со скоростью м/с в однородное магнитное поле. Вектор скорости заряда и вектор индукции магнитного поля взаимно перпендикулярны. Найти величину и направление силы, действующей на заряд. Индукция магнитного поля Тл.

Сила, действующая на заряд в магнитном поле, определяется выражением

Так как направление скорости  и индукции перпендикулярны, то , поэтому

Ответ: Н

Задача 2.

Точечный заряд Кл влетает со скоростью м/с в однородное магнитное поле с индукцией Тл.  Вектор скорости заряда и вектор индукции магнитного поля составляют . Найти величину и направление силы, действующей на заряд.

Сила, действующая на заряд в магнитном поле, определяется выражением

Ответ: Н

Задача 3.

Протон движется со скоростью м/с перпендикулярно однородному магнитному полю с индукцией Тл. Найти силу, действующую на протон, и радиус окружности, по которой он движется.

Сила будет равна:

Радиус окружности найдем из формулы для центростремительного ускорения:

Ответ: Н, м.

Задача 4.

Частица массой кг и зарядом  Кл движется в однородном магнитном поле с индукцией Тл. Кинетическая энергия частицы Дж. Какой путь пройдет частица за время, в течение которого ее скорость изменит направление на ? Магнитное поле перпендикулярно скорости частицы.

Кинетическая энергия частицы равна:

Откуда скорость:

Тогда сила, действующая в поле на частицу, равна:

Так как скорость должна изменить направление на противоположное, то понятно, что, двигаясь по окружности, частица должна пройти полкруга, и тогда скорость ее будет иметь противоположное направление.

Тогда

Ответ: м

Задача 5. В магнитном поле, индукция которого 2 мТл, по винтовой линии радиусом см и шагом см движется электрон. Определить его скорость.

Скорость электрона будет иметь две составляющие: во-первых, поступательная составляющая: скорость движения вперед,  во-вторых, скорость, направленная по касательной и обеспечивающая движение электрона по окружности. Начнем с движения по окружности. На электрон действует сила:

С такой скоростью электрон будет преодолевать окружность длиной за время :

За время прохождения полного круга электрон продвигается вперед на шаг винтовой линии :

Так как обе составляющие скорости взаимно перпендикулярны, то определить скорость электрона поможет теорема Пифагора:

Подставим  числа:

Ответ:

Задача 6.

Электрон ускоряется однородным  электрическим полем, напряженность которого кВ/м . Пройдя в электрическом поле некоторый путь, он влетает в однородное магнитное поле и начинает двигаться по окружности радиусом мм. Какой путь прошел электрон в электрическом поле? Индукция магнитного поля Тл. Начальная скорость электрона – нулевая.

В электрическом поле электрон ускорился, и в итоге приобрел некоторую скорость, которую можно найти, зная радиус. А если узнаем скорость, то сможем определить и путь электрона.

С одной стороны,

С другой стороны,

Тогда, приравнивая, имеем:

Для определения пути при равноускоренном движении можно воспользоваться формулой:

Ускорение найдем из соотношения:

Тогда:

Подставим числа:

Ответ: 19,8 см.

В этой главе…

• Оцениваем электрический заряд и электрическую силу
• Сканируем электрическое поле
• Изучаем электрическое поле с помощью точечных зарядов
• Создаем простое электрическое поле между пластинами конденсатора
• Постигаем электрические потенциалы, измеряя напряжение
• Связываем электрический потенциал с точечными зарядами

Вокруг нас все пронизано электричеством. В каждом атоме его собственные заряды вращаются с невероятной скоростью. Иногда электрические заряды проявляются совершенно неожиданно, например, ощущаются, как острое покалывание в момент касания наэлектризованной металлической дверной ручки или дверцы автомашины. А порой, наоборот, включая электрический свет, мы внезапно узнаем, что так остро необходимые электрические заряды куда-то пропали.

В этой главе повествование курса постепенно “электризуется”: в ней описываются причины того, почему избыток заряда на нашей одежде (например, из-за скопления слишком большого количества электронов) доставляет нам столь острые ощущения в момент разряда. Это пример типичного проявления статического электричества. Кроме того, в этой и следующей главах говорится о том, как ведут себя электрические заряды и как они становятся тем, что принято называть электрическим током. В данной главе речь идет об электрических зарядах, электрическом потенциале, электрических полях, силах, действующих между зарядами, и о многом другом. А все это начинается с мельчайших носителей заряда.

Плюс и минус: заряды электрона и протона

Атомы состоят из ядра с заряженными протонами и нейтральными нейтронами, а также из легких заряженных электронов, стремительно вращающихся вокруг ядра.

У заряженных частиц, электронов и протонов одинаковая величина заряда, равная:

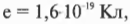
где Кл означает кулон — используемая в СИ единица заряда (см. главу 2). Заряды протона и электрона соответственно равны +1,6·10^-19 Кл и -1,6·10^-19 Кл (считать заряд электрона отрицательным — это не более чем достигнутая в свое время договоренность). Таким образом, электроны — это частицы-носители электричества: как статического — при отсутствии движения заряженных частиц, так и динамического — с учетом движения заряженных частиц (например, электрический ток, который протекает по проводам). Итак, если имеется заряд, равный целому кулону, то какому количеству электронов он соответствует? Поскольку величина заряда каждого электрона равна 1,6·10^-19 Кл, то получается, что:

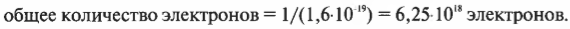
Итак, чтобы получить заряд в 1 Кл, надо собрать 6,25·10¹⁸ электронов. Но если собрать вместе огромное количество электронов, то произойдет интересная вещь. Электроны разлетятся в сторону, подобно родственникам, разбегающимся в конце скучного семейного мероприятия.

Тяни и толкай: электрические силы

Воздействие электрических зарядов друг на друга проявляется в виде силы. Например, чтобы удержать в одном месте 6,25·10¹⁸ электронов, придется приложить немало усилий. Все объекты вокруг нас содержат электрические заряды, но если некий объект имеет избыточное количество электронов, то он обладает суммарным отрицательным зарядом, а если, наоборот, электронов ему не хватает, то этот объект обладает суммарным положительным зарядом.

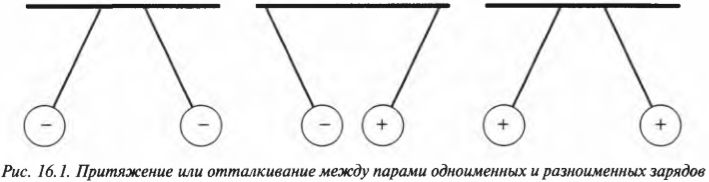
Как известно, одноименные полюсы магнитов отталкиваются, а разноименные — притягиваются. На рис. 16.1 показаны шарики, подвешенные на ниточках и имеющие электрический заряд. Так вот, как и в случае с магнитами, пары шариков с одноименными зарядами (+ и + или — и -) будут отталкиваться друг от друга, а пары с разноименными зарядами (+ и — или — и +) — наоборот, притягиваться друг к другу.

Подбираемся к закону Кулона

Недостаточно просто говорить о положительности или отрицательности заряда, надо еще указывать их числовые значения. Насколько велики силы, действующие между заряженными телами? Это зависит от того, насколько велики заряды и насколько далеко они находятся друг от друга. В главе 5 говорится о другой силе, действующей между телами, — силе всемирного тяготения:

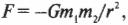
где ​( F )​ — это сила, ​( G )​ — универсальная гравитационная постоянная, ​( m_1 )​ — масса первого тела, ( m_2 ) — масса второго, а ​( r )​ — расстояние между ними. Аналогично, в результате лабораторных измерений можно убедиться, что сила взаимодействия электрических зарядов выражается таким образом:

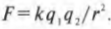
В данном случае ( q_1 ) и ( q_2 ) — это два взаимодействующих заряда, измеренных в кулонах, ​( r )​ — расстояние между ними, а ​( k )​ — коэффициент пропорциональности.

(В системе СГСЭ единица измерения заряда выбрана таким образом, что коэффициент ​( k )​ = 1, а сам символ ( k ) принято опускать в формуле закона Кулона. В системе СИ ​( k )​ ≈ 8,99·10⁹ Н·м²·Кл^-2, причем обычно он выражается формулой:

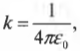
где ​( delta_0 )​ ≈ 8,85·10^-12 Кл²·Н^-1·м^-2 — электрическая постоянная. Здесь и далее автор использует систему СИ. — Примеч. ред.)

Формула ​( F=kq_1q_2/r^2 )​ называется законом Кулона. Этот закон определяет величину силы, действующей между электрическими зарядами. Обратите внимание, что если заряды имеют одинаковый знак, то действующая между ними сила является положительной, т.е. заряды будут отталкиваться друг от друга. А если заряды имеют противоположные знаки, то действующая между ними сила является отрицательной, т.е. заряды будут притягиваться друг к другу.

Притягиваем заряды

Важным компонентом закона Кулона является расстояние между заряженными телами (см. два предыдущих раздела). Допустим, два точечных объекта разнесли на 1 м друг от друга и придали каждому из них заряд в 1 Кл: одному — отрицательный, а другому — положительный. Какую силу нужно приложить, чтобы преодолеть их притяжение друг к другу? Подставим численные значения в формулу закона Кулона:

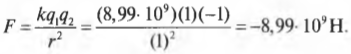
Чтобы не дать шарикам сойтись, нужно приложить силу в 8,99·10⁹Н. Значение неправдоподобно большое — оно равносильно весу груза с массой примерно 560000 т или весу 10 наполненных нефтяных танкеров. Забавный вывод: следует хорошо подумать, прежде чем придавать точечным объектам заряды в 1 Кл. Как видите, между такими зарядами возникает чудовищно большое электрическое взаимодействие.

Вычисляем скорость электронов

Благодаря круговой орбите электрона можно связать между собой две силы: электростатическую и центростремительную (глава 10). Известно, что каждый атом водорода состоит из одного электрона, который вращается вокруг одного протона. Размеры атома водорода слишком малы, чтобы все это увидеть, но известно, что электрон носится вокруг протона очень быстро. Тогда возникает вопрос — насколько быстро? Как известно, между протоном и электроном действует электростатическая сила притяжения. При условии, что орбита электрона круговая, эта сила обеспечивает центростремительную силу (глава 10). Таким образом, электростатическую силу по закону Кулона можно приравнять к центростремительной силе:

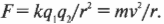
Масса электрона и радиус его орбиты равны соответственно 9,1·10^-31 кг и 5,29·10^-11 м. Итак, взяв значения, требуемые для вычисления электростатической силы (константу ​( k )​, а также заряды электрона и протона), получим:

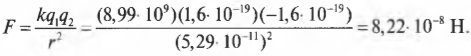
Полученная сила, действующая между электроном и протоном, обеспечивает центростремительную силу, поэтому:

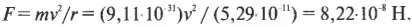
Вычисление дает для ​( v )​ значение 2,19·10⁶ м/с или около 7,88 млн. км/ч! Попробуйте представить себе эту скорость; она равна где-то 1% от скорости света.

Изучаем силы, действующие между несколькими зарядами

Если в задаче рассматривается взаимодействие зарядов, то совсем не обязательно, что их будет только два. И если зарядов все-таки больше двух, то для вычисления результирующей силы, приложенной к любому из них, придется использовать векторы. (Подробнее о векторах можно узнать в главе 4.)

Посмотрите на рис. 16.2, где показаны три взаимодействующие заряда: один положительный и два отрицательных. Какова результирующая сила, действующая на положительный заряд?

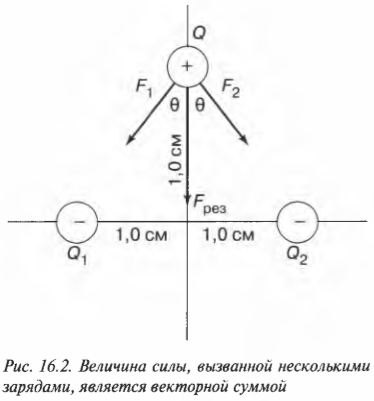
На положительный заряд ​( Q )​ действуют силы, вызванные двумя отрицательными зарядами ​( Q_1 )​ и ( Q_2 ); на рис. 16.2 эти силы обозначены, как ( F_1 ) и ( F_2 ). Суммой ( F_1 ) и ( F_2 ) является ( F_{рез} ). Пусть ( Q_1 ) = ( Q_2 ) = -1,0·10^-8 Кл, ​( Q )​ = 3,0·10^-8 Кл, а все заряды, как показано на рисунке, расположены на осях X и Y в 1,0 см от начала координат. Чему равна( F_{рез} )? С помощью теоремы Пифагора (глава 2) получаем ​( theta )​ = 45°. По величине ​( F_1=F_2 )​, поэтому:

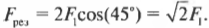
Какова величина ( F_1 )?

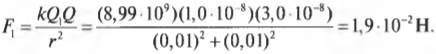
Итак, ( F_1 ) равняется 1,9·10^-2 Н, и можно найти результирующую силу, действующую на положительный заряд:

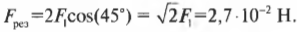
Итак, величина результирующей силы, действующей на положительный заряд, получена в виде векторной суммы (глава 4) и равняется 2,7·10^-2 Н.

Действие на расстояние: электрические поля

Чтобы найти силу, действующую между двумя зарядами, надо знать величину (значение) каждого из них. А когда зарядов целое множество, то не исключено, что и их значений также целое множество. Что если к имеющемуся множеству зарядов кто-то другой захочет добавить еще и пробный заряд (т.е. заряд, используемый специально для измерения действующих на него сил)? Допустим, что величина этого нового пробного заряда не известна. Может, 1 Кл? А почему бы не 1,0·10^-8 Кл или 1,0·10³ Кл?

Чтобы описать, как имеющееся множество зарядов будет воздействовать на чей-то другой пробный заряд, физики ввели понятие электрическое поле. Для определения силы взаимодействия поля от имеющегося множества зарядов достаточно умножить величину пробного заряда на величину напряженности поля в той точке, где он находится. Вот как определяется напряженность ​( mathbf{E} )​ электрического поля:

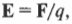
где ( mathbf{F} ) обозначает силу, действующую на пробный заряд со стороны имеющегося множества зарядов, a ​( q )​ — величина пробного заряда. Напряженность выражается в ньютонах на один кулон (Н·Кл^-1). Обратите внимание, что речь идет о векторной величине, т.е. имеющей модуль и направление (глава 4).

Другими словами, напряженность электрического поля в той или иной точке — это сила, которая бы действовала в ней на пробный заряд в один кулон. Направление напряженности совпадает с направлением силы, вызываемой в данной точке каким-либо положительным зарядом.

Представим, что вы перемещаете по горизонтали заряд в 1 Кл. День солнечный, погода прекрасна, но тут нежданно-негаданно заряд оказывается в электрическом поле с напряженностью 5 Н/Кл, направленной противоположно его движению (рис. 16.3).

Что же происходит? На объект с зарядом 1 Кл внезапно действует сила, направленная противоположно его движению:

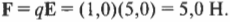
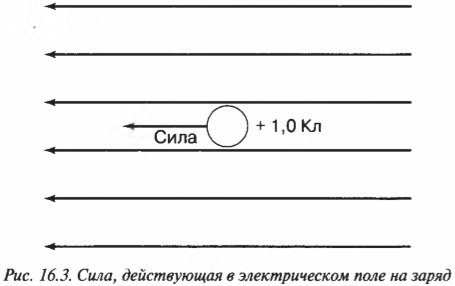
Если изменить направление движения объекта с зарядом 1 Кл, то эта сила будет направлена уже по ходу его движения. Польза понятия “электрическое поле” состоит в следующем: по напряженности поля можно определить силу, действующую на заряд в этом поле. Если заряд в точке положительный, то направление этой силы будет совпадать с направлением напряженности поля в этой точке, а если заряд отрицательный, то сила будет направлена в противоположную сторону.

Так как напряженность электрического поля в любой точке — это результирующий вектор (обладающий, как известно, величиной и направлением), то его можно вычислить путем сложения составляющих его векторов (об особенностях такого сложения говорится в главе 4). Посмотрите на рис. 16.4, где показаны (в виде векторов напряженности) два исходных электрических поля, “горизонтальное” и “вертикальное”, расположенные в одной и той же области. Образуемое ими общее электрическое поле имеет напряженность, равную векторной сумме их напряженностей.

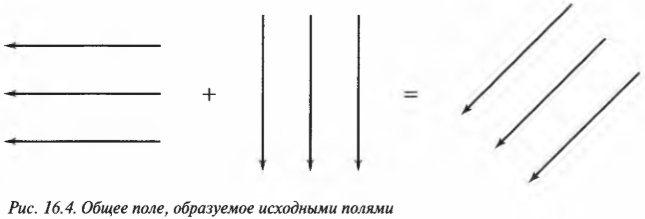
По всем направлениям: электрические поля от точечных зарядов

Не все электрические поля выглядят так просто как те, что показаны на рис. 16.3. Как, например, выглядит электрическое поле от точечного заряда? Под точечным подразумевается заряд очень малого физического объекта. Известно, что заряд ​( Q )​ создает электрическое поле, но какое? Благодаря формуле напряженности электрического поля, ​( E=F/q )​, ответить на этот вопрос достаточно просто. Пусть имеется пробный заряд ​( q )​, с помощью которого можно в разных точках измерять силу, вызываемую зарядом ​( Q )​. Вот эта сила, вычисляемая по формуле из предыдущего раздела этой главы:

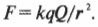
Итак, чему равна напряженность электрического поля? Надо разделить эту силу на величину пробного заряда ​( q )​:

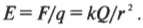
Напряженность электрического поля от точечного заряда — это ​( E=kQ/r^2 )​. Она является вектором (глава 4), но куда направлен этот вектор? Чтобы узнать это, вернемся к пробному заряду ​( q )​ и предположим, что он является положительным (помните, что напряженность электрического поля определяется как сила, действующая на положительный заряд в один кулон).

В любом месте электрического поля сила, действующая из ​( Q )​ на ( q ), является радиальной, т.е. направленной по прямой, которая соединяет центры двух зарядов. Если заряды ( Q ) и ( q ) положительны, то сила, действующая на ( q ), будет направлена не к ( Q ), а в противоположную сторону. Таким образом, напряженность электрического поля в любой точке будет также направлена в противоположную от ( Q ) сторону. Это можно увидеть на рис. 16.5, где электрическое поле изображено в виде так называемых линий поля, использовать которые впервые предложил Майкл Фарадей в XIX веке.

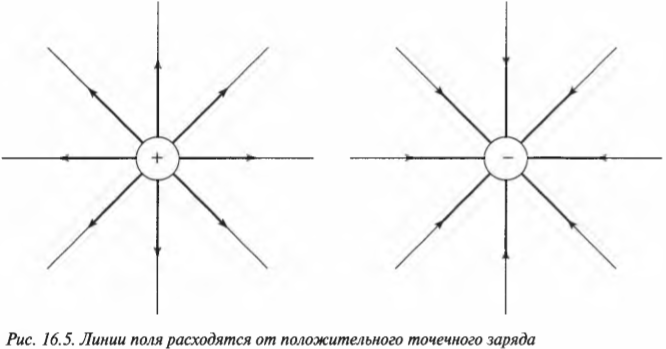
Глядя на линии поля, можно получить хорошее качественное представление электрического поля (не путать с количественным представлением, т.е. в виде У ^ / чисел). И когда в точке А линии поля ближе друг к другу, чем в точке В, то это значит, что в точке А поле сильнее, чем в точке В. Кроме того, обратите внимание, что линии поля расходятся от положительных зарядов и, наоборот, сходятся к отрицательным зарядам (рис. 16.5).

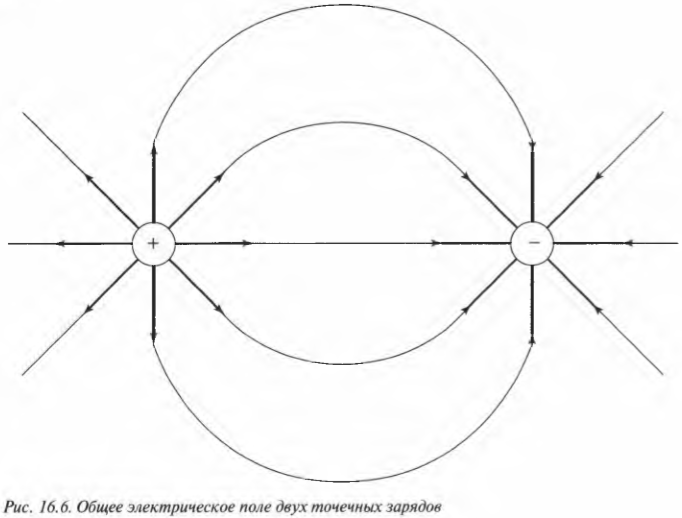
Как определить величину электрического поля от нескольких зарядов? В таком случае напряженности полей в каждой точке надо складывать как векторы. Например, имея два точечных заряда, положительный и отрицательный, получим электрическое поле, показанное на рис. 16.6.

Линии поля (как те, что показаны на рис. 16.6) начинаются на положительном заряде и заканчиваются на отрицательном заряде, т.е. они не могут начинаться или заканчиваться в точке пространства без заряда.

Заряжаем конденсатор: электрические поля между плоскими пластинами

Вычисление электрического поля от множества точечных зарядов, о котором говорилось в предыдущем разделе, в общем случае представляет собой довольно сложную задачу сложения векторов (глава 4). Чтобы облегчить себе жизнь, физики используют модели простых полей. Рассмотрим модель простого поля в плоском конденсаторе. Вообще говоря, конденсатором (не обязательно плоским) называется объект, способный сохранять заряд: положительный и отрицательный заряды хранятся отдельно, чтобы они притягивались друг к другу, но не могли самостоятельно соединиться.

На рис. 16.7 показан пример конденсатора с двумя плоскими пластинами: на одной пластине равномерно распределен заряд ​( +q )​, а на другой — заряд ​( -q )​. Все компоненты напряженностей полей, созданных точечными зарядами, на этих пластинах взаимно компенсируют друг друга, за исключением тех компонент, которые направлены перпендикулярно пластинам. Другими словами, между параллельными пластинами конденсатора создаются постоянные электрические поля, работать с которыми легче, чем с полями точечных зарядов.

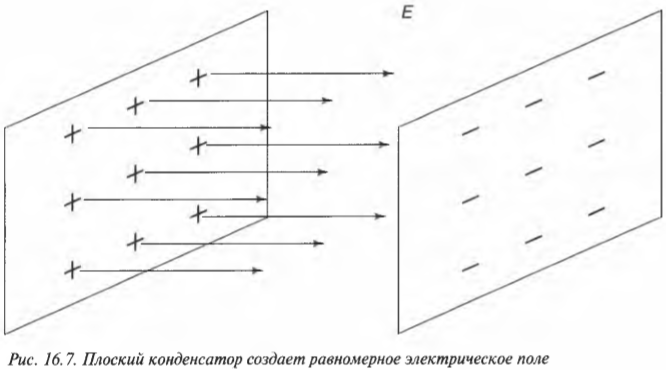
В результате достаточно долгих вычислений можно сделать вывод, что электрическое поле между пластинами постоянно (если пластины находятся друг от друга достаточно близко), а его напряженность равна:

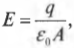
где ​( varepsilon_0 )​ — это электрическая постоянная, равная 8,85·10^-12 Кл²·Н^-1·м^-2 (см. один из предыдущих разделов этой главы), ​( q )​ — общий заряд на каждой из пластин (на одной и на другой из них заряд соответственно равен ( +q ) и ( -q )), ( A ) — это площадь каждой пластины. Формулу еще можно записать с помощью плотности заряда ​( sigma )​ на каждой пластине, где ​( sigma=q/A )​ (заряд, приходящийся на единицу площади). Тогда формула будет выглядеть таким образом:

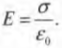
Модель плоского конденсатора значительно облегчает жизнь физика потому, что напряженность электрического поля постоянна и имеет постоянное направление (с положительной пластины на отрицательную), поэтому для вычисления напряженности поля не важно, в каком месте между пластинами измеряется напряженность поля.

Повышаем напряжение: электрический потенциал

Электрические поля (см. предыдущий раздел) — это еще не все, что относится к электричеству. Для изучения электричества придется использовать и другие понятия. Например, для работы с электрическими силами удобно использовать понятие потенциальной энергии, или энергии, “запасенной” в теле или в системе тел. В механике вполне естественно связывают работу силы и потенциальную энергию: например, подъем груза в поле силы тяжести связывается с увеличением потенциальной энергии ​( Delta W )​, т.е. энергии, накапливаемой в теле благодаря его новому положению:

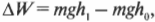
где ​( m )​ означает массу, ​( g )​ — ускорение свободного падения в поле силы тяжести, ​( h_1 )​ и ( h_2 ) — соответственно конечную и начальную высоту. Так как в электрическом поле на заряды действует сила, то можно говорить о потенциальной энергии и в электрических полях. Такой энергией является потенциальная энергия электрического поля, а ее изменение создает новую величину, которая называется напряжением и является движущей силой электрического тока.

Вычисляем потенциальную энергию электрического поля

Потенциальная энергия электрического поля — это потенциальная энергия, “запасенная” в электрическом поле. При знакомстве с понятием энергии в главе 8 мы также познакомились с понятием работы. Предположим, что положительный заряд перемещается по направлению к положительно заряженной пластине, как показано на рис. 16.8. Как они будут взаимодействовать друг с другом? Линии поля идут от положительных зарядов к отрицательным, а показанный на рисунке одиночный положительный заряд взаимодействует с положительно заряженной пластиной. Поскольку этот заряд имеет положительный знак, то действующая на него сила будет отталкивать его от положительно заряженной пластины, то есть вправо в плоскости рисунка. Кроме того, одиночный заряд будет притягиваться отрицательно заряженной пластиной справа от него.

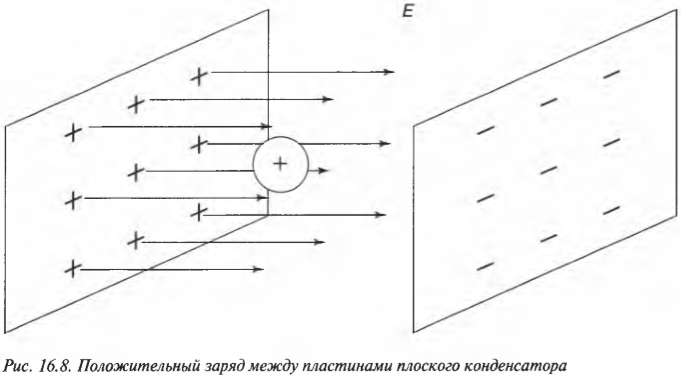
Итак, каким будет изменение потенциальной энергии положительного заряда при перемещении его между пластинами справа налево против силы, направленной в обратную сторону? Работа ​( A )​ по перемещению заряда должна равняться увеличению его потенциальной энергии. Формула такой работы имеет следующий вид:

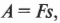
где ​( F )​ и ​( s )​ означают соответственно силу и перемещение. Сила, приложенная к положительному заряду, равна ​( qE )​, где ​( q )​ — это величина заряда, а ​( E )​ — напряженность электрического поля, в котором он находится. В результате получаем для формулы работы следующее выражение:

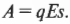
Эта величина работы равна увеличению потенциальной энергии заряда ​( Delta W )​. Если электрическое поле постоянно по направлению к модулю напряженности, то можно сказать, что изменение потенциальной энергии:

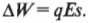
Для характеристики электрического поля физики придумали понятие напряженность электрического поля, которая определяется, как сила, действующая со стороны поля на точечный объект с зарядом 1 Кл (см. один из предыдущих разделов этой главы о действии на расстоянии с помощью электрического поля). Аналогично, для характеристики изменения потенциальной энергии электрического поля между точками А и Б физики ввели понятие электрическое напряжение.

Потенциалы и напряжение

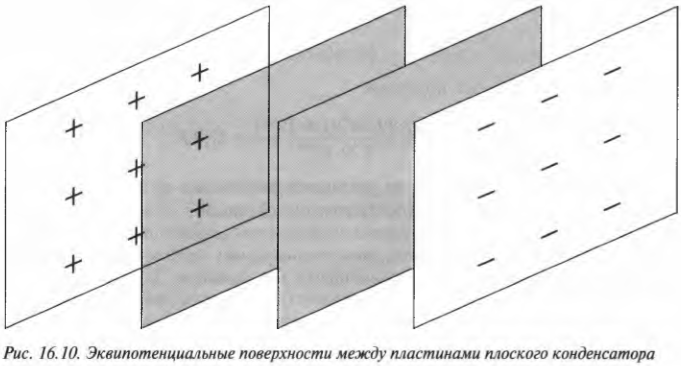
На языке физики напряжение — это разность электрических потенциалов (т.е. потенциальной энергии электрического поля, приходящейся на единицу заряда), или просто разность потенциалов. Эта величина определяется как отношение работы электрического поля при переносе пробного заряда из точки А в точку Б к величине пробного заряда. Единицей измерения напряжения в системе СИ является вольт (В), 1 В = 1 Дж/1 Кл. Напряжение обозначается символом ​( U )​.

Электрический потенциал ​( U )​ в определенной точке представляет собой электрическую потенциальную энергию ​( W )​ пробного заряда, деленную на величину этого заряда ​( q )​:

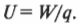
Таким образом, напряжение — это изменение потенциальной энергии заряда в один кулон. Работа ​( A )​ по перемещению в плоском конденсаторе положительного заряда ​( q )​ с отрицательной пластины на расстояние ​( s )​ по направлению к положительной пластине (см. выше) равна:

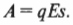
Эта работа равна изменению потенциальной энергии заряда при перемещении на расстояние ​( s )​ от отрицательной пластины, поэтому потенциал в месте нахождения заряда вычисляется по следующей формуле:

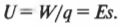
Предположим, что ваше внимание привлекла машина, стоящая на обочине дороги с открытым капотом. На вопрос: “В чем дело?” водитель отвечает: “Машина не едет”.

Желая помочь бедняге, вы достаете свой вольтметр и пытаетесь протестировать аккумулятор машины. Вольтметр показывает 12 В и, похоже, проблема совсем не в этом, но поскольку вы увлечены самим процессом изучения электричества, то вас уже не остановить.

Если 12 В — это изменение потенциальной энергии при перемещении заряда в один кулон от одной клеммы аккумулятора к другой, то какую работу нужно выполнить для перемещения между этими клеммами одного электрона? Как известно:

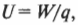
поэтому

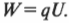
Попавший в затруднение водитель с интересом наблюдает за этими манипуляциями. Поскольку величина заряда электрона равна 1,6·10^-19 Кл (см. выше первый раздел в этой главе о заряде электрона и протона), то, подставляя в эту формулу численные значения, получим:

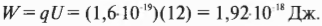
Спустя несколько мгновений вы гордо заявляете: “На перемещение одного электрона между клеммами аккумулятора требуется 1,92·10^-18 джоулей”.

У водителя пропадает всякая надежда, и не удивительно, что после ваших слов он смотрит на вас со странным выражением лица…

Оказывается, энергия сохраняется даже в электрическом поле

Как известно, при переходе системы объектов из состояния 1 с полной энергией ​( E_1 )​ в состояние 2 с полной энергией ( E_2 ) (где полная энергия является суммой кинетической ​( K )​ и потенциальной ​( W )​ энергии, см. главу 8) полная энергия сохраняется:

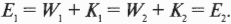
Оказывается, что полная энергия системы объектов сохраняется и в электрическом поле. Допустим, что пылинка с массой 1,0·10^-5 кг столкнулась с отрицательно заряженной пластиной плоского конденсатора и получила заряд —1,0·10^-5 Кл. Очевидно, что отрицательно заряженная пылинка будет притягиваться положительной пластиной и начнет движение к ней.

Разность потенциалов между пластинами составляет 30 В. Какова будет скорость пылинки, когда она столкнется с положительной пластиной (если не учитывать сопротивление воздуха)? Так как полная энергия сохраняется, то потенциальная энергия пылинки на отрицательной пластине к моменту ее столкновения с положительной пластиной уменьшится на величину возрастания кинетической энергии (​( Delta K={}^1!/!_2mv^2 )​). Величину уменьшения потенциальной энергии пылинки можно найти с помощью формулы:

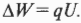
Подставляя в нее численные значения, получим:

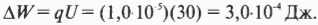
Это уменьшение потенциальной энергии превращается в увеличение кинетической энергии:

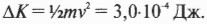
Подставляя численные значения, получим:

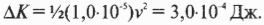
В результате несложных вычислений получим:

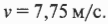
Иными словами, пылинка столкнется с положительной пластинкой на скорости, примерно равной 7,75 м/с, или 27,9 км/ч.

Электрический потенциал точечных зарядов

Разность потенциалов, или напряжение ​( U )​ (см. предыдущий раздел), между пластинами конденсатора зависит от расстояния ​( s )​ между положительно и отрицательно заряженными пластинами (подробнее о конденсаторах рассказывается выше в этой главе):

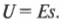
Сложнее определить потенциал точечного объекта с зарядом ​( Q )​, ведь его электрическое поле совсем не такое постоянное, как между пластинами конденсатора. Как вычислить потенциал на произвольном расстоянии от точечного заряда? Сила, действующая на пробный заряд ​( q )​, вычисляется по формуле:

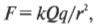
где ​( k )​ означает константу, равную 8,99·10⁹ Н·м²/Кл², а ​( r )​ — расстояние между точечным объектом с зарядом ​( Q )​ и пробным зарядом ​( q )​.

Напомним, что напряженность ​( E )​ в любой точке вокруг точечного заряда ​( Q )​ выражается формулой:

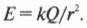
Итак, чему равен электрический потенциал точечного заряда? На бесконечности он равен нулю.

Если перенести пробный заряд на более близкое расстояние ​( r )​ от точечного заряда, то изменение его потенциала ​( U )​ будет равно выполненной работе ​( A )​, деленной на величину пробного заряда ​( q )​:

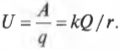
Это потенциал в вольтах, полученный для любой точки на расстоянии ​( r )​ от точечного заряда ​( Q )​ и равный нулю на расстоянии ​( r=infty )​. Сказанное имеет смысл, если не забывать, что потенциал — это работа по переносу пробного заряда в определенное место, деленная на величину пробного заряда. Возьмем, например, протон ​( Q )​ = +1,6·10^-19 Кл, расположенный в центре атома водорода. На расстоянии 5,29·10^-11 м от протона по свой обычной орбите движется электрон. Какой потенциал будет на таком расстоянии от протона? Вам известно, что:

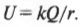
Подставив в формулу числа, получаем:

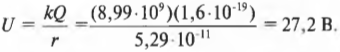
Итак, электрический потенциал на указанном расстоянии от протона равен 27,2 В. А это немало для столь крошечного (почти точечного) заряда.

Как и электрические поля, электрический потенциал можно представить графически (только не в виде линий поля, а в виде эквипотенциальных поверхностей). Эквипотенциальными называются поверхности с одинаковым потенциалом. Так как, например, потенциал точечного заряда зависит от расстояния (или радиуса сферы), то эквипотенциальными поверхностями точечного заряда являются сферы, расположенные вокруг этого заряда (рис. 16.9).

А как насчет эквипотенциальных поверхностей между пластинами плоского конденсатора? Как вам известно, при перемещении положительного заряда с отрицательно заряженной пластины на расстояние ​( s )​ по направлению к положительно заряженной пластине разность потенциалов имеет вид:

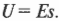
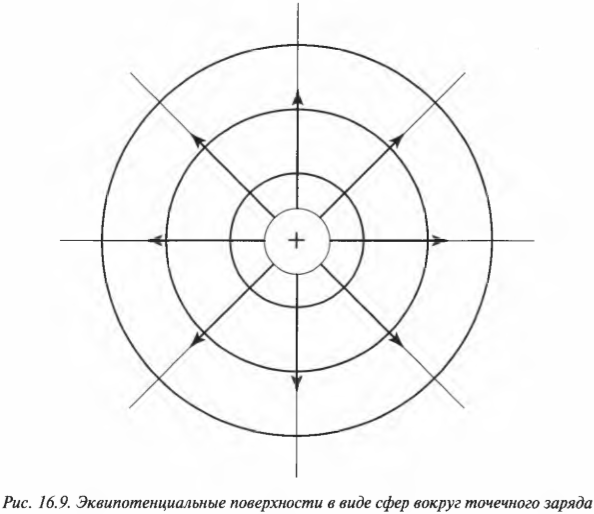
Иначе говоря, потенциал на эквипотенциальной поверхности зависит только от расстояния до пластин. Например, на рис. 16.10 две эквипотенциальные поверхности показаны между пластинами конденсатора.

Сохраняем заряд с помощью емкости

Конденсатор способен хранить противоположные электрические заряды. Они удерживаются отдельно так, чтобы они притягивались друг к другу, но не могли самостоятельно соединиться, например перейти с одной пластины на другую в плоском конденсаторе.

Каков заряд конденсатора? Он зависит от емкости ​( C )​ конденсатора. Заряды на обеих пластинах конденсатора равны друг другу (только противоположны по знаку) и связаны с напряжением ​( U )​ между пластинами и емкостью ( C ) конденсатора следующей формулой:

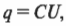
где ( q ) и ( C ) — это соответственно заряд и емкость. В плоском конденсаторе напряженность ( E ) электрического поля определяется следующей формулой:

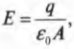
где ​( varepsilon_0 )​ — электрическая постоянная, а ​( A )​ — площадь пластины. Для связи напряжения ​( U )​ между пластинами, расположенными на расстоянии ​( s )​ друг от друга, и напряженности ​( E )​ электрического поля используется следующая формула:

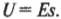
Поэтому:

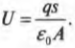
Так как ​( q = CU )​, то из предыдущей формулы получим:

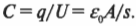
В системе СИ единицей измерения емкости является фарада (Ф), 1 Ф = 1 Кл/1 В.

Неплохо, но это еще не все. В большинстве конденсаторов между пластинами находится не воздух, а специальный наполнитель — диэлектрик. Диэлектрик — это материал, который плохо проводит электрический ток и увеличивает емкость конденсатора пропорционально своей диэлектрической проницаемости ( varepsilon ). Итак, если пространство между пластинами плоского конденсатора заполнено диэлектриком с диэлектрической проницаемостью ( varepsilon_0 ), то емкость увеличивается в соответствии с формулой:

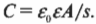
Например, диэлектрическая проницаемость слюды (минерала, широко используемого в конденсаторах) примерно равна 5,4, таким образом делая емкость конденсатора примерно в 5,4 раза большей, чем у того же конденсатора с вакуумом между пластинами, потому что диэлектрическая константа вакуума равна 1.

Конденсатор содержит заряды, расположенные отдельно друг от друга, но способные соединиться, и потому обладает связанной с этим потенциальной энергией. Ведь, чтобы разделить эти заряды, нужно затратить определенную работу. Чему равна энергия конденсатора? Путем несложных вычислений можно определить, что энергия конденсатора ( W_c ) равна:

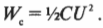
Пусть имеется две незаряженные пластины конденсатора с разностью потенциалов ​( U )​. Чтобы перенести часть заряда ​( dq )​ с одной пластины на другой (и таким образом создать заряд ​( +dq )​ на одной пластине и ​( -dq )​ на другой), нужно совершить работу ​( A=dq!cdot!U )​. Поскольку ​( q = CU )​, то работа ( A=q!cdot!dq/C ) и для определения полной работы по перенесению заряда ​( Q )​ нужно вычислить интеграл:

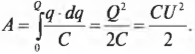
Теперь по формуле ​( W_c={}^1!/!_2CU^2 )​ можно вычислять энергию, хранящуюся в плоском конденсаторе, и выражать ее в джоулях (Дж).

Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.

Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.

Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:

F = k · (|q₁| · |q₂|) / r²

где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.

Коэффициент k в СИ принято записывать в форме:

k = 1 / (4πε₀ε)

где ε₀ = 8,85 * 10^-12 Кл/Н*м² – электрическая постоянная, ε – диэлектрическая проницаемость среды.

Для вакуума ε = 1, k = 9 * 10⁹ Н*м/Кл².

Сила взаимодействия неподвижных точечных зарядов в вакууме:

F = [1 /(4πε₀)] · [(|q₁| · |q₂|) / r²]

Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:

F = [1 /(4πε₀)] · [(|q₁| · |q₂|) / r²] = k · (1 /π) · [(|q₁| · |q₂|) / r²]

Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.

Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).

Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.

Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:

F_1,2 = -F_2,1

Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.

Вектор силы F_2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).

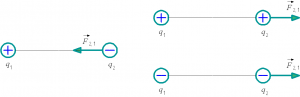
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.

Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.

В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.

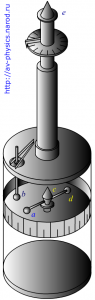
Рис. 1.10. Опыт Кулона (крутильные весы).

При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.

2017-07-12   

Точечный заряд $q_{1} = 1,0 cdot 10^{-5} Кл$ массой $m_{1} = 1,0 cdot 10^{-5} кг$ движется по оси одноименно с ним заряженного кольца. Какую наименьшую скорость должен иметь точечный заряд на очень большом расстоянии от кольца, чтобы пролететь сквозь него? Масса кольца $m_{2} = 2,0 cdot 10^{-5} кг$, его радиус $R = 5,0 cdot 10^{-2} м$, а величина заряда $q_{2} = 3,0 cdot 10^{-5} Кл$. Кольцо не закреплено и первоначально покоится.

Решение:

Законы сохранения импульса и энергии для системы «точечный заряд + кольцо» имеет вид;

$m_{1}v_{min} = m_{1}v + m_{2}v$,

$frac{m_{1}v_{min}^{2}}{2} = frac{m_{1}v^{2}}{2} + frac{m_{2}v^{2}}{2} + k frac{q_{1}q_{2}}{R}$.

Здесь $v_{min}$ — скорость точечного заряда на бесконечности, $v$ — скорости точечного заряда и кольца в момент, когда заряд оказывается в центре кольца. $frac{kq_{1}q_{2}}{2}$ – потенциальная энергия кулоновского взаимодействия точечного заряда и заряда кольца в тот же момент.

Отсюда $v_{min} = sqrt{ frac{2kq_{1}q_{2}(m_{1} + m_{2})}{Rm_{1}m_{2}}} = 4 cdot 10^{3} м/с$.

Закон Кулона <<	Оглавление (Глава 5)	>> Уравнения Максвелла

---

Пусть точечный заряд находится в начале системы отсчёта . Сила, с которой он действует на “пробный” заряд в системе , равна:

Найдём, как будет выглядеть это же взаимодействие в “неподвижной” системе отсчёта , мимо которой система движется с постоянной скоростью . Выпишем ещё раз законы преобразования различных величин. Базовыми являются преобразования Лоренца (стр. pageref{lorenz_vec0}):

(EQN)

где и . Из них непосредственно следует закон сложения скоростей:

(EQN)

Кроме этого, в третьей главе (стр. pageref{lorenz_force}) был получен закон преобразования силы , который мы запишем в обратном виде (слева сила в системе , а справа — в системе ):

(EQN)

Рассмотрим момент времени (когда начала систем совпадают). В этом случае из преобразований Лоренца () следует ( H):

(EQN)

Умножая при на (), приходим к соотношению ( H):

Подставим в правую часть преобразования () силу Кулона для неподвижного заряда в системе () и выражения для , , :

При переходе ко второму равенству учтено, что .

Приводя к общему знаменателю и выражая через при помощи (), окончательно находим силу, действующую на в “неподвижной” системе :

(EQN)

Если бы кулоновская сила в () была регуляризована (стр.pageref{kulon_a}), то в знаменателе дополнительно появилось бы слагаемое .

Обратим внимание, что при выводе () мы использовали постулат инвариантности заряда частицы. Аналогично инвариантности массы, мы считаем, что заряд — это собственная характеристика объекта, не зависящая от его скорости. Другими словами:

Выражение для силы () разбивается на два слагаемых, второе из которых зависит от скорости пробного заряда . Напомним, что в системе , связанной с зарядом , сила действия на пробный заряд не зависела от его скорости. Однако, если заряд, создающий поле, движется, теория относительности приводит к тому, что должна появиться ещё одна компонента силового воздействия, зависящая не только от положения пробного заряда, но и от его скорости. Её удобно выделить в виде отдельного поля. В результате получается сила Лоренца:

где введены электрическое и магнитное поля:

(EQN)

Подчеркнём, что появление магнитного поля (а точнее, силового воздействия , зависящего от скорости пробной частицы) — это чисто релятивистский эффект, возникающий благодаря преобразованию силы между двумя системами отсчёта. Как мы увидим чуть позже, уравнения Максвелла — это “лишь” закон Кулона плюс преобразования Лоренца! Магнит, притягивающий металл, является самым первым известным человечеству релятивистским эффектом (конечно, после видимого света).

Выражение для напряжённости электрического поля может быть записано следующим образом:

(EQN)

где , а — угол между радиус-вектором и скоростью.

Изучим подробнее характер электрического и магнитного полей, создаваемых движущимся зарядом. На одном и том же расстоянии эти поля достигают минимального значения в точках, находящихся на линии движения заряда , когда в (), и максимального на плоскости, перпендикулярной к скорости и проходящей через заряд . Например, для электрического поля:

“Густота” линий напряженности символизирует величину поля, поэтому электрическое поле движущегося заряда выглядит примерно так, как изображено на левом рисунке:

Образно говоря, силовые линии “сплющиваются”, прижимаясь к плоскости, перпендикулярной скорости заряда .

На правом рисунке изображены силовые линии магнитного поля. Так как равно векторному произведению скорости на электрическое поле , то магнитные силовые линии оказываются замкнутыми (см. правило штопора, стр. pageref{m_vectors}). В отличие от электрической составляющей силы, для которой линии напряжённости начинаются на заряде, магнитное поле не имеет зарядов. Это кинематический эффект, родственный замедлению времени, аберрации и т.п.

В книге принята система единиц, в которой . Для “восстановления” константы мы должны умножить величины, имеющие размерность времени в некоторой степени, на в той же степени. При применении этого правила сила делится на . Чтобы при этом нерелятивистский закон Кулона не изменился, заряд необходимо разделить на , поэтому:

Учитывая, что для скорости , сила Лоренца и связь магнитного и электрического полей с восстановленной константой имеют вид:

Дальше мы будем по-прежнему использовать систему , считая, что восстановление в любой формуле не составит для Читателя труда.

В первом разделе при помощи закона Кулона для неподвижного заряда и принципа суперпозиции мы получили уравнения электростатики (), стр.pageref{electrostatic}, для электрического поля. Выясним, каким дифференциальным уравнениям удовлетворяют электрическое и магнитное поля движущегося заряда.

Проведя регуляризацию, вычислим ( H) дивергенцию от электрического поля движущегося заряда:

где введена функция:

При , если , функция равна нулю. При , она стремится к бесконечности. Убедимся, что в этом пределе не зависит от скорости и равна -функции Дирака. Проинтегрируем электрическое поле по сфере, окружающей заряд ():

Интегрирование проводится по сферическим углам на фиксированном расстоянии от заряда. Ось направлена вдоль скорости. Интеграл по углу даёт множитель . В интеграле по сделаем замену :

Первообразная интеграла проверяется прямым дифференцированием. Таким образом, поток через сферу, окружающую заряд, при равен . Следовательно, для движущегося заряда по-прежнему справедливо электростатическое уравнение:

(EQN)

Мы видим, что, несмотря на то, что вектор напряжённости электрического поля не обладает сферической симметрией, дивергенция имеет такое же сингулярное значение, как и в случае неподвижного заряда.

Найдём теперь дивергенцию от магнитного поля:

Так как , ротор электрического поля равен:

(EQN)

Так как для смешанного произведения , то дивергенция магнитного поля равна нулю во всём пространстве, включая положение электрического заряда:

(EQN)

Выше мы выбрали момент времени , когда заряд находился в началах систем и . Так как заряд вместе с движется, поле в фиксированной точке неподвижной системы отсчёта изменяется. Поэтому для произвольного положения заряда необходимо везде подставить (звёздочку будем опускать). В частности:

Производную электрического поля по времени можно вычислить следующим образом (по сумма от 1 до 3):

Используя это соотношение, найдём ротор магнитного поля ():

Во втором равенстве применена формула “бац минус цаб”. Воспользовавшись уравнением и подставив вместо производную электрического поля по времени, получаем:

(EQN)

где называется плотностью тока точечного заряда.

Аналогично производной электрического поля, производная магнитного поля по времени равна:

В силу тождества ( H) можно вынести за оператор набла и получить ( H):

где для краткости . Учитывая, что , в правой части получим ротор электрического поля (), поэтому:

(EQN)

Если магнитное поле постоянно или отсутствует, ротор электрического поля равен нулю, как это было в электростатике. В общем же случае ротор отличен от нуля.

Соотношения (),(),(),() являются дифференциальными уравнениями, которым удовлетворяют электрическое и магнитное поля движущегося с постоянной скоростью заряда. Эти уравнения линейны, что является отражением принципа суперпозиции. Поэтому, если в пространстве находится множество зарядов, движущихся с различными постоянными скоростями, результирующее электромагнитное поле будет равно векторной сумме напряжённостей полей, создаваемых каждым зарядом. В этом случае плотность заряда и плотность тока равны сумме — функций Дирака:

где — положение -того заряда , а — его скорость. Выше предполагалось, что скорости всех зарядов постоянны. Соответственно, их траектории равны .

Так же, как это было сделано в электростатике, можно перейти к непрерывному пределу, усредняя точечные заряды в некотором небольшом объёме (если эти заряды расположены достаточно близко). Тогда плотность заряда будет “гладкой” функцией координат. Аналогично гладкой становится векторная функция, определяющая плотность тока зарядов , где — средняя скорость движения зарядов в объёме.

---

Закон Кулона <<	Оглавление (Глава 5)	>> Уравнения Максвелла

---

Релятивистский мир – лекции по теории относительности, гравитации и космологии