Как найти скорость точек ремня

АННОТАЦИЯ

Актуальность и цель. Объект исследования – ременная передача, состоящая из двух шкивов и ремня. Предмет исследования – тяговые характеристики ремня. Тяговая способность ремня и ременной передачи характеризуется экспериментальными графиками зависимостей относительного скольжения ремня и коэффициента полезного действия от коэффициента тяги передачи. Задача состоит в разработке математической модели ременной передачи, позволяющей теоретически оценивать тяговую способность ремня и рациональный режим работы в зоне упругого скольжения.

Материалы и методы. Кинематический и силовой расчет ременной передачи построен на теории упругого скольжения ремня по шкивам, разработанной Н. П. Петровым и Н. Е. Жуковским. В соответствии с этой теорией на шкивах существуют дуги упругого скольжения ремня. При этом вследствие упругого скольжения отношение скоростей точек ведомой и ведущей ветвей ремня линейно связано с относительным скольжением ремня, равным разности относительных удлинений ветвей. В статье предложена математическая модель ременной передачи, в основу которой положены новое полученное уравнение связи между скоростями точек ведущей и ведомой ветвей ремня и уравнения движения ремня как сплошной среды.

Результаты. Разработана математическая модель ременной передачи, позволяющая изучать тяговые характеристики ремня и определять рациональный режим работы. Разработана компьютерная модель, с помощью которой получены оценки тяговых характеристик.

Новизна. Предложено новое уравнение связи между скоростями точек ведущей и ведомой ветвей ремня.

Выводы. В режиме отсутствия буксования ремня эффективность ременной передачи возрастает при уменьшении коэффициента запаса сцепления. Коэффициент полезного действия достигает максимума при такой нагрузке, когда коэффициент запаса сцепления на одном из шкивов уменьшается до минимально допустимого. Чтобы поддерживать заданный коэффициент запаса сцепления, при изменении нагрузки силу натяжения ремня целесообразно регулировать.

ABSTRACT

Background. The object of research is belt transmission that consists of two pulleys and a belt. Subject of research is the traction characteristics of a belt. The challenge is to develop a mathematical model of the belt transmission, allowing in theory to evaluate the traction capacity of a belt and a rational mode of operation.

Materials and methods. Mathematical model of belt transmission is based on equation relationship between the velocities of lead and driven belt branches points and the equations of motion of the belt.

Results. The developed mathematical model of the belt transmission allows to study the belt traction characteristics and to determine a rational mode of operation. It was developed the computer model to estimate the traction experimental characteristics.

The novelty. It is proposed the new equation relationship between the speeds of points of leading and driven belt branches.

Conclusions. Belt transmission efficiency increases with decreasing safety factor of adhesion. Coefficient of efficiency reaches its maximum at this load, when the factor of adhesion on one of the pulleys is reduced to the minimum. To maintain the specified factor of adhesion, when changing the load force it is advisable to adjust the belt tension.

Введение

Кинематический и силовой расчет ременной передачи построен на теории упругого скольжения ремня по шкивам, разработанной Н. П. Петровым и Н. Е. Жуковским [2]. В соответствии с этой теорией на шкивах существуют дуги упругого скольжения ремня. При этом вследствие упругого скольжения отношение скоростей точек ведомой и ведущей ветвей ремня линейно связано с относительным скольжением ремня, равным разности относительных удлинений ветвей.

Статья посвящена разработке математической модели ременной передачи, в основу которой положены новое полученное уравнение связи между скоростями точек ведущей и ведомой ветвей ремня и уравнения движения ремня как сплошной среды.

1. Объект исследования и основные обозначения

Ременная передача – это механическая система, состоящая из ведущего шкива, ведомого шкива и соединяющего их ремня.

Введем следующие обозначения (рис. 1):

R₁, R₂ – радиус шкива 1 и шкива 2 соответственно, м;

L – расстояние между осями шкивов 1 и 2, м;

s – площадь поперечного сечения плоского ремня, м²;

δ – половина толщины ремня, м;

α₁, α₂ – радиальный угол охвата ремнем ведущего и ведомого шкива, рад;

r₁, r₂ – радиус цапфы вала ведущего и ведомого шкива, м;

,  – относительное удлинение cрединного волокна ведущей и ведомой ветви ремня соответственно;

₁, ₂ – угловая скорость шкива 1 и шкива 2 соответственно, рад/с;

,  – скорость набегающей на шкив точки ремня ведущей и ведомой ветви соответственно, м/с;

u – передаточное отношение;

ρ – плотность ремня, кг/м³;

,  – величина силы натяжения ведущей и ведомой ветви ремня соответственно без учета веса, Н;

 – начальная сила натяжения ремня без учета веса, Н;

E – модуль упругости ремня, Па;

 – начальное нормальное напряжение в сечении ремня, Н;

 – предел упругости ремня, Па;

f – коэффициент трения скольжения ремня со шкивом;

µ – коэффициент трения скольжения во вращательной паре “вал шкива − опора”;

M₁, M₂ – величина момента пары сил, приводящих в движение ведущий шкив 1, и пары сил полезного сопротивления (рабочей нагрузки), действующих на ведомый шкив 2 соответственно, Н м;

,  – величина момента силы трения во вращательной паре “вал − опора” ведущего и ведомого шкива относительно оси вращения соответствующего шкива, Н м;

P₁, P₂ – мощность момента M₁, M₂ пары сил соответственно, Вт;

η – коэффициент полезного действия ременной передачи.

2. Формулировка задачи

Тяговая способность ремня и ременной передачи характеризуется экспериментальными графиками зависимостей относительного скольжения ремня и коэффициента полезного действия от коэффициента тяги передачи [2, с. 137, 138]. Задача состоит в разработке математической модели ременной передачи, позволяющей теоретически оценивать тяговую способность ремня и рациональный режим работы в зоне упругого скольжения.

3. Кинематика ременной передачи

Рассмотрим ременную передачу с ведущим шкивом 1 и ведомым 2 при неизменной нагрузке и равномерных вращениях шкивов. В соответствии с исследованиями Н. П. Петрова и Н. Е. Жуковского дуга охвата шкива ремнем состоит из участков сцепления и скольжения [2, с. 130]. Пусть точки A, C и K, E– концевые точки дуги охвата ремнем ведущего и ведомого шкива соответственно (рис. 2). На участках AB и KD набегания ремня на ведущий и ведомый шкив ремень не скользит по шкиву. Следовательно, скорость  точек участка AB ведущей ветви ремня равна скорости точки A равномерно вращающегося шкива. При этом скорости точек участка BC ремня, касающегося ведущего шкива, уменьшаются до  в точке С схода, то есть участок BC ремня «отстает» от шкива из-за укорочения и скользит по нему. Аналогичные условия должны соблюдаться на дуге KE ведомого шкива. Скорость  точки K ведомой ветви ремня при набегании на шкив равна скорости точки K шкива. При этом скорости точек участка DE ремня, касающихся шкива, увеличиваются до  в точке E схода, то есть участок DE ремня «опережает» шкив из-за удлинения:

                                                                                               (1)

При буксовании ремня равенства (1) не соблюдаются.

Рассмотрим участок AC ремня, огибающий ведущий шкив. За время t его место займет участок AA₁ длиной  ведущей ветви, а участок AC займет положение CС₁ длиной  ведомой ветви:

 ; ..                                            (2)

Участки AA₁ и CС₁ в разные моменты времени представляют один и тот же участок AC ремня и имеют длину  в недеформированном состоянии. Следовательно,

                              ; .                                  (3)

Подставляя выражения для ,  из равенств (3) в равенства (2) и исключая время t, придем к такому равенству:

                                                     .                                                     (4)

По определению,

                                                             

или с учетом равенств (1), (4)

                                                     .                                           (5)

Формула (5) справедлива при отсутствии буксования ремня. Она доказывает, что передаточное отношение ременной передачи равно отношению радиусов ведомого и ведущего шкивов, умноженному на коэффициент пропорциональности, который не равен единице и зависит от относительных удлинений ведущей и ведомой ветвей ремня.

4. Динамика шкива и ремня

Установим соотношения между величинами моментов M₁, M₂ . Вес ремня учитывать не будем. Можно доказать, что он не влияет на работу движущих сил. Примем, что при неизменной нагрузке 1) вращения шкивов равномерные; 2) движение ремня установившееся; 3) ремень находится в упругом состоянии растяжения.

Выделим часть ремня, охватывающую ведущий шкив, как сплошную среду (рис. 3). Среда ограничена контрольной поверхностью, состоящей из цилиндрических внутренних и внешних поверхностей, двух боковых поверхностей, перпендикулярных оси вращения шкивов, и двух плоских радиальных поперечных сечений набегания и схода ремня. На контрольной поверхности действуют следующие силы: 1) равнодействующие ,  сил натяжения ведущей и ведомой ветви соответственно; 2) равнодействующая  реакций ведущего шкива.

При неизменном сопротивлении движение ремня как сплошной среды – установившееся. Полагая, что плотности и площади поперечного сечения ведомой ветви и ремня в ненапряженном состоянии отличается незначительно, запишем уравнение сохранения масс в интегральном виде [3, с. 54]:

                                              ,

где ,  − плотности и площадь поперечного сечения ведущей ветви ремня.

Момент силы или количества движения материальной точки относительно оси шкива будем считать положительным, если при взгляде на рисунок сила или количество движения стремятся вращать шкив вокруг оси против хода стрелки часов. Уравнение моментов количества движения относительно оси O вращения шкива ремня на шкиве при установившемся движении запишем в интегральном виде [3, с. 54]:

 

или с учетом уравнения сохранения масс

        ,                  (6)

где  – величина момента силы  относительно оси шкива.

Уравнение равномерного вращения шкива 1 представим в виде уравнения равновесия моментов сил относительно оси вращения:

                                      .

Следовательно, уравнение (6) можно записать так:

         

или

  .         (7)

Рассматривая участок ремня, охватывающий ведомый шкив, придем к аналогичному уравнению:

         .         (8)

При неизменности общей длины ремня растяжение ведущей ветви «компенсируется» сжатием ведомой ветви, то есть уменьшение силы сжатия «компенсируется» увеличением силы растяжения:

                                                                                             (9)

или

                                              .                                              (10)

Найдем величины ,  моментов сил трения во вращательной паре ведущего и ведомого шкива. На ведущий шкив со стороны элемента ab ремня действует элементарная нормальная сила dN₁ и элементарная сила dT₁ трения сцепления, а на ведомый шкив – соответственно dN₂ и dT₂. На вал ведущего шкива со стороны опоры действует элементарная сила, уравновешивающая силу dN₁ и элементарная сила dQ₁ трения, а на вал ведомого шкива − силы dN₂, dQ₂ (рис. 4).

По определению,

                                                                                     (11)

Силы трения скольжения связаны с силами давления такими равенствами:

; .

Следовательно, формулы (11) можно переписать так:

                                                                                   (12)

Установим связь между силами растяжения ремня и силами давления ремня на шкив.

Рассмотрим элемент ab ремня на ведущем шкиве с элементарным радиальным углом dα (рис. 5). На него действуют силы растяжения  и , вес, нормальная и касательная составляющие реакции шкива, элементарные равнодействующие которых равны dN и dT. Приращение  вектора  имеет проекцию  на ось касательной к окружности шкива и проекцию  на ось нормали к окружности шкива:

                                                     

Расчеты показали, что касательное ускорение точек ремня, обусловленное его деформацией, приводит к изменению сил натяжения ремня менее чем на 1% и им можно пренебречь. Вес ремня не влияет на работу движущих сил, и его также не будем учитывать. Рассмотрим предельный случай, когда скорость точки элемента ремня наибольшая и давление ремня на шкив наименьшее. Уравнения движения центра масс элемента ab ремня массы  на ведущем шкиве в естественном виде [1] запишем так:

                                                       

Проинтегрируем обе части уравнений по всем элементам ab ремня на дуге охвата ремня по окружности шкива 1:

                                                                (13)

Формулы (12) с учетом равенств (9), а также (13) и аналогичных для ведомого шкива примут такой вид:

                                                                  (14)

По определению, условие отсутствия буксования ремня на ведущем шкиве можно записать так:

                                               

или с учетом равенств (13)

                                                                      (15)

Условие отсутствия буксования для ведомого шкива выводится аналогично:

                                                                      (16)

Сцепление ремня с ведущим и ведомым шкивом характеризуется соответственно коэффициентом β₁, β₂ запаса сцепления:

                                                            (17)

Уравнения (4), (7), (8), (10) позволяют найти четыре неизвестные , , , . Они справедливы при отсутствии буксования ремня.

Отметим, что искомые неизвестные являются константами, если момент пары сил нагрузки не изменяется. Если момент пары сил изменяется и задан как функция времени, то при малом моменте сил инерции шкивов четыре неизвестные , , ,  определяются из тех же уравнений как функции от времени.

5. Алгоритм расчета

1. Задаем исходные данные: R₁ [м]; R₂ [м]; L [м]; r₁ [м]; r₂ [м]; s [м²]; ρ [кг/м³]; ₁ [рад/с]; M₂ [Н м];  [Па]; E [Па];  [Па]; f ; µ.

2. Определяем углы охвата ремней, скорость точки ведущей ветви по формуле (1), начальной силы растяжения ремня и моментов холостого хода по формулам (14).

; ; ; ;

; .

3. Отмечаем, что три уравнения (4), (8), (10) содержат три неизвестные , , .  Они приводятся к кубичному уравнению относительно переменной z:

                                      ,

где  ; ; ; .

4. Находим единственный корень z кубического уравнения на отрезке [0, 1] численным методом (например, методом Ньютона) и определяем скорость точки ведомой ветви ремня: .

5. Определяем неизвестные ,  из уравнений (4), (10):

; ;

6. Определяем силы натяжения и момент пары движущих сил из уравнений (7):                 , Н; , Н; 

, Н м.

7. Проверяем условия (15), (16) отсутствия буксования:

; 

8. Проверяем условие упругости ремня по среднему слою: .

9. При выполнении условий в п. 7, 8 определяем угловую скорость ведомого шкива по формуле (1): , рад/с.

10. Определяем передаточное отношение по формуле .

11. Определяем мощности движущих сил и сил сопротивления:

;     .

12. Оцениваем коэффициент полезного действия ременной передачи:

.

13. Оцениваем относительное скольжение  ремня по формуле

.

14. Оцениваем коэффициент  тяги передачи по формуле .

15. Оцениваем коэффициенты запаса сцепления по формулам (17).

6. Анализ тяговых характеристик

Рассчитаем тяговые характеристики ременной передачи (табл. 1).

1. Исходные данные

R1, м	R2, м	L, м	r1, мм	r2, мм	s, мм2	δ, мм	ρ, кг/м3	1, об/мин	M2, Н м	, MПа	E, МПа	, МПа	f	µ
0,1	0,2	0,7	10	20	160	2	1200	800	40	1,6	160	2,2	0,3	0,12

Расчет произведем по формулам алгоритма, полагая, что единицы измерения исходных данных приведены к системе СИ.

Сила растяжения и относительное удлинение ведущей ветви ремня увеличиваются, а ведомой − уменьшаются с увеличением момента пары сил нагрузки (рис. 6). При этом коэффициент  тяги и относительное скольжение возрастают (рис. 7, слева).

Коэффициент полезного действия передачи увеличивается с увеличением момента пары сил нагрузки от 5 до 40 Н м и увеличении коэффициента тяги (рис. 7, справа).

 

С увеличением нагрузки коэффициент β₁ запаса сцепления ремня с ведущим шкивом и β₂ с ведомым шкивом уменьшаются (рис. 8, слева).

При уменьшении коэффициента запаса сцепления на одном из шкивов до 1 эффективность ременной передачи возрастает. Коэффициент полезного действия достигает максимума при такой нагрузке и тяге, когда коэффициент запаса сцепления на одном из шкивов уменьшится до минимально допустимого.

Чтобы поддерживать заданный коэффициент запаса сцепления, при повышении нагрузки силу натяжения ремня необходимо регулировать, увеличивая ее прямо пропорционально моменту пары сил нагрузки (рис. 8, справа).

Рассмотрим вариант модели, когда в исходных данных вместо начальной силы натяжения ремня или начального нормального напряжения  в сечении ремня задано значение β коэффициента запаса сцепления .Тогда равенство (10) с учетом (17) можно переписать так:

                               ,                              (18)

где 

Уравнения (4), (7), (8), (18) позволяют найти четыре неизвестные , , , . Начальная сила натяжения ремня определяется по формуле (10):

.

Как показали расчеты, если коэффициент запаса сцепления на одном из шкивов равен 1, то есть дуги упругого скольжения и охвата шкива ремнем совпадают, то справедлива формула Эйлера без учета «вклада» сил инерции, деформации и толщины ремня: .

Снижение модуля упругости ремня в процессе эксплуатации приводит к ухудшению характеристик передачи (рис. 9).

При снижение эксплуатационных характеристик ремня дополнительное растяжение позволяет уменьшить коэффициент запаса сцепления и увеличить коэффициент полезного действия передачи.

Выводы

1. Компьютерная модель ременной передачи позволяет оценить тяговые характеристики ремня.

2. В режиме отсутствия буксования ремня эффективность ременной передачи возрастает при уменьшении коэффициента запаса сцепления. Коэффициент полезного действия достигает максимума при такой нагрузке, когда коэффициент запаса сцепления на одном из шкивов уменьшится до минимально допустимого.

3. Чтобы поддерживать заданный коэффициент запаса сцепления, при изменении нагрузки силу натяжения ремня целесообразно регулировать.

Список литературы:

Передаточные
механизмы предназначены для передачи
вращения от одною вала. называемого
ведущим, к другому, называемому ведо­мым.
Если оси ведущего и ведомого валов
параллельны или пересекают­ся, то
вращение можно передать с помощью
фрикционной или зубчатой передачи (рис.
10.8 – 10.11).

Во
фрикционной
передаче вращение передается вследствие
действия силы сцепления на поверхности
соприкасающихся колес, в зубчатой
передаче – от зацепления зубьев.
Вращательная скорость

в точке соприкасания колес относится
к точкам обоих колес, т. е. ее модуль
определяется как

.

откуда

.

Таким
образом, угловые
скорости колес фрикционной или зубчатой
передачи обратно пропорциональны
радиусам колес.

Отношение
угловой скорости ведущего колеса к
угловой скорости ведо­мого колеса
называется передаточным числам:

.

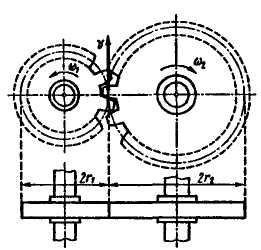
Рис.
10.8 Рис. 10.9

Рис.
10.10 Рис. 10.11

Передаточное
число можно вычислить как обратное
отношение радиусов колес:

.

Так
как числа зубьев пропорциональны длинам
окружностей и, следовательно, радиусам,
то передаточное число определяется и
по числу зубьев:

.

При
внешнем зацеплении (рис. 10.8) направление
вращения ведущего и ведомого колес
противоположное, а при внутреннем (рис.
10.9) – одинаковое.

Кроме
фрикционной и зубчатой передач существует
передача на расстоянии с помощью гибкой
связи (ремня, троса, цепи) (рис. 10.11).

Taк как скорости
всех точек ремня одинаковы и ремень не
скользит по поверхности шкива, то к
ременной передаче относятся те же
соот­ношения:

.

Применяются
также серии колес с неподвижными осями
вращения в виде последовательного ряда
с паразитными
колесами (рис. 10.12) и последовательного
ряда
с
кратным
зацеплением
(рис. 10.13), называемые рядовыми
соединениями колес.

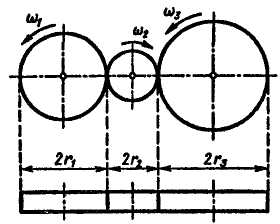
Рис.
10.12 Рис. 10.13

Определим
передаточное число фрикционной передачи
в виде рядо­вого соединения с паразитными
колесами:

для
колес 1-2

;

для
колес 2-3

.

Перемножаем
левые и правые части, получаем

.

Для
зубчатых колес

.

Передаточное
число рядового соединения с паразитными
колесами равно отношению радиусов
(чисел зубьев) ведомого и ведущего колес
и не зависит от радиусов (чисел зубьев)
паразитных колес.

Определим
передаточное число рядового соединения
с кратным зацеплением.

Частное
передаточное число для колес 1-2

.

Частное
передаточное число для колес 3-4

.

Так
как колеса 2—3 соединены жестко, т. е.

то общее передаточное число

равно произведению передаточных чисел:

.

Для
зубчатых колес

.

Таким
образом, общее
передаточное число рядового соединения
колес с кратным зацеплением равно
произведению чисел зубьев ведомых
колес, деленному на произведение чисел
зубьев ведущих колес.

В
рассмотренных выше передачах при
равномерном вращении ведущего вала
ведомый вал вращается тоже равномерно.

Для
получения переменной угловой скорости
ведомого вала приме­няются передачи,
в которых расстояние от точки соприкасания
колес до оси одного из валов или обоих
валов изменяется.

Рис.
10.14 Рис. 10.15

Во
фрикционной передаче, изображенной на
рис. 10.14, колесо 1 пере­мещается вдоль
его оси и отношение угловых скоростей
зависит от переменного расстояния х:

.

На
рис.10.15 изображены эллиптические колеса,
оси вращения которых находятся в фокусах
эллипсов. Отношение угловых скоростей
зависит от переменных расстояний

и

,

где

.

Пример
1.
Вал начинает вращаться равноускоренно
из состояния покоя. В
первые 20
с
он совершает
100 оборотов.
Каковы его
угловые
скорость и ускорение по истечении
20 с?

Решение.
Так как вал начинает вращаться из
состояния покое, то ω₀=0.
В этом
случае уравнения
при

имеют вид

,

(1)

Из
уравнения
(1) находим

,

где

.

Пример
2. Лебедка
(рис. 2.2.1), поднимающая груз по наклонной
плоскости, состоит из двух валов 1 л 2 с
шестернями (зубчатыми колесами), числа
зубьев которых равны соот­ветственно
z₁
= 12 и z₂=
48. К валу 2 прикреплен барабан радиусом
r=
0,3 м,
на который наматывается грузовой трос.
Вал 1 вращается равноускоренно с угловым
ускоре­нием ε₁
= 8 с^–2.
Определить скорость, ускорение и
переме­щение груза, а также ускорение
точки В
барабана в мо­мент времени t
= 1 с.
В начальный момент времени систе­ма
находилась в покое.

Рис.
2.2.1

Решение.
Найдем угловую скорость ω₁
ведущего вала 1 из условия, что оно
вращается с угловым ускорени­ем ε₁
= const,
учитывая, что

.
Интегрируя послед­нее уравнение по
времени, получаем

.

Постоянную
интегрирования получаем из начального
условия: при t=
0 ω₁
= 0 (система находилась в покое),
следовательно C₁
= 0.

Итак,
угловая скорость вала 1 определяется
уравнени­ем

.

При
t
= 1 с получаем

.

Шестерни
1 и 2 взаимодействуют без проскальзыва­ния.
Поэтому скорости точек их касания (точка
А)
будут одинаковы:

.

Отсюда
находим угловую скорость ω₂
вала 2, учитывая, что

:

.

Угловое
ускорение вала 2 равно

.

Поскольку
трос нерастяжим и относительно барабана
не проскальзывает, то скорость груза v
будет равна скоро­сти любой из точек
на ободе барабана, в частности, скоро­сти
точки В:
v
= v_B
= ω₂r
= 0,6t=|_t=1
c
=0,6 м/с.

Ускорение
точки В
равно векторной сумме касатель­ного
(вращательного) и нормального
(центростремитель­ного) ускорений:

.

Направление
вращательного ускорения определяется
направлением углового ускорения ε₂,
а его модуль равен

м/с².
Центростремительное ускорение на­правлено
к оси вращения вала 2 и равно по модулю

м/с².

Модуль
ускорения точки В

м/с².

Ускорение
груза можно найти, взяв производную по
времени от его скорости, так как это
касательное ускоре­ние:

м/с².

Перемещение
груза определяется интегрированием
модуля скорости по времени:

м.

Ответ:
v
= 0,6 м/с;
а
= 0,6 м/с²;
s
= 0,3 м;
а_B
= = 1,34 м/с².

Пример
3. Маховик
радиусом R
= 0,5 м
вращается так, что его угловая скорость
меняется в соответствии с уравнением

.
Для момента времени t
= 0,5 с
после нача­ла движения определить
скорость и ускорение точки на ободе
маховика. Установить, за какое время
маховик сде­лает 100 полных оборотов.

Рис.
2.2.2

Решение.
Для момента времени t
= 0,5 с
получаем ω = 0,680 с^–1,
и скорость точки на ободе маховика равна
v
= ωR
= 0,340 м/с.

Угловое ускорение
маховика

.

Ускорение
точки на ободе маховика равно сумме
двух составляющих ускорений:

,
где

и

— каса­тельное (вращательное) и
нормальное (центростремитель­ное)
ускорения точки.

Учитывая,
что вращательное ускорение равно по
мо­дулю

,
найдем

=0,680
м/с²;
центростремительное ускорение

.
Модуль полного ускорения точки

м/с.

Направления
скорости и ускорений по­казаны на
рис. 2.2.2.

Поскольку
значения величин угловой скорости и
углового ускорения имеют одинаковые
знаки, вращение тела уско­ренное.
Соответственно, совпадают по направлению
угловая скорость и угловое ускорение
тела, а также скорость точки и вращательное
ускорение.

Поворот
маховика на 100 полных оборотов
соответ­ствует углу его поворота φ
= 200π
рад.
Выражение для угла поворота найдем из
уравнения

.

Имеем

.

Итак,

,
откуда находим t
= 2,19 с.

Пример
4.
Вращение
маховика в
период пуска
машины определяется уравнением

где t
– в
с,
φ
– в рад.
Определить модуль и направление
ускорения точки, отстоящей от оси
вращения на расстоянии
50 см,
в тот момент, когда ее ско­рость равна
8
м/с.

Рис.
2.2.3

Решение.
По уравнению вращения маховика находим
его угловые скорость и ускорение согласно
формулам:

(1)

(2)

Пользуясь
формулой,
находим момент времени t₁,
когда скорость точки М
равна
8 м/с:

По
этому значению

из (1) находим
t₁:

По
уравнению
(2) вычисляем
ε,
а затем по формулам

модули
вращательного,
центростремительного
и полного
ускорений точки М
в этот момент времена:

Как
видно, модуль полного ускорения точки
весьма мало отличается от модуля
центростремительного ускорения точки
(рис. 2.2.3).

Направление
ускорения
точки
определяется
углом β,
образованным уско­рением
и радиусом
СМ:

Пример
5. Груз А,
подвешенный к нити АВ,
намотанной на барабан, опу­скается
равноускоренно из состояния покоя,
приводя во вращение барабан. За первые
3 с
барабан совершает 9 оборотов.
Определить в конце 5-й секунды скорость
и ускорение точки обода барабана, а
также груза А,
если диаметр барабана D
= 30 см
(рис. 2.2.4, а).

Рис.
2.2.4

Решение.
Барабан вращается равноускоренно
согласно уравнению:

.

Формула
угловой скорости имеет вид:

.

Для
того чтобы начальное значение угла
поворота

было равно нулю, следует неподвижную
полуплоскость поместить в начальном
положении под­вижной полуплоскости,
вращающейся с барабаном. Выполним это
и получим

.

При
вращении из состояния покоя начальная
угловая скорость барабана равна нулю

.
При этих условиях

;
(1)

.
(2)

Так
как при t
= 3 с

рад,
то из уравнения (1) определим угловое
ускорение

:

.

Из
уравнения (2) найдем угловую скорость
барабана в конце 5-й секунды:

.

Определим
в точке В
обода барабана (рис. 2.2.4, б)
модули вращательной скорости, вращательного
и центростремительного ускорений в
этот же момент времени по формулам:

(модуль
вращательного ускорения точки тела при
равнопеременном вращении одинаков для
всех моментов времени);

.

Модуль
полного ускорения точки обода барабана
определяется по формуле:

.

Вследствие
незначительной величины модуля
вращательного ускорения по сравнению
с модулем центростремительного ускорения
полное ускорение прибли­женно равно
центростремительному.

.

Ускорение
груза (рис. 2.2.4,
б) равно
вращательному ускорению точки обода:

.

Пример
6. Центробежный
регулятор вращается с постоянной угловой
скоростью ω
вокруг вертикальной оси. Угол АСВ
равен 60^о,
а ускорение шаров А
и В
равно по величине 100g,
где g=980
см/с².
Стержни АС,
ВС,
АD
и BD
одинаковой длины l=10
см.
Сколько оборотов в минуту делает
регулятор (рис. 2.2.5)?

Рис.
2.2.5

Решение.
Для того чтобы найти величину угловой
скорости регулятора, напишем зависимость
ускорения шара от параметров регулятора.
Так как регулятор вращается с постоянной
скоростью, то ускорение шара будет
центростремительным ускорением, модуль
которого определяется формулой

,

где
r
– кратчайшее расстояние шара до оси
вращения.

С
другой стороны, согласно условию,

.
Приравнивая эти два выражения нормального
ускорения шара, находим:

.

Угловая
скорость регулятора будет равна

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Два диска, соединенные невесомым нерастяжимым ремнем, равно-
мерно вращаются без скольжения ремня на дисках. Первый диск радиуса
R=0,2 м вращается с частотой n = 60 об/мин, второй – с угловой скоростью
омега= 251,2 рад\с
рад/с. Найти линейную скорость точек ремня и радиус второго
диска.

Примеры решения задач по теме «Кинематика твёрдого тела»

Подробности

Обновлено 13.08.2018 21:04

Просмотров: 795

«Физика – 10 класс»

При решении задач по этой теме обращайте внимание на связь кинематических характеристик поступательного и вращательного движений. При этом могут быть в одних случаях одинаковыми угловые скорости (например, задача 2), а в других — линейные скорости движения (например, задача 1).

Задача 1.

Два шкива соединены ременной передачей, передающей вращение от одного шкива к другому. Ведущий шкив вращается с частотой ν₁ = 3000 об/мин, ведомый шкив — с частотой ν₂ = 600 об/мин. Ведомый шкив имеет диаметр D₂ = 500 мм. Какой диаметр D₁ у ведущего шкива?

Р е ш е н и е.

Ведущий шкив вращается с угловой скоростью ω₁ = 2πν₁, а ведомый — со скоростью ω₂ = 2πν₂. Скорость приводного ремня равна линейной скорости точек окружностей того и другого шкива: υ = ω₁R₁ = ω₂R₂.

Отсюда Следовательно, искомый диаметр

Задача 2.

Колесо, радиус которого 40 см, катится по горизонтальной дороге со скоростью 2 м/с. Определите скорости относительно дороги точек колеса, находящихся на концах его вертикального и горизонтального диаметров, а также ускорения этих точек.

Р е ш е н и е.

Точка О₁ неподвижна относительно земли (рис. 1.64), следовательно, υ₁ = 0. Если считать, что через точку О₁ проходит мгновенная ось вращения, то относительно неё скорости всех точек, согласно уравнению (1.29), будут равны υ = ωr, где r — расстояние от точки O₁ до выбранной точки обода. Угловая скорость вращения ω = υ₀/R.

Тогда υ_c = υ_D = ωR√2 = υ₀√2 ≈ 2,8 м/с.

Скорость точки A υ_A = 2ωR = 2υ₀ = 4 м/с.

Все точки обода относительно оси вращения движутся с одинаковыми линейными скоростями и, следовательно, с одинаковым ускорениями

Заметим, что эту задачу также можно решить на основе закона сложения скоростей. Так, например, скорость точки D равна сумме скорости ₀ подвижной системы отсчёта, связанной с осью колеса, и скорости ₁ точки обода D относительно этой оси.

Задача 3.

Катушка с намотанной на неё нитью может катиться по поверхности горизонтального стола без скольжения. С какой скоростью υ₀ и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью υ? Радиус внутренней части катушки r, внешней — R (рис. 1.65).

Р е ш е н и е.

Скорость υ — скорость движения нити — совпадает со скоростью точки А внутренней части катушки. О_мгн — мгновенная ось вращения. Угловая скорость относительно мгновенной оси вращения ω = υ/(R – r), так как расстояние О_мгнА = R – r. Отсюда υ₀ = ωR = υR/(R – r).

Очевидно, что катушка перемещается в направлении движения конца нити. Скорость перемещения катушки будет больше, чем скорость нити.

Задача 4.

Шарик радиусом r катится со скоростью υ₀ по двум рельсам, расположенным на расстоянии 2а друг от друга. Определите скорости точек А и В относительно рельсов (рис. 1.66, а).

Р е ш е н и е.

Мгновенная ось вращения О_мгн в данном случае показана на рисунке 1.66, б. Угловая скорость поворота шарика относительно этой оси ω = υ₀/OM,

где

Отсюда

следовательно,

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика – Физика, учебник для 10 класса – Класс!ная физика

Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»