Как найти скорость точек вращающегося тела

Рассмотрим определение скоростей и ускорений точек вращающегося твердого тела:
Скорости и ускорения точек вращающегося твердого тела

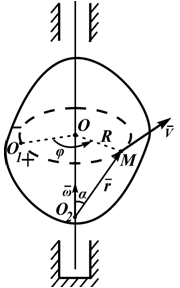
Рисунок 2.4

При вращении твердого тела вокруг неподвижной оси каждая точка тела движется по окружности. Радиус окружности R равен расстоянию от точки до оси вращения.

Закон движения точки может быть задан естественным способом (рисунок 2.4): траектория – окружность; начало отсчета точка O₁ и положительное направление движения выбраны, длина дуги (дуговая координата) определяется по формуле

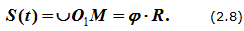
длина дуги (дуговая координата)

Скорости точек

Скорость точки вращающегося твердого тела определяется выражением

V=dS/dt=dφ∙R/dt=ωR (2.9)

где ω — угловая скорость вращения твердого тела.

Скорость направлена по касательной к траектории, поэтому можно написать

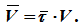
Вектор скорости можно получить векторным произведением:

V=ω × r,
V=ω × r × sinα=ω×R.

Ускорения точек

Ускорение точки при естественном способе задания движения определяется как сумма касательного и нормального ускорений (см. вывод формулы (1.10)):

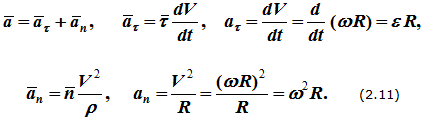
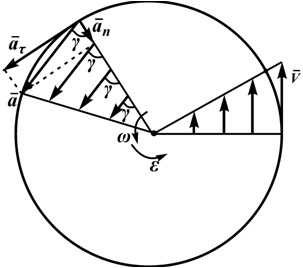
Угол, который составляет полное ускорение с радиусом

Рисунок 2.5

Эти же выражения можно получить, взяв производную от векторного произведения V=ω × r.

Угол, который составляет полное ускорение с радиусом, может быть определен из соотношения (рисунок 2.5)

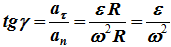
То есть эти углы для всех точек тела одинаковы и не зависят от их расположения на теле. На этом же рисунке представлены законы распределения скоростей и ускорений точек во вращающемся теле в зависимости от расстояния их до оси вращения. Эти законы распределения соответствуют формулам:

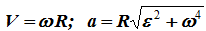
>> Передаточные механизмы

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Решение задач и лекции по технической механике, теормеху и сопромату

Источник

Найдиготовую курсовую работувыполненное домашнее заданиерешённую задачуготовую лабораторную работунаписанный рефератподготовленный докладготовую ВКРготовую диссертациюготовую НИРготовый отчёт по практикеответы и шпаргалкиполные лекцииполные семинарызаполненную рабочую тетрадьподготовленную презентациюпереведённый текстнаписанное изложениенаписанное сочинениеготовую статью

72,7% бесплатных материалов

964 руб. средняя цена курсовой работы

351 руб. средняя цена домашнего задания

119 руб. средняя цена решённой задачи

160 руб. средняя цена лабораторной работы

174 руб. средняя цена реферата

168 руб. средняя цена доклада

1608 руб. средняя цена ВКР

664 руб. средняя цена диссертации

596 руб. средняя цена НИР

358 руб. средняя цена отчёта по практике

276 руб. средняя цена ответов (шпаргалок)

201 руб. средняя цена лекций

222 руб. средняя цена семинаров

280 руб. средняя цена рабочей тетради

188 руб. средняя цена презентации

67 руб. средняя цена перевода

137 руб. средняя цена изложения

150 руб. средняя цена сочинения

308 руб. средняя цена статьи

Гарантия возврата средств

Скорости точек тела, вращающегося вокруг неподвижной оси. Формула Эйлера

2020-06-032021-03-09СтудИзба

Скорости точек тела, вращающегося вокруг неподвижной оси. Формула Эйлера

Скорость любой точки тела, вращающегося вокруг неподвижной оси, называется линейной. Заметим, что скорости точек на ободе маховика или вращающегося диска называются также окружными скоростями.

Так как движение точки в этом случае движения тела задано естественным образом, то величина линейной скорости будет равна

υ=|s| = R|φ|,

или

υ =Rω.

Следовательно, линейная скорость точки тела, вращающегося вокруг неподвижной оси, по величине равна произведению радиуса вращения на величину угловой скорости. Линейная скорость направлена по касательной к окружности в сторону вращения и, таким образом, перпендикулярна радиусу вращения R (рис 50).

Покажем, что линейная скорость точки тела, вращающегося вокруг неподвижной оси, равна векторному произведению угловой скорости тела на радиус-вектор точки.

Действительно, пусть тело вращается вокруг неподвижной оси против часовой стрелки. Тогда вектор угловой скорости ω будет направлен в положительную сторону оси вращения Оz,. Положение рассматриваемой точки тела определим радиусом-вектором r. Радиус вращения R будет равен

Отзывы студентов

Добавляйте материалы
и зарабатывайте!

Продажи идут автоматически

588

Средний доход
с одного платного файла

Обучение Подробнее

Источник

1.
Скорости точек тела. Рассмотрим
какую-нибудь точку М твердого
тела, находящуюся на расстоянии h от
оси вращения (см. рис.9). При вращении
тела точка М будет
описывать окружность радиуса h,
плоскость которой перпендикулярна оси
вращения, а центр С лежит
на самой оси. Если за время dt происходит
элементарный поворот тела на угол dφ,
то точка М при
этом совершает вдоль своей траектории
элементарное перемещение ds=hdφ.
Тогда числовое значение скорости точки
будет равно отношению ds к dt, т.е

Скорость в
отличие от угловой скорости тела называют
иногда еще линейной
или окружной скоростью точки М.

Таким образом,
числовое значение скорости точки
вращающегося твердого тела равно
произведению угловой скорости тела на
расстояние от этой точки до оси
вращения.

Направлена
скорость по касательной к описываемой
точкой окружности или перпендикулярно
плоскости, проходящей через ось вращения
и точку М.

Так
как для всех точек тела имеет
в данный момент времени одно и то же
значение, то скорости точек вращающегося
тела пропорциональны их расстояниям
от оси вращения.

Скорость и
ускорение точки вращающегося тела

Следовательно,
линейная скорость любой точки вращающегося
тела равна произведению угловой скорости
на расстояние от данной точки до оси
вращения. Направлена эта скорость всегда
по касательной к окружности, которую
описывает данная точка при своем
движении.

В
каждый данный момент времени угловые
скорости точек вращающегося тела равны.
Поэтому линейные скорости точек тела
пропорциональны их расстоянию до оси
(рис.3.4), т.е. скорость изменяется
полинейному закону.

Так
как точки тела совершают криволинейное
движение (траектории точек – окружности),
то полное ускорение слагается из
нормального и касательного ускорений,
которыеопределяются ,

(3.14)

Таким
образом полное ускорение точки
будет (3.15) Из
формул (3.15) следует, что полное ускорение
точки вращающегося тела пропорционально
ее расстоянию до оси вращения.

При
вращательном движении тела вокруг оси
нормальное ускорение  называют
еще центростремительным  (вектор
направлен по радиусу к центру
кривизны),  касательное
ускорение называют
и иначе – вращательным ускорением  (вектор
ускорения направлен по касательной).

47.Скорость и ускорение точки при векторном способе заданиядвижения

С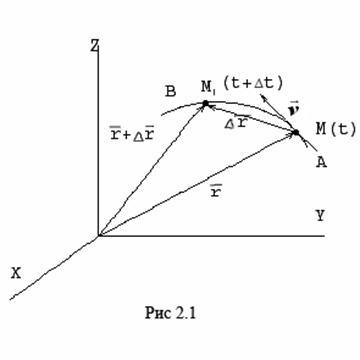корость
точки – это величина, характеризующая
как быстро и в каком направлении меняется
положение точки в пространстве. Поскольку
она определяет направление перемещения
точки, скорость является величиной
векторной. Пусть за время Δt радиус-вектор
точки М изменился на величину Δ. Тогда
средней скоростью называется векторная
величина (2.1)

Этот
вектор направлен так же, как и .
Предельное значение ,
при стремящемся к нулю ,
определит мгновенное значение скорости
в данный момент времени

(2.2)

При
стремлении  к
нулю хорда ММ₁,
а значит и вектор  поворачивается
вокруг точки М, приближаясь к касательной
к траектории в точке М и в пределе,
совпадая с ней. Поэтому вектор  направлен
по касательной к траектории точки в
сторону движения.

         В
общем случае криволинейного движения
вектор скорости изменяется по величине
и направлению в функции времени.
Следовательно, за время  вектор  можно
представить в виде . Ускорение точки
в криволинейном движении характеризует
быстроту изменения вектора  по
величине и направлению. Тогда средняя
величина ускорения определится ,
а мгновенное значение ,
или

(2.3)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Макеты страниц

Установив в предыдущих параграфах характеристики движения всего тела в делом, перейдем к изучению движения отдельных его точек.

1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис. 134).

При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время происходит элементарный поворот тела на угол то точка М при этом совершает вдоль своей траектории элементарное перемещение Тогда числовое значение скорости точки будет равно отношению т. е.

или

Скорость v в отличие от угловой скорости тела называют иногда еще линейной или окруокной скоростью точки М.

Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.

Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.

Так как для всех точек тела со имеет в данный момент времени одно и то же значение, то из формулы (44) следует, что скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Поле скоростей точек вращающегося твердого тела имеет вид, показанный на рис. 136.

Рис. 136

Рис. 137

2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами

В нашем случае . Подставляя значение v из равенства (44) в выражения получим:

или окончательно:

Касательная составляющая ускорения направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при замедленном); нормальная составляющая всегда направлена по радиусу МС к оси вращения (рис. 137).

Полное ускорение точки М будет или

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом который вычисляется по формуле [вторая из формул (22)]. Подставляя сюда значения из равенств (45), получаем

Так как имеют в данный момент времени для всех точек тела одно и то же значение, то из формул (46) и (47) следует, что ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол , с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис. 138.

Рис. 138

Рис. 139

Формулы (44) — (47) позволяют определить скорость и ускорение любой точки тела, если известен закон вращения тела и расстояние данной точки от оси вращения. По этим же формулам можно, зная движение одной точки тела, найти движение любой другой его точки, а также характеристики движения всего тела в целом.

3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов v и а, проведем из произвольной точки О оси АВ радиус-вектор точки М (рис. 139). Тогда а и по формуле (44)

Таким образом, – модуль векторного произведения равен модулю скорости точки М. Направления векторов тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно,

т. е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Формулу (48) называют формулой Эйлера.

Беря от обеих частей равенства (48) производные по времени, получим

или

Формула (49) определяет вектор ускорения любой точки вращающегося тела.

Вектор направлен, как и вектор , т. е. по касательной к траектории точки Вектор же направлен вдоль МС, т. е. по нормали к траектории точки М, а так как Учитывая все эти результаты, а также формулы (45), заключаем, что

Задача 54. Вал, делающий об/мин, после выключения двигателя начинает вращаться равнозамедленно и останавливается через с. Определить, сколько оборотов сделал вал за это

Решение. Так как вал вращается равиозамедленно, то для него, считая будет

Начальной угловой скоростью при замедленном вращении является та, которую вал имел до выключения двигателя. Следовательно,

В момент остановки при угловая скорость вала. Подставляя эти вначения во второе из уравнений (а), получаем:

Если обозначить число сделанных валом за время оборотов через N (не смешивать с n; — угловая скорость), то угол поворота за то же время будет равен Подставляя найденные значения в первое из уравнений (а), получим

откуда

Задача 55. Маховик радиусом пращаегся равномерно, делая об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.

Решение. Скорость точки обода где угловая скорость w должна быть выражена в радианах в секунду. Тогда

Далее, так как то и, следовательно,

Ускорение точки направлено в данном случае к оси вращения.

Задача 56. Полагая, что при разгоне маховик вращается по закону

определить значения постоянных коэффициентов и k из условий, что при должно быть и что предельная угловая скорость, до которой разгоняется маховик а его угловое ускорение при разгоне не должно превышать значения

Найти также, какое ускорение будет при этом у точек обода маховика в момент времени , если радиус маховика

Решение. Из уравнения (а) видно, что при если

Далее из уравнения (а) находим, что Следовательно, при если

При этих значениях уравнение (а) примет вид

Отсюда находим

Первое из равенств (в) показывает, что со временем растет и при стремится к предельному значению следовательно, Из второго же равенства видно, что со временем убывает, стремясь к нулю, а наибольшее чение имеет при следовательно,

Но по условиям задачи Тогда должно быть откуда При этих значениях k и равенство (б) дает окончательно следующий закон вращения маховика:

Тогда, что видно и из равенств (в), будет

момента времени 1 с, учитывая, что получим Следовательно, в этот момент времени

Задача 57. Груз В (рис. 140) приводит во вращение вал радиусом и сидящую на одной оси с валом шестерню ральуссч Движение груза начинается из состояния покоя и происходит с постоянным ускорением а. Определить, по какому закону будет при этом вращаться находящаяся в зацеплении с шестерней шестерня 2 радиуса .

Рис. 140

Решение. Так как груз В начинает двигаться без начальной скорости, то его скорость в любой момент времени t равна Эту скорость будут иметь и точки обода вала. Но, с другой стороны, скорости этих точек равны где общая для вала и шестерни 1 угловая скорость. Следовательно,

Теперь найдем Так как скорость точки сцепления С должна быть одной и той же для обеих шестерен, то откуда

Итак, угловая скорость шестерни 2 растет пропорционально времени. Учитывая, что где — угол поворота шестерни 2, получим

Отсюда, беря от обеих частей интегралы и считая, что при угол найдем окончательно закон равноускоренного вращения шестерни 2 в виде

Оглавление

ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
ВВЕДЕНИЕ
Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
§ 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
§ 3. СВЯЗИ И ИХ РЕАКЦИИ
Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
§ 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
§ 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
§ 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
§ 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
§ 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
§ 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
§ 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
§ 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
§ 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
§ 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
§ 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
§ 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
§ 17. РЕШЕНИЕ ЗАДАЧ
§ 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
§ 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
§ 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
§ 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
Глава VI. ТРЕНИЕ
§ 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
§ 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
§ 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
§ 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
§ 27. ТРЕНИЕ КАЧЕНИЯ
Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
§ 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
§ 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
§ 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
Глава VIII. ЦЕНТР ТЯЖЕСТИ
§ 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
§ 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
§ 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
§ 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
§ 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
§ 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
§ 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
§ 38. ВЕКТОР СКОРОСТИ ТОЧКИ
§ 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
§ 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
§ 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
§ 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
§ 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
§ 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
§ 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
§ 46. РЕШЕНИЕ ЗАДАЧ
§ 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
§ 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
§ 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
§ 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
§ 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
§ 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
§ 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
§ 57. РЕШЕНИЕ ЗАДАЧ
§ 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
§ 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
§ 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
§ 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
§ 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
§ 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
§ 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
§ 67. РЕШЕНИЕ ЗАДАЧ
Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
§ 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
§ 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
§ 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
§ 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
Раздел третий. ДИНАМИКА ТОЧКИ
Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
§ 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 75. СИСТЕМЫ ЕДИНИЦ
§ 76. ОСНОВНЫЕ ВИДЫ СИЛ
Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
§ 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
§ 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
§ 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
§ 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
§ 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
§ 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
§ 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
§ 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
§ 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
§ 87. РАБОТА СИЛЫ. МОЩНОСТЬ
§ 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
§ 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
§ 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
§ 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
§ 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
§ 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
§ 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
§ 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
§ 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
§ 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
§ 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
§ 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
§ 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
§ 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
§ 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
§ 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
§ 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
§ 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
§ 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
§ 109. РЕШЕНИЕ ЗАДАЧ
Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
§ 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
§ 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
§ 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
§ 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
§ 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
§ 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
§ 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
§ 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
§ 118. РЕШЕНИЕ ЗАДАЧ
§ 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
§ 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
§ 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
§ 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
§ 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
§ 124. РЕШЕНИЕ ЗАДАЧ
§ 125. СМЕШАННЫЕ ЗАДАЧИ
§ 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
§ 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
§ 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
§ 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
§ 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
§ 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
§ 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
§ 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
§ 135. РЕШЕНИЕ ЗАДАЧ
§ 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
§ 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
§ 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
§ 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
§ 140. РЕШЕНИЕ ЗАДАЧ
§ 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
§ 143. ОБОБЩЕННЫЕ СИЛЫ
§ 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
§ 145. УРАВНЕНИЯ ЛАГРАНЖА
§ 146. РЕШЕНИЕ ЗАДАЧ
Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
§ 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
§ 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
§ 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
§ 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
§ 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
§ 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
§ 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
§ 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
§ 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА

Источник

Скорости точек

Ускорения точек

Решение задач и лекции по технической механике, теормеху и сопромату

Популярные услуги по физике

Скорости точек тела, вращающегося вокруг неподвижной оси. Формула Эйлера

Рекомендуемые материалы

Отзывы студентов

47.Скорость и ускорение точки при векторном способе заданиядвижения

Добавить комментарий Отменить ответ

Скорости точек

Ускорения точек

Решение задач и лекции по технической механике, теормеху и сопромату

Популярные услуги по физике

Скорости точек тела, вращающегося вокруг неподвижной оси. Формула Эйлера

Рекомендуемые материалы

Отзывы студентов

47.Скорость и ускорение точки при векторном способе заданиядвижения

Вам также может понравиться

Как найти блокировщик рекламы на компьютере

Как найти работу в москве любую

Как найти любовницу на долго

Добавить комментарий Отменить ответ