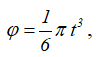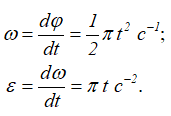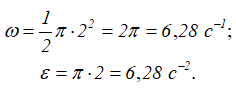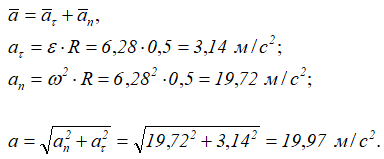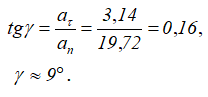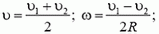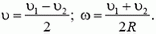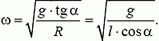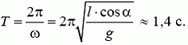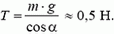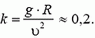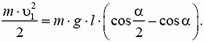Пример решения задачи по определению в заданный момент времени скорости, ускорения и угла между вектором ускорения точки, лежащей на ободе диска и радиусом, вращающегося по известному закону диска.
Задача
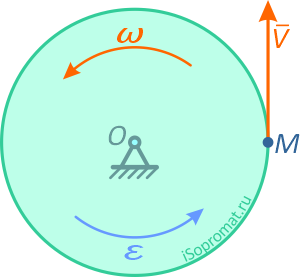
Диск радиуса R=0,5 м вращается по закону:
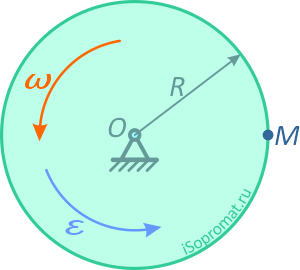
Рисунок 2.8
В момент времени t=2 c определить скорость точки M, лежащей на ободе диска, её ускорение и угол между вектором ускорения и радиусом диска.
Другие примеры решений >
Помощь с решением задач >
Решение
При заданном законе вращения угловая скорость и угловое ускорение определяются по формулам (2.3) и (2.4)
Для момента времени t=2 c:
Скорость точки M:
Вектор скорости направлен по касательной к траектории движения точки, т.е. по касательной к окружности (рисунок 2.9).
Рисунок 2.9
Ускорение точки M:
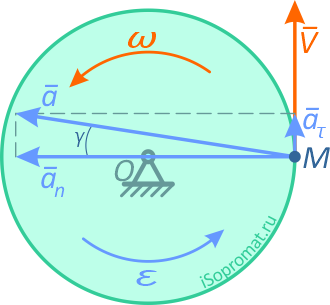
Касательное и нормальное ускорения направлены соответственно по касательной и по нормали (рисунок 2.10).
Рисунок 2.10
Угол между радиусом и вектором ускорения γ:
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Асламазов Л.Г. Движение по окружности // Квант. — 1972. — № 9. — С. 51-57.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время Δt описывает дугу, угловая мера которой Δφ, то угловая скорость 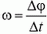
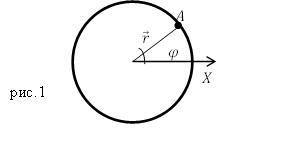
Угловая скорость ω связана с линейной скоростью υ соотношением υ = ω·r, где r — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.
Рис. 1.
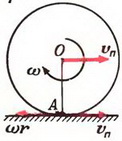
Задача 1. Диск радиуса r катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна υп. С какой угловой скоростью при этом вращается диск?
Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью υп вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью ω.
Для нахождения ω воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения υп равна по величине и противоположна по направлению линейной скорости вращательного движения υвр = ω·r. Отсюда сразу получаем 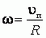
Рис. 2.
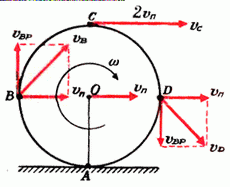
Задача 2. Найти скорости точек В, С и D того же диска (рис. 3).
Рис. 3.
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна 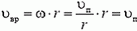
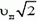
Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно 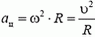
Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению 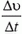
Задача 3. Найти ускорения точек А, В, С и D диска радиуса r, катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна υп (рис. 3).
В системе координат, связанной с центром диска, диск вращается с угловой скоростью ω, а плоскость движется поступательно со скоростью υп. Проскальзывание между диском и плоскостью отсутствует, следовательно, 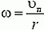
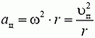
Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона 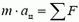
Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.
Задача 4. Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости υ = 70 км/ч и коэффициенте трения шин о дорогу k =0,3.
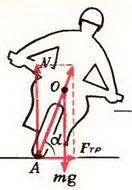
На автомобиль действуют сила тяжести Р = m·g, сила реакции дороги N и сила трения Fтp между шинами автомобиля и дорогой. Силы Р и N направлены вертикально и равны по величине: P = N. Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: 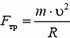
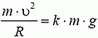
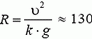
Сила реакции дороги N при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля 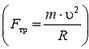
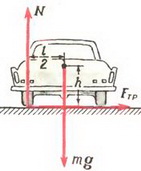
Задача 5. При какой скорости автомобиль, движущийся по дуге окружности радиуса R = 130 м, может опрокинуться? Центр тяжести автомобиля находится на высоте h = 1 м над дорогой, ширина следа автомобиля l = 1,5 м (рис. 4).
Рис. 4.
В момент опрокидывания автомобиля как сила реакции дороги N, так и сила трения Fтp приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью υ на него действует сила трения 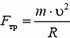
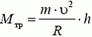
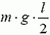
Откуда 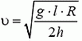
Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения 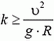
Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).
Задача 6. Мотоциклист едет по горизонтальной дороге со скоростью υ = 70 км/ч, делая поворот радиусом R = 100 м. На какой угол α к горизонту он должен при этом наклониться, чтобы не упасть?
Сила трения между мотоциклом и дорогой 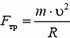
Рис. 5.
Подставляя сюда значения Fтp и N, находим что или
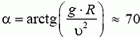
Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.
Задача 7. С какой максимальной скоростью υ может двигаться автомобиль по наклонному треку с углом наклона α при радиусе закругления R и коэффициенте трения шин о дорогу k?
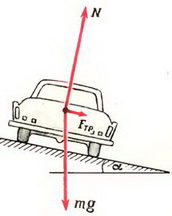
На автомобиль действуют сила тяжести m·g, сила реакции N, направленная перпендикулярно плоскости трека, и сила трения Fтp, направленная вдоль трека (рис. 6).
Рис. 6.
Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна 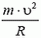
Сумма проекций всех сил на вертикальное направление равна нулю:
N·cos α – m·g – Fтp·sin α = 0.
Подставляя в эти уравнения максимальное возможное значение силы трения Fтp = k·N и исключая силу N, находим максимальную скорость 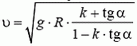
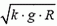
Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.
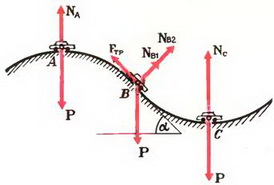
Задача 8. Автомобиль массы m = 1,5 т движется со скоростью υ = 70 км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса R = 200 м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?
Рис. 7.
В точке А на автомобиль действуют сила тяжести Р = m·g и сила реакции дороги NA. Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: 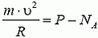
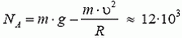
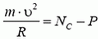
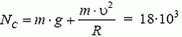
В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги NB1, причем 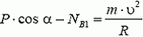

Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину 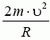
При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.
Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно k·N, где k — коэффициент трения между шинами автомобиля и дорогой, N — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.
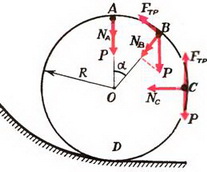
Задача 9. Автомобиль массой m = 0,5 т, движущийся со скоростью υ = 200 км/ч, совершает «мертвую петлю» радиуса R = 100 м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли А; в точке В, радиус-вектор которой составляет угол α = 30º с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения шин о дорогу k = 0,5?
Рис. 8.
В верхней точке петли сила тяжести и сила реакции дороги NA направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: 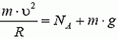
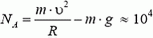
Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе NА.
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: 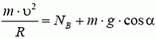
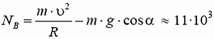
Легко видеть, что NB > NA; с увеличением угла α сила реакции дороги увеличивается.
В точке С сила реакции 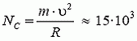
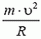
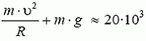
, таким образом, является минимальным значением силы реакции.
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения k·N во всех точках петли. Это условие заведомо выполняется, если минимальное значение 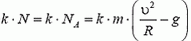
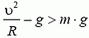
Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.
Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.
Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.
Задача 10. Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли R = 100 м, масса автомобиля m = 0,5 т.
Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?
Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги 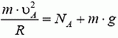
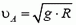
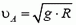
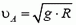
Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость 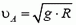
Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем
Подставляя сюда значение 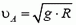
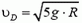
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.
Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:
Подставляя сюда значение 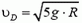

Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке B:
Н.
Аналогично можно найти силу давления в любой другой точке «мертвой петли».
Упражнения
1. Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения Т = 88 мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии R = 200 км от поверхности Земли.
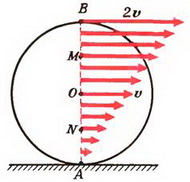
2. Диск радиуса R помещен между двумя параллельными рейками. Рейки движутся со скоростями υ1 и υ2. Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.
3. Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.
4. Самолет движется по окружности с постоянной горизонтальной скоростью υ = 700 км/час. Определить радиус R этой окружности, если корпус самолета наклонен на угол α = 5°.
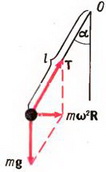
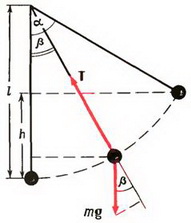
5. Груз массы m = 100 г, подвешенный на нити длины l = 1 м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол α = 30°. Определить также натяжение нити.
6. Автомобиль движется со скоростью υ = 80 км/ч по внутренней поверхности вертикального цилиндра радиуса R = 10 м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?
7. Груз массой m подвешен на нерастяжимой нити, максимально возможное натяжение которой равно 1,5m·g. На какой максимальный угол α можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол α/2 с вертикалью?
Ответы
I. Угловая скорость искусственного спутника Земли 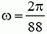
2. Здесь возможны два случая (рис. 1). Если угловая скорость диска ω, а скорость его центра υ, то скорости точек, соприкасающихся с рейками, будут соответственно равны
в случае a) υ1 = υ + ω·R, υ2 = υ – ω·R;
в случае б) υ1 = υ + ω·R, υ2 = ω·R – υ.
(Мы приняли для определенности, что υ1 > υ2). Решая эти системы, находим:
а)
б)
Рис. 1.
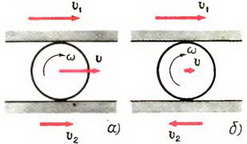
3. Скорость любой точки М, лежащей на отрезке ОВ (см. рис. 2), находится по формуле υM = υ + ω·rM, где rM — расстояние от точки М до центра диска О. Для любой точки N, принадлежащей отрезку ОА, имеем: υN = υ – ω·rN, где rN — расстояние от точки N до центра. Обозначим через ρ расстояние от любой точки диаметра ВА до точки А соприкосновения диска с плоскостью. Тогда очевидно, что rM = ρ – R и rN = R – ρ = –(ρ – R). где R — радиус диска. Поэтому скорость любой точки на диаметре ВА находится по формуле: υρ = υ + ω·(ρ – R). Так как диск катится без проскальзывания, то 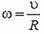
Рис. 2.
Доказанное утверждение позволяет нам сделать вывод, что сложное движение точек, находящихся на диаметре ВА, можно в каждый данный момент рассматривать как простое вращение вокруг неподвижной точки А с угловой скоростью ω, равной угловой скорости вращения вокруг центра диска. В самом деле, в каждый момент скорости этих точек направлены перпендикулярно диаметру ВА, а по величине равны произведению ω на расстояние до точки А.
Оказывается, что это утверждение справедливо для любой точки диска. Более того, оно является общим правилом. При любом движении твердого тела в каждый момент существует ось, вокруг которой тело просто вращается — мгновенная ось вращения.
4. На самолет действуют (см. рис. 3) сила тяжести Р = m·g и подъемная сила N, направленная перпендикулярно плоскости крыльев (так как самолет движется с постоянной скоростью, то сила тяги и сила лобового сопротивления воздуха уравновешивают друг друга). Равнодействующая сил Р и N должна быть направлена к центру окружности, по которой движется самолет, и создавать центростремительное ускорение 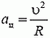
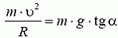
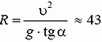
Рис. 3.
5. Равнодействующая силы тяжести Р = m·g и силы натяжения нити Т должна создавать центростремительное ускорение ац = ω2·R, где R = l·sin α — радиус круга, по которому вращается груз. Из рисунка 4 получаем:
m·ω2·R = m·g·tg α, откуда
Период обращения груза
Натяжение нити
Рис. 4.
6. На автомобиль действуют (рис. 5) сила тяжести Р = m·g, сила реакции со стороны цилиндра N и сила трения Fтp. Так как автомобиль движется по горизонтальному кругу, то силы Р и Fтp уравновешивают друг друга, а сила N создает центростремительное ускорение 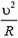
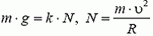
Рис. 5.
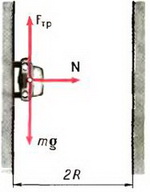
7. Груз будет двигаться по окружности радиуса l (рис. 6). Центростремительное ускорение груза 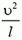
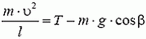
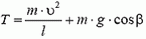
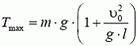
Используя это соотношение, для максимального значения натяжения нити получаем формулу: Tmax = m·g·(3 – 2 cos α). По условию задачи Tmах = 2m·g. Приравнивая эти выражения, находим cos α = 0,5 и, следовательно, α = 60°.
Определим теперь натяжение нити при 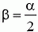
Подставляя значение υ1 в формулу для силы натяжения, находим:
Рис. 6.
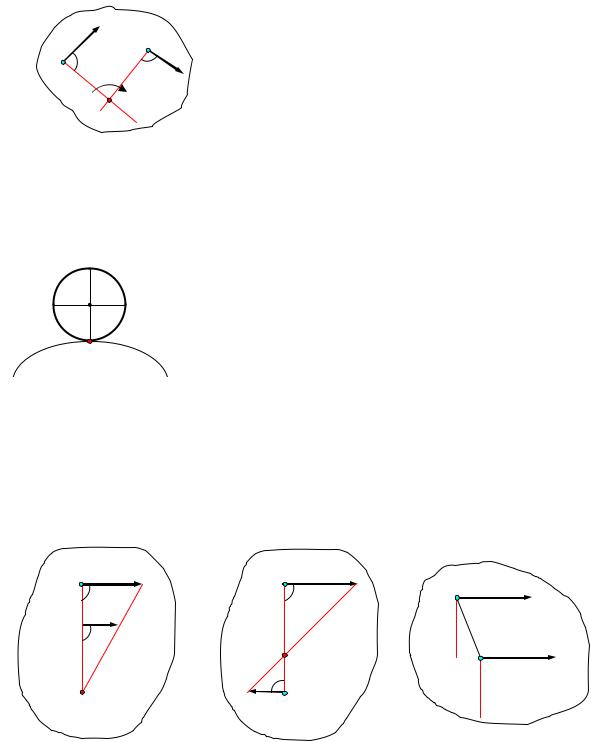
Рис.12
Способы нахождения мгновенного центра скоростей
Для определения положения мгновенного центра скоростей плоской фигуры необходимо знать только направления скоростей двух ее точек.
Указанные свойства позволяют определить положение мгновенного центра скоростей плоской фигуры в различных случаях.
|
VA |
1. Если скорости двух точек не параллельны, |
||
|
А |
В |
VB |
то мгновенный центр скоростей лежит в точке |
|
900 |
пересечения перпендикуляров к ним, что следует из |
||
|
900 |
|||
|
теоремы о существовании мгновенного центра ско- |
Рростей (рис.12).
2. Если плоское движение осуществляется
качением без скольжения одного твердого тела по неподвижной поверхности другого, то точка их контакта Р имеет в данный момент скорость, равную нулю, и, следовательно, будет мгновен-
ным центром скоростей (рис.13).
3. Если скорости двух точек А и В плоской фигуры параллельны и с прямой, соединяющей эти точки, составляют прямые углы, то мгновенный центр скоростей Р находится как точка пересечения об-
Рщего перпендикуляра, восстановленного к скоро-
|
Рис.13 |
стям в данных точках, и прямой, проходящей через |
|
концы векторов скоростей (рис.14 и рис.15). |
4. Если скорости двух точек параллельны и с прямой, соединяющей точки образуют острые углы, то мгновенный центр скоростей не суще-
ствует (находится в бесконечности). В этом случае скорости всех точек плоской фигуры равны, а угловая скорость равна нулю (рис. 16).
|
А |
VA |
А |
VA |
А |
VA |
||
|
90 |
0 |
90 |
0 |
||||
В
Р VB
В
|
Р |
900 |
|
|
В |
||
|
VB |
||
|
Рис. 14 |
Рис. 15 |
Рис. 16 |
10
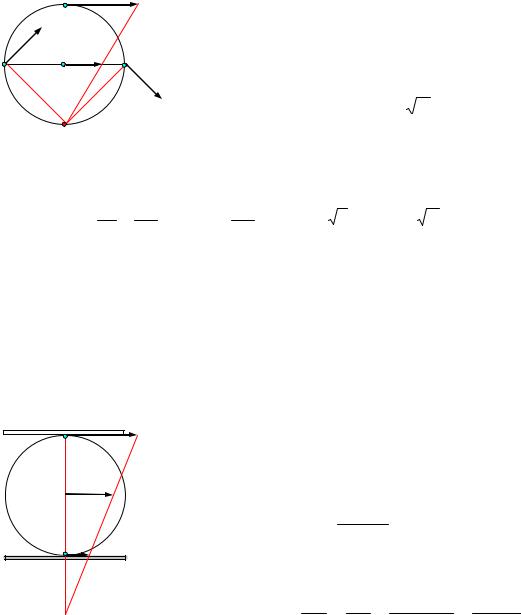
Решение задач с помощью мгновенного центра скоростей.
Задача 1. Найти скорости точек А, В и D обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра колеса С равна VC.
|
Определить скорости точек А, В, D и угловую скорость колеса. |
|||||||||||||||||
|
Решение. Мгновенный центр скоростей |
Р колеса находится (рис.177) в |
||||||||||||||||
|
точке контакта колеса с неподвижной плоскостью. Скорости точек А, В, D |
|||||||||||||||||
|
VD |
перпендикулярны к отрезкам, соединяющим эти |
||||||||||||||||
|
D |
точки с точкой Р, модули скоростей пропорцио- |
||||||||||||||||
|
VA |
нальны их длинам: |
||||||||||||||||
|
С |
VC |
В |
Расстояния точек А и В до мгновенного цен- |
||||||||||||||
|
А |
тра скоростей одинаковы, |
следовательно, скоро- |
|||||||||||||||
|
VB |
сти этих точек равны |
||||||||||||||||
|
VA =VB =VC |
2. |
||||||||||||||||
|
Скорость точки D равна 2VC , так как рас- |
|||||||||||||||||
|
P |
|||||||||||||||||
|
стояние точки D |
до мгновенного центра скоро- |
||||||||||||||||
|
Рис.17 |
|||||||||||||||||
|
VA = |
стей в два раза больше расстояния СР . |
||||||||||||||||
|
AP |
; V |
=V AP ; |
AP = R 2, V |
=V 2. |
|||||||||||||
|
V |
CP |
A |
C CP |
A |
C |
||||||||||||
|
C |
VC |
VC |
|||||||||||||||
|
Угловая скорость колеса равна |
ω = |
= |
. |
||||||||||||||
|
CP |
R |
Задача.2. Диск зажат между двумя рейками, (рис.18) которые движутся со скоростями V1 и V2 (V1 > V2).
Определить угловую скорость диска и скорость его центра, если его радиус равен R.
АVAa
С
ВVB
b
Р
Рис.18
Решение. Скорость точки А диска равна скорости верхней рейки, а скорость точки В – скорости нижней рейки. Мгновенный центр скоростей находится в точке Р (рис.16). Скорость точки С является средней линией трапеции ВАав:
VC = V1 +2V2 .
Угловая скорость
ω = VAPA = VBPB = APVA −−VBPB = V12−RV2 .
Задача 3. Кривошипно-шатунный механизм
11
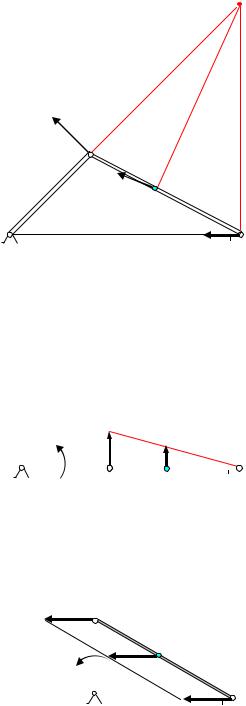
Угловая скорость кривошипа равна ωОА. Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.
Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна VA =ωOA OA. , а скорость точки В направлена по
|
горизонтальной прямой. |
||||||||||||||||||||||||||||||||||||
|
1. Кривошип ОА образует острый угол с горизонтальной прямой |
||||||||||||||||||||||||||||||||||||
|
P |
(рис.19). В этом случае мгновенный |
|||||||||||||||||||||||||||||||||||
|
центр скоростей шатуна находится в |
||||||||||||||||||||||||||||||||||||
|
точке Р, где пересекаются восстановлен- |
||||||||||||||||||||||||||||||||||||
|
ные в точках А и В перпендикуляры к |
||||||||||||||||||||||||||||||||||||
|
скоростям в этих точках. |
||||||||||||||||||||||||||||||||||||
|
VA |
AP |
BP |
||||||||||||||||||||||||||||||||||
|
VA |
= BP |
VB =VA AP . |
||||||||||||||||||||||||||||||||||
|
VB |
||||||||||||||||||||||||||||||||||||
|
A |
Скорость точки С направлена перпенди- |
|||||||||||||||||||||||||||||||||||
|
VC |
C |
кулярно отрезку РС и находится из про- |
||||||||||||||||||||||||||||||||||
|
порции: |
||||||||||||||||||||||||||||||||||||
|
O |
VC |
= |
CP |
V |
=V |
CP . |
||||||||||||||||||||||||||||||
|
VB |
VA |
AP |
C |
A |
AP |
|||||||||||||||||||||||||||||||
|
B |
Угловая скорость шатуна равна |
|||||||||||||||||||||||||||||||||||
|
Pис.19 |
ωAB = |
VA |
||||||||||||||||||||||||||||||||||
|
AP |
||||||||||||||||||||||||||||||||||||
|
2. Кривошип и шатун расположены на одной прямой (рис.20). |
||||||||||||||||||||||||||||||||||||
|
В этом положении мгновенный центр скоростей находится в точке В, |
||||||||||||||||||||||||||||||||||||
|
VA |
поэтому скорость VB |
равна нулю. Ско- |
||||||||||||||||||||||||||||||||||
|
VC |
рость точки С находится из пропорции: |
|||||||||||||||||||||||||||||||||||
|
VC |
CB |
CB |
||||||||||||||||||||||||||||||||||
|
O |
= |
V =V |
. |
|||||||||||||||||||||||||||||||||
|
VA |
AB |
C |
A |
AB |
||||||||||||||||||||||||||||||||
|
A |
C |
|||||||||||||||||||||||||||||||||||
|
B |
Угловая скорость шатуна равна |
|||||||||||||||||||||||||||||||||||
|
Рис.20 |
ωAB = |
VA |
. |
|||||||||||||||||||||||||||||||||
|
AB |
||||||||||||||||||||||||||||||||||||
|
VA A |
3. |
Кривошип |
занимает |
|||||||||||||||||||||||||||||||||
|
вертикальное положение (рис.21). В |
||||||||||||||||||||||||||||||||||||
|
VC |
C |
этом случае мгновенный центр скоростей |
||||||||||||||||||||||||||||||||||
|
шатуна находится в бесконечности, скоро- |
||||||||||||||||||||||||||||||||||||
|
O |
VВ |
B |
сти всех его точек равны, угловая скорость |
|||||||||||||||||||||||||||||||||
|
шатуна равна нулю. |
||||||||||||||||||||||||||||||||||||
|
Рис. 21 |
||||||||||||||||||||||||||||||||||||
12
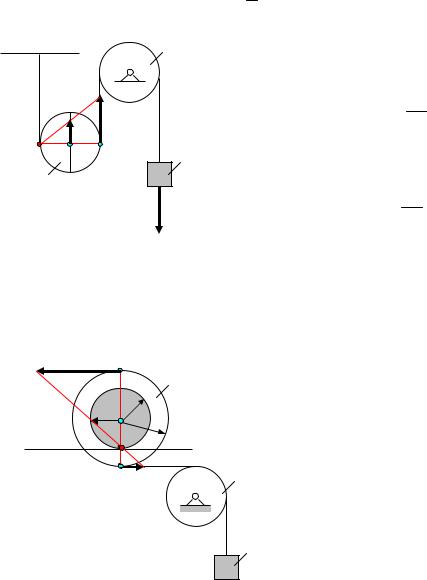
Задача 4. Определить скорости точек А, В, Р подвижного блока 3 (рис.22) и его угловую скорость, если скорость тела 1 равна V1
Решение. Подвижный блок совершает плоское движение. Скорость точки контакта Р подвижного блока с неподвижной нитью равна нулю: VР = 0, т.е. точка Р – мгновенный центр скоростей подвижного блока.
Скорость точки С перпендикулярна отрезку, соединяющему ее с мгновенный центром скоростей: VC CP .
|
2 |
|||
|
О |
|||
|
VС |
VА |
||
|
Р С |
А |
1 |
|
|
3 |
B |
||
|
Рис.22 |
V1 |
||
Скорости точек при плоском движении пропорциональны расстояниям до мгновенного центра скоростей
VC = CP .
VA AP
VA = V1, так как точка А и тело 1 связаны нерастяжимой нитью, тогда
VC = 0,5R .
V1 R
Следовательно, VC = 0,5 VA = 0,5 V1.
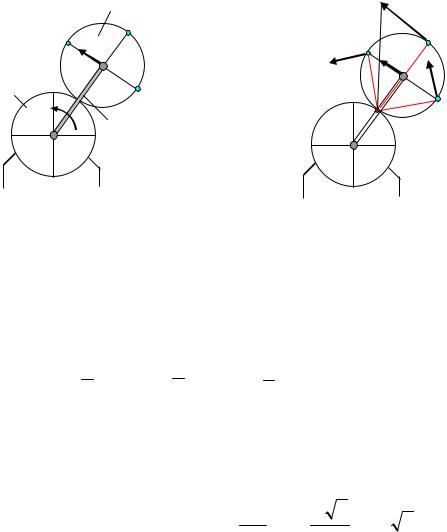
Задача 5. Определить угловую скорость и скорости точек А, В, С и Р катушки 3 (рис.23), если скорость груза 1 равна V1.
|
VA |
A |
3 |
|
|
VC |
С |
R |
|
|
r |
|||
|
P |
B VB |
2 |
|
|
O |
Рис.23

Решение. Скорость точки В катушки равна скорость груза 1, так как они связаны нерастяжимой нитью: VВ = V1.
При качении без скольжения в точке контакта катушки с рельсом находится мгновенный центр скоростей Р. Скорости точек А и С перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром скоростей и пропорциональны их расстояниям до мгновенного центра скоростей, поэтому
|
VC |
= |
CP |
; |
VC |
= |
r |
. |
|||
|
V |
BP |
V |
R −r |
|||||||
|
B |
B |
|
Отсюда |
VC |
= VB |
r |
= V1 |
r |
|||
|
R − r |
R |
|||||||
|
Аналогично определим скорость точки А. |
||||||||
|
VA = |
AP |
; |
VA = |
r +R |
. |
|||
|
BP |
||||||||
|
V |
V |
R −r |
||||||
|
B |
B |
Следовательно,
13
|
V |
=V |
r +R |
=V |
r +R |
. |
|||
|
B R −r |
||||||||
|
A |
B R −r |
Задача 6. Определить угловую скорость и скорости точек А, В, D, E шестерни 3 (рис.24), которую приводит в движение кривошип ОА, вращающийся вокруг оси О неподвижной шестерни 1 с угловой скоростью ωОА.
|
3 |
VD |
|||||
|
D |
||||||
|
В VA |
В |
D |
||||
|
А |
VВ |
VA |
||||
|
VE |
||||||
|
1 |
Е |
|||||
|
А |
Е |
|||||
|
ωАВ |
P |
|||||
|
2 |
||||||
Решение. Скорость точки А, принадлежащей кривошипу ОА, перпендикулярна кривошипу и равна VA = ωAB AB.
Шестерня 3 совершает плоское движение, ее мгновенный центр скоростей находится в точке зацепления Р с неподвижной шестерней 1 (рис. 24а). Скорости точек В, Е и D перпендикулярны отрезкам, соединяющим их с мгновенным центром скоростей.
VB BP , VD DP , VE EP .
Скорости точек пропорциональны отрезкам, соединяющим эти точки с мгновенным центром скоростей Р.
VB =VE , так как расстояния этих точек до мгновенного центра скоростей равны: ВР = ЕР.
|
VA |
= AP ; откуда VB =VA BP |
=VA |
R |
2 |
=VA 2. |
||||
|
V |
R |
||||||||
|
BP |
AP |
||||||||
|
B |
|||||||||
|
Аналогично определяем скорость точки D. |
|||||||||
|
VA |
= |
AP ; |
откуда VD =VA DP =VA 2R |
= 2VA. |
|||||
|
V |
DP |
AP |
R |
||||||
|
D |
Задача 7. Определить скорости точек А, В, С, D и угловые скорости звеньев механизма, изображенного на рис. 25, если угловая скорость криво-
шипа ОА равна ωОА.
Решение. Во всех вариантах скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.
14

Звенья ОА и ОВ механизма (рис.25) совершают вращательное движение. Скорость точки А, являющейся концом кривошипа ОА, равна VA = ωОА OA и перпендикулярна кривошипу.
|
Скорость VB OB .Звенья АС и ВD совершают плоское движение. Звено |
||||||||||||||||||||||
|
Р2 |
СD движется |
поступательно, по- |
||||||||||||||||||||
|
этому скорости точек C и D равны: |
||||||||||||||||||||||
|
VB |
VC = VD . |
|||||||||||||||||||||
|
A |
Мгновенный |
центр |
скоростей |
|||||||||||||||||||
|
VA |
B |
звена АС лежит в точке Р1 пересе- |
||||||||||||||||||||
|
ωOA O |
чения перпендикуляров к скоростям |
|||||||||||||||||||||
|
в точках А и С. |
||||||||||||||||||||||
|
VC С |
D |
V |
= |
CP |
, |
CP |
||||||||||||||||
|
VD |
C |
1 |
V |
=V |
||||||||||||||||||
|
V |
AP |
1 . |
||||||||||||||||||||
|
A |
C |
A AP |
||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||||
|
Угловая скорость звена АС равна |
||||||||||||||||||||||
|
ωAC = |
VA |
. |
||||||||||||||||||||
|
Рис.25 |
||||||||||||||||||||||
|
Р1 |
AP1 |
|||||||||||||||||||||
|
Проведем |
перпендикуляры к |
|||||||||||||||||||||
|
скоростям VВ |
и VD , точка их пересечения Р2 |
|||||||||||||||||||||
|
– мгновенный центр скоростей |
|
VB |
BP2 |
BP |
||
|
звена ВD. V |
= DP , откуда |
2 |
||
|
VB =VD DP . |
||||
|
D |
2 |
2 |
||
|
Угловая скорость звена ВD равна |
||||
|
ωBD = |
VB |
. |
||
|
BP2 |
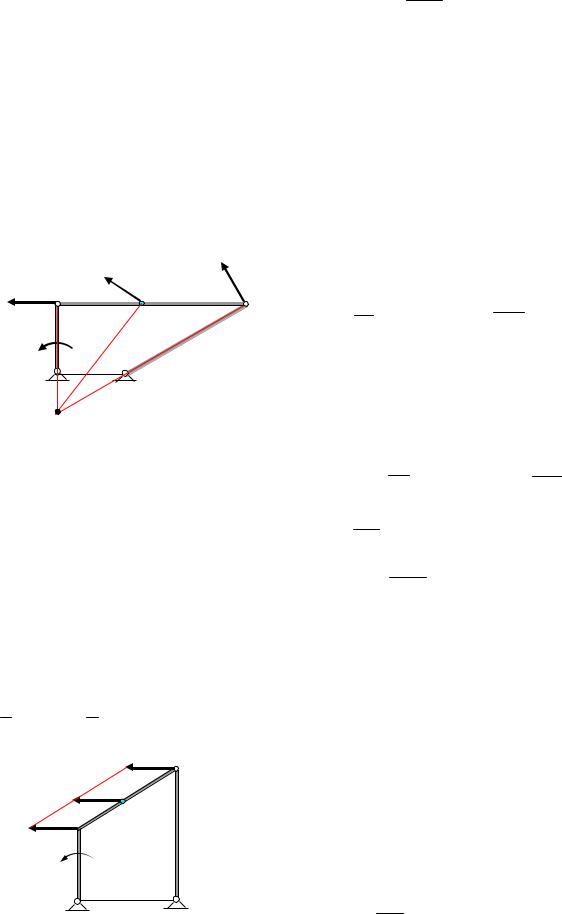
Задача 8. Определить скорости точек А, D и угловые скорости звеньев механизма, изображенного на рис. 26, если угловая скорость кривошипа ОА
равна ωОА.
Скорость точки А равна VA = ωОА OA и перпендикулярна кривошипу ОА. Звено АВ совершается плоское движение, скорость точки В направлена вертикально вниз. Мгновенный центр в данный момент находится в бесконечности, поэтому скорости всех его точек равны, а угловая скорость ωAB = 0 .
Скорость точки D перпендикулярна кривошипу О2D, следовательно, мгновенный центр скоростей звена ВD совпадает с точкой О2.
|
Тогда |
VD = |
DO2 ; |
откуда |
|||||||
|
О1 |
А |
D |
VB |
BO2 |
||||||
|
DO2 . |
||||||||||
|
ωОА |
VD |
90 |
0 |
V |
=V |
|||||
|
D |
B |
BO2 |
||||||||
|
VA |
В |
О2 |
BD |
|||||||
|
Угловая скорость |
звена |
|||||||||
|
равна ωBD = |
VB |
= VD . |
||||||||
|
VB |
BO2 |
DO2 |
||||||||
|
Угловая скорость кривошипа O2D равна ωBD |
= VD . |
||||||||||
|
DO2 |
|||||||||||
|
Задача 9. Определить скорости точек А, С, D и угловые скорости звень- |
|||||||||||
|
ев механизма, изображенного на рис. 25, |
если угловая скорость кривошипа |
||||||||||
|
ОА равна ωОА (рис.27). |
|||||||||||
|
Решение. Звенья О1А и О2В совершают вращательные движения, поэто- |
|||||||||||
|
му скорость точки А направлена перпендикулярно кривошипу О1А и равна |
|||||||||||
|
VA = ωОА· OA. |
|||||||||||
|
Скорость точки D перпендикулярна звену О2D. |
|||||||||||
|
Звено АD совершает плоское движение, мгновенный центр скоростей |
|||||||||||
|
этого звена лежит в точке Р пересечения перпендикуляров, проведенных в |
|||||||||||
|
VD |
точках А и D к скоростям VA и VD. |
||||||||||
|
VC |
Скорость точки D находим из про- |
||||||||||
|
VA |
А |
D |
|||||||||
|
С |
порции |
VD |
DP |
. VD |
=VA DP . |
||||||
|
= |
|||||||||||
|
ωОА |
VA |
AP |
AP |
||||||||
|
Соединим |
точек |
С с мгновенным |
|||||||||
|
О1 |
|||||||||||
|
О2 |
центром скоростей Р, скорость точки С |
||||||||||
|
будет направлена перпендикулярно от- |
|||||||||||
|
Р |
резку СР. |
||||||||||
|
Рис.27 |
Модуль этой скорости найдем из |
||||||||||
|
пропорции |
VC |
= CP |
, VC =VA CP . |
||||||||
|
VA |
AP |
AP |
|||||||||
|
Угловая скорость звена АD равна ωAD = |
VA . |
||||||||||
|
AP |
VD . |
||||||||||
|
Угловая скорость кривошипа равна |
ω |
= |
|||||||||
|
O2D |
O2 D |
||||||||||
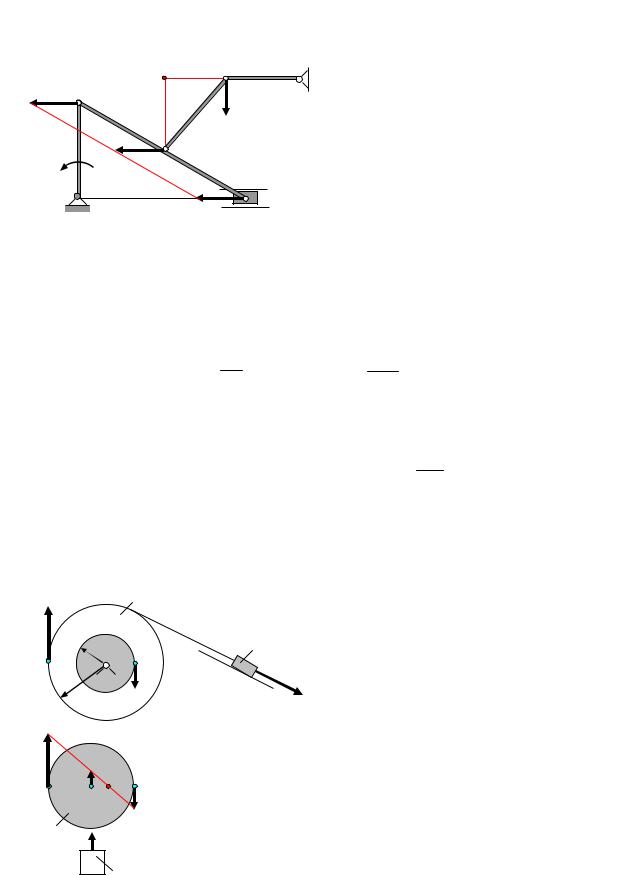
Задача 10. Определить скорости точек А, В, С, и угловые скорости звеньев механизма, изображенного на рис. 28, если угловая скорость криво-
шипа ОА равна ωОА.
Решение. Звенья ОА и DB совершают вращательные движения, поэтому
VA OA , VB
VC
VA
ωОА 
О
BD . Скорость точки А равна VA = ωОА· OA. Звено совершает
|
VВ |
плоское движение, так как скорости точек А и В |
||
|
В |
параллельны, то мгновенный центр скоростей |
||
|
С |
этого звена находится в бесконечности, поэтому |
||
|
скорости всех его точек геометрически равны |
|
VA = VB = VC. |
|
|
Угловая скорость звена AВ равна нулю. Уг- |
|
|
D |
ловая скорость кривошипа ВD равна |
|
ωBD = VB . |
|
|
BD |
Рис.28
16
|
Задача 11. Определить скорости точек А, В, С, D и угловые скорости |
|||||||||
|
звеньев механизма, изображенного на рис. 29, |
если угловая скорость криво- |
||||||||
|
Р |
D |
шипа ОА равна ωОА. |
|||||||
|
О2 |
Решение. |
Скорость точки А |
|||||||
|
VA |
А |
||||||||
|
VD |
перпендикулярна |
кривошипу |
и |
||||||
|
равна VA = ωОА· OA. Звено АВ со- |
|||||||||
|
VC |
С |
вершает |
плоское |
движение, |
ско- |
||||
|
ωОА |
рость VВ точки В направлена гори- |
||||||||
|
О1 |
VВ |
В |
зонтально влево. В данном положе- |
||||||
|
нии |
мгновенный |
центр скоростей |
|||||||
|
Рис.29 |
звена АВ находится в бесконечно- |
||||||||
|
сти, поэтому скоростей всех |
его |
||||||||
|
точек геометрически равны: VA = VB = VC. |
|||||||||
|
Звено CD совершает плоское движение, мгновенный центр скоростей |
|||||||||
|
этого звена лежит в точке Р пересечения перпендикуляров, проведенных к |
|||||||||
|
скоростям в точках С и D. Скорость точки D найдем из пропорции |
|||||||||
|
VC = |
CP |
, VD =VC |
DP . |
||||||
|
V |
DP |
CP |
|||||||
|
D |
|||||||||
|
Угловая скорость звена СD равна ωCD = VC . |
|||||||||
|
CP |
= VD . |
||||||||
|
Угловая скорость кривошипа О D равна |
ω |
||||||||
|
2 |
O2D |
DP |
|||||||
Задача 12. Определить скорость точки С и угловую скорость подвижного блока 3 (рис.30), если скорость тела 1 равна V1, r = 0,5R.
Решение. Блок 2 вращается вокруг точки О, скорость его точки В по ве-
|
VB |
2 |
личине равна скорости тела 1, так |
||||||||||||||||||
|
как они связаны нерастяжимой ни- |
||||||||||||||||||||
|
r O |
1 |
тью: VB = V1.Скорость |
точек |
при |
||||||||||||||||
|
B |
A |
вращательном |
движении пропор- |
|||||||||||||||||
|
R |
VA |
V1 |
циональны |
их |
радиусам |
вращения, |
||||||||||||||
|
поэтому |
VA |
= |
r |
= |
0,5R |
= 0,5 . |
Сле- |
|||||||||||||
|
VD |
VB |
R |
R |
|||||||||||||||||
|
VC |
довательно, VA = 0,5 VB. |
|||||||||||||||||||
|
D |
К |
Подвижный |
блок 3 совершает |
|||||||||||||||||
|
плоское движение, |
при этом |
VD = |
||||||||||||||||||
|
С |
P |
|||||||||||||||||||
|
VE |
VB, VК = VA, так как соответствую- |
|||||||||||||||||||
|
3 |
||||||||||||||||||||
|
V4 |
щие точки связаны нерастяжимыми |
|||||||||||||||||||
|
нитями. |
||||||||||||||||||||
|
4 |
||||||||||||||||||||
|
Рассмотрим движение блока 3. |
||||||||||||||||||||
|
Рис.30 |
Мгновенный центр скоростей нахо- |
|
|
дится в точке пересечения Р общего |
||
|
17 |
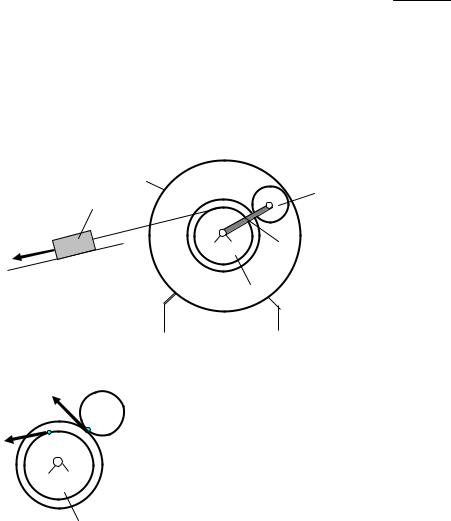
перпендикуляра, проведенного к скоростям VD и VК , и прямой, проходящей через концы этих векторов. Конец вектора скорости VС точки С лежит на прямой, соединяющей концы векторов скоростей VD и VК .
VК = VA = 0,5VB, VD = VB , тогда VК = 0,5VD.
Составим пропорцию:
VK = KP
VD DP .
Обозначив СР = х, тогда KP = R – x, DP = R + x. Подставив эти значения в пропорцию, получим
|
0,5 V |
R − x |
R |
|||||
|
V |
D = |
, |
откуда x = |
. |
|||
|
R + x |
|||||||
|
3 |
|||||||
|
D |
Тогда расстояние точки К до мгновенного центра скоростей Р равно KP = R – x = 2/3 R, т.е. расстояние точки С до мгновенного центра скоростей в два раза меньше, чем то же расстояние до точки К, поэтому скорость точки будет в два раза меньше скорости точки К. VC = 0,5· VK = 0,5 VA = 0,25 V1.
Угловая скорость блока 3 равна ω3 = CPVC = 0,25RV1 3 = 0,75VR1 .
Скорость груза 4, подвешенного на нити в точке С, равна скорости точки С.
V4 = VC = 0,25 V1.
Задача 13. Определить скорость точки С и угловую скорость кривошипа ОС указанного на рис.31 механизма, если скорость тела 1 равна V1 (радиусы тел 3 и 5 заданы).
|
2 |
5 |
Решение. Данный механизм со- |
||||||||||
|
C |
||||||||||||
|
1 |
стоит из пяти, соединенных между |
|||||||||||
|
V1 |
O |
4 |
собой тел. |
|||||||||
|
1. Тело 1, двигаясь вниз по на- |
||||||||||||
|
клонной плоскости, сообщает телу 3 |
||||||||||||
|
3 |
вращательное движение вокруг точ- |
|||||||||||
|
ки О. |
||||||||||||
|
Рис.31 |
В свою очередь тело 3, находясь |
|||||||||||
|
в зацеплении с телом 5, сообщает |
||||||||||||
|
VK |
ему плоское движение. |
|||||||||||
|
5 |
Точка С тела 5 приводит в движение кривошип ОС, кото- |
|||||||||||
|
VA |
K |
рый вращается вокруг точки О. |
||||||||||
|
A |
2. Рассмотрим движение тела 3 (рис.31а). Скорость |
|||||||||||
|
O |
точки А равна скорости груза 1, так как они связаны не- |
|||||||||||
|
растяжимой нитью. Определим скорость точки К. |
||||||||||||
|
3 |
Скорости точек вращающегося тела относятся как |
|||||||||||
|
их радиусы вращения: |
||||||||||||
|
Рис. 31 а |
VA |
= |
r |
. |
||||||||
|
VK |
||||||||||||
|
R |
18

Отсюда скорость
|
VC |
P |
VK =VA |
R |
=V1 |
R |
. |
|
|
r |
|||||||
|
5 |
r |
||||||
|
K |
C |
3. Рассмотрим движение тела 5 (рис.31 |
|||||
|
б). |
Точка Р является мгновенным центром |
||||||
скоростей, так как в этой точке тело 5 находится в зацеплении с неподвижной шестер-
3ней 2. Скорость точки находим из пропорции
|
VC |
= |
CP |
||||||||||||||||
|
, |
||||||||||||||||||
|
Рис. 31 б |
VK |
KP |
||||||||||||||||
|
CP |
r3 |
=VK |
=V1 R . |
|||||||||||||||
|
VC |
VC =VK |
= |
||||||||||||||||
|
KP |
||||||||||||||||||
|
C 5 |
2r3 |
2 |
2 r |
|||||||||||||||
|
4. Кривошип вращается (рис.31в) вокруг точки О |
||||||||||||||||||
|
определим по форму- |
||||||||||||||||||
|
O |
4 |
с угловой скоростью, которую |
||||||||||||||||
|
VC |
||||||||||||||||||
|
ле |
ωOC = |
. |
||||||||||||||||
|
OC |
3
Рис. 31 в
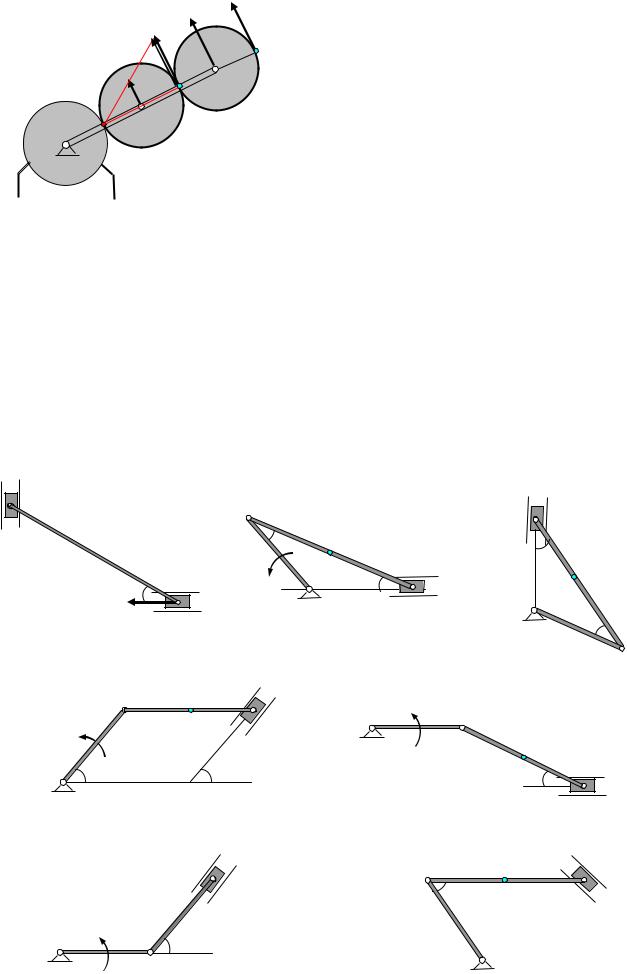
Задача 14. Кривошип ОС соединяющий центры трех шестерен одинакового радиуса R (рис.32), вращается вокруг точки О с угловой скоростью ω.
|
VС |
Шестерня |
1 закреплена |
неподвижно, |
|||
|
шестерни 2 и 3 приводятся в движение |
||||||
|
D |
||||||
|
кривошипом. Определить скорости точек |
||||||
|
VA |
С |
контакта |
между шестернями, скорость |
|||
|
точки D и угловые скорости подвижных |
||||||
|
ω |
||||||
|
А |
3 |
шестерен. |
||||
|
О |
2 |
Решение. |
||||
|
1. Рассмотрим движение кривошипа. |
||||||
|
1 |
||||||
|
Скорости точек А и С (рис.32) на- |
||||||
|
правлены |
перпендикулярно |
кривошипу |
||||
|
Рис.32 |
ОС и равны |
VA = ω·OA = 2 ω R, VC = ω·OC = 4 ω R.
2. Рассмотрим движение шестерни 2.
Шестерня 2 совершает плоское движение, (рис.32 а) скорость точки А известна. В точке контакта с неподвижной шестерней 1 находится мгновенный центр скоростей Р.
19
|
VD |
Скорость VK направлена перпендику- |
||||||||||||
|
лярно отрезку КР, |
модуль ее определяет- |
||||||||||||
|
VК |
VС |
||||||||||||
|
D |
ся из пропорции |
||||||||||||
|
VK |
= |
KP |
= |
2R |
= 2 , |
||||||||
|
VA |
С |
VA |
AP |
R |
|||||||||
|
А |
К |
откуда VK = 2 VA = 4ω R. |
|||||||||||
|
О Р |
Угловая скорость шестерни 2 равна |
||||||||||||
|
ω2 |
= |
VA |
= |
2ω R |
= 2ω . |
||||||||
|
R |
|||||||||||||
|
AP |
|||||||||||||
|
Рис.32 а |
3. Определим характер движения шес- |
терни 3.
Скорости точек С и D шестерни 3 равны по модулю и параллельны, следовательно, шестерня 3 совершает поступательное движение, угловая скорость такого движения равна нулю.
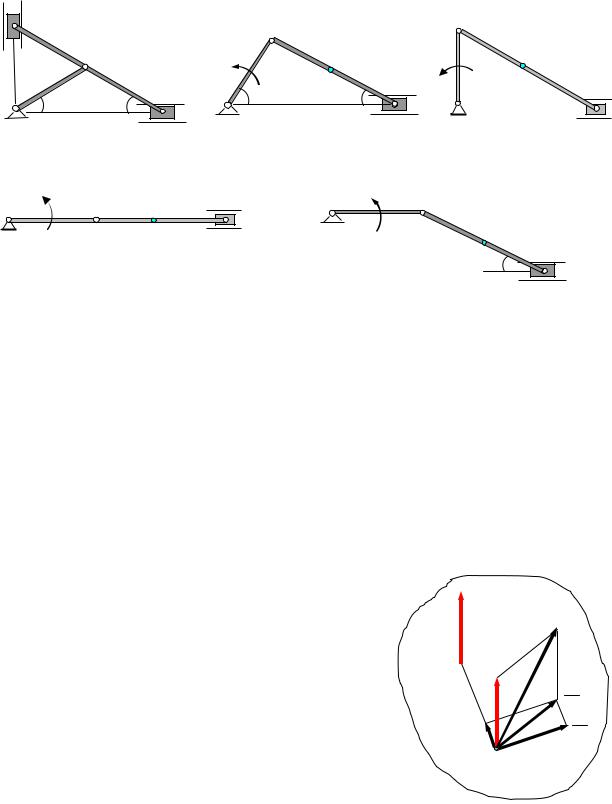
Упражнения.
Определить с помощью мгновенного центра скоростей скорости точек А, В и С в механизмах, представленных на чертежах
|
А |
В |
||||||||||
|
А |
|||||||||||
|
300 |
C |
300 |
|||||||||
|
30 |
0 |
В |
ωОА |
О |
300 |
В |
C |
||||
|
О |
|||||||||||
|
VВ |
|||||||||||
|
Рис.1 |
Рис.2 |
300 |
|||||||||
|
А |
|||||||||||
|
В |
Рис. 3 |
||||||||||
|
A |
C |
ωОА |
|||||||||
|
O |
A |
||||||||||
|
ωОА |
|||||||||||
|
C |
|||||||||||
|
O |
450 |
450 |
30 |
0 |
В |
||||||
|
Рис.5 |
|||||||||||
|
Рис.4 |
|||||||||||
|
B |
А |
C |
В |
||||||||
|
600 |
|||||||||||
|
O |
ωОА |
450 |
О |
||||||||
|
A |
20 |
||||||||||
Ускорения точек плоской фигуры.
Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.
Следовательно, ускорение любой точки при плоском движении равно
геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.
Пусть известно ускорение точки А плоской фигуры, тогда ускорение другой точки этой фигуры будет равно (рис.33).
aB = aA + aBA ,
где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:
aBA = aBAτ + aBAn .
aA
aB
A
aA
a BA a n a BAτ
BA B
Рис.33
Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно
21
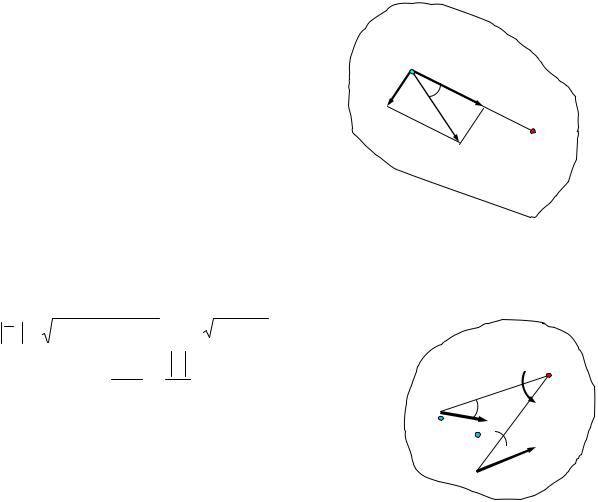
aτBA = ε BA.
Нормальное ускорение направлено по отрезку ВА к полюсу А и равно
aBAn =ω2 BA.
Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:
aB = aA +aBAn +aBAτ .
Мгновенным центром ускорений называется точка, принадлежащая связанной с плоской фигурой плоскости, ускорение которой в данный момент равно нулю.
Если за полюс выбрать мгновенный центр ускорений, то ускорение произвольной точки плоской фигуры определяется как ускорение вращательного движения вокруг мгновенного центра ускорений (рис.34).
|
aA = aAL = aALn + aALτ , |
|||||
|
где L –мгновенный |
центр ускорений, aALn |
– |
|||
|
нормальное |
τ |
касательное ус- |
А |
||
|
ускорение, aAL – |
aALτ |
ε aALn |
|||
|
корение точки А вращательного движения пло- |
|||||
|
ской фигуры вокруг мгновенного центра уско- |
L |
||||
|
рений. |
aALn =ω2 AL, |
aτAL =ε AL. |
aA |
||
|
Ускорение aALn |
– направлено по AL , уско- |
||||
|
рение aALτ |
– перпендикулярно AL. Ускорение |
Рис.34 |
|||
|
aA точки А образует угол α с отрезком AL со- |
|||||
единяющим точку А с мгновенным центром ускорений и равно (рис.35)
|
aA = (aALn )2 +(aτAL )2 = AL ω4 +ε2 , |
||||
|
tgα = aτAL |
= |
ε |
. |
L |
|
aALn |
ω2 |
А |
ε |
|
Таким образом, если известно ускорение точки А плоской фигуры, то, чтобы найти положение мгновенного центра ускорений, следует это ускорение повернуть вокруг точки А на угол α в сторону вращения фигуры и на полученной прямой отложить расстояние
22
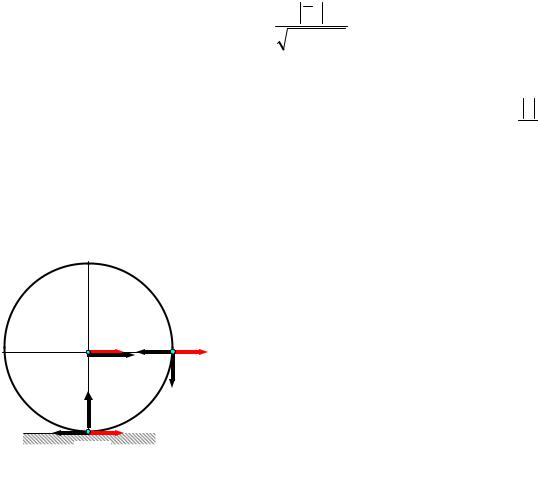
Если известны направления ускорений двух точек плоской фигуры, то мгновенный центр ускорений определяется как точка пересечения получен-
ных поворотом этих ускорений на один и тот же угол α = arctq ωε2 в сторону вращения.
Задача1. Центр колеса, катящегося без скольжения по горизонтальной плоскости, в данный момент имеет скорость VC = 2 м/c и ускорение аC = 1,6 м/c. Радиус колеса R = 0,4 м. Определить точек В и Р (рис. 36).
Решение. Так как скорость и ускорение точки С известны, то принимаем точку С за полюс.
|
С |
aC |
В |
aC |
Тогда aB = aC +aBCn +aBCτ |
|||
|
aP = aC +aPCn +aPCτ , |
|||||||
|
VC |
|||||||
|
aPCn |
a n |
где |
|||||
|
BC |
|||||||
|
τ |
aBCn = ω2 BC = ω2 R, |
aPCn = ω2 PC = ω2 R, |
|||||
|
aPC |
Р |
aC |
τ |
= ε BC = ε R, |
τ |
||
|
Рис. 36 |
aBC |
aPC = ε BC = ε R. |
Мгновенный центр скоростей колеса находится в точке Р – точке каса-
|
ния колеса с неподвижной плоскостью, поэтому |
||||||||||||||||||
|
VC = ωCP =ω R, откуда ω = |
VC |
, при t = 1c, ω =ω = |
2 |
=5 (1/ c). |
||||||||||||||
|
R |
0,4 |
|||||||||||||||||
|
Угловое ускорение колеса |
||||||||||||||||||
|
ε = |
dω |
= |
1 |
dVC |
= |
aC |
, при t =1 c, ε = |
1,6 |
= 4 (1/ c2 ) |
|||||||||
|
dt |
dt |
0,4 |
||||||||||||||||
|
R |
R |
|||||||||||||||||
|
Тогда |
aC |
aC |
||||||||||||||||
|
aτBC = ε R = |
R = aC , |
aτPC = ε R = |
R = aC . |
|||||||||||||||
|
R |
||||||||||||||||||
|
R |
Ускорение точки Р будет направлено к центру колеса точке С и равно
aP = aBCn =ω2 R = 52 0,4 =10 (м/ c2 ) .
Для определения ускорения в точке В спроектируем векторное равенство aB = aC +aBCn +aBCτ на горизонтальную ось x и вертикальную ось у:
23
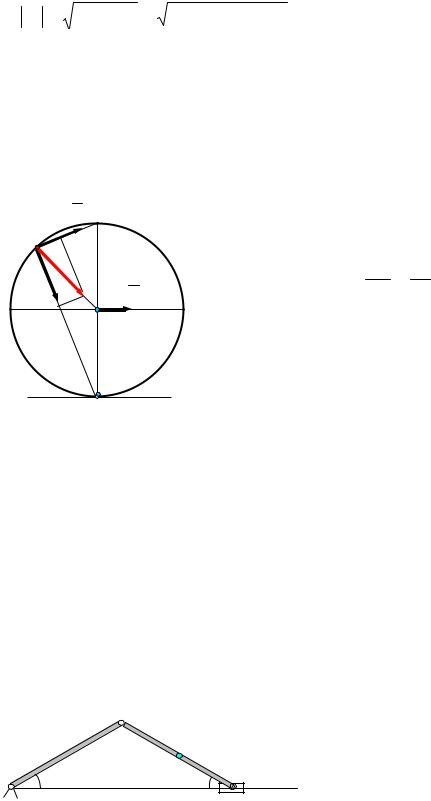
|
aBx |
= aC − aBCn = aC −ω2 R =1,6 −52 0,4 = −8,4 ( м/ с2 ) |
|
aBy |
= −aτDC = −aC = −1,6 ( м/ c2 ) |
|
aB = |
aBx2 + aBy2 = (−8,4)2 +(−1,6)2 ≈ 8,55 ( м/ c). |
Задача 2. Колесо радиуса R = 0,4 м катится без скольжения так, что центр колеса имеет постоянную скорость VC =2 м/c. Определить ускорения точек Р и М обода колеса(рис.37)
Решение. Так как скорость центра колеса является постоянной, то его
ускорение рений.
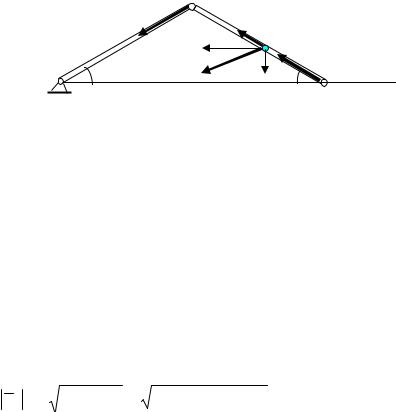
aMτ
M
aMn
aC = 0 , следовательно, точка С будет мгновенным центром уско-
VM
aMC VC

Мгновенный центр скоростей находится в точке Р – точке контакта с неподвижной плоскостью. Значит
ω = CPVC = VRC = const.
Отсюда следует,
|
& |
tgα = |
ε |
= 0, α = 0. |
|
|
чтоε =ω = 0, |
ω |
2 |
||
Следовательно, ускорения всех точек колеса будут направлены к центру колеса и равны
|
aM =ω2 |
2 |
|||
|
Рис.37 |
CM = ω2 R = VC . |
|||
|
R |
Ускорение точки М, находящейся на ободе колеса, являясь полным ускорением криволинейного движения, раскладывается на касательное, направленное по скорости в этой точке, и нормальное ускорение, направленное по перпендикуляру к скорости, т.е. по прямой, соединяющей точку М с мгновенным центром скоростей. (рис.37.).
aM = aMn + aMτ ; aMn = aM cosα, aτM = aM sin α.
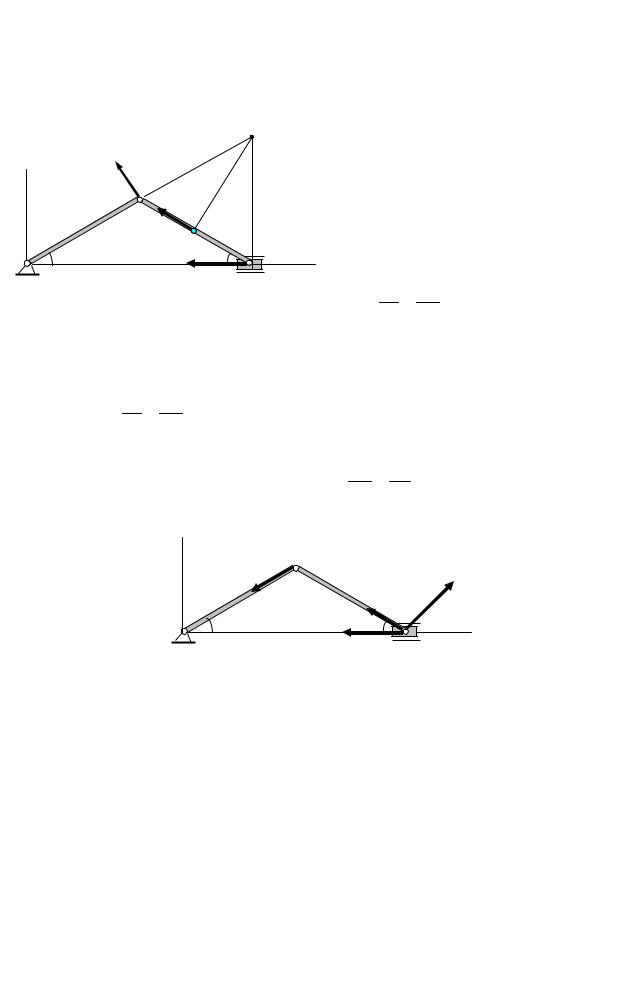
Задача 3. Определить скорости точек А, В, С и ускорения точек А и В кри- вошипно-шатунного механизма (рис.38), если кривошип вращается с посто-
|
y |
янной угловой скоростью ωОА = 2 |
|||||||
|
А |
1/с, ОА = АВ = 0,6 м, МВ = 0,3 м, ϕ |
|||||||
|
C |
=300. |
|||||||
|
О |
ϕ |
ϕ |
В x |
Решение. Скорость точки А |
||||
|
(рис. 39) перпендикулярна криво- |
||||||||
|
Рис.38 |
шипу ОА и равна |
|||||||
|
VA =ωOA OA =1,2 м/c. |
24
|
Звено АВ совершает плоское движение/ Скорость точки В направлена |
|||||||||||
|
горизонтально, что обусловлено направляющими, вдоль которых движется |
|||||||||||
|
ползун В. |
|||||||||||
|
Для определения скоростей точек А и В, принадлежащих шатуну АВ, оп- |
|||||||||||
|
ределим положение мгновенного центра скоростей этого звена. Проведем |
|||||||||||
|
P |
перпендикуляры |
к |
скоростям |
в |
|||||||
|
точках А и В, мгновенный центр |
|||||||||||
|
y |
VA |
скоростей Р находится в точке их |
|||||||||
|
A |
пересечения. |
||||||||||
|
VC |
Скорости точек при плоском |
||||||||||
|
C |
движении пропорциональны рас- |
||||||||||
|
О |
300 |
300 |
x |
стояниями до мгновенного центра |
|||||||
|
В |
скоростей. |
||||||||||
|
VB |
VB = |
AP |
|||||||||
|
Рис.39 |
. В треугольнике АВР: |
||||||||||
|
АР = ВР, следовательно, VB=VA=1,2 м/с. |
VA |
BP |
|||||||||
|
Скорость VC |
точки С направлена перпендикулярно отрезку СР, соеди- |
||||||||||
|
няющему точку С с мгновенным скоростей. Значение скорости VC находим |
|||||||||||
|
из пропорции: VC |
= CP . Из треугольника АСР: |
СР =AP sin 60. |
|||||||||
|
VA |
AP |
||||||||||
|
Следовательно, VC= VA sin 600 = 1,03 м/с. |
|||||||||||
|
Угловая скорость шатуна равна |
ωAB = VA |
= 1,2 |
= 2 |
м/c. |
|||||||
|
AP |
0,6 |
||||||||||
|
y |
А |
||||||||||
|
aAn |
|||||||||||
|
аВАn |
aBAτ |
||||||||||
|
О |
300 |
||||||||||
|
aB |
В |
x |
|||||||||
|
Рис.40 |
|||||||||||
|
Ускорение точки А представляет собой нормальное ускорение аАn , на- |
|||||||||||
|
правленное по кривошипу (рис. 40) |
|||||||||||
|
aAn =ωOA2 |
OA =2,4 м/c. |
||||||||||
|
Ускорение точки В направлено по оси х и определяется векторным равенст- |
|||||||||||
|
вом: |
aB = aAn +aBA = aAn +aBAn +aBAτ , |
||||||||||
|
(а) |
|||||||||||
|
где векторы aBAn |
и aBAτ |
представляют собой составляющие ускорения вра- |
|||||||||
|
щательного движения звена АВ вокруг точки А. Вектор |
aBAn |
направлен по |
|||||||||
|
радиусу вращения ВА , ускорение aBAτ |
– перпендикулярно АВ. |
||||||||||
|
25 |
Нормальное ускорение
aBAn =ωAB2 AB =2,4 м/с.
Таким образом, в уравнении (а) неизвестными являются ускорения aB и aBAτ . Для их определения спроектируем равенство (а) на оси х и у.
|
На ось х: |
−aB |
= −aAn cos 300 |
−aBAn cos 300 |
+ aτBA sin 300 . |
(б) |
|||||||
|
На ось у: |
0 = −aAn sin 300 |
+aBAn |
sin 300 +aτBA cos300 . |
(в) |
||||||||
|
Из уравнения (в) находим aτBA = aAn tg300 −aBAn |
tg300 =0. |
|||||||||||
|
Угловое ускорение шатуна равно нулю. |
||||||||||||
|
Из уравнения (б) получаем aB =2,06 м/с. |
||||||||||||
|
Определим ускорение точки С (рис.41 ). |
||||||||||||
|
aC = aAn +aCA = aAn +aCAn +aCAτ |
(г) |
|||||||||||
|
аАn |
А |
|||||||||||
|
n |
||||||||||||
|
аCx |
аCА |
|||||||||||
|
аn |
||||||||||||
|
О |
300 |
аC |
аCy |
ВА В |
x |
|||||||
|
Рис.41 |
||||||||||||
|
Касательное ускорение |
aCAτ = 0 |
|||||||||||
|
Нормальное ускорение |
aCAn =ω2 AC = 22 0,6 =1,2 (м/ c2 ). |
Находим проекции уравнения (г)на оси Ох и Оу:
|
aCx = −aAn cos300 −aCAn cos300 |
= −1,82 (м/ c2 ). |
|
aC y = −aAn sin 302 +aCAn sin 300 = −2,4 0,5 +1,2 0,5 = −0,6( м/ c2 ). |
|
|
Ускорение точки С равно |
|
|
aC = aCx2 +aCy2 = (1,82)2 +(−0,6)2 |
=1,91 ( м/ c2 ) |
26
Контрольрые вопросы
1.Определение плоскопараллельного движения.
2.Уравнения движения плоской фигуры.
3.Определение скоростей точек плоской фигуры.
4.Теорема Жуковского.
5.Мгновенный центр скоростей. Свойства м.ц.с.
6.Способы нахождения мгновенного центра скоростей.
7.Решение задач с помощью мгновенного центра скоростей.
8.Ускорения точек плоской фигуры.
Библиографический список
1.Бутенин Н.В и др. Курс теоретической механики.
Лань, 2002.- 736 стр.
2.Тарг С.М. Краткий курс теоретической механики. Высшая школа, 2004. – 416 стр.
3.Яблонский А.А., Никифорова В.М. Курс теоретической механики. Интеграл-Пресс, 2004. – 608 стр.
4.Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. Интеграл-Пресс, 2004. – 384 стр.
27
Соседние файлы в папке Термех
- #
- #
- #
- #
- #
- #
- #
- #
Линейная скорость через угловую, теория и онлайн калькуляторы
Линейная скорость через угловую
Определение
Мгновенной (истинной) скоростью ($overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):
[overline{v}={mathop{lim }_{Delta tto 0} frac{Delta overline{r}}{Delta t}=frac{doverline{r}}{dt} }left(1right).]
$Delta overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $Delta t$.
Выражение линейной скорости через угловую скорость
Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.
Так как вектор перемещения $Delta overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $Delta overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.
Скорость прохождения пути ($s$) определяют:
[v={mathop{lim }_{Delta tto 0} frac{Delta s}{Delta t}=frac{ds}{dt}left(2right). }]
Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.
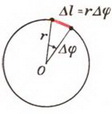
Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($varphi $), который образует радиус-вектор ($overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).
Быстроту изменения угла поворота $varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $omega $. Угловая скорость равна:
[omega =frac{dvarphi }{dt}left(3right).]
Вращение называют равномерным, если угловая скорость постоянна $omega =const$. При равномерном вращении $omega $ можно называть угловой частотой.
Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$ R=const$, то длину дуги найдем как:
[s=Rvarphi left(4right).]
Продифференцируем обе части выражения (4) по времени, имеем:
[frac{ds}{dt}=frac{dleft(Rvarphi right)}{dt}=Rfrac{dvarphi }{dt}left(5right).]
Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:
[v=Romega left(6right).]
Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ – радиус кривизны траектории в месте нахождения частицы.
В векторном виде выражение (6) записывают так:
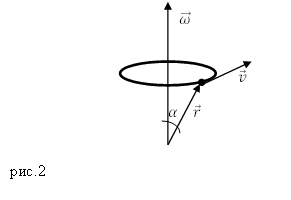
[overline{v}=overline{omega }times overline{r}left(7right),]
$overline{r}$ – вектор, соединяющий ось вращения и движущуюся точку (рис.2). Модуль скорости, используя формулу (7) найдем как:
[v=omega r{sin alpha left(8right), }]
где $alpha $ – угол между вектором угловой скорости и $overline{r}.$
Угловая скорость через линейную
Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:
[omega =frac{v}{R}left(9right).]
Или используя формулу (8) угловую скорость выразим как:
[omega =frac{v}{r{sin alpha }}left(10right).]
Примеры задач с решением
Пример 1
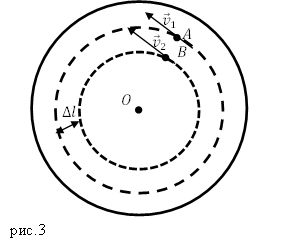
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($omega $)?
Решение. Основой для решения задачи будет формула:
[omega =frac{v}{R}left(1.1right).]
Угловые скорости движения точки A и B одинаковы (${omega }_A={omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):
[{omega }_A=frac{v_1}{R_1};; {omega }_B=frac{v_2}{R_2}left(1.2right).]
$R_1$ – расстояние от точки O до точки A; $R_2=R_1-Delta l$ – расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:
[frac{v_1}{R_1}=frac{v_2}{R_1-Delta l}to R_1=frac{Delta lcdot v_1}{v_1-v_2}left(1.3right).]
Найдем угловую скорость точки A:
[{omega }_A=v_1cdot frac{v_1-v_2}{Delta lcdot v_1}=frac{v_1-v_2}{Delta l}.]
Ответ. Угловая скорость всех точек диска равна $omega =frac{v_1-v_2}{Delta l}$
Пример 2
Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с
законом: $varphi left(tright)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени,
равный $t’=1 (с)$.
Решение. В качестве основы для решения задачи воспользуемся формулой:
[v=Romega left(2.1right).]
Используя уравнение $varphi left(tright)$ и связь угла поворота и угловой скорости найдем $omega $:
[omega =frac{dvarphi }{dt}=frac{d}{dt}left(A+Bt^3right)=3Bt^2(2.2).]
Подставим результат (2.2) в (2.1), имеем:
[v=Rcdot 3Bt^2.]
Вычислим искомую скорость:
[v=1cdot 3cdot 5cdot 1^2=15 left(frac{м}{с}right).]
Ответ. $vleft(t’right)=15frac{м}{с}$
Читать дальше: масса и плотность вещества.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.