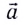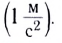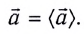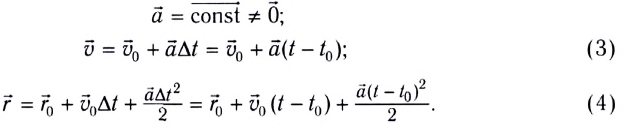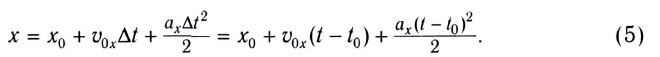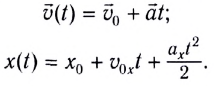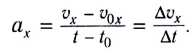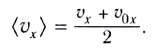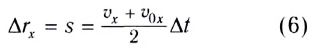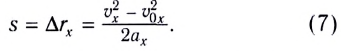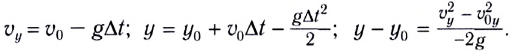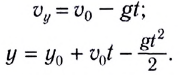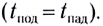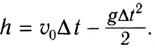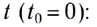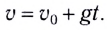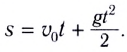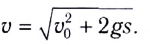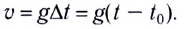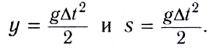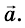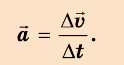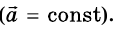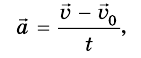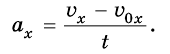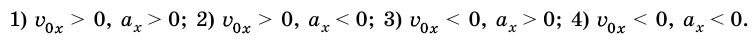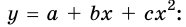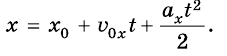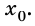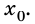Здесь, в этой статье, мы обсудим, как найти конечную скорость с ускорением и расстоянием и как на нее влияют импульс и сила.
Мы рассчитываем конечную скорость объекта, используя различные уравнения, содержащие силу, массу, время, расстояние и импульс. Для каждой переменной мы можем использовать разные уравнения для определения конечной скорости.
Например, чтобы найти конечную скорость, используя импульс объекта, можно использовать уравнение импульса, котороеР = мв где m — масса объекта, P — импульс объекта, а v — скорость объекта.
Это уравнение содержит скорость, импульс и массу, поэтому оно может помочь в вычислении конечной скорости, когда известны масса и импульс. Точно так же, если масса дана без импульса, то мы можем использовать математическую форму второго закона движения Ньютона, то есть F = ma, где m — масса объекта, F — передняя работа над объектом, а a — ускорение объекта. Наконец, для времени и расстояния кинематические уравнения движения являются лучшими инструментами для определения скорости кого-либо или объекта.
График силы, импульса, ускорения и скорости
Как найти конечную скорость через силу, массу и время?
Как я уже упоминал, математическая форма второго закона движения Ньютона для нахождения конечной скорости с использованием силы, массы и времени. Математическая форма второго закона движения F = ма, где m — масса объекта, F — передняя работа над объектом, а — ускорение объекта.
Уравнение содержит непосредственно силу, массу и ускорение.
Как мы знаем, ускорение — это «скорость изменения скорости по отношению ко времени».
Итак, по этой формуле мы можем найти скорость, зная массу, силу и время. Если тело движется с переменной скоростью, что влечет за собой изменение скорости и/или направления, считается, что изменение происходит в этом движении.
Второй закон движения Ньютона, который подразумевает, как сила производит корректировку в движении, касается этого движения. Второй закон движения Ньютона иллюстрирует числовую связь между силой, массой и ускорением и используется для количественной оценки того, что происходит в сценариях, включающих силы и движение. Второй закон чаще всего формулируется численно как F = ма
Как найти конечную скорость через расстояние и время?
Используя первое, второе и третье уравнения движения.
Первое кинематическое уравнение v=u+at представляет собой комбинацию конечной скорости, начальной скорости, ускорения, расстояния и времени. То, какое уравнение следует использовать, будет зависеть от конкретного случая. Иногда можно использовать более одного уравнения.
Чтобы найти конечную скорость, когда известны начальная скорость и расстояние, третье уравнение движения, которое v2=u2+ 2к может быть использован. И если время дано с расстоянием, и нам нужно вычислить конечную скорость, то, во-первых, мы можем узнать начальную скорость, используя второе уравнение движения, которое s=ut+1/2 в2 а затем, используя третье уравнение движения, которое v2 = ты2+ 2к, мы можем рассчитать конечную скорость объекта.
Вычисление начальной и конечной скорости является частью нескольких физических формулировок и уравнений. В моделях для сохранение импульса или законы движения, разрыв между начальной и конечной скоростью говорит вам о скорости предмета до и после, что угодно происходит. Это может быть сила, приложенная к предмету, удар или что-то еще, что изменяет траекторию и скорость объекта.
Соответствующее уравнение движения можно использовать для вычисления конечной скорости объекта, испытывающего постоянное ускорение. Чтобы связать их друг с другом, эти уравнения требуют сочетания расстояния, начальной скорости, конечной скорости, ускорения и времени.
Как найти конечную скорость по импульсу?
Используя уравнение импульс то есть P = mv], где m — масса объекта, P — импульс объекта, а v — скорость объекта.
Это уравнение содержит массу объекта и скорость объекта. Выражение, подобное приведенному выше, можно рассматривать как технику решения вопросов. Можно определить последнюю переменную в формуле, имея целочисленные данные всех переменных, кроме одной, в формулах.
Точно так же выражение можно рассматривать как фразу, объясняющую значимое отношение между двумя переменными. В выражении две переменные можно рассматривать либо как линейно коррелированные, либо как обратно связанные. И масса, и скорость прямо пропорциональны импульсу. При неизменной скорости увеличение массы приведет к увеличению импульса, переносимого предметом.
Соответственно, увеличение скорости (при неизменной массе) приведет к увеличению мамы предмета.энтум. Мы можем предсказать, насколько сильно изменение одной переменной повлияет на другую, рассматривая и вычисляя пропорционально количества. Импульс — это элемент вектора, который имеет величину (математическую величину), а также направление. Вектор импульса обычно движется по той же траектории, что и вектор скорости.
С импульс – это вектор, сложение двух векторов импульса выполняется так же, как сложение любых двух других векторов. Когда два вектора направлены в разные стороны, один из них считается отрицательным, а другой — положительным. В большинстве вопросов этой группы задач для эффективного решения необходимо учитывать векторный характер импульса.
Как найти конечную скорость после столкновения?
Использование выражения для упругих и неупругих столкновений.
Импульс P, то есть P = mv, где m — масса объекта, P — импульс объекта, а v — скорость объекта.
По закону сохранения импульса: «Импульс до столкновение = импульс после столкновение»
Выражение для упругих столкновений
Формула для расчета конечной скорости данного объекта
v1f=m1-m2/m1+m2 (v1) +2m1-m2/m1+m2 (v2i)
Формула для расчета конечной скорости сталкивающегося объекта
v2f=m2-m1/m1+m2 (v1) +2m1-m2/m1+m2 (vi)
Выражение для неупругого столкновения
m1v1+m2v2=m1v1f+m2v2f
где m1 – масса объекта до столкновения, v1 – скорость данного объекта до столкновения, m2 – масса сталкивающегося объекта до столкновения, v2 – скорость сталкивающегося объекта до столкновения, а v1f – конечная скорость данного объекта, а v2f – конечная скорость сталкивающегося объекта.
Эластичный или неэластичный столкновения возможны. Оба импульс и кинетическая энергия сохраняются при упругих столкновениях, а кинетическая энергия не сохраняется при неупругих столкновениях. Неупругие столкновения происходят, когда кинетическая энергия не сохраняется, например, при столкновении транспортных средств. Сохранение импульс относится к неупругим столкновениям.
В результате импульс до удара равен импульсу после контакта. Слово «импульс» соответствует количеству переменных, содержащихся в движущемся предмете. Произведение массы на скорость — вот как это называется. а его единицы – кгм/с.
Можно эффективно определить скорость транспортного средства после столкновения, используя приведенную ниже формулу, если мы знаем начальную массу и скорость транспортного средства и сталкивающегося объекта.
Когда частицы сталкиваются в неупругое столкновение, они не действуют как упругие во время столкновения. Это указывает на то, что частицы не деформируются упруго в месте столкновения; вместо этого они могут необратимо деформироваться, что приводит к рассеиванию энергии во время столкновения. Это отличается от упругого столкновения, при котором частицы упруго изгибаются в месте удара, ведя себя как безупречно упругие пружины, поглощая и высвобождая равное количество энергии.
Как найти конечную скорость без учета времени?
С помощью третьего уравнения движения.
Третье уравнение движения не содержит времени, поэтому оно не зависит от времени.
Третье уравнение движения, которое есть v2=u2+2asis комбинация начальной скорости, конечной скорости, ускорения и расстояния. Таким образом, мы можем легко вычислить конечную скорость, когда известны другие переменные. И ему не нужно время, чтобы быть Познанным.
Если положение объекта меняется относительно стандартного местоположения, считается, что он находится в движении относительно этой стандартной точки, а если нет, то считается, что он находится в неподвижном состоянии относительно этой точки. Мы создаем несколько классических формул, относящихся к определениям расстояния, смещения, скорости, скорости и ускорения объекта, с помощью формул, называемых уравнениями движения для хорошего понимания или взаимодействия с различными условиями покоя и движения.
Как найти конечную скорость без ускорения?
Как мы обсуждали ранее, приведенная ниже формула содержит начальную скорость объекта и сталкивающегося объекта до столкновения, а также массу объекта и сталкивающегося объекта до столкновения и конечную скорость. Итак, отсюда легко вычислить конечную энергию объекта, не зная его ускорения.
Учитывая м1 – масса объекта до столкновения, v1 – скорость данного объекта до столкновения, м2 – масса сталкивающегося объекта до столкновения, v2 – скорость сталкивающегося объекта до столкновения, а v1f – конечная скорость данного объекта и v2f – конечная скорость сталкивающегося объекта.
Для упругого столкновения;
v1f=m1-m2/m1+m2 (v1) +2m1-m2/m1+m2 (v2i)
v2f=m2-m1/m1+m2 (v1) +2m1-m2/m1+m2 (v1i)
Для неупругого столкновения;
m1v1+m2v2=m1v1f+m2v2f
Если у нас есть исходная масса и скорость предоставленного объекта и сталкивающегося предмета, мы можем использовать приведенную ниже формулу для вычисления скорости предмета после столкновения.
Как найти конечную скорость без начальной скорости?
Если начальная скорость объекта не указана, то можно считать, что изначально объект находился в состоянии покоя.
Таким образом, мы можем рассчитать конечную скорость по различным формулам, таким как кинематические уравнения, приравняв начальную скорость к нулю. Также мы можем найти скорость объекта по числовой форме второго закона движения, если известна масса объекта. Другой способ найти скорость — использовать формулу импульса, если известны масса и импульс объекта.
Примеры
Пример 1
Допустим, автомобиль массой 100 кг движется со скоростью 80 м/с. Другой автомобиль массой 120 кг движется со скоростью 100 м/с. Они сталкиваются друг с другом. Конечная скорость первого автомобиля после столкновения равна 100 м/с. Какой будет конечная скорость второго автомобиля после столкновения?
Столкнулись две машины
Решения
В этом случае масса m1 то есть масса первого автомобиля до столкновения, скорость v1 первого автомобиля перед столкновением, масса m2 второго автомобиля до столкновения, скорость v2 второго автомобиля перед столкновением и конечной скоростью v1f первого автомобиля после столкновения известны.
Данный;
m1= 100 кг
v1= 80 м/см2= 120 кг
v2= 100 м / с
v1f = 100 м / с
Используя формулу упругого столкновения, мы можем вычислить конечную скорость второго автомобиля после столкновения.
v2f=m2-m1/m1+m2 (vf)+m1-m2/m1+m2 (vi)
v2f=(120- 100/120+ 100)100+(120(100+20))80
v2f= (0.090) 100 + 43.6363
v2f= 52.64 м / с
Таким образом, конечная скорость второго автомобиля после столкновения равна v.2f= 52.64 м / с.
Пример 2
Автомобиль начал двигаться с начальной скоростью 30 м/с и преодолел расстояние 5 км. Автомобиль достигает ускорения a=10 м/с.2. Какой должна быть конечная скорость автомобиля и сколько времени это займет?
В этом примере известна начальная скорость автомобиля, ускорение автомобиля и перемещение автомобиля, а конечная скорость автомобиля и время, затраченное автомобилем, задаются.
Для нахождения конечной скорости мы будем использовать третье уравнение движения, которое представляет собой комбинацию начальной скорости, конечной скорости, смещения и ускорения.
Данный;
Начальная скорость, u = 30 м / с
Ускорение, а=10м/с2
Водоизмещение, с=5000м
Для нахождения конечной скорости мы будем использовать третье уравнение движения, то есть;
v2 = u2 + 2as
где v — конечная скорость объекта, u — начальная скорость объекта, а — ускорение объекта при смещении объекта.
Ввод заданных значений в приведенную выше формулу
v2= 30 м / с2+2(10м2s2)(5000м)
v2= 900 m2s2+(20м/s2)(5000м)
v2= 900 m2s2+100000m2/s2
v2= 100900 m2/s2
v = 317.645 м / с
Значит, конечная скорость автомобиля будет равна 317.645 м/с.
Теперь, чтобы найти время, необходимое для покрытия заданного перемещения, мы будем использовать первое уравнение движения, которое имеет вид v=u+at.
Подставляя заданные значения в это уравнение, мы получим
317.645 м/с=30 м/с+ 10 м/с2t
317.645 м/с-30 м/с= 10м/с2t
287.645 м/с = 10м/с2t
t=287.645 м/с / 10 м/с}
t = 28.7 с
Таким образом, время, которое потребуется машине, чтобы добраться до конечной точки, составляет 28.7 секунды.
Часто задаваемые вопросы | Часто задаваемые вопросы
В. С точки зрения физики, что такое импульс?
Импульс — это двумерная величина, которая включает в себя как величину, так и направление. Поскольку у импульса есть направление, его можно использовать для прогнозирования направления и скорости движения сталкивающихся тел.
В. Какую роль играет импульс в движении?
Когда два тела сталкиваются друг с другом, тело, имеющее большую скорость, что приводит к большему импульсу, передает большую мощность телу, имеющему меньшую скорость или движущемуся медленнее.
Тело с малой стартовой скоростью должно сместиться с большей скоростью и импульсом по сравнению с телом с большей скоростью при старте после столкновения.
В. Каковы подходы к сохранению импульса?
Переменная, называемая импульсом, которая определяет движение в замкнутом наборе компонентов и никогда не меняется в соответствии с принципом сохранения импульса; то есть «общий импульс системы остается постоянным».
Импульс эквивалентен импульсу, необходимому для остановки предмета за заданный промежуток времени, когда его масса умножается на его скорость. Общий импульс набора сущностей равен сумме их различных импульсов.
Однако, поскольку импульс — это вектор, который включает в себя как направление, так и амплитуда движения, импульсы объектов, движущихся в противоположных направлениях, могут компенсироваться, давая общую сумму нулю.
Как найти мгновенную скорость в конце пути, если известны только V среднее и Vo?
В задаче не указано очень важное условие: как изменялась скорость? Попробуем решить задачу, полагая, что это было равноускоренное движение.
$S=v_ct$ (1)
$S=frac{v^2-v_0^2}{2a}$ (2)
$a=frac{v-v_0}{t}$ (3)
Подставим из (3) значение ускорения а в (2) и затем приравняем правые части (1) и (2):
$frac{v^2-v_0^2}{frac{2(v-v_0)}{2}}=v_ct$ (4)
Разность квадратов в числителе левой части (4) можно представить как произведение разности членов на их сумму. Тогда (4) принимает вид:
$frac{(v-v_0)(v+v_0)}{2(v-v_0)}=v_ct$ (5)
После сокращения получаем
$v+v_0=2v_c$ (6)
Откуда находим
$v=2v_c-v_0$
Второй закон Ньютона тут на фиг не нужен, потому что все тела, независимо от их массы, на высоте трёх метров нгаз землёй движутся с одним и тем же ускорением – g. Равным 9,81 м/с². То есть это задачка чисто кинематическая, а не на динамику.
Ну и учитывая уровень самой задачки, можно не заморачиваться “разложением скорости на составляющие”. Ясен пень, что направлена она по вертикали, причём совершенно по фигу, вверх или вниз, потому что даже если вверх, то потом при движении вниз ЭТУ точку тело пройдёт С ТОЙ ЖЕ скоростью. Поэтому ответ АлексаМ12, в котором приращение скорости рассматривается с точки зрения баланса энергий, по направлению мысли верный, но арифметически – с грубой ошибкой, потому что складвать скорости надо квадратично, а не “+ начальные 3 метра”.
Итак, будем считать, что скорость направлена вниз (раз по фигу куда). Тогда из закона сохранения энергии имеем gH+v_о²/2 = v_к²/2 (v_о – начальная скорость, v_к – конечная), откуда v_к = корень из (2gH+v_о²). И вся любовь.
Числа подставьте сами.
Разумеется, можно это решить и без привлечения закона сохранения энергии, а через квадратное уравнение S = gt²/2+v_ot, или же збавиться от времени, вспомнив, что v_о+gt = v_к, a S = 1/2 (v_о+v_к)t.
Содержание:
Прямолинейное равноускоренное движение:
Движение с изменяющейся скоростью называют неравномерным. Простейшим видом неравномерного движения является прямолинейное движение с постоянным ускорением, т. е. прямолинейное равноускоренное движение. Впервые такое движение выделил и исследовал Галилей.
Равноускоренным называется движение, при котором скорость тела (МТ) за любые равные промежутки времени изменяется одинаково.
Ускорением
В СИ основной единицей ускорения является метр в секунду за секунду
При прямолинейном равноускоренном движении ускорение 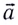
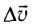
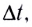
где 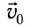
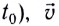
При таком движении ускорение 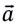
Кинематические уравнения равноускоренного движения имеют вид:
При прямолинейном равноускоренном движении тела (МТ) вдоль оси Ох зависимость координаты от времени выражается уравнением
Если 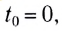
Поскольку ускорение при прямолинейном равноускоренном движении постоянно 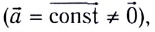
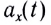
В случае, когда проекция ускорения положительна 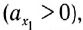
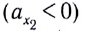
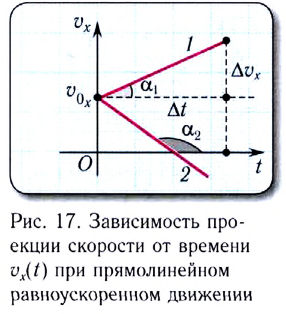
График зависимости проекции скорости от времени 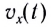
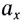
Если проекция скорости на выбранную ось Ох положительна 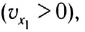
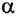
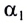
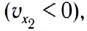
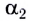
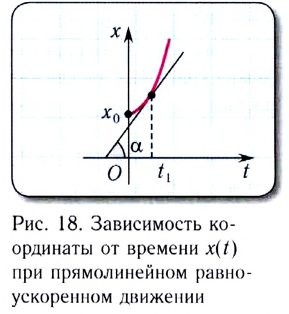
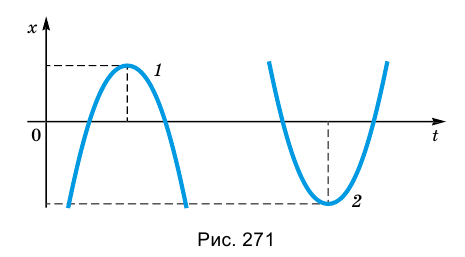
График зависимости координаты от времени x(t) при прямолинейном равноускоренном движении представляет собой ветвь параболы (рис. 18). Проекция скорости 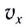
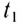
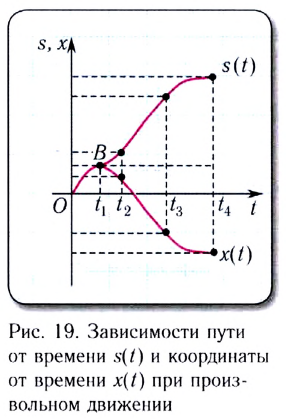
Подчеркнем, что в процессе движения путь, пройденный материальной точкой, все время увеличивается, в то время как проекция перемещения (координата) может уменьшаться. Вследствие этого график зависимости пути от времени s(t) будет совпадать с графиком зависимости координаты от времени х(t) (рис. 19) на тех участках, где координата увеличивается (см. участок от начала координат до точки В на рисунке).
Соответственно, на тех участках, где координата уменьшается, график зависимости пути от времени является «зеркальным» отражением кривой х(t) от горизонтальной плоскости, проходящей через точку, с которой началось уменьшение координаты (см. точку В на рисунке).
Так как зависимость проекции скорости прямолинейного движения тела вдоль оси Ох от времени 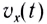
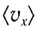
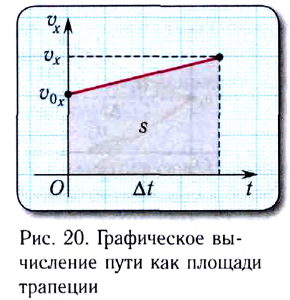
Соответственно, в этом случае проекция перемещения на ось Ох (путь)
численно равна площади закрашенной трапеции (рис. 20).
Исключая время t из уравнений прямолинейного равноускоренного движения для скорости v(t) и координаты x(t), можно получить еще одну часто используемую формулу
Прибор для измерения ускорения называется акселерометром.
Примером равноускоренного прямолинейного движения является свободное падение тел, при котором на тело действует только сила тяжести, и оно движется с ускорением 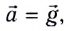
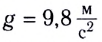
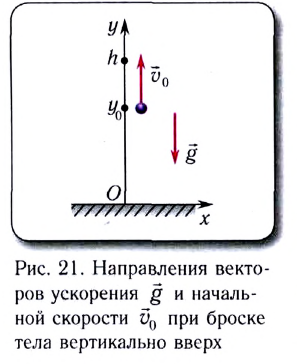
Если ось Оу направлена вертикально вверх, а ось Ох — вдоль поверхности Земли (рис. 21), то движение тела (МТ), брошенного вертикально вверх со скоростью 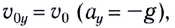
В случае, когда 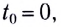
Время подъема тела (МТ) на максимальную высоту, на которой 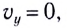
Скорость в момент возвращения тела (МТ) в исходную точку О определяется по формуле 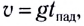
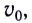
Докажите самостоятельно, что без учета сопротивления воздуха время подъема тела (МТ) равно времени его падения.
Высоту подъема h тела (МТ) (см. рис. 21) за промежуток времени 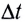
Максимальная высота подъема тела (МТ) определяется по формуле
Модуль скорости на высоте h (см. рис. 21) можно найти ио формуле
При движении тела (МТ) из начальной точки 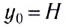
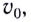
Пройденный телом (МТ) путь s определяется по формуле
Скорость в конце пути s:
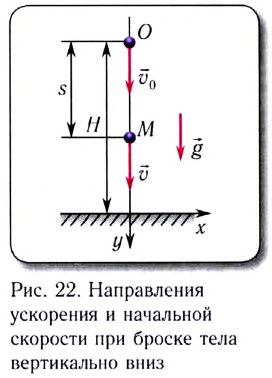
Падение тел с высоты Н без начальной скорости 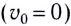
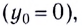
При 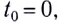
Координата у и пройденный путь s определяются соответственно по формулам:
Продолжительность свободного падения с высоты Н:
Скорость тела при свободном падении с высоты Н:
Равноускоренное движение
Прямолинейное равномерное движение, то есть движение с постоянной скоростью, -редкое явление в окружающей среде. Значительно чаще придется иметь дело с такими движениями, в которых скорость не является постоянной, а со временем изменяется. Такие движения называют неравномерными.
На всех современных транспортных средствах устанавливают специальные приборы -спидометры (рис. 266), показывающие значение скорости в данный момент времени.
Понятно, что по спидометру нельзя определить направление скорости. Для некоторых средств транспорта, например для морских кораблей и самолетов, необходимо знать также направление скорости движения. Тогда, кроме спидометра, устанавливают еще и другие навигационные приборы, в самом простом случае – компас.
Следовательно, теперь мы знаем, что при неравномерном движении скорость движения тела не является постоянной величиной и в разные моменты времени имеет свое направление и значение.
Для упрощения будем рассматривать такое неравномерное движение, при котором скорость движения тела за каждую единицу времени и вообще за любые равные интервалы времени изменяется одинаково. Такое движение называют равноускоренным.
Движение тела, при котором его скорость за любые равные интервалы времени изменяется одинаково, называют равноускоренным движением.
Во время такого движения скорость может изменяться.
Если за некоторый интервал времени 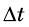
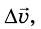
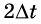
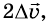
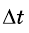
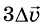
При этом если значение 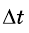
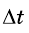
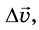
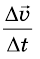
приращению времени будет таким же, как и раньше. Следовательно, в
данном равноускоренном прямолинейном движении отношение 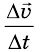
Вектор 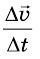
Ускорением тела в его равноускоренном прямолинейном движении называют векторную физическую величину, характеризующую изменение скорости за единицу времени и равную отношению изменения скорости движения тела к интервалу времени, за которое это изменение произошло:
Из определения равноускоренного движения следует, что его ускорение является постоянной величиной
Если в выбранный начальный момент времени t = 0 скорость движения тела равна 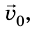
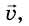
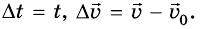
где 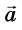
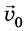
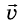
Как видно из этой формулы, за единицу ускорения следует взять ускорение такого прямолинейного равноускоренного движения, при котором за единицу времени скорость изменяется также на единицу. И это означает: ускорение равно единице, если за 1 с скорость движения тела изменяется на 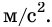
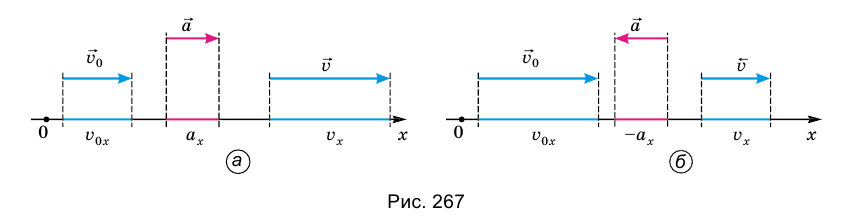
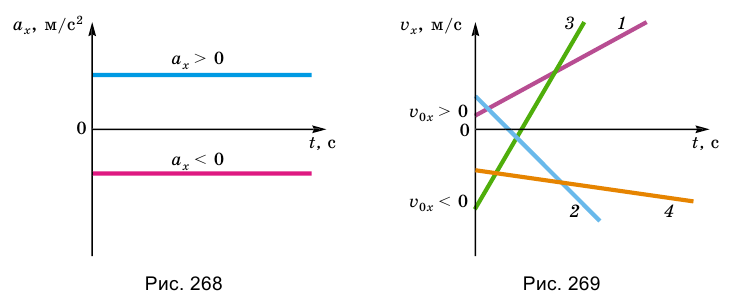
Равноускоренное движение может быть ускоренным или замедленным. Рассмотрим ускорение и скорость равноускоренного движения в проекциях на ось Ох (рис. 267), тогда ускорение будет приобретать вид:
Если 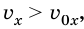
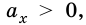
Если 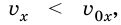
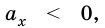
Вам уже известно, как графически изображается равномерное прямолинейное движение тела. Попробуем аналогично представить графически равноускоренное прямолинейное движение.
- Заказать решение задач по физике
Графики равномерного прямолинейного движения тела
Рассмотрим график проекции ускорения движения тела 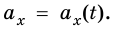
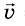
График проекции скорости движения тела 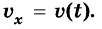
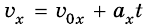
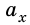
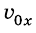
Если 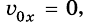
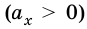
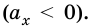
График движения тела х = x(t). Кинематические уравнения движения являются квадратичной функцией вида
Поэтому графиком зависимости координаты тела от времени является парабола, ветви которой согласно параметрам движения имеют разное направление. Например, если 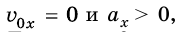
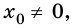
Если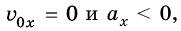
Если 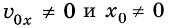
- Сложение скоростей
- Ускорение в физике
- Скорость при равнопеременном движении
- Перемещение, координата и путь при равнопеременном движении
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
Как найти модуль скорости
Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько быстро тело передвигается в пространстве. Перемещение предполагает изменение координат.

Инструкция
Введите систему координат, относительно которой вы будете определять направление и модуль скорости. Если в задаче уже задана формула зависимости скорости от времени, вводить систему координат не нужно – предполагается, что она уже есть.
По имеющейся функции зависимости скорости от времени можно найти значение скорости в любой момент времени t. Пусть, например, v=2t²+5t-3. Если требуется найти модуль скорости в момент времени t=1, просто подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
Когда задача требует найти скорость в начальный момент времени, подставьте в функцию t=0. Таким же образом можно найти время, подставив известную скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t²+5t-3=0. Отсюда t=[-5±√(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а поскольку время не может быть отрицательным, остается только t=1/2.
Иногда в задачах уравнение скорости дается в завуалированной форме. Например, в условии сказано, что тело двигалось равноускоренно с отрицательным ускорением -2 м/с², а в начальный момент скорость тела составляла 10 м/с. Отрицательное ускорение означает, что тело равномерно замедлялось. Из этих условий можно составить уравнение для скорости: v=10-2t. С каждой секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, поэтому легко найти общее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд после начала движения тело остановится.
Помимо прямолинейного движения тела, существует еще и движение тела по окружности. В общем случае оно является криволинейным. Здесь возникает центростремительное ускорение, которое связано с линейной скоростью формулой a(c)=v²/R, где R – радиус. Удобно рассматривать также угловую скорость ω, причем v=ωR.
Источники:
- как находить зависимость пути от времени
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.