В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.
Ситуация 1
Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить.
Задача
Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 + 70 = 160 (км/ч) – скорость удаления.
2) 160 × 4 = 640 (км)
Ответ: 640 км будет расстояние между автомобилями через 4 часа.
Ситуация 2
Представь, что вы с мамой идете навстречу друг другу.
В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.
Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить.
Задача
Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся?
1) 90 + 70 = 160 (км/ч) – скорость сближения
2) 640 : 160 = 4 (ч)
Ответ: автомобили встретятся через 4 часа.
Ситуация 3
Представь, что ты идешь по улице и видишь, что впереди идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость сближения.
Задача
Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?
1) 90 – 70 = 20 (км/ч) – скорость сближения
2) 120 : 20 = 6 ( ч)
Ответ: второй автомобиль догонит первый через 6 часов.
Ситуация 4
Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую.
Задача
Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 – 70 = 20 (км/ч) – скорость удаления
2) 20 × 4 = 80 (км)
Ответ: 80 км будет расстояние между автомобилями через 4 часа.
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Скорость время расстояние
Онлайн калькулятор поможет Вам рассчитать время пути из пункта А в пункт Б и среднюю скорость движения.
Смотрите также
в описании к калькулятору добавьте, что из-за особенностей Javascript он не принимает «,» даже не представляю сколько людей погорело у вас тут.
Спасибо.
Поддержку «,» добавили.
Два пешехода вышли навстречу друг другу. Скорость первого составляет 3 м/мин, а второго — 4 м/мин. Через
сколько минут они встретятся, если расстояние между ними 1680 метров?
Медвежат отвезли за 600 км от населенного пункта. Через 18 дней (432часа) они вернулись в посёлок. Вопрос: Это реально? И с какой скоростью они могли передвигаться в сутки?
За какое время пройдёт машина расстояние 10 метров со скоростью 170км/ч
задача.1 трактор ехал со скоростью 36 км.в час .2 трактор _32 км в час между ними .растояние 136км.нужно найти время когда встретятся.
От города A до города B расстояние 40 км. Два велосипедиста выехали из A и B навстречу друг другу, один со скоростью 10 км/ч, а другой — 15 км/ч. Муха вылетела с первым из A со скоростью 100 км/ч, долетела до второго, села ему на лоб и полетела обратно к первому, села ему на лоб, вернулась ко второму и так далее, пока они не столкнулись лбами и не раздавили ими муху. Сколько километров пролетела муха?
машина едет со скоростью 85 км в час ,за сколько минут проедет машина 78 км
Если пешеход вышел в деревню со скоростью 4.8 км/ч,возвращался со скоростью 6 км/ч и вернулся на час раньше. Какое расстояние от села до деревни?
Задачи на движение в одном направлении
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.

1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
Формула нахождения значений скорости, времени и расстояния
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+. +vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+. +Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
§ 1 Скорость сближения и скорость удаления
В этом уроке познакомимся с такими понятиями, как «скорость сближения» и «скорость удаления».
Для ознакомления с понятиями «скорость сближения» и «скорость удаления» рассмотрим 4 реальные ситуации.
Из двух городов навстречу друг другу одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается ли расстояние между автомобилями? Если да, то с какой скоростью?
Изобразим движение данных автомобилей на координатном луче.
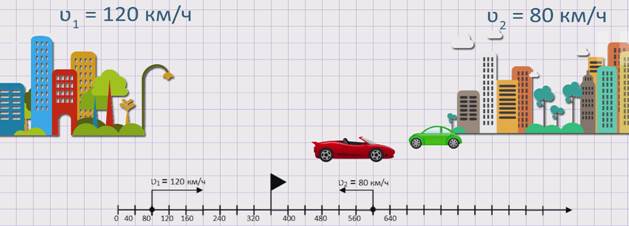
Из рисунка видно, что два автомобиля, двигаясь навстречу друг другу, приближаются. Значит, расстояние между ними сокращается. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо к скорости первого автомобиля прибавить скорость второго. А именно, скорость сближения равна сумме скоростей первого и второго автомобилей: ʋсбл. = ʋ1 +ʋ2.
Найдем скорость сближения данных автомобилей:
![]()
Значит, расстояние между автомобилями сокращается со скоростью 200 км/ч. Рассмотрим вторую ситуацию.
Из двух городов одновременно в одном направлении, вдогонку, выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается или увеличивается расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
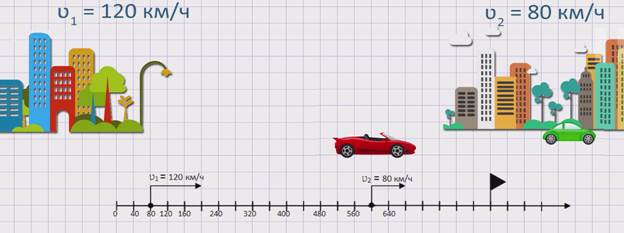
Из рисунка видно, что первый автомобиль движется быстрее второго автомобиля или же движется вдогонку второму автомобилю. Значит, расстояние между автомобилями будет сокращаться. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость сближения равна разности скоростей двух автомобилей: ʋсбл. = ʋ1 – ʋ2 .
Найдем скорость сближения данных автомобилей: ʋсбл. = ʋ1 – ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями сокращается со скоростью 40 км/ч.
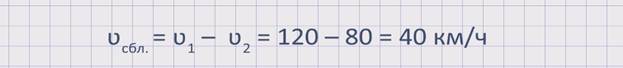
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Рассмотрим следующую третью ситуацию.
Из двух городов в противоположных направлениях одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Будет ли увеличиваться расстояние между автомобилями? Если да, то на сколько?
Изобразим движение данных автомобилей на координатном луче.
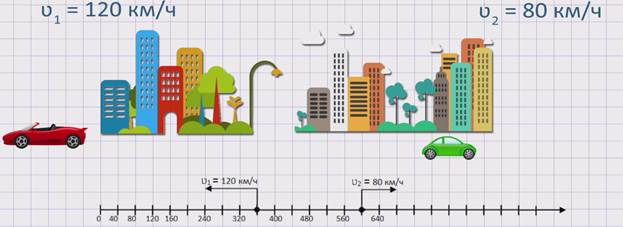
Из рисунка видно, что два автомобиля, двигаясь в противоположных направлениях, удаляются друг от друга. Значит, расстояние между ними увеличивается. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо к скорости первого автомобиля прибавить скорость второго автомобиля. А именно, скорость удаления равна сумме скоростей двух автомобилей: ʋуд. = ʋ1 + ʋ2 .
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 + ʋ2 = 120 + 80 = 200 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 200 км/ч.
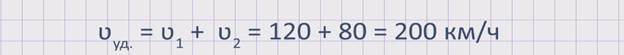
Рассмотрим последнюю четвертую ситуацию.
Из двух городов водном направление одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Причем второй автомобиль движется с отставанием. Будет увеличиваться или уменьшаться расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
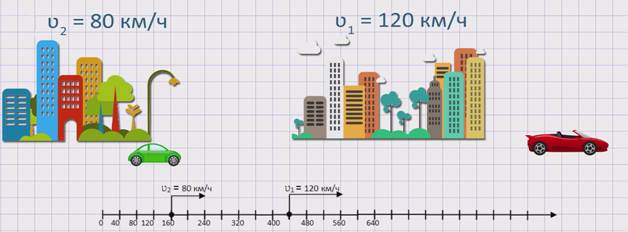
Из рисунка видно, что второй автомобиль движется медленнее первого автомобиля или же движется с отставанием от первого автомобиля. Значит, расстояние между автомобилями будет увеличиваться. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость удаления равна разности скоростей двух автомобилей: ʋуд. = ʋ1 – ʋ2 .
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 – ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 40 км/ч.
![]()
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость удаления». Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
§ 2 Краткие итоги по теме урока
1.Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
2.При движении двух объектов навстречу друг другу скорость сближения равна сумме скоростей этих объектов. ʋсбл. = ʋ1 + ʋ2
3.При движении вдогонку скорость сближения равна разности скоростей объектов движения. ʋсбл. = ʋ1 – ʋ2
4.Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
5.При движении двух объектов в противоположных направлениях скорость удаления равна сумме скоростей этих объектов. ʋуд. = ʋ1 + ʋ2
6.При движении с отставанием скорость удаления равна разности скоростей объектов движения. ʋуд. = ʋ1 – ʋ2

После долгой прогулки по парку Юра и Яра выехали в противоположных направлениях на автомобилях. Скорость автомобиля Юры — (75) км/ч, а скорость автомобиля, на котором едет Яра — (58) км/ч. Как и с какой скоростью изменится расстояние между ними?
Рассмотрим схему движения Юры и Яры.

Юра и Яра удаляются друг от друга, значит, расстояние между ними увеличивается.
Чтобы найти, с какой скоростью они удаляются друг от друга, рассмотрим правило вычисления скорости удаления.

Получается, что скорость удаления автомобилей Юры и Яры: (75 + 58 = 133) км/ч.
Рассмотрим ещё один пример.
Юра и Яра ехали на автомобилях в одном направлении, но с разной скоростью. Юра ехал первым со скоростью (69) км/ч, а Яра ехала следом со скоростью (46) км/ч. Уменьшится или увеличится расстояние между ними и с какой скоростью?
Рассмотрим схему движения Юры и Яры.

Скорость автомобиля Юры больше, чем автомобиля, на котором едет Яра, значит, расстояние между ними увеличивается. Перед нами движение с отставанием.
Чтобы найти, с какой скоростью удаляются друг от друга Юра и Яра, рассмотрим правило вычисления скорости удаления во время движения с отставанием.

Получается, что скорость удаления автомобилей Юры и Яры: (69) (– 46 = 23) км/ч.
Расстояние, на которое объекты удаляются друг от друга за единицу времени, называется скоростью удаления.
Сделаем вывод:
при движении в противоположных направлениях скорость удаления равна сумме скоростей:
vуд.=v1+v2
.
При движении с отставанием скорость удаления равна разности скоростей:
vуд.=v1
−v2
.
Для решения задач на движение стоит прояснить объекты сближаются или удаляются, ответ зависит от вида движения. Когда объекты двигаются навстречу друг другу из разных пунтков, то они сближаются:
(v_1+v_2=20+30=50) км/час скорость сближения
Когда объекты двигаются в противоположных направлениях из одного пункта, то они удаляются:
(v_1+v_2=20+30=50) км/час скорость удаления
Когда объекты двигаются в одном направление одновременно:
- Если они выезжают одновременно, то два объекта удаляются друг от друга, так как скорость у них разная, для того чтобы найти скорость их удаления надо из большей скорости вычесть меньшую.
(v_y=v_2-v_1)
- Если они выезжают с интервалом, то два объекта могут удаляться или сближаться в зависимости от их скоростей:
1) если скорость объекта, который впереди больше, то они удаляются. (v_2>v_1)
2) если скорость объекта, который впереди меньше, то они сближаются . (v_1>v_2)
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
