В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.
Ситуация 1
Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить.
Задача
Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 + 70 = 160 (км/ч) – скорость удаления.
2) 160 × 4 = 640 (км)
Ответ: 640 км будет расстояние между автомобилями через 4 часа.
Ситуация 2
Представь, что вы с мамой идете навстречу друг другу.
В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.
Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить.
Задача
Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся?
1) 90 + 70 = 160 (км/ч) – скорость сближения
2) 640 : 160 = 4 (ч)
Ответ: автомобили встретятся через 4 часа.
Ситуация 3
Представь, что ты идешь по улице и видишь, что впереди идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость сближения.
Задача
Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?
1) 90 – 70 = 20 (км/ч) – скорость сближения
2) 120 : 20 = 6 ( ч)
Ответ: второй автомобиль догонит первый через 6 часов.
Ситуация 4
Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую.
Задача
Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 – 70 = 20 (км/ч) – скорость удаления
2) 20 × 4 = 80 (км)
Ответ: 80 км будет расстояние между автомобилями через 4 часа.
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Памятка «Учимся решать задач на движение»
В задачах на движение рассматриваются три взаимосвязанные величины:
S – расстояние (пройденный путь),
t – время движения и
V – скорость – расстояние, пройденное за единицу времени.
Расстояние – это произведение скорости на время движения
S = V ● t
Скорость – это частное от деления расстояния на время движения
V = S : t
Время – это частное от деления расстояния на скорость движения
t = S : V
Задачи на встречное движение
Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V
Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?
Схема к задаче:

Решение:
S = V ● t
V сближ. = 1V + 2V
1 способ:
1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи
2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи
3) 36 + 42 = 78 (км)
2 способ:
1) 12 + 14 = 26 (км/ч) – скорость сближения
2) 26 • 3 = 78 (км)
Ответ: расстояние между посёлками 78 км.
Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?
Схема к задаче:

Решение:
V сближ. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость сближения
2) 280 : 140 = 2 (ч)
Ответ: машины встретятся через 2 часа.
Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?
Схема к задаче:

Решение:
V = S : t
2V = V сближ. – 1V
1) 340 : 2 = 170 (км/ч) – скорость сближения
2) 170 – 80 = 90 (км/ч)
Ответ: 90 км/ч. скорость второй машины
Задачи на движение в противоположных направлениях
Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях.
V удал. = 1V + 2V
Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?
Схема к задаче:

Решение:
S = V ● t
1 способ
1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч
2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч
3)36 + 42 = 78 (км)
2 способ
V удал. = 1V + 2V
S = V ● t
1)12 + 14 = 26 (км/ч) – скорость удаления
2)26 • 3 = 78 (км)
Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.
Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?
Схема к задаче:

Решение:
V удал. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость удаления
2) 280 : 140 = 2 (ч)
Ответ: через 2 часа расстояние между машинами будет 280 км
Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?
Схема к задаче:

Решение:
V = S : t
2V = V удал. – 1V
1) 340 : 2 = 170 (км/ч) – скорость удаления машин
2) 170 – 80 = 90 (км/ч)
Ответ: скорость второй машины 90 км/ч.

После долгой прогулки по парку Юра и Яра выехали в противоположных направлениях на автомобилях. Скорость автомобиля Юры — (75) км/ч, а скорость автомобиля, на котором едет Яра — (58) км/ч. Как и с какой скоростью изменится расстояние между ними?
Рассмотрим схему движения Юры и Яры.

Юра и Яра удаляются друг от друга, значит, расстояние между ними увеличивается.
Чтобы найти, с какой скоростью они удаляются друг от друга, рассмотрим правило вычисления скорости удаления.

Получается, что скорость удаления автомобилей Юры и Яры: (75 + 58 = 133) км/ч.
Рассмотрим ещё один пример.
Юра и Яра ехали на автомобилях в одном направлении, но с разной скоростью. Юра ехал первым со скоростью (69) км/ч, а Яра ехала следом со скоростью (46) км/ч. Уменьшится или увеличится расстояние между ними и с какой скоростью?
Рассмотрим схему движения Юры и Яры.

Скорость автомобиля Юры больше, чем автомобиля, на котором едет Яра, значит, расстояние между ними увеличивается. Перед нами движение с отставанием.
Чтобы найти, с какой скоростью удаляются друг от друга Юра и Яра, рассмотрим правило вычисления скорости удаления во время движения с отставанием.

Получается, что скорость удаления автомобилей Юры и Яры: (69) (– 46 = 23) км/ч.
Расстояние, на которое объекты удаляются друг от друга за единицу времени, называется скоростью удаления.
Сделаем вывод:
при движении в противоположных направлениях скорость удаления равна сумме скоростей:
vуд.=v1+v2
.
При движении с отставанием скорость удаления равна разности скоростей:
vуд.=v1
−v2
.
§ 1 Скорость сближения и скорость удаления
В этом уроке познакомимся с такими понятиями, как «скорость сближения» и «скорость удаления».
Для ознакомления с понятиями «скорость сближения» и «скорость удаления» рассмотрим 4 реальные ситуации.
Из двух городов навстречу друг другу одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается ли расстояние между автомобилями? Если да, то с какой скоростью?
Изобразим движение данных автомобилей на координатном луче.
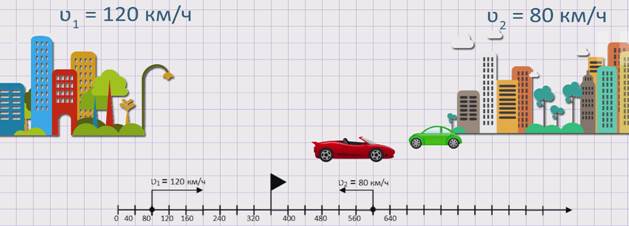
Из рисунка видно, что два автомобиля, двигаясь навстречу друг другу, приближаются. Значит, расстояние между ними сокращается. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо к скорости первого автомобиля прибавить скорость второго. А именно, скорость сближения равна сумме скоростей первого и второго автомобилей: ʋсбл. = ʋ1 +ʋ2.
Найдем скорость сближения данных автомобилей:
![]()
Значит, расстояние между автомобилями сокращается со скоростью 200 км/ч. Рассмотрим вторую ситуацию.
Из двух городов одновременно в одном направлении, вдогонку, выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Сокращается или увеличивается расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
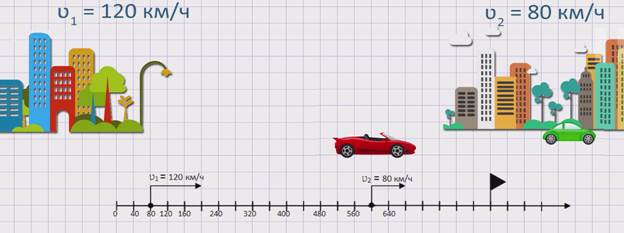
Из рисунка видно, что первый автомобиль движется быстрее второго автомобиля или же движется вдогонку второму автомобилю. Значит, расстояние между автомобилями будет сокращаться. Чтобы узнать, с какой скоростью сокращается расстояние между автомобилями или же с какой скоростью сближаются два автомобиля, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость сближения равна разности скоростей двух автомобилей: ʋсбл. = ʋ1 – ʋ2 .
Найдем скорость сближения данных автомобилей: ʋсбл. = ʋ1 – ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями сокращается со скоростью 40 км/ч.
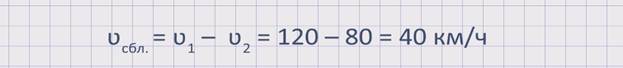
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Рассмотрим следующую третью ситуацию.
Из двух городов в противоположных направлениях одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Будет ли увеличиваться расстояние между автомобилями? Если да, то на сколько?
Изобразим движение данных автомобилей на координатном луче.
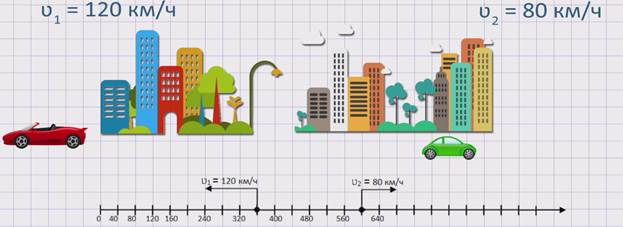
Из рисунка видно, что два автомобиля, двигаясь в противоположных направлениях, удаляются друг от друга. Значит, расстояние между ними увеличивается. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо к скорости первого автомобиля прибавить скорость второго автомобиля. А именно, скорость удаления равна сумме скоростей двух автомобилей: ʋуд. = ʋ1 + ʋ2 .
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 + ʋ2 = 120 + 80 = 200 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 200 км/ч.
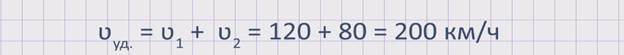
Рассмотрим последнюю четвертую ситуацию.
Из двух городов водном направление одновременно выехало два автомобиля. Скорость первого автомобиля ʋ1 = 120 км/ч, а скорость второго автомобиля ʋ2 = 80 км/ч. Причем второй автомобиль движется с отставанием. Будет увеличиваться или уменьшаться расстояние между автомобилями и на сколько?
Изобразим движение данных автомобилей на координатном луче.
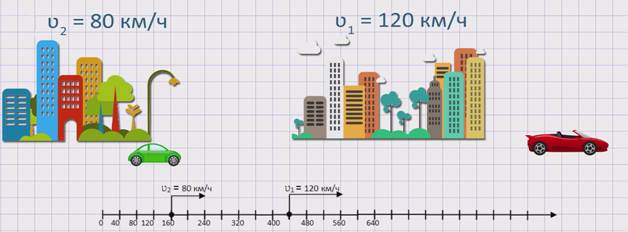
Из рисунка видно, что второй автомобиль движется медленнее первого автомобиля или же движется с отставанием от первого автомобиля. Значит, расстояние между автомобилями будет увеличиваться. Чтобы узнать, с какой скоростью увеличивается расстояние между автомобилями или же с какой скоростью удаляются два автомобиля друг от друга, необходимо из скорости первого автомобиля вычесть скорость второго автомобиля. А именно, скорость удаления равна разности скоростей двух автомобилей: ʋуд. = ʋ1 – ʋ2 .
Найдем скорость удаления данных автомобилей: ʋуд. = ʋ1 – ʋ2 = 120 – 80 = 40 км/ч. Значит, расстояние между автомобилями увеличивается со скоростью 40 км/ч.
![]()
Рассматривая приведенные выше ситуации, мы познакомились с понятием «скорость удаления». Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
§ 2 Краткие итоги по теме урока
1.Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
2.При движении двух объектов навстречу друг другу скорость сближения равна сумме скоростей этих объектов. ʋсбл. = ʋ1 + ʋ2
3.При движении вдогонку скорость сближения равна разности скоростей объектов движения. ʋсбл. = ʋ1 – ʋ2
4.Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
5.При движении двух объектов в противоположных направлениях скорость удаления равна сумме скоростей этих объектов. ʋуд. = ʋ1 + ʋ2
6.При движении с отставанием скорость удаления равна разности скоростей объектов движения. ʋуд. = ʋ1 – ʋ2
Для решения задач на движение стоит прояснить объекты сближаются или удаляются, ответ зависит от вида движения. Когда объекты двигаются навстречу друг другу из разных пунтков, то они сближаются:
(v_1+v_2=20+30=50) км/час скорость сближения
Когда объекты двигаются в противоположных направлениях из одного пункта, то они удаляются:
(v_1+v_2=20+30=50) км/час скорость удаления
Когда объекты двигаются в одном направление одновременно:
- Если они выезжают одновременно, то два объекта удаляются друг от друга, так как скорость у них разная, для того чтобы найти скорость их удаления надо из большей скорости вычесть меньшую.
(v_y=v_2-v_1)
- Если они выезжают с интервалом, то два объекта могут удаляться или сближаться в зависимости от их скоростей:
1) если скорость объекта, который впереди больше, то они удаляются. (v_2>v_1)
2) если скорость объекта, который впереди меньше, то они сближаются . (v_1>v_2)
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
