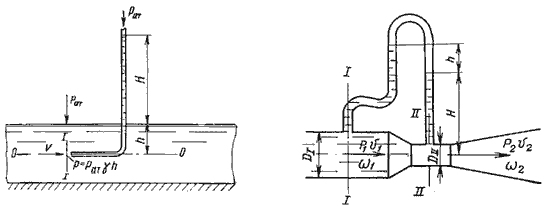
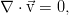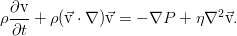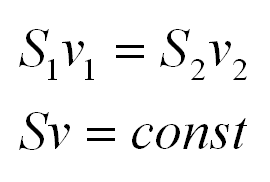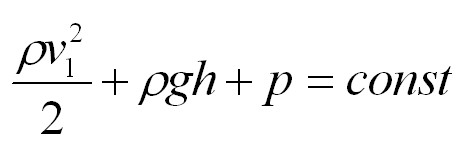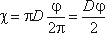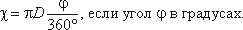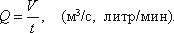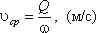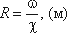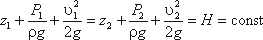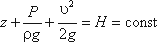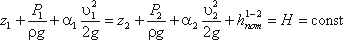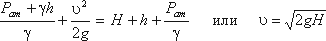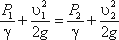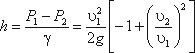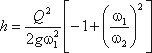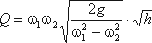Как найти скорость в гидродинамике

Как найти скорость в гидродинамике

Рисунок из «Гидродинамики» Д. Бернулли: из-за течения по трубе, компенсирующего расход через правое отверстие О, давление в трубе меньше, чем в сосуде слева.

Механика сплошных сред
BernoullisLawDerivationDiagram.svg
Сплошная среда

Классическая механика

Закон сохранения массы · Закон сохранения импульса

Теория упругости

Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость

Гидродинамика

Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение

Основные уравнения

Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука

См. также: Портал:Физика

Зако́н Берну́лли[1] (также уравне́ние Берну́лли[2][3], теоре́ма Берну́лли[4][5] или интегра́л Берну́лли[2][6][7]) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением. Согласно этому закону, если вдоль линии тока давление жидкости повышается, то скорость течения убывает, и наоборот. Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости[2] (то есть без вязкости и теплопроводности).

История[править | править код]

Для случая несжимаемой жидкости результат, эквивалентный современному уравнению Бернулли, был опубликован в 1738 году Даниилом Бернулли[K 1]. В современном виде интеграл был опубликован Иоганном Бернулли в 1743 году[11] для случая несжимаемой жидкости, а для некоторых случаев течений сжимаемой жидкости — Эйлером в 1757 году[12].

Интеграл Бернулли в несжимаемой жидкости[править | править код]

Полное давление
Размерность {displaystyle L^{-1}MT^{-2}}
Единицы измерения
СИ Дж/м3 = Па
СГС эрг/см3
Примечания
Постоянно вдоль линии тока стационарного течения несжимаемой жидкости.

Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что величина {displaystyle rho v^{2}/2+rho gh+p} сохраняет постоянное значение вдоль линии тока:

{displaystyle {frac {rho v^{2}}{2}}+rho gh+p={text{const}}.}

Здесь

rho  — плотность жидкости;
v — скорость потока;
h — высота;
p — давление;
g — ускорение свободного падения.

Элементарный вывод уравнения Бернулли из закона сохранения энергии

BernoullisLawDerivationDiagram.png

Элементарный вывод уравнения Бернулли из закона сохранения энергии приведён, например, в учебнике Д. В. Сивухина[13]. Рассматривается стационарное движение жидкости вдоль линии тока, изображённое на рисунке. Слева на объем жидкости, первоначально заключённый между двумя сечениями A_{1} и A_{2}, действует сила {displaystyle F_{1}=p_{1}A_{1}}, а справа — противоположного направления сила {displaystyle F_{2}=-p_{2}A_{2}}. Скорость v и давление p в сечениях 1 и 2, а также их площади обозначены нижними индексами 1 и 2. За бесконечно малое время Delta t левая граница этого объёма жидкости сместилась на малое расстояние {displaystyle s_{1}=v_{1}Delta t}, а правая — на расстояние {displaystyle s_{2}=v_{2}Delta t}. Работа, совершённая силами давления, равна:

{displaystyle W=F_{1}s_{1}+F_{2}s_{2}=Delta tleft(v_{1}A_{1}p_{1}-v_{2}A_{2}p_{2}right).}

В начале интервала времени Delta t объем жидкости, заключённый между двумя поверхностями A_{1} и A_{2}, состоит из левого голубого элемента и средней синей части, в конце этого интервала сместившийся объём состоит из средней синей части и правого голубого элемента. Так как течение стационарное, вклад синего фрагмента в энергию и массу обсуждаемого объёма жидкости не меняется, а сохранение массы позволяет заключить, что масса левого голубого элемента равна массе правого голубого элемента: {displaystyle Delta m=Delta tv_{1}A_{1}rho _{1}=Delta tv_{2}A_{2}rho _{2}.} Поэтому работа сил, выражение для которой можно преобразовать к виду: {displaystyle Delta W=Delta mleft({frac {p_{1}}{rho _{1}}}-{frac {p_{2}}{rho _{2}}}right),} равна изменению энергии, равному, в свою очередь, разности энергий правого голубого элемента {displaystyle Delta E_{2}} и левого голубого элемента {displaystyle Delta E_{1}}.

Для несжимаемой жидкости можно, во-первых, в выражении для работы положить {displaystyle rho _{1}=rho _{2}=rho } и, во-вторых, в выражении для энергии элемента жидкости ограничиться кинетической и потенциальной энергией: {displaystyle Delta E_{1}=Delta mleft({frac {v_{1}^{2}}{2}}+gh_{1}right),} {displaystyle Delta E_{2}=Delta mleft({frac {v_{2}^{2}}{2}}+gh_{2}right).} После этого равенство {displaystyle Delta W=Delta E_{2}-Delta E_{1}} даёт: {displaystyle p_{1}+rho gh_{1}+{frac {rho v_{1}^{2}}{2}}=p_{2}+rho gh_{2}+{frac {rho v_{2}^{2}}{2}}}, или {displaystyle p+rho gh+{frac {rho v^{2}}{2}}={rm {const}}}.

Константа в правой части (может различаться для различных линий тока) иногда называется полным давлением[2]. Могут также использоваться термины «весовое давление» rho gh, «статическое давление» p и «динамическое давление» {displaystyle rho v^{2}/2}. По словам Д. В. Сивухина[13], нерациональность этих понятий отмечалась многими физиками.

Размерность всех слагаемых — единица энергии на единицу объёма. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Третье слагаемое по своему происхождению является работой сил давления (см. приведённый выше вывод уравнения Бернулли), но в гидравлике может называться «энергией давления» и частью потенциальной энергии[14]).

Вывод формулы Торричелли из закона Бернулли[править | править код]

Иллюстрация формулы Торричелли

В применении к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда закон Бернулли даёт равенство полных давлений на свободной поверхности жидкости и на выходе из отверстия:

{displaystyle rho gh+p_{0}={frac {rho v^{2}}{2}}+p_{0},}

где

h — высота столба жидкости в сосуде, отсчитанная от уровня отверстия,
v — скорость истечения жидкости,
p_{0} — атмосферное давление.

Отсюда: v={sqrt {2gh}}. Это — формула Торричелли. Она показывает, что при истечении жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты h. Или, если истекающую из малого отверстия в сосуде струю направить вверх, в верхней точке (в пренебрежении потерями) струя достигнет уровня свободной поверхности в сосуде[15].

Другие проявления и применения закона Бернулли[править | править код]

Закон Бернулли объясняет эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем в широкой части

Приближение несжимаемой жидкости, а с ним и закон Бернулли справедливы и для ламинарных течений газа, если только скорости течения малы по сравнению со скоростью звука[16].

Вдоль горизонтальной трубы координата z постоянна и уравнение Бернулли принимает вид {displaystyle {frac {rho v^{2}}{2}}+p={text{const}}}. Отсюда следует, что при уменьшении сечения потока из-за возрастания скорости давление падает. Эффект понижения давления при увеличении скорости потока лежит в основе работы расходомера Вентури[17] и струйного насоса[1].

Закон Бернулли объясняет, почему суда, движущиеся параллельным курсом, могут притягиваться друг к другу (например, такой инцидент произошёл с лайнером «Олимпик»)[18].

Применение в гидравлике[править | править код]

Последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Для технических приложений часто уравнение Бернулли записывается в виде, в котором все члены разделены на «удельный вес» {displaystyle rho g}:

{displaystyle H=h+{frac {p}{rho g}}+{frac {v^{2}}{2g}}={text{const}},}

где имеющие размерность длины члены в этом уравнении могут иметь следующие названия:

Напор[19]
Размерность L
Единицы измерения
СИ метр
Примечания
Полное давление, делённое на удельный вес.
H — гидравлическая высота[4] или напор[19],
h — нивелирная высота[4],
{displaystyle {frac {p}{rho g}}} — пьезометрическая высота[4] или (в сумме с нивелирной высотой) гидростатический напор[19],
{displaystyle {frac {v^{2}}{2g}}} — скоростная высота[4] или скоростной напор[19].

Закон Бернулли справедлив только для идеальных жидкостей, в которых отсутствуют потери на вязкое трение. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, приближённо учитывающих различные «гидравлические потери напора»[19].

Интеграл Бернулли в баротропных течениях[править | править код]

Уравнение Бернулли может быть выведено и из уравнения движения жидкости[K 2][K 3]. При этом течение предполагается стационарным и баротропным. Последнее означает, что плотность жидкости или газа не обязательно постоянна (как у предполагавшейся ранее несжимаемой жидкости), но является функцией только давления: {displaystyle rho =rho (p)}, что позволяет ввести функцию давления[22] {displaystyle {mathcal {P}}=int {frac {mathrm {d} p}{rho (p)}}.} В этих предположениях величина

{displaystyle {frac {v^{2}}{2}}+gh+{mathcal {P}}={text{const}}}

постоянна вдоль любой линии тока и любой вихревой линии. Соотношение справедливо для течения в любом потенциальном поле, при этом gh заменяется на потенциал массовой силы varphi .

Вывод интеграла Бернулли для баротропного течения

Для безвихревых баротропных течений, скорость которых может быть выражена в виде градиента потенциала скорости {displaystyle {vec {v}}=operatorname {grad} psi }, интеграл Бернулли в виде {displaystyle {frac {partial psi }{partial t}}+{frac {left(operatorname {grad} psi right)^{2}}{2}}+gh+{cal {P}}=mathrm {const} }[K 4] сохраняется также в нестационарных течениях, причём постоянная в правой части имеет одинаковое значение для всего течения[25].

Формула Сен-Венана — Ванцеля[править | править код]

Если в течении совершенного газа выполняется адиабатический закон[26]

{displaystyle p={frac {p_{0}}{rho _{0}^{gamma }}}rho ^{gamma },qquad rho ={frac {rho _{0}}{p_{0}^{1/gamma }}}p^{1/gamma },qquad {cal {P}}=-{frac {gamma }{gamma -1}}{frac {p_{0}}{rho _{0}}}left[1-left({frac {p}{p_{0}}}right)^{(gamma -1)/gamma }right],}

то уравнение Бернулли выражается так[27] (вкладом от силы тяжести обычно можно пренебречь):

{displaystyle {frac {v^{2}}{2}}-{frac {gamma }{gamma -1}}{frac {p_{0}}{rho _{0}}}left[1-left({frac {p}{p_{0}}}right)^{(gamma -1)/gamma }right]=mathrm {const} } вдоль линии тока или вихревой линии. Здесь
gamma ={frac {C_{p}}{C_{V}}} — показатель адиабаты газа, выражающийся через теплоёмкости при постоянном давлении и при постоянном объёме,
{displaystyle p, rho } — давление и плотность газа,
{displaystyle p_{0}, rho _{0}} — условно выбранные постоянные (одинаковые для всего течения) значения давления и плотности.

С помощью полученной формулы находят скорость газа, вытекающего из сосуда с высоким давлением через малое отверстие. Удобно давление и плотность газа в сосуде, скорость газа в котором равна нулю, принять за {displaystyle p_{0}, rho _{0},} тогда скорость истечения выражается через внешнее давление p по формуле Сен-Венана — Ванцеля[28]:

{displaystyle v^{2}={frac {2gamma }{gamma -1}}{frac {p_{0}}{rho _{0}}}left[1-left({frac {p}{p_{0}}}right)^{(gamma -1)/gamma }right].}

Термодинамика закона Бернулли[править | править код]

Из термодинамики следует, что вдоль линии тока любого стационарного течения идеальной жидкости

{displaystyle {frac {v^{2}}{2}}+w+varphi ={text{const}},quad s={text{const}},}

где w — энтальпия единицы массы, varphi  — гравитационный потенциал (равный {displaystyle gz} для однородной силы тяжести), s — энтропия единицы массы.

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

Интеграл Бернулли применяют в инженерных расчётах, в том числе для сред, весьма далёких по своим свойствам от идеального газа, например для водяного пара, используемого в качестве теплоносителя в паровых турбинах. При этом могут использоваться так называемые диаграммы Молье, представляющие удельную энтальпию (по оси ординат) как функцию удельной энтропии (по оси абсцисс), и, например, давления (или температуры) в виде семейства изобар (изотерм). В этом случае последовательность состояний вдоль линии тока лежит на некоторой вертикальной линии ({displaystyle s={text{const}}}). Длина отрезка этой линии, отсекаемого двумя изобарами, соответствующими начальному и конечному давлению теплоносителя, равна половине изменения квадрата скорости[31].

Обобщения интеграла Бернулли[править | править код]

Интеграл Бернулли также сохраняется при переходе потока через фронт ударной волны, в системе отсчета, в которой ударная волна покоится[32]. Однако при таком переходе энтропия среды не остаётся постоянной (возрастает), поэтому соотношение Бернулли является лишь одним из трёх соотношений Гюгонио, наряду с законами сохранения массы и импульса, связывающих состояние среды за фронтом с состоянием среды перед фронтом и со скоростью ударной волны.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений[33]), в магнитной гидродинамике[34], феррогидродинамике[35]. В релятивистской гидродинамике, когда скорости течения становятся сравнимыми со скоростью света c, интеграл формулируется в терминах релятивистски инвариантных[36] удельной энтальпии и удельной энтропии[37].

Комментарии[править | править код]

  1. ↑ В записи Д.Бернулли в явном виде не фигурировало внутреннее давление в жидкости[8][9][10].
  2. ↑ «…[Вывод теоремы Бернулли из уравнения энергии] обедняет содержание теоремы Бернулли … Интеграл Бернулли, вообще говоря, не зависит от уравнения энергии, хотя действительно совпадает с ним для изоэнтропического и адиабатического движения совершенного газа»[20].
  3. ↑ «Два … пути получения уравнения Бернулли не эквивалентны. При энергетическом выводе нет необходимости в предположении об изэнтропичности течения. При интегрировании уравнения движения интегралы Бернулли получаются не только вдоль линий тока, но и вдоль вихревых линий»[21].
  4. ↑ В русскоязычной литературе интеграл Бернулли для потенциальных течений несжимаемой или баротропной жидкости известен как интеграл Коши — Лагранжа[25]

Примечания[править | править код]

  1. ↑ 1 2 Ландсберг Г. С. Закон Бернулли, 1985.
  2. ↑ 1 2 3 4 Вишневецкий С. Л. Бернулли уравнение, 1988.
  3. ↑ Титьенс О., Прандтль Л. Гидро- и аэромеханика, 1933.
  4. ↑ 1 2 3 4 5 Лойцянский Л. Г. Механика жидкости и газа, 2003, §24. Теорема Бернулли.
  5. ↑ Милн-Томсон Л. М. Теоретическая гидродинамика, 1964.
  6. ↑ Седов Л. И. Механика сплошной среды, 1970.
  7. ↑ Чёрный Г. Г. Газовая динамика, 1988.
  8. ↑ Трусделл К. Очерки по истории механики, 2002.
  9. ↑ Михайлов Г. К., 1999, с. 17.
  10. ↑ Darrigol O. A history of hydrodynamics, 2005, с. 9.
  11. ↑ Трусделл К. Очерки по истории механики, 2002, с. 255, 257.
  12. ↑ Euler L. Continuation des recherches, 1755 (1757), с. 331.
  13. ↑ 1 2 Сивухин Д. В. Механика, 1989, §94. Стационарное движение идеальной жидкости. Уравнение Бернулли.
  14. ↑ Чугаев Р. Р. Гидравлика. — Л.: Энергия, 1975. — 600 с.
  15. ↑ Сивухин Д. В. Механика, 1989, §95. Примеры на применение уравнения Бернулли. Формула Торричелли.
  16. ↑ Сивухин Д. В. Механика, 1989, §94, формула (94.6).
  17. ↑ Молоканов Ю. К. Процессы и аппараты нефтегазопереработки. — М.: Химия, 1980. — С. 60. — 408 с.
  18. ↑ Я. И. Перельман. Отчего притягиваются корабли? Дата обращения: 27 декабря 2018. Архивировано 11 мая 2012 года.
  19. ↑ 1 2 3 4 5 Напор, 1992.
  20. ↑ Бэтчелор Дж. Введение в динамику жидкости, 1973, Примечание Г. Ю. Степанова, с. 208.
  21. ↑ Гольдштейн Р. В., Городцов В. А. Механика сплошных сред, 2000, с. 104.
  22. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (9).
  23. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (7).
  24. ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VIII. §2, уравнение (2.1).
  25. ↑ 1 2 Лойцянский Л. Г. Механика жидкости и газа, 2003, §42. Интеграл Лагранжа — Коши.
  26. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (29).
  27. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (30).
  28. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (31).
  29. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (2.4).
  30. ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
  31. ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
  32. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, §85.
  33. ↑ Голубкин В. Н., Сизых Г. Б. О некоторых общих свойствах плоскопараллельных течений вязкой жидкости // Известия АН СССР, серия Механика жидкости и газа : журнал. — 1987. — № 3. — С. 176–178. — doi:10.1007/BF01051932.
  34. ↑ Куликовский А. Г., Любимов Г. А. Магнитная гидродинамика. — М.: Физматлит, 1962. — С. 54. — 248 с.
  35. ↑ Розенцвейг Р. Феррогидродинамика / Пер. с англ. под ред. В. В. Гогосова. — М.: Мир, 1989. — С. 136. — 359 с. — ISBN 5-03-000997-3.
  36. ↑ Зубарев Д. Н., Релятивистская термодинамика, 1994.
  37. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (134.11).

Литература[править | править код]

  • Бэтчелор Дж. Введение в динамику жидкости / Пер. с англ. под ред. Г. Ю. Степанова. — М.: Мир, 1973. — 760 с.
  • Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова-Бома эффект — Длинные линии. — С. 187. — 704 с.
  • Гольдштейн Р. В., Городцов В. А. Механика сплошных сред. Часть 1. — М.: Физматлит, 2000. — 256 с. — ISBN 5-02-015555-1.
  • Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
  • Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 5-е, стереотипное. — М.: Физматлит, 2001. — 736 с. — («Теоретическая физика», том VI). — ISBN 5-9221-0121-8.
  • Лойцянский Л. Г. Механика жидкости и газа. — М.: Дрофа, 2003. — 842 с. — ISBN 5-7107-6327-6.
  • Милн-Томсон Л. М. Теоретическая гидродинамика. — М.: Мир, 1964. — 656 с.
  • Михайлов Г. К. Становление гидравлики и гидродинамики в трудах петербургских академиков (XVIII) // Известия Академии наук, серия Механика жидкости и газа : журнал. — 1999. — Вып. 6. — С. 7–25.
  • Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный компрессор — Пойнтинга теорема. — С. 242. — 672 с. — ISBN 5-85270-019-3.
  • Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
  • Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
  • Сивухин Д. В. Общий курс физики. — Издание 3-е, исправленное и дополненное. — М.: Наука, 1989. — Т. I. Механика. — 576 с. — ISBN 5-02-014054-6.
  • Титьенс О., Прандтль Л. Гидро- и аэромеханика. — М.–Л.: ГТТИ, 1933. — Т. 1. — 224 с.
  • Трусделл К. Очерки по истории механики. — М. — Ижевск: Институт компьютерных исследований, 2002. — 316 с. — ISBN 5-93972-192-3.
  • Фабер Т. Е. Гидроаэродинамика / Пер. с англ. под ред. А. А. Павельева. — М.: Постмаркет, 2001. — 560 с. — ISBN 5-901095-04-9.
  • Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — 424 с. — ISBN 5-02-013814-2.
  • §182. Закон Бернулли // Элементарный учебник физики / Под ред. Г. С. Ландсберга. — М.: Наука, 1985. — Т. 1. Механика. Теплота. Молекулярная физика.
  • Darrigol O. Worlds of flow. A history of hydrodynamics from the Bernoullis to Prandtl. — Oxford: Oxford University Press, 2005. — 356 с. — ISBN 978-0-19-856843-8.
  • Euler L. Continuation des recherches sur la théorie du mouvement des fluides // Mémoires de l’Académie royale des sciences et belles lettres. — Berlin, 1755 (1757). — Т. 11. — С. 316—361.
  • Truesdell, Clifford Ambrose. Rational fluid mechanics, 1687–1765. Editor’s introduction to Euleri Opera omnia II 12 // Leonardi Euleri. Opera Omnia. — Lausanne: Auctoritate et Impensis, Societas Scientiarum Naturalium Helveticae, 1954. — Т. 12. — С. I—CXXV. — (II).

Ссылки[править | править код]

  • Русский перевод трактата Даниила Бернулли, в котором впервые появляется интеграл (закон) Бернулли
Источник

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 1023 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс

колдовства

преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

  • конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
  • давления окружающих элементов жидкости
  • просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v” = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

Продолжать?

Проголосовали 492 пользователя.

Воздержался 91 пользователь.

Источник

4.2.1. Гидравлический радиус и эквивалентный диаметр

При движении
жидкости через сечение любой формы,
отличной от круглой, в качестве расчетного
линейного размера принимают гидравлический
радиус или эквивалентный диаметр.

Под гидравлическим
радиусом rг
(м) принимают отношение площади
затопленного сечения трубопровода или
канала, через которое протекает жидкость,
т.е. живого сечения потока, к смоченному
периметру:

,

где S
– площадь сечения потока жидкости, м2;

П
– смоченный периметр, м.

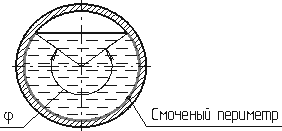
Смоченный периметр
П
– часть
периметра живого сечения, ограниченное
твердыми стенками (рисунок 15, выделен
двойной линией).

Рисунок 15 – Смоченный
периметр

Для круглой трубы

,

Для круглой трубы
с внутренним диаметром d
и, значит, площадью свободного сечения


при сплошном заполнении его жидкостью

,
откуда гидравлический радиус:

,

Диаметр, выраженный
через гидравлический радиус, представляет
собой эквивалентный
диаметр:

,

Следовательно:

,

Для канала
прямоугольного сечения со сторонами a
и b,
полностью заполненного жидкостью,
гидравлический радиус:

,

А эквивалентный
диаметр:

,

Для канала кольцевого
поперечного сечения, в котором жидкость
ограничена внутренней и наружной
окружностями с диаметром dв
и
dн
соответственно, эквивалентный диаметр:

,

Для круглой трубы

[1-5].

4.2.2. Скорость и расход жидкости

Рассмотрим движение
жидкости по трубе постоянного сечения.

Количество жидкости,
протекающей через поперечное сечение
потока («живое сечение», т.е. затопленное
сечение трубопровода (рисунок 16)) в
единицу времени, называют расходом
жидкости.

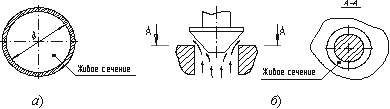
Рисунок 16 – Живые
сечения: а – трубы, б – клапана

Различают Q
– объемный расход [м3/с],
и массовый расход М
[кг/с].

В разных точках
живого сечения потока скорость частиц
жидкости неодинакова. Поэтому в расчетах
используют не истинные (локальные)
скорости, а фиктивную среднюю скорость.

Средняя скорость

– выражается
отношением объемного расхода жидкости
к площади живого сечения потока [1,3,4].

,

где Q
– объемный расход, м3/с;

S
– площадь живого сечения, м2.

Откуда объемный
расход:

,

Массовый расход
М
[кг/с ]:

,

где ρ – плотность
жидкости кг/м3.

4.3. Виды движения жидкости

Основными видами
движения жидкости являются: движение
установившееся и неустановившееся,
равномерное и неравномерное, напорное
и безнапорное, сплошное и прерывистое.

Установившимся
движением называется такое движение
жидкости, при котором давление и скорость
не изменяются во времени в каждой
фиксированной точке пространства, через
которую проходит жидкость.


,

Движение, при
котором скорость и давление изменяются
не только от координат пространства,
но и от времени, называется неустановившимся
или
нестационарным


,

.

Примером
неустановившегося движения может
служить истечение жидкости из отверстия
при переменном уровне ее в резервуаре:
с понижением высоты столба жидкости
скорость истечения уменьшается во
времени.

Установившееся
движение в свою очередь подразделяется
на равномерное
и неравномерное.

Равномерным
называется
такое установившееся движение, при
котором живые
сечения вдоль потока не изменяются: в
этом случае
;
средние скорости
по длине потока также не изменяются,
т.е.
.
Примером равномерного движения является:
движение жидкости в цилиндрической
трубе,
в канале постоянного сечения при
одинаковых глубинах.

Установившееся
движение называется неравномерным,
когда
распределение
скоростей в различных поперечных
сечениях неодинаково; при этом средняя
скорость
и площадь поперечного сечения потока
могут быть и
постоянными вдоль потока. Примером
неравномерного движения может быть
движение жидкости в конической трубе
или в речном русле переменной ширины.

Напорным
называется
движение жидкости, при котором поток
полностью
заключен в твердые стенки и не имеет
свободной поверхности. Напорное движение
происходит вследствие разности давлений
и под действием
силы тяжести. Примером напорного движения
является движение жидкости
в замкнутых трубопроводах (например, в
водопроводных трубах).

Безнапорным
называется
движение жидкости, при котором поток
имеет свободную поверхность. Примером
безнапорного движения может быть:
движение жидкости в реках, каналах,
канализационных и дренажных трубах.
Безнапорное
движение происходит под действием силы
тяжести и за счет начальной
скорости. Обычно на поверхности
безнапорного потока давление атмосферное.

Следует
отметить еще один вид движения: свободную
струю.
Свободной
струей называется
поток, не ограниченный твердыми стенками.
Примером
может служить движение жидкости из
пожарного брандспойта, гидромонитора,
водопроводного крана, из отверстия
резервуара и т. п. В этом случае
движение жидкости происходит по инерции
(т. е. за счет начальной скорости)
и под действием силы тяжести.

Для упрощения
выводов, связанных с изучением потока
жидкости, вводится
понятие о плавно
изменяющемся
движении жидкости.

Плавно
изменяющимся называется
такое движение жидкости, при котором
кривизна струек незначительна (равна
нулю или близка к нулю) и угол
расхождения между струйками весьма мал
(равен нулю или близок к нулю),
т. е. практически поток жидкости мало
отличается от параллельно
струйного. Это предположение вполне
оправдывается при изучении
многих случаев движения жидкости в
каналах, трубах и других сооружениях.

Свойства потока
при плавно изменяющемся движении:

1) поперечные
сечения потока плоские, нормальные к
оси потока;

2) распределение
гидродинамических давлений по сечению
потока подчиняется закону гидростатики,
т.е. гидродинамические давления по
высоте
сечения распределяются по закону прямой.
Это свойство легко можно доказать,
если внутри потока выделить частицу
жидкости и спроектировать все
действующие на нее силы на плоскость
живого сечения. Вследствие того, что
скорости и ускорения в этом случае будут
перпендикулярны сечению, силы
инерции в уравнение не войдут; поэтому
уравнение равновесия и закон распределения
давления в плоскости живого сечения не
будет отличаться от такового
для жидкости, находящейся в покое;

3) удельная
потенциальная энергия (т. е. потенциальная
энергия единицы веса
жидкости) по отношению к некоторой
плоскости сравнения для всех точек
данного сечения потока жидкости есть
величина постоянная. [2-4].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #

    15.05.2015135.17 Кб18генетическая карта русских.doc

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

закон уравнение бернулли

Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».

Кто такой Бернулли?

Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».

закон уравнение бернулли

Д. Бернулли (1700-1782)

Идеальная жидкость и течение идеальной жидкости

Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это  жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.

Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.

Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.

Поток жидкости– совокупность частиц движущейся жидкости.

Поток жидкости

Поток жидкости

Вывод уравнения Бернулли

Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.

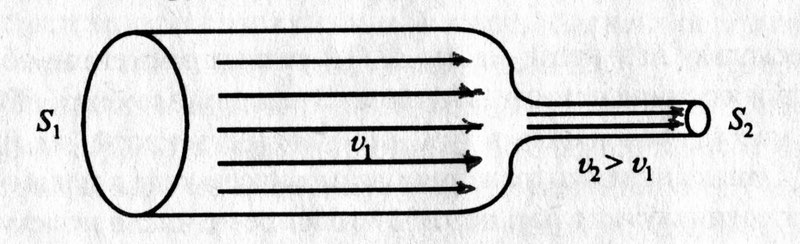
Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2.  При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.

Уравнение Бернулли

Данное уравнение – уравнение неразрывности струи.

К выводу уравнения Бернулли

К выводу уравнения Бернулли

Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:

Уравнение Бернулли

Смысл уравнения Бернулли

Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.

Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.

Иван

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Главная страница

Содержание

Введение

Основы гидростатики

Основы гидродинамики

Гидравлические сопротивления

Истечние жидкости из отверстий, насадков и из-под затворов

Гидравлический расчет простых трубопроводов

Гидравлические машины

Лекция 3. ОСНОВЫ ГИДРОДИНАМИКИ

Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие
с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде
такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную
к направлению течения. Например, живое сечение трубы – круг (рис.3.1, б); живое сечение клапана – кольцо с
изменяющимся внутренним диаметром (рис.3.1, б).

Рис. 3.1. Живые сечения: а – трубы, б – клапана

Смоченный периметр χ (“хи”) – часть периметра живого сечения, ограниченное твердыми
стенками (рис.3.2, выделен утолщенной линией).

Рис. 3.2. Смоченный периметр

Для круглой трубы

если угол в радианах, или

Расход потока Q – объем жидкости V, протекающей за единицу времени t через живое
сечение ω.

Средняя скорость потока υ – скорость движения жидкости, определяющаяся отношением расхода
жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения
и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она
равна нулю.

Гидравлический радиус потока R – отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется
такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z)

P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени,
называется неустановившимся или нестационарным

υ = f1(x, y, z, t)

P = φ f1(x, y, z, t)

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор
скорости в данный момент времени направлены по касательной.

Трубка тока – трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением.
Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 3.3. Линия тока и струйка

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах
без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением).
Безнапорное – течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые
каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

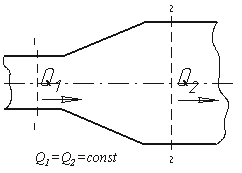
Рис. 3.4. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений.
Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении
постоянен, т.е. Q1=Q2= const, откуда

ω1υ1 = ω2υ2

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно
дает связь между давлением P, средней скоростью υ и пьезометрической высотой z
в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого
уравнения решается большой круг задач.

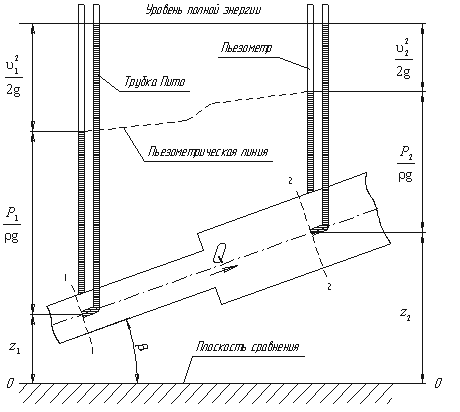
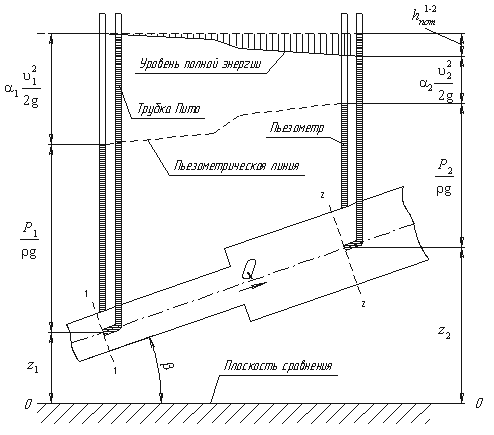
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом
β (рис.3.5).

Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и
сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой
равен Q.

Для измерения давления жидкости применяют пьезометры – тонкостенные стеклянные трубки, в которых
жидкость поднимается на высоту 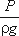. В каждом сечении установлены
пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой
направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также
поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2
поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы
получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой
плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет
отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет
следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть
величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 – удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и
2-2;
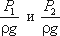
– удельные энергии давления, характеризующие потенциальную
энергию давления в тех же сечениях;
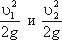
– удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении
постоянна.

Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет
линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 – геометрические высоты сечений 1-1
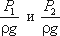
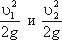
и 2-2 над плоскостью сравнения; – пьезометрические высоты;
– скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной
высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых
жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше
полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный
напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень
первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться
из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного
напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые
называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного
режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями
жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

= hлин + hмест

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два
сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ,
g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго
сечения используют уравнение постоянства расхода жидкости υ1ω
1 = υ2ω2.

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка
Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости
в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения
1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н – столб жидкости в трубке Пито.

Рис. 3.7. Трубка Пито и pасходомер Вентури

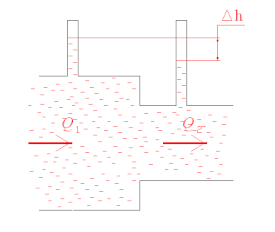
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого
основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с
цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры,
то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и
II-II:

или

Используя уравнение неразрывности

Q = υ1ω1 = υ2ω2

сделаем замену в получено выражении:

Решая относительно Q, получим

Выражение, стоящее перед 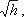, является постоянной величиной, носящей название постоянной
водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в
виде тарировочной кривой h от Q, которая имеет параболический характер.

Проверить себя ( Тест )

Наверх страницы

Источник

Добавить комментарий