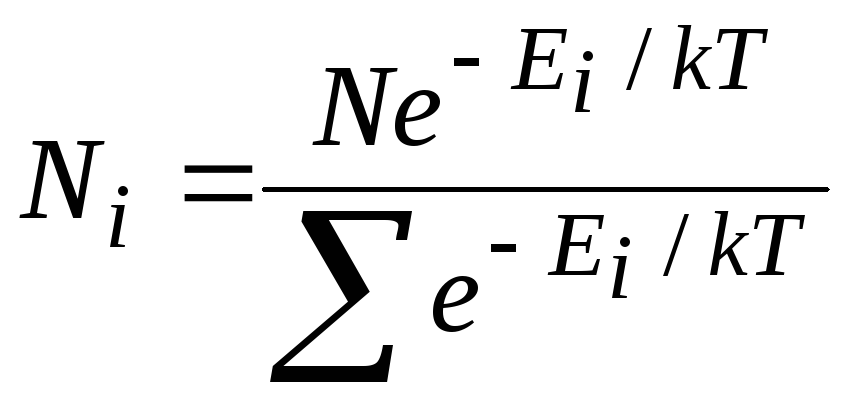Как найти скорость в молекулярной физике

Молекулярная физика Основные формулы

1. Основы молекулярно-кинетической теории. Газовые законы

1.1 Количество вещества

m — масса;

μ — молярная масса вещества;

N — число молекул;

N_A = 6,02·10²³ моль^-1 — число Авогадро

1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;

m — масса одной молекулы;

n = N/V — концентрация молекул;

V — объем газа;

N — число молекул;

— среднее значение квадрата скорости молекул.

1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10^-23 Дж/К — постоянная Больцмана;

R = kN_A = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T = t+273 — абсолютная температура;

t — температура по шкале Цельсия.

1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;

k — постоянная Больцмана;

T — абсолютная температура.

1.6 Закон Бойля-Мариотта

p — давление;

V — объем газа.

1.7 Закон Шарля

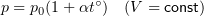
p₀ — давление газа при 0 °С;

α = 1/273 °C^-1 — температурный коэффициент давления.

1.8 Закон Гей-Люссака

V₀ — объем газа при 0 °С.

1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

p_i — парциальное давление i-й компоненты смеси газов.

2. Основы термодинамики

2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;

R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T — абсолютная температура.

2.2 Элементарная работа, совершаемая газом,

при изменении объема на бесконечно малую величину dV

p — давление газа.

При изменении объема от V₁ до V₂

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;

ΔA — работа, совершаемая веществом;

ΔU — изменение внутренней энергии вещества.

2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;

ΔT — изменение температуры на этом участке процесса.

Molecular speed is defined as the speed of the group of molecules in an ideal gas. Molecular speed is an important concept in the kinetic theory of gases. According to the kinetic theory of gases, the molecules of a gas are in constant motion and move in a straight line until they collide with another molecule. All the molecules of an ideal gas undergo elastic collision. It explains why small molecules diffuse more rapidly than large molecules. The molecular speed of a gas is directly proportional to its speed and inversely proportional to its molar mass. The molecular speed of a gas increases with an increase in the temperature of the gas. For example, Helium has the lowest molecular mass and thus has the highest molecular speed.

Types of Molecular Speed

The concept of molecular speed states that a cluster of atoms moves at a typical rate. The particles in an ideal gas don’t come into contact with one another. Let us see different types of molecular speed and how to calculate them. Molecular speed can be of 3 types which are as follows:

Average Molecular Speed

It is the average speed of a group of molecules in a gas. It is denoted using . It can be calculated using the formula:

where, 

• T is the temperature of the gas in Kelvin
• M is the molar mass
• R is the Ideal gas constant, 8.314 kg*m²/s²*mol*K

Root Mean Square Speed

It is the measure of the speed of the particles in particular gas. It is denoted by v_rms and can be calculated using the formula:

where,

• T is the temperature of the gas in Kelvin
• M is the molar mass
• R is the Ideal gas constant, 8.314 kg*m²/s²*mol*K

Most Probable Speed

It is the speed which is acquired by most of the molecules in a gas. It is denoted by v_p and can be calculated using the following formula:

where,

• T is the temperature of the gas in Kelvin
• M is the molar mass
• R is the Ideal gas constant, 8.314 kg*m²/s²*mol*K

Relation between Molecular Speeds

The volume of a gas molecule is little in relation to the whole volume of the container when it comes to the molecular speeds of a particle. The gas particles travel freely and with complete mobility. The force of attraction between the gaseous molecules is therefore absent.

• The relationship between average molecular speed, root mean square speed, and most probable speed is:

• The ratio between average molecular speed, root mean square speed, and most probable speed is:

Maxwell Distribution of Molecular Speeds

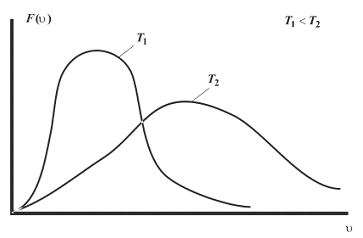
Maxwell and Boltzmann derived an equation to find the distribution of various types of molecular speeds in a gas. The number of molecules per unit speed is indicated on the y-axis of the Maxwell-Boltzmann distribution graph. The quantity of molecules in the gas is represented by the total area under the whole curve. The peak of the graph will move to the right if we heat the gas to a greater temperature (since the average molecular speed will increase). The graph grows higher and more narrow as the gas gets colder, similar to how the graph shortens and widens as the gas heats up.

Inferences from the Graph

• The most probable speed is represented by the peak of the curve. The average molecular speed is the speed that is just a little higher than the most probable speed. The root mean square speed coincides with the average kinetic energy of the gas molecules.
• The curve will spread and flatten out when we observe the gas at increasing temperatures. 
• The shape of the curve is dependent upon the molar mass and temperature of the gas. 
• The curve gets taller and flatter when we consider gases of increasing molar mass.
• With the increase in temperature, the most probable speed increases, and the peak of the curve shifts to the right. The particles of gas also tend to move faster. 

Solved Examples on Molecular Speed

Example 1: The temperature of gas with a molar mass of 2 g/mol is 900K. Calculate the root mean square speed of the particles of gas.

Solution:

Given, M = 2g/mol, T = 900K

R = 8.314

Example 2: Calculate the most probable speed of Helium gas at 800K.

Solution:

Given, T = 800K

For Helium, M = 4g/mol and R = 8.314

Example 3: Determine the speed of particles of m = 1 gr/mol and temperature 1500 k.

Solution:

Given, M = 1g/mol, T = 1500K and R = 8.314

Example 4: Compare the following quantities, the RMS velocity of oxygen at 80 °C and the RMS velocity of Hydrogen at 45 °C. 

Solution:

To compare the quantities, we shall calculate the rms for oxygen and hydrogen for the given conditions.

Oxygen:

Given T = 80C = 353K, Molar mass of oxygen (M) = 16g/mol

Hydrogen:

Given, T = 45°, C = 318K, Molar mass of Hydrogen (M) = 2g/mol

Thus, rms velocity of hydrogen is more than Oxygen at the given conditions.

Example 5: Find the average molecular speed of gas with a molar mass 19 g at 500K.

Solution:

Given, T = 500K, M = 19g/mol

FAQs on Molecular Speed

Question 1: What is meant by the kinetic theory of gases?

Solution:

Based on the notion that a gas is made up of atoms or molecules that are moving quickly, kinetic theory describes how gases behave.

Question 2: Why do smaller gas atoms travel more quickly?

Solution:

Because of the molecular mobility of molecules, smaller gas particles travel more quickly. At all temperatures higher than absolute zero, they have kinetic energy. The average kinetic energy of gas molecules and temperature are directly inversely correlated. At the same temperature and pressure, lighter gases will also move at speeds that are higher than heavier gases.

Question 3: What is meant by the degree of freedom?

Solution:

The amount of independent ways that the system’s path and configuration might vary is referred to as the degree of freedom.

Question 4: Describe mean energy.

Solution:

The mean energy or internal energy of one mole of gas is called the mean energy. It is represented by the letter U.

Last Updated :
11 Oct, 2022

Like Article

Save Article

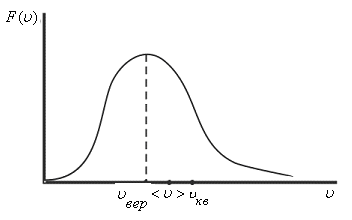
Средние скорости молекул

Найдём
наиболее
вероятную скорость,
соответствующую максимуму
функции
распределения.
Эта скорость определяется из условия

,
т.е.

Проведя
дифференцирование произведения функций,
получим

Средняя
скорость
молекул
(имеется в видусредняя
арифметическая скорость)
по определению из формулы статического
усреднения

Средняя
скорость входит в
коэффициенты диффузии, вязкости,
теплопроводности и, соответственно
используется в расчётах этих процессов.

Среднеквадратичная
скорость
;

,
откуда

Эта
скорость входит в основное уравнение
молекулярно-кинетической теории.
Качественно
положение характерных (средних) скоростей
показано на рис. 8.6

	Проанализируем, как будет меняться ход кривой при изменении температуры газа. При увеличении температуры (или уменьшении массы молекулы) максимум кривой смещается вправо (из ) и становится ниже (площадь под кривойостаётся неизменной) (Рис. 8.7)
Рис. 8.6
Рис. 8.7

3.
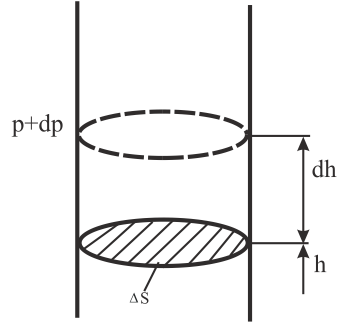
Барометрическая формула.

Атмосферное
давление на высоте h
обусловлено весом вышележащих слоёв
газа. Давление на высоте h+dh
будет P+dP
(dh>0,
dP<0,
т.к. вес и
давление с высотой убывают).

Разность
давлений
P
и P+dP
обусловлена
весом газа, заключённого в объёме
цилиндра, с площадью основания, равной
и высотойdh
(Рис. 8.8).

	, где – плотность газа на высоте, отсюда (*) При нормальных условиях воздух можно считать идеальным газом. Тогда можно найти из уравнения состояния идеального газа , здесь
Рис. 8.8

М
– средняя масса моля воздуха. Плотность

,
подставим в (*), получим

.
Поделим обе части на Р:

.
Возьмём интеграл от левой и правой
частей:

.

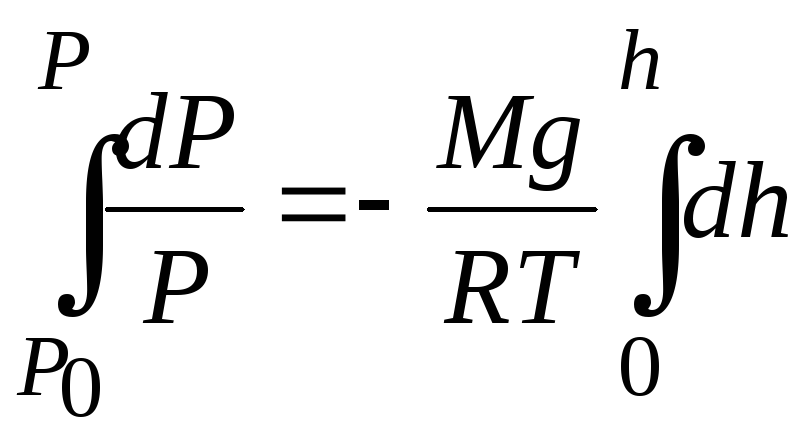Предел
давление на уровнеh=0.
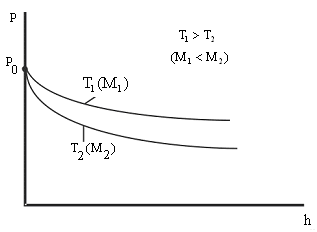
Для случая, когда температура постоянная
(изотермическая атмосфера), интегрируя,
получим:

,
отсюда получаем барометрическую
формулу.

	Графическая иллюстрация этой формулы на рис. 8.9 Давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже температура.
Рис. 8.9

Распределение Больцмана

В
барометрической формуле в отношении
M/R
разделим и
числитель и знаменатель на число Авогадро
.

,
где

масса
одной молекулы,

постоянная
Больцмана.

Вместо
Р
и
подставим соответственно.(см. лекцию №7), гдеплотность
молекул на высотеh,
плотность
молекул на высоте.

Из барометрической
формулы в результате подстановок и
сокращений получим распределение
концентрации молекул по высоте в поле
силы тяжести Земли.

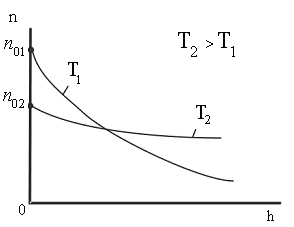
Из
этой формулы следует, что с понижением
температуры число частиц на высотах,
отличных от нуля, убывает (рис. 8.10),
обращаясь в 0 при Т=0 (при
абсолютном нуле все молекулы расположились
бы на поверхности Земли). При высоких
температурах n
слабо убывает с высотой, так

	что молекулы оказываются распределёнными по высоте почти равномерно. Распределение молекул по высоте является результатом конкуренции между притяжением молекул к Земле и тепловым движением, стремящимся разбросать молекулы по всем высотам. На разной высоте молекула обладает различным запасом потенциальной энергии
Рис. 8.10

.Следовательно,
распределение
молекул по высоте является и распределением
их по значениям потенциальной энергии.

(*)

где
плотность молекул в том месте пространства,
где потенциальная энергия молекулы
имеет значение;плотность
молекул в том месте, где потенциальная
энергия равна 0.

Больцман
доказал, что распределение (*) справедливо
не только в случае потенциального поля
сил земного тяготения, но и в любом
потенциальном поле сил для совокупности
любых одинаковых частиц, находящихся
в состоянии хаотического теплового
движения.

Таким
образом, закон
Больцмана (*) даёт распределение частиц,
находящихся в состоянии хаотического
теплового движения, по значениям
потенциальной энергии.
(рис. 8.11)

Рис. 8.11

1. Распределение
   Больцмана при дискретных уровнях
   энергии.

Полученное
Больцманом распределение относится к
случаям, когда молекулы находятся во
внешнем поле и их потенциальная энергия
может применяться непрерывно. Больцман
обобщил полученный им закон на случай
распределения, зависящего от внутренней
энергии молекулы.

Известно,
что величина внутренней энергии молекулы
(или атома) Е
может принимать лишь дискретный ряд
дозволенных значений
.
В этом случае распределение Больцмана
имеет вид:

,

где
число
частиц в состоянии с энергией;

коэффициент
пропорциональности, который удовлетворяет
условию

,

где
N
– полное число частиц в рассматриваемой
системе.

Тогда
и в результате для случая дискретных
значений энергии распределение Больцмана

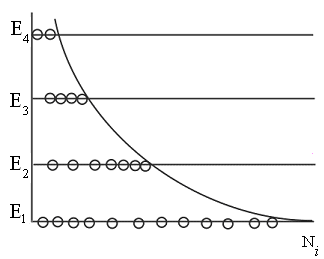
	Качественная иллюстрация этого распределения представлена на рис. 8.12. Это распределение характерно для состояния термодинамического равновесия. Заметим, что в активных средах лазеров населённость уровней с большим значением энергии может быть выше, чем с меньшим. Это так называемая инверсная населённость уровней.
Рис. 8.12

Но
состояние системы в этом случае
термодинамически неравновесное.

1. Статистика
   Максвелла-Больцмана

Распределение
Максвелла и Больцмана можно объединить
в один закон Максвелла-Больцмана,
согласно которому число молекул,
компоненты скорости которых лежат в
пределах от
до,
а координаты в пределах отx,
y,
z
до x+dx,
y+dy,
z+dz,
равно

где
,плотность
молекул в том месте пространства, где;;;полная
механическая энергия частицы.

Распределение
Максвелла-Больцмана устанавливает
распределение молекул газа по координатам
и скоростям при наличии произвольного
потенциального силового поля.

Примечание:
распределение Максвелла и Больцмана
являются составными частями единого
распределения, называемого распределением
Гиббса (этот вопрос подробно рассматривается
в спецкурсах по статической физике, и
мы ограничимся только упоминанием этого
факта).

Вопросы для
самоконтроля.

1. Дайте определение
   вероятности.

2. Каков смысл функции
   распределения?

3. Каков смысл условия
   нормировки?

4. Запишите
   формулу для определения среднего
   значения результатов измерения величины
   x
   с помощью функции распределения.

5. Что представляет
   собой распределение Максвелла?

6. Что
   такое функция распределения Максвелла?
   Каков ее физический смысл?

7. Постройте
   график функции распределения Максвелла
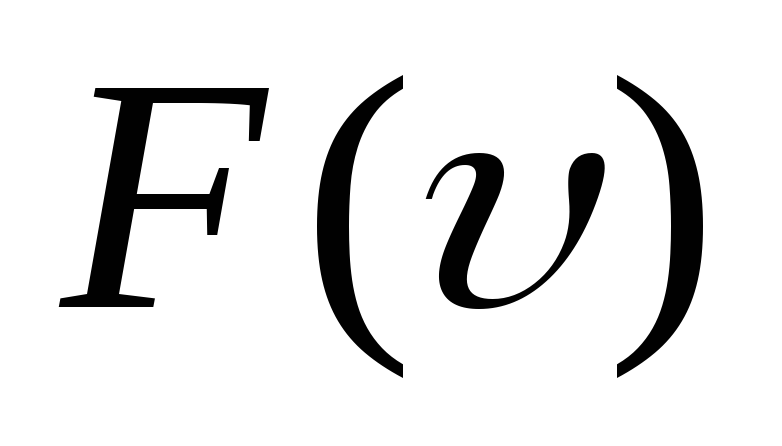   и укажите характерные особенности этой
   функции.

8. Укажите
   на графике
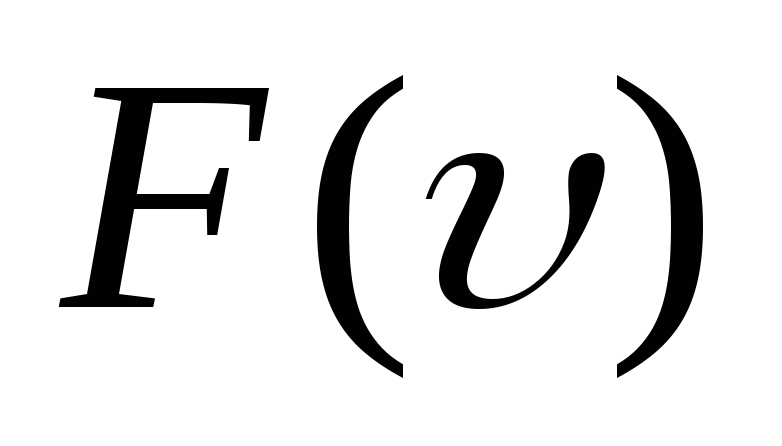   наиболее вероятную скорость.
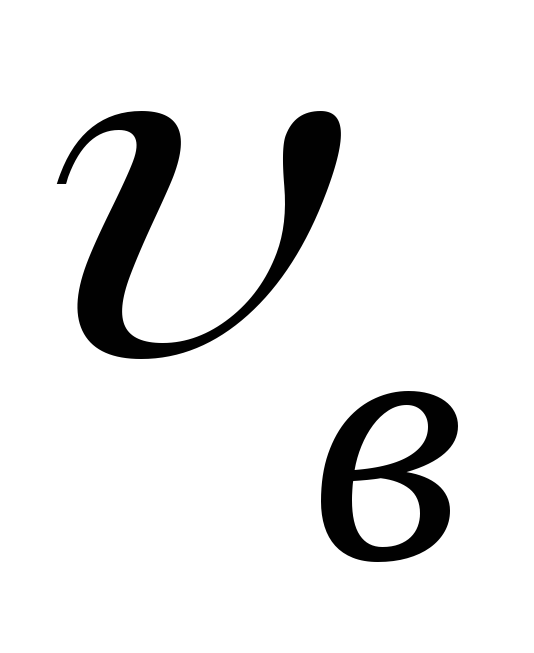   Получите выражение для.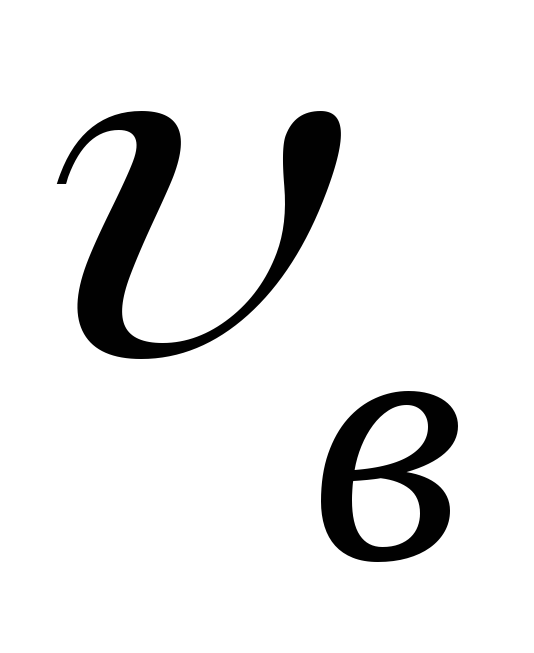
   Как изменяется график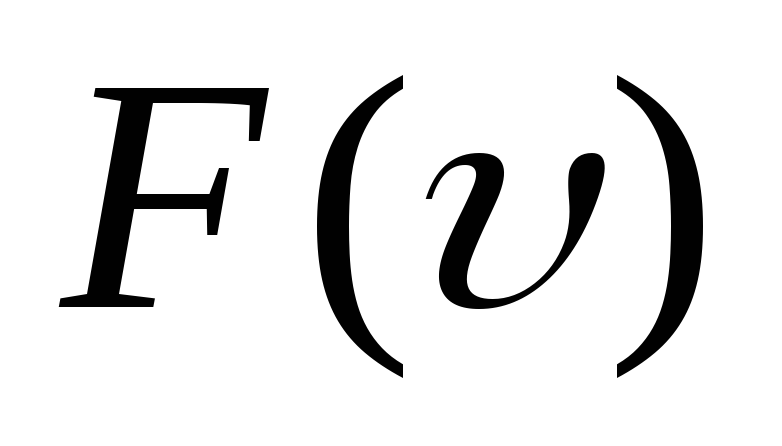при повышении температуры?

9. Получите
   барометрическую формулу. Что она
   определяет?

10. Получите
    зависимость концентрации молекул газа
    в поле силы тяжести от высоты.

11. Запишите
    закон распределения Больцмана а) для
    молекул идеального газа в поле силы
    тяжести; б) для частиц массой m,
    находящихся в роторе центрифуги,
    вращающейся с угловой скоростью
    .

12. Объясните
    физический смысл распределения
    Максвелла-Больцмана.

Лекция №9

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.

Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см³ при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.

Что такое средняя скорость движения молекул

Среднюю скорость движения молекул часто именуют скоростью их теплового движения.

Как определить среднюю квадратичную скорость движения молекул

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]

Ещё одно выражение для среднеквадратичной скорости:

[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

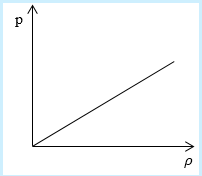
Напомним, что средняя скорость частиц:

[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m₀= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/N_a

PV = (m/μ)*RT = (N/N_a)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/N_a)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]