Загрузить PDF
Загрузить PDF
Скорость является функцией времени и определяется как абсолютной величиной, так и направлением.[1]
Часто в задачах по физике требуется найти начальную скорость (ее величину и направление), которой изучаемый объект обладал в нулевой момент времени. Для вычисления начальной скорости можно использовать различные уравнения. Основываясь на данных, приведенных в условии задачи, вы можете выбрать наиболее подходящую формулу, которая позволит легко получить искомый ответ.
-

1
Используйте подходящее уравнение. При решении физической задачи необходимо знать, какая формула вам понадобится. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, ускорение и время, для определения начальной скорости удобно использовать следующее соотношение:
- Vi = Vf – (a * t)
- В эту формулу входят следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- a — ускорение
- t — время
- Обратите внимание, что это стандартная формула, используемая для вычисления начальной скорости.
-

2
Подставьте в формулу известные величины. Выписав все исходные данные и записав необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Если вы где-либо допустили ошибку, то легко сможете найти ее, просмотрев свои записи.
-

3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для получения искомого результата. Если можно, используйте калькулятор, чтобы снизить вероятность просчетов при вычислениях.
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
- Запишем исходные данные:
- Vi = ?, Vf = 200 м/с, a = 10 м/с2, t = 12 с
- Умножим ускорение на время: a * t = 10 * 12 =120
- Вычтем полученное значение из конечной скорости: Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 м/с на восток
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
-

1
Используйте подходящую формулу. При решении какой-либо физической задачи необходимо выбрать соответствующее уравнение. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- Vi = (d / t) – [(a * t) / 2]
- В эту формулу входят следующие величины:
- Vi — начальная скорость
- d — пройденное расстояние
- a — ускорение
- t — время
-

2
Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Допустив ошибку в решении, вы сможете без труда найти ее, просмотрев свои записи.
-

3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для нахождения ответа. Если возможно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
- Запишем исходные данные:
- Vi = ?, d = 150 м, a = 7 м/с2, t = 30 с
- Умножим ускорение на время: a * t = 7 * 30 = 210
- Поделим произведение на два: (a * t) / 2 = 210 / 2 = 105
- Поделим расстояние на время: d / t = 150 / 30 = 5
- Вычтем первую величину из второй: Vi = (d / t) – [(a * t) / 2] = 5 – 105 = -100 Vi = -100 м/с в западном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
-

1
Используйте подходящее уравнение. Для решения физической задачи необходимо выбрать соответствующую формулу. Первым делом следует записать все начальные данные, указанные в условии задачи. Если известны конечная скорость, ускорение и пройденное расстояние, для определения начальной скорости удобно использовать следующее соотношение:
- Vi = √ [Vf2 – (2 * a * d)]
- Эта формула содержит следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- a — ускорение
- d — пройденное расстояние
-

2
Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Допустив где-либо ошибку, вы сможете без труда найти ее, просмотрев ход решения.
-

3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. По возможности используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
- Запишем исходные данные:
- Vi = ?, Vf = 12 м/с, a = 5 м/с2, d = 10 м
- Возведем в квадрат конечную скорость: Vf2= 122 = 144
- Умножим ускорение на пройденное расстояние и на 2: 2 * a * d = 2 * 5 * 10 = 100
- Вычтем результат умножения из квадрата конечной скорости: Vf2 – (2 * a * d) = 144 – 100 = 44
- Извлечем квадратный корень из полученного значения: = √ [Vf2 – (2 * a * d)] = √44 = 6,633 Vi = 6,633 м/с в северном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
-

1
Выберите подходящую формулу. При решении физической задачи необходимо использовать соответствующее уравнение. Прежде всего следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, время и пройденное расстояние, для определения начальной скорости можно использовать следующее соотношение:
- Vi = Vf + 2 (t – d)
- В данную формулу входят следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- t — время
- d — пройденное расстояние
-

2
Подставьте в формулу известные значения. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Внимательно изучите условие задачи и аккуратно записывайте каждый шаг при ее решении.
- Допустив ошибку, вы сможете без труда найти ее, просмотрев решение.
-

3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. Если можно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект преодолел расстояние 15 метров (49,2 фута) в течение 45 секунд, и его конечная скорость составляет 17 метров (55,8 фута) в секунду. Найдем начальную скорость объекта.
- Запишем исходные данные:
- Vi = ?, Vf = 17 м/с, t = 45 с, d = 15 м
- Вычтем расстояние из времени: (t – d) = (45 – 15) = 30
- Умножим полученное значение на 2: 2 ( t – d) = 2 (45 – 15) = 60
- Прибавим к этой величине конечную скорость: Vf + 2 (t – d) = 17 + 60 = 77 Vi = 77 м/с в южном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Допустим, объект преодолел расстояние 15 метров (49,2 фута) в течение 45 секунд, и его конечная скорость составляет 17 метров (55,8 фута) в секунду. Найдем начальную скорость объекта.
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (необязательно)
Об этой статье
Эту страницу просматривали 149 660 раз.
Была ли эта статья полезной?
Download Article
Download Article
Velocity is a function of time and defined by both a magnitude and a direction. [1]
Often in physics problems, you will need to calculate the initial velocity (speed and direction) at which an object in question began to travel. There are multiple equations that can be used to determine initial velocity. Using the information given in a problem, you can determine the proper equation to use and easily answer your question.
-

1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you have values for the final velocity, acceleration, and time involved, you can use the following equation:[3]
- Initial velocity: Vi = Vf – (a * t)
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- t stands for “time”
- Note that this equation is the standard equation used when finding initial velocity.
-

2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
Advertisement
-

3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.[4]
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
- Write the known information:
- Vi = ?, Vf = 200 m/s, a = 10 m/s2, t = 12 s
- Multiply the acceleration and time. a * t = 10 * 12 =120
- Subtract the product from the final velocity. Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 m/s east
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating east at 10 meters (32.8 ft) per second squared traveled for 12 seconds reaching a final velocity of 200 meters (656.2 ft) per second. Find the initial velocity of that object.
Advertisement
-

1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation.[5]
If you know values for the distance, time, and acceleration, you can use the following equation:- Initial velocity: Vi = (d / t) – [(a * t) / 2]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- d stands for “distance”
- a stands for “acceleration”
- t stands for “time”
-

2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-

3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
- Write the known information:
- Vi = ?, d = 150 m, a = 7 m/s2, t = 30 s
- Multiply the acceleration and time. a * t = 7 * 30 = 210
- Divide the product by two. (a * t) / 2 = 210 / 2 = 105
- Divide the distance by the time. d / t = 150 / 30 = 5
- Subtract your first quotient from the second quotient. Vi = (d / t) – [(a * t) / 2] = 5 – 105 = -100 Vi = -100 m/s west
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating west at 7 meters (23.0 ft) per second squared traveled a distance of 150 meters (492.1 ft) within 30 seconds. Calculate the initial velocity of that object.
Advertisement
-

1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, acceleration, and distance, you can use the following equation:[7]
- Initial velocity: Vi = √ [Vf2 – (2 * a * d)]
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- a stands for “acceleration”
- d stands for “distance”
-

2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-

3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 12 m/s, a = 5 m/s2, d = 10 m
- Square the final velocity. Vf2= 122 = 144
- Multiply the acceleration by the distance and the number two. 2 * a * d = 2 * 5 * 10 = 100
- Subtract this product from your previous one. Vf2 – (2 * a * d) = 144 – 100 = 44
- Take the square root of your answer. = √ [Vf2 – (2 * a * d)] = √44 = 6.633 Vi = 6.633 m/s north
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object accelerating north at 5 meters (16.4 ft) per second squared traveled 10 meters (32.8 ft), ending up at a final velocity of 12 meters (39.4 ft) per second. Calculate the object’s initial velocity.
Advertisement
-

1
Know the right equation to use. In order to solve any physics problem you must know which equation to use. Writing down all of the known information is the first step to finding the right equation. If you are given the final velocity, time, and distance, you can use the following equation:[9]
- Initial velocity: Vi = 2(d/t) – Vf
- Understand what each symbol stands for.
- Vi stands for “initial velocity”
- Vf stands for “final velocity”
- t stands for “time”
- d stands for “distance”
-

2
Fill in the known information. Once you have written the known information and determined the proper equation, you can fill in values for the appropriate variables. Carefully setting up each problem and writing out every step of the process is important.
- If you make a mistake, you can easily find it by looking back at all of your previous steps.
-

3
Solve the equation. With all of the numbers in place, use the proper order of operations to finish the problem. If you’re allowed, use a calculator to limit the number of simple math mistakes.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
- Write the known information:
- Vi = ?, Vf = 3 m/s, t = 15 s, d = 45 m
- Divide distance by time. (d/t) = (45/15) = 3
- Multiply that value by 2. 2 (d/t) = 2 (45/15) = 6
- Subtract final velocity from the product. 2(d/t) – Vf = 6 – 3 = 3 Vi = 3 m/s south
- Write your answer correctly. Include a unit of measurement, usually meters per second or m/s, as well as a direction the object was traveling in. Without providing information about the direction, you only have a measurement of speed rather than velocity.
- For example: An object with a final velocity of 3 meters (9.8 ft) traveled south for 15 seconds and covered a distance of 45 meters (147.6 ft). Calculate the object’s initial velocity.
Advertisement
Add New Question
-
Question
What are the difficulties some people have in understanding acceleration?

Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.

Academic Tutor
Expert Answer
One of the difficulties people face is the unit for acceleration, which is meters per second squared. To understand this with a real-world example, think about a rock being dropped off a cliff. Acceleration due to Earth’s gravity is 9.8 meters per second squared, so we can round up to 10 for this example. Neglecting friction, when you first let go of the rock, its velocity is zero. After one second of falling, the speed of the stone will be 10 meters a second. After two seconds of falling, the speed of the stone will be 20 meters a second. After three seconds of falling, the speed of this will be 30 meters per second. It gains 10 meters a second of speed for each second that it is falling.
-
Question
A bullet of 60 gm is fired using a rifle of mass 12kg. Rifle recoils with a velocity of 2.5m/s. What is the initial velocity?

Kinetic energy -> Kinetic energy
0.5mv^2 -> 0.5mv^2
0.5 x 12 x 2,5^2 = 0.5 x 0.06 x v^2
6 x 6.25 = 0.03 x v^2
37.5 = 0.03 x v^2
sqrt(37.5/0.03) = v
sqrt(1250) = v
v = 35.3 m/s -
Question
If displacement and time are related as s = 3.5t + 5t2, what is the initial velocity?

Initial velocity is 3.5. The equation is s = ut + 1/2at^2, where s – distance, u – inititial velocity, and a – acceleration.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Pencil
- Paper
- Calculator (optional)
About This Article
Article SummaryX
To find initial velocity, start by multiplying the acceleration by the time. Then, divide that number by 2 and write down the quotient you get. Next, divide the distance by the time and write down that quotient as well. Finally, subtract your first quotient from your second quotient to find the initial velocity. To learn how to find initial velocity using the final velocity, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 834,362 times.
Did this article help you?
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!

Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
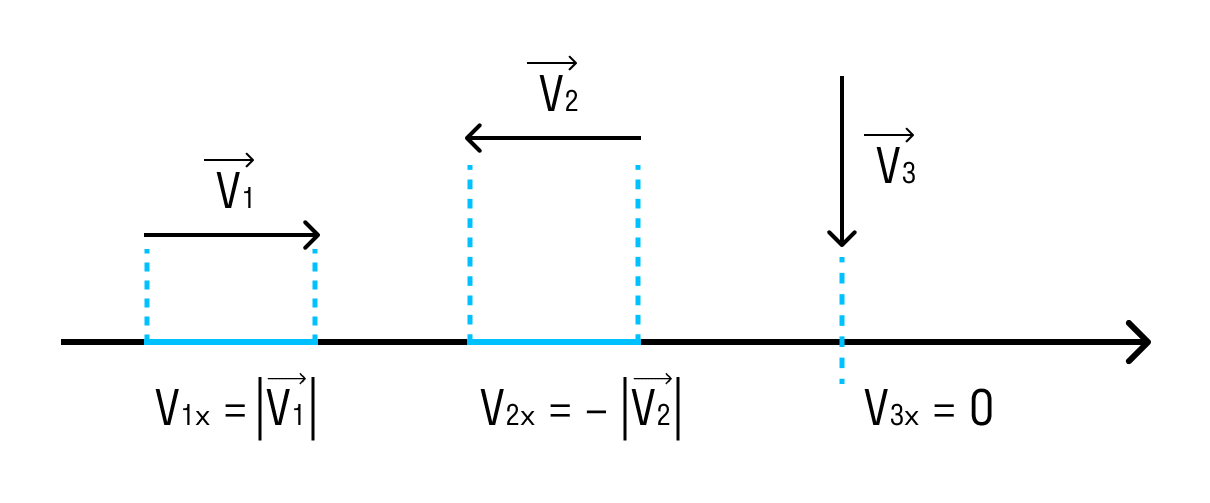
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
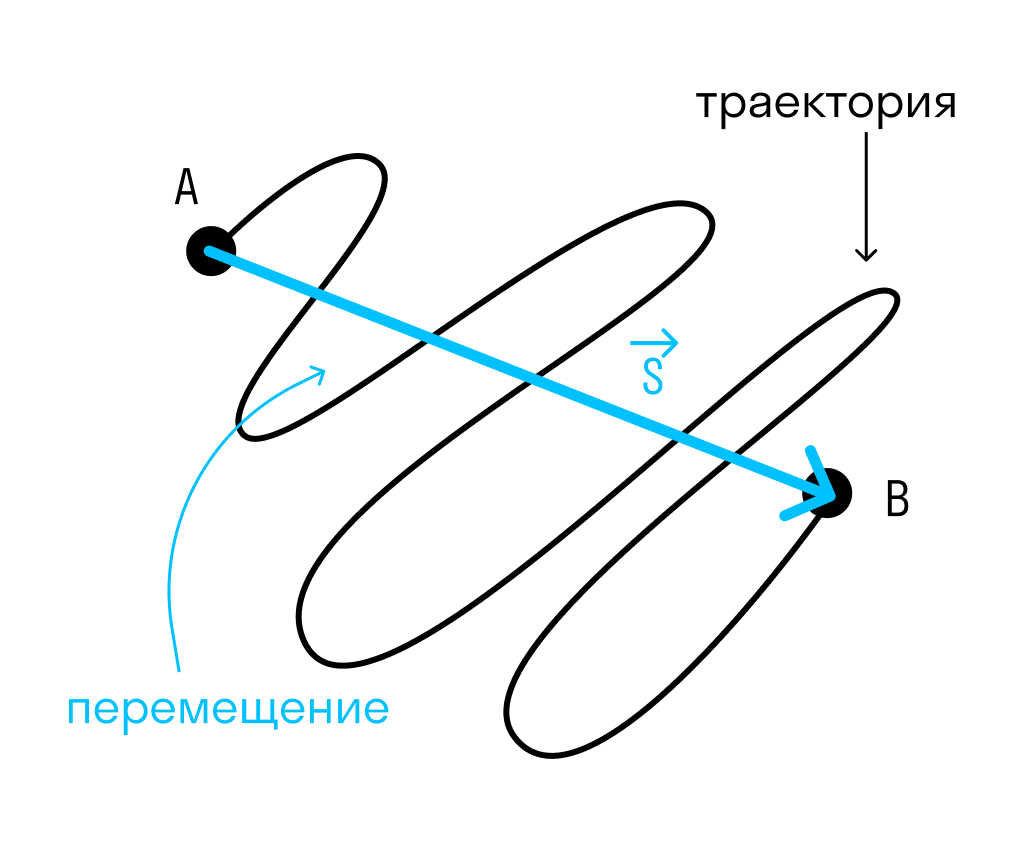
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это
длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) = x0 + vxt
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси
x(t) = x0 − vxt
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
Уравнение движения для равноускоренного движения
x(t) = x0 + v0xt + axt2/2
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с2]
Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:
Формула конечной скорости
— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с2]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места,
. Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt2/2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки:
км
Ответ: через полчаса координата автобуса будет равна 150 км.
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении:![]()
s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение.
Проекция скорости на ось ОХ:
![]()
sx — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы).
Знак модуля скорости зависит от направления вектора скорости и оси координат:
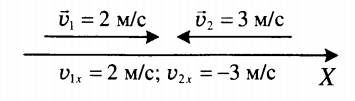
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Дополнительные единицы измерения
- 1 км/ч (километр в час) = 1000 м/3600 с.
- 1 км/мин (километр в минуту) = 1000 м/60 с.
- 1 км/с (километр в секунду) = 1000 м/с.
- 1 м/мин (метр в минуту) = 1 м/60 с.
- 1 см/с (сантиметр в секунду) = 0,01 м/с.
Спидометр — прибор для измерения модули скорости тела.
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:
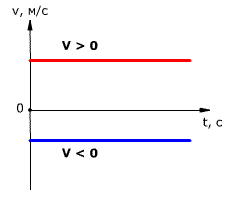
Определение направления движения по графику скорости
- Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
- Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
- Если график скорости совпадает с осью времени, тело покоится.
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
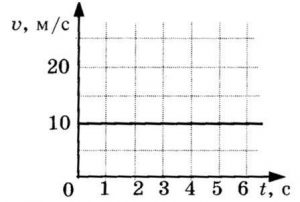
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
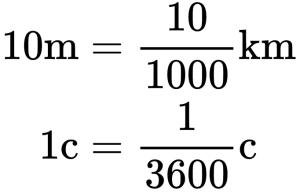
Теперь нужно разделить километры на часы:
![]()
Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.
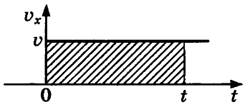
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
![]()
Вектор перемещения равен произведению вектора скорости на время движения:
![]()
Внимание!
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
![]()
График проекции перемещения
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
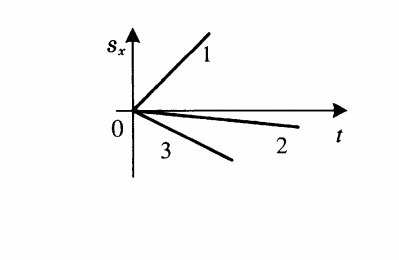
Определение направления движения по графику проекции перемещения
- Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
- Если луч лежит ниже оси времени, тело движется против оси ОХ.
- Если луч совпадает с этой осью, тело покоится.
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
График координаты
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
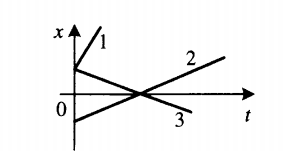
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:![]()
Определение направления движения тела по графику координаты
- Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
- Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
- Если координата не изменяется, тело покоится.
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
Пример №2. График зависимости координаты тела от времени имеет вид:
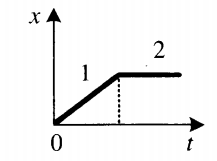
Изучите график и на его основании выберите два верных утверждения:
- На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
- Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
- На участке 1 тело движется равномерно, а на участке 2 оно покоится.
- На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
- Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
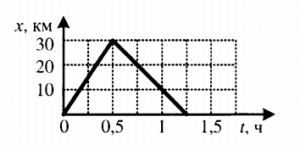
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
1,5 – 0,5 = 1 (час).
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
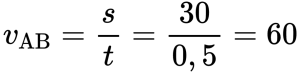
Скорость во время движения от В к А равна:
![]()
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
Задание EF17553
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…

Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18768
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.
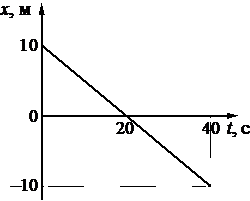
Какой из графиков соответствует зависимости от времени для проекции υx скорости этого тела на ось Ox?
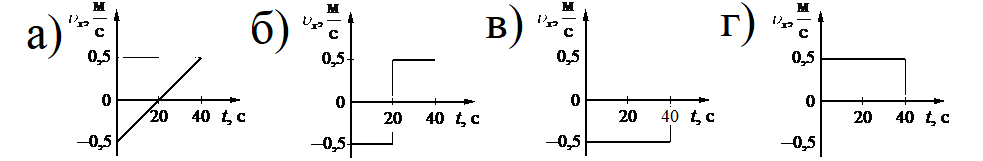
Алгоритм решения
- Записать уравнение координаты при равномерном прямолинейном движении.
- Выразить из уравнения проекцию скорости.
- Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
- Вычислить проекцию скорости.
- Выбрать соответствующий график.
Решение
Уравнение координаты при равномерном прямолинейном движении имеет вид:
![]()
Отсюда проекция скорости равна:
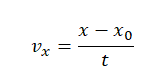
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
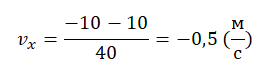
Этому значению соответствует график «в».
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.

Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1 и s2, а затем сложим их:

s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.5k
В данной статьи изложены мысли, которые возникали при решении задач с сайта “Решу ЕГЭ” в разделе – https://phys-ege.sdamgia.ru/test?theme=204. Рисунки взяты оттуда же.
1. Общий подход
Анализ и использование данного графика базируется на формуле перемещения тела S, м:
Как видно из формулы площадь под графиком равна перемещению тела. Например, тело с 1 по 2 секунду на графике, представленном на рис. 1 прошло S = V * t = 2м/с * (2с – 1с) = 2м/с *1с = 2м
2. Чуть посложнее
Если мы захотим найти перемещение тела с начала движения t = 0c до 4-ой секунды движения тела согласно графику на рис. 2, то нам необходимо найти сумму площадей трех геометрических фигур: с 0с по 1с – треугольник, с 1с по 2с прямоугольник, со 2с по 4с – трапеция.
S треугольника = (1/2) * длину высоты треугольника * длину сторону треугольника, к которой проведена высота =
=(1/2) * 2м/с * (1с – 0с) = 1/2 * 2м/с * 1с = 1м
S прямоугольника мы находили в начале статьи = 2м
S трапеции = (1/2) * сумму оснований трапеции * высоту трапеции =
=(1/2) * (2м/с + 6м/с) * (4с – 2с) = (1/2) * 8м/с * 2с = 8м
Итого S = 1м + 2м + 8м = 11м
3. А если скорость равна нулю?
Не стоит пугаться нулевых скоростей на каком-либо интервале времени. Например с 3с по 5с на графике, представленном на рис. 3 перемещение тела равно 0м, т. к. площадь фигуры с 3с по 5с равна 0.
4. А если скорость ушла “в минус”?
А вот отрицательная скорость может вызвать некоторые затруднения. Здесь надо очень внимательно читать задание и не перепутать очень похожие физические величины: путь и перемещение. Путь – величина скалярная и поэтому для ее нахождения с помощью графика на рис. 4 надо зеркально отобразить отрицательные участки скорости и сложить площади фигур (см. Рис. 5)
Перемещение – величина векторная и поэтому при определении этой величины необходимо учитывать знак площади. Например, если нужно найти перемещение тела с 0с по 10с (см. рис. 5), то нужно площадь треугольника с 0с по 4с сложить с площадью треугольника с 8с по 10с и из полученного результата вычесть площадь треугольника с 4с по 8с.
5. Когда можно и не считать!
Иногда требуется визуальный анализ графиков. Например, необходимо определить какой автомобиль из 4-х с 0с до 15с проехал наибольшее расстояние?
Рассматривая площади геометрических фигур под графиками (см. рис. 6) видим, что площадь больше у графика (и машины) №3.
6. Переходим к ускорению
До сих пор мы на линейных графиках с координатами скорости и времени (см. рис. 7) видели скорость, время и перемещение (или путь).
А тут ещё прячется ускорение. Давайте попробуем его найти. Вспоминаем формулу равноускоренного движения
Рассматривая график на рис. 7 определим Vo при t = 0с => Vo = 2м/с.
А теперь возьмём на графике точку в момент времени t = 1c и определим по графику скорость в этот момент времени => V = 4м/с.
Подставляем найденные значения в формулу 2 =>
4м/с = 2м/с + a * 1c => а = (4м/с – 2м/с) / 1с = 2м/с2
Возвращаемся к графику (см. рис. 8)
Теперь мы можем сказать, что на рис. 8 представлен график линейного уравнения V = Vo + a*t = 2 + 2*t. Эти знания расширяют область использования графика на рис. 8. Например мы можем сказать, что при
t = 10c скорость будет равна V = 2м/с + 2м/с2*10с = 22м/с
7. Ищем ускорение на произвольном прямолинейном участке графика
Нас могут попросить найти ускорение тела на произвольном прямолинейном участке графика. Например с 6с по 10с на графике, представленном на рис. 9.
Для этого получим формулу для ускорения, усложнив формулу 2 заменив t на (t – to):
Возвращаемся к поиску ускорения:
а = (5м/с – (-5м/с))/(10с – 6с) = 10м/с / 4с = 2.5м/с2
8. Ищем координаты тела
Зная начальные координаты тела, начальную скорость, ускорение тела и время перемещения можем найти координаты тела в любой момент времен (формула 4)
9. Ищем скорость в пространстве
Мы можем знать значение проекций скорости на оси: х, y и z. Нас могут попросить найти модуль скорости. Ищем по формуле 5:
Для понимания формулы 5 можно представить модуль скорости диагональю параллелепипеда, а проекции скорости сторонами параллелепипеда (см. рис. 11)
Заключение
Пока, это все мысли, которые появлялись во время решения задач в разделе сайта “Решу ЕГЭ” по адресу https://phys-ege.sdamgia.ru/test?theme=204. Пишите в комментариях, если что-то напрашивается добавить.
Автор с благодарностью примет любые пожертвования на развитие канала “От сложного к простому” https://money.yandex.ru/to/4100170126360.

