Как найти скорость в наивысшей точке подъема? Формула или объяснение.
Профи
(579),
закрыт
12 лет назад
Евгений Бубнов
Мудрец
(18039)
12 лет назад
Скорость — это производня от расстояния по времени. Наивысшая точка — это когда скорость меняет свой знак с плюса на минус. Т. е. в наивысшей точке скорость равнап нулю. Геометрический смысл производной — тангенс угла наклона касательной к раектории. В наивысшей токе линия ускорения будет горизонтальна, т. е. нагенс угла наклона тоже будет равен нулю
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
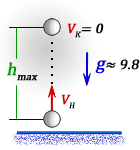
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула максимальной высоты (h max):
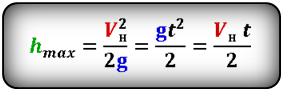
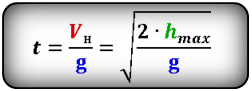
Формула времени за которое тело достигло максимальную высоту (t):
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
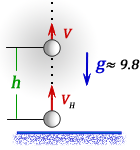
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
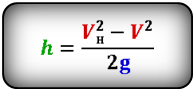
Формула скорости тела в момент времени t (V):
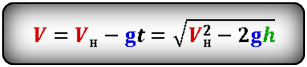
Формула начальной скорости тела (Vн):
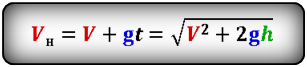
Формулы высоты тела в момент времени t (h):
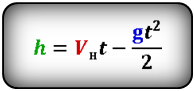
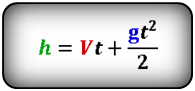
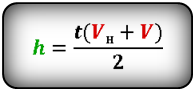
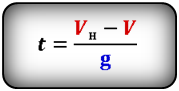
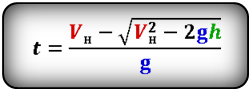
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
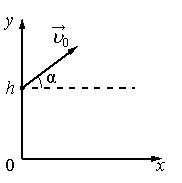
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
![]()
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 42.8k
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:

Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
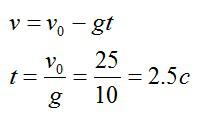
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
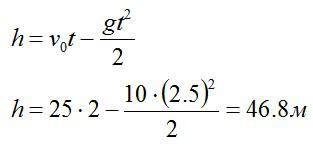
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
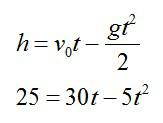
Мы получили квадратное уравнение. Упростим его и найдем корни:
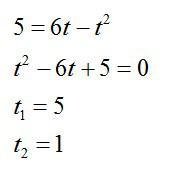
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
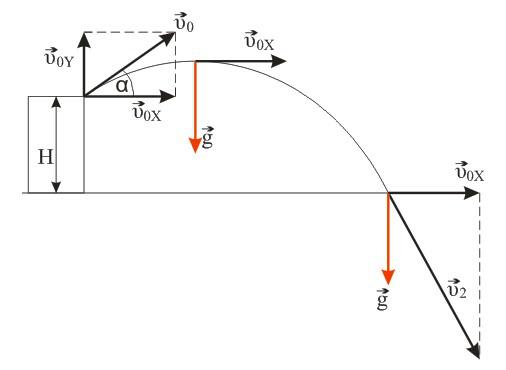
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
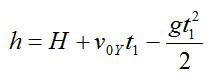
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
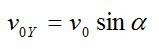
Подставив выражение для скорости в первое уравнение, получим:
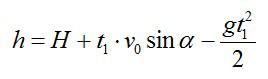
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
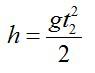
Для высоты дома можно записать:
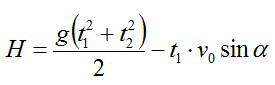
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
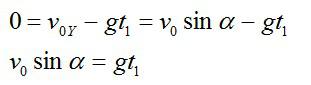
Подставляем в формулу для высоты H и вычисляем:
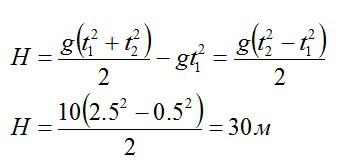
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
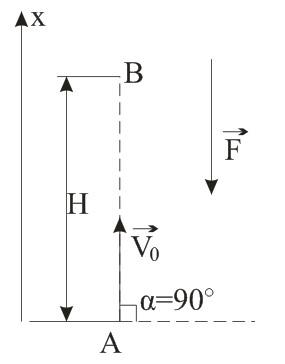
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
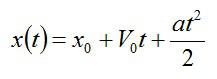
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
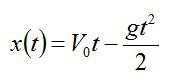
Далее будем использовать еще одно общее кинематическое соотношение:

где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
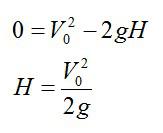
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
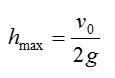
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:

Скорость тела в момент падения с высоты h:
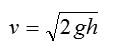
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
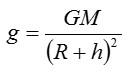
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Рекорд свободного падения для человека на данный момент принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который в 2012 году прыгнул с высоты 39 километров и находился в свободном падении 36 402,6 метра.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
