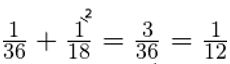Как найти скорость в задаче на работу

2-й способ решения — без таблицы

Как обойтись без составления таблицы?

Сразу составить уравнение.

Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.

Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.

Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.

А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.

Во-первых, сравним формулы:

Движение	Работа
( displaystyle v=frac{S}{t})	( displaystyle P=frac{A}{t})
Скорость движения	Скорость выполнения работы, т.е. производительность
Пройденный путь	Выполненная работа
Потраченное на движение время	Потраченное на работу время

Теперь рассмотрим задачу:

Пример №1

Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.

Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?

Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).

Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:

( displaystyle frac{112}{x}=frac{112}{x+1}+2).

То же самое уравнение! Вот и получается, что работа и движение – одно и то же.

Как решать задачи на совместную работу

Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).

Пример №2

Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).

За какое время они заполнят бассейн, работая вместе?

Решение

Во-первых, давай придумаем аналогию с движением.

Придумал?

Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).

А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.

Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!

Тогда что нас просят найти? Время, через которое они встретятся.

Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.

Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).

Итак,

( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).

Тогда время, за которое с такой производительностью будет выполнена работа ( A):

( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)

Итак, правило:

При совместной работе производительности складываются

А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.

Пример 8

На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?

Решение:

Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).

Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).

Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).

( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.

То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).

Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:

Задачи на совместную работу

Рассмотрим задачи, в которых речь идёт о совместном выполнении некоторой работы. При этом всё равно, какую работу выполняют и чем эту работу измеряют — числом деталей, количеством вспаханных гектаров и т. п. Если, например, некоторая работа выполняется за  10  часов, то за  1  час, очевидно, выполняется    всей работы, а вся работа составляет десять таких частей  .  Поэтому обычно в таких задачах всю работу принято считать равной единице, объём выполненной работы выражают как часть этой единицы.

Под совместной работой можно понимать и одновременную работу двух труб при наполнении бассейна, и прохождение некоторого пути при движении навстречу друг другу и т. п. Метод решения остаётся тем же.

Для решения задач на совместную работу используются уравнения и системы уравнений. Применение уравнений для решения задач в 4 классе является дискуссионым, однако часто без них никак.

Задачи на совместную работу многообразны. Это могут быть и бригады рабочих, выполняющие одну и ту же работу, и трубы, наполняющие бассейн и выводящие из него воду, землекопы, копающие траншеи и пр.

Принципы решения задач на совместную работу схожи с принципами решения задач на движение. В задачах на движение путь – это произведение скорости на время.

В задачах на совместную работу аналогом пройденного пути выступает объём сделанной работы, который вычисляется как скорость производства чего бы то ни было (скорость наполнения воды в бассейне, копания канавы и пр.), умноженная на время.

В задачах на движение скорости двух объектов, движущихся навстречу друг другу, складываются, а в случае, когда один объект догоняет другой, то скорость сближения определяется как разность скоростей двух объектов.

Аналогично в задачах на совместную работу скорости выполнения работ – если это работа в одно направлении, складываются, и вычитаются, если это работы в противоположном направлении. Например, если две трубы заполняют бассейн с определённой скоростью, то для вычисления времени, за который бассейн будет заполнен двумя трубами, надо сложить скорости заполнения каждой из труб – этот случай аналогичен движению объектов навстречу друг другу (у них одна цель, т.е. они делают одну и ту же работу).

Если же у нас из одной трубы в бассейн втекает объём воды с определённой скоростью, а из другой трубы вытекает с другой (меньшей) скоростью, то для нахождения времени заполнения бассейна нам надо из скорости первой трубы вычесть скорость второй трубы. Это аналогично случаю, когда более быстрый объект догоняет более медленный. У них разные цели – один хочет оторваться от преследования, второй хочет его догнать, и их скорости вычитаются. Точно так же у двух труб разные цели – одна хочет бассейн наполнить, а вторая опустошить.

Рассмотрим конкретные примеры.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Задача 1

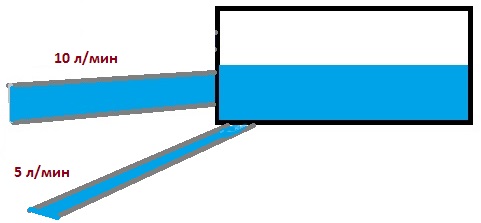
2 трубы наполняют бассейн. Одна со скоростью 5 литров в минуту, вторая со скоростью 10 литров в минуту. Объём бассейна 300 литров. За какое время две трубы наполнят бассейн?

Решение

Две трубы делают одну и ту же работу, поэтому для нахождения суммарной скорость их работы надо сложить скорость наполнения бассейна первой трубой со скоростью наполнения второй трубой.

V = 5 + 10 = 15 л/мин.

Объём бассейна нам известен – 300 л. Следовательно, для того, чтобы найти, за какое время он будет наполнен, надо объём бассейна разделить на скорость наполнения, которую мы только что нашли.

t = 300 / 15 = 20 минут.

Ответ: бассейн наполнится за 20 минут

Задача 2

В изначально пустой бассейн объёмом 400 литров поступает вода из трубы со скоростью 30 литров в минуту. Из второй трубы меньшего диаметра вода вытекает из бассейна со скоростью 20 литров в минуту. За какое время наполнится бассейн?

Решение

В данном случае трубы выполняют противоположную работу, поэтому для нахождения итоговой скорости работы надо из большей скорости вычесть меньшую скорость.

V = 30 – 20 = 10 л/мин

10 л/мин – это итоговая скорость наполнения бассейна. Если у нас за одну минуту в бассейн вылилось 30 литров воды, и за эту же минуту 20 литров вытекло из него, то осталось всего 10 литров – это и есть скорость наполнения.

Время заполнения бассейна водой мы находим аналогично первой задаче:

t = 400/10 = 40 мин.

Ответ: бассейн заполнится за 40 минут

Задача 3

Первая бригада может выполнить задание за 36 ч, а вторая бригада может выполнить то же задание за 18 ч. За сколько часов это задание выполнят две бригады при совместной работе?

Решение. 1 способ – с помощью дробей

В старших классах такая задача решается просто с помощью дробей.

Примем всю работу за единицу, тогда за 1 ч первая бригада выполняет 1/36 работы, а вторая бригада за 1 час сделает 1/18 работы. При совместной работе за 1 ч две бригады выполняют всей работы, поэтому всю работу они выполнят

всей работы. Таким образом, если за 1 час выполняется 1/12 всей работы, то вся работа целиком будет сделана за 12 часов.

Ответ: 12 часов

Решение. 2 способ – по действиям без дробей

Если первая бригада всю работу делает за 36 часов, то мы можем представить, что работа состоит из 36 частей, каждая из которых равна 1 часу.

1. Определим, какую часть работы делает за 1 час первая бригада.

Для этого разделим общее количество частей, из которых состоит работа, на то время, за которое первая бригада делает всю работу

36:36 = 1 часть

2. Определим, какую часть работы делает за 1 час вторая бригада.

Делаем как в первом действии

36:18 = 2 части.

3. Найдём, сколько частей работы делают за один час две бригады в месте

2 + 1 = 3 части

4. Найдём, за какое время обе бригады сделают всю работу.

Для этого общее количество частей (36) разделим на суммарную скорость работы двух бригад, т.е. 3 части в час.

36:3 = 12 часов.

Как видим, при решении вторым способом мы получили тот же ответ, что и при решении с помощью дробей.

Ответ: 12 часов

Одна труба может наполнить бассейн водой за 12 часов, а другая – за 20 часов. За какое время бассейн будет наполнен водой, если две трубы будут работать одновременно?

Решение

В 4-м классе дети дробей ещё не знают, поэтому задачу надо решать через части.

Итак, нам надо всю работу обозначить каким-то количеством частей, и далее, исходя из этого, определить скорость работы труб в частях.

Наиболее простой способ определения количества частей – перемножить 12 на 20 и получить 240 частей. В этом случае скорость работы первой трубы – 20 частей в час (12 – это 1/20 от 240), а скорость второй трубы – 12 частей в час (20 – это 1/12 от 240).

Суммарная скорость работы двух труб: 20+12 = 32 части в час.

Чтобы найти время, за которое наполнится бассейн, надо 240 поделить на 32. Дробных чисел дети в 4-м классе ещё не знают, поэтому поделим нацело 240 на 32 и найдём частное и остаток:

240:32 = 7 остаток 16.

16 – это половина от 32

Суммарная скорость двух труб – 32 части в час, значит 16 частей бассейна заполняются за полчаса, то есть 30 минут.

Ответ – 7 часов 30 минут.

Общее количество частей можно определить не путём перемножения времени работы первой трубы на время работы второй, а путём нахождения наименьшего общего кратного (НОК) этих двух чисел.

Для 12 и 20 НОК равен 60. 60 – наименьшее число, которое без остатка делится и на 12 и на 20.

Таким образом, если вся работа – 60 частей, то

скорость первой трубы – 60:12 = 5 частей в час

скорость второй трубы – 60:2- = 3 части в час.

Суммарная скорость двух труб: 5+3 = 8 частей в час.

Теперь для нахождения времени заполнения бассейна нам надо 60 поделить на 8.

60:8 = 7 остаток 4.

Суммарная скорость двух труб – 8 частей в час, значит 4 части бассейна заполняются за полчаса, то есть 30 минут.

Таким образом, общее время наполнения бассейна – 7 часов 30 минут. Мы получили то же самое время, что и в первом способе, когда у нас вся работа состояла из 240 частей.

Ответ: 7 часов 30 минут

Задача 5

За пять недель пират Ерёма

Способен выпить бочку рома

А у пирата, у Емели

Ушло б на это две недели.

За сколько дней прикончат ром

Пираты, действуя вдвоём?

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Решение

Эту задачу можно решить через дроби. 5 недель – это 35 дней, 2 недели – 14 дней, далее нужно 1/35 (скорость выпивания бочки в день пирата Ерёмы) сложить с 1/14 (скорость Емели), привести дроби к общему знаменателю, получить суммарную скорость в 1/10, и, соответственно, ответ в 10 дней.

Но можно решить эту задачу и без использования дробей.

Аналогично предыдущей задачи про бассейн, выразим всю работу в частях, при этом так, чтобы это число делилось без остатка и на 35 и на 14.

Наименьшее число, которое делится без остатка и на 35 и на 14 – это 70. (Если мы испытываем сложности с нахождением минимального числа, то всегда можно перемножить 35 на 14 и получить 490).

Итак, всю бочку рома мы приняли равной в 70 частей. Акцентирую ваше внимание, что мы вместо 70 могли бы взять любое другое количество частей – это не повлияло бы на логику решения задачи, но, т.к. в 4-м классе дети не умеют работать с дробными числами, то мы берём то число частей, которое без остатка делится на скорость работы всех работников, которые есть в условии задачи. В нашем случае работники – это два пирата, работа которых заключается в выпивании рома.

Таким образом, если Ерёма выпивает всю бочку за 35 дней, то его скорость это

70:35 = 2 части в день

Скорость Емели, который ту же бочку выпивает за 14 дней:

70:14 = 5 частей в день.

Суммарная скорость выпивания рома Ерёмы и Емели – 5 + 2 = 7 частей в день.

Таким образом, если весть объём рома – это 70 частей, а оба пирата за день выпивают 10 частей, то весь ром они выпьют за

70:7 = 10 дней.

Ответ: 10 дней.

Задача 6

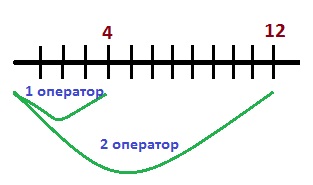
Два оператора могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 4 ч, а второй 12 ч, то они выполнят всю работу. За какое время может набрать весь текст каждый оператор, работая отдельно?

Решение

введём обозначения

x – объём текста, который в час печатает первый оператор

y – объём текста, который в час печатает второй оператор

С одной стороны, весь объём работы можно выразить как

8x + 8y (два оператора набирают текст за 8 часов).

С другой стороны, этот же объём работы:

4x + 12y

Т.к. это одинаковые объёмы работы, то составим уравнение:

8x + 8y = 4x + 12y

8x – 4x = 12y – 8y

4x = 4y

x = y

Отсюда делаем вывод, что операторы работают с одинаковой скоростью.

Рассмотрим случай, когда первый оператор будет работать 4 ч, а второй 12 ч.

Вот схема их работы:

Первые 4 часа оба оператора работают вместе, и за это время они сделают половину всей работы (т.к. работая вместе 8 часов, они сделают всю работу).

После 4 часов работы первый оператор прекращает работать и продолжает работать второй оператор. Всего он по условию задачи работает 12 часов – то есть ещё 8 часов после того, как прошли первые 4 часа.

И если за первые 4 часа сделана половина работы, то оставшиеся 8 часов работы второго оператора – это вторая половина работы.

То есть второй оператор половину работы делает за 8 часов, и, следовательно, всю работу он сделает за 16 часов. Как мы уже выяснили ранее, скорости работы операторов равны, поэтому первый оператор также всю работу выполнит за 16 часов.

Ответ: и первый и второй оператор всю работу по отдельности выполнят за 16 часов.

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Задача 7

Первая труба наполняет резервуар объемом 180 литров, а вторая труба наполняет резервуар объемом 120 литров. При этом известно, что одна из труб пропускает на 1 литр воды в минуту меньше, чем другая. Необходимо определить, сколько литров в минуту пропускает первая труба, если резервуары полностью заполняются за одинаковое время.

Решение

Как мы уже говорили в начале этого урока, принципы решения задач на совместную работу схожи с принципами решения задач на движение.

Рассматриваемая задача схожа с задачами на движение, в которых один объект догоняет другой. Напомню, что в таких задачах, если у нас известно первоначальное расстояние между двумя объектами, и скорости этих объектов, то время, за которое второй объект догонит первый, рассчитывается как первоначальное расстояние, поделённое на скорость сближения объектов, где скорость сближения – разница между скоростью догоняющего объекта и догоняемого.

В этой задаче про два резервуара известно, что они наполняются за одинаковое время, хотя их объёмы разные. То есть скорость наполнения первого, более большого резервуара, очевидно выше, чем скорость наполнения второго, меньшего по объему. Разница между скоростями наполнения известна – 1 литр в минуту.

Таким образом, если проводить аналогии с задачами на движение, где один объект догоняет второй, мы можем сказать, что скорость догона в нашем случае – это тот самый 1 литр в минуту, а первоначальное расстояние между объектами – это разница в объёмах двух резервуаров, то есть 180-120 = 60 л. И чтобы найти, за какое время один объект догонит другой – то есть в нашем случае, когда они полностью заполнятся, надо разницу в объёмах разделить на разницу в скоростях заполнения.

То есть 60/60 = 1 час.

1 час равен 60 минутам.

По условию задачи нам надо определить, сколько литров в минуту пропускает первая труба.

Для этого объём первого резервуара надо поделить на время, за которое он полностью заполняется.

То есть 180 литров /60 минут = 3 литра в минуту.

Ответ: скорость первой трубы – 3 литра в минуту.

Мы понимаем, что приведённые при решении этой задачи рассуждения могут показаться неочевидными. Для того, чтобы вы могли убедиться, что данная методика является верной, проиллюстрируем её на примере с меньшими цифрами.

Пусть у нас есть два бака, один объёмом 15 литров, второй объёмом 18 литров. Первый наполняется со скоростью 5 литров в минуту, а второй – со скоростью 6 литров в минуту.

Несложно подсчитать, что время заполнения у них будет одинаковое – 3 минуты (15:5 = 3, 18:6 = 3).

Эти же три минуты можно получить по другому:

Разница в объёмах баков – 3 литра (18- 15 = 3). Разница в скоростях наполнения – 1 литр в минуту (6 – 5 = 1).

Соответственно, время, за которое второй, более объёмный бак, “догонит” первый, меньший по объёму, составляет 3:1 = 3 минуты.

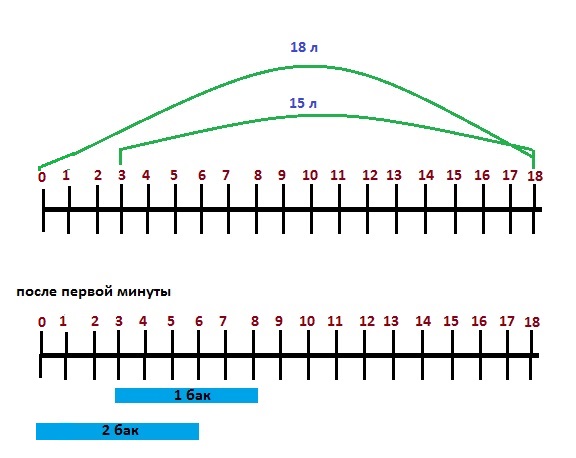
Проиллюстрируем это на рисунке.

На горизонтальной шкале отложим объём – от нуля до 18 литров.

Для первого бака, который объёмом 15 литров, отсчёт будем вести от отметки в 3 л и до 18 л. То есть как будто бы его объём тоже 18 литров, но на три литра он уже заполнен, и осталось заполнить 15 литров.

Таким образом отметка в 3 литра – это первоначальное “расстояние” между двумя баками.

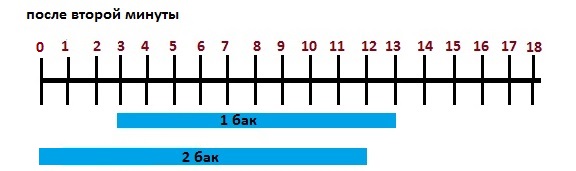
После первой минуты первый бак заполнился на 5 литров, и мы рисуем синюю полоску от отметки 3 л до отметки 8 л. Второй бак заполнился на 6 литров, и мы рисуем синюю полоску от 0 до 6 л. Таким образом, за первую минуту разница в объёмах воды в двух баках (“расстояние” между ними) сократилось с первоначальных 3 литров до 2 литров.

После второй минуты первый бак заполнился ещё на 5 литров (итого за 2 минуты на 10 литров), и мы рисуем синюю полоску от отметки 3 литра до отметки 13 литров. Второй бак заполнился ещё на 6 литров (итого на 12 литров за 2 минуты), и мы рисуем синюю полоску от отметки 0 до 12 литров. Разница в объёмах воды в баках сократилась с 2 литров до 1 литра.

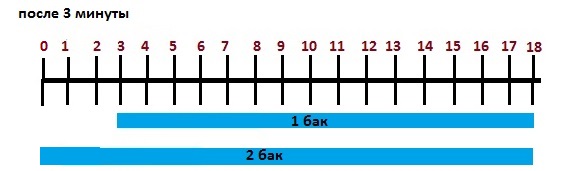
После третьей минуты первый бак заполнился ещё на 5 литров (итого за 3 минуты на 15 литров), и мы рисуем синюю полоску от отметки 3 литра до финальной отметки 18 литров. Второй бак заполнился ещё на 6 литров (итого на 18 литров за 3 минуты), и мы рисуем синюю полоску от отметки 0 до 18 литров. Разница в объёмах воды в баках сократилась с 1 литров до нуля. Оба бака заполнились полностью.

Таким образом, из данного рисунка следует, с каждой минутой разница в объёмах воды в баках сокращается ровно на величину, равную разнице скоростей наполнения баков.

Поэтому применённая нами формула для решения этой задачи, согласно которой время наполнения – это разница в объёмах резервуаров, делённая на разницу скоростей, является рабочей.

Что такое работа?

Работа это первичное понятие и под ним понимают некоторый объем физически выполнимого труда выполняемых людьми или механизмами. Обозначается работа обычно через A или Q. В арифметических задачах всю работу часто принимают за 1 единицу.

Что такое производительность труда?

Производительность труда есть работа выполняемая за одну единицу времени. Обозначается через q и вычисляется как

q=A/t

вся работа делённое на время за которое она выполняется.

Из этой формулы вытекает ещё две:

A= q*t – вся работа равна производительности умноженной на время

t= A/q – время равно всей работе делённой на производительность.

Эти формулы используются для решения задач на работу.

Интересно проследить аналогия между задачами на движение.

Скорость движения тела есть путь пройденный телом за одну единицу времени

v = S/t

Таким образом производительность q = Q/t есть скорость выполнения работы

Также есть аналогия и между ценой товара, стоимостью покупки и его количеством

Ц = C/K

С – стоимость всей покупки

K – количество купленного товара

Ц – цена товара.

Задача 203 б)

примем всю работу за 1 единицу.

1) Если вся работа 1 единица, а первый ученик выполняет её за 20 мин, то его производительность равна 1/20 (по определению производительности)

2) Если вся работа 1 единица, а второй ученик выполняет её за 30 мин, то его производительность равна 1/30 .

3) Если первый ученик имеет производительность 1/20, а второй 1/30, то общая производительность равна сумме 1/20 + 1/30 = 5/60 (т.к. общая производительность равна сумме производительностей ) .

3) Если вся работа 1 единица, а общая производительность равна 5/60, то время за которое выполнят оба ученика работая вместе будет равно
1 : (5/60)= 60 /5 = 12 мин. (т.к. время равно работе делённой на производительность).

Ответ: оба ученика, работая вместе, уберут класс зв 12 минут

Задача 208

Примем всю работу за 1 единицу.

1) Если первая бригада может выполнить единицу работы за 9 дней, то её производительность равна 1/9.

2) Если производительность первой бригада 1/9 и она работала 3 дня то она выполнила 3*(1/9) = 3/9 всей работы.

3) Если выполнено 3/9 работы, то осталось выполнить 1- 3/9 = 6/9 все работы

4) Если вторая бригада может выполнить единицу работы за 12 дней, то её производительность равна 1/12.

4) Если осталось выполнить 6 /9 всей работы с производительностью 1/12, то это займет (6/9) : (1/12) = (6*12)/)9 = 8 дней

5) Если первая бригада работала 3 дня,а вторая 8 дней и выполнили всю работу, то всего было затрачено 3 + 8 = 11 дней.

Ответ: вся работа выполнена за 11 дней.

Задача 212.

Весь воз сена примем за 1 единицу.

1) Если лошадь съедает воз сена за 1 месяц, то её производительность еды равна 1/1 = 1

2) 1) Если коза съедает воз сена за 2 месяца, то её производительность еды равна 1/2

3) Если овца съедает воз сена за 3 месяца, то её производительность еды равна 1/3

4) Если у лошади производительность еды равна 1, у козы 1/2, у овцы 1/3, то их общая производительность еды равна 1+1/2+1/3 = 11/6

5) Если воз сена принят за 1 единицу, а общая производительность равна 11/6, то вместе лошадь, коза и овца съедят воз сена за 1:(11/6) = 6 /11 месяца или приблизительно 30 * 6 /11 = 180 /11 = 16 дней.

Ответ: вместе лошадь, коза и овца съедят воз сена за 6 /11 месяца.

Суть задач на производительность следующая: некоторую работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Они могут выполнять эту работу либо по отдельности, либо совместно друг с другом. Алгоритм решения здесь такой же, как и алгоритм решения задач на движение:

1. Анализ данных.
2. Составление таблицы.
3. Составление уравнения.
4. Решение уравнения.

Основные особенности решения задач на производительность:

• Задачи на производительность схожи с задачами на движение. Основная формула при решении: V = v·t. Сравните её с формулой для решения задач на движение S = v·t. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.
• Объем работы может быть не дан по условию и его не нужно находить при решении задачи (нам просто напросто не важно, какой объем работы выполняется). В таком случае его можно обозначить какой-нибудь буквой, например, V или A. В процессе решения эта переменная, которой мы обозначили объем, сократится и её значение не придется находить.
• Также, если объем работы не дан по условию, удобно принять его просто за 1; тогда время t, требующееся для выполнения всей работы, иv – производительность труда, связаны формулой:

$ t=frac{1}{upsilon}. $

• В отличие от задач на движение, в задачах на производительность скорости выполнения работы не могут вычитаться, а могут только складываться друг с другом. Если два человека или механизма по отдельности работают с производительностями v₁ и v₂, то вместе они будут работать быстрее (никак не медленнее), с суммарной производительностью v₁ + v₂, а время совместной работы будет равно:

$ t=frac{1}{upsilon_{1}+upsilon_{2}} $

Пример:

Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

Решение:

В задаче требуется найти производительность второго рабочего. Примем его скорость за x. Заполним таблицу.

	v, дет/ч	t, ч	V, дет
Первый рабочий	x + 5	$ frac{200}{x+5} $	200
Второй рабочий	x	$ frac{200}{x} $	200

В условии задачи сказано, что первый рабочий выполняет заказ на 2 часа быстрее, чем второй. На основании этого составим уравнение:

$ {frac{200}{x+5}+2=frac{200}{x} frac{200+2x+10}{x+5}=frac{200}{x}.} $

2x² + 210x = 200x + 1000;

x² + 5x – 500 = 0.

Получаем два корня, x₁= 20 и x₂= –25. Второй корень не подходит, так как производительность не может быть отрицательной.

Ответ: 20 дет/ч.

Виды задач на производительность:

1. Задачи на совместную работу:

Задачи на совместную работу — это тип задач, в которых объектами, выполняющими работу, являются люди или группы людей: рабочие, ученики, операторы, бригады рабочих и т п. Объекты могут выполнять работу по отдельности, а могут — вместе.

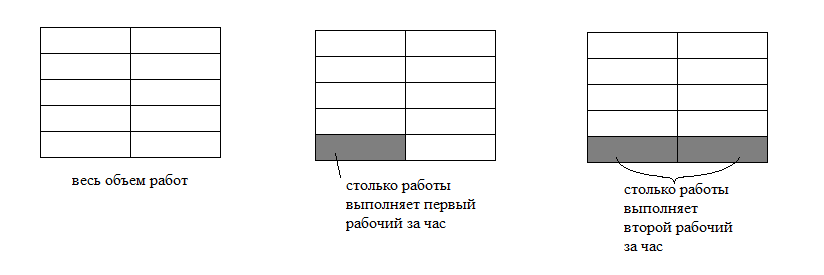
Разберем простой пример. Двум рабочим требуется выполнить работу. Допустим, первый рабочий выполняет всю работу за 10 часов, а второй — за 5. Давайте найдем, за сколько часов рабочие справятся с работой, выполняя её вместе.

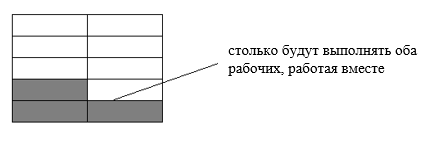
Получается, что если принять весь объем работ за 1, то первый рабочий выполняет $ frac{1}{10} $ всей работы за час, а второй $ frac{1}{10} $ то есть $ frac{1}{10} $ всей работы за час. На рисунке весь объем работ — это 10 «кирпичиков», первый выполняет 1 «кирпичик» за час, а второй — 2. Тогда вместе они будут выполнять $ frac{1}{10}+ frac{1}{5}= frac{3}{10} $  всей работы за час, или 3 «кирпичика»:

Чтобы найти совместную производительность рабочих, мы сложили друг с другом их собственные производительности. Теперь, чтобы найти время, за которое оба рабочих справятся с работой, выполняя её вместе, разделим полный объем работ на совместную производительность:

$ 1/frac{3}{10}=frac{10}{3}=3frac{1}{3} $

То есть вместе рабочие справятся с работой за 3 $ frac{1}{3} $ часа, или за 3 часа 20 минут.

2. Задачи на бассейны и трубы:

Отдельно можно выделить группу задач на производительность — задачи на заполнение бассейна несколькими трубами. В таких задачах рабочим будут соответствовать насосы (или трубы) разной производительности, а объему работы — объем бассейна или иного резервуара.

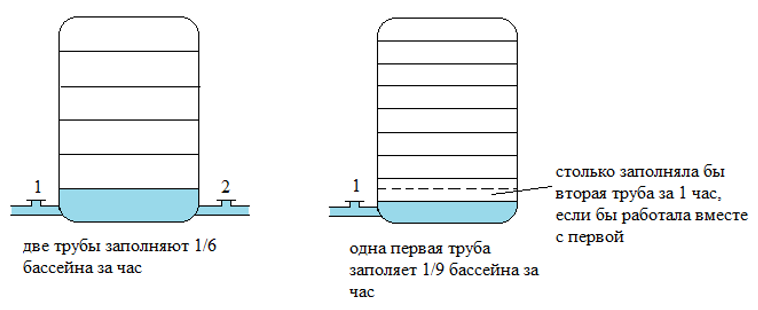
Рассмотрим пример. Две трубы наполняют бассейн за 6 часов, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?

Получается, что за 1 час две трубы наполняют $ frac{1}{6} $ часть бассейна, а одна первая труба наполняет $ frac{1}{9} $ часть бассейна: Так как вместе трубы наполняют бассейн водой со скоростью, равной сумме скоростей отдельно каждой из труб, то вторая труба наполняет бассейн со скоростью $ frac{1}{6}- frac{1}{9}= frac{1}{18} $.

Таким образом, вторая труба заполнит бассейн за $ 1/frac{1}{18}=18 $ часов.