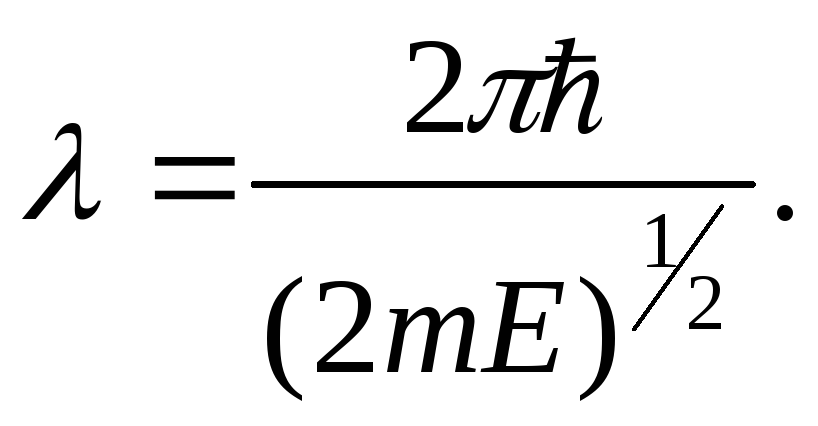Как найти скорость волны де бройля - Сайт, где вы сможете решить свои вопросы

Квантовая механика
Введение^[en] История^[en] Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект Эффект Комптона
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Представление фазового пространства Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Локальная^[en] Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения Глоссарий^[en] ЭПР-парадокс
См. также: Портал:Физика

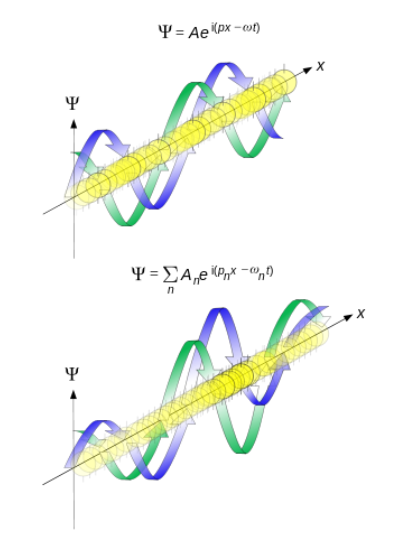
Волна́ де Бро́йля — волна вероятности (или волна амплитуды вероятности^[1]), определяющая плотность вероятности обнаружения объекта в заданном интервале конфигурационного пространства. В соответствии с принятой терминологией говорят, что волны де Бройля связаны с любыми частицами и отражают их волновую природу.

Идея о волнах, связанных не только с квантами света, но и массивными частицами, предложена Луи де Бройлем в 1923—1924 годах^[2] и называется гипотезой де Бройля. Хотя трактовка квадрата модуля амплитуды волны как плотности вероятности в конфигурационном пространстве принадлежит Максу Борну^[3], по традиции и в знак признания заслуг французского физика говорят о волнах де Бройля.

Идея волн де Бройля полезна для приблизительных выводов о масштабах проявления волновых свойств частиц, но не отражает всей физической реальности и потому не лежит в основе математического аппарата квантовой механики. Вместо дебройлевских волн эту роль в квантовой механике выполняет волновая функция, а в квантовой теории поля — полевые операторы.

Корпускулярно-волновой дуализм фотонов и массивных частиц[править | править код]

Физика атомов, молекул и их коллективов, в частности кристаллов, а также атомных ядер и элементарных частиц изучается в квантовой механике. Квантовые эффекты являются существенными, если характерное значение действия (произведение характерной энергии на характерное время или характерного импульса на характерное расстояние) становится сравнимым с hbar (постоянная Планка). Если частицы движутся со скоростями много меньше, чем скорость света в вакууме , то применяется нерелятивистская квантовая механика; при скоростях, близких к , — релятивистская квантовая механика.

В основе квантовой механики лежат представления Планка о дискретном характере изменения энергии атомов, Эйнштейна о фотонах, данные о квантованности некоторых физических величин (например, импульса и энергии), характеризующих в определённых условиях состояния частиц микромира. В то же время было твёрдо установлено, что свет проявляет свойства не только потока частиц, но и волны, то есть обладает корпускулярно-волновым дуализмом.

Де Бройль выдвинул идею о том, что волновой характер распространения, установленный для фотонов, имеет универсальный характер. Он должен проявляться для любых частиц, обладающих импульсом . Все частицы, имеющие конечный импульс , обладают волновыми свойствами, в частности, подвержены интерференции и дифракции^[4].

Природа волн де Бройля[править | править код]

Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определённые места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль.

Формулы де Бройля[править | править код]

Формула де Бройля устанавливает зависимость длины волны lambda , связанной с движущейся частицей вещества, от импульса частицы, а полной энергии — от частоты , в виде релятивистски инвариантных соотношений:

${displaystyle lambda ={frac {h}{p}},}$

где — постоянная Планка.

Другой вид формул де Бройля:

${mathbf {p}}={frac {h}{2pi }}{mathbf {k}}=hbar {mathbf {k}},$

где ${mathbf {k}}={frac {2pi }{lambda }}{mathbf {n}}$ — волновой вектор, модуль которого $k={frac {2pi }{lambda }}$ — волновое число — есть число длин волн, укладывающихся на 2pi единицах длины, — циклическая частота, — единичный вектор в направлении распространения волны, ${displaystyle hbar ={frac {h}{2pi }}approx 1{,}05cdot 10^{-34}}$ Дж·с.

Полная энергия ${displaystyle E=E_{K}+m_{0}c^{2}}$ включает кинетическую энергию $E_{K}$ и энергию покоя ${displaystyle E_{0}=m_{0}c^{2}}$ , в терминах которых

${displaystyle lambda ={frac {h}{p}}=hc[E_{K}(E_{K}+2m_{0}c^{2})]^{-1/2},}$

где hc=1240 эВ×нм, и значения ${displaystyle m_{0}c^{2}}$ равны 0 для фотона и других безмассовых частиц, ${displaystyle m_{e}c^{2}=}$ 511 кэВ для электрона, и ${displaystyle m_{p}c^{2}=}$ 938 МэВ для протона.

Нерелятивистский предел[править | править код]

У частиц с дорелятивистскими энергиями, движущимися со скоростью vll c (скорости света), для импульса справедлива формула p=mv (где — масса частицы), для кинетической энергии ${displaystyle W=E-mc^{2}}$ — формула ${displaystyle W=mv^{2}/2}$ . Тогда длина волны де Бройля

${displaystyle lambda ={frac {h}{p}}={frac {h}{mv}}={frac {h}{sqrt {2mW}}}.}$

В частности, для электрона, который ускорился в электрическом поле с разностью потенциалов вольт

${displaystyle lambda ={frac {12{,}25}{sqrt {Delta varphi }}};mathrm {AA} .}$

Ультрарелятивистский предел[править | править код]

Для частиц в ультрарелятивистском случае, когда их скорость близка к скорости света, ${displaystyle vrightarrow c,Egg mc^{2}}$ , длины волны равна ${displaystyle lambda ={frac {hc}{E}}}$ ^[5].

Формулы де Бройля для четырёх векторов[править | править код]

В четырёхмерном виде формулы де Бройля связывают четырёхвектор энергии-импульса ${displaystyle p^{mu }}$ с четырёхмерным волновым вектором и имеют вид^[6]:

${displaystyle p^{mu }={begin{pmatrix}p_{0}\p_{1}\p_{2}\p_{3}end{pmatrix}}={begin{pmatrix}E/c\p_{x}\p_{y}\p_{z}end{pmatrix}}=hbar {begin{pmatrix}omega /c\k_{x}\k_{y}\k_{z}end{pmatrix}}.}$

Энергия и импульс любого материального объекта связаны соотношением:

${displaystyle {frac {E^{2}}{c^{2}}}=m^{2}c^{2}+p_{x}^{2}+p_{y}^{2}+p_{z}^{2}.}$

Аналогичным соотношением связаны частота и волновой вектор^[6]:

${displaystyle {frac {omega ^{2}}{c^{2}}}={frac {m^{2}c^{2}}{hbar ^{2}}}+k_{x}^{2}+k_{y}^{2}+k_{z}^{2},}$

где ${displaystyle {frac {mc}{hbar }}}$ — комптоновское волновое число, обратное приведенной комптоновской длине волны ${displaystyle {frac {lambda _{C}}{2pi }}.}$

Фазовая и групповая скорость волн де Бройля[править | править код]

Фазовая скорость волн де Бройля свободной частицы

${displaystyle v_{f}={frac {omega }{k}}={frac {E}{p}}={frac {mc^{2}}{mv}}={frac {c^{2}}{v}}simeq {frac {c^{2}}{h}}mlambda ={frac {c^{2}p^{2}}{2Wh}}lambda .}$

Последние соотношения — нерелятивистское приближение. Зависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию. Фазовая скорость $v_{f}$ волны де Бройля хотя и больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).

Групповая скорость волны де Бройля равна скорости частицы :

$u={frac {domega }{dk}}={frac {dE}{dp}}=v$

Иллюстрация[править | править код]

Иллюстрация волны де Бройля

Для частицы массой , покоящейся в инерциальной системе отсчёта псевдоевклидовой плоскости 4-пространства Минковского, движущейся со скоростью относительно условно неподвижной системы вдоль положительного направления оси , формула квантовомеханической амплитуды вероятности обнаружить её в каком-либо месте пространства всюду одна и та же. Однако фаза — есть функция времени:

${displaystyle ae^{(-iomega _{0})t'}}$

,^[7]

где: ${displaystyle omega _{0}={frac {E_{0}}{hbar }}={frac {mc^{2}}{hbar }}={frac {2pi cdot c}{lambda _{C}}}}$ ;

Здесь: omega_0 — частота изменения фазы;

$E_{0}$

— энергия покоящейся частицы;

$hbar ={frac {h}{2pi }}$

— приведённая постоянная Планка:

— скорость света;

${displaystyle lambda _{C}={frac {h}{mc}}}$

— комптоновская длина волны покоящейся частицы массой

^[8].

На рисунке обозначено:
${displaystyle lambda _{C}=O'A_{1}}$ . Линиями равных фаз в этой системе будут линии одновременности, проведённые через точки временной оси параллельно пространственной оси . Эти линии представляют собой плоскую волну, которая описывается волновой функцией

${displaystyle psi _{(x',t')}=ae^{(-iomega _{0})t'}=ae^{(-i/hbar )E_{0}t'}}$

;

На Рисунке 1 показаны только две линии равных фаз, проведённые через точки $A_{1}$ и $A_{2}$ , в которых фазы амплитуды вероятности имеют то же значение, что и в точке , принятой за начальное.
Для нештрихованной системы отсчёта фаза амплитуды вероятности обнаружить частицу в какой-либо точке является уже функцией не только времени, но и пространства^[7].

Линии равных фаз системы пересекают как временную, так и пространственную оси системы , разбивая при этом каждую из них на равные отрезки.

Фаза амплитуды вероятности является инвариантной величиной. Это означает, если в штрихованной системе в пространственно-временных точках $C_{1}$ и B_1 фаза отличается на целое число 2pi относительно фазы в точке , то и в нештрихованной системе в этих точках фазы должны отличаться на то же число 2pi .^[8] Отсюда следует, что отрезки по осям и представляют собой длины волн как во времени, так и в пространстве.

Согласно релятивистской концепции, применяя преобразования Лоренца,^[9] из рисунка следует:

${displaystyle OC_{1}=O'A_{1}{sqrt {1-(V/c)^{2}}}=cT=lambda _{C}{sqrt {1-(V/c)^{2}}}}$

где: — период изменения фазы в нештрихованной системе.
Из последнего равенства этой цепочки равенств следует:

где: omega — круговая частота изменения фазы в системе ;

${displaystyle E=mc^{2}/{sqrt {1-(v/c)^{2}}}}$

— полная энергия частицы в системе отсчета

;

Здесь учтено, что скорость частицы равна скорости перемещения штрихованной системы, в которой эта частица покоится.

Из треугольника ${displaystyle OB_{1}C_{1}}$ , принимая во внимание, что ${displaystyle operatorname {tgalpha } ={frac {V}{c}}}$ и учитывая, что , получим:

${displaystyle B_{1}O={frac {lambda _{C}{sqrt {1-(v/c)^{2}}}}{operatorname {tgalpha } }}={frac {h}{p}}=lambda }$

где: lambda — длина волны де Бройля;

— импульс частицы.

Выражение для фазы амплитуды вероятности волны де Бройля в системе можно получить, используя преобразование Лоренца для времени при переходе из штрихованной системы к нештрихованной:

${displaystyle t'={frac {t-(V/c^{2})x}{sqrt {1-(V/c)^{2}}}}}$

;

Заменив на в выражении для амплитуды в штрихованной системе отсчета, получим:

${displaystyle ae^{(-i/hbar )E_{0}t'}=ae^{-{(i/hbar )left[left(E_{0}t/{sqrt {1-(V/c)^{2}}}right)-left(E_{0}Vx/{c^{2}{sqrt {1-(V/c)^{2}}}}right)right]}}}$

;

Отождествляя полную энергию частицы ${displaystyle E=E_{0}/{sqrt {1-(v/c)^{2}}}}$ и её импульс ${displaystyle p=E_{0}v/c^{2}{sqrt {1-(v/c^{2}}}}$ с полученным при преобразовании выражением для фазы, учитывая, что , формула амплитуды волны де Бройля запишется так:

${displaystyle ae^{-{(i/hbar )left[Et-pxright]}}}$

;^[7]

Фазовая скорость волны, то есть скорость, с которой перемещаются точки волны с постоянной фазой (например, на Рисунке 1 перемещение одноимённой фазы из точки B_1 в точку $C_{1}$ ) определяется непосредственно из треугольника ${displaystyle OB_{1}C_{1}}$ :

${displaystyle v_{f}={frac {c^{2}}{v}}}$

;

Монохроматическая волна де Бройля характеризуется соотношениями и . То есть, такой волновой объект имеет вполне определённый импульс и совершенно неопределённую область локации.^[10] Именно это и содержится в утверждении, когда говорится, что существует одинаковая амплитуда вероятности обнаружить частицу во всех точках пространства.

Явление корпускулярно-волнового дуализма присуще всем видам материи, но в разной степени. Частице массой ${displaystyle m=10^{-5}}$ г, движущейся со скоростью м/с, соответствует волна де Бройля с длиной волны ${displaystyle lambda =6{,}6cdot 10^{-22}}$ см. Такие длины волн лежат за пределами доступной наблюдению области. Поэтому в механике макроскопических тел волновые свойства несущественны и не учитываются.^[8]

Зависимость длины волны от скорости частицы[править | править код]

Механизм изменения длины волны де Бройля в зависимости от изменения скорости частицы заключается в следующем.

При возрастании скорости перемещения штрихованной системы, которая является собственной для покоящейся в ней частицы, координатные оси этой системы словно лезвия ножниц, вращаясь относительно начала , поворачиваются в сторону положения биссектрисы квадранта, образованного положительными направлениями осей нештрихованной системы.^[9] Точка $A_{1}$ (Рисунок 1) пересечения временной оси ct' с инвариантной (единичной) гиперболой^[9] ${displaystyle lambda _{C}^{2}=c^{2}t^{2}-x^{2}}$ , которая определяет длину в штрихованной системе, неограниченно приближается к биссектрисе квадранта, принимая бесконечные положительные значения координатных осей и . При этом, линия одновременности (линия равных фаз), проведенная через эту точку, стремится к положению биссектрисы, и точка B_1 пересечения этой линии с осью устремляется к началу O. То есть, при длина волны , а импульс частицы ${displaystyle p=mv/{sqrt {1-(v/c)^{2}}}rightarrow infty }$ .

При уменьшении скорости перемещения собственной системы отсчёта частицы — координатные оси этой системы опять же, словно лезвия ножниц, раздвигаются относительно положения биссектрисы квадранта. Угол alpha наклона оси ct' к оси и оси к оси стремится к нулю. Точка $A_{1}$ пересечения единичной гиперболы с осью времени штрихованной системы приближается к точке . При этом, линия равных фаз штрихованной системы, проведённая через точку $A_{1}$ , стремится к параллельности с осью , а точка B_1 пересечения этой линии с осью устремляется в бесконечность в сторону отрицательных значений оси . Это означает, что при длина волны , а импульс частицы . В этом предельном случае фаза амплитуды вероятности будет уже функцией только времени. И параметром волны будет комптоновская длина волны ${displaystyle lambda _{C}=OA}$ .

Подытоживая результаты обоих предельных случаев, когда произведение длины волны и импульса частицы принимает вид неопределённостей типов и можно утверждать: , что находит своё подтверждение в соотношении де Бройля: ${displaystyle lambda ={frac {h}{p}}}$ .

Экспериментальная проверка[править | править код]

Гипотеза де Бройля объясняет ряд экспериментов, необъяснимых в рамках классической физики^[11]:

Опыт Дэвиссона — Джермера по дифракции электронов на кристаллах никеля.
Опыт Дж. П. Томсона по дифракции электронов на металлической фольге.
Эффект Рамзауэра аномального уменьшения сечения рассеяния электронов малых энергий атомами аргона.
Дифракция нейтронов на кристаллах (опыты Г. Хальбана, П. Прайсверка и Д. Митчелла).

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным. Впрочем, наблюдать квантовые эффекты можно и в макроскопическом масштабе, особенно ярким примером этому служат сверхпроводимость и сверхтекучесть.

См. также[править | править код]

Волновой пакет
Комптоновская длина волны
Ток вероятности

Примечания[править | править код]

↑ Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике. Вып. 3–4, 1976, с. 221–222, 412.
↑ Louis de Broglie «The Reinterpretation of Wave Mechanics» Foundations of Physics, Vol. 1 No. 1 (1970) (недоступная ссылка)
↑ М. Борн. Размышления и воспоминания физика: Сборник статей / Отв. ред. Э. И. Чудинов. — М.: Наука, 1977. — С. 16. — 280 с.
↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — С. 17-18
↑ Волна де Бройля — статья из Физической энциклопедии
↑ ¹ ² Паули В. Общие принципы волновой механики. — М.: ОГИЗ, 1947. — С. 14
↑ ¹ ² ³ Фейнман Ричард Филлипс. Том 3. Квантовая механика Архивная копия от 2 марта 2021 на Wayback Machine Гл. 5. § 1, § 2.
↑ ¹ ² ³ Вихман Э. Квантовая физика. — М.: Наука, 1977. — С. 156—157, 185, 187—188. — 415 с.
↑ ¹ ² ³ Угаров В. А. Специальная теория относительности. – М.: Наука, 1977, – С. 60 – 62, 64 – 65, 121 – 124. – 384 с.
↑ Г. А. Зисман, О. М. Тодес. Курс общей физики, том III. — М.: Наука, 1972. — С. 282—283. — 496 с.
↑ Архивированная копия. Дата обращения: 25 декабря 2009. Архивировано из оригинала 26 апреля 2009 года.Архивированная копия. Дата обращения: 25 декабря 2009. Архивировано из оригинала 26 апреля 2009 года.

Литература[править | править код]

Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Вып. 3–4. — 3-е изд. — М.: Мир, 1976. — 496 с.
www.e-libra.su/read/464761-tom-3-kvantovaya-mehanika.html# — Фейнман Ричард Филлипс. Том 3. Квантовая механика читать онлайн. Гл. 5. § 1, § 2.

Ссылки[править | править код]

Волны де Бройля / лекция «Элементы квантовой механики»
Соотношение де Бройля // «Элементы»

Источник

Как определить длину волны де Бройля для электрона

Содержание:

Волна де Бройля или волна амплитуды вероятности
Природа волн де Бройля, фазовая и групповая скорость
Какой формулой определяется длина волны
Как определить длину волны де Бройля для электрона

Волна де Бройля или волна амплитуды вероятности

Волна де Бройля является волной вероятности или волной амплитуды вероятности, которая определяет плотность вероятности обнаружения объекта в конкретной точке конфигурационного пространства.

Согласно определения волн де Бройля, можно сделать вывод об их взаимодействии с какими-либо частицами и их волновой природе. Формулировка волн материи была введена в науку в 1924 году французским физиком-теоретиком Луи де Бройлем. Благодаря теории, свойство корпускулярно-волнового дуализма (или двойственности) было распространено на любые проявления материи, включая излучение и какие-либо частицы вещества.

В современной квантовой теории «волна материи» понимается несколько иначе. Однако название данного физического феномена, связанного с частицами вещества, включая водород, сформулировано в честь автора гипотезы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В 1913 году Н. Бор предложил полуклассическую модель атома, в основе которой было два постулата:

Момент импульса электрона в атоме строго определен. Величина в любом случае пропорциональна nh/2π, где n – какое-либо целое число, начиная с 1, а h – постоянная Планка, присутствие которой в формуле ясно свидетельствует о том, что момент импульса частицы квантован. Таким образом, атом включает комплекс разрешенных орбит, по которым только и может перемещаться электрон. Когда электрон расположен на этих орбитах, излучение (то есть потеря энергии) отсутствует.
Атомный электрон излучает или поглощает энергию в процессе перехода с одной орбиты на другую в количестве, определяемом, как разность энергий на этих орбитах. В связи с тем, что промежуточные состояния между разрешенными орбитами отсутствуют, излучение строго квантуется. Показатель его частоты составляет (E1 – E2)/h, что является выводом из формулы Планка для энергии E = hν.

Таким образом, боровская модель атома не предусматривает излучение электрона на орбите, его нахождение между орбитами. Однако согласно простой рассматриваемой модели, движение электрона рассматривают с классической точки зрения, как вращение планеты вокруг Солнца.

В процессе поиска ответа на вопрос о поведении электрона Де Бройль предположил, что электрону в любом случае должна соответствовать определенная волна. Благодаря ей, частица «выбирает» исключительно такие орбиты, на которых данная волна укладывается целое число раз. В этом и заключался смысл целочисленного коэффициента в постулированной Бором формуле.

Гипотеза приводит к выводу, что электронная волна де Бройля не является электромагнитной, а волновые параметры должны быть характерны для любых материальных частиц, а не только для электронов в атоме. Ученому удалось получить важное соотношение, с помощью которого можно определить тип этих рассматриваемых волновых свойств. Формула расчета волны де Бройля:

(λ = h/p)

где λ – является длиной волны, p – определяет импульс частицы в уравнении.

Де Бройль объединил в одном соотношении корпускулярную и волновую характеристики материи: такие, как импульс и длина волны. Данные параметры связывает постоянная Планка, величина которой примерно составляет (6,626*10^{-27} эрг∙с) или (6,626*10^{-34} Дж∙с), задающая масштаб проявления волновых свойств вещества.

Природа волн де Бройля, фазовая и групповая скорость

Следует отметить, что волны де Бройля, называемые электронными волнами, не являются электромагнитными. В 1927 году американским физикам Дэвиссону и Джермеру удалось подтвердить гипотезу де Бройля. Ученые обнаружили дифракцию электронов на кристалле никеля. В процессе получилось определить дифракционные максимумы, которые соответствуют формуле Вульфа-Брэггов:

(2dsinj = nl)

Расчет брэгговской длины волны подтвердил ее соответствие формуле:

Расчет брэгговской длины волны

Источник: bog5.in.ua

Дифракционная картинка

Источник: bog5.in.ua

В дальнейшем гипотеза де Бройля была подтверждена опытным путем Л.С. Тартаковским и Г. Томсоном. Ученым удалось зафиксировать дифракционную картину, когда пучок быстрых электронов при Е≈ 50 кэВ проходит сквозь фольгу из разных металлов.

Чуть позже получилось обнаружить дифракцию нейтронов, протонов, атомных пучков и молекулярных пучков. В дальнейшем были изобретены инновационные методики исследования вещества, включая нейтронографию и электронографию, сформировалось направление электронной оптики.

Макротела должны характеризоваться аналогичными свойствами. В случае, если m = 1кг, (l = 6,62*10^{-31} м) – невозможно обнаружить современными методами – поэтому макротела рассматриваются только в качестве корпускул.

В том случае, когда частица с массой m перемещается со скоростью v, фазовая скорость волн де Бройля будет определяться по формуле:

фазовая скорость волн де Бройля

Источник: bog5.in.ua

волновое число

Источник: bog5.in.ua

Исходя из того, что c > v, фазовая скорость волн де Бройля превышает скорость света в вакууме. Можно отметить, что фазовая скорость Vф может быть больше и может быть меньше с, в отличие от групповой скорости. Формула групповой скорости:

Формула групповой скорости

Источник: bog5.in.ua

Скорость

Источник: bog5.in.ua

Таким образом, групповая скорость волн де Бройля соответствует скорости движения частицы. В случае фотона она будет равна:

групповая скорость волн де Бройля соответствует скорости движения частицы

Источник: bog5.in.ua

В результате, значение групповой скорости равно скорости света.

Волны де Бройля подвержены дисперсии. Если подставить выражение:

Волны де Бройля подвержены дисперсии

Источник: bog5.in.ua

в формулу:

в формулу

Источник: bog5.in.ua

получим следующее равенство:

(Vф= f(λ))

Примечание

Так как присутствует дисперсия, волны де Бройля невозможно представить, как волновой пакет. В противном случае, он мгновенно «расплывется», то есть исчезнет, в течение 10-26 с.

Какой формулой определяется длина волны

Количественные соотношения, которые связывают корпускулярные и волновые способности частиц, аналогичны свойствам фотонов:

длина волны

Источник: bog5.in.ua

Гипотеза де Бройля основана на универсальном характере данного равенства, что справедливо в условиях любых волновых процессов. Какой-либо частице, которая обладает импульсом р, соответствует волна. Ее длину можно определить с помощью формулы де Бройля:

формула де Бройля

Источник: bog5.in.ua

p =mv– является импульсом частицы, h – определяется, как постоянная Планка.

Как определить длину волны де Бройля для электрона

Рассчитать длину волны де Бройля для электрона можно на конкретном примере. Предположим, то требуется определить длину волны де Бройля λ для электрона, кинетическая энергия которого составляет:

W1 = 10 кэВ;
W2 = 1 МэВ.

В первую очередь стоит записать исходные данные:

(m_{e}=9,1*10^{-31} кг)

(W1 = 10 кэВ = 10*10^{3}*1,6*10^{-19} = 1,6*10^{-15}Дж)

(W2 = 1 МэВ = 10*10^{6}*1,6*10^{-19}= 1,6*10^{-13} Дж)

Требуется найти λ.

Решение:

Формула волны де Бройля:

Формула волны де Бройля

Источник: bog5.in.ua

Так как известна кинетическая энергия электронов, можно рассчитать их скорость:

кинетическая энергия электронов

Источник: bog5.in.ua

Формула

Источник: bog5.in.ua

формула

Источник: bog5.in.ua

Далее можно определить длину волны де Бройля:

длинf волны де Бройля

Источник: bog5.in.ua

В том случае, когда скорость v частиц соизмерима со скоростью света с, длину волны де Бройля можно рассчитать по формуле:

длину волны де Бройля можно рассчитать по формуле

Источник: bog5.in.ua

Источник

Лекция
4

2.Двойственная
корпускулярно-волновая природа

частиц вещества

2.1. Гипотеза де
Бройля

В 1924 г. французский
физик Луи де Бройль выдвинул гипотезу,
согласно которой движение электрона,
или какой-либо другой частицы, связано
с волновым процессом. Длина волны этого
процесса:

а
частота ω
= Е/ħ,
т.е. корпускулярно-волновой дуализм
присущ всем без исключения частицам.

Если
частица имеет кинетическую энергию Е,
то ей соответствует длина волны де
Бройля:

Для
электрона, ускоряемого разностью
потенциалов
,
кинетическая энергия
,и
длина волны

Å.
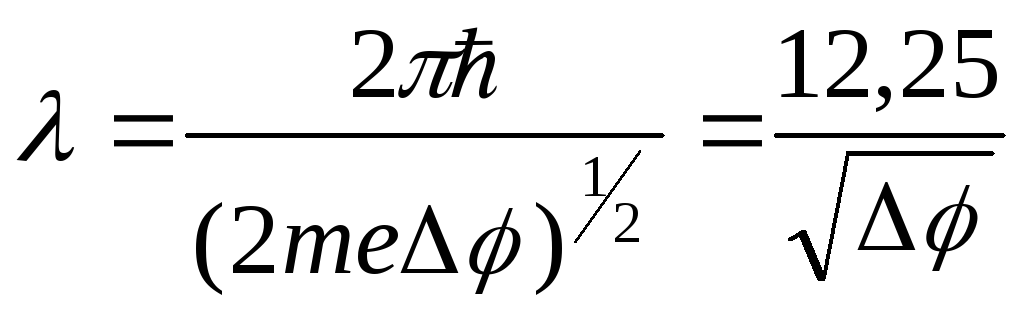
(2.1)

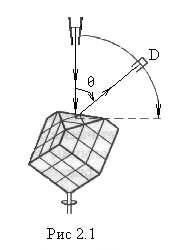
Опыты Дэвиссона и Джермера (1927). Идея
их опытов заключалась в следующем.
Если пучок электронов обладает волновыми
свойствами, то можно ожидать, даже не
зная механизма отражения этих волн,
что их отражение от кристалла будет
иметь такой же интерференционный
характер, как у рентгеновских лучей.

В
одной серии опытов Дэвиссона и Джермера
для обнаружения дифракционных
максимумов (если таковые есть) измерялись
ускоряющее напряжение электронов и
одновременно положение детектора D
(счетчика отраженных
электронов). В опыте использовался
монокристалл никеля (кубической системы),
сошлифованный так, как показано на
рис.2.1.

Если его повернуть вокруг
вертикальной оси в положение,
соответствующее рисунку, то в этом
положении сошлифованная поверхность
покрыта правильными рядами атомов,
перпендикулярными к плоскости падения
(плоскости рисунка), расстояние между
которыми d=0,215
нм.

Д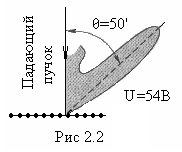етектор
перемещали в плоскости падения, меняя
угол θ.
При угле θ
= 50° и ускоряющем напряжении U=54В
наблюдался особенно
отчётливый максимум отраженных
электронов, полярная диаграмма которого
показана на рис.2.2.

Этот максимум можно истолковать как
интерференционный максимум первого
порядка от плоской дифракционной
решетки с периодом

, (2.2)

что видно из рис.2.3. На этом
рисунке каждая жирная точка представляет
собой проекцию цепочки атомов,
расположенных на прямой, перпендикулярной
плоскости рисунка. Период d
может быть измерен
независимо, например, по дифракции
рентгеновских лучей.

В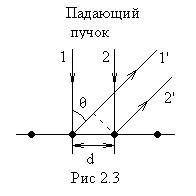ычисленная
по формуле (2.1) дебройлевская длина
волны для U=
54В равна 0,167 нм. Соответствующая
же длина волны, найденная из формулы
(2.2), равна 0,165 нм. Совпадение настолько
хорошее, что полученный результат
следует признать убедительным
подтверждением гипотезы де Бройля.

Другая серия опытов Дэвиссона
и Джермера состояла в измерении
интенсивности I
отраженного электронного пучка при
заданном угле падения, но при различных
значениях ускоряющего напряжения
U.

Теоретически должны появиться при этом
интерференционные максимумы отражения
подобно отражению рентгеновских лучей
от кристалла. От различных кристаллических
плоскостей кристалла в результате
дифракции падающего излучения на атомах
исходят волны, как бы испытавшие
зеркальное отражение от этих
плоскостей. Данные волны при интерференции
усиливают друг друга, если выполняется
условие Брэгга-Вульфа:

,

m=1,2,3,…,
(2.3)

где d
— межплоскостное
расстояние, α
— угол скольжения.

Н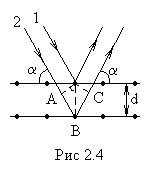апомним
вывод этой формулы. Из рис. 2.4 видно, что
разность хода двух волн, 1 и 2, отразившихся
зеркально от
соседних атомных слоев, АВС
=.
Следовательно, направления, в которых
возникают интерференционные максимумы,
определяются условием (2.3).

Теперь подставим в
формулу (2.3) выражение (2.1) для
дебройлевской длины волны. Поскольку
значения α и d
экспериментаторы
оставляли неизменными, то из формулы
(2.3) следует, что

~т, (2.4)

т.е. значения
,
при которых образуются максимумы
отражения, должны быть пропорциональны
целым числам т =
1, 2, 3, …, другими словами, находиться на
одинаковых расстояниях друг от друга.

Э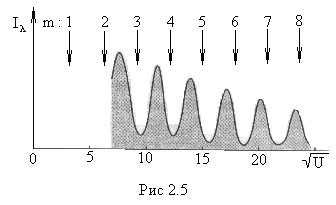то
и было проверено на опыте, результаты
которого представлены на рис.2. 5, где
U
представлено в вольтах.
Видно, что максимумы интенсивности
I
почти равноудалены друг от друга (такая
же картина возникает и при дифракции
рентгеновских лучей от кристаллов).

Полученные Дэвиссоном и Джермером
результаты весьма убедительно подтверждают
гипотезу де Бройля. В теоретическом
отношении, как мы видели, анализ дифракции
дебройлевских волн полностью совпадает
с дифракцией рентгеновского излучения.

Итак, характер зависимости
(2.4) экспериментально подтвердился,
однако наблюдалось некоторое расхождение
с предсказаниями теории. А именно,
между положениями экспериментальных
и теоретических максимумов (последние
показаны стрелками на рис. 2.5) наблюдается
систематическое расхождение, которое
уменьшается с увеличением ускоряющего
напряжения U.
Это расхождение, как
выяснилось в дальнейшем, обусловлено
тем, что при выводе формулы Брэгга-Вульфа
не было учтено преломление дебройлевских
волн.

О преломлении
дебройлевских волн.
Показатель преломления п
дебройлевских волн,
как и электромагнитных, определяется
формулой

, (2.5)

где

и
—
фазовые скорости этих волн в вакууме и
среде (кристалле).

Фазовая скорость дебройлевcкой
волны — принципиально ненаблюдаемая
величина. Поэтому формулу (2.5) следует
преобразовать так, чтобы показатель
преломления п можно было выразить
через отношение измеряемых величин.
Это можно сделать следующим образом.
По определению, фазовая скорость

,
(2.6)

где k
—
волновое число. Считая аналогично
фотонам, что частота и дебройлевских
волн тоже не меняется при переходе
границы раздела сред (если такое
предположение несправедливо, то опыт
неизбежно укажет на это), представим
(2.5) с учетом (2.6) в виде

(2.7)

П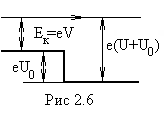опадая
из вакуума в кристалл (металл), электроны
оказываются в потенциальной яме.
Здесь их кинетическая энергия

возрастает на «глубину»
потенциальной ямы (рис. 2.6). Из формулы
(2.1), где
,
следует, что λ~

Поэтому выражение
(2.7) можно переписать так:

(2.8)

где U₀
— внутренний
потенциал кристалла.
Видно, что чем больше U
(относительно
),
тем п ближе
к единице. Таким образом, п
проявляет себя особенно
при малых U,
и формула Брэгга-Вульфа
принимает вид

(2.9)

Убедимся, что формула
Брэгга-Вульфа (2.9) с учетом преломления
действительно объясняет положения
максимумов интенсивности

на рис. 2.5. Заменив в (2.9) п
и λ
согласно формулам
(2.8) и (2.1) их выражениями через ускоряющую
разность потенциалов U,
т.е.

(2.10)

получим:

(2.11)

Теперь учтем, что распределение

на рис.2.5 получено для никеля при значениях
U₀=15
B,
d=0,203
нм и α=80°.
Тогда (2.11) после несложных преобразований
можно переписать так:

(2.12)

Вычислим по этой формуле
значение
,
например, для максимума
третьего порядка (m
= 3), для которого расхождение с
формулой Брэгга-Вульфа
(2.3) оказалось наибольшим:

Совпадение с действительным положением
максимума 3-го порядка не требует
комментариев.

Итак, опыты Дэвиссона и Джермера
следует признать блестящим
подтверждением гипотезы де Бройля.

Опыты Томсона и Тартаковского. В
этих опытах пучок электронов
пропускался через поликристаллическую
фольгу (по методу Дебая при изучении
дифракции рентгеновского излучения).
Как и в случае рентгеновского излучения,
на фотопластинке, расположенной за
фольгой, наблюдалась система дифракционных
колец. Сходство обеих картин поразительно.
Подозрение, что система этих колец
порождается не электронами, а вторичным
рентгеновским излучением, возникающим
в результате падения электронов на
фольгу, легко рассеивается, если на пути
рассеянных электронов создать магнитное
поле (поднести постоянный магнит).
Оно не влияет на рентгеновское излучение.
Такого рода проверка показала, что
интерференционная картина сразу же
искажалась. Это однозначно свидетельствует,
что мы имеем дело именно с электронами.

Г. Томсон осуществил опыты
с быстрыми электронами
(десятки кэВ), II.С.
Тарковский — со сравнительно медленными
электронами (до 1,7
кэВ).

Опыты с нейтронами и
молекулами. Для успешного наблюдения
дифракции волн на кристаллах необходимо,
чтобы длина волны этих волн была сравнима
с расстояниями между узлами кристаллической
решетки. Поэтому для наблюдения дифракции
тяжелых частиц необходимо пользоваться
частицами с достаточно малыми
скоростями. Соответствующие опыты по
дифракции нейтронов и молекул при
отражении от кристаллов были проделаны
и также полностью подтвердили гипотезу
де-Бройля в применении и к тяжелым
частицам.

Благодаря этому было
экспериментально доказано, что волновые
свойства являются универсальным
свойством всех частиц.
Они не обусловлены какими-то особенностями
внутреннего строения той или иной
частицы, а отражают их общий закон
движения.

О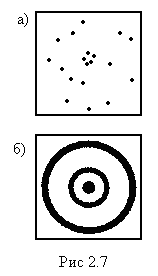пыты
с одиночными электронами. Описанные
выше опыты выполнялись с использованием
пучков частиц. Поэтому возникает
естественный вопрос: наблюдаемые
волновые свойства выражают свойства
пучка частиц или отдельных частиц?

Чтобы ответить на этот вопрос, В.
Фабрикант, Л. Биберман и Н. Сушкин
осуществили в 1949 г. опыты, в которых
применялись столь слабые пучки электронов,
что каждый электрон проходил через
кристалл заведомо поодиночке и каждый
рассеянный электрон регистрировался
фотопластинкой. При этом оказалось, что
отдельные электроны попадали в
различные точки фотопластинки совершенно
беспорядочным на первый взгляд образом
(рис.2.7,а). Между тем при достаточно
длительной экспозиции на фотопластинке
возникала дифракционная картина
(рис.2.7, б), абсолютно идентичная картине
дифракции от обычного электронного
пучка. Так было доказано, что волновыми
свойствами обладают и отдельные
частицы.

Таким образом, мы имеем дело
с микрообъектами, которые обладают
одновременно как
корпускулярными, так и волновыми
свойствами. Это позволяет нам в дальнейшем
говорить об электронах, но выводы, к
которым мы придем, имеют совершенно
общий смысл и в равной степени
применимы к любым частицам.

Из формулы де Бройля следовало, что
волновые свойства должны быть присущи
любой частице вещества, имеющей массу
и скорость
.
В 1929г. опыты Штерна доказали, что формула
де Бройля справедлива и для пучков
атомов и молекул. Он получил следующее
выражение для длины волны:

Ǻ,

где μ – молярная масса вещества,
N_А – число
Авогадро, R –
универсальная газовая постоянная, Т
– температура.

При отражении пучков атомов и молекул
от поверхностей твердых тел должны
наблюдаться дифракционные явления,
которые описываются теми же соотношениями,
что и плоская (двумерная) дифракционная
решетка. Опыты показали, что кроме
частиц, рассеянных под углом, равным
углу падения, наблюдаются максимумы
числа отраженных частиц под другими
углами, определяемыми формулами двумерной
дифракционной решетки.

Формулы де Бройля оказались справедливыми
также для нейтронов. Это подтвердили
опыты по дифракции нейтронов на
приемниках.

Таким образом, наличие волновых свойств
у движущихся частиц, обладающих массой
покоя, есть универсальное явление, не
связанное с какой-либо спецификой
движущейся частицы.

Отсутствие волновых свойств у
макроскопических тел объясняется
следующим образом. Подобно
той роли, которую играет скорость
света при решении вопроса о применимости
ньютоновской (нерелятивистской) механики,
существует критерий, показывающий в
каких случаях можно ограничиться
классическими представлениями. Этот
критерий связан с постоянной Планка ħ.
Физическая размерность
ħ
равна (энергия)x(время),
или (импульс)x(длина),
или (момент
импульса). Величину
с такой размерностью называют действием.
Постоянная Планка
является квантом действия.

Если в данной физической
системе значение некоторой характерной
величины Н с
размерностью действия
сравнимо с ħ,
то поведение этой системы может быть
описано только в рамках квантовой
теории. Если же значение Н
очень велико по
сравнению с ħ,
то поведение системы с высокой точностью
описывают законы классической физики.

Отметим, однако, что данный
критерий имеет приближенный характер.
Он указывает лишь, когда следует проявлять
осторожность. Малость действия Н
не всегда свидетельствует
о полной неприменимости классического
подхода. Во многих случаях она может
дать некоторое качественное представление
о поведении системы, которое можно
уточнить с помощью квантового подхода.

2.2Свойства
волн де Бройля

Рассмотрим
движение свободного электрона. По де
Бройлю, ему соответствует длина волны:

Будем
называть ее электронной волной. Известно,
что λ
=
_фаз/,
где
_фаз
– фазовая скорость распространения
волны. Найдем фазовую скорость волны
де Бройля:

т. е. фазовая скорость зависит
от частоты
,
а значит дебройлевские волны обладают
дисперсией даже
в вакууме. В соответствии с современной
физической интерпретацией фазовая
скорость дебройлевских волн имеет чисто
символическое значение, поскольку
эта интерпретация относит их к числу
принципиально ненаблюдаемых величин.

Т.к. c >
,
то фазовая скорость волн де Бройля
больше скорости света в вакууме.

Найдем групповую скорость волны де
Бройля:

где

– скорость частицы.

Установление того факта, что групповая
скорость дебройлевских волн равна
скорости частицы, сыграло в свое время
важную роль в развитии принципиальных
основ квантовой физики, и в первую
очередь в физической интерпретации
дебройлевских волн. Сначала была сделана
попытка рассматривать частицы как
волновые пакеты весьма малой протяженности
и таким образом решить парадокс
двойственности свойств частиц. Однако
подобная интерпретация оказалась
ошибочной, так как все составляющие
пакет гармонические волны распространяются
с разными фазовыми скоростями. При
наличии большой дисперсии, свойственной
дебройлевским волнам даже в вакууме,
волновой пакет «расплывается». Для
частиц с массой порядка массы электрона
пакет расплывается практически
мгновенно, в то время как частица является
стабильным образованием.

Таким образом, представление частицы
в виде волнового пакета оказалось
несостоятельным. Проблема двойственности
свойств частиц требовала иного подхода
к своему решению.

Прежде всего убедимся, что
гипотеза де Бройля не противоречит
понятиям макроскопической физики.
Возьмем в качестве макроскопического
объекта, например, пылинку, считая, что
ее масса т =
1 мг и скорость

=1 мкм/с. Соответствующая
ей дебройлевская длина волны

Т.е. даже у такого небольшого
микроскопического объекта как пылинка
дебройлевская длина волны оказывается
неизмеримо меньше размеров самого
объекта. В таких условиях никакие
волновые свойства, конечно, проявить
себя не могут.

Иначе обстоит дело, например,
у электрона с кинетической энергией

и импульсом
.
Его дебройлевская
длина волны

где

в эВ. При

= 150 эВ дебройлевская
длина волны электрона равна λ
~0,1 нм или ~1.
Такой же порядок величины имеет постоянная
кристаллической решетки. Поэтому,
аналогично тому, как в случае рентгеновских
лучей, кристаллическая структура
может быть подходящей решеткой для
получения дифракции дебройлевских
волн электронов.

Сведем
корпускулярные и волновые свойства
свободных частиц в таблицу и покажем
их связь:

Корпускулярные
свойства Волновые свойства

Скорость

,
импульс

Длина волны де Бройля

Энергия

Частота волны де
Бройля ω
=

Групповая
скорость волн де Бройля

Фазовая
скорость волн де Бройля

Волны
де Бройля не электромагнитные.
Распространение их не связано с
распространением в пространстве
какого-либо электромагнитного поля.
Волны де Бройля, связанные с частицами
вещества, имеют специфическую квантовую
природу, не имеющую аналогов в классической
физике. Вопрос о природе волн, связанных
с частицами вещества, в квантовой
механике рассматривают как вопрос о
физическом смысле амплитуды этих волн.
Вместо амплитуды рассматривают
интенсивность волны, которая пропорциональна
квадрату модуля амплитуды.

В
опытах по дифракции электронов было
доказано неодинаковое распределение
пучков электронов, отраженных или
рассеянных по различным направлениям.
Выделялись направления, в которых
рассеивалось большее число электронов.
Наличие максимума числа электронов в
некоторых направлениях означает, что
эти направления соответствуют наибольшей
интенсивности волн де Бройля, т.е.
интенсивность волн в данной точке
пространства определяет число электронов,
попавших в эту точку за 1 секунду. Таким
образом, квадрат модуля амплитуды волн
де Бройля в данной точке является мерой
вероятности того, что частица находится
в этой точке.

Подтвержденная
на опыте идея де Бройля о корпускулярно-волновом
дуализме микрочастиц принципиально
изменила представления об облике
микромира. Поскольку всем микрообъектам
(частицам) присущи и волновые и
корпускулярные свойства, то любую из
этих частиц нельзя считать ни частицей,
ни волной в классическом понимании этих
слов. Возникла потребность в такой
теории, в которой волновые и корпускулярные
свойства материи выступали бы не как
исключающие, а как взаимно дополняющие
друг друга. В основу такой теории –
квантовой механики – и легла гипотеза
де Бройля.

Соседние файлы в папке квантовая

#
#
08.03.2015376.32 Кб4115.doc
#
#
#
#
#
#
#
#
#

Источник

Сергей Феликсович Савельев

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Определение 1

Волны де Бройля – волны вероятности, которые определяют плотность вероятности обнаружения объекта в заданной точке конфигурационного пространства.

Формула для определения длины волны записывается следующим образом:

Корпускулярно – волновая природа материи является одним из основных аспектов квантовой механики: каждый материальный объект может проявлять волновые свойства, а это значит, что он может обладать свойствами дифракции и интерференции.

В связи с тем, что длина волны электронов и материи чрезвычайно мала по сравнению с длиной волны света, электроны подходят для наблюдения за мелкими объектами. Это было использовано, в частности, для построения электронного микроскопа, который имеет разрешение во много раз выше, чем оптический микроскоп.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Эти соображения относятся к свободному движению частиц (которые соответствуют плоским волнам).

Рисунок 1. Распространение Волн Де Бройля

Пример для макроскопического объекта

Макроскопические объекты можно рассматривать как волны де Бройля, а длина волны настолько мала, что она становится неизмерима. Говорят, что макроскопические объекты не раскрывают их собственной волны. Например, можно рассчитать, что для человека $50$ – кг, движущегося со скоростью $10$ км/ч длина волны равна

Это значение настолько мало, что невозможно обнаружить волновые свойства человека.

Гипотеза де Бройля

Де Бройль, в $1924$ году, защищая кандидатскую диссертацию, предположил, что, свет имеет как волнообразные и частицеподобные свойства, так и электроны имеют волновые свойства.

«Волны Де Бройля» 👇

где $lambda $ – длина волны фотона.

Таким образом, де Бройль предложил ввести отношение между импульсом и длиной волны фотона, так что длина волны была выражена импульсом частицы.

Эта гипотеза не имела экспериментальной базы и была чисто теоретическим предположением.

Но в дальнейшем эти результаты были подтверждены Джорджом Томсоном в Шотландии, за которую в $1937$ году он получил Нобелевскую премию по физике.

Фазовая скорость

В квантовой механике, частицы ведут себя как волны с комплексными фазами. Фазовая скорость равна произведению частоты, умноженной на длину волны.

Используя релятивистские соотношения для энергии и импульса, мы имеем

где${rm E}$ является полной энергией частицы, ${rm p}$ импульс, $gamma $ фактор Лоренца.

Групповая скорость

Альберт Эйнштейн впервые объяснил корпускулярно – волновой дуализм света в $1905$ году.

И в релятивистской и нерелятивистской квантовой физике, мы можем определить групповую скорость частицы волновой функцией со скоростью частицы. Квантовая механика очень четко продемонстрировала эту гипотезу, и отношение было показано для частиц такого размера, как молекулы.

где${rm E}$ является полной энергией частицы, ${rm p}$ импульс, $h$ является постоянной Планка.

Пример 1

Электрон обладает кинетической энергией $T=1,02$ МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия $T$ электрона уменьшится вдвое?

Решение:

Связь длины волны де Бройля с кинетической энергией $E_к$ в классическом приближении

[lambda =frac{h}{sqrt{2cdot mcdot E_к}}]

В релятивистском случае длину волны нужно вычислять по формуле

[lambda =frac{hcdot c}{sqrt{left(E_кleft(E_к+2m_ec^2right)right)}}]

Где $m_ec^2-$ масса покоя электрона и равна $0,511$ МэВ.

В нашем случае кинетическая энергия $E_к$ сравнима с массой покоя электрона и поэтому нужно использовать формулу для релятивистского случая.

Тогда

[lambda =frac{hcdot c}{sqrt{left(E_кleft(E_к+2m_ec^2right)right)}}]

[{lambda }^,=frac{hcdot c}{sqrt{left({E^,}_кleft({E^,}_к+2m_ec^2right)right)}}=lambda =frac{hcdot c}{sqrt{left({0,5E}_кleft(0,5E_к+2m_ec^2right)right)}}]

Поэтому искомая величина равна

[frac{{lambda }^,}{lambda }=frac{sqrt{left(E_кleft(E_к+2m_ec^2right)right)}}{sqrt{left({0,5E}_кleft(0,5E_к+2m_ec^2right)right)}}=sqrt{frac{left(E_к+2m_ec^2right)}{0,5cdot left(0,5E_к+2m_ec^2right)}}]

Подставляем числа (переводя одновременно все величины в систему СИ).

[frac{{lambda }^,}{lambda }=sqrt{frac{left(1,02 МэВ+2cdot 0,51 МэВright)}{0,5cdot left(0,5cdot 1,02 МэВ+2cdot 0,51 МэВright)}}=1,63]

Ответ: длина волны де Бройля увеличится в $1,63$ раз.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Корпускулярно-волновой дуализм фотонов и массивных частиц[править | править код]

Природа волн де Бройля[править | править код]

Формулы де Бройля[править | править код]

Нерелятивистский предел[править | править код]

Ультрарелятивистский предел[править | править код]

Формулы де Бройля для четырёх векторов[править | править код]

Фазовая и групповая скорость волн де Бройля[править | править код]

Иллюстрация[править | править код]

Зависимость длины волны от скорости частицы[править | править код]

Экспериментальная проверка[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Как определить длину волны де Бройля для электрона

Волна де Бройля или волна амплитуды вероятности

Природа волн де Бройля, фазовая и групповая скорость

Какой формулой определяется длина волны

Как определить длину волны де Бройля для электрона

Пример для макроскопического объекта

Гипотеза де Бройля

Фазовая скорость

Групповая скорость

Вам также может понравиться

Как найти производную от sin куб

Где найти отзывы как

Как составить брачный договор перед браком

Добавить комментарий Отменить ответ