Длина волны
О чем эта статья:
Волна: продольная и поперечная
Начнем с того, что волна — это распространение колебания в пространстве.
Волны бывают механическими и электромагнитными.
Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.
- Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.
Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.
Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.
Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.
Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.
Электромагнитные волны — это те волны, которые мы потрогать не можем.
- Например, радиоволны, Wi-Fi и свет.
Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10 8 м/с. И источники у них разные.
Волны также принято делить на продольные и поперечные:
Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.
- Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.
Поперечные — волны, у которых колебание происходит поперек направления распространения волны.
- Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
- Видимый свет и дрожание гитарной струны — тоже поперечные волны.
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
Формула периода колебания волны
T = t/N
N — количество колебаний [—]
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости
𝑣 = S/t
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
𝑣 = λ/T
λ — длина волны [м]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
Возьмем формулу скорости:
Нам известна длина волны, но не дан период. Период вычисляется по формуле:
Теперь подставляем величины в формулу
Резонанс
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
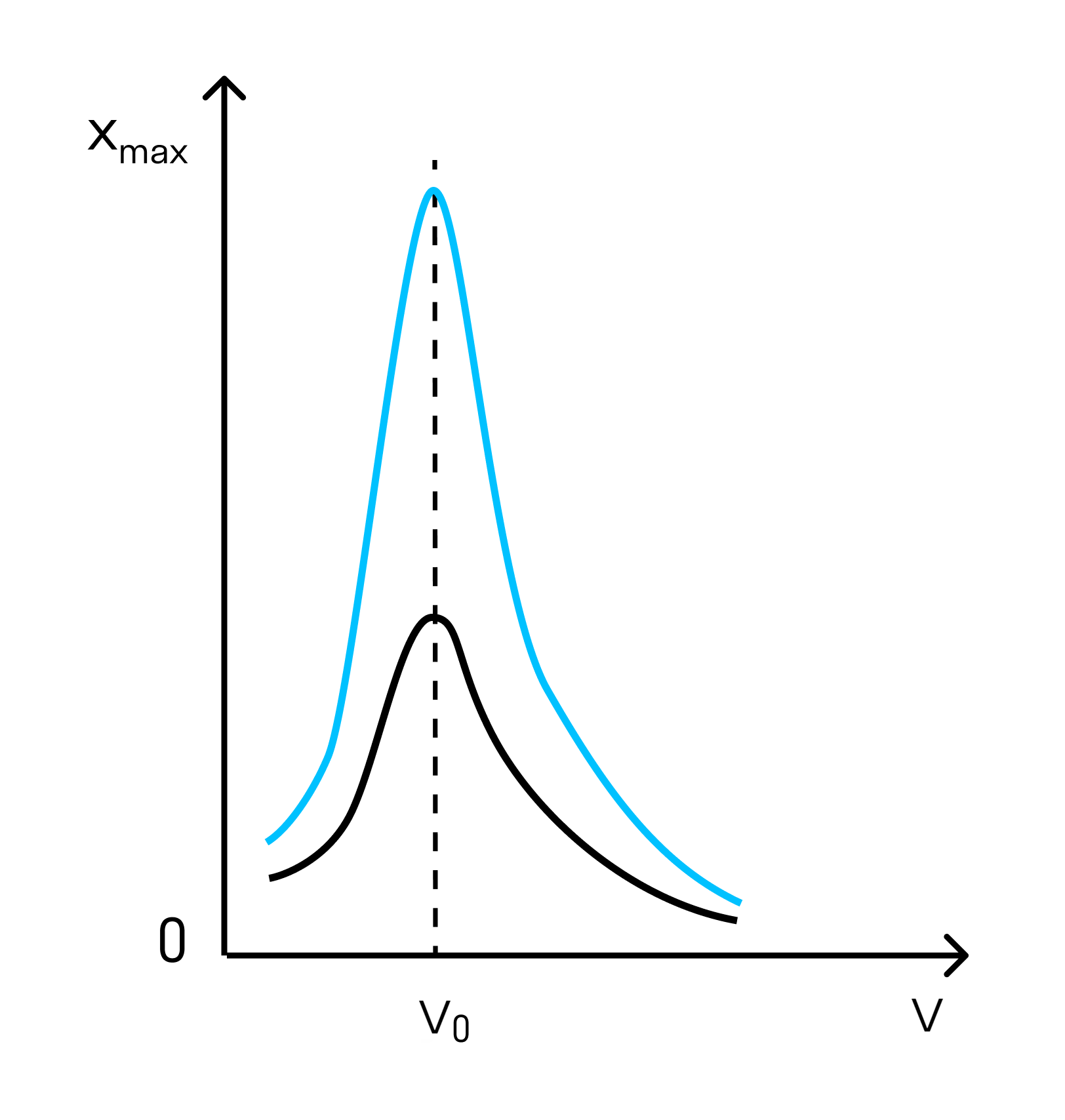
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Формула частоты
ν = N/t
N — количество колебаний [—]
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Как найти скорость распространения волны по уравнению
274 дн. с момента
до конца учебного года
Длина волны. Скорость распространения волны.
Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λ = υ T . Так как период Т и частота v связаны соотношением T = 1 / v, то скорость волны:
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [ λ ] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц
Длина и скорость волны.
Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
,
где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.
Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
,
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
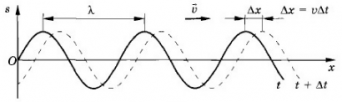
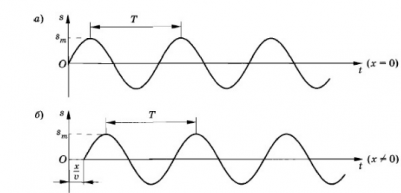
Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направлением распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
[spoiler title=”источники:”]
http://www.sites.google.com/site/opatpofizike/teoria/9-klass/dlina-volny-skorost-rasprostranenia-volny
http://www.calc.ru/Dlina-I-Skorost-Volny.html
[/spoiler]
Отдельные частицы любого тела — твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-то частица начинает колебаться, то благодаря взаимодействию между частицами это движение с некоторой скоростью начинает распространяться во все стороны.
Определение
Волна — колебания, распространяющиеся в пространстве с течение времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря силам упругости. Эти силы осуществляют связь между отдельными частями тела. В образовании волн на поверхности воды играют роль сила тяжести и сила поверхностного натяжения. Такие волны позволяют наиболее наглядно рассмотреть главные особенности волнового движения.
Волна на поверхности воды представляет собой бегущие вперед валы округлой формы. Расстояние между валами, которые также называют гребнями, примерно одинаковы. Волны распространяются в среде с определенной скоростью. Так, если чайка летит вперед, а по ней в любой момент времени оказывается один и тот же гребень, то скорость распространения волны можно принять равной скорости полета чайки. Волны на воде наблюдать удобно потому, что скорость их распространения невелика.
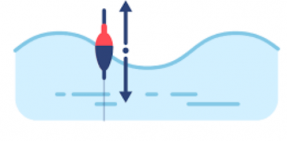
Если бросить в воду легкий предмет, он не будет увлекаться волной, а начнет совершать колебания вверх и вниз, оставаясь примерно на одном месте, как поплавок. Это говорит о том, что частицы воды остаются на месте в то время, как волна распространяется на большие расстояния.
Если же резко толкнуть горизонтальную пружину, можно будет наблюдать, как в одних местах она разрежается, в других — уплотняется. Это тоже волна. Видно, что энергия, полученная от толчка руки, переносится через пружину, хотя ее частицы остаются на месте.
Примеры с поплавком на воде и горизонтальной пружиной позволяют сделать вывод, что волна переносит энергию, но не переносит вещество среды.
Виды механических волн
По характеру колебаний частиц среды относительно положения равновесия различают два вида волн:
Определения
- Поперечная волна — волна, при которой частицы среды колеблются перпендикулярно направлению распространения этой волны.
- Продольная волна — волна, при которой частицы среды колеблются параллельно направлению распространения этой волны.
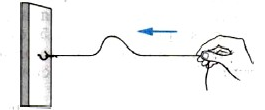
Волны, распространяющиеся вдоль резинового шнура, являются поперечными (см. рисунок ниже). Чтобы появилась волна, нужно взять конец шнура, прикрепленного к вертикальной опоре, и дернуть его. При этом волна побежит к вертикальной опоре, а сам шнур будет менять свою форму. Каждая частица шнура станет совершать колебания относительно своего неизмененного положения равновесия сверху вниз (перпендикулярно направлению распространения волны).
Рассмотрим поперечные волны подробнее. Каждый участок шнура обладает массой и упругостью. При деформации шнура в любом его сечении появляются силы упругости. Эти силы стремятся возвратить шнур в исходное положение. Благодаря инертности участок колеблющегося шнура не останавливается в положении равновесия, а проходит его, продолжая двигаться до тех пор, пока силы упругости не остановят этот участок в момент максимального отклонения от положения равновесия.
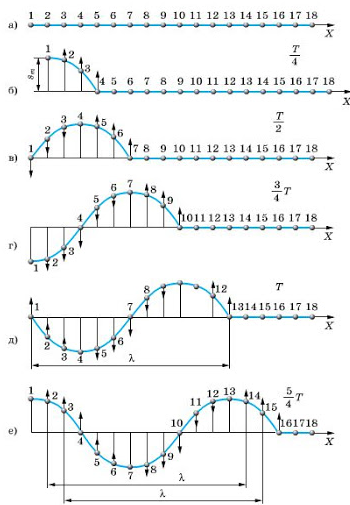
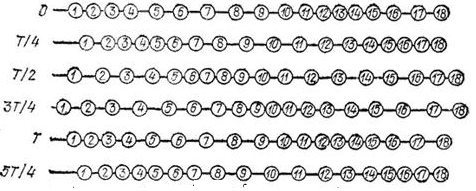
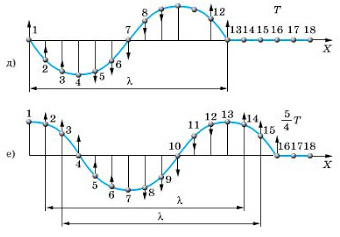
На рисунках а, б, в, г, д и е изображен процесс распространения поперечной волны. На них показаны положения частиц среды в последовательные моменты времени.
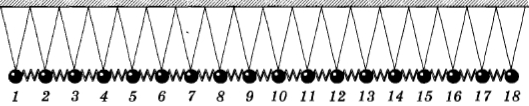
Теперь рассмотрим распространение в среде продольной волны. Такую волну можно наблюдать, собрав установку из цепочки массивных шариков, связанных пружинками. Шары подвешены так, чтобы они могли колебаться только вдоль цепочки (см. рисунок ниже).
Если первый шар привести в колебательное движение, то вдоль цепочки побежит продольная волна, состоящая из чередующихся уплотнений и разрежений шаров. Уплотнения и разрежения (см. рисунок ниже) появляются вследствие горизонтальных колебаний шаров у положения равновесия. Волна также распространяется горизонтально.
Физические характеристики волны
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Определение
Длина волны — расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ2, колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
v=λT
Но мы знаем, что период равен величине, обратной частоте колебаний:
T=1ν
Тогда скорость распространения волны равна:
v=λν
Скорость волны равна произведению длины волны на частоту колебаний.
При распространении волны мы имеем дело с периодичностью двоякого рода:
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
ν=nt
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v=λν=λnt=1·105=2 (мс)
Уравнение бегущей волны
Определение
Бегущая волна — волна, распространяющаяся в пространстве.
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
s = s(x, t)
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = smaxsin ωt
smax — амплитуда колебаний (рис. а).
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
τ=xv
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Уравнение бегущей волны
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s(x, t)=0,1sin(2πt−xπ2). Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω=2π (радс)
v=4 (мс)
Циклическую частоту также можно рассчитать по формуле:
ω=2πν
Тогда частота волны равна:
ν=ω2π=2π2π=1 (Гц)
Тогда длина волны равна:
λ=vν=41=4 (м)
Задание EF18242
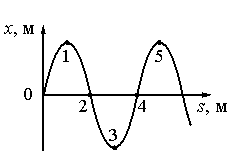
Ответ:
а) π/3
б) π/2
в) π
г) 2π
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу, которая связывает скорость волны с ее частотой и длиной.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Частота звуковой волны: ν = 400 Гц.
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν=4·400=1600 (мс)
Ответ: 1600
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18803
На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Расстояние наблюдателя до источника звука: s = 510 м.
Звук от удара проделает путь, равный одинарному расстоянию от наблюдателя до источника звука. Следовательно, для нахождения времени, через которое наблюдатель услышит звук, нужно разделить этот путь на скорость звука в воздухе:
t=sv=510340=1,5 (с)
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.1k
Формула скорости волны в физике
Формула скорости волны
Определение
Фронт волны (волновая поверхность) – это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ – период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ – модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период – величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Волны на поверхности жидкости; волна, пробегающая по веревке, если дернуть ее за один из концов; даже звук – всё это примеры механических волн. Сегодня мы познакомимся с параметрами, которые количественно характеризуют волны.
Вспомним определение: волна – это изменение некоторой совокупности физических величин, которое распространяется в пространстве от места возникновения с течением времени.
Представим себе бильярдные шары, расставленные в ряд с интервалом в несколько сантиметров (см. рис. 1).
Рис. 1. Расставленные бильярдные шары
После удара по крайнему шару (см. рис. 2) мы увидим, как он перемещается и сталкивается со вторым шаром.
Рис. 2. Шар ударяет крайний шар
Затем второй шар ударяет третий и так далее. Таким образом, мы наблюдаем распространение волны. Изменение величин (в данном случае это перемещение, скорость, кинетическая энергия шаров) распространяется в пространстве с течением времени (см. рис. 3).
Рис. 3. Принцип распространения волны
- Такая волна является одиночной – изменение физических величин распространяется разово.
- Цунами, волна, пробегающая по веревке, если дернуть ее за один из концов, даже продвижение на одного человека привычной нам очереди за мороженым – тоже примеры одиночных волн.
- Очередь за мороженым
Представим очередь за мороженым (см. рис. 4).
Рис. 4. Продвижение очереди
Люди, стоящие в очереди, находятся на равном расстоянии друг от друга. Затем, расплатившись и получив свое мороженое, довольный покупатель покидает очередь. Человек, стоящий за ним, смещается на шаг к прилавку, тоже освобождая свое место.
Дальше смещение на шаг вперед совершит третий покупатель, затем четвертый и т. д. То есть смещение будет распространяться в пространстве от места возникновения (от начала очереди к концу) с течением времени.
Такая волна является одиночной – смещение каждого покупателя происходит однократно.
Повторно волна «прокатится» по очереди лишь после того, как следующий покупатель отойдет от прилавка и стоящий за ним сместится на его место – то есть возникнет уже новое смещение, новое изменение физической величины.
А что будет происходить, если соединить шары пружинками? Тогда при перемещении первого шара прикрепленная к нему пружина будет сжиматься и в ней будет возникать сила упругости, которая с одной стороны будет толкать второй шар и передавать ему энергию, а с другой стороны – возвращать первый шар в исходное положение (см. рис. 5).
Рис. 5. Сила упругости в пружине
Описанная ситуация моделирует упругую среду (газ, жидкость, твердое тело).
Между частицами упругих сред присутствуют силы упругого взаимодействия, которые препятствуют деформации этой среды. При смещении частиц эти силы, подобно пружинкам в нашем примере, стремятся вернуть их в исходные положения (см. рис. 6).
Рис. 6. Действие сил упругого взаимодействия
Благодаря этому в упругих средах могут распространяться не только разовые изменения физической величины (одиночные волны), но и периодические изменения физической величины (колебания).
Волна – это изменение физической величины, распространяющееся в пространстве. И если это изменение физической величины будет периодическим, то есть будет представлять собой колебания, оно также будет распространяться.
Для частиц упругой среды выполняются оба условия возникновения колебаний – при отклонении возникает сила, возвращающая их в исходное положение (см. рис.
7) и, так как частицы обладают массой, они продолжают движение по инерции при прохождении этого положения.
Рис. 7. Возвращающая сила
При этом колебания распространяются в упругой среде и передают энергию в другие точки, хотя частицы остаются вблизи своих исходных положений.
Один из примеров механической волны, представляющей собой распространение колебаний, – это столь привычный нам способ обмена информацией – звук. Подробнее о его свойствах пойдет речь на следующем уроке.
Скорость распространения волны
Волна распространяется с течением времени, и естественно говорить о скорости ее распространения. Действительно, если мы будем ехать по волнорезу на велосипеде со спидометром рядом с гребнем волны, на спидометре мы увидим скорость волны (см. рис. 8).
Рис. 8. Скорость распространения волны
Разберемся, скорость чего мы измерили. Это не скорость движения воды, волна не переносит вещество. Волна переносит энергию колебаний, но четко определить координату и перемещение энергии нельзя. Можно определить координату точки, которая колеблется, и значит, обладает энергией (см. рис. 9).
Рис. 9. Движение точки
Таким образом, мы рассматриваем перемещение возмущения, отклонения точки от положения равновесия. Чтобы измерить координату точно, выберем точное значение отклонения, например максимум отклонения. При проходе волны сначала одна точка максимально отклоняется, затем соседняя и так далее (см. рис. 10).
Рис. 10. Прохождение точек через максимальное отклонение
Сами точки при этом вдоль волны не движутся, в этом мы убедимся, посмотрев на поплавок, прыгающий на волнах, а движется возмущение, скорость которого мы и измеряем.
Как и в механике, скорость – это перемещение в единицу времени:
Скорость распространения волны – это расстояние, на которое распространяется волна в единицу времени. Единицы измерения – метры в секунду.
Например, найдем скорость распространения волны в нашем примере с бильярдными шарами.
За время между перемещениями первого и последнего шаров волна распространилась от начала до конца выстроенного ряда, то есть расстояние от первого до последнего шара в ряду. То есть волна за время прошла расстояние , тогда ее скорость равна (см. рис. 11).
Рис. 11. Определение скорости распространения волны
Скорость распространения механических волн зависит от плотности среды. Как правило, чем плотнее среда – тем скорость распространения механических волн в ней выше.
К примеру, скорость распространения звуковых волн в твердых телах выше, чем в жидкостях, а в жидкостях – выше, чем в газах.
Причиной этого является то, что чем плотнее среда, тем сильнее проявляются ее упругие свойства.
В случае когда в пространстве распространяются колебания, их параметры будут характеризовать и волну в целом. Вспомним параметры колебаний, о которых идет речь.
Параметры колебаний
Амплитуда колебаний – это максимальное смещение периодически изменяющейся величины от равновесного значения. Обозначение и единицы измерения определяются типом изменяющейся величины. Это может быть и электрический заряд, и температура, и скорость, и т. д.
- Период колебаний – это время, за которое совершается одно полное колебание.
- Обозначается латинской буквой , измеряется в секундах.
Частота колебаний – это количество полных колебаний за единицу времени. Обозначается греческой буквой , измеряется в герцах.
В случае когда механическая волна представляет собой распространение колебаний, ее характеризует еще один параметр – длина волны – это расстояние, на которое распространяются колебания за один период (см. рис. 12).
Рис. 12. Длина волны
Обозначается длина волны греческой буквой , измеряется в метрах.
Наблюдая за волной на воде, легко заметить, что она обладает «пространственным периодом»: гребни и впадины чередуются через равные интервалы. Этот интервал и есть длина волны.
В этом случае можно записать еще одно выражение для скорости распространения волны. Т. к.
за период T волна распространяется на расстояние λ – значит, скорость распространения волны будет равна:
Задача 1
Определите скорость звука в воде, если источник, колеблющийся с периодом 0,002 с, возбуждает в ней волны длиной 3 м (см. рис. 13).
Рис. 13. Рисунок к задаче 1
- Порассуждаем:
- — требуется найти скорость распространения механической волны в воде;
- — при этом нам известен период и длина волны;
— длина волны – это расстояние, на которое волна распространяется за один период (см. рис. 14);
Рис. 14. Длина волны в задаче 1
- — значит, скорость распространения волны будет равна отношению ее длины к периоду:
- Подставим данные из условия и рассчитаем ответ:
- Задача решена.
Задача 2
Пока рыба не клевала, рыболов заметил, что за время t = 20 c его поплавок поднимался на гребни бегущих к берегу волн N = 30 раз. Определите скорость волн, если расстояние между соседними гребнями = 1 м.
Порассуждаем:
— Поплавок находится в некоторой точке волновой поверхности и колеблется вместе с ней. Значит, параметры, описывающие его колебания, будут характеризовать и волну в целом.
- — Из условия известно, что за время t поплавок совершил N колебаний. Значит, период колебаний поплавка и период механической волны равен:
- (делим суммарное время на количество полных колебаний, которые произошли за это время)
- — Также нам известна длина волны – расстояние, на которое волна распространяется за один период.
- — Значит, скорость распространения волны будет равна отношению ее длины к периоду:
- Подставим сюда выражение для периода и получим окончательное выражение для скорости распространения волны:
- Остается подставить данные из условия и вычислить ответ:
- Задача решена.
Источник: https://100ballov.kz/mod/page/view.php?id=2603
Длина волны — формулы, свойства и расчеты

Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
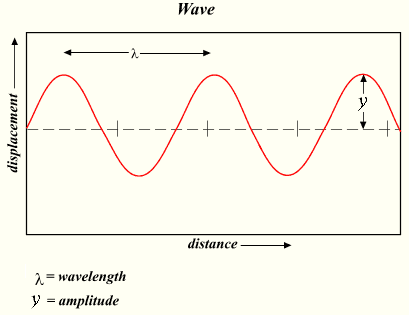
На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн
Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
- Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
- Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:

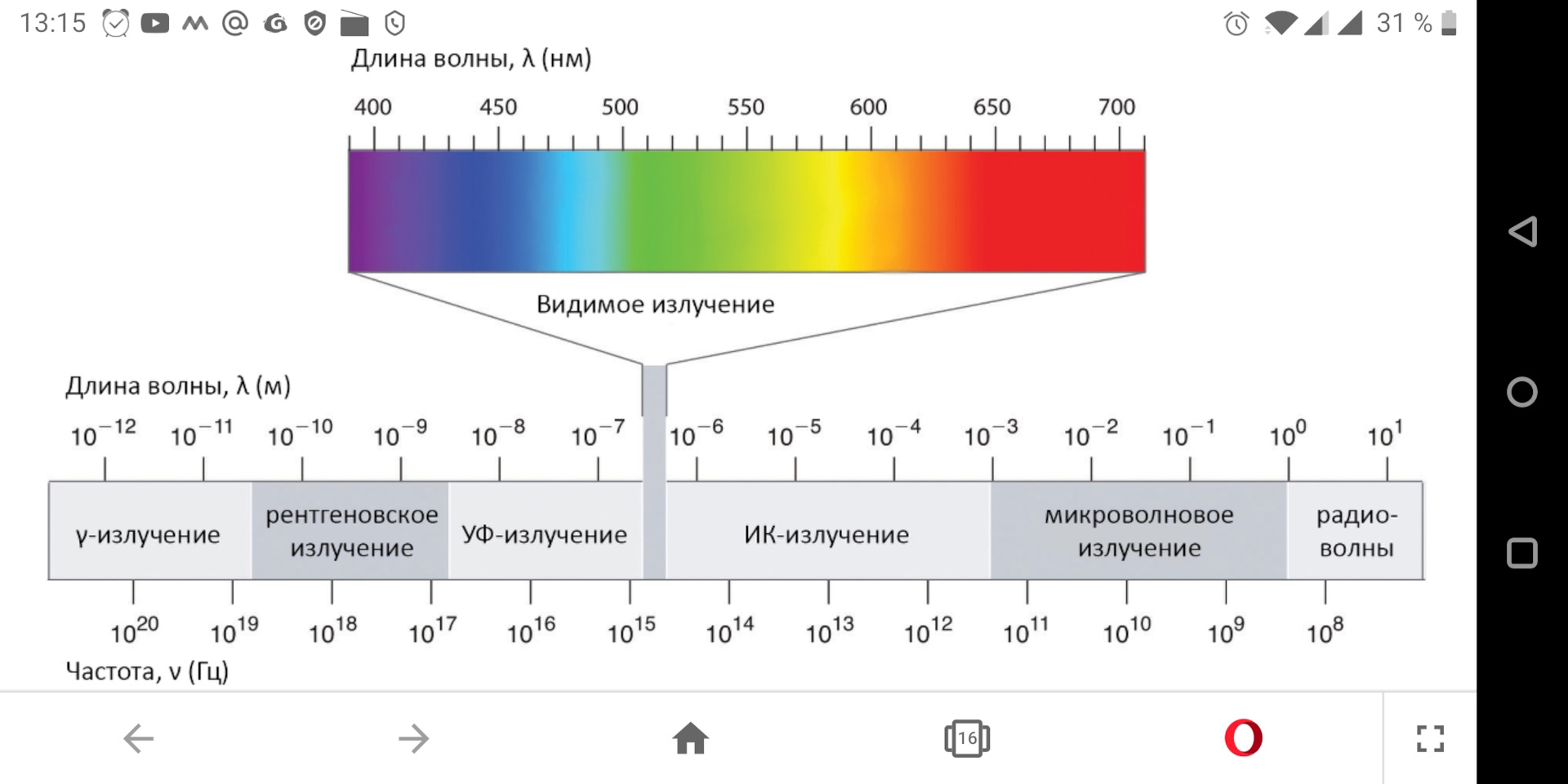
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Источник: https://nauka.club/fizika/dlina-volny.html
Теория радиоволн: ликбез

Радиоволна

«УКВ», «ДВ», «СВ»
Сверхдлинные волны — v = 3—30 кГц (λ = 10—100 км).
Имеют свойство проникать вглубь толщи воды до 20 м и в связи с этим применяются для связи с подводными лодками, причем, лодке не обязательно всплывать на эту глубину, достаточно выкинуть радио буй до этого уровня.
Эти волны могут распространяться вплоть до огибания земли, расстояние между земной поверхностью и ионосферой, представляет для них «волновод», по которому они беспрепятственно распространяются.
Длинные волны(ДВ) v = 150—450 кГц (λ = 2000—670 м).

Средние волны (СВ) v = 500—1600 кГц (λ = 600—190 м).

Короткие волны (КВ) v= 3—30 МГц (λ = 100—10 м).

Ультракороткие Волны(УКВ) v = 30 МГц — 300 МГц (λ = 10—1 м).

Так к примеру при радиотрансляции с останкинской телебашни высотой 500 м на приемную антенну высотой 10 м, дальность связи при условии прямой видимости составит около 100 км.
Высокие частоты (ВЧ-сантиметровый диапазон) v = 300 МГц — 3 ГГц (λ = 1—0,1 м).
Не огибают препятствия и имеют хорошую проникающую способность. Используются в сетях сотовой связи и wi-fi сетях. Еще одной интересной особенностью волн этого диапазона, является то, что молекулы воды, способны максимально поглощать их энергию и преобразовывать ее в тепловую. Этот эффект используется в микроволновых печах. Как видите, wi-fi оборудование и микроволновые печи работают в одном диапазоне и могут воздействовать на воду, поэтому, спать в обнимку с wi-fi роутером, длительное время не стоит.
Крайне высокие частоты (КВЧ-миллиметровый диапазон) v = 3 ГГц — 30 ГГц (λ = 0,1—0,01 м).
Отражаются практически всеми препятствиями, свободно проникают через ионосферу. За счет своих свойств используются в космической связи.
AM — FM
Зачастую, приемные устройства имеют положения переключателей am-fm, что же это такое:
AM — амплитудная модуляция

FM — частотная модуляция

Еще термины
Интерференция — в результате отражений волн от различных препятствий, волны складываются. В случае сложения в одинаковых фазах, амплитуда начальной волны может увеличиться, при сложении в противоположных фазах, амплитуда может уменьшиться вплоть до нуля.
Это явление более всего проявляется при приеме УКВ ЧМ и ТВ сигнала. Поэтому, к примеру внутри помещения качество приема на комнатную антенну ТВ сильно «плавает».
Дифракция — явление, возникающее при встрече радиоволны с препятствиями, в результате чего, волна может менять амплитуду, фазу и направление.
Данное явление объясняет связь на КВ и СВ через ионосферу, когда волна отражается от различных неоднородностей и заряженных частиц и тем самым, меняет направление распространения. Этим же явлением объясняется способность радиоволн распространяться без прямой видимости, огибая земную поверхность. Для этого длина волны должна быть соразмерна препятствию.
PS:
Источник: https://habr.com/post/158161/
Свойства волн: длина, частота и скорость
Физика > Длина волны, частота в соотношении со скоростью
Характеристика волны – длина, скорость и частота. Узнайте, что такое частота на графике волны, фазовая и групповая скорость, распространение волны и амплитуда.
Волны характеризуются по частоте, длине и амплитуде. Есть также два типа скорости: фазовая и групповая.
Задача обучения
- Рассмотреть главные характерные свойства волн.
Основные пункты
- Длина волны – пространственный период.
- Частота – число циклов за временной промежуток. Нельзя смешивать с угловой частотой.
- Фазовую скорость можно определить в качестве произведения длины и частоты.
Термины
- Скорость волны – абсолютный показатель скорости, при которой проходит фаза любого частотного компонента волны.
- Частота – соотношение числа периодического явления к временному промежутку: f = n/t.
Пример
Если мы рассмотрим видимый свет, то можем отобразить его как электромагнитную волну. Она будет представлена электрическими и магнитными полями, смещающимися в среде. Частоту определяют как цвет: 4 × 1014 Гц (красный), 8 × 1014 Гц (фиолетовый), а между ними – все остальные. Длина волны существует в обратной пропорциональности частоте: чем больше частота, тем короче длина.
Свойства волн
Волны характеризуются по их свойствам. Амплитуда представляет половину дистанции от гребня к впадине. Также можно заметить длину волны – пространственный период (от гребня к гребню), обозначающийся буквой λ.
Частота – количество пройденных циклов за определенный временной промежуток. В виде формулы:
Красная волна наделена низкочастотным синусом, поэтому наблюдается мало повторений циклов. А вот у фиолетовой высокая частота. Заметьте, что время растет по горизонтали
- f = 1/T (T – период колебаний).
- Частота и длина волны также могут быть связаны друг с другом по отношению к «скорости» волны. Получаем:
- v = fλ (v – скорость волны или фазовая скорость, с которой фаза волны распространяется в пространстве).
- Есть также групповая скорость волны – показатель, с которым общая форма волновых амплитуд (модуляция или огибающая волны) распространяется в пространстве.
Перед вами волна с групповой (положительная) и фазовой (отрицательная) скоростями, движущихся в разных направлениях
Читайте нас на Яндекс.Дзен
Источник: https://v-kosmose.com/fizika/dlina-volnyi-chastota-v-sootnoshenii-so-skorostyu/
Длина волны и скорость ее распространения
Абсолютно все в этом мире происходит с какой-либо скоростью. Тела не перемещаются моментально, для этого требуется время. Не являются исключением и волны, в какой бы среде они не распространялись.
Если вы бросите камень в воду озера, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Например, если вибрирующий железный лист засунуть концом в воду, то вода покроется рябью маленьких волн, однако скорость их распространения будет меньше, чем в железном листе.
Это несложно проверить даже в домашних условиях. Только не порежьтесь о вибрирующий железный лист…
Длина волны
Существует еще одна важная характеристика это длина волны. Длина волны это такое расстояние, на которое распространяется волна за один период колебательных движений. Легче понять это графически.
Если зарисовать волну в виде рисунка или графика, то длиной волны будет являться расстояние между любыми ближайшими гребнями либо впадинами волны, либо между любыми другими ближайшими точками волны, находящимися в одинаковой фазе.
Так как длина волны это расстояние, пройденное ею, то и найти эту величину можно, как и любое другое расстояние, умножив скорость прохождения на единицу времени. Таким образом, длина волны связана со скоростью распространения волны прямо пропорционально. Найти длину волны можно по формуле:
- λ=vT ,
- где λ длина волны, v скорость волны, T период колебаний.
- А учитывая, что период колебаний обратно пропорционален частоте этих же колебаний: T=1⁄υ, можно вывести связь скорости распространения волны с частотой колебаний:
- v=λυ .
Частота колебаний в разных средах
Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения.
Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае.
Нужна помощь в учебе?

Следующая тема: Источники звука и звуковые колебания: что это и как происходит
Источник: http://www.nado5.ru/e-book/dlina-volny-skorost-rasprostraneniya-voln
Длина, скорость и частота электромагнитной волны
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
Электромагнитные колебания — это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны (Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские либо гамма-лучи.
Длина волны, обозначаемая буквой λ и измеряемая в метрах — это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости света и составляет величину: v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где n > 1 — это показатель преломления среды. Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве. Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн, которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100…10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405…480 ТГц | 740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680…790 ТГц | 440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь существует некоторая путаница.
Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме, т. е. численно равной Kp = 1/n, где n — это, как мы помним, показатель преломления среды.
Другие, наоборот — как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду — если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а если Kp < 1, то n = 1/Kp.
Источник: https://vpayaem.ru/inf_wave1.html
Урок 12. волновые явления. длина волны. скорость распространения волн. — Физика — 9 класс — Российская электронная школа
- Конспект объясняющего модуля
- Тип урока — комбинированный
- Задачи:
- — личностные
- — метапредметные
- — регулятивные:
- — предметные:
- Цели учащихся:
- Различать поперечные и продольные волны;
- Описывать механизм образования волн.
- Называть характеризующие волны физические величины
- Называть величины, характеризующие упругие волны;
- Записывать формулы взаимосвязи между ними
- Организационный момент.
— Умение пользоваться методами научного исследования явлений природы — Познавательные: Строят логические цепи рассуждений. Устанавливают причинно- следственные связи. — Сличают свой способ действия с эталоном — Знать определение волн. Основные характеристики волн. Уметь определять период, частоту, амплитуду и длину волны
— Мотивационный модуль.
Выполнение заданий мотивационного модуля.
— Объяснение нового материала. Объясняющий модуль
Прослушать объяснения, выполнить задания.
Закрепление нового материала. Тренировочный модуль Выполнение заданий из тренировочного модуля
Контрольный модуль. Выполнение заданий контрольного модуля.
Тезаурус основных терминов и понятий:
— Колебания, распространяющиеся в пространстве с течением времени и удаляющиеся от места их возникновения, называются волной или бегущей волной
— Процесс распространения механических колебаний в среде называют механической волной. — Основное свойство волны.
- Распространяясь в пространстве волны, переносят энергию без переноса вещества
- — Волны, направление распространения которых перпендикулярно направлению колебаний частиц среды, называют поперечными.
- — Волны, направление распространения которых совпадает с направлением колебаний частиц среды, называют продольными
- Длина волны — это расстояние, на которое распространяется волна за время, равное периоду колебания:
— Поперечная вона. — Причина появление волны — изменение формы тела как следствие упругой дефрмации сдвига. Распространяется в твердых телах.
— Продольная волна. Причина появления волны — изменение объема тела, как следствие упругой деформации растяжения или сжатия.
$$upsilon = frac{ lambda} {T} = lambda
u$$
Источник: https://resh.edu.ru/subject/lesson/3017/main/
Если бросить камень в воду, то в месте его падения частицы воды начинают колебаться, двигаясь вверх и вниз. Соседние частицы, связанные с ними силами сцепления, также приходят в колебание. Однако для передачи колебания соседним частицам требуется некоторое время. То есть, чем дальше отстоят частицы от места, где начались колебания, тем позже эти частицы будут вовлечены в колебательное движение. Таким образом, от места падения камня волна бежит во все стороны с определенной скоростью, которая называется скоростью распространения волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. Если считать скорость волны постоянной, то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
Так как период колебаний в волне обратно пропорционален частоте,
,
то можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
Калькулятор ниже позволяет по двум известным параметрам формулы посчитать неизвестный.
Скорость и длина волны
Точность вычисления
Знаков после запятой: 3