Как определить скорость распространения волны по уравнению
274 дн. с момента
до конца учебного года
Длина волны. Скорость распространения волны.
Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.

Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λ = υ T . Так как период Т и частота v связаны соотношением T = 1 / v, то скорость волны:
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [ λ ] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц
Длина и скорость волны.
Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
,
где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.
Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
,
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направлением распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Волновое движение в физике – формулы и определение с примерами
Содержание:
Волновое движение:
Процесс распространения колебаний в упругой среде называют механической волной. Для механических волн нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию, она должна обладать инертными и упругими свойствами.
Различают поперечные и продольные волны. Продольные волны могут распространяться в любых средах: твердых, жидких и газообразных; поперечные – только в твердых средах.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. Волны переносят энергию колебаний.
Изучив страницу, вы сможете:
- исследовать образование стоячих звуковых волн в воздухе;
- объяснять механизм образования стоячих волн, определять узлы и пучности, используя графический метод;
- исследовать интерференцию от двух источников на поверхности воды;
- объяснять принцип Гюйгенса и условия наблюдения дифракционной картины механических волн.
Уравнение бегущей волны
Колебательное движение тела в упругой среде является источником механической волны.
Волну, переносящую энергию, называют бегущей волной.
В однородной среде скорость распространения волны остается величиной постоянной. Смещение y (x, t) от положения равновесия частиц среды при распространении волны зависит от координаты x на оси 0х, вдоль которой распространяется волна, и от времени t по закону:
где
Введем волновое число тогда уравнение бегущей волны примет вид
Смещение точек упругой среды в волне, бегущей в противоположном направлении выбранной оси 0х, можно определить по формуле:
Вспомните! Основные характеристики волн. Волны, созданные источником, совершающим гармонические колебания, характеризуются амплитудой колебания частиц среды A, частотой длиной волны и скоростью распространения
Длиной волны называют расстояние между двумя соседними точками на оси 0х, колеблющимися в одинаковых фазах. Расстояние, равное длине волны , волна пробегает за период Т, следовательно, В однородных средах скорость распространения волны величина постоянная.
Физический смысл волнового числа
Запишем формулу (2), выразив циклическую частоту через период с учетом определения длины волны получим:
Бегущая волна обладает двойной периодичностью – во времени и в пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны Волновое число является пространственным аналогом циклической частоты
Фронт волны и волновая поверхность
Волна за время, равное периоду колебаний, достигает точек пространства, расположенных от источника на расстоянии длины волны. Совокупность этих точек представляет собой фронт волны, который отделяет колеблющиеся точки среды от точек, не вовлеченных в колебательное движение. Фронт волны от точечного источника представляет собой сферу, от плоской пластины – плоскость, от струны – форму цилиндра (рис. 79–81).
Фронт волны – это геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Направление распространения волны указывает луч, который перпендикулярен фронту волны.
В волне можно рассмотреть множество поверхностей, все точки которых совершают колебания синфазно, их называют волновыми поверхностями. При множестве волновых поверхностей, фронт волны только один.
Геометрическое место точек пространства, которые совершают колебания в одинаковой фазе в данный момент времени, называют волновой поверхностью.
Стоячие волны
Уравнение стоячей волны При отражении от более плотной среды волна, изменив свое направление на обратное, меняет фазу на то есть на противоположную. В результате сложения падающей и отраженной волн образуется стоячая волна. Она имеет вид, представленный на рисунке 83. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.
Получим уравнение стоячей волны путем сложения уравнений бегущих волн:
Заменив волновое число его значением запишем уравнение стоячей волны в виде:
Координаты точек пучностей и узлов определяются из условий наибольшего и наименьшего значений амплитуды. При образуется пучность с амплитудой равной 2 А (рис. 84). Расстояния от источника стоячей волны до пучностей равны:
При образуются узлы, амплитуда колебаний в этой точке равна 0. Расстояния от источника волны до узлов равны:
Расстояния между двумя соседними пучностями или двумя соседними узлами равны:
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не переносится в другие части струны. В каждом таком отрезке происходит дважды за период превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Отсутствие переноса энергии является отличительной особенностью стоячей волны.
Пример:
Уравнение бегущей волны, изображенной на рисунке (рис. 85): . Уравнение отраженной волны:
А. Получите уравнение стоячей волны как сумму падающей и отраженной волн.
В. Полученное выражение запишите, заменив волновое число и циклическую частоту через длину волны и период.
С. Определите положение узлов и пучностей.
Дано:
Решение: А. Уравнение стоячей волны определятся сложением уравнений бегущих волн:
В.
С. При образуется пучность с амплитудой 2А. Расстояние от источника до пучностей
С. Расстояние от узлов определим из условия тогда
Ответ:
Интерференция волн
Если в некоторой среде несколько источников возбуждают механические волны, то они распространяются независимо друг от друга. Все точки среды принимают участие в колебаниях, вызванных каждой волной в отдельности. Наложение волн, в результате которой появляется устойчивая картина чередующихся максимумов и минимумов колебаний частиц среды, называют интерференцией.
Интерферировать могут только волны, имеющие одинаковую частоту и постоянный сдвиг фаз. Такие волны называют когерентными, их создают источники, колеблющиеся с одинаковой частотой и постоянным значением сдвига фаз.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Интерференция бывает стационарной и нестационарной. Стационарную интерференционную картину могут давать только когерентные волны: например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников (рис. 87).
Запомните! Волны называют когерентными, если их источники совершают колебания одной частоты с постоянным сдвигом фаз.
Условие максимума и минимума при интерференции двух волн
Амплитуда колебаний при наложении волн определяется в соответствии с принципом суперпозиции (рис. 88). Если в некоторой точке среды накладываются гребни когерентных волн, то происходит усиление колебаний, амплитуда принимает значение, равное сумме амплитуд. Если накладывается гребень одной волны с впадиной другой волны, то при равенстве амплитуд отдельно взятых волн данная точка пространства не совершает колебания. Если амплитуды отличаются, то колебания в этой точке совершаются с амплитудой равной разности амплитуд распространяющихся волн.
Для определения результата интерференции волн, распространяющихся от двух источников А и В, находящихся на расстоянии от точки С, достаточно определить разность хода волн и сравнить с длиной волны. Если разность хода равна целому числу длин волн, то в точке С произойдет наложение гребней или впадин, амплитуда колебаний возрастет (рис. 89). Выполняется условие максимума:
где − разность хода волн, – натуральное число, равное 0, 1, 2, 3 … Разность хода лучей соответствует разности фаз колебаний:
так как волна за период пробегает расстояние равное длине волны периоду Т соответствует фаза
Минимум колебаний в рассматриваемой точке среды наблюдается в том случае, если от двух когерентных источников распространяются волны со сдвигом фаз, равным нечетному числу p, а разность хода лучей кратна нечетному числу полуволн. В этом случае колебания происходят в противофазе (рис. 90).
Возьмите на заметку:
Интерференция волн приводит к перераспределению энергии колебаний между частицами среды. Это не противоречит закону сохранения энергии, так как в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.
Распространение волн. Принцип Гюйгенса – Френеля
На основе принципа Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн, невозможно объяснить, почему источники вторичных волн создают фронт только по направлению распространения волны. Для объяснения явлений распространения волны французский физик О. Френель в 1815 г. дополнил принцип Х. Гюйгенса представлениями о когерентности и интерференции вторичных волн. При наложении вторичных когерентных волн происходит интерференция, в результате которой амплитуда колебаний в различных точках пространства становится разной: по направлению распространения волны усиливается, в обратном направлении – уменьшается. Огибающая фронты вторичных волн является фронтом результирующей волны (рис. 92).
Дифракция механических волн
Вторичные волны, созданные точками среды, которые находятся на краю отверстия или препятствия, искривляются и волна огибает препятствие (рис. 93 а–г).
Дифракция – это явление огибания волнами препятствий.
Все волны способны огибать препятствия, если длина волны соизмерима с размерами препятствия. Дифракция становится заметной, если размеры препятствия меньше длины волны.
Физика в нашей жизни:
Струнные музыкальные инструменты
Интересно знать! Адырна (рис. 96 а) – один из древнейших казахских струнных инструментов. В его форме отобразилась воинственность кочевников-казахов: он напоминает изогнутый лук воина. Деревянный корпус инструмента легкий, так как он пустотелый. Струны изготавливают из кусков специально выделанной кожи или сплетенных из верблюжьей шерсти нитей. Музыкант играет, перебирая струны. Их в инструменте 13. Жетыген (рис. 96 б) – семиструнный музыкальный инструмент. Он имеет прямоугольную форму, изготовлен из дерева, струны – из конского волоса. Легенда о жетыгене раскрывает причину использования именно семи струн. Старик, потерявший семерых сыновей, вылил свое горе, исполняя кюи о них. Вспоминая каждого из сыновей, он натягивал новую струну на музыкальном инструменте.
Условие возникновения стоячей волны в струне
Стоячая волна в струне возникает только в том случае, если длина струны равняется целому числу длин полуволн:
Набору значений длин волн соответствует набор возможных частот Каждая из частот и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота называется основной частотой, все остальные частоты называются гармониками.
В отличие от груза на пружине или маятника, у которых имеется единственная собственная частота, струна обладает бесконечным числом собственных резонансных частот. На рисунке 96 в изображены несколько типов стоячих волн в струне. Стоячие волны различных типов могут одновременно присутствовать в колебаниях струны.
Визуализация звуковых волн
Существует несколько способов демонстрации стоячей волны, один из них – фигуры Хладни (рис. 97). Немецкий физик Эрнст Хладни получал узор, посыпая пластинку песком и проводя по краю смычком. Движения смычка заставляли пластинку колебаться на некоторой резонансной частоте. Песок скапливался и лежал неподвижно в узлах, а на участках, где отраженная волна усиливала бегущую, песок смещался.
Интересно знать! В Шотландии есть рослинская капелла св. Матвея, на одной из арок которой есть 213 резных каменных кубов, с вырезанным на них геометрическим рисунком. Многие исследователи пытались понять, что зашифровано в рисунках на кубах. Отставной генерал ВВС Томас Митчел со своим сыном, пианистом Стюартом Митчелом предложили оригинальный способ расшифровки послания. Они сопоставили геометрические рисунки с фигурами Хладни и пришли к выводу, что на кубах записаны ноты. Собрав ноты воедино и творчески обработав их, они представили миру произведение «Рослинский Мотет».
Итоги:
Глоссарий
Волновая поверхность – геометрическое место точек, имеющих одинаковую фазу колебаний.
Дифракция – явление огибания волнами препятствий.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Когерентные волны – волны, имеющие одинаковую частоту и постоянный сдвиг фаз.
Механическая волна – процесс распространения колебаний в упругой среде.
Фронт волны – геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Распространение колебаний в упругих средах. Продольные и поперечные волны
Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. В качестве примера достаточно вспомнить, что измерение пульса осуществляется на запястье, хотя сердце расположено внутри грудной клетки. Такие явления связаны с распространением механических волн.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Механические волны не могут распространяться в вакууме.
Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц за большой промежуток времени равно нулю.
Рассмотрим основные характеристики волны.
Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.
Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.
Основными характеристиками волны являются (рис. 208):
- амплитуда (A) — модуль максимального смещения точек среды из положений равновесия при колебаниях;
- период (T) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны);
- частота— число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;
- скорость— скорость перемещения гребня волны (это не скорость частиц!):
- длина волны— наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника
Рассмотрим колебания источника волны, происходящие с циклической частотой и амплитудой А:
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна v, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии r от источника, описывается функцией
где k — волновое число фаза волны.
Выражение х(t, r) называется уравнением плоской волны, распространяющейся (бегущей) вдоль направления радиус-вектора
Бегущую волну можно наблюдать, проведя следующий опыт: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна, описываемая уравнением плоской волны.
Рассмотрим классификацию бегущих волн по направлению колебаний частиц среды, в которой они распространяются.
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 209).
При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в воздухе и жидкости.
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. С помощью длинной пружины можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно пружине (рис. 210).
Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.
Продольные колебания симметричны относительно линии распространения ВС, и их действие на любой регистрирующий прибор не изменяется, если прибор будет поворачиваться вокруг направления распространения.
Действие поперечных волн на регистрирующий прибор зависит от того, в какой плоскости, проходящей через линию распространения, происходит колебание. Эта особенность поперечных волн носит название поляризации. Если колебания происходят в одной плоскости, то волну называют плоско или линейно поляризованной. Если конец вектора колебаний, например вектора смещения, скорости, напряженности электрического поля, описывает эллипс или окружность, то волну называют эллиптически или циркулярно-поляризованной.
До сих пор мы рассматривали волны, распространяющиеся в какой-либо среде. Волны, которые распространяются на границе раздела двух сред, называются поверхностными волнами. Примером данного типа волн служат волны на поверхности воды.
Звуковые волны. Скорость звука. Ультразвук
Звуком называются колебания среды, воспринимаемые органами слуха.
Раздел физики, в котором изучаются звуковые явления, называется акустикой.
Звуковая волна — упругая продольная волна, представляющая собой зоны сжатия и разрежения упругой среды (например, воздуха), распространяющиеся в пространстве с течением времени. Таким образом, в процессе распространения звуковой волны меняются такие характеристики среды, как давление и плотность.
Звуковые волны классифицируются по частоте следующим образом:
- инфразвук
- слышимый человеком звук
- ультразвук
- гиперзвук
Многие животные могут воспринимать ультразвуковые частоты. Например, собаки могут слышать звуки до 50 000 Гц, а летучие мыши — до 100 000 Гц. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.
Звуковые волны приносят человеку жизненно важную информацию — с их помощью мы общаемся, наслаждаемся мелодиями, узнаем по голосу знакомых людей. Мир окружающих нас звуков разнообразен и сложен, однако мы достаточно легко ориентируемся в нем и безошибочно можем отличить пение птиц от шума городской улицы.
Одной из важнейших характеристик звуковых волн является спектр. Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.
В сплошном спектре присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.
В
дискретном спектре — конечное число волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал.
По типу спектра звуки разделяются на шумы и музыкальные тона.
Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).
Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты. На основе музыкальных тонов создана музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию па различных музыкальных инструментах.
Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить
основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр.
Любой звук, помимо частоты, характеризуется интенсивностью.
Интенсивность I — это энергия переносимая волной в единицу времени = 1 с через единичную площадку площадью расположенную перпендикулярно к направлению распространения волны:
Другими словами, интенсивность любой волны — мощность, переносимая волной через единичную площадку, расположенную перпендикулярно к направлению распространения волны.
Единицей интенсивности в СИ является ватт на метр в квадрате
Чтобы вызвать звуковые ощущения, волна должна обладать некоторой минимальной интенсивностью, называемой порогом слышимости.
С возрастом порог слышимости человека возрастает.
Интенсивность звуковых волн, при которой возникает ощущение боли, называют порогом болевого ощущения или болевым порогом. Интенсивность звука, улавливаемого ухом человека, лежит в широких пределах: от (порог слышимости) до (порог болевого ощущения). Человек может слышать и более интенсивные звуки, но при этом он будет испытывать боль.
Реактивный самолет может создать звук интенсивностью мощные усилители на концерте в закрытом помещении — до поезд метро — около
Уровни интенсивности звука L определяют обычно, используя шкалу, единицей которой является бел (Б) или, что гораздо чаще, децибел (дБ) (одна десятая бела). 1 Б самый слабый звук, который воспринимает наше ухо. Единица названа в честь изобретателя телефона А. Г. Белла. Измерение уровня интенсивности в децибелах проще, поэтому принято в физике и технике.
Уровень интенсивности L любого звука в децибелах вычисляется через интенсивность звука по формуле
где I — интенсивность данного звука, — интенсивность соответствующая минимально возможной интенсивности звука, улавливаемого ухом человека.
Так, поезд метро создает уровень интенсивности звука 100 дБ, мощные усилители — 120 дБ, а реактивный самолет — 150 дБ. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками.
Физическим характеристикам звука соответствуют определенные (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это связано с тем, что восприятие звука — процесс не только
физический, но и физиологический. Действительно, человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека).
Основными физиологическими характеристиками звука являются громкость, высота и тембр.
Громкость (степень слышимости звука) определяется как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах, т. е. его способностью улавливать звуки различных частот. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 Гц до
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://www.calc.ru/Dlina-I-Skorost-Volny.html
http://www.evkova.org/volnovoe-dvizhenie-v-fizike
[/spoiler]
План урока:
Распространение колебаний в среде
Волны. Продольные и поперечные волны. Волны сжатия и разрежения
Упругие волны. Основное общее свойство бегущих в среде волн
Длина волны
Скорость распространения волны. Частота волны
Частоты и период волны
Распространение колебаний в среде
Чтобы понять, что такое колебания в среде достаточно представить несколько простых примеров:
- камень бросили в воду, по поверхности воды тут же расходятся круги – это и есть колебания поверхности воды;
- игра на гитаре – струна начинает колебаться после прикосновения музыканта.
Рассмотрим простую ситуацию распространения колебаний в среде: длинная пружинка, закрепленная с одной стороны, а с другой на нее оказывается периодическое внешнее воздействие, например, равномерные толчки рукой (см. рисунок 1).

После первого толчка часть пружинки, которая находится ближе к руке, сожмется (см. рисунок 1а), а потом из-за упругих свойств пружины, разожмется, воздействуя на витки, лежащие правее первоначального сжатия (см. рисунок 1б). Таким образом сжатие будет «продвигаться» вправо (влево – нет, так как ему мешает рука, блокирующая левый край пружины). После следующего толчка рукой образуется новое сжатие, которое тоже будет «продвигаться» вправо, потом следующее сжатие и т.д. (см. рисунок 1в).
Обобщить все сказанное можно следующим образом: колебания в среде или даже колебания среды (ведь пружинка – это среда) представляют собой некое возмущение, распространяющееся от места их возникновения без переноса вещества. Источником таких возмущений является колеблющееся тело (или некое периодическое воздействие). Такое возмущение и называется волной. Рассмотрим это явление подробнее.
Волны. Продольные и поперечные волны. Волны сжатия и разрежения
Волна – это колебание, распространяющиеся в какой-либо среде с течением времени.
Волны бывают разные. В рассмотренном ранее примере с пружинкой (см. рисунок 1) волна распространяется вправо, а частицы вещества (пружины) сжимаются и разжимаются вдоль направления волны – такие волны называются продольными.
Продольная волна – волна, в которой направление колебаний частиц среды параллельно направлению распространения волны.
Теперь рассмотрим иной случай:волна в гитарной струне. Схематично ее колебание показано на рисунке 2. Направление распространения волны – вправо, а направление смещения частиц – вверх и вниз.

Рисунок 2 – Поперечная волна
Поперечная волна– волна, в которой направление колебаний частиц среды перпендикулярно направлению распространения волны.
Важно отметить, что при возникновении поперечных волн в струне происходит деформация сдвига, а значит, колебания будут происходить под действием сил упругости, старающихся вернуть струну в исходное положение. Деформация сдвига и силы упругости могут возникнуть только в твердых телах (представьте, что один слой жидкости или газа смещается относительно другого – силы упругости в этом случае не возникают). Следовательно, поперечные волны распространяются только в твердых телах.
Продольные волны распространяются в любой среде, в том числе в жидкости и в газах. В любом типе вещества этот тип волны представляет собой чередование сгущений и разрежений частиц, поэтому продольные волны называются так же волнами сжатия и разрежения.
Продольными волнами является, например, звук.
Упругие волны. Основное общее свойство бегущих в среде волн
Волны могут распространяться в разных средах, однако особо выделяют волны, которые распространяются в упругих средах.
Упругая волна – это механическое возмущение или деформация, распространяющееся в упругой среде. Или, другими словами, это распространение колебаний в упругой среде.
*Для справки: тело (среда) называется упругим, если после прекращения воздействия на него оно возвращается в исходное состояние. Упругие деформации – обратимые, то есть те, после которых тело еще способно вернуться в исходное состояние. Например, если взять тонкий деревянный стержень, можно его немного согнуть, но как только воздействие прекратится, он вернется в начальное положение – это будет упругая деформация. Если согнуть стержень слишком сильно, так, чтобы он сломался, будет неупругая деформация.
Ранее рассматривалось разделение волн на продольные и поперечные. Помимо этого, все волны можно так же разделить на стоячие и бегущие.
Бегущие волны – тип волн, при котором происходит перенос энергии без переноса вещества.
В примере с пружинкой (рисунок 1) как раз рассматривается бегущая волна. Как известно, сжатая пружина обладает потенциальной энергией, следовательно, «продвигающееся» сжатие в пружине переносит с собой потенциальную энергию. При этом не происходит переноса вещества.
Основное общее свойство бегущих в среде волн: перенос энергии без переноса вещества.
Стоячие волны – такой тип волн, при котором не происходит переноса энергии. Стоячие волны являются суперпозицией (наложением друг на друга) бегущих волн. Это сложное явление, которое не изучается в курсе физики для 9-го класса. Однако, следует помнить, что такие волны существуют.
Основные характеристики волн
Из определения понятия «волна» следует, что волна – это колебание, а значит, ей будут присущи все характеристики колебаний: амплитуда, период и частота. Помимо этого, определение волны говорит, что она куда-то распространяется, следовательно, волны будут характеризоваться скоростью. И последняя характеристика – длина волны. С нее и начнется подробный разбор.
* Напоминание: скорость – векторная величина, а значит, она включает в себя и модуль скорости волны, и направление ее распространения.
Длина волны
Рассмотрим простой пример: веревка, которую с одной стороны держит ученик, а с другой она закреплена за опору (рисунок 3). Ученик начинает периодически встряхивать веревочку, вследствие чего по ней начинают идти волны.

Упрощенно можно сказать, что распространение колебаний волны в веревочке представляет собой чередование «горбов» и «впадин». Можно заметить, что расстояние между каждыми двумя соседними «горбами» или «впадинами» везде одинаковое. Это и есть длина волны для конкретно взятого примера. Длина волны обозначается буквой λ (читается как «лямба» или, иногда, «ламбда»). В СИ:

Чтобы обобщить понятие длины волны, нужно ввести другие характеристики.
Скорость распространения волны
Под скоростью распространения волны понимают скорость распространения колебаний (возмущения). Так же можно сказать, что скорость продольной или поперечной волны – это скорость переноса энергии бегущей волны. Скорость, как и всегда, обозначается буквой ν (в данном случае, скорость – вектор, в эту величину включается и модуль, и направление движения; если в условиях конкретной задачи необходим только модуль скорости, он обозначается ν).

Волны, распространяющиеся в пространстве, удобно рассматривать, используя функции. Обратимся к примеру, с пружиной, представленному ранее. Вдоль пружины можно выбрать координатную ось х. Волны, бегущие в пружине – это волны уплотнения и растяжения. Тогда можно задать относительную деформацию ε как функцию от координаты х:

То есть, пользуясь этой функцией, мы сможем вычислить деформацию в каждой точке пружины, а также можно построить график – рисунок 4.

Как уже говорилось ранее, волна распространяется (бежит) по пружине с течением времени (t). Скорость бегущей волны v. Чтобы учесть это, воспользуемся свойством смещения графика функции, и зададим плотность так:

График функции, заданной в таком виде, при равномерном увеличении t будет ползти вправо. То есть каждая точка графика будет двигаться вправо со скоростью v (рисунок 5).

Для задания волны, бегущей влево, нужно задать смещение с противоположным знаком:

Приведенные выражения называются уравнениями бегущей волны. Удобство такого рассмотрение заключается в том, что наложение множества волн с разными характеристиками можно рассматривать просто как математическую функцию, и использовать для этого весь мат. аппарат. В программе старших классах будет разобрано, как это применяется для исследования свойств одной волны и наложения двух и трех волн.А пока достаточно знать, как по виду функции определить, в каком направлении движется волна.
*Математическое отступление.
Напомним, что математическая функция в узком смысле – это закон, который в соответствие одному числу ставим другое. В записи:


Частоты и период волны
Если вернутся к примеру на рисунке 3, можно сказать, что частота волны – это количество гребней, проходящих мимо наблюдателя за единицу времени (то есть за секунду в СИ). Частота обозначается буквой v(«ню»). Напомним, что:

Даже свет и цвета, которые мы видим – это тоже особый вид волн, которые называются электромагнитными (они будут рассматриваться чуть позже). Например, красный цвет – это волны, длины которых находятся в диапазоне от 620 до 760 нанометров. Длина всех волн света (или световых волн) колеблется в промежутке примерно от 380 до 760 нанометров.
Длина волны. Скорость волны
Гипермаркет знаний>>Физика и астрономия>>Физика 11 класс>> Длина волны. Скорость волны
§ 44 ДЛИНА ВОЛНЫ. СКОРОСТЬ ВОЛНЫ
Рассмотрим физические характеристики волны — длину волны и скорость. После того как колебания при распространении поперечной волны достигнут 13-го шара, 1-й и 13-й шары будут колебаться совершенно одинаково. Когда 1-й шар находится в положении равновесия и движется влево (если смотреть вдоль цепочки шаров; см. рис. 6.7, д), то и 13-й шар находится в положении равновесия и тоже движется влево. Спустя еще четверть периода 1 й шар оказывается максимально отклоненным влево и в гаком же положении находится 13-й шар (см. рис. 6.7, е). Колебания этих шаров происходят в одинаковых фазах1.
1Точнее, колебания 13-го шара отстают по фазе от колебаний 1-го на 2![]() . Но так как cos (
. Но так как cos (![]() t – 2
t – 2![]() ) = cos
) = cos ![]() t, то такая разность фаз не приводит к различию в состояниях колеблющихся шаров, и можно считать поэтому, что их колебания происходят в одинаковых фазах.
t, то такая разность фаз не приводит к различию в состояниях колеблющихся шаров, и можно считать поэтому, что их колебания происходят в одинаковых фазах.
Кратчайшее расстояние между точками, колеблющимися в одинаковых фазах, называется длиной волны. Следо-иательно, расстояния между 1-ми 13-м, 2-м и 14-м, 3-м и 15-м шарами равны длине волны (см. рис. 6.7, д, с). Длина полны обозначается греческой буквой ![]() (лямбда).
(лямбда).
Длина продольной волны согласно рисунку 6.8, б равна расстоянию между 4-м и 16-м шарами или между 2-м и 14-м шарами.
При распространении волны разные частицы среды (шары в рассматриваемой модели) колеблются с различными фазами, если только расстояние между ними не равно ![]() n (где n — целое число).
n (где n — целое число).
Шары 1-й и 7-й (см. рис. 6.7), находящиеся на расстоянии ![]() /2, колеблются в противоположных фазах: когда 1-й шар от положения равновесия движется вверх, то 7-й — вниз (см. рис. 6.7, d).
/2, колеблются в противоположных фазах: когда 1-й шар от положения равновесия движется вверх, то 7-й — вниз (см. рис. 6.7, d).
За один период волна распространяется на расстояние ![]() (см. рис. 6.7, д).
(см. рис. 6.7, д).
![]() =
= ![]() T. (6.1)
T. (6.1)
Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний. Так как период Т и частота v связаны соотношением
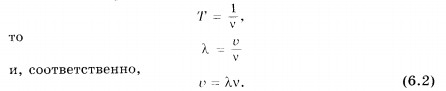
При распространении волны вдоль шнура мы наблюдаем два вида периодичности.
Во-первых, каждая частица шнура совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по закону синуса или косинуса) частота и амплитуда колебаний частиц одинаковы во всех точках шнура. Эти колебания различаются только фазами.
Во-вторых, в каждый момент времени форма волны (т. е. профиль шнура) повторяется на протяжении шнура через отрезки длиной ![]() . На рисунке 6.9 черной линией показан профиль шнура в определенный момент времени t (мгновенный снимок волны). С течением времени этот профиль перемещается.
. На рисунке 6.9 черной линией показан профиль шнура в определенный момент времени t (мгновенный снимок волны). С течением времени этот профиль перемещается.
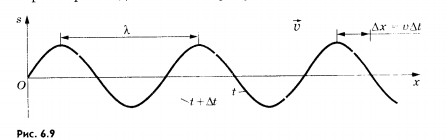
Спуста промежуток времени![]() t волна будет иметь вид, изображенный на том же рисунке синей линией.
t волна будет иметь вид, изображенный на том же рисунке синей линией.
Для продольной волны также справедлива формула (6.2), связывающая скорость распространения волны, длину волны и частоту колебаний.
Все волны распространяются с конечной скоростью. Длина волны зависит от скорости ее распространения и частоты колебаний.
![]()
1. Что называют длиной волны?
2. Как связаны скорость волны и длина волны!
3. Определите по рисунку 6.8, какова разность фаз колебаний двух соседних шаров; двух шаров, находящихся на расстоянии, равном длине волны.
Мякишев Г. Я., Физика. 11 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с : ил.
Физика для 11 класса, учебники и книги по физике скачать, библиотека онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Помимо скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

где
v — скорость волны; T — период колебаний в волне; λ (греческая буква «ламбда») — длина волны.
Выбрав направление распространения волны за направление оси x и обозначив через y координату колеблющихся в волне частиц, можно построить график волны. График синусоидальной волны (при фиксированном времени t) изображен на рисунке 45. Расстояние между соседними гребнями (или впадинами) на этом графике совпадает с длиной волны λ.
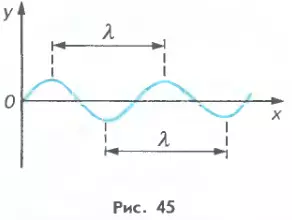
Формула (22.1) выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте, т. е. T = 1/ν, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
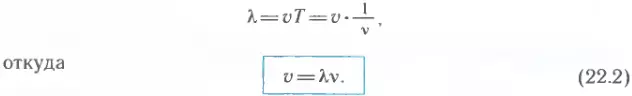
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
1. Что понимают под скоростью волны? 2. Что такое длина волны? 3. Как длина волны связана со скоростью и периодом колебаний в волне? 4. Как длина волны связана со скоростью и частотой колебаний в волне? 5. Какие из следующих характеристик волны изменяются при переходе волны из одной среды в другую: а) частота; б) период; в) скорость; г) длина волны?
Экспериментальное задание. Налейте воду в ванну и посредством ритмичных касаний воды пальцем (или линейкой) создайте на ее поверхности волны. Используя разную частоту колебаний (например, касаясь воды один и два раза в секунду), обратите внимание на расстояние между соседними гребнями волн. При какой частоте колебаний длина волны больше?
Каждая волна имеет свои параметры движения.
Скорость волны — скорость распространения возмущения.
Пример:
воздействуя на стальной стержень с одного конца, можно вызвать волны сжатия и разрежения со скоростью (5000 frac{м}{с}).
Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.
Помимо скорости, важной характеристикой волны является длина волны.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).
Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.
![]()
Рис. (1). Модель упругой среды для демонстрации колебаний
Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.
Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.

Рис. (2). Изображение максимального смещения от положения равновесия первого шарика
В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.

Рис. (3). Изображение максимального смещения от положения равновесия четвёртого шарика
Между седьмым и четвёртым шариком, а также седьмым и десятым (1/4) часть колебания (рис. (4)).

Рис. (4). Изображение максимального смещения от положения равновесия седьмого шарика
Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.

Рис. (5). Изображение максимального смещения от положения равновесия десятого шарика
Начиная с тринадцатого шарика, мы можем отсчитывать новую волну (рис. (6)).

Рис. (6). Изображение модели новой волны
Длину волны измеряют расстоянием, на которое перемещается волновая поверхность за один период колебания источника волн;
Длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, который колеблется в одинаковой фазе:
, где (λ) («лямбда») — длина волны, (upsilon) — скорость волны, (T) — период колебания.
Период колебаний можно выразить как величину, обратную частоте колебаний:
T=1ν
.
Тогда выразим длину волны как отношение скорости и частоты:
λ=υν
.
Длина волны прямо пропорциональна скорости волны и обратно пропорциональна частоте колебаний (прямо пропорциональна периоду колебаний).
Поперечные и продольные волны описываются одними и теми же законами.
Выразим скорость волны:
как отношение длины волны к периоду колебаний:
υ=λT
;
как произведение длины волны на частоту колебаний:
υ=λν
.
За длину волны (λ) примем расстояние между шариками, колеблющимися в одинаковых фазах. Например (см. рис. (6)), между четвёртым и шестнадцатым, третьим и пятнадцатым.
Колебания проходят шарики, начиная с первого и заканчивая двенадцатым, проходят все фазы колебания. Новая волна начинается с тринадцатого шарика. Каждый шарик совершает одно полное колебание за время, которое называют периодом колебаний (T). За это время колебательный процесс проходит расстояние, называемое длиной волны (λ.)
Модель распространения продольных волн представлена на рисунке (7).
Длиной волны будет расстояние между соседними центрами сжатия пружины.
Рис. (7). Распространение продольных волн в упругой пружине
Источником колебаний генерируется волна той же частоты, поэтому вынужденные колебания совпадают по частоте с осциллятором и не зависит от плотности среды, в которой движется волна.
Если в ходе движения волна переходит в среду другой плотности, то скорость движения волны изменяется, а частота колебаний остаётся прежней.
Источники:
Рис. 1. Модель упругой среды для демонстрации колебаний. © ЯКласс.
Рис. 2. Изображение максимального смещения от положения равновесия первого шарика. © ЯКласс.
Рис. 3. Изображение максимального смещения от положения равновесия четвёртого шарика. © ЯКласс.
Рис. 4. Изображение максимального смещения от положения равновесия седьмого шарика. © ЯКласс.
Рис. 5. Изображение максимального смещения от положения равновесия десятого шарика. © ЯКласс.
Рис. 6. Изображение модели новой волны. © ЯКласс.
Рис. 7. Распространение продольных волн в упругой пружине. © ЯКласс.
