Определение угловой скорости маятника
Кинетическая
энергия вращательного движения маятника
![]() ,
,
где![]() – момент инерции маятника с грузами,
– момент инерции маятника с грузами,
переходит в потенциальную энергию,
равную работе по закручиванию нити.
Найдем её величину. Используя закона
Гука, упругий момент нитиMпропорционален углу поворотамаятника:![]() .
.
(3)
где
![]() – постоянная момента упругих сил.
– постоянная момента упругих сил.
Элементарная
работа против сил упругости по закручиванию
нити на угол
![]() равна
равна![]() .
.
После интегрирования обеих частей
равенства имеем:![]() .
.
(4)
Закон сохранения
механической энергии в этом случае
запишется в виде:
![]() . (5)
. (5)
где
![]() .
.
Из выражения (5) получим:
![]() , (6)
, (6)
где
![]() – наибольший угол поворота маятника.
– наибольший угол поворота маятника.
Используя основной
закон динамики вращательного движения
твердого тела: ![]() .
.
(7)
с
учетом выражения (3) можно записать
уравнение колебаний баллистического
маятника в виде:
![]() . (8)
. (8)
или
![]() . (9)
. (9)
Частным решением
этого уравнения является:
![]() ,
,
где величина![]()
– есть круговая частота
![]() ,которая по определению равна
,которая по определению равна![]() .
.
Таким образом, маятник будет совершать
гармонические колебания с периодом:
![]() . (10)
. (10)
Заменяя в формуле
(10) величину
![]() ее значен6ием из выражения (6), получим
ее значен6ием из выражения (6), получим![]() ,
,
откуда искомая начальная угловая
скорость маятника равна:
![]() . (11)
. (11)
Определение момента инерции маятника
Для определения
момента инерции маятника
![]() воспользуемся формулой (10), переписанной
воспользуемся формулой (10), переписанной
в виде:
![]() . (12)
. (12)
Применим формулу
(12) для двух положений грузов на расстоянии
![]() и
и![]() от оси вращения
от оси вращения
![]()
![]() (13)
(13)
где
![]() и
и![]() – периоды колебаний маятника, соответствующие
– периоды колебаний маятника, соответствующие
положениям грузов![]() и
и![]() .
.
Из системы уравнений
(13) получим:
 (14)
(14)
Подставляя выражение
(11) и (14) в (2), получим окончательную
формулу для определения скорости полета
снаряда:
 . (15)
. (15)
Порядок выполнения работы
Задача работы:
определение скорости полета снаряда
при помощи крутильного баллистического
маятника.
Описание экспериментальной установки
О бщий
бщий
вид унифилярного подвеса показан на
рис. 2. Основание I оснащено регулируемыми
ножками 2, которые позволяют выставлять
горизонтальное положение прибора. На
основании закреплена колонна 3, к которой
крепятся верхний 4, средний 5 и нижний 6
кронштейны.
К среднему кронштейну
прикреплен пружинный пистолет 7,
обеспечивающий полет пули, а также
прозрачный экран с нанесенной на него
шкалой 8 для отсчета угла поворота
маятника при попадании в него груза.
Кронштейны 4 и 6 имеют зажимы, служащие
для крепления стальной проволоки, на
которой подвешен маятник. Маятник
состоит из двух стержней 9, перемещаемых
грузов 10, двух кювет, наполненных
пластилином 11, указателем 12, перекрывающим
световой поток идущий к фотоэлектрическому
датчику 13. Фотоэлектрический датчик
соединен с секундомером, шкала которого
выведена на переднюю панель прибора.
На лицевой панели
14 размещены следующие клавишные
переключатели: «ПУСК» – начало измерения,
«СТОП» – окончание измерения. На задней
панели установки находятся: клавишный
переключатель «СЕТЬ» – включение прибора
в сеть и выходное гнездо, служащее для
подключения фотоэлектрического датчика
и заземляющий зажим.
Для
приготовления прибора к работе необходимо:
-
заземлить
прибор; -
произвести
выравнивание прибора; -
включить
сетевой шнур в сеть. Прибор готов к
работе сразу после включения сетевого
напряжения и не нуждается в нагреве. -
установить
мишень в рамку, убедиться, что мишень
находиться на линии «выстрела», а флажок
рамки пересекает оптическую ось
фотодатчика. -
установить
грузы на рамке.
Определение
скорости полёта снаряда проводится по
следующей схеме:
-
Обнулить
маятник, т.е. установить маятник в таком
положении, чтобы черта на шкале показывала
угол отклонения
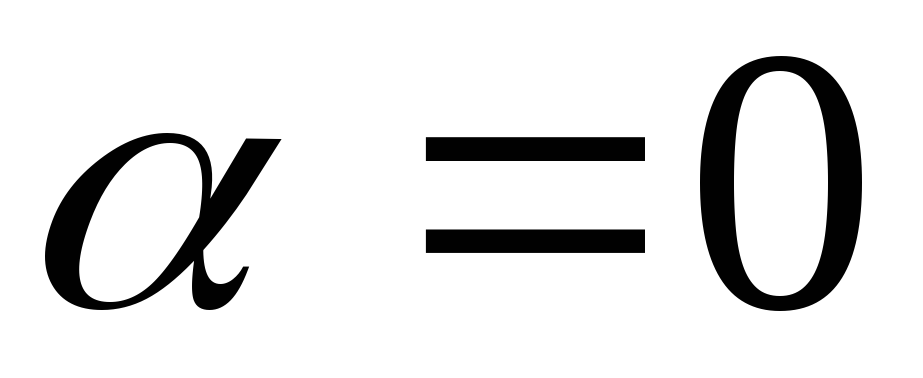 ;
; -
Установить
«снаряд» на направляющий стержень
спускового устройства, взвести пружину
и произвести «выстрел». Визуально
определить максимальный угол отклонения
 рамки по шкале угловых перемещений с
рамки по шкале угловых перемещений с
помощью флажка, закрепленного на рамке
ирасстояние
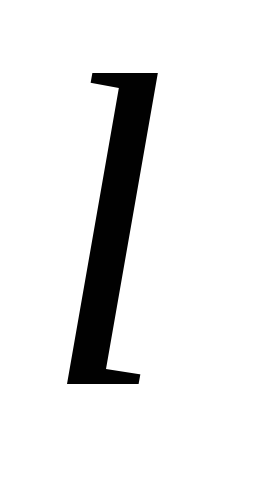 от оси вращения рамки до центра отпечатка
от оси вращения рамки до центра отпечатка
«снаряда», залипшего в мишени (с помощью
линейки); -
Измерения
повторить 5 раз. -
отклонить
рамку на угол 300градусов и
зафиксировать ее с помощью электромагнита,
нажав кнопку «СЕТЬ» на задней панели
блока; -
нажать
кнопку «ПУСК» и измерить время десяти
полных колебаний t.
Вычислить период колебанийT.
Нажатие клавиши “СТОП” произвести
после десятого колебания;
![]() ,
,
-
снять
грузы с рамки и повторить измерения
периода десяти колебаний рамки без
грузов. Определить период
 ;
; -
скорость
полета снаряда

вычислить по формуле (15). Иметь в
виду, что ,M– масса грузов,m– масса «снаряда».
,M– масса грузов,m– масса «снаряда». -
Данные
записать в таблицу.
|
Образец |
|||||||
|
№ п.п. |
m, |
, |
, |
l, |
T, |
T1, |
V, |
|
1 |
|||||||
|
… |
|||||||
|
5 |
-
Выполнить
статистическую обработку результатов
измерения с использованием метода
Стьюдента.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Период вращения маятника по окружности
Определение ускорения свободного падения при помощи маятника.
Отличие равномерного циклического движения по окружности и колебания.
Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.
Колебание — возвратно-поступательное движение, то есть движение с остановками и изменением скорост и( ускорением и торможением) и соответственно направления движения.
Движение по окружности не является возвратно поступательным, и считаться колебательным не может. Это частный случай криволинейного движения по замкнутой траектории не имеющее особой точки равновесия.
Характеристики колебательного процесса:
- Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, ( м )
- Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), ( с )
- Частота — число колебаний в единицу времени, ( Гц, с −1 ) .
Период колебаний и частота — обратные величины;
и
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота (рад/с, Гц, с −1 ) , показывающая число колебаний за единиц времени:
Понятие частот ы( любой) напрямую через радианы или градусы сводится к понятию угловой скорости, то есть если имеется одна единица измерения c -1, частота и угловая скорость отличаются между собой только кратностью угла и считаться разными физическими величинами не могут.
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания: от угла, если выражаться просто.
Другое распространённое обозначение
Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
Численно циклическая частота равна числу циклов (колебаний, оборотов) за 2 π секунд
Вот только колебания тут не при чем, и движение происходит по дуге окружности. И 2 пи годится только для движения по окружности как кратность в градусах или радианах полному обороту. Как только колебания – это уже движение «туда» и «обратно» в пределах именно того угла, в котором и происходит движение. Кратность именно этому углу и никакому другому. Ниже будет показана справедливость данного уточнения.
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
,
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.
Это так сказать предисловие к рассмотрению движения маятника, чтоб даже и не заикались о различии формулы, использованной Гюйгенсом в модели математического маятника для вычисления периода колебаний, с формулой для определения угловой скорости при равномерном движении по окружности.
В опыте с математическим маятником имеется не просто ошибка с жестким определением периода качания маятника. Это заранее и с умыслом спланированная
Неточность. А по существу намеренный подгон.
По Гюйгенсу период составляет
w – угловая скорость. 1/ w —частота. 2 пи- кратность полному обороту или движение в половине окружности «туда» и «обратно»
время,
g – ускорение свободного падения.
Однако Гюйгенс, а вместе и все остальные забывают, что данный период относится только к равномерному круговому движению с постоянной угловой скоростью.
Это движения опять же описано Гюйгенсом и им же введено центростремительное ускорение.
Для движения по кругу радиуса R длина окружности будет C = 2π R . Если период вращения есть T , то угловая скорость вращения ω будет равна:
Период колебаний связан соотношением взаимной обратности с частотой, количеством колебаний за единицу времени .( сек^-1):
Период колебаний и частота — обратные величины;
и
2пи лишь коэффициент кратности угла.
2 p именно для движения по окружности, а маятник в опыте конкретно этого движения не совершает.
Мало того, реально вообще период величина не постоянная.
В большинстве опытов он колеблется в половине круга, в пределах явно меньших одного p , и период может составлять T = p / w . Надо учитывать при этом, что угловая скорость движения маятника не имеет ничего общего со скоростью равномерного движения по окружности. Она меняется!!
На рисунке и представлен угол, в пределах которого в опыте и именно в большинстве опыто в( от 45 0 до -45 0 =90 0 и далее только с уменьшением) как раз и совершается движение груза маятника. При больших углах отклонения у реального нежесткого маятника натяжение нити резко падает.
То есть собственно и происходит более или менее свободное падение, которому не особо мешает жесткий и нерастяжимый подвес на опоре, рычаг.
А вот и углы, в которых это свободное более или менее падение можно наблюдать.
Измерил угловую скорость на малом угле, сделал это последовательно на нескольких углах, вычислил ускорение. Нате вам, пожалуйста, ускорение свободного падения. Не очень точное.
Так это и проще делается, путем бросания без всякого подвеса.
А вообще то—ускорение свободного падения—это направленное движения четко вниз, оно при нормальном падении и определяется, без всяких колебаний–движений в сторону от вертикали. И если такое отклонение имеется, значит имеется и путь проделанный в эту сторону, движение по дуге с ускорением, не направленным по вертикали, мало того это ускорение знакопеременно, так как направление меняется. Угловое оно.
а математическая модель что маятника, что осциллятор а- -даже для отмазки никуда не годится.
А вот угол, который в качестве жесткого приближения используется в модели математического маятника.
2пи «туда» и «обратно».
При этом рассматриваются углы, в которых вроде как и работает модель. Самоограничение наложенное опытом на математику Гюйгенса. Вот эти малые углы.
Только при таких малых углах
Период является временем одного цикла колебательного движения маятника в обе стороны «туда» и «обратно», величина, не меняющаяся только при «таком опыте с малыми углами» даже при затухающем процессе. И круговое равномерное движение нельзя считать колебательным процессом, поскольку нет возвратно-поступательного .
Общая скорость движения математического маятника за один период не меняется, то есть не меняется и частота колебаний при неизменной длине подвеса. Однако первую четверть периода 2пи маятник движется ускоренно вниз, вторую четверть периода замедленно вверх. Закон этого движения для малых углов отклонения якобы описывается моделью математического маятника, где аналогом принимается совершенно отличный от рассматриваемог о( ускоренного) вид движения. Но период тогда не должен меняться при любых углах отклонения, чего в опыте не наблюдается.
То есть в расчетной формуле для свободного падения
При применении допустима величина предельного угла отклонения в 45 градусов, то есть 90 туда сюда, Пи радиан,
Пропадае т( сокращается) двойка в знаменателе. Там она входит в состав периода (2п/ w )
После чего ускорение свободного падения вдвое больше общепринятого по Гюйгенсу g =19.6 вместо 9.8 м/сек^2.
Этот вариант является основным, использованным Гюйгенсом для якобы доказательства справедливости его формулы для равноускоренного движения и соответственно всего, что касается ускорения свободного падения.
Это так сказать рассмотрен первый вариант неработоспособности модели. А он использован Гюйгенсом, для доказательства (подтверждения его расчетов) в кинематике равноускоренного движения. И как оказывается, может быть с успехом оспорено в различных вариантах.
Условие нерастяжимого подвеса. Нерастяжимый одновременно предполагает нерастяжимость не только по длине, но и по толщине подвеса. То есть подвес просто предельно жесткий и невесомый.
В противном случае это не модель, а подгон под чей то явно не благовидный интерес.
А посему математический, да и реальный, маятник можно отпускать из любого положения вплоть до максимально возможного.
Полный угол качания при этом составит в ту и другую сторону 4 пи.
Что опять ведет к сокращению уже в числителе. Что явно показывает, еще мягко говоря, абсурдность методики, примененной Гюйгенсом.
В теории математического маятника не оговаривается обязательность угла отклонения. Есть рекомендации, и от фонаря, применимости метода только на малых углах. Однако 2пи это два движения “туда” и “обратно” в половине окружности, которое может совершать математический маятник. А применено только к малым углам. Вопрос почему? Так он и по полной может. !И меет право.
А имеет право совершать движение и в пределах п /2. и вообще в любых углах..
Вопрос волюнтаризма выбора угла отклонения Гюйгенсом. Маятник математический и математика точная наука. Гюйгенс совершил то, что в математике недопустимо, применил произвольный подход (какой ему было выгодно) к выбору угла отклонения, включил «жестко» это недоразумение в формулу, позволяющую трактовать свою математику как угодно.
А совершенно точное максимальное значение угла-4п, а не 2 пи, как ограничение, наложенное Гюйгенсом, а минимальное 0 и вообще не наблюдается никакого падения.
То есть, отпуская маятник из крайнего верхнего положения, совершено действие аналогичное сделанному Гюйгенсом. И ничего в этом зазорного и противоречащего логике модели нет. И применимость метода тут не при чем. Просто сделано уточнение на более общий случай угла отклонения именно математического маятник а( с его начальными допущениями) и пока только доказана вопиющая неточность, допущенная Гюйгенсом в теории математического маятника.
Тогда если считать, что в формуле Гюйгенса все кроме этого коэффициента правильно, то явно виден волюнтариз м( свобода выбора) в его определении времени одного колебания.
Теперь посмотрим на одну очень примечательную « отмазку ».
Не смотря на то, что маятник не совершает никаких циклических круговых движений, отмазка предполагает замену колебательного (возвратно-поступательного по дуге) движения с бухты барахты круговым, причем с применением толкающей сторонней силы, помимо силы для отклонения груза от вертикали. Называется, автор упростил, одно более или менее простое движение заменил, не задумываясь, принципиально другим еще более усложнив саму задачу, где колебания под действием силы тяжести совсем не рассматривается. Оно просто отсутствует. Вместо колебания в реальном опыте будет постоянное уменьшение радиуса окружности.
Рис. Колебания маятника в плоскости (а) и движение по конусу (б)
»При качаниях маятника груз движется ускоренно по Дуге ВА (рис. а) под действием возвращающей силы Р 1 , которая меняется при движении. Расчет движения тела под действием непостоянной силы довольно сложен .»
Автор явно лукавит или вообще не понимает сути процесса качания маятника. Сила, в общем-то, постоянная, это сила тяжести.
Она постоянно действует как на подвес, так и на груз.
Непостоянна реакция опоры и вес тела, напрямую зависящий от скорости движения и ускорения.
«Поэтому мы для упрощения поступим следующим образом. Заставим маятник совершать не колебание в одной плоскости, а описывать конус так, чтобы груз двигался по окружности (рис. б). Это движение может быть получено в результате сложения двух независимых колебаний: одного — по-прежнему в плоскости рисунка и другого — в перпендикулярной плоскости.
Очевидно, периоды обоих этих плоских колебаний одинаковы, так как любая плоскость качаний ничем не отличается от всякой другой. Следовательно, и период сложного движения — обращения маятника по конусу — будет тот же, что и период качания в одной плоскости. Этот вывод можно легко иллюстрировать непосредственным опытом, взяв два одинаковых маятника и сообщив одному из них качание в плоскости, а другому — вращение по конусу .»
можно с ума сойти. Сложили и получили… математически равномерное движение по окружности…. И круговое движение не является колебанием в силу определения колебания и отсутствия точки равновесия.
Но период обращения «конического» маятника равен длине описываемой грузом окружности, деленной на скорость:
Заметим, угловую скорость. Или скорость по реальной дуге, а не секущей ее хорде. И ни какого не маятника ….. ну нет тут никакого возвратно поступательного движения.
Если спроецировать реальное движение на бумагу, то получится сужающаяся спираль.
Логика и только логика и здравый смысл делают нереальным данное воображаемое приближение, а проще выдумывание на пустом месте.
Теперь посмотрим на формулу Гюйгенса для периода математического маятника.
Берем формулу:
и вычисляем g просто исходя из угловой скорости. Качание одно (туда сюда), до понятия частоты не дотянули чисто по физическим причинам, 2пи сокращается, обе части уравнения возводятся в квадрат, имеем:
L – длина подвеса , w -угловая скорость.
угловая скорость при этом постоянна, как ни странно. А это исходя из равномерного движения по окружности, Гюгенсово известное определение . Вопрос, а где оно угловое ускорение? Когда стоит буква g -ускорение свободного падения, направленное не к центру, а эта формула — центростремительное ускорение по Гюйгенсу!
Рассматривается чисто кинематическая трактовка модели. Никаких масс и причин, вызвавших движение.
Рассматриваем тот вариант, первоначальный, и никакие последующие, хоть в малой части использующие гюйгеновскую кинематику теории, во внимание не принимаются, поскольку априори базируются на ней самой.
Короче ни динамика, ни теория гармонический колебаний, как инструмент тыканья носом не годятся, здесь как раз и идет речь о корне этих дисциплин.
И ускорение это должно быть направлено вертикально вниз, в направлении противоположном центростремительному , то есть со знаком минус.
И что самое замечательное и смешное, в модели реально центростремительное ускорение ПРОПАЛО.
Что интересно, все это маскируется совершенно наглым образом:
В википедии в статье про гармонический осциллятор
Ускорение теперь просто ускорение, не угловое, и даже не свободного падения, а просто взятое со знаком минус и полученное из квадрата скорости. Что само по себе вызывает усмешку, квадрат скорости, поскольку в дифференциалах появляется квадрат угла, но это к слову и рассмотрено в http :// fatyf . narod . ru / cinema 7. htm
Ускорение может быть также выражено как функция перемещения:
То есть ускорение направлено в сторону, обратную центростремительному. !к оторое записывается точно такой же формулой. Но его почему-то вместе с угловым ускорением не стало в принципе.
Далее следует поразительная чехарда с буквами и явно видимая замена одного ускорения, другим. Красным помечено как это делается.
В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ с ускорением свободного падения g даётся формулой
Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от ускорения свободного падения g , поэтому при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.
Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускорения пропорционально синусу координаты:
не синусу а косинусу. !и вовсе не угловому а просто неизвестно какому a ( t )!
Когда угол θ мал, можно считать, что sin θ ≈ θ , и выражение принимает вид:
а ускорение то g -свободного падения, но вдруг, откуда не возьмись
что делает угловое ускорение прямо пропорциональным углу θ , а это удовлетворяет определению простого гармонического движения.
Спрашивается, а какого рожна заменен один вид движения на другой?
А у маятника скорость меняется и маятник движется в пределах от и до градусов угла отклонени я( математический) и меньше по опыту, в одну сторону ускоренно в другую замедленно. У реального маятника уменьшается и угол качания-амплитуда .
А геометрия такая! как у криволинейного движения. Дуга окружности Гюйгенсом заменяется хордой, которая явно короче истинного пути, что и определяет малость угла отклонения в опыте, то есть сопоставимость хорды и дуги, чем больше угол отклонения, тем больше погрешность.
А апологеты до сих пор выясняют, а почему модель работает только при малых углах и в процентах. прикидывают погрешность, хотя она математически точно рассчитывается.
и оказывается период то нам и не нужен вовсе. !п ри таком подходе.
ведь угловая скорость не меняется она усреднена. и все движение приведено к углу, в котором этого движения не наблюдается.
Определение из учебников.
Мгновенная скорость есть первая производная пути по времени =
v= ( ds / dt )= s ‘
где символы d / dt или штрих справа вверху у функции обозначают производную этой функции.
Иначе – это скорость v = s / t при t , стремящимся к нулю.
И это пишут в учебниках, не смотря вообще на опыт, просто обзывают скорость несвойственным ей наименованием от фонаря – МГНОВЕННОЙ, ТО ЕСТЬ ОТСУТСТВИЕМ ВРЕМЕНИ, поскольку в природе-физике мгновенного нет. Просто это малый интервал времени. Как не крути с наименованием, этот интервал измеряем. А если не измеряем, это уже не физика, а фантазии математиков.
»При отсутствии ускорения в момент измерения – мгновенная равна средней за время периода движения без ускорений Vмгн . = Vср . =S/ t за этот период .»
Скорость есть путь за время. На флоте есть прибор, называется лаг. Сколько узлов ушло за время, такова и скорость за это время независимо от порывов ветра, то есть это измерение не зависит от изменений скорости во время движения. Хотите поймать эти изменения, чаще ставьте узлы и делайте меньше отрезки времени измерения.
А что такое средняя скорость? Это скорость в предположении равномерного движения без конца и начала, без ускорений. В природе такого не бывает.
В общем имеется не «средняя» скорость, а сумма скоростей—скорость общая.
Только говорят, что 600 км за десять часов, со средней скоростью 60 км в час. Это если не стоять, не стартовать и не тормозить. Двигаться все время равномерно. Нет у такого движения ни начала ни конца. Фикция это, а не движение. Бесконечность не есть предмет измерения. Такое движение можно наблюдать только в космосе у планет.
Самим так двигаться—помрешь на ходу.
Это будет общей скоростью, 600 км за 10 часов, а скорость на малом отрезке пути—дифференцированная скорость.
Общая скорость это сумма малых отрезков, сумма дифференциалов скоростей (отношений пути к времени), интеграл, вычисление которого дает путь . у скорение это сумма скоростей, соотнесенная к общему времени движения – интеграл (путь за время в квадрате), вычисление которого дает скорость.
А текущая скорость это, скорость на последнем малом отрезке. В предположении дальнейшего равномерного движения.
Именно так и работает спидометр. Он показывает и пересчитывает обороты двигателя именно на данный измеряемый не мгновенно интервал времени. В предположении дальнейшего не ускоренного движения без учета сопротивления.
Иначе все время надо на газ поднажимать.
И она является при единичном отрезке времени и общей. И ускорение равносильно скорости на единичном интервале времени.
То есть если я сделал один шаг с места, это и скорость и ускорение. Поскольку шаг – один.
Мгновенных скоростей не бывает. А средние только вычисляются .
м гновенности получить не удастся, физика этого не позволяет. мгновенность это отсутствие времени. И обзывать первую производную от пути по времени мгновенной не имеет смысла. Это просто скорость на малом отрезке пути, за известный промежуток времени который одинаков для всех неодинаковых отрезков общего пути.
В физике нет бесконечно малых величин.
Оперировать с бесконечностью в физике неблагодарная и опасная затея. Физика не занимается абстрактными и не измеряемыми величинами.
Камень, и очень большой в электростатику с ее обособленным зарядом.
Итак, использование Гюйгенсом равномерного движения по окружности привело к тому, что из уравнения для периода качания маятника включающего в себя отношение длины подвеса к ускорению свободного падения получилась формула для центростремительного ускорения, направленного совершенно в противоположную сторону.
Вывод приведен выше.
Это отношение ( l / g ) без надлежащего вывода и обоснования и используется во всех остальных якобы способах доказательства правильности модели математического маятника. Мало того это отношение многие называют эмпирикой Гюйгенса и до сих пор не понимают, как оно получено, используют вслепую, вместе с непониманием, а почему это работает только на малых углах отклонения. Результат –к аша из математических наворотов для гармонического осциллятора целиком и полностью основанных на центростремительном ускорении при равномерном движении по окружности.
И на графической анимации представленной в википедии явно видно как в фазовом представлении все точки совершают равномерное движение по окружности.
Направления ускорений на криволинейной траектории (по Гюйгенсу) и направление силы (ускорений) в модели математического маятника. Перевернем первый рисунок и что получим. Как это прикажете понимать?
И что более всего впечатляет, это отсутствие даже намека на действительное угловое ускорение (ускорение по дуге) через дифферециалы ! во всех способах описания математического маятника и гармонического осциллятора, как будто корова языком слизала это ускорение при ускоренном движении. Его в данной модели просто нет и никакими ухищрениями, кроме как опытом его не получить. Понятно почему, ускоренное движение по дуге окружности подменено равномерным , без ускорения. Подлог. А В место центростремительного введено ускорение свободного падения.
Центростремительного тоже нет в модели.
Модель математического маятника по Гюйгенсу с его допущениями вообще не годится для определения ускорения свободного падения как и сам маятник. Поскольку есть опора, мешающая этому свободному падению.
А раз нет углового ускорения, то какое такое ускорение свободного падения, если при малых углах маятник практически не падает, а просто висит за счет жесткости опоры? Мало того она не жесткая абсолютно и пружинит, да в разные стороны и чем угол отклонения меньше, тем точнее работает модель. Абсурд, движения меньше— модель лучше.
Движения не т- -идеал.
Слов нет, смех сквозь слезы.
Какое такое ускорение свободного падения, если тело вообще не движется.
Его и не будет в модели никогда, поскольку по всей математике видно, что маятник этот выдуманный движется равномерно. А поскольку равномерно, то ускорение центростремительное, а не ускорение свободного падения. что и видно из формул невооруженным взглядом.
и все что связано с такой модель ю- -чистого вида подгон под желаемое.
и все притянуто за уши.
механика такая—-сякая–по Гюйгенсу.
Вместе с кинематикой равноускоренного движения, оправдать Формулы которой Гюйгенс попытался двойным обманом.
Моделью, которая в принципе не отражает существа дела, и формулой для периода, где один вид движения заменен на другой.
А теперь разберем такую штуку, как говорят релятивисты,
«Все у нас подтверждается опытами», в применении к Гюйгенсу.
Маятник длиной 1 метр качается 40 раз при 20 градусах угла отклонения. Мелочи малых погрешностей игнорируем, дело принципиально рассматриваем.
Время одного колебания-2 секунды – период.
Рассчитывается как отношение времени к числу колебаний.
У Гюйгенса другая формула для периода, тянутая из равномерного движения по окружности.
Что самое интересное, только с современной точки зрения приравнивание этих двух периодов с первого взгляда логично.
Но, только с позиции математики 17 века такое никак не получается. НЕ было ни теории гармонических колебаний, на Гюйгенсовом и построенной, ни лангражиана , и вообще никаких примочек, чтоб доказать справедливость данного приравнивания.
Его надо доказывать. Мало это формулу просто назвать периодом.
Нынче делают это без зазрения совести.
Подставляя значения в формулу Гюйгенса имеем
T=2*3.1415*sqrt(1./ 9,80665) [сек]
Квадратный корень извлекаем с помощью калькулятора Windows
и получаем 3.131557. Далее
Т=2*3.14159 / 3.131557 = 2*1.003204=
=2.006408
Но у Гюйгенса обоснований самой формулы не имеется, А кроме как его собственной кинематики равномерного движения по окружности других способов и не было.
А посему, это дело требует проверки с позиции семнадцатого века,
Где период является произведением 2пи -к оэффициента кратности на время.
То есть выражение sqrt ( L / G )—время одного колебания. Для простоты обозначим t .
И получается следующее, если делать алгебраический вывод для значения длины из формулы
T=2ПИ sqrt ( l / g ),
где возвести обе части уравнения T=2pi*sqrt(L/ g ) в квадрат, получим Т^2=4pi^2 * L/ g и не зная значения L вычислить его, получается
L=T^2 g /4pi^2
где сущность периода остается той же самой, по гюйгенсу .
T =2 pi * t , Где t —время одного колебания без всякого круга.
и сравниваем с исходной измеренной предварительно 1 метр .
Ничего не получается. Цифра запредельная.
Т это период по Гюйгенсу, 2 пи это коэффициент и ко времени отношения не имеет, размерность времени только у второй части формулы. ОН, этот период, ничем не отличается от периода равномерного движения по окружности.
T=2pi/ w w= 1/ t –будет частота. И взяться 2пи, кроме как оттуда, просто неоткуда.
Что надо, чтобы получить нужный Гюйгенсу «результат»?
Чтобы расчет вышел и никто явно не заметил. Да смухлевать с этим периодом, чего проще?
Подменяем, по ходу дела период T =2 pi * t периодом T = t / n , благо что называются одинаково, и всяко забыв, откуда получено 2пи, да и сама расчетная формула для длины.
То есть, исключаем эти злочастные и мешающие 2пи из числителя формулы. И говорим, что эти периоды одно и то же.
То есть 2пи входит во время одного колебания и не является коэффициентом кратности, и все что касается движения по окружности, к данному вопросу якобы не относится.
считаем: L=4*9.8/(4*3.14*3.14) ==0.99 ура сошлось.
Да сошлось, по-еврейски.
При полном забывании того, что вывод формулы делался с учетом этих 2пи, и след остался в знаменателе. А его бы, по крайней мере, при такой левой подстановке тоже сократить надо.
Маятник то полный оборот по кругу только в одном случае делает!
И этот случай представлен выше. В остальных 2пи мешает. Да и не работает.
Для этого и исключается 2пи, чтоб совпадало по любому.
2пи есть в периоде равномерного движения по окружности . н о ее не может быть в формуле для периода маятника, который вычисляется как отношение времени качаний к количеству. T= t / n . но Гюйгенс приравнял вообще все три периода—- свой ,з атем тянутый из кругового, и реальный. = t / n , а потом по ходу свой использовал для расчета, и убрал 2пи, чтоб по любому вышло.
Так что приравнивание этих формул мухлеж еще тот. Изощренный.
Долго, наверное, думал. Так что и не удивительно, что никто внимания не обращает на такую математику, если это можно назвать математикой.
Проко л- -самый главный, которого ликвидировать никак, неспособность академиков к математике, мешающая аналитическому получению углового ускорения при качании маятника. Только опытным путем, да и то не хотят.
Приходится делать это вместо них.
а это интструмент.
Будут рассматриваться возражения, только по существу рассматриваемого вопроса. Кинематика. Из динамики не предлагать, из гармонического осциллятора тоже и из теории гармонических колебаний. Они все на кинематике Гюйгенса и основываются, с которой и приходится иметь дело.
Фатьянов Ф.В. 1.02.2013 Спб . Исправления и добавления после обсуждений 28.03.2013.
[spoiler title=”источники:”]
http://fatyf.narod.ru/cinema6.htm
[/spoiler]

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Формула угловой скорости
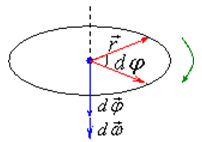
Угловая скорость характеризует скорость вращения тела и измеряется в радианах за секунду.
![Rendered by QuickLaTeX.com [ omega = frac{Delta varphi}{Delta t} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7e32a8d9a166dd6194c728f6712a8a00_l3.png)
При равномерном вращении угловая скорость равна циклической частоте вращения и связана с периодом вращения (T) формулой:
![Rendered by QuickLaTeX.com [ omega = frac{2 pi}{T} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f394d50f47d64f5d0243e2fb6eebe8d3_l3.png)
Угловая скорость является псевдовектором, направление которого зависит от направления вращения и определяется по правилу правого винта.
Примеры решения задач по теме «Угловая скорость»
| Понравился сайт? Расскажи друзьям! | |
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,660 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,971 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
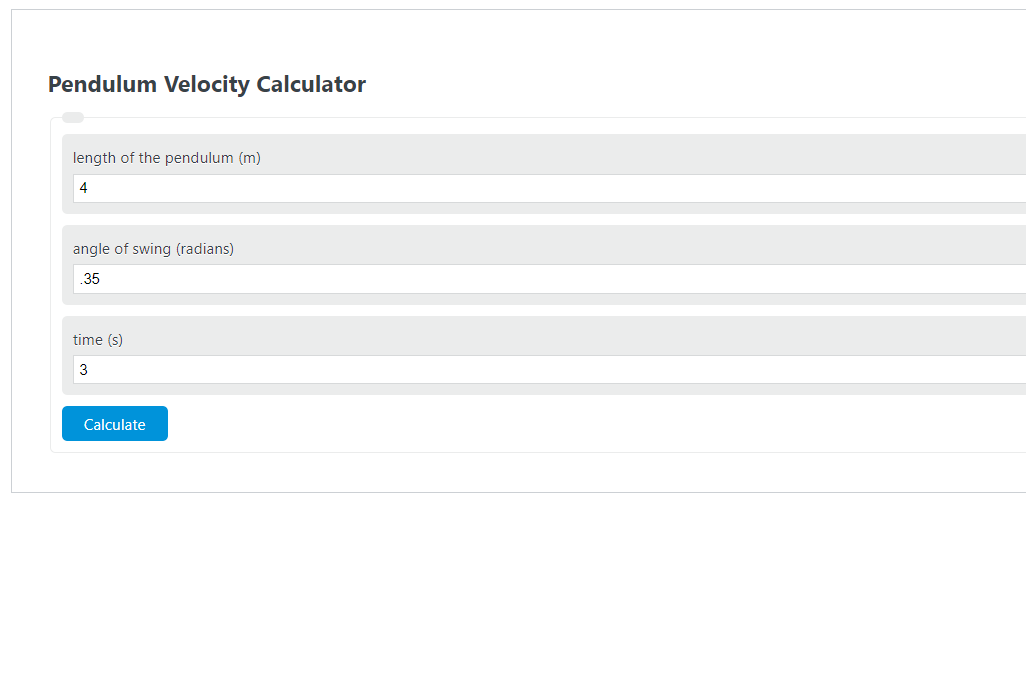
Enter the angle, length, and time into the calculator to determine the pendulum velocity.
- All Velocity Calculators
- Pendulum Force Calculator
- Pendulum Calculator (Frequency & Period)
- Downward Force Calculator
Pendulum Velocity Formula
The following equation is used to calculate the Pendulum Velocity.
V = a * SQRT( L*g) *sin (sqrt ( g/L) * t)
- Where V is the pendulum velocity (m/s)
- L is the length of the pendulum (m)
- a is the angle of swing
- t is the time (s)
What is a Pendulum Velocity?
Definition:
Pendulum velocity describes the instantaneous tangential velocity of a pendulum at any given angle.
How to Calculate Pendulum Velocity?
Example Problem:
The following example outlines the steps and information needed to calculate Pendulum Velocity.
First, determine the length of the pendulum. In this example, the length of the pendulum is found to be 4m.
Next, determine the angle of the swing. For this problem, the angle of swing is found to be .35 radians.
Next, determine the time. In this case, the time is measured to be 3s.
Finally, calculate the Pendulum Velocity using the formula above:
V = a * SQRT( L*g) *sin (sqrt ( g/L) * t)
V = .35 * sqrt( 4*9.81) *sin (sqrt ( 9.81/4) * 3)
V = 2.19 m/s