Памятка
по математике 4 класс по теме
«Скорость, время, расстояние»
S – расстояние ( путь); измеряется в км, м и т.д.
V – скорость ( это расстояние, преодолеваемое за единицу времени); измеряется в км/ч, м/ мин и т.д.
t- время; измеряется в часах, минутах и т.д.
- Чтобы найти расстояние, нужно скорость умножить на время. S =V х t
- Чтобы найти скорость, нужно расстояние разделить на время.
V = S : t
- Чтобы найти время, нужно расстояние разделить на скорость.
t = S :V
Задача на нахождение расстояния
Пешеход шёл со скоростью 5 километров в час. Какой путь он пройдёт за 3 часа?
5 х 3 = 15 ( км)
Ответ: 15 километров пройдёт пешеход.
Задача на нахождение скорости
Пешеход за 3 часа прошёл 15 километров. С какой скоростью шёл пешеход?
15 : 3 = 5 ( км/ч)
Ответ: 5 км/ ч скорость пешехода.
Задача на нахождение времени
Пешеход шёл со скоростью 5 километров в час и прошёл 15 километров. Сколько времени шёл пешеход?
15 : 5 = 3 ( ч)
Ответ: 3 часа шёл пешеход.

Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.

Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Дискуссии, как правильно воспринимать время, не утихают до сих пор. Платон считал, что оно есть не что иное, как движение. Аристотель предполагал, что время – количественное измерение перемещения. Оно было добавлено к классической геометрии Евклида, действующей на ограниченное число измерений. В итоге стало рассматриваться четырёхмерное пространство.
Сегодня так и нет ответов на следующие вопросы о времени:

- из-за чего происходит его течение;
- почему оно определяется только в одном направлении;
- является ли параметр одномерным, как многие учёные считают;
- можно ли обнаружить кванты характеристики.
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
- начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
- пройденное расстояние можно определить, отняв из конечных координат начальные;
- изменение положения будет нулевым, когда d = p.
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:

- Из населённого пункта А в точку Б выехала колонна грузовиков. Навстречу им отправился легковой автомобиль. Скорость грузоперевозчиков составляет 80 км/ч, а пассажирской машины 60 км/ч. Встретились они в точке C через полтора часа. Определить расстояние между А и Б. Решение этой задачи будет состоять из нескольких шагов. На первом можно найти путь, который проехала колона: 80 * 1,2 = 96 км. На втором вычислить пройденное расстояние второй: 60 * 1,2 = 72 км. Отсюда общий путь будет равен сумме: АС + СБ = 72 + 96 = 168 км.
- Корабль, скорость которого в стоячих водах равна 30 км/ч, идёт по течению, а после возвращается. Скорость реки равняется трём километрам в час, промежуточная остановка занимает 5 часов. Путь от начала до возврата корабль проходит за 30 часов. Найти, сколько километров составляет весь рейс. Чтобы решить задачу, удобно составить таблицу. В столбцах нужно записать расстояние, скорость и время, а в строках расчётные данные для таких событий, как стоянка, ход по и против течения. Учитывая условие, рабочая формула примет вид: (S / 28) + (S / 22) + 5 = 30. Выражение можно упростить. В итоге должно получиться: 25 * S / 308 = 25 → S = 308. Так как путь корабля состоял из двух одинаковых расстояний, искомое расстояние будет: P = 2 * S = 308 * 2 = 616 км.
- Железнодорожный состав проезжает мост за 45 секунд. Длина переправы составляет 450 метров. При этом стрелочник, смотря прямо, видит проходящий поезд всего 15 секунд. Найти длину состава и скорость его движения. Если принять, что поезд движется со скоростью V, то его длина будет равняться D = 15 * V. Так как состав за 45 секунд проходит расстояние 45 * V = 450 + 15 * V, из равенства легко определить скорость: V = 45 * V – 15 * V = 450 → V = 450 / 3 0 = 15 м / с. Следовательно, длина состава: D = 15 * 15 = 225 м.
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Содержание
- Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
- Как найти время, зная скорость и расстояние?
- Как найти скорость, если известно время и расстояние?
- Как найти расстояние, если известно время и скорость?
- Единицы измерения
- График зависимости скорости тела от времени: фото
- Таблица 4 класс: скорость, время, расстояние
- Примеры решения задач на скорость, время, расстояние за 4 класс
- ВИДЕО: Задачи на движение
Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S. Скорость обозначается буквой v. А время, за которое пройден путь, обозначается буквой t.
- Путь — S
- Скорость — v
- Время — t
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.

Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту . Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?

Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.

Пишем в черновик эти данные например так:
Расстояние до норы — 3 километра
Скорость Зайца — 1 километр за 1 минуту
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S — 3 километра
V — 1 км/мин
t — ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S : v
Теперь запишем решение задачи цифрами:
t = 3 : 1 = 3 минуты
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.
- Из условия задачи определяем, что нужно найти скорость
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
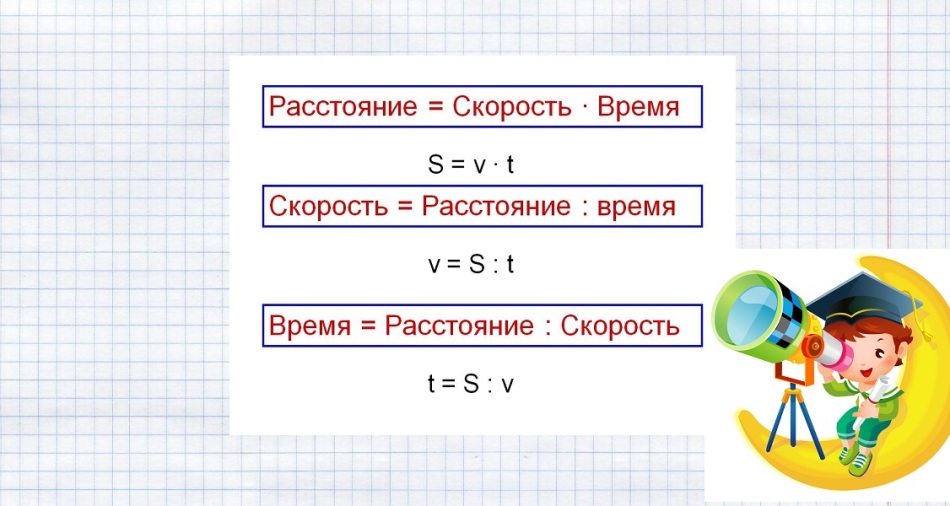
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S — 3 километра
t — 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S : t
Теперь запишем решение задачи цифрами:
v = 3 : 3 = 1 км/мин

Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Расстояние — неизвестно
Теперь, то же самое запишем математическими знаками:
v — 1 км/мин
t — 3 минуты
S — ?
Вспоминаем формулу для нахождения расстояния:
S = v ⋅ t
Теперь запишем решение задачи цифрами:
S = 3 ⋅ 1 = 3 км

Как научиться решать более сложные задачи?
Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.

Единицы измерения
Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.
ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.
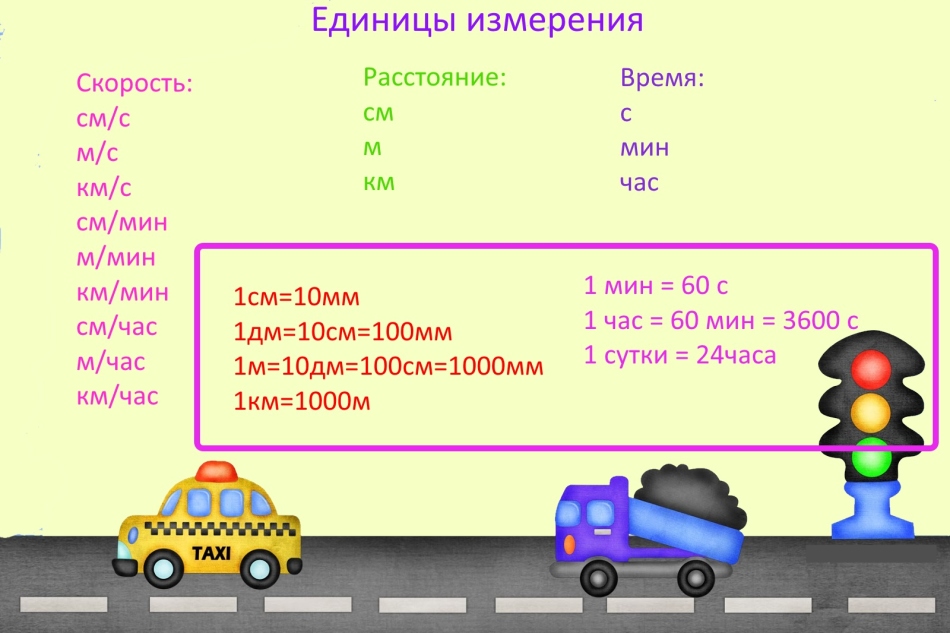
Для любознательных: Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.

Задача про удава: Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)

Решение:
Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
Запишем эти данные:
Скорость мартышки — 60 см/сек
Скорость слоненка — 20 см/сек
Время — 5 секунд
Расстояние неизвестно
Запишем эти данные математическими знаками:
v1 — 60 см/сек
v2 — 20 см/сек
t — 5 секунд
S — ?
Запишем формулу для расстояние, если известна скорость и время:
S = v ⋅ t
Посчитаем, какое расстояние прошла мартышка:
S1 = 60 ⋅ 5 = 300 см
Теперь посчитаем, сколько прошел слоненок:
S2 = 20 ⋅ 5 = 100 см
Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
S = S1 + S2 = 300 + 100 = 400 см
График зависимости скорости тела от времени: фото
Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
- Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?

Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.

Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)

Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
- 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
- 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
- Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
- Ответ: 24 км, 36 км.
Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.
ВИДЕО: Задачи на движение
Математика, 4 класс
Урок № 36. Связь между скоростью, временем и расстоянием
Перечень вопросов, рассматриваемых в теме:
– как скорость взаимосвязана с величинами время, расстояние?
– как определить скорость по известному расстоянию и времени движения?
– как определить расстояние по известной скорости и времени движения?
– как определить время движения по известному расстоянию и скорости?
Глоссарий по теме:
Скорость — это расстояние, пройденное за единицу времени.
Скорость, расстояние и время можно измерять и сравнивать, значит это величины.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Чтобы узнать расстояние, нужно скорость умножить на время.
Чтобы найти время, нужно расстояние разделить на скорость.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 – М.; Просвещение, 2017. – с.6-8.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.
Теоретический материал для самостоятельного изучения
В таблицах даны скорости вороны и комара, льва и кенгуру. Определи, какое расстояние пролетит ворона за 2 мин, а комар за 3 с. Какой путь преодолеет лев за 4 ч, а кенгуру за 30 мин?

Мотоциклист едет со скоростью 41 км/ч. Какое расстояние он преодолеет за 5 ч, если будет двигаться с той же скоростью?

Для того чтобы узнать расстояние, необходимо скорость, 41 км в час умножить на время, 5 часов. Таким образом, расстояние, которое преодолел мотоциклист равно 205 км.
41 · 5 = 205 км
Чтобы найти расстояние, нужно скорость умножить на время.
Будем учиться записывать задачи в таблицу и решать их.
Задача 1.
Черепаха двигалась со скоростью 5 м/ мин. Какое расстояние прошла она за 3 минуты?
Задача 2.
Слон двигался со скоростью 100 м/мин. Какое расстояние он прошёл за 10 мин?
Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения.
Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения. Расстояние, которое прошли черепаха и расстояние, которое прошёл слон, нам неизвестны. Поставим в таблице знаки «вопрос».
5 м/мин – это скорость черепахи, 100 м/мин – это скорость слона. Запишем данные в колонку «Скорость». 3 минуты это время движения черепахи, 10 минут – время, которое находился в пути слон. Запишем эти данные в третью колонку.
|
Скорость |
Время |
Расстояние |
|
|
Черепаха |
5 м/мин |
3 мин |
? |
|
Слон |
100 м/мин |
10 мин |
? |
Мы теперь знаем, чтобы найти расстояние, нужно скорость умножить на время. Запишем решение и ответ.
Скорость 5 м/мин умножим на время 3 мин, получится 15 метров. Это расстояние, которое прошла черепаха.
Скорость 100 м/мин умножим на время 10 мин, получится 1000 метров. Это расстояние, которое прошёл слон.
5 · 3 = 15 (м)
100 · 10 = 1000 (м)
Ответ: черепаха за 3мин прошла 15 м, а слон за 10 мин прошёл 1000 м.
Итак, чтобы найти расстояние, нужно скорость умножить на время.
А теперь рассмотрим задачу на нахождение времени.
Расстояние от города до посёлка 20 км. Из города вышел пешеход со скоростью 5 км/ч. Сколько времени потребуется пешеходу, чтобы пройти весь путь?
Это задача на движение, значит, речь идет о величинах скорость, время, расстояние. Заполним таблицу.
В задаче нужно узнать время движения пешехода. Оно нам неизвестно, поставим знак вопроса. Известно, что расстояние, которое нужно пешеходу равно 20 км.5 км/ч это скорость движения.
|
Скорость |
Время |
Расстояние |
|
5 км/ч |
? |
20 км |
Правило: чтобы найти время, нужно расстояние разделить на скорость. Запишем решение:
20 : 5 = 4 (ч)
Ответ: пешеход будет в пути 4 часа.
Запоминаем правило нахождения времени: чтобы узнать время, расстояние разделить на скорость.
Задания тренировочного модуля:
1. Заполните кроссворд.

Решите кроссворд.
По горизонтали:
2. Плот проплыл 630 м со скоростью 90 м/мин. Чему равно время движения плота?
3. Анника за 6 мин проехала на велосипеде 600 м. Чему равно время движения Анники?
По вертикали:
1. За 7 мин улитка проползла 7 дм. Чему равна скорость движения улитки?
Правильные ответы:
По горизонтали: 2.семь. 3. сто.
По вертикали: 1. десять.
2. Распределите единицы измерения величин по группам. Перенесите данные в соответствующие столбики.

Варианты ответа:
1. 85 см/мин
2. 120 с
3. 548 км
4. 12 мин
5. 850 м/с
6. 600 км/ч
7. 10 ч
8. 2500 м
9. 41 дм
Правильный вариант:
|
Скорость |
Время |
Расстояние |
|
85 см/мин 850 м/с 600 км/ч |
120 с 12 мин 10 ч |
548 км 2500 м 41 дм |
3. Вставьте пропущенное слово, выбирая из списка правильный ответ.
Как пройденный путь зависит от скорости?
Если скорость движения увеличить в несколько раз, то пройденный путь_______ во столько же раз.
Варианты ответа: уменьшится, увеличится.
Правильный вариант: увеличится.
Памятка “СКОРОСТЬ. ВРЕМЯ. РАССТОЯНИЕ.”
Скачать материал
без ожидания
Скачать материал
без ожидания


аудиоформат


- Сейчас обучается 30 человек из 18 регионов




Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 258 172 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 25.04.2018
- 334
- 0
- 25.04.2018
- 496
- 5
- 25.04.2018
- 2019
- 253
- 25.04.2018
- 367
- 4
- 25.04.2018
- 249
- 0
- 25.04.2018
- 637
- 1
- 25.04.2018
- 588
- 6
- 25.04.2018
- 223
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Психолого-педагогические аспекты инклюзивного образования в условиях реализации ФГОС»
-
Курс повышения квалификации «Система образовательной организации в начальном общем образовании в условиях реализации ФГОС»
-
Курс повышения квалификации «Организация краеведческой деятельности детей в учебно-воспитательном процессе начальной школы»
-
Курс повышения квалификации «Содержательные аспекты профессионального и личностного развития педагогических работников в рамках реализации профессионального стандарта»
-
Курс повышения квалификации «Психолого-педагогическая диагностика в современном образовательном процессе»
-
Курс повышения квалификации «Разработка адаптированных образовательных программ в условиях ФГОС СПО»
-
Курс повышения квалификации «Организация работы с обучающимися с ограниченными возможностями здоровья (ОВЗ) в соответствии с ФГОС»
-
Курс повышения квалификации «Техники креативного мышления как инструмент формирования общих компетенций по ФГОС»
-
Курс повышения квалификации «Сурдопедагогика: организация обучения, воспитания, коррекция нарушений развития и социальной адаптации глухих, слабослышащих, позднооглохших обучающихся в условиях реализации программы ФГОС»
-
Курс повышения квалификации «Новые методы и технологии преподавания в начальной школе по ФГОС»
-
Курс повышения квалификации «Формирование и развитие ключевых компетенций школьников в интересах устойчивого развития региона»
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Цымбалюк Лариса Анатольевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 7 лет и 4 месяца
- Подписчики: 2
- Всего просмотров: 661189
-
Всего материалов:
611
