|
Как решить задачу по математике? Полное условие задачи: Из двух городов, расстояние между которыми 520 км, одновременно вышли навстречу друг другу два поезда и встретились через 4 ч. Один поезд шёл со скоростью 60 км/ч. С какой скоростью шёл другой поезд?
Чисто теоретически можно предположить и заявить, что поезда мчались с абсолютно одинаковой скоростью. Но в жизни такое бывает крайне редко. Чаще они ухитряются на одном и том же маршруте в одном и том же направлении приходить на станцию то вовремя, а то опаздывать. И время опоздания в каждом случае разное. А потому придётся нам всё-таки посчитать, один паровозик двигался быстрее или медленнее другого?
Первым делом нужно выяснить, что мы можем посчитать, чтобы приблизиться к ответу? Но вариантов у нас не много. Из того, что предоставлено в условиях задания, можно выбрать только время в пути и скорость одного из поездов. Умножив одно на другое, мы получим то расстояние, которое ему удалось преодолеть.
У нас с вами появилось новое число. Чем оно может нам помочь? По-моему, если его вычесть из общего расстояния в 520 километров, мы получим другое расстояние – именно то, которое преодолел другой состав. Как его можно вычислить? Достаточно общего расстояния вычесть путь, пройденный первым поездом.
Оценив ситуацию опытным взглядом, уже можно сказать, что это расстояние больше первого. Следовательно и поезд, который его прошёл, должен был двигаться существенно быстрее тихохода. Но пока это только слова. Давайте приступим к дальнейшим подсчётам и выясним, с какой же скоростью мчался второй паровозик? Как это можно сделать?Вполне достаточно пройденной расстояние разделить на всё те же самые 4 часа. Ведь именно столько потратили оба состава на дорогу к моменту встречи.
Если кому-то интересно, можно вычесть из семидесяти шестьдесят и таким образом узнать на сколько именно быстрее летел второй поезд – на целых десять километров в час. Но делать это по условию задачи было не обязательно. автор вопроса выбрал этот ответ лучшим
НатВас 2 года назад Зная по условию, что один из поездов за час проходит расстояние в 60 км, можно вполне узнать, какое расстояние пройдёт этот поезд за 4 часа: 4 • 60 = 240 (км). Поезда движутся навстречу друг другу. Значит, второй поезд до встречи пройдёт такое расстояние: 520 – 240 = 280 (км). Время в пути до встречи у поездов одинаковое – 4 часа. Значит, теперь можно найти и скорость второго поезда, то есть сколько километров он проходил за один час: 280 : 4 = 70 (км/ч). ________________________ Можно решить задачу и другим способом. Раз поезда одновременно движутся навстречу друг другу, то скорости их суммируются. Следовательно, можно найти общую скорость поездов, с которой они преодолели расстояние в 520 км за 4 часа: 520 : 4 = 130 (км/ч). Скорость одного из поездов нам известна – это 60 км/ч. Теперь осталось найти скорость второго поезда: 130 – 60 = 70 (км/ч). В обоих вариантах ответ получился одинаковым – 70 км/ч.
Sagavaha 2 года назад В этом задании нам известна скорость одного из участников движения и общее время до момента встречи. Первым делом получаем расстояние, которое было покрыто за эти четыре часа первым поездом – для этого скорость умножаем на время 60х4=240 Следующим действием вычислим, сколько же пути должен был покрыть второй жд-состав. Для этого мы отнимаем найденный участок от общей длины пути 520-240=280 Теперь, имея на руках и время, и километраж – просто находим искомую скорость, с которой двигался второй поезд. Для это мы разделим километры на те же четыре часа 280/4=70 Таким образом, искомая скорость семьдесят км/ч
В Рокотов 2 года назад У нас есть два состава, вышедшие навстречу друг другу, из разных городов с разной скоростью, прежде чем они встретились. Задача станет интереснее, если потребуется узнать скорость второго состава чтобы перевести стрелки и предотвратить катастрофу. Первое что нужно сделать – выяснить какое расстояние пройдет первый состав за 4 часа. 4умножаем на 60 получаем 240 км. Узнаем сколько пройдет до встречи второй поезд: из общей суммы 520вычитаем получившееся в первом действии число 240 и получаем расстояние пройденное вторым поездом = 280км. Остается это расстояние 280разделить на 4 часа, так мы узнаем его скорость в час. Ответ 70 км/ч. Второй способ искать через скорость сближения общее растояние делим на 4 часа получаем 130 км/час. Скорость второго поезда получаем вычитанием из скорости сближения скорости первого поезда тоже 70 км в час.
Урания 2 года назад Так как поезда шли навстречу друг другу, условно предположим, что первый поезд (с известной скоростью в 60 км) вышел из пункта А, а второй (с неизвестной) – из пункта В. По условию задачи следует, что за четыре часа, которые шли поезда, они встретились, а значит – они покрыли расстояние, равное 520 км (между пунктами А и В) Определим, сколько километров прошел поезд с известной скоростью в 60 км, вышедший из пункта А за 4 часа: 60 х 4 = 240 км. Следовательно, второй поезд, вышедший из пункта В прошел за это время: 520 – 240 = 280 км. Зная время следования второго поезда из пункта В (4 часа), определим его скорость: 280 : 4 = 70 км. Следовательно, второй поезд шел со скоростью 70 км в час.
Alex2837 2 года назад Из условия задачи сразу же напрашивается возможность узнать, какое расстояние проехал один поезд, поскольку мы знаем его скорость и время нахождения в пути. Для этого скорость 60 км/ч × 4 ч = 240 км. Теперь мы можем узнать, какое расстояние проехал второй поезд. Для этого от общего расстояния пути 520 км – 240 км = 280 км. Далее узнаем скорость второго поезда. Для этого расстояние пути 280 км ÷ 4 ч = 70 км/ч. Таким образом, задача в три действия выглядит следующим образом: 60×4=240 км. (проехал первый поезд) 520-240=280 км (проехал второй поезд) 280÷4=70 км/ (скорость второго поезда) Ответ: 70 км/ч.
Kuzmich291192 2 года назад Задачи подобного рода, когда два тела двигаются навстречу друг другу, встречаются довольно часто как в физике, так и в математике. Данная задача не представляет особой сложности, предложенные ответы других пользователей в полной мере отражают суть решения. Но, бывают задачи, где с ходу общая картина не всегда сразу ясна, хочу предложить универсальный способ для решения задач подобного рода. Суть способа: если два тела двигаются навстречу друг другу со скоростями v1 и v2, то мы, условно, одно из тел останавливаем, а другому придаём скорость (v1+v2) и задача намного упрощается в понимании. Применим данный способ к нашей задаче: Дано: v1=60 км/ч; S=520 км; t= 4 ч. Найти: v2-? Решение: Остановим, например, первый поезд, следовательно для второго поезда будет справедливо: S=(v1+v2)*t; Отсюда выражаем v2: v2=S/t-v1. Подставляем данные и производим расчёт: v2=520/4-60; v2=130-60=70 км/ч. Ответ: v2=70 км/ч. Примечание: при решении задач желательно переводить все данные в СИ, что бы не ошибиться в расчётах, но в данной задаче опустим данный шаг, так как кроме километров, часов, и километров в час иных единиц измерения не фигурирует.
Поскольку первый поезд до встречи прошёл путь: 60км/ч * 4ч = 240км, то тогда второй поезд прошёл путь до встречи: 520км – 240км = 280км, а потому его скорость в: 280км / 240км = 1.(6) раза больше, чем скорость первого, а значит, скорость второго: 60км/ч * 1.(6) = 70км/ч
m3sergey 2 года назад Если понять условие задачи и решать ее последовательно по шагам, то никаких сложностей для школьника она не представляет:
Ответ: второй поезд ехал со скоростью 70 км/ч.
Polomatel 2 года назад Раз поезда встретились, значит на двоих они преодолели все расстояние между городами 520 км. за 4 часа. Легко вычислить скорость их взаимного сближения: 520 км. : 4 часа = 130 км/час. Зная скорость одного в 60 км/час, легко вычислить скорость второго: 130 – 60 = 70 км/час. Ответ: второй поезд шел со скоростью 70 км/час. 1) 520:4=130(км/ч)-скорость сближения поездов 2) 130-60=70(км/ч)-скорость второго поезда Ответ: 70 км/ч. При встречном движении находится скорость сближения: V=V1+V2 PC-352353F 2 года назад 60*4=240(км)Прошёл первый поезд. 520-240=280(км)Прошёл 2 поезд. 280:4=70(км/ч)Скорость 2 поезда Ответ:Скорость 2 поезда 70км/ч Знаете ответ? |

Чтобы решать задачи на встречное движение, вспомним основные понятия и формулы для решения задач на движение:
(v) — скорость;
и
v2
— скорость первого и второго объектов;
— скорость сближения;
(t) — время;
— время до встречи;
(s) — первоначальное расстояние;
— расстояние между объектами через определённый промежуток времени после начала движения объектов.
Рассмотрим первую ситуацию.

Яра и Юра давно не виделись и договорились встретиться в парке. Расстояние между друзьями составляет (315) км. Юра поехал на автомобиле со скоростью (60) км/ч, а Яра — на автобусе со скоростью (45) км/ч.
Через какое время друзья встретятся?
Начертим схему.

Стрелки на схеме показывают, с какой скоростью едут Юра и Яра. Флажком обозначено место встречи друзей. А дугой показано расстояние между героями — (315) км.
По схеме видно, что друзья едут навстречу друг другу, то есть расстояние между ними сокращается. Перед нами — встречное движение.
Первоначально необходимо найти скорость сближения по формуле:

1. (60 + 45 = 105) км/ч.
Теперь найдём, через какое время произойдёт встреча Юры и Яры:
2. (315 : 105 = 3) ч.
Ответ: через (3) часа друзья встретятся в парке.
Рассмотрим вторую ситуацию.

С двух станций одновременно начали движение два поезда навстречу друг другу. Скорость первого поезда равна (90) км/ ч, а второго — (70) км/ч. Чему равно расстояние между станциями, если встреча поездов произошла через (2) часа после начала отправления?
Начертим схему.

Найдём скорость сближения двух поездов: (90 + 70 = 160) км/ч.
Определим расстояние между станциями до начала отправления поездов: (160 · 2 = 320) км.
Ответ: расстояние между станциями составляет (320) км.
Рассмотрим третью ситуацию.

Тракторист и таксист едут навстречу друг другу из двух сёл, расстояние между которыми составляет (400) км. Скорость трактора — (25) км/ ч, а такси — (50) км/ч. Как изменится расстояние между ними через (1) час? Через (2) часа? Через (4) часа?
Заполним таблицу:
|
(t) ч |
(d) км |
|
(0) |
(400) |
|
(1) |
(400) (– (25 + 50) · 1 = 325) |
|
(2) |
(400) (– (25 + 50) · 2 = 250) |
|
(4) |
(400) (– (25 + 50) · 4 = 100) |
Источники:
Изображения: схема, робот, космонавт, транспорт. © ЯКласс.
§ 1 Встречное движение
В этом уроке мы познакомимся с задачами на встречное движение.
При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».
Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.
Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.
Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.
В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.
Говоря о задачах на встречное движение, используют понятие «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени. Обозначается ʋсбл..
Чтобы найти скорость сближения при встречном движении, зная скорости объектов, надо найти сумму этих скоростей: ʋсбл. = ʋ1 + ʋ2. Чтобы найти скорость сближения, зная время и расстояние, необходимо расстояние разделить на время: ʋсбл. = S : t.
§ 2 Решение задач
Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на встречное движение.
ЗАДАЧА 1. От двух станций, расстояние между которыми 564 км, одновременно навстречу друг другу вышли два поезда. Скорость одного из них – 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
Изобразим движение поездов на схеме:
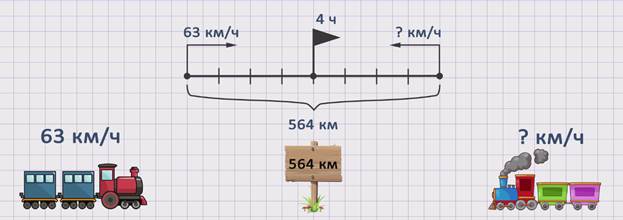
скорость первого поезда обозначим буквой ʋ1 = 63 км/ч. Скорость второго поезда обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t = 4 ч. Расстояние, которое прошли оба поезда, – буквой S = 564 км.

Поскольку, чтобы найти неизвестную скорость, необходимо знать время, а оно известно и равно 4 часам, и расстояние, прошедшее вторым поездом до встречи, которое не указано в условиях задачи, то необходимо найти это расстояние.. Из условия задачи нам известно все расстояние S = 564 км, скорость первого поезда ʋ1 = 63 км/ч и время t = 4 ч. Зная расстояние, которое прошел до встречи первый поезд, мы сможем узнать и расстояние, которое прошел второй поезд. S1 = ʋ1 · t = 63 · 4 = 252 км. Значит, S2 = S – S1 = 564 – 252 = 312 км. Найдя расстояние, которое прошел до встречи второй поезд, можем найти и скорость второго поезда. ʋ2 = S2 : t = 312 : 4 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.

Рассмотрим второй вариант.
Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость первого поезда, из условий задачи она известна ʋ1 = 63 км/ч, и скорость сближения, которая не оговаривается условиями задачи, то надо найти скорость сближения, используя данные задачи, а именно расстояние S = 564 км и время встречи t = 4 часа. Чтобы найти скорость сближения поездов, можно расстояние разделить на время. ʋсбл. = S : t = 564 : 4 = 141 км/ч. Теперь, зная скорость сближения, можем найти скорость второго поезда. ʋ2 = ʋсбл. – ʋ1 = 141 – 63 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.
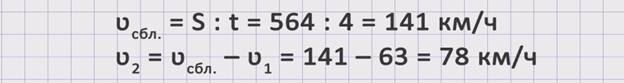
ЗАДАЧА 2. Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится, чтобы встретиться, если скорость первого составляет 20 км/час, а второго – 25 км/час?
Изобразим движение теплоходов на схеме.
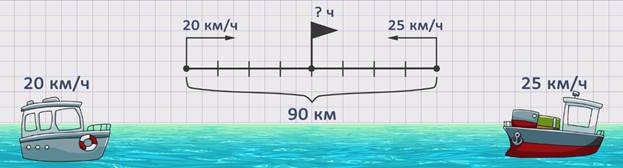
Скорость первого теплохода обозначим буквой ʋ1 = 20 км/ч. Скорость второго теплохода обозначим буквой ʋ2 = 25 км/ч. Расстояние между пристанями обозначим буквой S = 90 км. Время – буквой t = ? часов.
Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость сближения, так как t = S : ʋсбл.. Поскольку расстояние нам известно из условия задачи, надо найти скорость сближения. ʋсбл. = ʋ1 + ʋ2 = 20 + 25 = 45 км/ч. Теперь, зная скорость сближения, можем найти неизвестное время. t = S : ʋсбл = 90 : 45 = 2 ч. Получаем, что теплоходам понадобится 2 часа, чтобы встретиться.
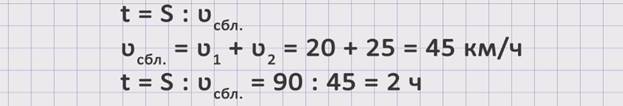
ЗАДАЧА 3. Из поселка и города навстречу друг другу одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость – 50 км/час?
Покажем движение автобусов на схеме.
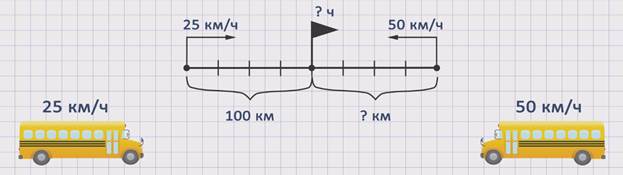
Скорость первого автобуса обозначим буквой ʋ1 = 25 км /ч. Скорость второго автобуса обозначим буквой ʋ2 = 50 км/ч. Расстояние, которое до места встречи проехал первый автобус, обозначим буквой S1 = 100 км. Расстояние, которое проехал до встречи второй автобус – буквой S2 = ? км, а время – буквой t.
Чтобы ответить на вопрос задачи, необходимо знать скорость второго автобуса и время, которое он был в пути до встречи, так как S2 = ʋ2 · t. Поскольку скорость второго автобуса известна из условия задачи, надо найти время. Если мы найдем время, которое был в пути первый автобус, то мы найдем и время, которое был в пути второй автобус, так как они выехали одновременно, а это значит, что до момента встречи автобусы были в пути одинаковое количество времени. Чтобы найти время, можно расстояние, которое проехал первый автобус, разделить на его скорость. t = S1 : ʋ1 = 100 : 25 = 4 часа. Теперь, зная время, можем найти расстояние, которое второй автобус проехал до момента встречи. S2 = ʋ2 · t = 50 · 4 = 200 км. Получили, что второй автобус проехал до встречи 200 км.
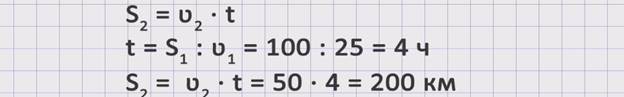
§ 3 Краткие итоги по теме урока
При решение задач на встречное движение следует помнить, что в задачах такого типа выполняются следующие условия:
1.Объекты начинают свое движение одновременно навстречу друг другу, т.е. находятся в пути до встречи одинаковое количество времени; время обозначается латинской буквой t = S : ʋсбл;
2.Расстояние S – это сумма расстояний двух объектов до встречи; S = S1 + S2 или S = ʋсбл· t;
3.Объекты сближаются с определенной скоростью – скоростью сближения, обозначающейся латинской буквой ʋсбл. = S : t или ʋсбл = ʋ1 + ʋ2, соответственно ʋ1 = S1 : t и ʋ2 = S2 : t.
Контрольные задания > С двух станций, расстояние между которыми равно 25,6 км, одновременно в одном направлении вышли два поезда. Первый поезд шёл впереди со скоростью 58,4 км/ч, и через 4 ч после начала движения его догнал второй поезд. Найдите скорость второго поезда.
Ответ:
[1) 58,4 cdot 4 = 233,6 (км) – проехал ]
[первый поезд.]
[2) 233,6 + 25,6 = 259,2 (км) – проехал ]
[второй поезд.]
[3) 259,2 :4 = 64,8 left( frac{км}{ч} right) – скорость ]
[второго поезда.]
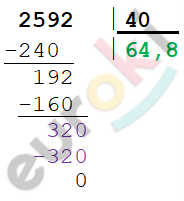
[Ответ:64,8 frac{км}{ч}text{. }]
Придумай задачу на движение вдогонку, в которой надо узнать:
а) время до встречи;
б) скорость одного из движущихся объектов;
в) первоначальное расстояние между ними.

reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 28 урок. Движение вдогонку. Номер №5
Решение а
Из двух городов в одном направлении выехали два поезда. Скорость первого поезда 120 км/ч, а скорость второго 100 км/ч. Расстояние между городами 200 км. Через сколько часов произойдет встреча?
Решение:
200 : (120 − 100) = 200 : 20 = 10 (ч) − пройдет до встречи.
Ответ: через 10 часов
Решение б
Из двух городов в одном направлении выехали два поезда. Скорость первого поезда 120 км/ч. Найди скорость второго поезда, если известно, что расстояние между городами 200 км, а встреча произошла через 10 часов?
Решение:
120 − (200 : 10) = 120 − 20 = 100 (км/ч) − скорость второго поезда.
Ответ: 100 км/ч
Решение в
Из двух городов в одном направлении выехали два поезда. Скорость первого поезда 120 км/ч, а скорость второго 100 км/ч. На каком расстоянии находятся города, если поезда встретились через 10 ч?
Решение:
(120 − 100) * 10 = 20 * 10 = 200 (км) − расстояние между городами.
Ответ: 200 км


