Для школьников.
Во всех колебательных системах, при выводе их из положения равновесия, кроме возвращающей силы присутствуют силы трения или силы сопротивления, препятствующие их колебательным движениям. Поэтому полная энергия колебательной системы, расходуемая на работу против сил трения (сопротивления), уменьшается, колебания затухают и прекращаются.
На рисунке слева показан график зависимости смещения колеблющейся точки от положения равновесия от времени для затухающего колебания. Пунктирной линией изображено изменение амплитуды затухающего колебания.
Быстрота затухания определяется величиной силы сопротивления. Если сила сопротивления очень большая, то колебания прекращаются после первого прохождения через положение равновесия (нижняя кривая рисунка справа) или даже до первого перехода через положение равновесия (верхняя кривая рисунка справа). Такое движение колеблющегося тела называется апериодическим.
Уравнение, описывающее затухающее колебание, имеет вид:
Здесь
– коэффициент затухания, зависящий от силы сопротивления, которая при малых скоростях пропорциональна скорости.
Выражение для амплитуды затухающих колебаний имеет вид:
где А (с индексом ноль) – амплитуда в начальный момент времени.
Строго затухающее колебание не является периодическим, но если затухание невелико, то можно говорить о периоде.
Период затухающих колебаний зависит от силы сопротивления и определяется формулой:
Здесь буквой “омега”
обозначена круговая частота затухающего колебания, а буквой
круговая частота гармонического колебания.
Чем больше сила сопротивления, тем больше коэффициент затухания, тем быстрее уменьшается амплитуда А и тем больше период затухания Т.
При очень малом трении, когда коэффициент затухания очень мал, период затухающего колебания близок к периоду незатухающего свободного колебания.
На практике быстроту затухания часто характеризуют логарифмическим декрементом затухания, обозначаемым буквой “лямбда”
Логарифмический декремент затухания равен натуральному логарифму отношения двух последовательных амплитуд, отстоящих друг от друга за период времени Т:
Коэффициент затухания и логарифмический декремент затухания связаны между собой зависимостью:
Задача.
Логарифмический декремент затухания маятника равен 0,02. Во сколько раз k уменьшится амплитуда маятника после n = 50 полных колебаний? Считать, что период затухающих колебаний близок к периоду свободных незатухающих колебаний.
Решение. Амплитуда затухающего колебания изменяется по закону:
По условию задачи время 50 колебаний:
Подставив два последних уравнения в уравнение амплитуды затухающего колебания, получим
Тогда амплитуда после n = 50 колебаний уменьшится в k раз:
Здесь е – основание натурального логарифма (е = 2,71828).
Ответ: после совершения 50 колебаний амплитуда уменьшилась в е раз. (Время, в течение которого амплитуда колебаний уменьшается в е раз, называется временем затухания).
На практике в одних случаях надо уменьшать затухание колебаний (например, при работе балансира механических часов), в других случаях, наоборот, увеличивать (например, надо чтобы стрелка электроизмерительных приборов быстро останавливалась).
Для этого в электроизмерительном приборе используется металлическая пластинка, соединённая со стрелкой прибора, в которой при её движении между полюсами электромагнита возникают вихревые токи, тормозящие движение пластинки.
Приведём задачу на затухающие колебания, на переход энергии колеблющейся системы в работу по преодолению сил трения.
Интересен тот факт, что небольшие силы трения мало влияют на период колебаний, тогда как на амплитуду колебаний они влияют гораздо больше. Этот факт используется в работе маятниковых часов.
Ещё Галилеем было сказано о возможности использования маятника в часах. Первые часы с маятником были созданы в 1673 году Гюйгенсом.
Таким образом, все реальные свободные колебания являются затухающими. Но при малых силах трения (сопротивления) колебания в течение достаточно долгого промежутка времени остаются близкими к гармоническим и тогда период затухающих колебаний можно считать равным периоду свободных незатухающих колебаний.
Быстрота затухания характеризуется коэффициентом затухания, логарифмическим декрементом затухания. Коэффициент затухания – это величина, обратная времени, в течении которого амплитуда колебаний уменьшается в е раз.
https://yandex.ru/video/preview/?text=%D0%B4%D0%B5%D0%BC%D0%BE%D0%BD%D1%81%D1%82%D1%80%D0%B0%D1%86%D0%B8%D1%8F%20%D0%B7%D0%B0%D1%82%D1%83%D1%85%D0%B0%D1%8E%D1%89%D0%B8%D0%B5%20%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F&path=wizard&parent-reqid=1638616551229540-1048262997957332495-sas3-0841-245-sas-l7-balancer-8080-BAL-1765&wiz_type=vital&filmId=7663491726844988663
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Сложение гармонических колебаний.
Следующая запись: Вынужденные колебания. Резонанс.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 5 8.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
готово
Уравнения и графики затухающих колебаний
§6 Затухающие колебания
Декремент затухания. Логарифмический декремент затухания.
Добротность
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.
Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.
Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
где r – коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости.
Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона
где β – коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
– дифференциальное уравнение затухающих колебаний.
– у равнение затухающих колебаний.
ω – частота затухающих колебаний:
Период затухающих колебаний:
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Если затухания выражены слабо (β→0), то . Затухающие колебания можно
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
В уравнении (1) А0 и φ0 – произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
τ – время релаксации.
Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:
Логарифмический декремент затухания равен логарифму D :
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания – постоянная для данной системы величина.
Еще одной характеристикой колебательной система является добротность Q .
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.
Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.
Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
§7 Вынужденные колебания.
Резонанс
В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.
По второму закону Ньютона:
(1)
– дифференциальное уравнение вынужденных колебаний.
Это дифференциальное уравнение является линейным неоднородным.
Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:
Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:
(2)
Частное решение этого уравнения будем искать в виде:
т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,
Это комплексное число удобно представить в виде
где А определяется по формуле (3 ниже), а φ – по формуле (4), следовательно, решение (2),в комплексной форме имеет вид
Его вещественная часть, являвшаяся решением уравнения (1) равна:
(3)
(4)
Слагаемое Хо.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ωрез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).
Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то
При ω→0 все кривые приходят к значению – статическое отклонение.
Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие “солнышко” за счет изменения положения центра тяжести система.(То же в “лодочках”.) См. §61 .т. 1 Савельев И.В.
Затухающие колебания в контуре и их уравнение
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, – затухающие.
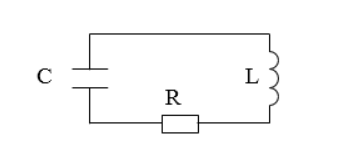
Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.
Характеристики затухающих колебаний
Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:
m a = – k x – y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .
Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,
Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e – период времени уменьшения амплитуды в e раз.
Для R L C контура применима формула с ω частотой.
При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C – собственная частота, отсюда ω ≈ ω 0 .
При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :
Q = 1 R L C = ω 0 L R , где R , L и C – сопротивление, индуктивность, емкость, а ω 0 – частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:
Q = R L C = R ω 0 L .
R является входным сопротивлением параллельного контура.
Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:
Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.
Уравнения затухающих колебаний
Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:
q ( t ) = q 0 e ( – β t ) cos ω t + a ‘ 0 = q 0 e – β t cos ( ω t ) .
Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.
Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.
Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .
Функция изображается аналогично рисунку 2 .
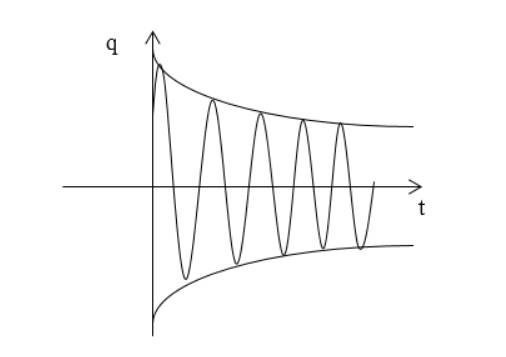
Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту – ω 0 .
Решение
Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C – контуре:
q ( t ) = q 0 e ( – β t ) cos ω t + a ‘ 0 = q 0 e – β t cos ( ω t ) .
Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение
Для нахождения I ( t ) :
I ( t ) = – ω 0 q 0 e ( – 2 β t ) sin ( ω t + α ) , где t g α = β ω .
Очевидно, что электрическая энергия W q запишется как:
W q = q 2 2 C = q 0 2 2 C e ( – 2 β t ) cos 2 ( ω t ) = W 0 e ( – 2 β t ) cos 2 ( ω t ) .
Тогда значение магнитной энергии контура W m равняется:
W m = L 2 ω 0 2 q 0 2 e ( – 2 β t ) sin 2 ω t + a = W 0 e – 2 β t sin 2 ω t + a .
Запись полной энергии будет иметь вид:
W = W q + W m = W 0 e ( – 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( – 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .
Где sin α = β ω 0 .
Ответ: W ( t ) = W 0 e ( – 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.
Решение
Если колебания в контуре затухают медленно, то:
Очевидно, выражение энергии, запасенной в контуре, вычислим из
W ( t ) = W 0 e ( – 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( – 2 β t ) .
Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .
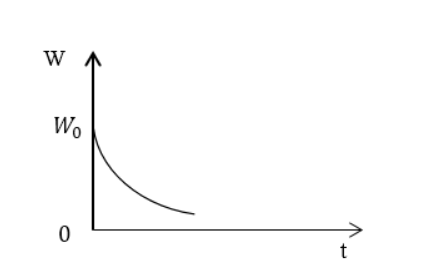
Ответ: W ( t ) = W 0 e ( – 2 β t ) . Энергия в контуре убывает по экспоненте.
1.6. Свободные затухающие колебания
Гармонические колебания, существующие вечно, являются одной из физических абстракций. В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии. Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания. Затухание колебаний всегда будет наблюдаться в системах с трением.
Уравнение затухающих колебаний
Рассмотрим в качестве примера пружинный маятник, помещенный в вязкую среду. Помимо силы упругости на тело будет действовать сила сопротивления, пропорциональная скорости

где r — соответствующий коэффициент, зависящий от вязкости среды, размеров и формы тела. Поэтому уравнение движения примет вид:


Здесь  новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если
новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если  .
.
Другой пример — электромагнитный контур. Если помимо конденсатора С и индуктивности L в контуре имеется еще и активное сопротивление R, то ЭДС самоиндукции равна сумме напряжения на конденсаторе и падения напряжения на сопротивлении. Поэтому уравнения (1.15) примут теперь вид:

Подставляем первое уравнение во второе:


Напомним, что комбинация L/R уже встречалась нам в теории электромагнетизма, где она характеризовала характерное время затухания (появления) экстратоков замыкания-размыкания. Таким образом, величина b имеет размерность обратного времени, совпадающую с размерностью циклической частоты.
Анализ решений
Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:


Дифференцируя функцию x(t), получаем:

Подставляем эти выражения в (1.67):
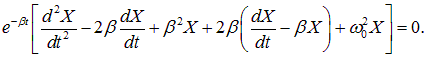
Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной  . Получаем в итоге дифференциальное уравнение для функции X(t):
. Получаем в итоге дифференциальное уравнение для функции X(t):

Здесь возможны два случая. Пусть сначала  . Тогда можно ввести параметр
. Тогда можно ввести параметр

так что уравнение (1.71) примет вид:

Но это — стандартное уравнение гармонических колебаний, общее решение которого мы знаем:
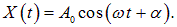
Значит, мы нашли общее решение уравнения затухающих колебаний (1.67):

Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний:  . Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой
. Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой  и с амплитудой, изменяющейся по закону (рис. 1.22)
и с амплитудой, изменяющейся по закону (рис. 1.22)


Рис. 1.22. Свободные затухающие колебания
Коэффициент затухания  определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.
определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.
Период затухающих колебаний равен:

Пусть первое наибольшее положительное отклонение достигается в момент времени  . Последующие наибольшие отклонения того же знака (A’, A”, A”’ и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:
. Последующие наибольшие отклонения того же знака (A’, A”, A”’ и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:

Определим количество колебаний, которое совершит система за время  . За это время амплитуда уменьшается в е раз, а число колебаний равно:
. За это время амплитуда уменьшается в е раз, а число колебаний равно:

Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляется величина, называемая добротностью:

которая пропорциональна числу колебаний Nе, совершаемых системой за то время  , за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при
, за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при  находим:
находим:

Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании (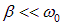 ) имеем:
) имеем:

где E0 — значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:


то есть при слабом затухании добротность, с точностью до множителя  , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
, равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
При увеличении затухания частота колебаний

стремится к нулю, а период колебаний растет. В предельном случае

период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при  движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/elektromagnitnye-kolebanija-volny/zatuhajuschie-kolebanija-v-konture/
http://online.mephi.ru/courses/physics/optics/data/course/1/1.6.html
[/spoiler]
При любых колебаниях энергия системы
расходуется на работу против сил
сопpотивления сpеды. Поэтому амплитуда
колебаний со временем убывает, и колебания
прекращаются.
Допустим, что сила сопротивления линейно
зависит от скорости, т. е.
Fс = – r υ = – r
dx/dt,
здесь r– коэффициент сопротивления
среды. Знак минус указывает, что силаFси скорость
имеют противоположные направления.
С учётом всех сил второй закон Ньютона
записывается в виде
![]() или
или![]() .
.
(1.17)
Величину
= r / (2m) (1.18)
называют коэффициентом затухания.
Выражение (1.17) является дифференциальным
уравнением затухающих колебаний.Его решением служит функция
x = A0 e–
t сos(ω t + ).
(1.19)
Обpатим внимание на то, что
![]()
– циклическая частота затухающихколебаний, а ω0–собственнаяциклическая частота, т. е. частота
колебаний той же колебательной системы
в отсутствие сил сопpотивления (r =
0).
Амплитуда затухающих колебаний (рис.
1.14) изменяется по экспоненциальному
закону
A = A0 e –
t
. (1.20)
Сравним периоды затухающих и незатухающих
колебаний:
![]() .
.
Видно, что для очень малого коэффициента
затухания ( <<
ω0)T = T0 = 2
/ ω0.


При > ω0период является мнимой величиной, а
движение точки носитапериодический
(непериодический) характер (рис. 1.15).
С тепень
тепень
затухания характеризуетлогарифмический
декремент затухания – натуральный
логарифм отношения двух соседних
амплитуд, т.е. амплитуд, взятых через
период колебаний (рис. 1.14): (1.21)
(1.21)
Коэффициент затухания
и логарифмический декремент затухания являются
важнейшими хаpактеpистиками колебательного
пpоцесса. Они показывают, как быстpо
пpоисходит уменьшение во вpемени амплитуды
колебаний и, следовательно, как быстpо
pасходуется пеpвоначально запасенная
энеpгия, пpопоpциональная квадpату
амплитуды.
Рассмотpим физический смысл и. Пpедставим, что
за вpемяе амплитуда колебаний уменьшилась в “е”
pаз (e – основание натурального
логаpифма), пpичем за это вpемя пpоизошлоNeполных колебаний (по смыслуNe = е
/T). Пользуясь фоpмулой (1.20), получим
для отношения амплитуд
![]() откуда
откуда
коэффициент затухания= 1 /е, т.е.
это величина,обpатная вpемени, в
течение котоpого амплитуда уменьшается
в e pаз. Тогда из фоpмулы (1.21) следует,
что
![]() Следовательно,логаpифмический
Следовательно,логаpифмический
декpемент затухания обpатно пpопоpционален
числу полных колебаний, по истечении
котоpых амплитуда уменьшается в “e”
pаз.
В соответствии с физическим смыслом β
и δ коэффициент затухания измеpяется в
c-1, а логаpифмический декpемент
затухания является величиной безpазмеpной.
П р и м е р 8. Дифференциальное
уравнение затухающих колебаний имеет
вид
![]() .
.
Найти коэффициент затухания и циклическую
частоту этих колебаний.
Р е ш е н и е. Приведем уравнение к виду
(1.17):
![]()
откуда найдем
![]()
Тогда циклическая частота затухающих
колебаний
![]()
П р и м е р 9. После десяти полных
колебаний материальной точки ее амплитуда
уменьшается от 10 см до 6 см. Коэффициент
затухания равен 0,2c-1.
Записать закон движения точки.
Р е ш е н и е. Для записи закона
движения в уравнении (1.19) необходимо
найти циклическую частоту затухающих
колебаний.
Отношение амплитуд по истечении
10 колебаний
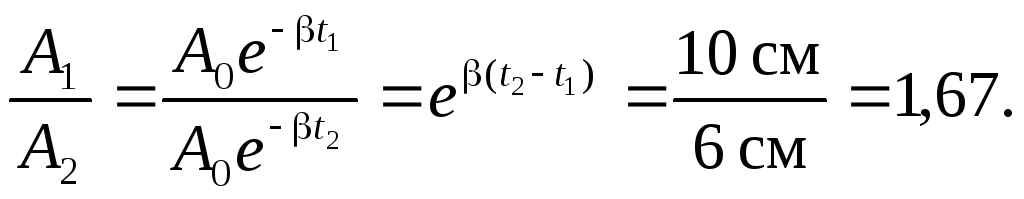
Промежуток времени между колебаниями
(t2 – t1)
= 10T, так как прошло
десять полных колебаний. Тогда
![]()
![]()
Найдем циклическую частоту затухающих
колебаний
ω =2π/T= 2π∙10β/ln1,67 = 7,8π,
с-1.
Полагая начальную фазу равной нулю,
запишем уравнение колебаний, выражающее
закон движения точки:
3.1. Механические затухающие колебания
3.2. Электромагнитные затухающие колебания
3.3. Характеристики затухающих колебаний
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
Уравнение колебаний – решение дифференциального уравнения.
Амплитуда затухающих колебаний зависит от времени.
Частота и период зависят от степени затухания колебаний.
Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
3.1. Механические затухающие колебания
Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:
Упругая сила. ![]() , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
, где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): ![]() . Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
. Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
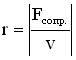 Закон движения пружинного маятника – это второй закон Ньютона: ma = Fупр. + Fсопр.
Закон движения пружинного маятника – это второй закон Ньютона: ma = Fупр. + Fсопр.
Учитывая, что ![]() и
и 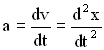 , запишем второй закон Ньютона в виде:
, запишем второй закон Ньютона в виде:
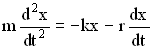 .
.
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
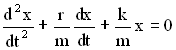
Обозначим ![]() , где β – коэффициент затухания,
, где β – коэффициент затухания, ![]() , где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
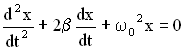 . Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения:
. Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения: ![]()
![]() .
.
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.
Частота затухающих колебаний:
![]() (физический смысл имеет только вещественный корень, поэтому
(физический смысл имеет только вещественный корень, поэтому ![]() ).
).
Период затухающих колебаний: 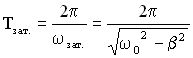 .
.
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: ![]() .
.
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
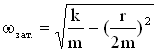 ,
, 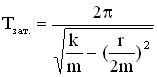 . Амплитуда затухающих колебаний:
. Амплитуда затухающих колебаний: ![]() , для пружинного маятника
, для пружинного маятника ![]() .
.
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
Графики зависимости смещения от времени ![]() и амплитуды от времени
и амплитуды от времени ![]() представлены на Рисунках 3.1 и 3.2.
представлены на Рисунках 3.1 и 3.2.
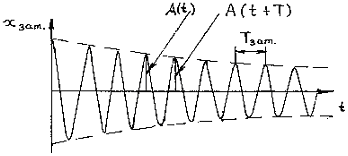
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний

Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний
3.2. Электромагнитные затухающие колебания
Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).
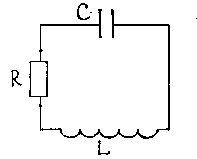
Рисунок 3.3.
Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура: ![]()
Падение напряжения:
– на активном сопротивлении: ![]() , где I – сила тока в контуре;
, где I – сила тока в контуре;
– на конденсаторе (С): ![]() , где q – величина заряда на одной из обкладок конденсатора.
, где q – величина заряда на одной из обкладок конденсатора.
ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: ![]() (закон Фарадея).
(закон Фарадея).
Подставим значения UR, UC, ![]() в уравнение, отражающее закон Кирхгофа, получим:
в уравнение, отражающее закон Кирхгофа, получим:
![]() .
.
Сила тока определяется как производная от заряда ![]() , тогда
, тогда 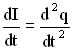 , и дифференциальное уравнение примет вид:
, и дифференциальное уравнение примет вид:
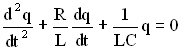 .
.
Обозначим ![]() ,
, ![]() , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
, получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
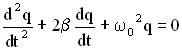
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
![]() или
или
![]() .
.
Амплитуда затухающих колебаний заряда имеет вид:
![]() , где
, где ![]() .
.
Частота затухающих колебаний в LCR – контуре:
 .
.
Период затухающих электромагнитных колебаний:
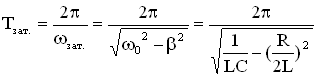 .
.
Возьмем уравнение для заряда в виде ![]() , тогда уравнение для напряжения на обкладках конденсатора можно записать так
, тогда уравнение для напряжения на обкладках конденсатора можно записать так 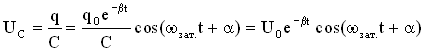 .
.
Величина 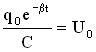 называется амплитудой напряжения на конденсаторе.
называется амплитудой напряжения на конденсаторе.
Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение ![]() и векторную диаграмму.
и векторную диаграмму.
Окончательное уравнение для силы тока таково:
![]() ,
,
где 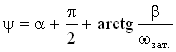 – начальная фаза.
– начальная фаза.
Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.
Энергия колебаний в контуре складывается из энергии электрического поля
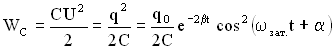
и энергии магнитного поля
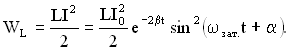
Полная энергия в любой момент времени:
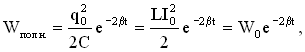
где W0 – полная энергия контура в момент времени t=0.
1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону: ![]() .
.
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 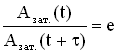 , а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем
, а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем 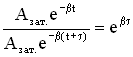 . Из этих соотношений следует βτ = 1, отсюда
. Из этих соотношений следует βτ = 1, отсюда
![]() .
.
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ – физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
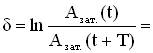
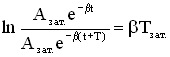
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
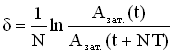 ,
,
где Азат.(t) и Азат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
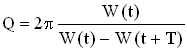 . Так как энергия пропорциональна квадрату амплитуды, то
. Так как энергия пропорциональна квадрату амплитуды, то 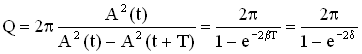 .
.
При малых значениях логарифмического декремента δ добротность колебательной системы равна
![]() ,
,
где Ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна 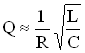 , а добротность пружинного маятника –
, а добротность пружинного маятника – 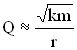 .Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
.Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω0 = β частота затухающих колебаний становится равной нулю ωзат. = 0, а Тзат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.
При ω0 = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω0 = β запишется так: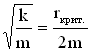 , откуда найдем величину критического коэффициента сопротивления:
, откуда найдем величину критического коэффициента сопротивления:
![]() .
.
Для LCR – контура условие 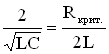 позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:
позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:
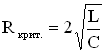 .
.
Затухание колебаний
Свободные колебания в реальных условиях не могут продолжаться вечно. Для механических систем всегда имеет место сопротивление среды, вследствие чего энергия движения объекта рассеивается при трении. В электромагнитных контурах колебания затухают за счет сопротивления проводников.
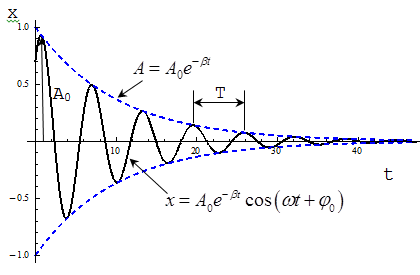
Уравнение затухающих колебаний
Уравнение затухающих колебаний описывает движение реальных колебательных систем. В дифференциальной форме оно записывается следующим образом:
Из этого выражения можно получить еще одну каноническую форму:
либо
Здесь x и t – координаты пространства и времени, А – первоначальная амплитуда. – коэффициент затухания, который зависит от сопротивления среды r и массы колеблющегося объекта m:
Чем больше сопротивление среды, тем больше энергии рассеивается при вязком трении. И наоборот – чем больше масса (а значит, инерционность) тела, тем дольше оно будет продолжать движение.
Циклическая частота свободных колебаний (такой же системы, но без трения) учитывает силу упругости в системе (например, жесткость пружины k):
Строго говоря, в случае затухающих колебаний нельзя говорить про период – время между повторяющимися движениями системы постоянно увеличивается. Однако если колебания затухают медленно, для них с достаточной точностью можно определить период Т:
Циклическая частота затухающих колебаний
Еще одна характеристика затухающих колебаний – циклическая частота:
Время релаксации – это коэффициент, показывающий, за какое время амплитуда колебаний уменьшится в е раз:
Отношение амплитуды изменяющейся величины в двух последовательных периодах называют декрементом затухания:
Эту же характеристику при расчетах часто представляют в виде логарифма:
Добротность Q характеризует, насколько силы упругости системы превышают силы сопротивления среды, препятствуя диссипации энергии:
Примеры решения задач
