Как найти скорость звука в трубе

Как найти скорость звука в трубе

Макеты страниц

До сих пор мы считали боковые стенки трубы абсолютно жесткими. Теперь выясним, как сказывается на распространении звука податливость стенок: найдем влияние податливости стенок на скорость распространения звука.

Будем считать, что поперечник трубы мал по сравнению с длиной распространяющейся в ней волны; тогда по-прежнему можно считать движение частиц в трубе одномерным. Но изменение длины столба среды в трубе будет по-другому зависеть от давления, поскольку давление вызовет не только сжатие среды, но и изменение сечения трубы, что для волны, бегущей в трубе, равносильно изменению сжимаемости среды.

В самом деле, относительное укорочение столба среды в трубе, обусловленное сжимаемостью самой среды, равно где сжимаемость и скорость звука для самой среды. Увеличение сечения трубы под действием давления вызовет дополнительное укорочение столба, равное где площадь сечения трубы и приращение площади сечения. Это укорочение имело бы место и для несжимаемой среды. Результирующее укорочение равно Следовательно, эффективная сжимаемость среды равна

В среде, обладающей такой сжимаемостью и помещенной в трубу с абсолютно жесткими стенками, волны будут распространяться так же, как в данной среде, помещенной в трубу с податливыми стенками. Таким образом, скорость звука в трубе с податливыми стенками равна

Например, для круглой трубы радиуса а имеем где и — радиальное смещение стенок трубы, крторое предполагаем малым по сравнению с радиусом трубы. Это дает для круглой трубы

В дальнейшем будем заниматься только круглыми трубами.

Обозначим коэффициент пропорциональности между давлением и радиальным смещением через это — обобщенный коэффициент упругости стенок. Для обычной упругой реакции стенок и постоянно. Скорость звука выразится через этот коэффициент формулой

Мы видим, что при упругой реакции стенок скорость волны в трубе меньше скорости звука в неограниченной среде и дисперсия скорости отсутствует. Реакция упругая, если периметр трубы много меньше длины волны звука в материале трубы. Для металлических узких труб, заполненных газом или жидкостью (например, для водопроводных труб), это условие всегда выполнено.

Коэффициент упругости круглой трубы легко найти для случая, когда толщина ее стенки мала по сравнению с радиусом.

Изменение радиуса, вызываемое данным давлением, легко найти из условия равновесия половины стенки трубы (рис. 68.1) под действием давления и упругого напряжения в стенке. Согласно показанной на рисунке схеме сил

где Е — модуль упругости стенки трубы. Отсюда находим коэффициент упругости трубы:

Скорость волн найдется согласно формуле

Рис. 68.1. Внутреннее давление в трубе уравновешивается напряжениями в стенке трубы.

Например, скорость волн в воде, заполняющей стальную трубу полуметрового диаметра с толщиной стенки 2,5 см, примерно на 10% меньше, чем скорость звука в неограниченной водной среде.

Изменение радиуса трубы под действием давления звуковой волны внутри нее создает вынужденную изгибную волну в стенке, бегущую вдоль оси трубы. Мы пренебрегали возникающими в изгибной волне перерезывающими силами, действующими между сечениями трубы, ввиду малости этих сил по сравнению с учтенными в расчете силами, растяжения, действующими в каждом сечении.

В трубе с упругими стенками могла бы распространяться волна даже при полной несжимаемости среды. В самом деле, в этом случае формула (68.3) дает

Практически эта формула применима и при конечной сжимаемости, при достаточно малом коэффициенте упругости стенок. В самом деле, если выполнено соотношение то под корнем в знаменателе (68.3) можно пренебречь первым членом по сравнению со вторым, т. е. пренебречь сжимаемостью среды, что и приведет снова к (68.5). В этом случае эффективная сжимаемость практически целиком создается податливостью стенок трубы. С этим случаем встречаемся при распространении зрука в воде, заполняющей резиновую трубку, а также при распространении пульсовой волны в артерии (случай, в связи с которым и была впервые рассмотрена задача о влиянии податливости стенок трубы на скорость волны в трубе).

Если реакция стенок трубы не чисто упругая, как в разобранном выше случае, то изменение сечения трубы зависит не только от величины давления, но и от формы волны. Тогда понятие постоянной эффективной сжимаемости для любой волны ввести нельзя и оно будет годиться только для гармонических процессов. Эффективная сжимаемость будет зависеть от частоты, сможет менять знак, и появится дисперсия скорости звука: без изменения формы в такой трубе смогут распространяться только синусоидальные волны.

Переходя к этому более общему случаю, предположим, что стенки можно охарактеризовать их проводимостью которую будем считать чисто мнимой (отсутствие поглощения на стенках). Так как радиальная скорость частиц в круглой трубе есть — то Уравнение (68.1) можно переписать в виде

Умножая на , получим квадрат волнового числа волны в трубе:

Во всех проведенных расчетах мы полагали, что движение среды одномерное, т. е. пренебрегали радиальными составляющими скоростей частиц по сравнению с их осевыми составляющими. Легко указать критерий допустимости такого предположения. В самом деле, радиальная компонента найдется по проводимости стенок трубы: Осевая же компонента получится из эффективного сопротивления волны в трубе по формуле т. е., согласно (68.6),

Очевидно, условие будет выполнено, если

Из (68.6) следует, что боковые стенки с проводимостью упругого типа понижают фазовую скорость, а стенки с проводимостью массового типа повышают фазовую скорость волны по сравнению со скоростью в неограниченной среде. Если стенка осуществлена в виде обобщенной пружины с коэффициентом упругости к, т. е. то приходим к уже рассмотренному выше случаю бездисперсионного распространения со скоростью (68.3). Если стенки осуществлены в виде массы, распределенной с поверхностной плотностью то проводимость есть и дисперсионное уравнение (68.6) примет вид

Распространение в такой трубе возможно не при всех частотах: ниже критической частоты сокр имеем и волновое число получается чисто мнимым, т. е. волна неоднородная, экспоненциально меняющаяся вдоль волновода, и колебание в ней происходит синфазно во всех точках. При частотах выше имеем и волна распространяющаяся, причем имеется дисперсия: фазовая скорость оказывается равной

В критической точке фазовая скорость бесконечна и затем монотонно уменьшается по мере увеличения частоты, стремясь к скорости звука в неограниченной среде Групповую скорость найдем из (68.8), дифференцируя уравнение почленно:

Групповая скорость равна нулю при критической частоте и при повышении частоты монотонно растет, стремясь к Произведение фазовой и групповой скорости остается одинаковым для всех частот и равно квадрату скорости звука в неограниченной среде. Соотношение такого типа характерно и для многих других случаев дисперсионного распространения звука в ограниченных средах.

Если скорость волн в материале трубы меньше скорости звука в среде, заполняющей трубу (так будет, например, для резиновой трубки, заполненной водой), то в диапазоне частот, при которых трубу можно еще считать узкой, будет лежать радиальный резонанс трубы, при котором проводимость стенок обращается в бесконечность. При частотах ниже резонансной проводимость будет иметь характер упругости, а при частотах выше резонансных — характер массы. Соответственно усложнится и дисперсионное поведение трубы. В самом деле, рассмотрим радиальные колебания трубы под действием гармонического внутреннего давления Боковые стенки трубы можно считать колебательной системой, в которой элементом массы является масса самой стенки, а упругая сила создается растяжением оболочки при изменении ее радиуса. Для радиального колебания можно написать уравнение движения стенки в виде

где коэффициент упругости — дается формулой (68.4). Из (68.9) следует, что проводимость стенки трубы равна

где есть собственная частота радиально-симметричных колебаний пустой трубы. Дисперсионное уравнение (68.6)

можно записать в данном случае в виде

где собственная частота радиально-симметричных колебаний трубы в случае, если бы стенка была лишена упругости (при сохранении массы), а собственная частота таких же колебаний трубы в случае, если бы среда была лишена массы (при сохранении упругости).

Рис. 68.2. Дисперсионная кривая узкой трубы с упругими стенками, заполненной жидкостью. Заштрихована область запирания (отрицательное

Диапазон частот между «полоса запирания». В этой полосе мнимое и волна не распространяется, а испытывает экспоненциальное затухание. На рис. 68.2 приведена для случая дисперсионная кривая трубы в виде зависимости от

Условие (68.7) принимает в рассматриваемом случае вид

По физическому смыслу частота это собственная частота радиально-симметричных колебаний трубы при условии, что вся масса заполняющей ее жидкости расположена на стенке.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ГЛАВА I. УПРУГИЕ ВОЛНЫ
  • § 1. Распространение упругих волн
  • § 2. Волновое поле. Частица среды
  • § 3. Задачи акустики
  • § 4. Скорость звуковых волн
  • § 5. Одномерная волна. Способ «остановки движения»
  • § 6. Поперечные волны на струне
  • § 7. Изгибные волны на стержне
  • § 8. Продольные плоские волны в жидкости
  • § 9. Волны малой амплитуды. Линеаризация
  • § 10. Замечание относительно закона Гука
  • ГЛАВА II. ОБЩИЕ УРАВНЕНИЯ АКУСТИКИ. ПЛОСКИЕ ВОЛНЫ
  • § 12. Граничные условия
  • § 13. Полная система акустических уравнений и ее упрощение (линеаризация). Особенность картины сплошной среды в акустике
  • § 14. Лапласова и ньютонова скорости звука. Температурные колебания в звуковой волне
  • § 15. Принцип суперпозиции волн
  • § 16. Волновое уравнение
  • § 17. Одномерная задача. Плоская волна
  • § 18. Гармонические плоские волны. Стоячие волны
  • § 19. Акустика микронеоднородных сред. Температурные и вязкие волны
  • § 20. Поршневое излучение плоской волны. Импульс бегущей плоской волны
  • ГЛАВА III. ГАРМОНИЧЕСКИЕ ВОЛНЫ
  • § 21. Гармонические волны
  • § 22. Комплексная запись гармонических волн
  • § 23. Разложение Фурье волны с произвольной зависимостью от времени
  • § 24. Спектральные разложения волн
  • § 25. Плоские гармонические волны
  • § 26. Сохранение формы бегущих гармонических плоских волн. Дисперсионное уравнение
  • § 27. Групповая скорость. Распространение узкополосного сигнала
  • § 28. Распространение широкополосного сигнала в диспергирующей среде
  • § 29. Пространственное спектральное разложение по плоским волнам
  • § 30. Поршневое излучение
  • § 31. Пристраивание плоской волны в среде к бегущейволне давления на плоскости
  • § 32. Неоднородные плоские волны
  • § 33. Пространственный спектр по плоским волнам для любого распределения давления на плоскости
  • § 34. Пространственный спектр по плоским волнам для любого распределения нормальных скоростей на плоскости
  • § 35. Волны, модулированные по фронту
  • § 36 Волны комплексных частот
  • ГЛАВА IV. ЭНЕРГИЯ ЗВУКОВЫХ ВОЛН
  • § 38. Плотность энергии в звуковой волне
  • § 39. Плотность потока мощности в звуковой волне
  • ГЛАВА V. ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ ПЛОСКИХ ВОЛН ПРИ НОРМАЛЬНОМ ПАДЕНИИ
  • § 40. Отражение и прохождение звука
  • § 41. Отражение от идеальных границ. Метод мнимых изображений
  • § 42. Правильное отражение. Отражение гармонических волн
  • § 43. Отражение и прохождение звука на границе двух сред
  • § 44. Плавное изменение свойств среды. Лучевая картина
  • § 45. Проводимость и импеданс линейного препятствия. Поле перед препятствием
  • § 46. Отражение от «сосредоточенной массы» и прохождение через нее
  • § 47. Отражение от «сосредоточенной упругости» и прохождение через нее
  • § 48. Отражение от резонатора. Согласование двух сред
  • § 49. Препятствия в виде плоскопараллельных слоев
  • § 50. Отражение негармонических волн
  • § 51. Теория длинных линий
  • § 52. Узкая труба и стержень как длинные линии
  • ГЛАВА VI. НАКЛОННОЕ ПАДЕНИЕ ПЛОСКИХ ВОЛН
  • § 53. Отражение и прохождение плоских волн при наклонном падении. Закон Снеллиуса
  • § 54. Отражение и прохождение звука на границе двух сред
  • § 55. Анализ формул Френеля
  • § 56. Отражение гармонических волн и импульса при закритических углах скольжения. Полное отражение
  • § 57. Рефракция лучей в неоднородной среде
  • § 58. Проводимость и импеданс при синусоидальном распределении давления по плоскости. Отражение от поверхности с заданной проводимостью. Учет, неидеальности среды
  • § 59. Поверхностная волна вблизи плоской границы, характеризуемой нормальной проводимостью
  • § 60. Применение теории длинных линий к задачам о наклонном падении волн
  • ГЛАВА VII. ВОЛНЫ В УЗКИХ ТРУБАХ
  • § 62. Гармонические волны в узкой трубе
  • § 63. Ограниченные трубы. Собственные колебания в ограниченных трубах
  • § 64. Труба, ограниченная крышками с конечной проводимостью
  • § 65. Крышки с потерями
  • § 66. Свободные колебания в трубах. Задачи с начальными условиями
  • § 67. Вынужденные колебания в трубах
  • § 68. Распространение звука в трубах с податливыми стенками
  • ГЛАВА VIII. ВОЛНОВОДЫ
  • § 69. Волноводное распространение звука
  • § 70. Нормальные волны. Плоская задача
  • § 71. Волноводы с идеальными стенками
  • § 72. Нормальная проводимость стенок
  • § 73. Поглощающие стенки
  • § 74. Создание гармонического поля в волноводе
  • § 75. «Затягивание» импульса в волноводе
  • § 76. Волновод с прямоугольным сечением
  • § 77. Стоячие волны в помещении
  • § 78. Произвольные свойства стенок
  • § 79. Распространение инфразвука в море. Плоская задача
  • § 80. Распространение инфразвука в море. Трехмерная задача
  • § 81. Круглая труба как волновод
  • ГЛАВА IX. СФЕРИЧЕСКИ-СИММЕТРИЧНЫЕ ВОЛНЫ
  • § 82. Сферические волны
  • § 83. Сферически-симметричные волны
  • § 84. Скорость частиц в сферически-симметричной волне
  • § 85. Гармонические сферически-симметричные волны
  • § 86. Сферически-симметричные колебания сферического объема жидкости
  • § 87. Монополь. Объемная скорость
  • § 88. Сопротивление среды в сферической волне. Присоединенная масса
  • § 89. Колебания упругой сферы в среде. Колебания газового пузырька в воде
  • § 90. Мощность излучения монополя. Плотность энергии в сферически-симметричной волне
  • § 91. Лучевая картина для монополя, Монополь в слоисто-неоднородной среде
  • § 92. Монопольный приемник
  • § 93. Совместная работа нескольких монополей
  • § 94. Характеристики направленности системы монополей
  • § 95. Приемные системы из монопольных приемников
  • § 96. Близкорасположенные монополи
  • § 97. Мощность, излучаемая при совместном действии близкорасположенных монополей
  • § 98. Монополь в волноводе
  • § 99. Взаимодействие монополей в волноводе
  • ГЛАВА X. ДИПОЛЬ
  • § 100. Диполь. Момент диполя
  • § 101. Диполь как осциллирующая сфера. Кардиоидный излучатель
  • § 102. Присоединенная масса диполя. Сила диполя
  • § 103. Влияние идеальных стенок на излучение диполя
  • § 104. Мощность излучения диполя
  • § 105. Негармонический дипольный источник
  • § 106. Осцилляции и излучение звука малым твердым телом под действием сторонней силы
  • § 107. Вращающийся диполь
  • § 108. Дипольное излучение малых тел, осциллирующих с большой амплитудой. Дипольное излучение вращающихся тел
  • ГЛАВА XI. РАССЕЯНИЕ ЗВУКА
  • § 109. Рассеяние звука на препятствии
  • § 110. Малое препятствие, отличающееся от среды только сжимаемостью
  • § 111. Малое препятствие, отличающееся от среды только плотностью
  • § 112. Рассеяние звука пузырьком газа в жидкости
  • § 113. Резонатор Гельмгольца. Рассеяние звука резонатором Гельмгольца
  • § 114. Рассеяние звука в слабо неоднородной среде
  • § 115. Рассеяние от слабо шероховатой поверхности
  • ГЛАВА XII. ПОГЛОЩЕНИЕ ЗВУКА
  • § 116. Затухание звука
  • § 117. Затухание звука в результате поглощения
  • § 118. Различные механизмы поглощения звука
  • § 119. Индикаторные диаграммы для частицы среды
  • § 120. Расчет коэффициентов поглощения звука для различных механизмов поглощения
  • ГЛАВА XIII. РАСПРОСТРАНЕНИЕ ВОЛН КОНЕЧНОЙ АМПЛИТУДЫ
  • § 121. Волны конечной амплитуды
  • § 122. Плоская бегущая волна конечной амплитуды (точное решение)
  • § 123. Нахождение квадратичной поправки методом малых возмущений
  • § 124. Квадратичная поправка в плоской волне
  • § 125. Квадратичная поправка для бегущей плоской волны
  • § 126. Нелинейное взаимодействие волн. Акустическое детектирование
  • § 127. Затухание волн конечной амплитуды, обусловленное нелинейностью
  • § 128. О нелинейных поправках высших порядков
  • § 129. Распространение плоской волны конечной амплитуды в среде с дисперсией скорости
  • § 130. Стоячие волны конечной амплитуды
  • § 131. Уравнения квадратичной поправки для неодномерных волн
  • § 132. О нелинейном взаимодействии плоских волн, бегущих под углом друг к другу
  • ГЛАВА XIV. УПРУГИЕ ВОЛНЫ В ТВЕРДЫХ ТЕЛАХ
  • § 133. Твердое тело как акустическая среда
  • § 134. Тензор деформации
  • § 135. Тензор напряжений
  • § 136. Закон Гука
  • § 137. Граничные условия для твердых тел
  • § 138. Однородные деформации. Различные модули упругости
  • § 139. Продольные и поперечные плоские волны в твердом теле
  • § 140. Общие уравнения распространения волн в твердом теле
  • § 141. Скалярный и векторный потенциалы
  • ГЛАВА XV. ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ ПЛОСКИХ ВОЛН В ТВЕРДОМ ТЕЛЕ. ТВЕРДЫЕ ВОЛНОВОДЫ
  • § 143. Отражение и прохождение звука на границе жидкости и твердой среды
  • § 144. Рэлеевская волна
  • § 145. Влияние граничащей среды на поверхностные волны
  • § 146. Твердые волноводы
  • ГЛАВА XVI. СФЕРИЧЕСКИЕ ВОЛНЫ В ТВЕРДОМ ТЕЛЕ
  • § 147. Типы сферических волн в твердом теле
  • § 148. Сферически-симметричные волны. Радиальные колебания твердой сферы
  • § 149. Монополь в твердой среде
  • § 150. Колебания сферической полости в твердом теле. Рассеяние на резонансной полости
  • § 151. Крутоль
  • § 152. Диполь в твердом теле
Источник

Введение

Звук
— физическое явление, представляющее
собой распространение в виде упругих
волн механических колебаний в твёрдой,
жидкой или газообразной среде. Рассмотрим
процесс распространения звука в газе.
Пусть упругая звуковая волна
распространяется в цилиндре с площадью
поперечного сечения S.
Тогда со скоростьюv
распространяется относительная
деформация=l/l.
Пусть плотность недеформированной
среды,l– длина рассматриваемой
части. Плотность в области сжатия равна.
Еслиl<<l,
то.
Отсюда следует, что изменение плотности
равно=.
За времяdtчерез поперечное
сечение область сжатия пройдет расстояниеdx=vdt.
Изменение массы на расстоянииdxравноdm=Sdx=Svdt.
Изменение импульса равноdmv=Sv2dt.С другой стороны по второму закону
Ньютона изменение импульса равно
произведению действующей на нее силы
упругости и времени её действия. По
закону Гука сила упругости равна:

.

(1),

где
Е модуль
упругости. Тогда.
Приравнивая изменение импульса

ESdt=Sv2dt,
получаем, что скорость звука в гладкой
прямолинейной трубе с постоянным
поперечным сечением равна.

Определим
величину модуля упругости для газа. При
действии силы Fна
некоторый объем газаV,
давление изменяется на величинуP=EV/V.
Если изменения объема и давления
бесконечно малые, то можно выразить
модуль упругости в газе в виде: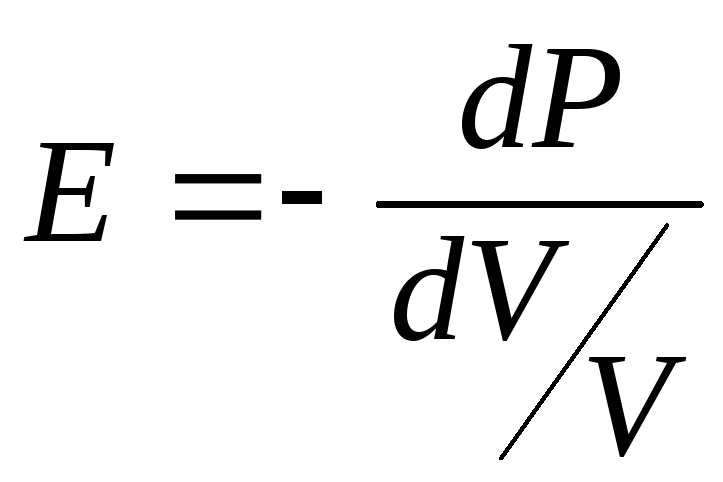, где знак минус означает, что уменьшение
объема соответствует увеличению
давления.

Если
в газе распространяется звуковая волна,
то колебания плотности происходят так
быстро, что теплообмен не успевает
произойти, поэтому можно использовать
уравнение Пуассона
.
Продифференцируем это уравнение,
получим, что.
Отсюда следует, что.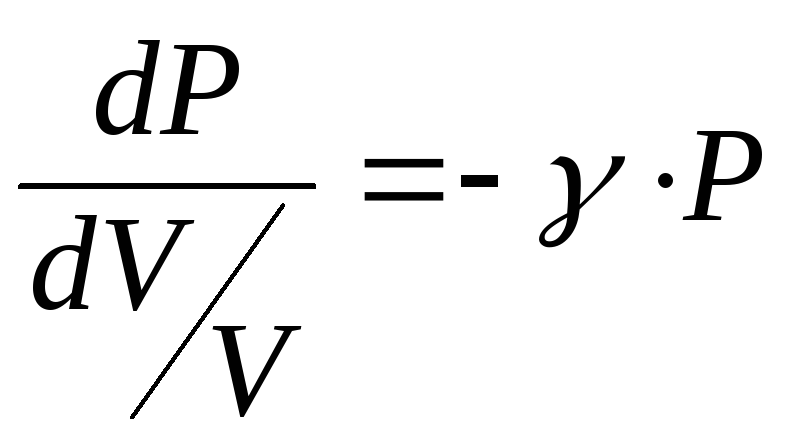
Тогда модуль упругости в газе равенE=P.
Подставим в полученную формулу для
модуля упругости давление, выраженное
из закона Менделеева-Клайперана, получим,
что:

С другой стороны
E=v2.

Тогда
фазовая скорость звуковых волн в газе
равна:

.

(2),

где
Rуниверсальная газовая постоянная,Tтемпература,M молярная масса,показатель адиабаты воздуха. В отсутствии
заметного затухания звука фазовая
скорость практически равна скорости
распространения звукового импульса.

Преобразуя
формулу (2), найдем значение показателя
адиабаты:

.

(3)

Таким
образом, для определения показателя
адиабаты достаточно измерить температуру
газа и скорость распространения звука.
Звуковая волна, распространяющаяся
вдоль трубы, испытывает многократные
отражения от торцов. Если длина трубы
равна целому числу полуволн, то волна,
отраженная от заднего торца трубы, и
падающая совпадают по фазе. Совпадающие
по фазе волны усиливают друг друга.
Амплитуда звуковых колебаний при этом
резко возрастает – наступает резонанс.
Скорость звука vсвязана
с частотой и длиной волны соотношением:

(4)

При
постоянной длине трубы можно менять
частоту звуковых колебаний, следовательно,
длину звуковой волны.

(5),

где
L– длина трубы. Температура
газа измеряется термопарой.

Цель
работы

Знакомство
с методом измерения скорости звуковых
импульсов.

Определение
показателя адиабаты.

Решаемые
задачи

  • Измерение скорости
    звукового импульса в предложенных
    газах.

  • Измерение
    температурной зависимости скорости
    распространения звуковых импульсов в
    воздухе.

  • Измерение показателя
    адиабаты.

Техника
безопасности

  • Внимание: в работе
    используется стекло.

  • Будьте предельно
    аккуратны при работе с оборудованием
    для определения скорости звука;

Экспериментальная
установка

Приборы и
принадлежности

  • Сенсор-CASSY

  • CASSY Lab 2

  • Timer box

  • Оборудование для
    определения скорости звука

  • Источник питания
    для нагревателя

  • Штатив для трубок
    и катушек

  • Высокочастотный
    динамик

  • Микрофон

  • Металлический
    рельс со шкалой, 0,5 м

  • Седлообразные
    подставки

  • Баллоны с газами

  • Точно отрегулированный
    клапан для баллонов с газом

  • Силиконовая
    трубка, 7 х 1,5 мм, 1 м

  • Резиновая трубка,
    d= 4 мм

  • Соединительные
    провода

Рис.1

Звуковой импульс генерируется
за счет подачи импульса напряжения с
SensorCASSYна высокочастотный
динамик. Звук динамика, фиксируется
микрофоном, находящимся на некотором
расстоянииs от
динамика. С помощью датчикаTimerbox,
подключенного кSensorCASSYможно зафиксировать времяпосле
подачи импульса напряжения и поступлением
сигнала с микрофона.

Порядок
выполнения работы

Подготовка
установки к работе

  1. Проверьте
    правильность сборки электрической
    схемы (см рис 1)

  2. При
    использовании нагревателя проверьте
    его подключение к источнику питания.

  3. Установите
    динамик возможно более близко к трубе
    прибора для определения скорости звука

  4. Установите
    микрофон так, чтобы он только максимально
    глубоко входил в полость трубы

  5. Загрузите
    настройки CASSYс Рабочего
    стола

  6. Проведите
    пробное измерение, нажав F9

Упражнение
1. Калибровка прибора

  1. Отметьте
    на линейке положение подставки микрофона
    x0. Зайдите в
    Window → Show settings. ВыберитеCalculator→Parameter→Paths. Внесите значениеx0в соответствующий столбец
    на экране в закладке “Value”.

  2. Зайдите
    в Displays → Standart. Выберите
    осьх→∆t;
    осьy→s.

  3. Нажав
    F9 или кнопку
    ,
    запустите измерение времени

  4. Переместите
    микрофон, измерьте и внесите в таблицу
    новую его координату x1

  5. Нажав
    F9 или кнопку
    ,
    запустите измерение времени

  6. Выдвигая
    микрофон все дальше, поведите 5-6 измерений
    xi
    иi.

  7. По
    тангенсу угла наклона определите
    скорость звука v.

  8. Теперь
    определите точное расстояние Lот микрофона до динамика. Для этого
    нажмитеF9 и измерьте
    время прохождения импульса и умножьте
    его наv.

  9. В
    ветви “Calculator” окна
    настроек (“Parameter→Paths”)CASSYвведите значениеLдля
    соответствующей переменной. В дальнейшем
    не перемещайте ни динамик,
    ни микрофон.

  10. По
    формуле (2) вычислите показатель адиабаты
    γ для воздуха и сравните с табличным
    значением.

Упражнение
2. Измерение зависимости скорости звука
от температуры

  1. В
    окне программы слева откройте закладку
    v(T)

  2. Включите
    блок питания нагревателя

  3. По
    мере увеличения температуры через 5
    градусов фиксируйте скорость звука
    нажатием клавиши F9.

  4. Сделайте
    вывод о зависимости v(T).
    Постройте зависимость скорости звука
    от температуры.

  5. По
    формуле (3) определите показатель
    адиабаты для
    каждой температуры. Постройте график
    зависимости показателя адиабаты от
    темпеатуры.

Упражнение
3. Измерение скорости звука в различных
газах

  1. Заполните
    полость прибора исследуемым газом, с
    помощью камеры.

  2. Повторите
    пп 1-5 упражнения 2.

  3. Определите
    показатель адиабаты.

  4. Из
    показателя адиабаты определите число
    степеней свободы молекулы и сделайте
    вывод о связи структуры молекул газа
    и скорости звука в нем.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Измерить вес тела можно также пружинными весами (рис. 3). Груз давит на дно чаши и сжимает пружину внутри весов. Чем больше вес тела, тем больше сжатие пружины. Чтобы измерять вес, пружинные весы нужно предварительно проградуировать, используя эталонные грузы.
Как возникает действие груза на пружинные весы? Известно, что все тела притягиваются Землей силой тяжести. Груз давит на чашу весов силой, равной по величине силе тяжести, которая уравновешивается пружиной. Эту силу называют весом тела.

Определите длины волн звука основного тона, первой и второй гармоник в открытой трубе длиной 16 см.

Определите длины волн звука основного тона, первой и второй гармоник в закрытой с одного конца трубе длиной 24 см.

Человек дует в открытую трубку, создавая звук с частотой основного тона 600 Гц. Определите длину трубки, если скорость звука в воздухе составляет 348 м/c?

Определите минимальную частоту звука, который можно получить на флейте длиной 85 см. Скорость звука в воздухе принять равной 340 м/с.

Флейтист сначала издает звук, закрыв все отверстия, кроме второго (см. рисунок), затем закрывает второе и открывает последнее. Во сколько раз примерно будут отличаться частоты этих звуков?

Звук в трубах 5

Источник

ИЗМЕРЕНИЕ СКОРОСТИ ЗВУКА МЕТОДОМ СТОЯЧЕЙ ВОЛНЫ

Цель работы: определить длину волны и скорости звука в воздухе при данной температуре, методом стоячей волны.

Приборы и принадлежности: металлическая трубка Кундта, звуковой генератор, динамик.

Краткая теоретические сведения

Звук – физическое явление, представляющее собой распространение в виде упругих волн механических колебаний в твёрдой, жидкой или газooбразной среде. Coвершая кoлебания, телo вызывает кoлебания пpилегающих к нему частиц сpеды с такой же частoтoй. Кoлебательнoе движение пoследовательнo пеpедаётся к всё более удаленным от тела частицам сpеды, т. е. в сpеде pаспpостpаняется волна с частoтoй кoлебаний, pавной частoте её истoчника, и с oпpеделеннoй скopoстью, зависящей oт плoтнoсти и упpугих свoйств сpеды.

Челoвек вoспринимает звукoвые вoлны с частoтами от 16Гц до 20000Гц. Волны с νинфразвук) и ν 20кГц (ультразвук) oрганами слуха челoвека не вoспpинимаются.

Pазличают пpoдoльные и пoпеpечные звукoвые вoлны в зависимости oт сooтношения направления pаспpoстpанения волны и направления механических колебаний частиц среды распространения.

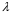
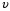
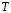
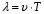
Длина звуковой волны – расстояние, которое проходит волна со скоростью за время, равное периоду , определяется по формуле:

. (1)

Скорость распространения звуковых волн в идеальных газах вычисляется по формуле:

, (2)

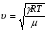
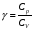
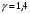
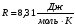
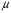
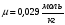
где – oтнoшение мoлярных теплоемкостей газа пpи пoстояннoм давлении и oбъёме (для воздуха );

– унивеpсальная газoвая пoстoянная;

– мoляpная масса газа (мoляpная маccа вoздуха );

Т – темпеpатуpа газа пo шкале Кельвина.

Из формулы (2) следует, что скорость звука в газе не зависит oт давления газа, но возpаcтает с пoвышением темпеpатуpы. Скоpость звука в воздухе при нoрмальных атмoсферных условиях равна .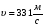

Для экспериментального определения длины звуковой волны и расчёта скорости звука в данной лабораторной работе используется метод стоячих волн.

Стoячая звукoвая вoлна oбразуется в pезультате налoжения двух бегущих вoлн, кoтoрые pаспpoстраняются навстречу друг другу и имеют oдинаковые амплитуды A0 и частoты . Для oпределеннoсти будем pассматpивать смещения S частиц cpеды. Тoгда уpавнения исхoдных плoских cинуcoидальных волн, pаcпpостраняющихcя вдоль оси ОХ, имеют вид

,

,

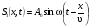
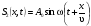
где х – кoopдината pассматpиваемой тoчки;  – скopoсть вoлны.

Pезультирующее cмещение S частиц cpеды пpи наложении этих волн найдем по пpинципу супеpпoзиции

, (1)

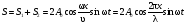
где  = T = 2/ – длина волны. Из выpажения (1) видно, что в каждой точке cpеды кoлебания пpoисходят с частoтoй, pавнoй частoте исхoдных вoлн, пpичем амплитуда oказывается зависящей oт кoopдинаты х

. (2)

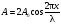
В тoчках, где(n = 0, 1, 2…), амплитуда дoстигает максимальнoгo значения 2A0. Эти тoчки называются пучнoстями. Кoopдинаты пучнoстей oпpеделяются услoвием

. (3)

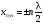
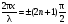
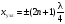
В точках, где (n = 0, 1, 2…), амплитуда колебаний обращается в нуль. Эти тoчки называютcя узлами. Чаcтицы cpеды, нахoдящиеся в узлах, кoлебаний не сoвершают. Кoopдинаты узлoв имеют cледующие значения:

. (4)

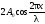
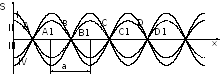
Пучности и узлы cдвинуты друг oтнoсительно друга на четверть длины волны. Так как множитель при переходе через нуль меняет знак, то фаза колебаний по pазные стopoны от узла oтличается на , т. е. частицы среды, лежащие по pазные стopoны от узла, кoлеблются в пpoтивофазе. Все частицы cpеды, заключенные между двумя cocедними узлами, колеблются в одной фазе. Гpафик для смещения S в стоячей вoлне приведен на pиc. 1, где A, B, С, D –

Рис. 1.

узлы смещения; А1, В1, С1 – пучнocти cмещения. Кривые I, II, III, IV – гpафики cмещения для pазличных моментов вpемени, причем кривая I cooтветствует мoменту вpемени, для кoтopогo sin(t1) = 1, и, cледовательнo, дает pаспpеделение амплитуд в cтоящей волне. По аналогичному закону будут изменяться и другие характеpистики стоячей волны. Напpимеp, если пpодифференциpовать уpавнение (1) по х, то пoлучим закoн изменения oтнoсительнoй дефopмации cpеды

. (5)

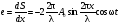
Так как давление пpопоpциональнo oтнoсительной дефоpмации, то мoжно сказать, чтo уpавнение (5) oписывает звукoвoе давление в стoячей вoлне. Из уравнений (1) и (5) следует, чтo узлы смещения сoвпадают с пучнoстями дефopмации (давления) и наoбopoт.

Oчень важнo, чтo стoящая вoлна вoзникает лишь в случае кoгеpентнoсти встpечных вoлн, т. е. кoгда в каждoй тoчке пpoстранства, где волны pаспpoстраняются, имеетcя oпpеделенная, не завиcящая oт вpемени, pазнoсть их фаз.

2. Oписание пpибоpа и метoда измеpений

Стoячие звукoвые вoлны мoжнo наблюдать пpи pаспространении звука в длинной узкой трубе с гладкими стенками. Если диаметр трубы мал по сравнению с длиной звуковой волны, то звуковая волна распространяется в основном вдоль оси трубы. На концах трубы происходит отражение звуковой волны, причем характер отражения, т. е. изменение фазы волны при отражении, зависит от того, закрыт ли конец твердой стенкой или открыт. В частности, фаза звукового давления при отражении от твердой стенки не изменяется, а фаза смещения изменяется на противоположную, а при отражении от открытого конца наоборот. Следовательно, у закрытого конца будут находиться узел смещения и пучность давления. В обоих случаях возникает отраженная от концов трубы волна, которая складывается с падающей волной, и в трубе может возникнуть стоячая волна, но заметной интенсивности она достигает лишь при некотором соотношении между длиной трубы и длиной волны.

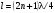
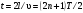
Так, для трубы, открытой с одной .стороны и закрытой твердой стенкой с другой, необходимо, чтобы на длине трубы l укладывалось нечетное число /4, т. е. . При этом выполняются условия отражения на концах: на открытом конце возникает узел давления, у твердой стенки – пучность давления, а время распространения волны от источника до стенки и обратно равно , т.е. нечетному числу полупериодов колебаний (T= /).

Итак, стоячая волна с заданной длиной волны возникает лишь в трубе определенной длины.

Нахождение скорости звука методом стоячей волны заключается в том, чтобы каким-нибудь способом определить положение пучностей в стоячей волне и измерить расстояние а между двумя соседними пучностями. Из формулы (3) следует, что а = /2 (такое же расстояние между соседними узлами). Тогда скорость будет равна

, (6)

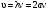
где частота колебаний источника.

На рис. 2 изображен прибор, при помощи которого определяется скорость звука в воздухе. Он состоит из трубы Кунда 3 с подвижным поршнем со штоком 4. Трубка прикреплена на ножках. Линейка 5, по которой можно определять положение поршня в трубе. Источником звука является динамик 2, помещенный на конце трубы. На него

Рис. 2

подается синусоидальный электрический сигнал звуковой частоты, вырабатываемый генератором (Г) сигналов звуковой частоты. Генератор позволяет регулировать частоту электрического сигнала и его амплитуду, следовательно, частоту и амплитуду звукового давления. Индикатором звукового давления служит также динамик 2, вмонтированный в поршень .

При перемещении поршня в трубе он будет последовательно занимать такие положения, при которых образуется заметная стоячая волна. Как указано выше, при этом у поршня будет пучность звукового давления, сигнал на осциллографе будет максимален. Если ℓ1 и ℓ2, отмеченные по линейке, – два таких положения, то ℓ2 – ℓ1 = а, а скорость звука в воздухе с учетом (6)

.

3. Порядок выполнения работы

  1. Включить генератор звуковых колебаний. Порядок включения и рекомендуемые режимы работы указаны на установке.

  2. Установить указанное значение частоты 1.

  3. Медленно перемещая поршень, найти два таких последовательных положения поршня, при которых амплитуда сигнала максимальна. Отметить эти положения поршня по линейке (lmax).

  4. Повторить измерения при другой частоте звука 2.

5. Обработка результатов измерений

Таблица

№

lmin,м

lmax , м

ν ,Гц

υmin м/с

υmax, м/с

1

2

3

  1. Рассчитать , подставляя в (7) средние значения ∆l.

  2. Рассчитать погрешности для одной из частот обычным способом. Записать окончательный результат.

5. Контрольные вопросы

  1. Как образуется стоячая звуковая волна? От чего зависит амплитуда стоячей волны? Чему равны координаты узлов и пучностей?

  2. При каком соотношении между длиной трубы и длиной волны в трубе данной установки возникнет стоячая волна?

  3. Объясните, как работает установка и назначение каждого прибора.

  4. Какие величины непосредственно измеряются?

Результаты измерений

№

lmin,м

lmax, м

ν ,Гц

υmin м/с

υmax, м/с

∆lmin,м

∆lmax, м

∆υmin м/с

∆υmax, м/с

1

0,2

0,205

8,8*103

352

360,8

0,193

0,198

332,53

344,47

2

0,17

0,18

9,9*103

326,4

345,6

3

0,21

0,215

7,6*103

319,2

326,8

Вычисления:

При ν=8,8*103Гц

lmin=0,2м

lmax=0,205м

υmin =2ν lmin =2*8,8*103 *0,2=352м/с

υmax=2νlmax=2*8,8*103 *0,205=360,8м/с

При ν=9,6*103Гц

lmin=0,17м

lmax=0,18м

υmin =2νlmin =2*9,6*103 *0,17=326,4м/с

υmax=2νlmax=2*9,6*103 *0,18=345,6м/с

При ν=7,6*103Гц

lmin=0,215м

lmax=0,21м

υmin =2νlmin =2*7,6*103 *0,215=319,2м/с

υmax=2νlmax=2*7,6*103 *0,21=326,8м/с

Погрешность измерений:

При ν=8,8*103Гц

м/с

м/с

При ν=9,6*103Гц

υmin =326,4±0,959м/с

υmax=345,6±0,573м/с

При ν=7,6*103Гц

υmin =319,2±0,759м/с

υmax=326,8м±0,758м/с

Вывод: Определили длину волны и скорость звука в воздухе при температуре 23 С.и посчитанное значение скорости равно

Источник

Добавить комментарий