Как найти скорость звуковой волны формула - Сайт, где вы сможете решить свои вопросы

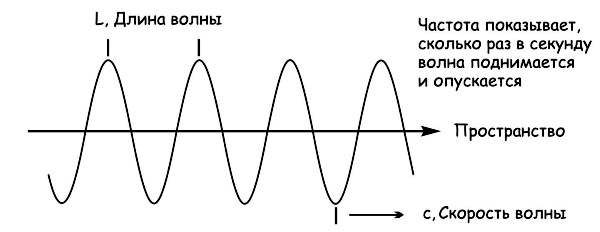
Звуковая волна – период, длина, частота и скорость распространения

Калькуляторы онлайн перевода длины звуковой, инфразвуковой или ультразвуковой
волны в частоту и наоборот. Таблица соответствия
нот полного звукоряда частотам.

Звуковая волна – это механические колебания, которые в результате колебаний молекул вещества распространяются в какой-либо
среде (в газе, жидкости или твёрдом теле) и, достигнув органов слуха человека, воспринимаются им как звук. Источник, создающий
возмущение (колебания воздуха), называется источником звука.
Как уже было сказано, для распространения звука необходима какая-либо упругая среда. Поэтому в вакууме ори, не ори – тебя никто не
услышит, по причине того, что звуковые волны распространяться не смогут, так как там нечему колебаться.., да и слушать там, по большому
счёту, тоже некому.

Так же, как и в случае с электромагнитными волнами, соотношение, связывающее длину звуковой волны с частотой колебаний,
в общем случае выглядит следующим образом:
λ (м) = V (м/сек) / F (Гц), где V (м/сек) – это скорость распространения
звука в среде.

Период колебаний также не претерпел никаких изменений и по-прежнему равен:

T(сек) = 1 / F (Гц) = λ (м) / V (м/сек).

Частота колебаний звукового сигнала F (Гц) – это параметр стабильный, практически не зависящий от среды распространения.

А вот скорость звука V (м/сек), а соответственно и длина звуковой волны – это величины, которые зависят
не только от плотности вещества, но и от его упругости, а в случае с жидкостями и газами ещё – и от температуры, и атмосферного
давления.

Зависимость скорости звуковой волны от свойств упругой среды легко прослеживается по следующей формуле:
V (м/сек) = √Eупр (паскаль) / ρ (кг/м³)
,
где Eупр представляет собой модуль объёмной упругости среды, а ρ – плотность среды.
Модуль упругости, так же как и плотность – это справочные величины, прописанные для конкретных материалов.

В качестве примера, ниже приведена таблица величины скорости распространения звука в различных средах:

Среда	Скорость звука, м/сек
Воздух при 0°	331
Воздух при 30°	350
Вода	1450
Медь	3800
Дерево	4800
Железо	4900
Сталь	5600

Для газов параметры модуля объёмной упругости и плотности имеют ярко выраженную зависимость от температуры и атмосферного давления.
Если углубиться, то скорость звука в газах можно вычислить по следующей формуле:

V (м/сек) = √γ*Ратм / ρ ,
где

γ = cp/сv – это отношение удельной теплоёмкости при постоянном давлении
к удельной теплоёмкости при постоянном объёме, а Pатм – атмосферное давление,
которое связано с температурой газообразной среды.

Поэтому, чтобы никого сильно не грузить, приведу и приближённую зависимость скорости звука (при нормальном
атмосферном давлении) от температуры среды:
V (м/сек) = (331 + 0,6 * T°), где 331 м/сек – это скорость звука при 0°С,
а T° – температура в градусах Цельсия.

Теперь можно совместить формулы и получить простое соотношение, связывающее длину звуковой волны с частотой колебаний с учётом
температуры среды:

λ (м) = (331 + 0,6 * T°) / F (Гц).

Всё это без лишнего напряга несложно посчитать при помощи листа бумаги или деревянных счёт, ну а для пущего упрощения жизни человека,
приведу и пару он-лайн считалок для перевода одного из параметров в другой.
Калькуляторы предполагают расчёты длины и частоты звуковой волны для воздушной среды при нормальном атмосферном
давлении (760 мм ртутного столба).

Онлайн калькулятор расчёта длины звуковой волны по частоте

Частота звуковых колебаний f
Температура Т(°С) (по умолчанию 20°)

Длина волны

Онлайн калькулятор расчёта частоты по длине звуковой волны

Длина волны λ при заданной Т
Температура Т(°С) (по умолчанию 20°)

Частота колебаний

Полный диапазон звуковых частот условно находится в пределах:
16…20 000 Гц.
Ниже ( 0,001…16Гц ) – инфразвук.
Выше ( 20…100кГц ) – низкочастотный ультразвук,
ещё выше (100кГц…1МГц) – высокочастотный ультразвук.

А для интересующихся приведу таблицу соответствия нот стандартного музыкального звукоряда частотам.

*Частота (Гц)*
*Октава*	*Нота*
До	До – диез	Ре	Ми – бемоль	Ми	Фа	Фа – диез	Си	Си- диез	Ля	Соль-бемоль	Соль
C	C#	D	Eb	E	F	F#	G	G#	A	Bb	B
0	16.35	17.32	18.35	19.45	20.60	21.83	23.12	24.50	25.96	27.50	29.14	30.87
1	32.70	34.65	36.71	38.89	41.20	43.65	46.25	49.00	51.91	55.00	58.27	61.74
2	65.41	69.30	73.42	77.78	82.41	87.31	92.50	98.00	103.8	110.0	116.5	123.5
3	130.8	138.6	146.8	155.6	164.8	174.6	185.0	196.0	207.7	220.0	233.1	246.9
4	261.6	277.2	293.7	311.1	329.6	349.2	370.0	392.0	415.3	440.0	466.2	493.9
5	523.3	554.4	587.3	622.3	659.3	698.5	740.0	784.0	830.6	880.0	932.3	987.8
6	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760	1865	1976
7	2093	2217	2349	2489	2637	2794	2960	3136	3322	3520	3729	3951
8	4186	4435	4699	4978	5274	5588	5920	6272	6645	7040	7459	7902

Источник

Скорость звука в различных средах^[1]

0 °C, 101325 Па	м/с	км/ч
Азот	333	1202,4
Аммиак	415	1494,0
Ацетилен	327	1177,2
Водород	1284	4622,4
Воздух	331	1191,6
Гелий	965	3474,0
Кислород	316	1137,6
Метан	430	1548,0
Угарный газ	338	1216,8
Неон	435	1566,0
Углекислый газ	259	932,4
Хлор	206	741,6
Жидкости
Вода	1403	5050,8
Ртуть	1383	4978,0
Твёрдые тела
Алмаз	12000	43200,0
Железо	5950	21420,0
Золото	3240	11664,0
Литий	6000	21600,0
Стекло	4800	17280,0

Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).

Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.

Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.

История измерения скорости звука[править | править код]

Уже у античных авторов встречается указание на то, что звук обусловлен колебательным движением тела (Птолемей, Евклид). Аристотель отмечает, что скорость звука имеет конечную величину, и правильно представляет себе природу звука^[2]. Попытки экспериментального определения скорости звука относятся к первой половине XVII в. Ф. Бэкон в «Новом органоне» указал на возможность определения скорости звука путём сравнения промежутков времени между вспышкой света и звуком выстрела.
Применив этот метод, различные исследователи (М. Мерсенн, П. Гассенди, У. Дерхам, группа учёных Парижской академии наук — Д. Кассини, Ж. Пикар, Гюйгенс, Рёмер) определили значение скорости звука (в зависимости от условий экспериментов, 350—390 м/с).

Теоретически вопрос о скорости звука впервые рассмотрел И. Ньютон в своих «Началах»; он фактически предполагал изотермичность распространения звука, поэтому получил заниженную оценку.
Правильное теоретическое значение скорости звука было получено Лапласом^[3]^[4]^[5]^[6].

В 2020 г. британские и российские физики впервые рассчитали максимально возможную скорость звука, которая составляет 36 км/с (этот показатель приблизительно втрое превышает скорость звука в алмазе (12 км/с), самом твёрдом известном материале в мире). Теория предсказывает наибольшую скорость звука в среде твёрдого атомарного металлического водорода, при давлении выше 1 млн атмосфер^[7]^[8].

Расчёт скорости звука в жидкости и газе[править | править код]

Скорость звука в однородной жидкости (или газе) вычисляется по формуле:

${displaystyle c={sqrt {frac {1}{beta rho }}}.}$

В частных производных:

${displaystyle c={sqrt {-v^{2}left({frac {partial p}{partial v}}right)_{s}}}={sqrt {-v^{2}{frac {C_{p}}{C_{v}}}left({frac {partial p}{partial v}}right)_{T}}},}$

где beta — адиабатическая упругость среды; rho — плотность; C_p — изобарная теплоёмкость; C_v — изохорная теплоёмкость; , , — давление, удельный объём и температура, — энтропия среды.

Для идеальных газов эта формула выглядит так:

${displaystyle c={sqrt {frac {gamma kT}{m}}}={sqrt {frac {gamma RT}{M}}}=alpha {sqrt {T}}={sqrt {frac {gamma }{3}}}v}$

где gamma — показатель адиабаты: 5/3 для одноатомных газов, 7/5 для двухатомных (и для воздуха), 4/3 для многоатомных; — постоянная Больцмана; — универсальная газовая постоянная; — абсолютная температура; — молекулярная масса; — молярная масса, $alpha = sqrt{frac{gamma R}{M}}$ ; — средняя скорость теплового движения частиц газа.

По порядку величины скорость звука в газах близка к средней скорости теплового движения молекул (см. Распределение Максвелла) и в приближении постоянства показателя адиабаты пропорциональна квадратному корню из абсолютной температуры.

Данные выражения являются приближёнными, поскольку основываются на уравнениях, описывающих поведение идеального газа. При больших давлениях и температурах необходимо вносить соответствующие поправки.

Для расчёта сжимаемости многокомпонентной смеси, состоящей из невзаимодействующих друг с другом жидкостей и/или газов, применяется уравнение Вуда. Это же уравнение применимо и для оценки скорости звука в нейтральных взвесях.

Для растворов и других сложных физико-химических систем (например, природный газ, нефть) данные выражения могут давать очень большую погрешность.

Влияние высоты на атмосферную акустику[править | править код]

Плотность и давление плавно уменьшаются с высотой, а температура (красный цвет) — нет. Скорость звука (синий цвет) зависит сложным образом от температуры на высоте и может быть рассчитана исходя из неё, поскольку влияние плотности и давления на скорость звука незначительно и зависит в основном от температуры. Скорость звука увеличивается с высотой в двух областях стратосферы и термосферы из-за разогрева газа в этих областях.

В атмосфере Земли температура выступает главным фактором, влияющим на скорость звука. Для данного идеального газа с постоянной теплоемкостью и составом скорость звука зависит исключительно от температуры. В таком идеальном случае эффекты пониженной плотности и пониженного давления на высоте нейтрализуют друг друга, за исключением остаточного влияния температуры.

Поскольку температура (и, следовательно, скорость звука) уменьшается с увеличением высоты до 11 км, звук преломляется вверх, удаляясь от слушателей на земле, создавая акустическую тень на некотором расстоянии от источника^[9]. Уменьшение скорости звука с высотой называется отрицательным градиентом скорости звука.

Однако выше 11 км в этой тенденции происходят изменения. В частности, в стратосфере на высоте более 20 км скорость звука увеличивается с высотой из-за повышения температуры в результате нагрева озонового слоя. Это дает положительный градиент скорости звука в этой области. Ещё одна область положительного градиента наблюдается на очень больших высотах, в слое, называемом термосферой (выше 90 км).

Твёрдые тела[править | править код]

Смотрите также: P-волна

Смотрите также: S-волна

В однородных твёрдых телах могут существовать два типа объёмных волн, отличающихся друг от друга поляризацией колебаний относительно направления распространения волны: продольная (P-волна) и поперечная (S-волна). Скорость распространения первой ${displaystyle (c_{P})}$ всегда выше, чем скорость второй ${displaystyle (c_{S})}$ :

${displaystyle c_{P}={sqrt {frac {K+{frac {4}{3}}G}{rho }}}={sqrt {frac {E(1-nu )}{(1+nu )(1-2nu )rho }}},}$

${displaystyle c_{S}={sqrt {frac {G}{rho }}}={sqrt {frac {E}{2(1+nu )rho }}},}$

где — модуль всестороннего сжатия, — модуль сдвига, — модуль Юнга, — коэффициент Пуассона. Как и для случая с жидкой или газообразной средой, при расчётах должны использоваться адиабатические модули упругости.

В многофазных средах из-за явлений неупругого поглощения энергии скорость звука, вообще говоря, зависит от частоты колебаний (то есть наблюдается дисперсия скорости). Например, оценка скорости упругих волн в двухфазной пористой среде может быть выполнена с применением уравнений теории Био-Николаевского. При достаточно высоких частотах (выше частоты Био) в такой среде возникают не только продольные и поперечные волны, но также и продольная волна II-рода. При частоте колебаний ниже частоты Био, скорость упругих волн может быть приблизительно оценена с использованием гораздо более простых уравнений Гассмана.

При наличии границ раздела, упругая энергия может передаваться посредством поверхностных волн различных типов, скорость которых отличается от скорости продольных и поперечных волн. Энергия этих колебаний может во много раз превосходить энергию объёмных волн.

Скорость звука в воде[править | править код]

В чистой воде скорость звука составляет около 1500 м/с (см. опыт Колладона — Штурма) и увеличивается с ростом температуры. Прикладное значение имеет также скорость звука в солёной воде океана. Скорость звука увеличивается с увеличением солёности и температуры. При увеличении давления скорость также возрастает, то есть, увеличивается с глубиной. Предложено несколько различных эмпирических формул для вычисления скорости распространения звука в воде.

Например, формула Вильсона 1960 года для нулевой глубины даёт следующее значение скорости звука:

${displaystyle c=1449,2+4,623 T-0,0546 T^{2}+1,39(S-35),}$

где

— скорость звука в метрах в секунду,

— температура в градусах Цельсия,

— солёность в промилле.

Иногда также пользуются упрощённой формулой Лероя:

${displaystyle c=1492,9+3(T-10)-0,006(T-10)^{2}-0,04(T-18)^{2} +}$

{displaystyle + 1,2(S-35)-0,01(T-18)(S-35)+z/61,}

где

— глубина в метрах.

Эта формула обеспечивает точность около 0,1 м/с для °C и при м.

При температуре +24 °C, солёности 35 промилле и нулевой глубине скорость звука равна около 1532,3 м/c. При °C, глубине 100 м и той же солёности скорость звука равна 1468,5 м/с^[10].

Коэффициенты формулы ЮНЕСКО

Коэффициент	Значение	Коэффициент	Значение
${displaystyle C_{00}}$	1402,388	${displaystyle A_{02}}$	7,166·10⁻⁵
${displaystyle C_{01}}$	5,03830	${displaystyle A_{03}}$	2,008·10⁻⁶
${displaystyle C_{02}}$	-5,81090·10⁻²	${displaystyle A_{04}}$	-3,21·10⁻⁸
${displaystyle C_{03}}$	3,3432·10⁻⁴	${displaystyle A_{10}}$	9,4742·10⁻⁵
${displaystyle C_{04}}$	-1,47797·10⁻⁶	${displaystyle A_{11}}$	-1,2583·10⁻⁵
${displaystyle C_{05}}$	3,1419·10⁻⁹	${displaystyle A_{12}}$	-6,4928·10⁻⁸
${displaystyle C_{10}}$	0,153563	${displaystyle A_{13}}$	1,0515·10⁻⁸
${displaystyle C_{11}}$	6,8999·10⁻⁴	${displaystyle A_{14}}$	-2,0142·10⁻¹⁰
$C_{12}$	-8,1829·10⁻⁶	${displaystyle A_{20}}$	-3,9064·10⁻⁷
${displaystyle C_{13}}$	1,3632·10⁻⁷	${displaystyle A_{21}}$	9,1061·10⁻⁹
${displaystyle C_{14}}$	-6,1260·10⁻¹⁰	${displaystyle A_{22}}$	-1,6009·10⁻¹⁰
${displaystyle C_{20}}$	3,1260·10⁻⁵	${displaystyle A_{23}}$	7,994·10⁻¹²
${displaystyle C_{21}}$	-1,7111·10⁻⁶	${displaystyle A_{30}}$	1,100·10⁻¹⁰
${displaystyle C_{22}}$	2,5986·10⁻⁸	${displaystyle A_{31}}$	6,651·10⁻¹²
${displaystyle C_{23}}$	-2,5353·10⁻¹⁰	${displaystyle A_{32}}$	-3,391·10⁻¹³
${displaystyle C_{24}}$	1,0415·10⁻¹²	${displaystyle B_{00}}$	-1,922·10⁻²
${displaystyle C_{30}}$	-9,7729·10⁻⁹	${displaystyle B_{01}}$	-4,42·10⁻⁵
${displaystyle C_{31}}$	3,8513·10⁻¹⁰	${displaystyle B_{10}}$	7,3637·10⁻⁵
${displaystyle C_{32}}$	-2,3654·10⁻¹²	${displaystyle B_{11}}$	1,7950·10⁻⁷
${displaystyle A_{00}}$	1,389	${displaystyle D_{00}}$	1,727·10⁻³
${displaystyle A_{01}}$	-1,262·10⁻²	${displaystyle D_{10}}$	-7,9836·10⁻⁶

Международная стандартная формула, применяемая для определения скорости звука в морской воде известна как формула ЮНЕСКО и описана в работе^[11]. Она более сложная, чем простые формулы, приведённые выше, и вместо глубины в неё входит давление как параметр. Оригинальный алгоритм ЮНЕСКО для расчётов по формуле описан в работе N. P. Fofonoff и R. C. Millard^[12].

В 1995 году коэффициенты, применяемые в данной формуле были уточнены^[13] после принятия международной температурной шкалы 1990 года. Конечная форма формулы ЮНЕСКО имеет следующий вид, входящие в формулу постоянные коэффициенты согласно^[13] приведены в таблице:

${displaystyle c(S,T,P)=C_{w}(T,P)+A(T,P)S+B(T,P)S^{3/2}+D(T,P)S^{2},}$

где ${displaystyle C_{w}(T,P)=C_{00}+C_{01}T+C_{02}T^{2}+C_{03}T^{3}+C_{04}T^{4}+C_{05}T^{5} +}$

${displaystyle + (C_{10}+C_{11}T+C_{12}T^{2}+C_{13}T^{3}+C_{14}T^{4})P +}$

${displaystyle + (C_{20}+C_{21}T+C_{22}T^{2}+C_{23}T^{3}+C_{24}T^{4})P^{2} +}$

${displaystyle + (C_{30}+C_{31}T+C_{32}T^{2})P^{3},}$

${displaystyle A(T,P)=A_{00}+A_{01}T+A_{02}T^{2}+A_{03}T^{3}+A_{04}T^{4} +}$

${displaystyle + (A_{10}+A_{11}T+A_{12}T^{2}+A_{13}T^{3}+A_{14}T^{4})P +}$

${displaystyle + (A_{20}+A_{21}T+A_{22}T^{2}+A_{23}T^{3})P^{2} +}$

${displaystyle + (A_{30}+A_{31}T+A_{32}T^{2})P^{3},}$

${displaystyle B(T,P)=B_{00}+B_{01}T+(B_{10}+B_{11}T)P,}$

${displaystyle D(T,P)=D_{00}+D_{10}P.}$

Здесь

— температура в градусах Цельсия (в диапазоне от 0 °С до 40 °С),

— солёность в промилле (в диапазоне от 0 до 40 промилле),

— давление в барах (в диапазоне от 0 до 1000 бар).

В библиотеке приводится исходный код алгоритма ЮНЕСКО на языке C#.

См. также[править | править код]

Скорость света
Эффект Доплера
Сверхзвуковая скорость
Сверхзвуковой самолёт
Звуковой барьер
Число Маха
Гиперзвуковая скорость
Сейсмическая волна

Примечания[править | править код]

↑ Скорость звука // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 4. Архивировано 9 марта 2011 года.
↑ Тимкин С. История естествознания
↑ The Speed of Sound. mathpages.com. Дата обращения: 3 мая 2015. Архивировано 25 июля 2020 года.
↑ Bannon, Mike; Kaputa, Frank The Newton–Laplace Equation and Speed of Sound. Thermal Jackets. Дата обращения: 3 мая 2015. Архивировано 15 августа 2020 года.
↑ Murdin, Paul. Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth (англ.). — Springer Science & Business Media, 2008. — P. 35—36. — ISBN 9780387755342.
↑ Fox, Tony. Essex Journal (неопр.). — Essex Arch & Hist Soc, 2003. — С. 12—16.
↑ Скорость звука: каков ее предел? / Блог компании ua-hosting.company / Хабр. Дата обращения: 26 декабря 2020. Архивировано 3 декабря 2020 года.
↑ Источник. Дата обращения: 26 декабря 2020. Архивировано 30 декабря 2020 года.
↑ Everest, F. The Master Handbook of Acoustics. — New York : McGraw-Hill, 2001. — P. 262–263. — ISBN 978-0-07-136097-5.
↑ Роберт Дж. Урик (Rodert J. Urick) Основы гидроакустики (Principles of underwater sound) Л: Судостроение, 1978; McGraw-Hill 1975.
↑ Chen‐Tung Chen, Frank J. Millero. Speed of sound in seawater at high pressures (англ.) // Journal of the Acoustical Society of America (англ.) (рус.. — 1977-11-01. — Vol. 62, iss. 5. — P. 1129—1135. — ISSN 0001-4966. — doi:10.1121/1.381646. Архивировано 5 августа 2019 года.
↑ Millard R. C., Jr; Fofonoff N. P. Algorithms for the computation of fundamental properties of seawater (англ.). — 1983. Архивировано 5 августа 2019 года.
↑ ¹ ² George S. K. Wong, Shi‐ming Zhu. Speed of sound in seawater as a function of salinity, temperature, and pressure (англ.) // Journal of the Acoustical Society of America (англ.) (рус.. — 1995-03-01. — Vol. 97, iss. 3. — P. 1732—1736. — ISSN 0001-4966. — doi:10.1121/1.413048. Архивировано 5 августа 2019 года.

Литература[править | править код]

Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1953;
Михайлов И. Г., Соловьев В. А., Сырников Ю. П., Основы молекулярной акустики, М., 1964;
Колесников А. Е., Ультразвуковые измерения, М., 1970;
Исакович М. А., Общая акустика, М., 1973.

Ссылки[править | править код]

Вычисление скорости звука
Таблицы скоростей звука
Акустические свойства различных материалов и скорости звука в них

Источник

Перед тем, как приступить к рассмотрению темы, дадим определение такому явлению, как звук.

Определение 1

Звук или звуковые волны – это волны, которые способно воспринять человеческое ухо.

При этом звуковые частоты имеют диапазон: примерно от 20 Гц до 20 кГц.

Определение 2

Инфразвук – звуковые волны, имеющие частоту менее 20 Гц.

Ультразвук – волны звука, имеющие частоту более 20 кГц.

Волнам звукового диапазона свойственно распространяться как в газе, так и в жидкости (продольные волны), и в твердом теле (продольные и поперечные волны). Особенно интересно для науки заниматься изучением распространения звуковых волн в газообразной среде, что по сути есть среда нашего обитания.

Определение 3

Акустика – это направление физики, занимающееся изучением звуковых явлений.

Когда звук получает распространение в газе, атомы и молекулы испытывают колебания вдоль направления распространения волны, следствием чего становится изменение локальной плотности ρ и давления p.

Замечание 1

Звуковые волны в газе зачастую называют волнами плотности или волнами давления.

В случае простых гармонических звуковых волн, получающих распространение вдоль оси OX, изменение давления p(x, t) имеет зависимость от координаты x и времени t, которая записывается так:

p(x,t)=p0cosωt±kx.

В аргументе косинуса мы видим два противоположных знака, что имеет отношение к двум направлениям распространения волны. Запишем выражение, которое покажет соотношение таких величин, как круговая частота ω, волновое число k, длина волны λ, скорость звука υ (соотношение будет таким же, как применимо для поперечных волн в струне или резиновом жгуте):

υ=λT=ωk; k=2πλ; ω=2πf=2πT.

Одной из ключевых характеристик звука является скорость распространения.

Определение 4

Скорость распространения – величина, описывающая звуковую волну, задаваемая инертными и упругими свойствами среды и определяемая для продольных волн в любой однородной среде при помощи формулы:

υ=Bρ.

В указанной формуле B является модулем всестороннего сжатия, ρ – средней плотностью среды.

Формула Лапласа

Первые попытки рассчитать значение скорости звука предпринял Ньютон, предположив равенство упругости воздуха атмосферному давлению pатм. В таком случае значение скорости звука в воздушной среде – менее 300 м/с, в то время как истинная скорость звука при нормальных условиях (температура 0 °С и давление 1 атм) равна 331,5 м/с, а скорость звука при температуре 20 °С и давлении 1 атм составит 343 м/с. Лишь по прошествии более ста лет было показано, почему предположение Ньютона не выполняется. Французский физик П. Лаплас указал, что ньютоновское видение равносильно предположению о быстром выравнивании температуры между областями разрежения и сжатия, и невыполнение его связано с плохой теплопроводностью воздуха и малым периодом колебаний в звуковой волне. В действительности между областями разрежения и сжатия газа появляется разность температур, существенным образом влияющая на упругие свойства. Лаплас, в свою очередь, выдвинул предположение, что сжатие и разрежение газа в звуковой волне происходят в соответствии с адиабатическим законом: в отсутствии влияния теплопроводности. В 1816 году физик вывел формулу, предназначенную для расчета скорости звуковой волны в воздухе и получившей название формулы Лапласа.

Определение 5

Формула Лапласа для определения скорости звука имеет запись:

υ=γpρ.

Где p является значением среднего давления в газе, ρ – средней плотности, а γ есть некоторая константа, находящаяся в зависимости от свойств газа.

В нормальных условиях скорость звука, рассчитанная по формуле Лапласа, равна υ=332 м/с.

В термодинамике имеется доказательство, что константа γ представляет собой отношение теплоемкостей при постоянном давлении Cp и постоянном объеме CV .

Формула Лапласа может быть записана несколько иначе, если использовать уравнение состояния идеального газа. Таким образом, окончательный вид формулы для определения скорости звука будет такой:

υ=γRTM.

В данной формуле T – абсолютная температура, M – молярная масса,
R=8,314 Дж/моль·К – универсальная газовая постоянная. Скорость звука находится в сильной зависимости от свойств газа: скорость звука тем больше, чем легче газ, в котором звуковая волна получает распространение.

Для наглядности приведем некоторые примеры.

Пример 1

Когда звук распространяется в воздушной среде (M=29·10–3 кг/моль) при нормальных условиях: υ=331,5 м/с;

Пример 2

Когда звук распространяется в гелии (M=4·10–3 кг/моль): υ=970 м/с;

Пример 3

Когда звук распространяется в водороде (M=2·10–3 кг/моль): υ=1270 м/с.

В жидкостях и твердых телах скорость звуковых волн еще больше. В воде, например, υ=1480 м/с (при 20 °С), в стали υ=5–6 км/с.

Характеристики звуковых волн

Помимо скорости распространения звук имеет и другие характеристики, связанные с восприятием его человеческими органами слуха.

Громкость звука

Рассуждая о том, как человеческое ухо воспринимает звук, в первую очередь мы говорим об уровне громкости, который зависит от потока энергии или интенсивности звуковой волны. А то, как воздействует звуковая волна на барабанную перепонку, зависит от звукового давления.

Определение 6

Звуковое давление – это амплитуда p0 колебаний давления в волне

Природа отлично потрудилась, создавая такое совершенное устройство, как человеческое ухо: оно способно воспринимать звуки в обширнейшем диапазоне интенсивностей. Мы имеем возможность слышать как слабый писк комара, так и грохот вулкана.

Определение 7

Порог слышимости – минимальное значение величины звукового давления, при котором звук этой частоты еще воспринимается человеческим ухом.

Болевой порог – это верхняя граница диапазона слышимости человека; та величина звукового давления, при котором звук вызывает в человеческом ухе ощущение боли.

Порог слышимости представляет собой значение p0около 10–10 атм, т. е. 10–5 Па: такой слабый звук характеризуется колебанием молекул воздуха в волне звука с амплитудой всего лишь 10–7 см! Болевой же порог соответствует значению p0 порядка 10–4 атм или 10 Па. Т.е., человеческое ухо способно к восприятию волн, в которых звуковое давление изменяется в миллион раз. Поскольку интенсивность звука пропорциональна квадрату звукового давления, диапазон интенсивностей оказывается порядка 1012!

Человеческое ухо, восприимчивое к звукам такого огромного диапазона интенсивности, допустимо сравнить с прибором, которым возможно измерить как диаметр атома, так и размеры футбольного поля.

Замечание 2

Для общей информированности заметим, что обычным разговорам людей в комнате соответствует интенсивность звука, примерно в 106 раз превышающая порог слышимости, а интенсивность звука на рок-концерте находится очень близко к болевому порогу.

Высота звука

Высота звуковой волны – еще одна характеристика звука, влияющая на слуховое восприятие. Человеческие ухо воспринимает колебания в гармонической звуковой волне как музыкальный тон.

Определение 8

Высокий тон – это звуки с колебаниями высокой частоты.

Низкий тон – это звуки с колебаниями низкой частоты.

Звуки, которые издают музыкальные инструменты, а также звуки голоса человека значимо отличаются друг от друга по высоте тона и по диапазону частот.

К примеру, диапазон наиболее низкого мужского голоса – баса – находится в пределах примерно от
80 до 400 Гц, а диапазон высокого женского голоса – сопрано – от 250 до 1050 Гц.

Определение 9

Октава – это диапазон колебаний звука, который соответствует изменению частоты колебаний в 2 раза.

Скрипка, к примеру, звучит в диапазоне примерно трех с половиной октав (196–2340 Гц),
а пианино – семи с лишним октав (27,5–4186 Гц).

Говоря о частоте звука, который извлекается при помощи струн любого струнного музыкального инструмента, будем иметь в виду частоту f1 основного тона. Однако колебания струн содержат также гармоники, частоты fn которых отвечают соотношению:

fn=nf1, (n=1, 2, 3,…).

Таким образом, звучащая струна способна излучать целый спектр волн с кратными частотами. Амплитуды An этих волн имеют зависимость от способа возбуждения струны, будь то смычок или молоточек. Эти амплитуды необходимы для придания музыкальной окраски звуку (тембру).

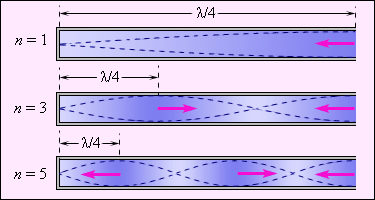
Аналогичный процесс мы наблюдаем, когда звучат духовые музыкальные инструменте. Трубы духовых инструментов служат акустическими резонаторами – акустическими колебательными системами, имеющими способность возбуждаться (резонировать) от звуковых волн определенных частот. Определенные же условия способствуют возникновению внутри трубы стоячей звуковой волны. Рисунок 2.7.1 демонстрирует несколько видов стоячих волн (мод) в органной трубе, закрытой с одного конца и открытой с другого. Звучание духовых инструментов, так же, как и струнных, состоит из целого спектра волн с кратными частотами.

Рисунок 2.7.1. Стоячие волны в трубе органа (закрыта лишь с одной стороны). Стрелки указывают направления движения частиц воздуха за один полупериод колебаний.

Музыкальные инструменты необходимо периодически настраивать.

Определение 10

Камертон – устройство для настройки музыкальных инструментов, состоящее из настроенных в резонанс деревянного акустического резонатора и соединенной с ним металлической вилки.

Удар молоточка по вилке вызывает возбуждение всей системы камертона с последующим звучанием чистого музыкального тона.

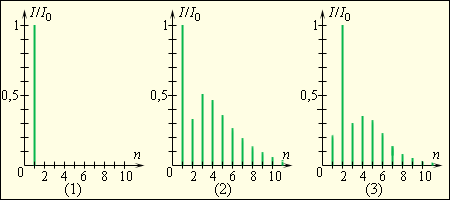
Гортань певца – по сути тоже акустический резонатор. Рисунок 2.7.2 демонстрирует спектры звуковых волн, издаваемых камертоном, струной пианино и низким женским голосом (альтом), звучащими на одной и той же ноте.

Рисунок 2.7.2. Относительные интенсивности гармоник в спектре волну звука при звучании камертона (1), пианино (2) и низкого женского голоса (альт) (3) на ноте «ля» контроктавы (f1=220 Гц). По оси ординат отложены относительные интенсивности II0 _.

Звуковые волны, чьи частотные спектры показаны на рисунке 2.7.2, имеют одну и ту же высоту, но различные тембры.

Биения

Разберем также такое явление, как биения.

Определение 11

Биение – это явление, возникающее, когда две гармонические волны с близкими, но все же имеющими отличия частотами, накладываются друг на друга.

Биения сопровождают, к примеру, одновременное звучание двух струн, имеющих настройки практически одинаковой частоты. Человеческий орган слуха воспринимает биения как гармонический тон с громкостью, периодически изменяющейся во времени. Запишем выражения, показывающие закономерность изменения звуковых давлений p1 и p2, которые осуществляют воздействие на ухо:

p1=A0cos ω1t и p2=A0cos ω2t.

Для удобства примем, что амплитуды колебаний звуковых давлений являются одинаковыми и равны p0=A0₀.

Согласно принципу суперпозиции полное давление, которое вызывается обеими волнами в каждый момент времени, есть совокупность звуковых давлений, задаваемых каждой волной в тот же момент времени. Запишем выражение, показывающее суммарное воздействие волн, используя тригонометрические преобразования:

p=p1+p2=2A0cosω1-ω22tcosω1+ω22t=2A0cos12∆ωtcosωсрt,

где ∆ω=ω1-ω2, аωср=ω1+ω22.

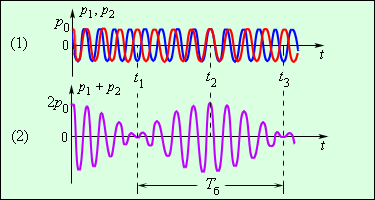
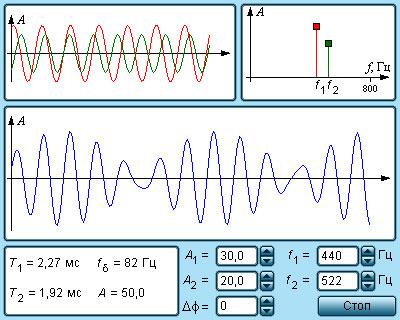
Рисунок 2.7.3(1) отображает, каким образом давления p1 и p2 зависимы от времени t. В момент времени t=0 оба колебания находятся в фазе, и их амплитуды суммируются. Поскольку частоты колебаний имеют хоть и небольшие, но отличия, через некоторое время t1 колебания войдут в противофазу. В этот момент суммарная амплитуда станет равна нулю: колебания взаимно «погасятся». К моменту времени t2=2t1 колебания вновь окажутся в фазе и т. д. (рисунок 2.7.3(2)).

Определение 12

Период биений Тб – это минимальное значение интервала между двумя моментами времени, которым соответствуют максимальная и минимальная амплитуда колебаний.

Формула, которая определяет медленно изменяющуюся амплитуду A результирующего колебания, имеет запись:

A=2A0cos12∆ωt.

Период Тб изменения амплитуды равен 2πΔω. Мы можем это продемонстрировать, приняв следующее предположение: периоды колебаний давлений в звуковых волнах T1 и T2 являются такими, что T1<T2 (т. е. ω1>ω2). За период биений Тб наблюдается некоторое число n полных циклов колебаний первой волны и (n–1) циклов колебаний второй волны:

Tб=nT1=(n-1)T2.

Отсюда следует:

Tб=T1T2T2-T1=2πω1-ω2=2π∆ω или fб=1Tб=1T1-1T2=f1-f2=∆f.

fб есть частота биений, определяемая как разность частот Δf двух звуковых волн, которые воспринимаются ухом одновременно.

Органы слуха человека способны к восприятию звуковых биений до частот 5–10 Гц. Прослушивание биений – это важный элемент техники настройки музыкальных инструментов.

Рисунок 2.7.3. Биения, возникающие, когда накладываются две звуковые волны с близкими частотами.

Рисунок 2.7.4. Модель явления биений.

Источник

Наше ухо постоянно слышит различные звуки. Чаще всего звук распространяется по воздуху, но может распространяться и в других средах. Эти среды называют упругими.

Если между ухом и источником звука удалить звукопередающую среду, то мы ничего не услышим. Это означает, что для передачи звука на расстояние необходима звукопередающая среда.

Пример:

Чтобы изолировать источник звука (будильник) от звукопередающей среды (воздуха), поместим его в установку, где сможем откачать воздух (рис. (1)).

Рис. (1). Эксперимент с будильником в вакууме

Для чистоты эксперимента послушаем будильник в воздушной среде под колоколом воздушного насоса. Звук слышен очень хорошо. Постепенно начнём откачивать воздух. Громкость звука уменьшается. При достижении вакуума под колоколом звук перестаёт передаваться — будильник не слышно. Этим экспериментом мы подтвердили утверждение о том, что в отсутствие упругой среды звук не передаётся.

Звуковые волны распространяются в упругой среде. Чем больше плотность вещества, тем лучше оно проводит звук.

Проведём эксперимент с доской из древесины (рис. (2)). Сможем ли мы расслышать тиканье часов на расстоянии, приложив ухо к одному концу доски, а к другому – наручные часы? Звук хорошо передаётся по доске.

Рис.(2). Эксперимент с доской из древесины

Если подвесить металлическую ложку на верёвочке (рис. (3)) и привязать другой конец к пальцам, то вибрация будет им передаваться. Проволока из металла будет лучше проводить звук.

Рис. (3). Эксперимент с ложкой и верёвочкой

Тела с низкой плотностью, не обладающие упругостью, содержащие звукоизолирующие слои (например, прослойку воздуха) проводят звук в меньшей степени. Например, пробка, поролон, вата.

Чтобы изолировать помещение от посторонних или ненужных звуков, необходимо облицевать потолок, стены и даже пол различными звукопоглощающими материалами. Для этих целей используют минеральную, базальтовую или хлопковую вату, а также газостекло, пенобетон, вспененный полиуретан и меламин и др. Все эти материалы в порах содержат воздух, что и способствует поглощению звука.

Таким образом,

звук может распространяться в любой среде (твёрдой, жидкой и газообразной), где есть молекулы. И не может распространяться там, где молекул нет, т.е. в вакууме.

Колебания источника звука создают в окружающей среде волну звуковой частоты, которая является упругой волной.

Восприятие звука слуховым аппаратом (рис. 4):

Волна, достигая наружного уха, воздействует на барабанную перепонку, что заставляет её колебаться с точно такой же частотой, с какой колеблется источник звука.
Колебания барабанной перепонки передаются на слуховые косточки в среднем ухе, далее — во внутреннее ухо.
Во внутреннем ухе колебания воздействуют на улитку, в которой есть волосковые клетки, которые преобразуют механические колебания в электрические нервные импульсы.
Слуховой нерв передаёт электрические нервные импульсы от улитки в головной мозг.
Мозг анализирует сигналы: распознаёт, сравнивает, интерпретирует.

Рис. (4). Строение слухового аппарата

В газах и жидкостях могут существовать только продольные упругие волны. Поэтому звук в воздухе передаётся продольными волнами, то есть чередующимися сгущениями и разрежениями воздуха, идущими от источника звука.

Звуковая волна распространяется в пространстве с определённой скоростью.

Наблюдая за стрельбой из оружия (например, из пушки), мы сначала видим вспышку и только потом (через некоторое время) слышим звук выстрела.

Измерив промежуток времени (t) между моментом появления вспышки и моментом, когда звук доходит до уха, а также расстояние между источником звука и наблюдателем, можно определить скорость распространения звука по формуле:

По опытным данным, при нормальном атмосферном давлении и температуре воздуха (0) °С скорость звука составляет (332) м/с.

В газах скорость звука прямо пропорциональна температуре.

Например, при (20) °С скорость звука в воздухе равна (343) м/с, при (60) °С — (366) м/с, при (100) °С — (387) м/с.

При повышении температуры среды увеличивается скорость движения молекул (или атомов) среды, что повышает интенсивность взаимодействия частиц среды. Значит, увеличивается передача энергии колебательного движения.

На скорость распространения звука оказывает влияние среда, в которой распространяется звук. Это связано не только с плотностью среды, но и расположением частиц этой среды относительно друг друга.

При решении задач скорость звука в воздухе обычно считают равной (340) м/с.

При температуре (0) °С скорость звука в водороде равна (1284) м/с, а в углекислом газе — (259) м/с. Это различие связано с массой молекул газов, в которых распространяется звук. Масса молекул водорода меньше массы молекул углекислого газа.

Для измерения скорости звука существуют специальные устройства, принцип действия которых связан с определением времени, за которое звук проходит определенное расстояние.

Плотности жидкостей и твёрдых тел значительно больше плотностей газов. Поэтому молекулы в этих средах находятся значительно ближе друг к другу, а следовательно, взаимодействие между ними более сильное. Это способствует более быстрому распространению звука.

Формулы для расчёта скорости механической волны

(upsilon) — скорость движения фронта волны:

1. звук распространяется равномерно:

υ=st

;
2. скорость пропорциональна длине волны:

υ=λT

;

3. скорость пропорциональна частоте колебаний:

υ=λν

Источники:

Источник

Получим формулу для расчета скорости звука в данной работе. Скорость волны связана с длиной бегущей волны λ и с частотой ν соотношением

υ
= λν. (12)

Из
формулы (11) следует, что λ = 2λ_ст,
тогда

υ
= 2λ_стν. (13)

По
формуле (13) можно
рассчитать
скорость звука при температуре
эксперимента.

Зависимость
скорости звука от температуры описывается
соотношением

υ
= υ₀, (14)

где
υ₀
– скорость звука при 0 ºС, t
– температура в ºС, α – температурный
коэффициент объемного расширения газа.
Для воздуха α = (3,67 
0,05)·10^–3
ºС^–1.
Из формулы (14) выразим скорость звука
при 0 ºС:

υ₀
=
.
(15)

Подставив
(13) в (15), получим расчетную формулу:

υ₀
=
.
(16)

Упрощенное описание установки и процессов, в ней происходящих

Установка
для определения скорости звука (рис. 2)
состоит из резонатора 1,
звукового генератора 2,
осциллографа 3
и отсчетной линейки 4.
Резонатор представляет собой закрытую
с обоих торцов трубу, в которую вмонтирован
телефон 5
и подвижный шток 6
с микрофоном 7.
Звуковой генератор создает электрические
колебания определенной частоты. Телефон
преобразует эти колебания в звуковые
колебания той же частоты. Звуковая волна
от телефона распространяется внутри
резонатора. В результате интерференции
прямой и отраженной звуковой волны в
резонаторе возникает стоячая волна,
которая представляет собой чередующиеся
сгущения и разрежения воздуха.

На
рис. 2 условно изображена стоячая волна,
пучностям которой соответствует
наибольшая амплитуда. Звук улавливается
микрофоном и преобразуется в электрический
сигнал, подаваемый на осциллограф. На
экране осциллографа наблюдается сигнал
синусоидальной формы, амплитуда которого
пропорциональна амплитуде звуковых
колебаний в данном месте резонатора.
Когда мембрана микрофона находится в
пучностях стоячей волны, амплитуда
воспринимаемых колебаний максимальна,
а когда в узлах – минимальна.

На
опыте обычно измеряют положение первого
максимума x₁
и последнего максимума x_k
и рассчитывают длину стоячей волны по
формуле

λ_ст
=
, (17)

где
k
– число максимумов.

В
несколько более точном представлении
схема эксперимента и происходящие в
ней явления выглядит иначе. Диаметр
микрофона равен внутреннему диаметру
резонатора. Таким образом, между
микрофоном и телефоном существует
замкнутое пространство, в котором
распространяются падающая и отраженная
волны. Стоячие волны возникают в том
случае, когда между мембранами телефона
микрофона укладывается целое число
длин волн λ_сти
возникает явление резонанса, отчетливо
воспринимаемое на слух и регистрируемое
осциллографом.

Порядок выполнения работы

Включить
звуковой генератор и установить частоту
колебаний по указанию преподавателя
(рекомендуемые частоты 900, 1000, 1100 Гц).
Перемещая
шток с микрофоном по направлению от
источника колебаний, определить число
максимумов k
с помощью осциллографа. По отсчетной
линейке найти положение первого
максимума x₁
и последнего максимума x_k.
Результаты измерений занести в таблицу.

Таблица

Результаты измерений
и вычислений

№ п/п	, Гц	k	x₁	x_k	_ст	υ₀, м/с

Для
каждого значения частоты выполнить не
менее трех измерений. При этом каждый
раз рекомендуется заново устанавливать
частоту на
звуковом генератое.
По
формуле (17) рассчитать длину стоячей
волны, а по формуле (16) – скорость звука
в воздухе при 0 ºС. Результаты
вычислений записать в таблицу.
Рассчитать
приближенное значение скорости звука
и оценить случайную погрешность υ_сл
по методу Стьюдента.
Вычислить
приборную погрешность в скорости звука
υ_сист.
Относительная приборная погрешность
рассчитывается по формуле

где
_ст
принять равной цене деления отсчетной
линейки, 
= 20 Гц, t
принять равной половине цены деления
шкалы термометра,

 =
510^–5
ºС^–1.
Абсолютная приборная погрешность будет
равна

υ_сист
= υ₀.

Определить
общую погрешность по формуле

υ=
.

Записать
окончательный результат с указанием
погрешности определения.
Рассчитать
по формуле (1) скорость звука в воздухе

(γ = 1,40;
М = 29·10^–3 кг/моль)
и сравнить с полученным на опыте
значением.

Сделать
выводы по работе.

Источник

Звуковая волна – период, длина, частота и скорость распространения

История измерения скорости звука[править | править код]

Расчёт скорости звука в жидкости и газе[править | править код]

Влияние высоты на атмосферную акустику[править | править код]

Твёрдые тела[править | править код]

Скорость звука в воде[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Формула Лапласа

Характеристики звуковых волн

Громкость звука

Высота звука

Биения

Получим формулу для расчета скорости звука в данной работе. Скорость волны связана с длиной бегущей волны λ и с частотой ν соотношением

Упрощенное описание установки и процессов, в ней происходящих

Порядок выполнения работы

Вам также может понравиться

Как грамотно составить заявление об отказе от страховки

Комерческое или коммерческое как правильно составить образец

Как найти звукозапись в windows 10

Добавить комментарий Отменить ответ