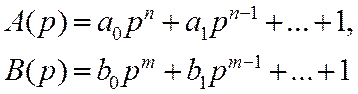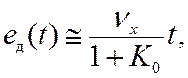Как найти скоростную ошибку

Как найти скоростную ошибку

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:
1. Введение в теорию автоматического управления
2. Математическое описание систем автоматического управления 2.1 — 2.3

В это части будут рассмотрены:
2.4 Основные виды входных воздействий
2.5. Основные положения и свойства интегральных преобразований Лапласа
2.6. Основные свойства преобразований Лапласа
2.7. Способы нахождения обратных преобразований Лапласа
2.8 Некоторые способы нахождения оригинала по известному изображению

Будет интересно познавательно и жестко.


На рисунке 3D график функции косеканс куба, к теме лекции отношения не имеет, но чертовски красив.

2.4 Основные виды входных воздействий

Для того, что бы определить свойства системы нужно осуществить воздействие и посмотреть на реакцию.

В теории управления техническими системами принят ряд стандартных входных воздействий, по реакции на которые определяются динамические свойства (характеристики) системы управления (звена). К таким воздействиям относятся: единичное импульсное воздействие, единичное ступенчатое воздействие, единичное гармоническое воздействие, линейное воздействие и др. Рассмотрим их более подробно…

2.4.1. Единичное ступенчатое воздействие

Данное воздействие является одним из наиболее «жестких» (неблагоприятных) воздействий, по реакции на которое сравниваются переходные свойства (переходной процесс) идентичных или близко идентичных систем.

Реакция системы (звена) на такое воздействие называется переходной функцией.

Единичное ступенчатое воздействие обозначается 1(t) и бывает 3-х видов: два асимметричных и одно симметричное.

$1(y) Rightarrow left[ begin{gathered} 1_+(t) 1(t) 1_-(t) end{gathered} right. mathbf{(2.4.1)}$

Рассмотрим каждый из этих видов воздействий:

$1(t)=left { begin{gathered} 1, если t>0 frac{1}{2}, если t=0 0, если t<0 end{gathered} right. 1_-(t) = left { begin{gathered} 1, если tgeq 0 0, если t<0 end{gathered} right. 1_+(t) = left { begin{gathered} 1, если t> 0 0, если tleq0 end{gathered} right. $

Рисунок 2.4.1 – Графики единичных ступенчатых воздействий

В теории управления наибольшее распространение имеет асимметричное воздействие 1+ (t), поскольку часто в анализе удобно рассматривать процесс, когда при t$leq$0 САР находится в равновесии, и анализ переходных процессов ведется только при t > 0.

Для удобства представления будем в дальнейшем записывать воздействие 1+(t), опуская индекс. 1+ (t) ≡ 1(t).

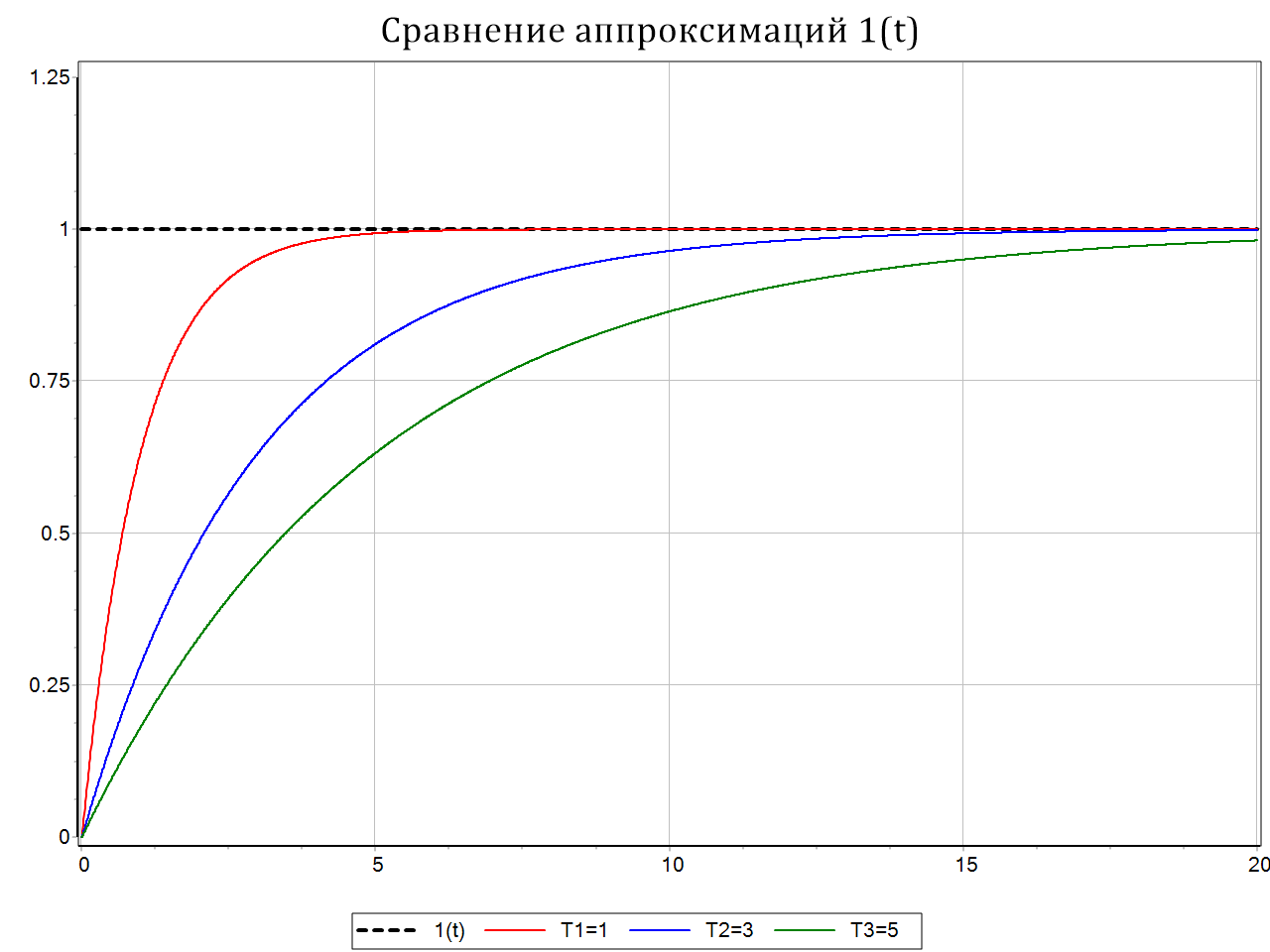
Поскольку рассматриваемое входное воздействие имеет разрыв при t = 0 (что часто нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать единичное ступенчатое воздействие, в виде неразрывной функции:

$1(t) = lim_{Tto0}(1 -e^{-frac{t}{T}}) mathbf{(2.4.2)}$

где Т – постоянная времени, а текущее время $t geq 0$

На рисунке 2.4.2 представлена графическая иллюстрация аппроксимации 1(t) по формуле (2.4.2).

Рисунок 2.4.1 – Графики единичных ступенчатых воздействий

2.4.2. Единичное импульсное воздействие: δ — функция Дирака

В математике различают три вида данного воздействия: одно симметричное и два асимметричных

$delta (t) Rightarrow left[ begin{gathered} delta_+(t) delta(t) delta_-(t) end{gathered} right. $

Рассмотрим все эти воздействия:
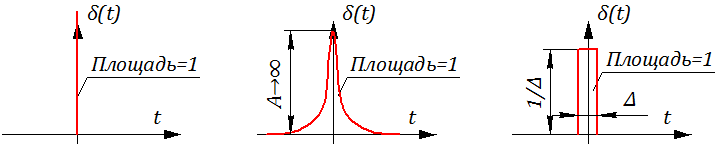
Симметричное единичное импульсное воздействие δ (t) определено как:

$delta (t) = left{ begin{gathered} 0, если t >0 infty, если t =0 0, если t <0 end{gathered} int_{-infty}^{+infty} delta(t) dt = 1; right.$

Графическая иллюстрация симметричного единичного импульсного воздействия представлена на рисунке 2.4.3. Фактически δ (t) – импульс (с длительностью стремящейся к нулю и амплитудой, равной бесконечности), площадь которого равна 1.

Рисунок 2.4.3 – Варианты представления симметричного импульсного воздействия

Для симметричного единичного импульсного воздействия δ(t) существует аналитическая форма представления:

$int_{-infty}^{+infty} delta(t)dt = int_{-infty}^{+infty} lim_{h to infty}frac{h}{sqrt{pi}}e^{-h^2t^2} = lim_{h to infty}frac{1}{sqrt{pi}}int_{-infty}^{+infty}e^{-(ht)^2} d(ht)$

Введем новую переменную $u = h cdot t$, тогда:

$frac{1}{sqrt{pi}} lim_{u to infty}int_{-infty}^{+infty}e^{-(u)^2} d(u) = frac{1}{sqrt{pi}} cdot sqrt{pi} = 1, поскольку lim_{u to infty}int_{-infty}^{+infty}e^{-(u)^2} d(u) = sqrt{pi}$

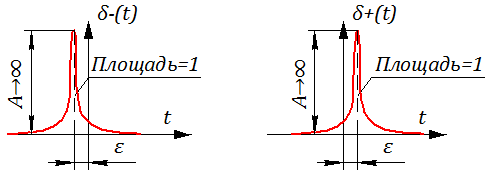
Смещенные (асимметричные) единичные импульсные воздействия определяются как:

$delta_- (t) = left{ begin{gathered} 0, если t leq 0 infty, если t =-epsilon 0, если t < epsilon end{gathered} right. delta_+ (t) = left{ begin{gathered} 0, если t > epsilon leq 0 infty, если t =epsilon 0, если t leq 0 end{gathered} right. int_{-infty}^{+infty} delta(t) dt = 1;$

где $epsilon -$сколь угодно малое положительное число (ε → 0)

Графическая иллюстрация смещенных единичных импульсных воздействий представлена на рисунке 2.4.4

Рисунок 2.4.4 – Смещенные единичные импульсные воздействия.

В дальнейшем в нашем курсе будет использоваться только δ+ (t). ==> Индекс «+» опускается… ==> δ+ (t) ≡ δ(t).

Поскольку смещенное единичное импульсное воздействие фактически имеет разрыва при t = 0 (что иногда нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать смещенное единичное импульсное воздействие:

$delta(t) = lim_{T to 0} frac{1}{T} e^{frac{-t}{T}} mathbf{(2.4.3)}$

где Т – постоянная времени, а текущее время t>0!!!
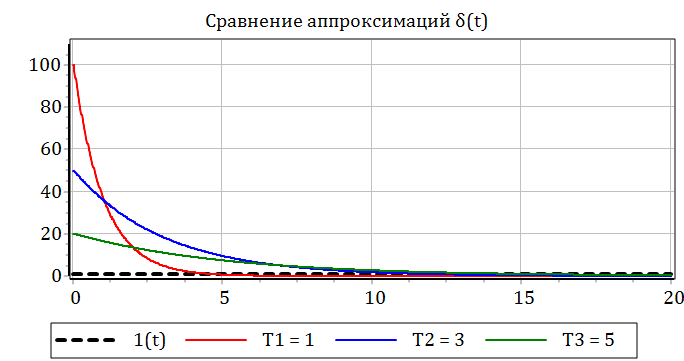
На рисунке 2.4.5 представлена графическая иллюстрация аппроксимации δ(t) по формуле (2.4.3).

Рисунок 2.4.5 – Графики аппроксимаций единичного импульсного воздействия

Реакция САУ (звена) на воздействие δ (t) называется весовой функцией.

2.4.3. Единичное гармоническое воздействие

Данное воздействие используется для анализа частотных характеристик САУ (звена) в установившемся режиме колебаний в системе, т.е. свойства САУ (звена) исследуются при больших значениях t (времени), когда влияние начальных условий пренебрежимо мало и движение (колебания) системы определяются только входным внешним воздействием.

$x(t) = sin (omega cdot t) mathbf{(2.4.4)} $

где ω — круговая частота, [1/с]; $ omega = 2 cdot picdot f$, где $f$ — частота в Герцах.

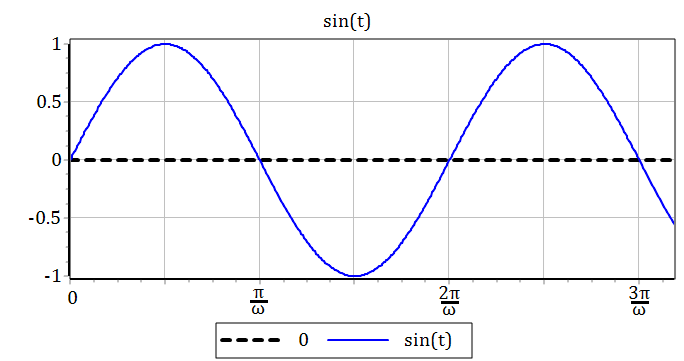
На рисунке 2.4.6 представлен график единичного гармонического воздействия.

Рисунок 2.4.6 – Гармоничное воздействие

Поскольку при анализе частотных характеристик САУ рассматривается режим установившихся вынужденных колебаний САУ (при больших значениях времени t, когда собственная составляющая переходного процесса пренебрежимо мала), то удобнее представить x(t) в показательной форме.

$x(t) = e^{omega cdot i cdot t} mathbf{(2.4.5)}$

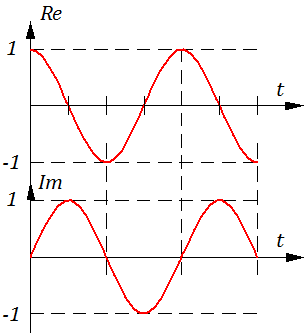
Необходимо отметить, что показательная форма – «комплексное» воздействие, и оно выглядит так (действительная и мнимая части условно показаны на рисунке 2.4.7):

$x(t)=e^{icdot omega cdot t} = underbrace{cos (omega cdot t)}_{Re}+ underbrace{i cdot sin(omega cdot t)}_{Im} mathbf{(2.4.6)} $

Рисунок 2.4.7 – Гармоничное воздействие действительна и менимая часть

Действительная часть «комплексного» воздействия (Re) – на самом деле косинусоидальное воздействие. Но так как частотные характеристики САУ определяются в режиме установившихся гармонических колебаний (т.е. при «очень-очень» больших значениях t), то не важно, по какому закону вводилось единичное гармоническое воздействие – по «синусу» или по «косинусу».

2.4.4. Линейное воздействие

Данный вид входного воздействия используется для оценки точности систем управления, а именно, для определения скоростных ошибок.

$x(t)= a cdot t mathbf{(2.4.7)}$

где t ≥ 0, а при t < 0 входное воздействие всегда равно нулю.

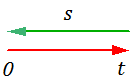
На рисунке 2.4.8 представлен график линейного входного воздействия

Рисунок 2.4.8 – Линейное входное воздействие

2.5. Основные положения и свойства интегральных преобразований Лапласа

Решение однородного обыкновенного дифференциального уравнения (ОДУ) усоб(t) записывается в виде (если нет повторяющихся корней):

$y_{соб.}(t) = sum_{j=0}^nc_je^{lambda_i}t$

т.е. все члены уравнения имеют одну и ту же форму. Этот результат наводит на мысль: «а нельзя ли ввести какое-то преобразование, в результате которого уравнение динамики (дифференциальное) можно привести к чисто алгебраическому, решение которого не представляет проблем.» А если затем сделать соответствующее обратное преобразование, то получим усоб (t), то есть получим цепочку:

Обыкновенное дифференциальное уравнение (ОДУ) $Rightarrow$ Алгебраическое уравнение $Rightarrow$ Решение $Rightarrow$ Обратное преобразование $Rightarrow$ Результат.

Именно такими соображениями руководствовался Лаплас, предлагая такое преобразование, называемое в настоящее время преобразованием Лапласа.

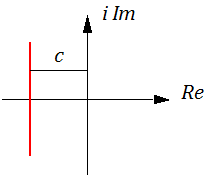
Предположим, что имеется нестационарный процесс f(t). Лаплас предложил ввести интегральное преобразование, которое отображает f(t) на комплексную плоскость согласно соотношению:

$F(s) = int_0^{infty}f(t) cdot e^{-st}dt mathbf{(2.5.1)}$

Рисунок 2.5.1

где s = c+i⋅ω: ω ∈ ] -∞; +∞ [; с – абсцисса абсолютной сходимости
(обычно в курсе «УТС» с = 0); f(t) – прообраз (оригинал); F(s) – изображение (образ);

Символическое обозначение преобразования Лапласа:

$f(t) Longrightarrow F(s) mathbf{(2.5.2)}$

Преобразование Лапласа существует, если при t<0 f(t ) = 0 и выполняется условия сходимости:

$int_0^infty mid f(t) mid cdot e^{-ct} dt < infty mathbf{(2.5.3)}$

В соответствии с соотношением (2.5.1) переходной процесс f(t) отображается на комплексную плоскость, где каждому значению оператора Лапласа «s» соответствует свой вектор. Линия, соединяющая концы векторов называется годографом.

Обратное преобразование Лапласа определяется следующим соотношением:

$f(t) = lim_{omega to infty} frac{1}{2pi cdot i} int_{c-icdot omega}^{c+i cdotomega} F(s) cdot e^{st}ds mathbf{(2.5.4)}$

Необходимо подчеркнуть, что если условие сходимости выполняется, то любому оригиналу соответствует изображение. Обратное преобразование Лапласа не всегда существует, т.е. если известно F(s), это не означает, что ему соответствует оригинал f(t)!

Прямое преобразование Лапласа символически обозначается:

$f(t) longrightarrow F(s) или L[f(t)] equiv F(s) mathbf{(2.5.5)}$

Обратное преобразование Лапласа обозначается:

$F(s) longrightarrow f(t) или L^{-1}[F(s)] equiv f(t) mathbf{(2.5.6)}$

Существует двухстороннее преобразование Лапласа $L_B [f(t)]$, частным случаем которого является обычное преобразование Лапласа

$L_B[f(t)] = int_{-infty}^{+infty}f(t) cdot e^{- s t} dt mathbf{(2.5.7)}$

Если при t ≤ 0 функция f(t) = 0, то $L_B [f(t)] ≡ L[f(t)]$

Частным случаем двухстороннего преобразования Лапласа (при с = 0, т.е. s = i⋅ω) является преобразование Фурье, определяемое соотношениями:

$Psi(i cdot omega) equiv L_B[f(t)]_{s=i cdot omega} = int_{ - infty}^{+infty}f(t) cdot e^{-i cdot omega cdot t} dt f(t) = frac{1}{2 pi}int_{ - infty}^{+infty}Psi(i cdot omega) cdot e^{-i cdot omega cdot t} d omega mathbf{(2.5.8)}$

2.5.1. Использование преобразования Лапласа для операции дифференцирования

Пусть известно $f(t)$ и его изображение по Лапласу: $f(t) longrightarrow F(s), $ выведем выражение для $ L[f(t)’ ]$.

Воспользуемся соотношением (2.5.1): $F(s) = int_0^{infty}f(t) cdot e^{-st}dt$, тогда получаем:

$L[f'(t)] = int_0^{infty}[f(t)'] cdot e^{-st}dtRightarrow left { begin{array} по частям u = e^{-st}; Rightarrow du = -s cdot e^{-st} ; d nu = f'(t)dt; Rightarrow nu = f(t). end{array} right. Rightarrow u cdot v mid_0^{infty}-int_0^{infty} v cdot dv Rightarrow$

$Rightarrow f(t) cdot e^{-st} mid_0^{infty}+ int_0^{infty}f(t)s cdot e^{-st} dt=[f(infty) cdot underbrace{e^{-scdot infty}}_{0}-f(0) cdot e^0]+s underbrace{int_0^{infty}f(t) cdot e^{-st}}_{F(s)}=$

$=s cdot F(s) - f(0) Rightarrow L[f'(t)] = s cdot F(s) - f(0), mathbf{(2.5.9)}$

где: $f(0) $ — начальное условия.
Если начальные условия равны нулю, то $f(0)=0$;

$L[f'(t)] = s cdot F(s); mathbf{(2.5.9.a)}$

Аналогичным способом найдем изображение 2-ой производной:

$L[f''(t)] = int_0^{infty}[f''(t)] cdot e^{-st}dtRightarrow left { begin{array} cu = e^{-st}; Rightarrow du = -s cdot e^{-st} ; d nu = f''(t)dt; Rightarrow nu = f'(t). end{array} right. Rightarrow Rightarrow f'(t) cdot e^{-st} mid_0^{infty}+s cdot underbrace{int_0^{infty} f'(t) cdot e^{-st} dt}_{L[f'(t)]} = -f'(0)+s cdot F[f'(t)] Rightarrow$

$ L[f''(t)] = s^2 cdot F(s) -s cdot f(0) - f'(0), mathbf{(2.5.10)}$

Если при $t=0, f(t) и f'(0)$ равны нулю (нулевые начальные условия), то:

$L[f''(t)] = s^2 cdot F(s) mathbf{(2.5.10.a)}$

Обобщая на производную n-го порядка при нулевых начальных условиях, имеем:

$L[f^{(n)}(t)] = s^n cdot F(s) mathbf{(2.5.11)}$

2.5.2. Использование преобразования Лапласа для операции интегрирования

Пусть известно $f(t)$ и его изображение по Лапласу: $f(t) longrightarrow F(s), $ выведем выражение для $ L[int f(t) ]$.

$L[int f(t)dt] = int_0^{infty}[f(t)dt] cdot e^{-st}dt Rrightarrow left { begin{array} e^{-st}dt = dv; Rightarrow v = - frac{1}{s}e^{-st}; int f(t)dt = u; Rightarrow du =f(t)dt; end{array} right. Rightarrow$

$[-1 frac{1}{s}e^{-st} cdot int f(t) dt] mid_0^{infty} + frac{1}{s} underbrace{int_0^{infty}f(t) cdot e^{-st} dt}_{F(s)} = frac {1}{s}F(s)+frac {1}{s}[int f(t) dt ] mid_0$

Окончательно:

$L[int f(t)dt] =frac {1}{s}F(s)+underbrace{frac {1}{s}[int f(t) dt ] mid_0}_{добавка н.у} mathbf{(2.5.12)}$

Если начальные условия равные нулю, то:

$L[underbrace{ intintint}_{n-раз} f(t)dt] =frac {1}{s^n}F(s) mathbf{(2.5.13)}$

Таким образом, операция интегрирования в оригинале функции приводит появлению в её изображении “добавке”, равной 1/s.

2.6. Основные свойства преобразований Лапласа

2.6.1. Свойство линейности

Пусть есть процессы описываемые функциями $f_1(t)$ и $f_2(t)$, каждый из которых имеет свое изображение по Лапласу: $f_1(t) longrightarrow F_1(s); f_2(t) longrightarrow F_2(s);$. Если $f(t) = f_1(t) pm f_2(t) $ то:

$L[f(t)]=L[f_1(t) pm f_2(t)] = F_1(s) pm F_2(s) mathbf{(2.6.1)}$

Если $f(t)= a cdot f_1(t)$, то:

$L[f(t)] = L[a cdot f_1(t)] = a cdot L[f_1(t)]= a cdot F_1(s) mathbf{(2.6.2)}$

2.6.2. Свойство подобия (свойство изменения масштаба)

Пусть $f(t) longrightarrow F(s)$ — известно, необходимо найти $L[f(a cdot t)]$

$L[f(a cdot t)] = frac{1}{a} int_0^{infty} f(a cdot t) cdot e^{-st cdot frac{a}{a}}d(at) = frac{1}{a} int_0^{infty} f(a cdot t) cdot e^{-frac{s}{a} cdot at}d(at) Rightarrow$

$L[f(at)]= frac{1}{a} F(frac{s}{a}) mathbf{(2.6.3)}$

2.6.3. Свойство запаздывания (теорема запаздывания)

Пусть $f(t) longrightarrow F(s)$ — известно, необходимо найти $L[f(t - tau )]$

Рисунок 2.6.1 – Иллюстрация переходного процесса с запаздыванием

$L[f(t - tau)] = int_0^ infty f(t -tau)e^{-s[t- tau+ tau]}d(t- tau) = e^{-s cdot tau} underbrace{int_0^infty f(t -tau)e^{-s[t- tau]}d(t- tau)}_{F(s)} $

$L[f(t pm tau)] = F(s) cdot e^{pm scdot tau} mathbf{(2.6.4)}$

2.6.4. Свойство смещения в комплексной плоскости

$L[f(t) cdot e^{pm s_0 cdot t}]= F(s pm s_0) mathbf{(2.6.5)} $

2.6.5. Первая предельная теорема

Если $f(t) longrightarrow F(s)$ — известно, а так же существует $lim_{s to infty}f(t)$, то:

$ lim_{t to infty}f(t) = lim_{s to 0}s cdot F(s) mathbf{(2.6.6)} $

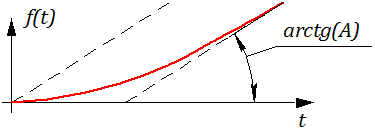
Рисунок 2.6.2 – Иллюстрация первой предельной теоремы

Это означает, что оси «t» и «s» формально направлены в противоположные стороны, т.е. чем больше t, тем меньше s и наоборот.

2.6.6.Вторая предельная теорема

$lim_{t to 0}f(t)= lim_{s to infty}s cdot F(s) mathbf{(2.6.7)}$

2.7. Способы нахождения обратных преобразований Лапласа по известному изображению

Вычисление оригиналов по известному (данному) изображению можно выполнить:
— по соответствующим таблицам преобразований Лапласа;
— по формулам Хэвисайда;
— разложением на элементарные дроби;
— другими способами.

В математических справочниках приводятся обширные таблицы, по которым можно найти оригиналы большинства изображений. Приведем основыные преобразования:

Таблица основных преобразований Лапласа

Однако, нередко бывают и случаи, когда необходимое преобразование отсутствует в таблицах. В этом случае используются различные специальные способы.

Например, если изображение F(s) можно представить в виде отношения полиномов по степеням «s», то наиболее общим и эффективным способом поиска оригинала является формула Хэвисайда.

Если $F(s) = frac{D_1(s)}{D_0(s)}$, где $D_1(s)$ и $D_0(s)$ – полиномы по степеням «s», то:

$ f(t)=sum_{j=1} frac{1}{(k_j-1)!} cdot lim_{s to s_j} frac{d^{k_j-1}}{ds^{k_j-1}}[(s-s_j)^{k_j} cdot F(s) cdot e^{st}], mathbf{(2.7.1)}$

где $s_j$ – полюса изображения, т.е. те значения «s» при которых полином $D_0(s)$ обращается в ноль;
$k_j$ – кратность j – го полюса.

Если уравнение $D_0(s)=0$ имеет n различных корней, то это означает что полюса F(s) имеют кратность, равную единице, т.е. нет повторяющихся полюсов.

Необходимо отметить, что использование формулы (2.7.1) будет корректно только в том случае, когда степень полинома $D_0(s)$ выше степени полинома $D_1(s)$. Если степени равны, то необходимо выделить целую часть (разделив «в столбик» полиномы) и чисто дробную часть, после чего для чисто дробной части корректна формула (2.7.1).

2.8 Некоторые способы нахождения оригинала по известному изображению

В качестве иллюстрации возможностей формулы Хэвисайда рассмотрим следующий пример:

Пример 1. Предположим, что изображение F(s) некоторого неизвестного процесса f(t) равно:

$F(s) = frac{A}{S^2(T cdot S+1)}; F(s) to f(t)=?$

$D_1(s) = A; D_0(s) = s^2(Ts+1)$

Найдем полюса:

$D_0(s) = s^2(Ts+1) Rightarrow S_1 =-frac{1}{T}; S_2=S_3=0; $

$ f(t) = S_1+S_2 для j=1; S_1=- frac{1}{T} Rightarrow lim_{s to -frac{1}{T}}[(s+frac{1}{T})cdot frac{A}{S^2(T cdot S+1)} cdot e^{st}] Rightarrow frac{1}{T}cdot frac{A}{frac{1}{T^2}} cdot e^{-frac{t}{T}}=A cdot T cdot e^{-frac{t}{T}}; для j =2,3 frac{1}{(2-1)!}lim_{s to 0} frac{d}{ds}[(s-0)^2 cdot frac{A}{S^2(T cdot S+1)} cdot e^{st}] = lim_{s to 0}[-frac{A}{(TS+1)^2} cdot T cdot e^{st}+t cdot e^{st} frac{A}{TS+1}] = =[-AT +At] Rightarrow f(t) =A cdot T cdot e^{-frac{t}{T}} - A cdot T+A cdot t = A[t - T(1 -e^{-frac{t}{T}})]; $

Рисунок 2.8.1 – График процесса построенный по изображению: $F(s) = frac{A}{S^2(T cdot S+1)}$.

Разложение на элементарные дроби.

$f(t) = ? F(s) = frac{D_1(s)}{D_0(s)}$

Если корни уравнение уравнения $D_0(s) = 0$ различны, т.е. нет совпадающих, то:

$F(s) = frac{D_1(s)}{D_0(s)}=frac{a_1}{s -s_1}+frac{a_2}{s -s_2}+ ..+frac{a_k}{s -s_k} +R(s)$

где $S_i$ — корни уравнения; $R(s)$ — остаточный член (не разлагается на действительные дроби);

$s_1,s_2,...,s_k in R s_{k+1},s_{k+2},...,s_n in C$

Используя свойства линейности преобразований Лапласа, мы можем представить $f(t) $ как сумму преобразований:

$f(t) = f_1(t)+f_2(t)+...+f_k(t)+f_{ост}(t)$

Пример 2

Имеем известное изображение:

$F(s)=frac{s+3}{s^2+3s+2}$

$f(t)$ — оригинал, при нулевых начальных условиях: $t =0, f(0)=0.$

Разложение на элементарные дроби:

$left | begin{gathered} s_1 = -1; s_2 = -2; end{gathered} right. Rightarrow F(s)=frac{a_1}{s+1}+frac{a_2}{s+2}.$

Используя метод неопределенных коэффициентов, приведем полученное выражение к общему знаменателю:

$a_1(s+2)+a_2(s+1) = s+3 left { begin{gathered} a_1+a_2 =1 2 cdot a_1+a_2 = 3 end{gathered} right. Rightarrow left { begin{gathered} a_1 =2 a_2 = -1 end{gathered} right. $

Тогда изображение разложенное на элементарные дроби принимает такой вид, что его решение можно получить из таблиц:

$F(s) = frac{2}{s+1} - frac{1}{s+2} и L^{-1} left[frac{2}{s+1}right] = 2 cdot L^{-1} left[frac{1}{s+1}right] = 2 cdot e^{-t} cdot 1(t) L^{-1} left[frac{1}{s+2}right] = e^{-2t} cdot 1(t) f(t) = f_1+f_2 =(2 cdot e^{-t} -e^{-2t})cdot 1(t) $

Рисунок 2.8.2 – График процесса построенный по изображению:$F(s)=frac{s+3}{s^2+3s+2}$.

Продолжение лекций: 2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

В заключение несколько полезных ссылок теме описанной в этой лекции:

  • Нижегородский государственный университет им. Н.И. Лобачевского. Учебно-методическое пособие ПРЕОБРАЗОВАНИЕ ЛАПЛАСА — www.lib.unn.ru/students/src/Laplace%20transform.pdf
  • Калькулятор Интегралов — www.integral-calculator.ru
  • СФУ Институт Космических и Информационых технологий Лекция ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ (МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД) — ikit.edu.sfu-kras.ru/files/3/L_10.pdf
  • Понятие полюсов и нулей в передаточных функциях — radioprog.ru/post/765
Источник

Расчеты скоростной ошибки εСт регулирования

Входной сигнал x(t)=Vtи изображением его является.
В соответствии с (1.56) скоростную ошибкуεСКследует вычислять по
формуле

(1.58)

1). Пусть в (1.58) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
скоростная ошибкаεСКбудет равна

В статической САУ скоростная ошибка
εСКбесконечно большая
и, поэтому, такая САУ неработоспособна.

2). Пусть в (1.58) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда скоростная ошибкаεСКбудет равна

В астатической САУ 1-го порядка имеется
скоростная ошибка εСК,
которую можно только уменьшить путем
увеличения общего коэффициента усиленияКразомкнутой САУ, но обратить в
ноль ее нельзя.

3). Пусть в (1.58) значение порядка νастатизма САУ равно 2:ν=2. Такая САУ
называется астатической 2-го порядка.
Тогда скоростная ошибкаεСКбудет равна

В астатической САУ 2-го порядка скоростная
ошибка εСКравна нулю,
т.е САУ является абсолютно точной.

Выводы по расчетам статической и скоростной ошибок регулирования:

1. Ошибки регулирования могут быть
уменьшены путем увеличения общего
коэффициента усиления Ки порядка
астатизмаνразомкнутой САУ.

2. При увеличении Кошибки регулирования
только уменьшаются. но не обращаются в
ноль.

3. При увеличении νСАУ становится
абсолютно точной – ошибка регулирования
становится нулевой.

3.6. Типовые регуляторы. Влияние п-, и- и д-регуляторов на прямые показатели качества сау: устойчивость, ошибки регулирования, колебательность, перерегулирование и быстродействие.

Для обеспечения при работе САУ заданных
показателей качества в ее структуру
вводят корректирующие устройства и
регуляторы. Корректирующие устройства
имеют передаточную функцию произвольного
вида. Регуляторами называются устройства,
передаточная функция которых имеет
стандартный вид.

Существуют три базовых простейших
регулятора – пропорциональный (П),
интегральный (И) и дифференциальный
(Д):

– П-регулятор имеет передаточную функцию
;

– И-регулятор имеет передаточную
функцию ;

– Д-регулятор имеет передаточную
функцию .

Из трех простейших можно получить еще
четыре составных регулятора:

– ПИ-регулятор с передаточной функцией ;

– ПД-регулятор с передаточной функцией ;

– ИД-регулятор с передаточной функцией ;

– ПИД-регулятор с передаточной функцией .

На практике широко применяются регуляторы
ПИ- и ПИД-типов. Регуляторы ПД- и ИД-типов
применяются редко из-за их низкой
помехоустойчивости (см. тему 1.17).

Простейшие
регуляторы обеспечивают улучшение
только некоторых показателей качества
САУ, а составные обеспечивают улучшение
работы САУ по комплексу показателей
качества. В практике проектирования
САУ и их эксплуатации крайне важно
понимание того, какие показатели качества
улучшает каждый из простейших регуляторов.

Будем рассматривать структурную схему
САУ, в которой регулятор и объект
управления включены последовательно
(рис.1.48а). Все характеристики САУ с
регулятором будем помечать индексом
СР, а без регулятора (рис.1.48б) –
индексомБР.

Из построений вытекают следующие
изменения косвенных показателей качества
ωсриγ:

– частота среза ωсрувеличится;

– запас по фазе γуменьшится.

Прямые
показатели качестваσ,t1иtППв
соответствии с соотношениями (1.59)
изменятся следующим образом:

– перерегулирование σувеличится,
возможна даже потеря устойчивости;

– быстродействие САУ по моменту t1первой установки возрастет;

– об изменении tППничего определенного сказать нельзя,
так какtППуменьшается при увеличенииωсри увеличивается при уменьшенииγ.

Качественные изменения графика
переходного процесса отображены на
рис.1.50.

При использовании П-регулятора порядок
астатизма САУ не изменяется, поэтому
ни одна из существующих ненулевых ошибок
регулирования не обратится в ноль, а
может быть только уменьшена за счет
того, что коэффициент передачи kПрегулятора будет взят большим единицы.

д). Эксплуатационные качества П-регулятора
являются наилучшими из всех простейших
регуляторов, так как П-регулятор не
обладает повышенной чувствительностью
к помехам (не ухудшает соотношение
“сигнал-помеха” для проходящего
через него сигнала), а его выходной
сигнал не подвержен дрейфу.

Выводы по применению П-регулятора
в САУ

Достоинства П-регулятора:

1. Повышает быстродействие САУ, оцениваемое
временем первой установки.

2. Эксплуатационные качества являются
наилучшими и, поэтому, в любом стандартном
регуляторе содержится П-часть.

Недостатки П-регулятора:

1. Увеличивает перерегулирование САУ.

2. Не обращает в ноль ни одну из ошибок
регулирования исходной САУ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Макеты страниц

§ 19.1. Статические и скоростные ошибки автоколебательных систем

В предыдущих главах исследовались симметричные автоколебания как результат свободного движения системы (т. е. без внешнего воздействия) при симметричных нелинейностях. Однако, как будет показано, важное практическое значение имеет также рассмотрение несимметричных автоколебаний.

Несимметрия автоколебаний может вызываться различными причинами;

1) несимметричностью нелинейной характеристики как при наличии, так и при отсутствии внешних воздействий;

2) наличием постоянного или медленно меняющегося внешнего воздействия при симметричных нелинейностях;

3) наличием постоянной или медленно меняющейся скорости изменения внешнего воздействия при симметричных нелинейностях (для тех случаев, когда постоянное воздействие не вызывает смещения центра колебаний; обычно это имеет место в следящих системах и вообще в астатических системах).

В самом деле, если имеется несимметричная нелинейная характеристика (например, рис. 19.1, а, б), то даже при симметричных колебаниях переменной возникают несимметричные по амплитуде колебания переменной (рис. 19.1, б).

Рис. 19.1.

Если же нелинейность симметрична (например, рис. 19.2, а, б), то при наличии постоянного внешнего воздействия (или в астатических системах при наличии постоянной скорости изменения внешнего

воздействия) смещается центр колебаний переменной вследствие чего колебания переменной становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, б).

Рис. 19.2.

Пусть задана автоматическая система, динамика которой описывается уравнением

В данном параграфе будем считать для статических систем или же для астатических систем. Астатической системой называется такая, в которой многочлен имеет общий множитель , т. е. .

Поэтому запишем уравнение (19.1) в виде

где соответственно

При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме

причем а, являются неизвестными постоянными.

С учетом величины смещения первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде

где при обозначении

Отсюда видно, что в общем случае все три коэффициента являются функциями трех неизвестных:

В частных случаях эти зависимости могут быть более простыми.

Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает

Это уравнение разбивается на два:

При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается нелинейная взаимосвязь обоих уравнений через соотношения (19.7).

Можно предложить два метода решения задачи.

Первый метод состоит в следующем. Уравнение (19.9) совпадает с прежним уравнением (18.33); отличие состоит лишь в том, что теперь коэффициенты q и согласно (19.7) зависят не только от а и , но и от смещения Поэтому, написав как прежде, характеристическое уравнение

заменив на ивыделив вещественную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:

Эти уравнения дают возможность определить амплитуду и частоту автоколебаний как функции постоянной составляющей

Для решения этой задачи можно применять любой из способов, описанных в § 18.2, в зависимости от того, какой из них лучше подходит к условиям заданной конкретной задачи. Таким же способом можно определить зависимость а и не только от но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики и , то здесь их необходимо строить в виде серии кривых при разных постоянных значениях (рис. 19.3).

После того как из уравнений (19.11) определены зависимости (19.12), можно, воспользовавшись первым из выражений (19.7), найти функцию смещения

Подставив ее в (19.8), получим алгебраическое уравнение

с одной неизвестной которая отсюда и определяется. Чаще всего это уравнение относительно является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда и частота

Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины смещения центра колебаний, характерную именно для нелинейных систем (в линейных системах смещение центра колебаний не играет роли), надо всегда иметь в виду.

Рис. 19.3.

При одних нелинейностях она может быть весьма существенной, при других — менее существенной.

Второй метод решения той же задачи состоит, наоборот, в том, что сначала решается уравнение (19.8), где согласно (19.7) будет или часто . Решение получает вид

Это решение подставляется затем в уравнения (19.11), которые, таким образом, буду! содержать только две неизвестные: Определив последние (по любому из способов § 18.2), вычисляем потом по (19.15) и величину которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия

Величина и является искомой статической или скоростной ошибкои соответственно для статической и астатической систем.

В тех случаях, когда передаточная функция линейной части системы имеет нулевой корень в знаменателе (что часто бывает), т. е. когда вместо (19.14) получаем уравнение

откуда определяется статическое отклонение или скоростная ошибка

В случае, когда при отсутствии внешнего воздействия определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью или же для которой

вместо уравнения (19.8) получаем

Оно решается любым из тех же двух методов, описанных выше для уравнения (19.8). Одновременно согласно (19.11) определяются

Если в этом случае знаменатель передаточной функции линейной части системы имеет нулевой корень, то и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид

откуда определяется Это означает, что в указанных системах возникает такое смещение колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F (т. е. обеспечивается ), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.

Приведем пример исследования совместного влияния двух внешних воздействий, причем из дальнейшего будет видно, что, в отличие от линейных систем, здесь нельзя просто складывать статические ошибки от отдельно взятых в ействий.

Уравнения автоматической системы (рис. 19.5) заданы в виде

где — простейшая симметричная релейная характеристика, показанная на рис. 19.5:

Чтобы воспользоваться выведенными выше общими формулами, надо сначала привести заданную систему уравнений (19.20) — (19.22) к одному уравнению типа (19.1).

Рис. 19.4.

Рис. 19.5.

В результате получаем

Пусть является задающим воздействием, изменяющимся с постоянной скоростью:

которое требуется воспроизвести на выходе системы в виде Допустим также, что второе внешнее воздействие является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):

Его влияние требуется свести к минимуму. Найдем установившуюся ошибку на выходе системы. Правая часть уравнения (19.24) будет при этом постоянной, и установившееся решение для х с учетом автоколебаний следует искать

в виде

Гармоническая линеаризация нелинейности (19.23) при этом согласно (19.6) дает

В данной задаче согласно (19.24) уравнение (19.9) для периодических составляющих получит вид

а уравнение (19.8) для постоянных составляющих будет

где согласно (19 24)-(19.26)

Выше были указаны два метода решения задачи. Для иллюстрации обоих методов решим данную задачу каждым из них.

Согласно первому методу сначала решается уравнение (19.29) для определения зависимостей

Характеристическое уравнение здесь будет

и уравнения (19.11) поэтому примут вид

Исключая отсюда находим частоту автоколебаний

Частота в данной задаче оказалась не зависящей от смещения , а следовательно, и от величины внешнего воздействия. Затем, подставляя в первое из уравнений (19.33) выражение q из (19.28) и из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний от смещения

где величина

представляет собой амплитуду автоколебаний в данной системе при отсутствии смещения (при ). Отсюда

Полученное выражение мояшо записать также в виде

если обозначить

Результат (19.37) или (19.38) и представляет собой искомую зависимость

Далее, согласно первому методу решения задачи подставим полученное значение амплитуды из (19.38) в выражение (19.28) для откуда с использованием (19.39) найдем функцию смещения

где А определяется через параметры системы формулой (19.36).

Подставив величину (19.40) в уравнение (19.30) для постоянных составляющих, с учетом (19.31) и (19.36) получим

Сравнивая это с формулой (19.39), видим, что для искусственно введенной ранее величины а можно записать следующее выражение:

Эта величина характеризует совокупность приложенных к системе внешних воздействий. Учитывая это, из формулы (19.38) находим амплитуду автоколебаний

Существенно то, что амплитуда автоколебаний зависит не только от параметров системы (см. (19.36)), но еще и от величины внешних воздействий. Эта зависимость нелинейная. В данном случае при увеличении внешних воздействий амплитуда уменьшается по закону косинуса, в то время как частота не зависит от внешних воздействий.

Из формулы (19.43) видно, что автоколебания существуют до тех пор, пока величины внешних воздействий удовлетворяют условию

При этом амплитуда автоколебаний изменяется в пределах

Таков первый метод определения установившихся величин смещения амплитуды и частоты автоколебаний при наличии внешних воздействий.

Проиллюстрируем также и второй метод. Согласно второму методу сначала решается уравнение (19.30). По (19.30) и первой из формул (19.28) находим

или, с учетом (19.31),

Для отыскания входящей сюда амплитуды а воспользуемся уравнением (19.29). Характеристическое уравнение для него будет (19.32), и уравнения (19.11) поэтому примут вид:

где согласно (19.28) и (19.45)

Исключая из уравнений (19.46) величину находим частоту автоколебаний

Подставив найденные выражения q в первое из уравнений (19.46), найдем амплитуду автоколебаний

где величина

является амплитудой автоколебаний при отсутствии внешних воздействий (при

Подставив найденное выражение амплитуды (19.49) в формулу (19.45) получим окончательно величину смещения

Как видно, второй метод в данной задаче приводит к тем же самым результатам значительно более коротким путем, чем первый, что очень важно для практических расчетов (принципиально же оба метода эквивалентны друг другу). По-видимому, большая простота второго метода будет иметь место и в большинстве других задач.

В этом втором методе, в отличие от первого, функция смещения не определяется. Однако последняя может понадобиться в дальнейшем для других целей. Но ее тоже легко можно определить при использовании второго метода. Здесь величины и их отношение выражены через величины внешних воздействий. Функция же смещения не должна содержать ни величин внешних воздействий, ни амплитуды зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим

а подставив это в первую из формул (19.28), сразу получим искомую функцию смещения

где А выражается только через параметры системы согласно (19.50).

Важно отметить, что функция смещения не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи.

Итак, двумя разными методами определена величина смещения автоколебаний на входе реле. Найдем теперь установившуюся ошибку на выходе системы Поскольку на выходе должно воспроизводиться внешнее воздействие то согласно рис. 19.5 и второму уравнению (19.20) ошибка данной системы выражается величиной установившееся решение для которой, следовательно, и надо искать. Выразив переменную через х, которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем

Учитывая (19.25) и (19.27), перепишем данное уравнение в виде

В соответствии с видом правой части установившееся решение этого линейного уравнения следует искать в виде

где — постоянные, а — периодическая составляющая.

Подставив это в (19.54), получим три уравнения для отыскания указанных величин:

Второе из них дает

Тогда из (19.56) находим

где определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной

где определяется формулой (19.49) через внешнее воздействие, а — формулой (19.48).

Итак, в данной системе имеются все три составляющие ошибки (19.55), зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной из них является составляющая возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при кос согласно (19.59) будет Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи на гибкую . Тогда в уравнении (19.54) величина заменится на :

Как видим, составляющая, пропорциональная времени, в правой части уравнения исчезла, вследствие чего установившееся решение для ошибки х в отличие от (19.55), будет

При этом из (19.62) находимз

причем изменяются, конечно, и формулы для (их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний ошибки можно сделать весьма малой.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 1.1. Понятие о замкнутых автоматических системах
  • § 1.2. Классификация автоматических систем по характеру внутренних динамических процессов
  • § 1.3. Примеры непрерывных автоматических систем
  • § 1.4. Примеры дискретных и релейных автоматических систем
  • ГЛАВА 2. ПРОГРАММЫ И ЗАКОНЫ РЕГУЛИРОВАНИЯ. АДАПТИВНЫЕ СИСТЕМЫ
  • § 2.1. Программы регулирования
  • § 2.2. Линейные и нелинейные законы регулирования
  • § 2.3. Системы с переменной структурой
  • § 2.4. Системы с самонастройкой программы (экстремальные системы)
  • § 2.5. Системы с самонастройкой параметров (собственно самонастраивающиеся системы)
  • § 2.6. Системы с самонастройкой структуры (самоорганизующиеся системы)
  • РАЗДЕЛ II. ОБЫКНОВЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 3.1. Линеаризация уравнений
  • § 3.2. О записи линеаризованных уравнений звеньев
  • ГЛАВА 4. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
  • § 4.2. Временные характеристики
  • § 4.3. Частотная передаточная функция и частотные характеристики
  • § 4.4. Логарифмические частотные характеристики
  • § 4.5. Позиционные звенья
  • § 4.6. Интегрирующие звенья
  • § 4.7. Дифференцирующие звенья
  • § 4.8. Неустойчивые и неминимально-фазовые звенья
  • § 4.9. Звенья с модулированным сигналом
  • ГЛАВА 5. СОСТАВЛЕНИЕ ИСХОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 5.1. Общий метод составления исходных уравнений
  • § 5.2. Передаточные функции систем автоматического регулирования
  • § 5.3. Законы регулирования
  • § 5.4. Использование структурных схем и графов
  • § 5.5. Многомерные системы регулирования
  • § 5.6. Управляемость и наблюдаемость
  • § 5.7. Уравнения следящей системы
  • ГЛАВА 6. КРИТЕРИИ УСТОЙЧИВОСТИ
  • § 6.1. Понятие об устойчивости систем регулирования
  • § 6.2. Критерий устойчивости Гурвица
  • § 6.3. Критерий устойчивости Михайлова
  • § 6.4. Построение областей устойчивости. D-разбиение
  • § 6.5. Критерий устойчивости Найквиста
  • § 6.6. Определение устойчивости по логарифмическим частотным характеристикам
  • § 6.7. Устойчивость двумерных систем с антисимметричными связями
  • ГЛАВА 7. ПОСТРОЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 7.2. Непосредственное решение исходного дифференциального уравнения
  • § 7.3. Сведение неоднородного уравнения к однородному
  • § 7.4. Использование преобразований Фурье, Лапласа и Карсона—Хевиеайда
  • § 7.5. Использование вещественных частотных характеристик
  • § 7.6. Использование вычислительных машин
  • ГЛАВА 8. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
  • § 8.2. Точность в типовых режимах
  • § 8.3. Коэффициенты ошибок
  • § 8.4. Определение запаса устойчивости и быстродействия по переходной характеристике
  • § 8.5. Приближенная оценка вида переходного процесса по вещественной частотной характеристике
  • § 8.6. Корневые методы
  • § 8.7. Диаграмма Вышнеградского
  • § 8.8. Интегральные оценки
  • § 8.9. Частотные критерии качества
  • § 8.10. Чувствительность систем регулирования
  • ГЛАВА 9. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 9.2. Теория инвариантности и комбинированное управление
  • § 9.3. Неединичные обратные связи
  • ГЛАВА 10. УЛУЧШЕНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
  • § 10.2. Последовательные корректирующие звенья
  • § 10.3. Параллельные корректирующие звенья
  • § 10.4. Обратные связи
  • § 10.5. Методы повышения запаса устойчивости
  • § 10.6. Примеры
  • ГЛАВА 11. СЛУЧАЙНЫЕ ПРОЦЕССЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 11.2. Случайные процессы
  • § 11.3. Стационарные случайные процессы
  • § 11.4. Корреляционная функция
  • § 11.5. Спектральная плотность стационарных процессов
  • § 11.6. Канонические разложения случайных функций
  • § 11.7. Прохождение случайного сигнала через линейную систему
  • § 11.8. Расчет установившихся ошибок в автоматических системах
  • § 11.9. Расчеты по минимуму среднеквадратичной ошибки
  • ГЛАВА 12. МЕТОДЫ СИНТЕЗА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 12.2. Корневой метод
  • § 12.3. Метод корневых годографов
  • § 12.4. Метод стандартных переходных характеристик
  • § 12.5. Метод логарифмических амплитудных характеристик
  • § 12.6. Синтез систем автоматического регулирования на основе частотных критериев качества
  • § 12.7. Об оптимальном синтезе
  • § 12.8. Использование классических вариационных методов
  • § 12.9. Динамическое программирование
  • § 12.10. Аналитическое конструирование регуляторов
  • РАЗДЕЛ III. ОСОБЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • ГЛАВА 13. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
  • § 13.2. Нахождение функции веса и построение переходных процессов
  • § 13.3. Передаточные функции
  • § 13.4. Устойчивость и качество регулирования
  • § 13.5. О синтезе систем с переменными параметрами
  • ГЛАВА 14. СИСТЕМЫ С ЗАПАЗДЫВАНИЕМ И СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
  • § 14.1. Уравнения линейных систем с запаздыванием
  • § 14.2. Уравнения линейных систем с распределенными параметрами
  • § 14.3. Исследование устойчивости и качества регулирования
  • ГЛАВА 15. ИМПУЛЬСНЫЕ СИСТЕМЫ
  • § 15.2. Использование z-преобразования
  • § 15.3. Передаточные функции
  • § 15.4. Устойчивость и качество импульсных систем регулирования
  • § 15.5. Случайные процессы в импульсных системах
  • РАЗДЕЛ IV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • ГЛАВА 16. СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 16.2. Уравнения систем с нелинейностью релейного типа
  • § 16.3. Уравнения систем с нелинейностью в виде сухого трения и зазора
  • § 16.4. Уравнения систем с нелинейностями других видов
  • ГЛАВА 17. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
  • § 17.1. Фазовые траектории и метод точечных преобразований
  • § 17.2. Теоремы прямого метода Ляпунова и их применение
  • § 17.3. Определение автоколебаний релейных систем методом припасовывания
  • § 17.4. Частотный метод В. М. Попова
  • § 17.5. Исследование систем с переменной структурой
  • ГЛАВА 18. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
  • § 18.1. Гармоническая линеаризация нелинейностей
  • § 18.2. Алгебраические способы определения автоколебаний и устойчивости в нелинейных системах первого класса
  • § 18.3. Примеры исследования нелинейных систем первого класса
  • § 18.4. Нелинейные системы второго класса
  • § 18.5. Вычисление высших гармоник и уточнение первой гармоники автоколебаний
  • § 18.6, Частотный метод определения автоколебаний
  • ГЛАВА 19. МЕДЛЕННО МЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
  • § 19.1. Статические и скоростные ошибки автоколебательных систем
  • § 19.2. Прохождение медленно меняющихся сигналов в автоколебательных системах
  • § 19.3. Гармоническая линеаризация нелинейностей при несимметричных колебаниях
  • ГЛАВА 20. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
  • § 20.1. Приближенное исследование колебательных переходных процессов
  • § 20.2. Примеры исследования колебательных переходных процессов
  • § 20.3. Система с нелинейным корректирующим устройством
  • § 20.4. Применение логарифмических частотных характеристик для исследования нелинейных законов рзгулирования
  • ГЛАВА 21. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
  • § 21.1. Симметричные одночастотные вынужденные колебания
  • § 21.2. Несимметричные вынужденные колебания с медленно меняющейся составляющей
  • § 21.3. Зависимость устойчивости и качества нелинейных систем от внешних вибраций
  • ГЛАВА 22. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
  • § 22.1. Статистическая линеаризация нелинейностей
  • § 22.2. Простейшие случайные процессы в нелинейных системах
  • § 22.3. Пример исследования влияния случайных помех на динамику нелинейной системы
  • ГЛАВА 23. НЕЛИНЕЙНАЯ ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • § 23.2. Синтез оптимальной системы с использованием принципа максимума
  • § 23.3. Последовательная оптимизация на базе нелинейного программирования
  • РАЗДЕЛ V. ЦИФРОВЫЕ И АДАПТИВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
  • ГЛАВА 24. СИСТЕМЫ РЕГУЛИРОВАНИЯ С ЦИФРОВЫМИ ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
  • § 24.2. О синтезе систем регулирования с ЦВМ
  • § 24.3. Дискретная коррекция
  • § 24.4. Периодические режимы, обусловленные квантованием по уровню
  • ГЛАВА 25. АДАПТИВНЫЕ СИСТЕМЫ
  • § 25.1. Системы экстремального регулирования
  • § 25.2. Самонастраивающиеся системы
  • ПРИЛОЖЕНИЕ 1. ТАБЛИЦА ФУНКЦИЙ
  • ПРИЛОЖЕНИЕ 2. ТАБЛИЦА ИНТЕГРАЛОВ
  • ЛИТЕРАТУРА
Источник

Определение динамических ошибок (по
скорости, по ускорению) для статической и астатических систем.

Точность АС
характеризуется величиной ошибки в установившемся режиме и зависит от характера
воздействия, а также структуры и параметров системы.

Реальные воздействия
в радиотехнических следящих системах описывается сложными (случайными)
функциями времени. Однако при анализе точности управления часто используют
простые детерминированные воздействия: постоянное ступенчатое, линейное,
квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить
в модели задающего воздействия наиболее существенные признаки (начальное
значение, скорость изменения, ускорение). Большинство систем радиоавтоматики
описываются передаточными функциями вида

,                                                 (11.1)

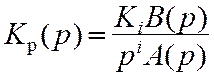
где Ki – общее усиление
разомкнутой системы, i – число интегрирующих
звеньев, определяющее порядок астатизма системы;

– полиномы, порядок которых определяется числом типовых
звеньев (n и m соответственно инерционных и форсирующих), а
коэффициенты полиномов – постоянными времени типовых звеньев.

11.1. Статические ошибки

Ошибка системы при постоянном
(ступенчатом) воздействии x(t)=x0=const при t³0
называется статическойeст.

Для установившейся
ошибки, учитывая, что изображение X(p)=x0/p,
запишем:

.  (11.2)

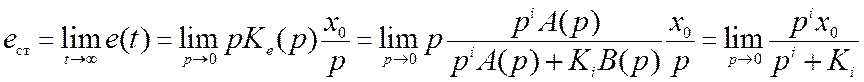
Для статической
системы (не содержащей интегрирующих звеньев) статическая ошибка равна

.                                                                      (11.3)

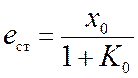
Таким образом, в
статических системах установившееся значение управляемой переменной не равно
заданному: меньше на величину ошибки, значение которой обратно пропорционально
усилению К0 по постоянному току (обычно К0>>1).

Для астатических
систем (i ³ 1) ошибка при постоянном воздействии

,

так как числитель в (11.2) равен нулю, а знаменатель равен
Кi.

Отсутствие
статической ошибки обусловило название таких систем – астатические.

11.2. Динамические ошибки

Ошибка,
характеризующая точность замкнутой системы при меняющемся воздействии,
называется динамической eд(t).

Любое детерминированное
воздействие (при условии существования его производных d(k)/dt(k),
k=1, 2, …) можно представить в виде ряда

,                                  (11.4)

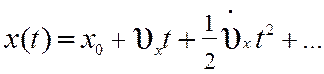
где x0 – начальное значение,  – скорость изменения, – ускорение и т. д.

Для вычисления
динамических ошибок при типовых воздействиях (линейном и квадратическом)
представим выражение для ошибки в операторной форме:

                                   (11.5)

Используя разложение
передаточной функции Ke(p) в ряд Маклорена по степеням
переменной р, перепишем (11.5) в виде

                           (11.6)

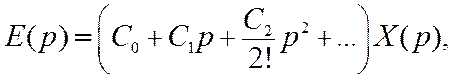
где C0, C1, C2,
… – коэффициенты ошибок, определяемые
как

                                        (11.7)

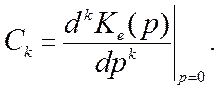
Установившееся
значение ошибки при произвольном воздействии x(t)
на основании (11.6) определяется временным рядом

                                       (11.8)

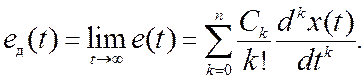
Чем меньше
коэффициенты ошибок, тем выше точность системы при произвольном
детерминированном воздействии. При вычислении коэффициентов Ck
обычно ограничиваются только первыми тремя (для систем с астатизмом не выше
второго порядка).

Коэффициент C0
в соответствии с (11.7) равен

.

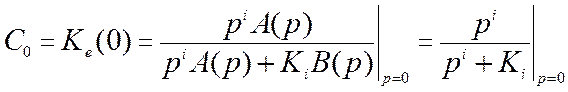
Для статических
систем (i=0) C0=1/(1+K0), а для
астатических систем C0=0.

Определим динамические
ошибки типовых систем при линейном воздействии (изменение с постоянной
скоростью) x(t)=nxt.

В соответствии с
формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как

.

Для статической
системы она равна

так как вклад составляющей C1nx
значительно меньше, чем C0 x(t), которая растет
линейно со временем. Таким образом, скоростная ошибка в статических системах
накапливается со временем со скоростью nx/(1+K0), что делает неприемлемым использование
таких систем при меняющемся воздействии. Для астатических систем C0=0 и скоростная ошибка

.

Нахождение
коэффициента ошибки C1 с использованием формулы (11.7)
затруднительно. Более простой способ его вычисления основан на сравнении
точного выражения для передаточной функции Ke(p) и
аппроксимирующего ее ряда:

                (11.9)

Уравнение (11.9)
можно представить в виде

              (11.10)

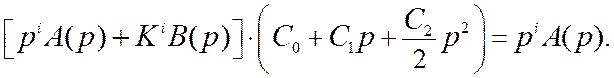
Полагая i= 1 (астатическая система первого порядка) и приравнивая
коэффициенты при переменной p в левой и правой частях уравнения, находим

или C1=1/K1, так как C0=0.

Таким образом,
скоростная ошибка системы первого порядка астатизма eд=nx/K1
определяется усилением разомкнутой системы K1 и не зависит от
времени. Параметр K1, имеющий размерность c –1,
называется добротностью системы по скорости (чем выше добротность, тем
точнее система).

Для астатической
системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C0=C1=0.
Равенство C1=0 вытекает из уравнения (11.10), так как в
правой части уравнения не содержится слагаемого, в которое входит переменная p
(есть только с p2 и выше).

Оценим динамические
ошибки типовых систем при квадратичном воздействии (изменение с постоянным
ускорением).

В соответствии с (11.8)
для динамической ошибки (ошибки по ускорению) запишем

.                                        (11.11)

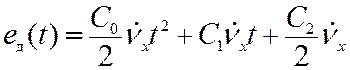
Для статической
системы ошибка по ускорению равна

                                    (11.12)

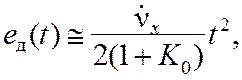
так как составляющие ошибки с коэффициентами C1 и C2
вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по
квадратичному закону исключает применение статических систем при наличии
ускорения.

Для системы первого
порядка астатизма ошибка по ускорению равна

                                      (11.13)

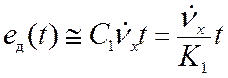
(вкладом составляющей  можно
пренебречь). Накопление ошибки со временем (со скоростью ) не позволяет применять такие
системы при наличии ускорения. Для астатической системы второго порядка ошибка
по ускорению равна

.                                      (11.14)

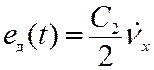
Определение
коэффициента ошибки C2 с использованием уравнения (11.7)
сводится к приравниванию коэффициентов при p2 в обеих частях
уравнения:

.                           (11.15)

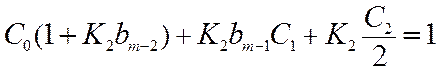
Откуда
C2/2=1/K2, так как C0=C1=0.

Источник

Скоростная ошибка

Cтраница 1

Скоростная ошибка в контуре самонастройки обратно пропорциональна квадрату произведения коэффициента усиления регулятора ( без множительного звена) на коэффициент усиления объекта.
 [1]

Скоростная ошибка, или первый член формулы ( 10 – 336), не изменилась и после введения форсировки. Это свойство сохраняется для первых членов рядов ошибок у всех астатических систем.
 [2]

Скоростная ошибка импульсной следящей САУ может быть получена, если задать входной сигнал в виде равномерно нарастающей решетчатой функции.
 [3]

Скоростная ошибка возникает при двигателях как постоянного, так и переменного тока. Она увеличивается с возрастанием скорости заводки Q и уменьшается при увеличении коэффициента усиления системы.
 [4]

Скоростная ошибка системы при этом уменьшается во столько же раз.
 [5]

Скоростные ошибки разомкнутого контура в этих схемах больше, так как в него входят или все ( рис. 2 6), или некоторые ( рис. 2 а) постоянные времени системы, охваченные относительно разомкнутого контура лишь местными обратными связями. Ниже при рассмотрении способа снижения частоты вычисления в цифровых САР будет показано, что применение этого варианта системы мало эффективно.
 [7]

Если скоростная ошибка мало отличается от общей ошибки установившегося режима, то добротность может быть численно приблизительно равна коэффициенту усиления К.
 [8]

Для устранения скоростной ошибки в схему дальномера может быть введено второе интегрирующее звено. Дальномер с двойным интегратором является системой регулирования с астатизмом второго порядка. В установившемся режиме при постоянной скорости изменения входного сигнала ошибка в такой системе равна нулю.
 [9]

Упругое звено на скоростную ошибку в данном случае влияния не оказывает. Однако могут быть случаи, когда это влияние имеет место.
 [10]

Упругое звено на скоростную ошибку в данном случае влияния не оказывает. Однако могут быть случаи, когда это влияние имеет место.
 [11]

Параметр ai компенсирует скоростную ошибку системы.
 [12]

Это значит, что скоростная ошибка обеих систем одинакова независимо от интервала дискретности.
 [13]

Примеры показывают, что установившиеся скоростные ошибки могут достигать значительных величин. Они могут быть сведены к нулю повышением порядка астатизма контуров настройки параметров до второго.
 [14]

Страницы:  

   1

   2

   3

   4

Источник

Добавить комментарий