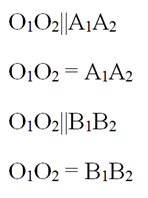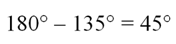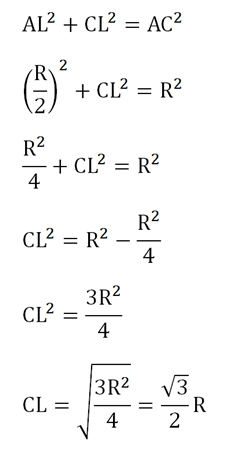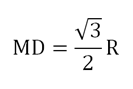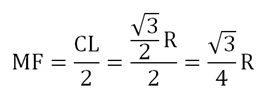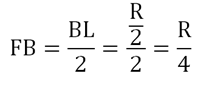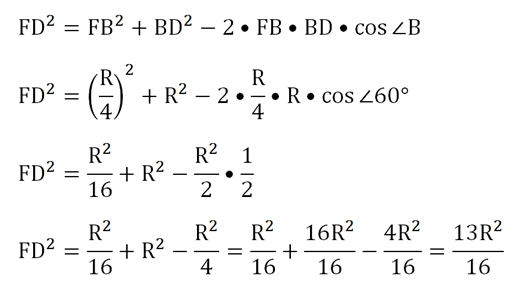Как найти скрещивающиеся прямые в параллелограмме - Сайт, где вы сможете решить свои вопросы

План урока:

Понятие скрещивающихся прямых

Сонаправленные лучи

Угол между прямыми

Задачи на скрещивающиеся прямые

Понятие скрещивающихся прямых

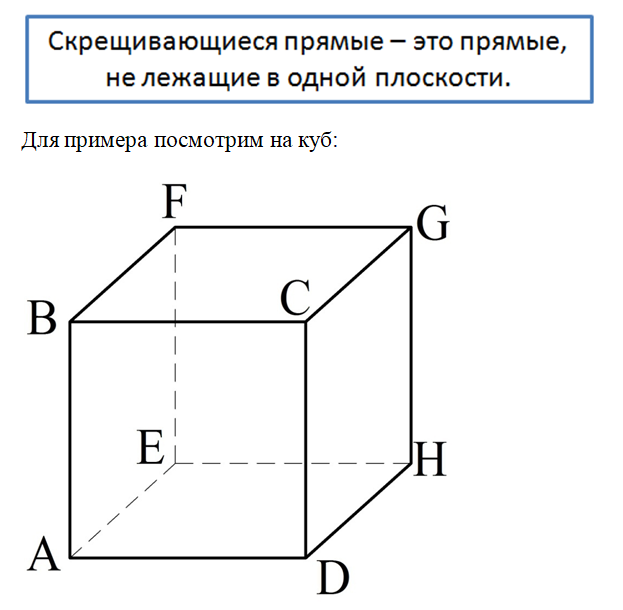
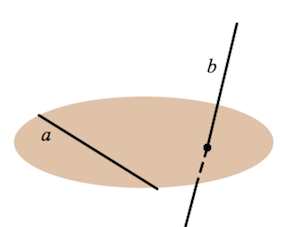
В пространстве можно построить две прямые так, что они не будут пересекаться, но и параллельными они также являться не будут. Для этого достаточно, чтобы прямые НЕ находились в одной плоскости. В этом случае их именуют скрещивающимися прямыми.

Здесь ребра ВС и АЕ как раз лежат на двух скрещивающихся прямых. Поэтому их можно так и называют – скрещивающиеся отрезки. По аналогии можно ввести понятие и скрещивающихся лучей.

Существует теорема, представляющая собой признак скрещивающихся прямых.

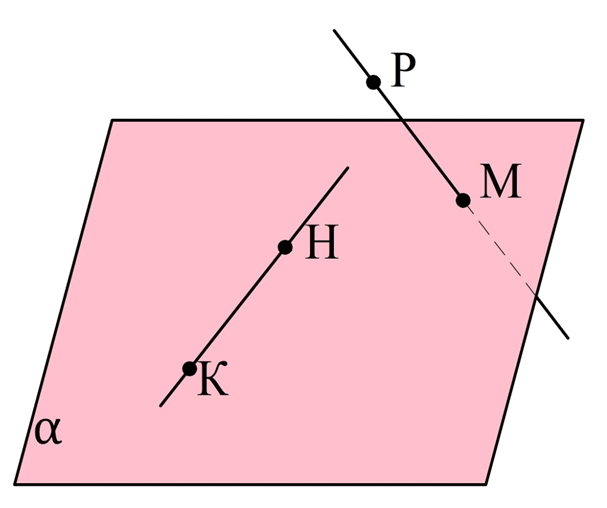
Действительно, пусть есть две прямые, НК и РМ. Обозначим как α плос-ть, проходящую через НК и точку М. Если РМ пересекает α, то это означает, что М – единственная общая точка у α и РМ. Получается, что Н, К, М и Р – это точки в различных плос-тях, и через них нельзя провести одну плос-ть. Значит, и прямые НК и РМ – скрещивающиеся.

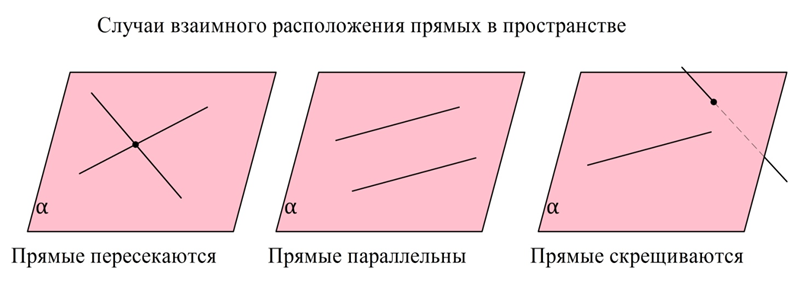
Таким образом, в стереометрии возможно всего три случая взаимного расположения двух прямых в пространстве:

1) прямые пересекаются, и тогда они обязательно находятся в одной плос-ти;

2) прямые располагаются в одной плос-ти, но не пересекаются – случай параллельных прямых;

3) прямые находятся в разных плос-тях – случай скрещивающихся прямых.

Докажем одну теорему:

Для доказательства возьмем произвольные скрещивающиеся прямые m и n. Отметим на n точку К и проведем через К прямую р, параллельную m:

Через пересекающиеся прямые nи p можно провести единственную плос-тьα. По признаку параллельности прямой и плос-ти можно заключить, что m||α.

Покажем, что кроме α нет других плос-тей, проходящих через n и параллельных m. Действительно, если бы такая плос-ть β существовала, то р имела бы с ней общую точку К, но полностью в β она бы не могла находиться, иначе α и β совпадали бы. Значит, р пересекала бы β. Но тогда ее обязательно пересекала бы и m по одну из свойств параллельных прямых. В этом случае m и β не были бы параллельными.

Сонаправленные лучи

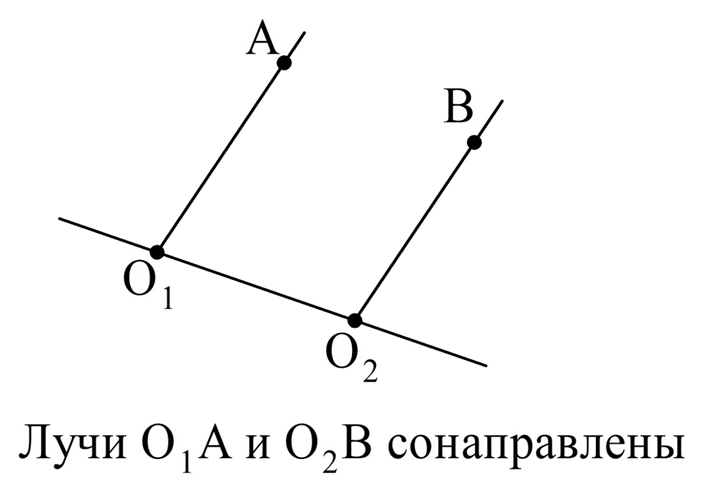
В планиметрии существует понятие сонаправленных лучей. Пусть на плос-ти есть два луча О₁А и О₂В. Проведем прямую О₁О₂. Она, как и всякая прямая, разделит плос-ть на две полуплоскости. Для того, чтобы лучи О₁А и О₂В считались сонаправленными, необходимо выполнение двух условий:

1) они должны оказаться в одной полуплоскости;

2) они должны быть параллельными.

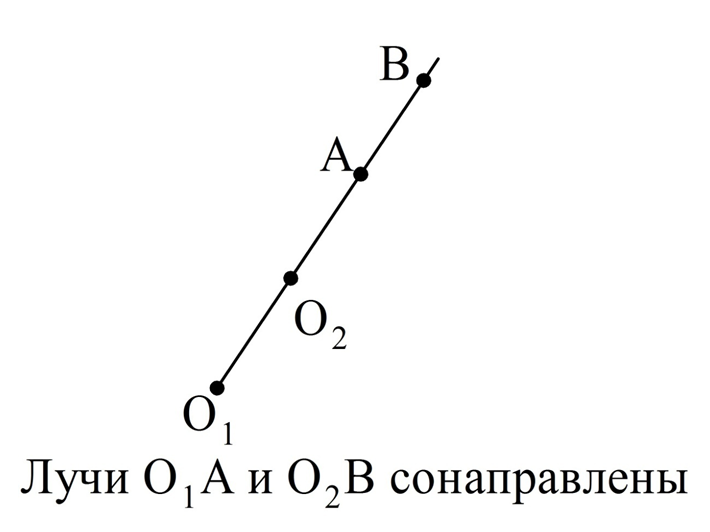
Здесь мы рассмотрели случай, когда лучи О₁А и О₂В находятся на разных прямых. Возможен частный случай, когда они располагаются на одной прямой. В таком случае для сонаправленности лучей достаточно, чтобы один из них полностью лежал на другом:

Рассмотрим теорему, касающуюся сонаправленных лучей, причем она верна не только в планиметрии, но и в стереометрии.

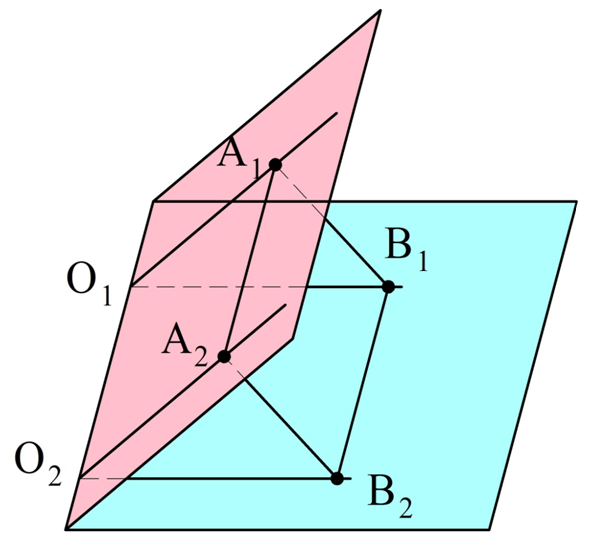
В доказательстве сразу рассмотрим случай углов, располагающихся в разных плос-тях. Пусть есть углы О₁ и О₂, стороны которых образуют попарно сонаправленные лучи. На одной паре лучей отметим точки А₁ и А₂ так, чтобы отрезки О₁А₁ и О₂А₂ были одинаковыми. На другой паре лучей аналогично отложим точки В₁ и В₂ так, чтобы одинаковыми были отрезки О₁В₁ и О₂В₂:

Заметим, что лучи О₁А₁ и О₂А₂ как сонаправленные должны располагаться в одной плос-ти, иначе они не будут параллельными. Тогда О₁А₁А₂О₂ – плоский четырехугольник. Отрезки О₁А₁ и О₂А₂ параллельны и одинаковы. Это значит, что О₁А₁А₂О₂ – параллелограмм. Аналогично легко убедиться, что параллелограммом является и четырехугольник О₁В₁В₂О₂. Это значит, что

Отсюда вытекает (по свойству транзитивности), что отрезки А₁А₂ и В₁В₂ также одинаковы и параллельны, а потому А₁А₂В₂В₁ – также параллелограмм. Значит, стороны А₁В₁ и А₂В₂ одинаковы. Получается, что у ∆О₁А₁В₁ и ∆О₂А₂В₂ одинаковы все стороны, поэтому ∆О₁А₁В₁ и ∆О₂А₂В₂ равны. Отсюда вытекает и равенство углов ∠А₁О₁В₁ и ∠А₂О₂В₂, ч. т. д.

Угол между прямыми

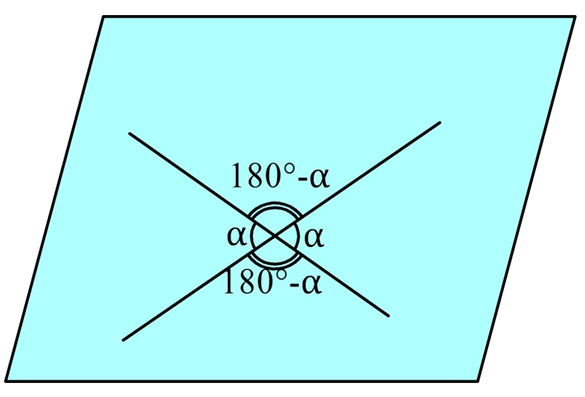
Напомним, какая величина считается углом между пересекающимися прямыми. При пересечении прямых образуется 4 угла. Зная один из них, легко вычислить и остальные углы. Понятно, что хотя бы один из углов будет не превышать 90°. Именно такой угол и принимается за угол между прямыми:

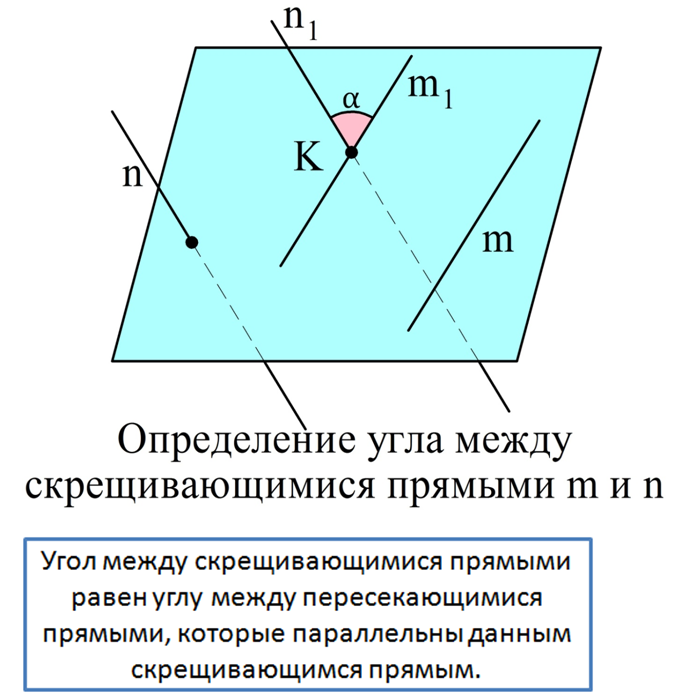
Теперь покажем, как определить угол между скрещивающимися прямыми. Пусть прямые m и n скрещиваются. Выберем в пространстве произвольную точку К. Через нее можно построить такие прямые m₁ и n₁, что m₁||m и n₁||n. Угол между m₁и n₁ как раз и принимается за угол между скрещивающимися прямыми m и n:

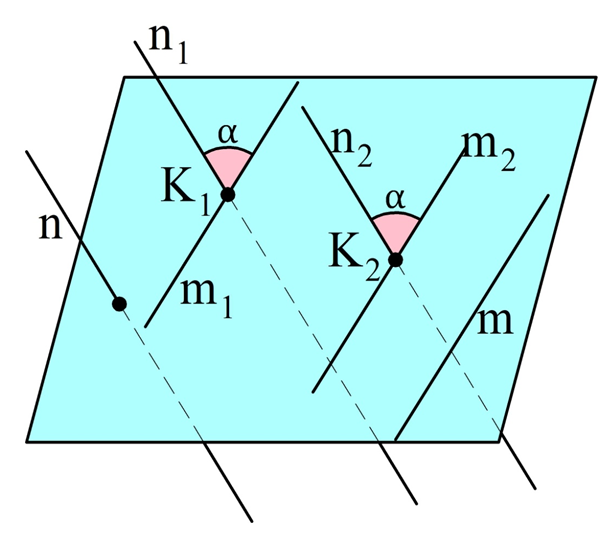
Возникает вопрос – зависит ли величина измеренного таким образом угла от того, какая именно точка К выбрана? Оказывается, что не зависит, и это можно доказать. Выберем две произвольные точки К₁ и К₂. Через К₁ проведем прямые n₁и m₁, а через К₂ проведем n₂и m₂, которые будут соответственно параллельны исходным прямым m и n.

Так как n₁||n и n₂||n, то по свойству транзитивности параллельности и n₁||n₂. Аналогично и m₁||m₂. Получается, что стороны углов в точках К₁ и К₂ соответственно сонаправлены. Значит, они одинаковы, ч. т. д.

Задачи на скрещивающиеся прямые

Теоретический материал закончился, осталось научиться применять полученные знания. Перед просмотром решения постарайтесь самостоятельно решить каждую задачу.

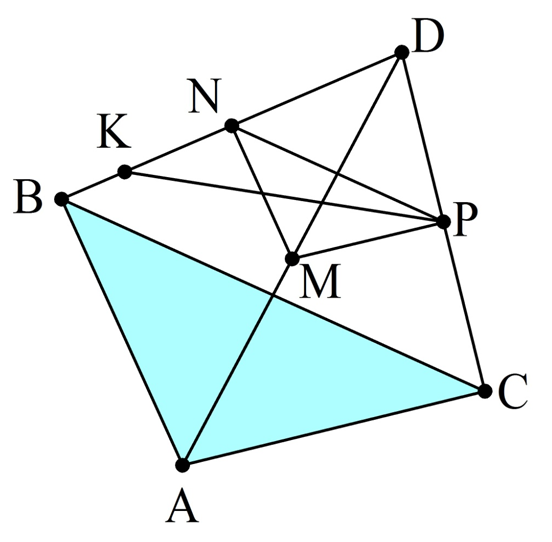
Задание. Точка D находится вне плос-ти ∆АВС. Середины отрезков АD, BD и СD обозначены буквами M, N и P соответственно. Точка K располагается на отрезке BN (и не совпадает с концами этого отрезка). Определите, как относительно друг друга располагаются прямые:

Решение. Сначала важно построить правильный рисунок по описанию задачи:

Теперь можно рассмотреть по отдельности каждый пункт.

а) АВ и DN. Прямая DN совпадает с прямой BD. Она в свою очередь пересекается с АВ в точке В. Значит, в данном случае прямые пересекаются.

б) РК и ВС. Рассмотрим плос-ть треугольника ∆ВСD. Рассматриваемые прямые как раз находятся в ней. То есть они уже точно не скрещиваются. Могут ли они быть параллельны? Обратите внимание на отрезок NP. Это средняя линия в ∆ВСD, поэтому NP||ВС. Через Р может быть проведена лишь одна прямая, параллельная ВС (по аксиоме параллельности), и это NP. Значит, KP пересекает ВС.

в) MN и АВ. В ∆АВDMN является средней линией, поэтому MN||АВ.

г) МР и АС. МР – это средняя линия в ∆АСD, значит, МР||АС.

д) KN и АС. Прямая KN совпадает с прямой BD. Она пересекает плос-ть АСВ, но точка пересечения (это В) не находится на АС. Тогда по признаку скрещивающихся прямых можно утверждать, что KN и АС скрещиваются.

е) MD и ВС. MD пересекается с плос-тью АСВ в точке А. Тогда из признака скрещивающихся прямых вытекает, что MD и DC скрещиваются.

Задание. Через точку Р, не находящуюся на прямой m, проведены две различные прямые, не пересекающиеся с m. Верно ли, что хотя бы одна из них точно скрещивается с m?

Решение. Каждая из этих двух прямых с m не пересекается. Тогда они либо параллельны m, либо скрещиваются с ней. Но обе прямые параллельны m не могут быть параллельны m, ведь тогда через Р будет проведено сразу две прямые, параллельные m, что невозможно. Значит, хотя бы одна из прямых действительно скрещивается с m.

Задание. MК и РН – скрещивающиеся прямые.Скрещиваются ли прямые МН и КР?

Решение. Ясно, что точки М, К, Р, Н располагаются в различных плос-тях. В противном случае, если бы существовала плос-ть α, в которой находились бы М, К, Р и Н, то в α также находились бы прямые МК и РН, и тогда они уже по определению не были бы скрещивающимися.

Теперь рассмотрим плос-ть КРН. В ней находится прямая КР. А прямая МН ее пересекает в точке К. Тогда, по признаку скрещивающихся прямых, МН и КР скрещиваются.

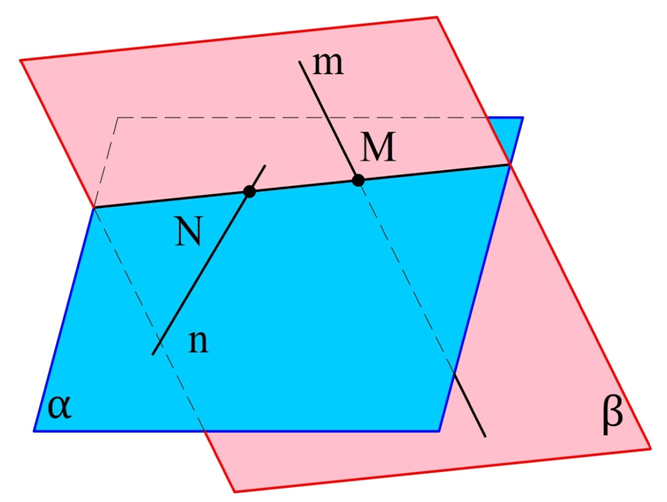
Задание. Прямые m и n скрещиваются. M – точка на m, N – точка на n. Через m и N проведена плос-ть α, а через n и M – плос-ть β. Пересекаются ли плос-ти α и β, и если да, то по какой линии?

Решение.

Посмотрим, есть ли у α и β общие точки. Плос-ть α проходит через n, то есть и через точку N тоже. Плос-ть β также проходит через N. Значит, N – общая точка. Аналогично можно показать, что и М – это общая точка. В итоге α и β пересекаются, причем на линии пересечения находятся точки M и N. Значит, именно прямая МN является границей этих двух плос-тей.

Задание. Известно, что MНКЕ – параллелограмм, а МНРТ – трапеция (РТ – её основание), причем они располагаются в разных областях. Каково расположение отрезков КЕ и РТ друг относительно друга.

Решение. Задачу можно решить и без рисунка. Если РТ – основание трапеции, то второе основание – это МН, и МН||РТ. В параллелограмме МНКЕ параллельны стороны МН и КЕ, ведь они противоположные. Тогда по свойству транзитивности параллельности из того факта, что МН||РТ и МН||КЕ, вытекает, что и РТ||КЕ.

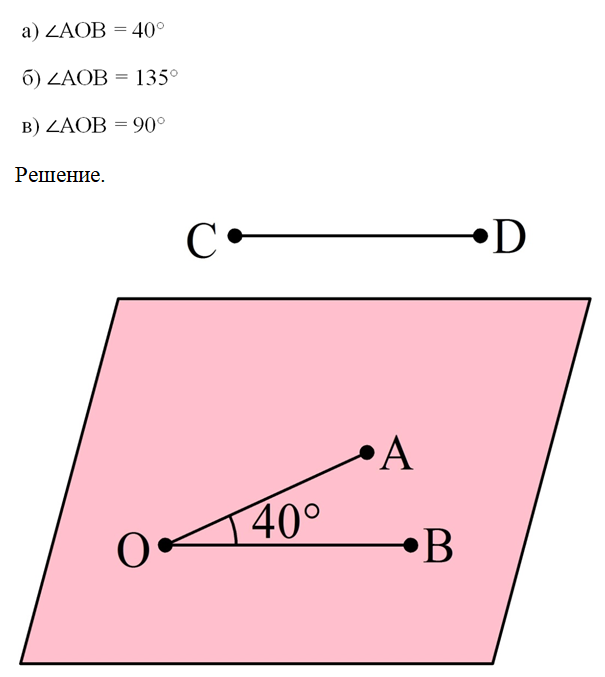
Задание. Известно, что ОА и СD – скрещивающиеся прямые, а ОВ||CD. Чему равен угол между ОА и CD, если

Если CD||ОВ, то угол между CD и ОА совпадает с углом между ОВ и ОА. В задании а) он совпадет с ∠АОВ и составляет 40°. В случае б) угол не может составлять 135°, так как он не должен превышать 90°. Поэтому он равен

Наконец, в случае в) он составит 90°.

Ответ: а) 40°; б) 45°; в) 90°.

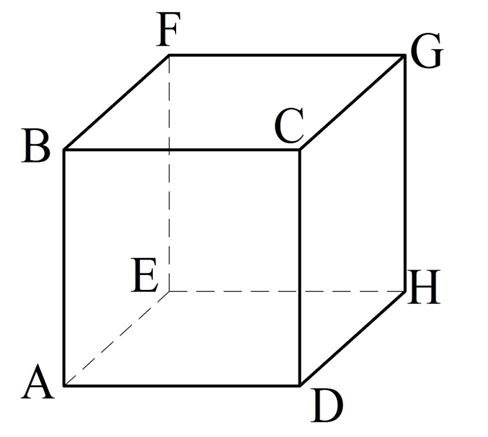
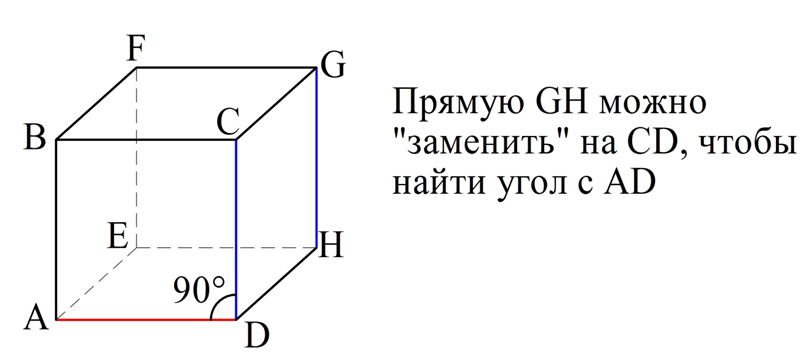
Задание. Дан куб, вершины которого обозначены так, как это показано на рисунке:

Найдите угол между прямыми:

Решение. Во всех трех случаях нам даны скрещивающиеся прямые. Для вычисления угла надо найти такие параллельные им прямые, которые будут пересекаться.

а) AD и GH. Заметим, что GH||СD, ведь это противоположные стороны квадрата СDHG, поэтому мы можем определить угол между AD и CD. Другими словами, мы просто заменяем в задаче GH на CD, так как эти отрезки параллельны. Так как отрезки AD и CD в свою очередь являются уже смежными сторонами в квадрате АВСD, то ∠ADC, который нам надо найти, составляет 90°.

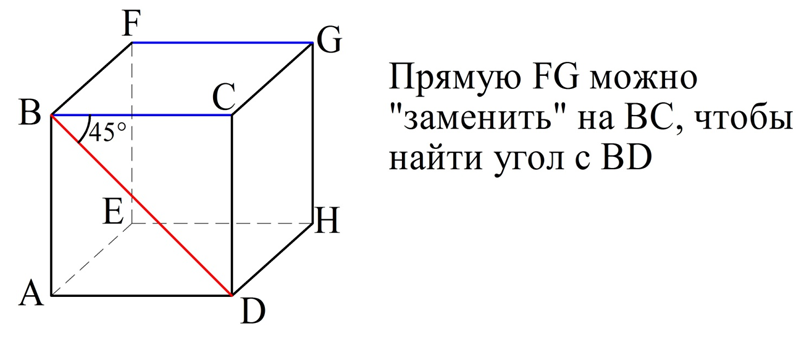
б) BD и FG. Здесь уже уместно заменить FG на ВС. Это можно сделать, ведь FG||ВС (это стороны квадрата). Тогда нам необходимо вычислить ∠СВD. Он составляет 45°, ведь диагональ квадрата делит его угол пополам.

в) BD и AF. Здесь есть смысл AF заменить на GD. Но для этого надо сначала показать, что AF||DG.Рассмотрим отрезки AD и FG. Каждый из них параллелен ВС (по свойству квадратов ABCD и ВСGH). Значит, по свойству транзитивности AD||FG, то есть эти отрезки располагаются в одной плос-ти. Тогда AFGD – плоский четырехугольник.

Заметим, что отрезки AD и FG ещё и одинаковы, так каждый из них равен ВС (вообще в кубе все ребра одинаковы). Получается, что в четырехугольнике AFGD стороны AD и FG одинаковы и параллельны, а потому AFGD – параллелограмм, по одному из его признаков. Отсюда и вытекает, что AF||DG.

Мы поняли, искомый нами угол между прямыми равен∠BDG. Как его вычислить? Для этого надо рассмотреть ∆BDG. Можно заметить, что он равносторонний. Действительно, отрезки BG, GD и BD – это диагонали в равных квадратах ВСGH, СDHG, АВСD, поэтому и сами эти диагонали также одинаковы. В любом равностороннем треугольнике все углы составляют по 60°, поэтому и ∠BDG равен этому же значению, то есть 60°.

Ответ: а) 90°; б) 45°; в) 60°.

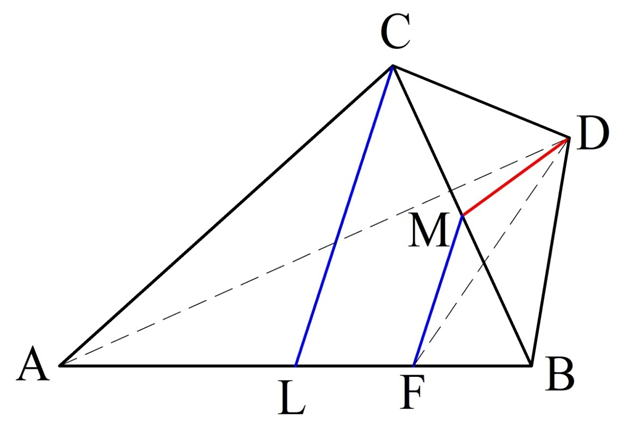
Задание (стереометрическая задача из ЕГЭ). Точки А, В, С и D в пространстве располагаются так, что расстояния между любыми двумя из этих точек одинаковы. Можно доказать (попробуйте сделать это самостоятельно), что такая ситуация возможна лишь в случае, когда точки не располагаются в одной плос-ти. М – середина ВС, а L – середина АВ. Найдите косинус угла между прямыми МD и CL.

Решение. Из условия вытекает, что ∆АВС, ∆ВСD, ∆ABD – равносторонние и притом равные друг другу. Проведем в ∆АВС отрезок такой отрезок MF, что MF||СL. Тогда нам необходимо вычислить ∠DMF (точнее, его косинус). Это можно сделать, используя теорему косинусов применительно к ∆MDF, но для этого сперва надо найти все стороны в этом треугольнике:

Для удобства обозначим длину отрезков АВ, ВС, АС, BD, AD и CD буквой R. Так как L– середина АВ, то CL– медиана в ∆АВС. Но в равностороннем треугольнике она одновременно будет и высотой. Тогда ∆АСL – прямоугольный. Запишем для него теорему Пифагора:

Аналогичным образом легко определить, что длина медианы DМ в ∆ВСD равна этому же значению:

Теперь исследуем ∆ВСL. Так как MF||CL и М – середина ВС, то MF оказывается средней линией в ∆ВСL. Значит, ее длина вдвое меньше, чем у СL:

Также из того факта, что МF – средняя линия, вытекает то, что F – середина LВ. Тогда можно вычислить FB:

Далее обратим внимание на ∆ВFD. ∠В в нем составляет 60°, ведь это одновременно и угол в равностороннем ∆АВD. Стороны FB и BD нам известны, а потому с помощью теоремы косинусов можно вычислить и FD:

Теперь можно составить и для ∆МDF уравнение на основе теореме косинуса, из которого удастся выяснить интересующий нас косинус ∠DMF:

В ходе сегодняшнего урока мы познакомились с новым понятием – скрещивающимися прямыми. Также мы узнали, как вычислять угол между ними. Подобные задачи могут встречаться и на ЕГЭ.

Источник

Опубликовано 3 года назад по предмету
Математика
от Vagabov1

какие в параллелограме прямые, скрещивающиеся?

Ответ

Ответ дан
padisova58

В параллелограмме нет скрещивающихся прямых,есть пересекающиеся.,если конечно вопрос ставится именно так как у вас
1. Ответ
  
  Ответ дан
  Vagabov1
  
  понятно, я вот тоже так думаю, но учитель написал скрещивающиеся

Самые новые вопросы

Математика – 3 года назад

Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x – 5,21 = 9,54

Информатика – 3 года назад

Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.

География – 3 года назад

Почему япония – лидер по выплавке стали?

Математика – 3 года назад

Чему равно: 1*(умножить)х? 0*х?

Русский язык – 3 года назад

В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Источник

11
Авг 2013

Категория: Справочные материалы

Скрещивающиеся прямые

2013-08-11
2013-08-11

Скрещивающиеся прямые – прямые, которые невозможно поместить в одну плоскость, то есть они не параллельны и не пересекаются.

Признак скрещивающихся прямых

Если одна из прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, отличной от точек первой прямой, то такие прямые – скрещивающиеся.

Расстояние между скрещивающимися прямыми

неп

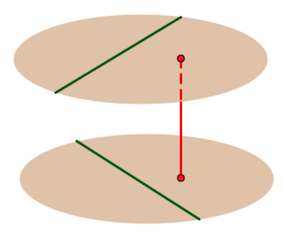
Через две скрещивающиеся прямые можно провести две параллельные плоскости (единственным образом).

Расстояние между скрещивающимися прямыми – есть расстояние между этими плоскостями.

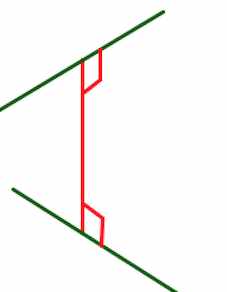
Общий перпендикуляр к двум скрещивающимся прямым

Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный каждой из двух скрещивающихся прямых, концы которого лежат на этих прямых.

Длина общего перпендикуляра равна расстоянию между скрещивающимися прямыми.

Угол между скрещивающимися прямыми

Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).

Автор: egeMax |

Нет комментариев

Источник

Комментарии преподавателя

1. Тема урока

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых

плоскости, параллельной другой прямой.

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых.

2. Определение скрещивающихся прямых

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

3. Теорема 1 (признак скрещивающихся прямых) и ее доказательство

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Доказательство

Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Рис. 1.

Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость – α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.

4. Возможные случаи расположения прямых

Три случая расположения прямых

1) Прямые a и b пересекаются в некоторой точке С: (Рис. 2.). Как мы знаем, через две пересекающиеся прямые проходит единственная плоскость.

Рис. 2.

2) Прямые a и b параллельны: a || b (Рис. 3.). Если прямые параллельны, то они лежат в одной плоскости и не пересекаются.

Рис. 3.

Заметим, что и в первом, и во втором случае прямые лежали в одной плоскости.

3) Прямые a и b скрещиваются (Рис. 4.). То есть прямые a и b не лежат в одной плоскости.

Рис. 4.

5. Пример скрещивающихся прямых в треугольной пирамиде

Пример

Дана треугольная пирамида ABCD, АВС – плоскость основания, точка D не лежит в плоскости АВС (Рис. 5.). Почему прямые АВ и DC скрещивающиеся?

Рис. 5.

Прямая DC пересекает плоскость АВС в точке С, не лежащей на прямой АВ, а прямая АВ лежит в плоскости АВС. Значит, по признаку, прямые АВ и DC – скрещивающиеся. То есть противоположные ребра треугольной пирамиды лежат на скрещивающихся прямых.

6. Теорема 2 и ее доказательство

Теорема 2.

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство.

Пусть нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.

Рис. 6.

Проведем через точку А прямую АЕ, параллельную прямой DC (Рис. 6.). По теореме о параллельных прямых, такая прямая существует и единственная. Тогда через две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α. Так как прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости α, значит, что прямая DC параллельна плоскости α, по признаку параллельности прямой и плоскости. Существование доказано.

Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямаяDC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α – единственная. Теорема доказана.

7. Задача 1

Точка D не лежит в плоскости треугольника АВС, точки M, N, P – середины отрезков DA, DB и DC соответственно, точка K лежит на отрезке BN (Рис. 7.). Выясните взаимное расположение прямых.

Рис. 7.

1) ND и AB.

Прямая ND – это другое обозначение прямой ВD. Прямая ВD и прямая АВ лежат в плоскости АВD и пересекаются.

2) PK и ВС.

Прямые PK и ВС лежат в одной плоскости. Значит, они либо параллельные, либо пересекаются. Проведем среднюю линию NP (N, P – середины отрезков DB и DC соответственно). По свойству средней линии, прямая NPпараллельна прямой ВС. Через точку Р можно провести только одну прямую, параллельную прямой ВС, и это прямая NP. Значит, любая другая прямая, проходящая через точку Р, не параллельна прямой ВС. Значит, PK иВС пересекаются.

3) MN и AB.

В треугольнике ABD точки M и N – середины сторон АD и ВD. Значит, МN – средняя линия. По свойству средней линии, МN параллельна АВ.

4) МР и АС.

В треугольнике ADС точки M и Р – середины сторон АD и СD. Значит, МР – средняя линия. По свойству средней линии, МР параллельна АС.

5) КN и АС.

Прямая КN и прямая ВD – это одна и та же прямая. Прямая АС лежит в плоскости АВС, прямая ВD пересекает плоскость АВС в точке, не лежащей на прямой АС. Значит, по признаку, прямые ВD и АС – скрещивающиеся. То есть, прямые КN и АС- скрещивающиеся.

6) МD и ВС.

Прямая МD и прямая АD – это одна и та же прямая. Прямая ВС лежит в плоскости АВС, прямая АD пересекает плоскость АВС в точке, не лежащей на прямой ВС. Значит, по признаку, прямые АD и ВС – скрещивающиеся. То есть, прямые МD и ВС – скрещивающиеся.

8. Задача 2

Докажите, что если АВ и СD скрещиваются, то АD и ВС тоже скрещиваются.

Доказательство

Предположим, что прямые АD и ВС не скрещивающиеся, то есть лежат в одной плоскости. Значит, все точки А, В, С, D лежат в этой плоскости, значит прямые АВ и СD тоже лежат в этой плоскости. Но прямые АВ и СDскрещивающиеся по условию. Получили противоречие. Значит, прямые АD и ВС – скрещивающиеся.

9. Итоги урока

Итак, мы познакомились со скрещивающимися прямыми: дали определение, доказали признак скрещивающихся прямых. Также мы доказали теорему о том, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теперь нам известны все случаи взаимного расположения прямых в пространстве: они могут пересекаться, быть параллельными, быть скрещивающимися.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/parallelnost-pryamyh-i-ploskostej/skreschivayuschiesya-pryamye-provedenie-cherez-odnu-iz-skreschivayuschihsya-pryamyh-ploskosti-parallelnoy-drugoy-pryamoy?seconds=0&chapter_id=210

http://www.metod-kopilka.ru/images/doc/54/49016/hello_html_m1b2a5d9c.png

http://festival.1september.ru/articles/593938/

http://www.proektant.ru/i/content/2014_II/4526_transportnaia_razviazka_02.jpg

Источник

Взаимное расположение прямых в пространстве

Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

– прямые совпадают.

Взаимное расположение прямых и их направляющие векторы

Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями

$l_{1}colon~frac{x-x_{1}}{a_{1}}=frac{y-y_{1}}{b_{1}}=frac{z-z_{1}}{c_{1}}, quad l_{2}colon~frac{x-x_{2}}{a_{2}}=frac{y-y_{2}}{b_{2}}=frac{z-z_{2}}{c_{2}},.$

где $M_{1}(x_{1},y_{1},z_{1}),,M_{2}(x_{2},y_{2},z_{2})$ — точки, принадлежащие прямым $l_{1}$ и $l_{2}$ соответственно, a $vec{p}_{1}=a_{1}vec{i}+b_{1}vec{j}+c_{1}vec{k},$ $vec{p}_{2}=a_{2}vec{i}+b_{2}vec{j}+c_{2}vec{k}$ — направляющие векторы (рис.4.34). Обозначим через $vec{m}=overrightarrow{M_{1}M_{2}}=(x_{2}-x_{1})vec{i}+(y_{2}-y_{1})vec{j}+(z_{2}-z_{1})vec{k}$ вектор, соединяющий заданные точки.

Перечисленным выше случаям взаимного расположения прямых $l_{1}$ и $l_{2}$ соответствуют следующие признаки:

– прямые $l_{1}$ и $l_{2}$ скрещивающиеся Leftrightarrow векторы $vec{m},,vec{p}_{1},,vec{p}_{2}$ не компланарны;

– прямые $l_{1}$ и $l_{2}$ пересекаются Leftrightarrow векторы $vec{m},,vec{p}_{1},,vec{p}_{2}$ компланарны, а векторы $vec{p}_{1},,vec{p}_{2}$ не коллинеарны;

– прямые $l_{1}$ и $l_{2}$ параллельные Leftrightarrow векторы $vec{p}_{1},,vec{p}_{2}$ коллинеарны, а векторы $vec{m},,vec{p}_{2}$ не коллинеарны;

– прямые $l_{1}$ и $l_{2}$ совпадают Leftrightarrow векторы $vec{m},,vec{p}_{1},,vec{p}_{2}$ коллинеарны.

Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:

$leftlanglevec{m},vec{p}_{1},vec{p}_{2}rightrangle= begin{vmatrix} x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\ a_{1}&b_{1}&c_{1}\ a_{2}&b_{2}&c_{2} end{vmatrix}.$

Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:

– прямые $l_{1}$ и $l_{2}$ скрещивающиеся Leftrightarrow определитель отличен от нуля;

– прямые $l_{1}$ и $l_{2}$ пересекаются Leftrightarrow определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е. $operatorname{rang}!begin{pmatrix}a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{pmatrix}=2,;$

– прямые $l_{1}$ и $l_{2}$ параллельные Leftrightarrow вторая и третья строки определителя пропорциональны, т.е. $operatorname{rang}!begin{pmatrix}a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{pmatrix}=1,,$ а первые две строки не пропорциональны, т.е. $operatorname{rang}!begin{pmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\a_{1}&b_{1}&c_{1}end{pmatrix}=2,;$

– прямые $l_{1}$ и $l_{2}$ совпадают Leftrightarrow все строки определителя пропорциональны, т.е. $operatorname{rang}!begin{pmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{pmatrix}=1,.$

Расстояние между параллельными прямыми

Найдем расстояние между параллельными прямыми, заданными каноническими уравнениями (рис.4.35)

Расстояние d между параллельными прямыми

$lcolon~frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}, quad l_{1}colon~frac{x-x_{1}}{a_{1}}=frac{y-y_{1}}{b_{1}}=frac{z-z_{1}}{c_{1}},$

где $M_{0}(x_{0},y_{0},z_{0}),,M_{1}(x_{1},y_{1},z_{1})$ — произвольные точки на прямых и $l_{1}$ соответственно, а координаты направляющих векторов прямых пропорциональны: $frac{a}{a_{1}}=frac{b}{b_{1}}=frac{c}{c_{1}},.$

Искомое расстояние равно высоте параллелограмма, построенного на векторах vec{p}=avec{i}+bvec{j}+cvec{k} и $vec{m}=overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k}$ , и может быть найдено по формуле (4.35).

Расстояние между скрещивающимися прямыми

Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.

Расстояние d между скрещивающимися прямыми

Найдем расстояние между скрещивающимися прямыми, заданными каноническими уравнениями

$lcolon_{1}~frac{x-x_{1}}{a_{1}}=frac{y-y_{1}}{b_{1}}=frac{z-z_{1}}{c_{1}}, quad l_{2}colon~frac{x-x_{2}}{a_{2}}=frac{y-y_{2}}{b_{2}}=frac{z-z_{2}}{c_{2}},$

где $M_{1}(x_{1},y_{1},z_{1}),,M_{2}(x_{2},y_{2},z_{2})$ — произвольные точки на прямых $l_{1}$ и $l_{2}$ соответственно.

Искомое расстояние равно высоте параллелепипеда, построенного на векторах $vec{m}=overrightarrow{M_{1}M_{2}}=(x_{2}-x_{1})vec{i}+(y_{2}-y_{1})vec{j}+(z_{2}-z_{1})vec{k},$ $vec{p}_{1}=a_{1}vec{i}+b_{1}vec{j}+c_{1}vec{k},$ $vec{p}_{2}=a_{2}vec{i}+b_{2}vec{j}+c_{2}vec{k},$ (рис.4.36), т.е.

$d=frac{|langlevec{m},vec{p}_{1},vec{p}_{2}rangle|}{|[vec{p}_{1},vec{p}_{2}]|},,$

(4.38)

где

$langlevec{m},vec{p}_{1},vec{p}_{2}rangle= begin{vmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{vmatrix}, quad [vec{p}_{1},vec{p}_{2}]= begin{vmatrix}vec{i}&vec{j}&vec{k}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{vmatrix}$

— смешанное и векторное произведения векторов. Как показано выше, прямые $l_{1}$ и $l_{2}$ скрещивающиеся тогда и только тогда, когда векторы $vec{m},vec{p}_{1},vec{p}_{2}$ некомпланарные, т.е.

$begin{vmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{vmatrix}ne0,.$

Отсюда следует, что вторая и третья строки не пропорциональны. Поэтому векторы $vec{p}_{1},vec{p}_{2}$ неколлинеарные, т.е. $|,[vec{p}_{1},vec{p}_{2}],|ne0$ и знаменатель в правой части (4.38) отличен от нуля.

Угол между прямыми

Угол между прямыми определяется как угол между их направляющими векторами. Поэтому величина varphi острого угла между прямыми

$l_{1}colon~frac{x-x_{1}}{a_{1}}=frac{y-y_{1}}{b_{1}}=frac{z-z_{1}}{c_{1}}, qquad l_{2}colon~frac{x-x_{2}}{a_{2}}=frac{y-y_{2}}{b_{2}}=frac{z-z_{2}}{c_{2}}$

вычисляется по формуле

$cosvarphi= frac{|,langlevec{p}_{1},vec{p}_{2}rangle,|}{|vec{p}_{1}|cdot|vec{p}_{2}|}= frac{|a_{1}cdot a_{2}+b_{1}cdot b_{2}+c_{1}cdot c_{2}|}{sqrt{a_{1}^2+b_{1}^2+c_{1}^2}cdotsqrt{a_{2}^2+b_{2}^2+c_{2}^2}},.$

(4.39)

Пример 4.16. Найти расстояние между прямой, проходящей через точки B(3;0;2), C(7;4;6) , и осью абсцисс. Найти величину varphi острого угла между этими прямыми.

Решение. Каноническое уравнение оси абсцисс имеет вид $frac{x}{1}=frac{y}{0}=frac{z}{0},,$ так как ось проходит через точку O(0;0;0) а vec{i} — ее направляющий вектор. Каноническое уравнение прямой получено в примере 4.15,”а”: $frac{x-3}{1}=frac{y}{1}=frac{z-2}{1}.$

Полагая vec{m}=overrightarrow{OB}=(3-0)vec{i}+(0-0)vec{j}+(2-0)vec{j}=3vec{i}+2vec{k}, $vec{p}_{1}=vec{i},$ $vec{p}_{2}=vec{i}+vec{j}+vec{k}$ по формуле (4.38) получаем:

$begin{gathered} langle,vec{m},vec{p}_{1},vec{p}_{2},rangle= begin{pmatrix}3&0&2\1&0&0\1&1&1end{pmatrix}=2, quad [,vec{p}_{1},vec{p}_{2},]= begin{pmatrix}vec{i}&vec{j}&vec{k}\1&0&0\1&1&1end{pmatrix}= -vec{j}+vec{k},\[4pt] d=frac{|,langle,vec{m},vec{p}_{1},vec{p}_{2},rangle,|}{|,[,vec{p}_{1},vec{p}_{2},],|}= frac{2}{sqrt{0^2+(-1)^2+1^2}}=sqrt{2},.end{gathered}$

Острый угол varphi находим по формуле (4.39):

$cosvarphi=frac{|,langle,vec{p}_{1},vec{p}_{2},rangle,|}{|,vec{p}_{1},|cdot|,vec{p}_{2},|}= frac{|1cdot1+0cdot1+0cdot1|}{sqrt{1^2+0^2+0^2}cdotsqrt{1^2+1^2+1^2}}= frac{1}{sqrt{3}}quad Rightarrow quad varphi=arccosfrac{1}{sqrt{3}},.$

Взаимное расположение прямой и плоскости

Возможны три случая взаимного расположения прямой и плоскости:

– прямая и плоскость пересекаются, т.е. имеют одну общую точку;

– прямая и плоскость параллельны, т.е. не имеют общих точек;

– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.

Получим признаки для всех этих случаев. Пусть прямая и плоскость rho заданы уравнениями:

$lcolon,frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}; qquad rhocolon,Acdot x+Bcdot y+Ccdot z+D=0,$

т.е. прямая проходит через точку $M_{0}(x_{0},y_{0},z_{0})$ коллинеарно вектору vec{p}=avec{i}+bvec{j}+cvec{k} а плоскость rho перпендикулярна вектору vec{n}=Avec{i}+Bvec{j}+Cvec{k},.

Перечисленным выше случаям взаимного расположения прямой и плоскости rho соответствуют следующие признаки:

– прямая и плоскость rho пересекаются Leftrightarrow векторы vec{p} и vec{n} не ортогональны (рис.4.37,а);

– прямая и плоскость rho параллельны Leftrightarrow векторы vec{p} и vec{n} ортогональны, а точка $M_{0}$ не принадлежит плоскости rho (рис.4.37,б);

– прямая лежит в плоскости rho~Leftrightarrow векторы vec{p} и vec{n} ортогональны, а точка $M_{0}$ принадлежит плоскости rho (рис.4.37,в).

Взаимное расположение прямой и плоскости

Учитывая свойство скалярного произведения векторов langle,vec{p},vec{n},rangle=acdot A+bcdot B+ccdot C получаем:

– прямая и плоскость rho пересекаются Leftrightarrow acdot A+bcdot B+ccdot Cne0 ;

– прямая и плоскость rho параллельны $Leftrightarrow~ begin{cases}acdot A+bcdot B+ccdot C=0,\ Acdot x_{0}+Bcdot y_{0}+Ccdot z_{0}+Dne0;end{cases}$

– прямая лежит в плоскости $rho~Leftrightarrow~ begin{cases}acdot A+bcdot B+ccdot C=0,\ Acdot x_{0}+Bcdot y_{0}+Ccdot z_{0}+D=0;end{cases}$

Угол между прямой и плоскостью

Угол между прямой и плоскостью rho определяется как угол между прямой и ее ортогональной проекцией на плоскость (рис.4.38). Из двух смежных углов varphi и varphi' , как правило, выбирают меньший. Если прямая перпендикулярна плоскости (ее ортогональная проекция на плоскость является точкой), то угол считается равным $textstyle{frac{pi}{2}}$ . Если обозначить psi и psi' углы, образованные наклонной с перпендикуляром к плоскости, то

sinvarphi=sinvarphi'=|cospsi|=|cospsi'|,.

Поскольку угол psi (или psi' ) равен углу между направляющим вектором vec{p} прямой и нормалью vec{n} к плоскости rho , то $sinvarphi= |cospsi|= frac{|langlevec{p},vec{n}rangle|}{|vec{p}|{cdot}|vec{n}|}$ . Записывая скалярное произведение через координаты множителей, получаем формулу вычисления угла varphi между прямой и плоскостью:

$sinvarphi= frac{|acdot A+bcdot B+ccdot C|}{sqrt{a^2+b^2+c^2}cdotsqrt{A^2+B^2+C^2}},.$

(4.40)

Отсюда, например, следует полученное ранее необходимое условие acdot A+bcdot B+ccdot C=0 параллельности прямой и плоскости.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Понятие скрещивающихся прямых

Сонаправленные лучи

Угол между прямыми

Задачи на скрещивающиеся прямые

какие в параллелограме прямые, скрещивающиеся?

Информация

Скрещивающиеся прямые

Признак скрещивающихся прямых

Расстояние между скрещивающимися прямыми

Общий перпендикуляр к двум скрещивающимся прямым

Угол между скрещивающимися прямыми

Комментарии преподавателя

1. Тема урока

2. Определение скрещивающихся прямых

3. Теорема 1 (признак скрещивающихся прямых) и ее доказательство

4. Возможные случаи расположения прямых

5. Пример скрещивающихся прямых в треугольной пирамиде

6. Теорема 2 и ее доказательство

7. Задача 1

8. Задача 2

9. Итоги урока

Взаимное расположение прямых в пространстве

Расстояние между параллельными прямыми

Расстояние между скрещивающимися прямыми

Угол между прямыми

Взаимное расположение прямой и плоскости

Угол между прямой и плоскостью

Вам также может понравиться

Как найти площадь основания окружности

Хрустит шрус как его исправить

Как быстро найти наименьшее общее кратное

Добавить комментарий Отменить ответ