Как найти скрещивающиеся прямые в пирамиде

Среди огромного количества стереометрических
задач в учебниках геометрии, в различных
сборниках задач, пособиях по подготовке в ВУЗы
крайне редко встречаются задачи на нахождение
расстояния между скрещивающимися прямыми.
Возможно, это обусловлено как узостью их
практического применения (относительно школьной
программы, в отличие от “выигрышных” задач на
вычисление площадей и объемов), так и сложностью
данной темы.

Практика проведения ЕГЭ показывает, что многие
учащиеся вообще не приступают к выполнению
заданий по геометрии, входящих в экзаменационную
работу. Для обеспечения успешного выполнения
геометрических заданий повышенного уровня
сложности необходимо развивать гибкость
мышления, способность анализировать
предполагаемую конфигурацию и вычленять в ней
части, рассмотрение которых позволяет найти путь
решения задачи.

Школьный курс предполагает изучение четырех
способов решения задач на нахождение расстояния
между скрещивающимися прямыми. Выбор способа
обусловлен, в первую очередь, особенностями
конкретной задачи, предоставленными ею
возможностями для выбора, и, во вторую очередь,
способностями и особенностями
“пространственного мышления” конкретного
учащегося. Каждый из этих способов позволяет
решить самую главную часть задачи – построение
отрезка, перпендикулярного обеим скрещивающимся
прямым (для вычислительной же части задач
деление на способы не требуется).

Основные способы решения задач на нахождение
расстояния между скрещивающимися прямыми

Нахождение длины общего перпендикуляра двух
скрещивающихся прямых, т.е. отрезка с концами на
этих прямых и перпендикулярного каждой из этих
прямых.

Нахождение расстояния от одной из
скрещивающихся прямых до параллельной ей
плоскости, проходящей через другую прямую.

Нахождение расстояния между двумя
параллельными плоскостями, проходящими через
заданные скрещивающиеся прямые.

Нахождение расстояния от точки, являющейся
проекцией одной из скрещивающихся прямых, на
перпендикулярную ей плоскость (так называемый
“экран”) до проекции другой прямой на ту же
самую плоскость.

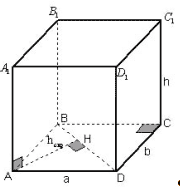
Проведем демонстрацию всех четырех способов на
следующей простейшей задаче: “В кубе с
ребром а найти расстояние между любым ребром
и диагональю не пересекающей его грани”. Ответ: .

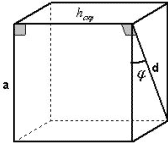
1 способ.

Рисунок 1

h_скр перпендикулярна плоскости боковой
грани, содержащей диагональ d и
перпендикулярна ребру, следовательно, h_скр
и является расстоянием между ребром а и
диагональю d.

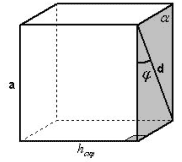
2 способ.

Рисунок 2

Плоскость A параллельна ребру и проходит через
данную диагональ, следовательно, данная h_скр
является не только расстоянием от ребра до
плоскости A, но и расстоянием от ребра до данной
диагонали.

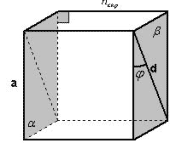
3 способ.

Рисунок 3

Плоскости A и B параллельны и проходят через две
данные скрещивающиеся прямые, следовательно,
расстояние между этими плоскостями равно
расстоянию между двумя скрещивающимися прямыми.

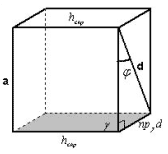
4 способ.

Рисунок 4

Плоскость A перпендикулярна ребру куба. При
проекции на A диагонали d данная диагональ
обращается в одну из сторон основания куба.
Данная h_скр является расстоянием между
прямой, содержащей ребро, и проекцией диагонали
на плоскость C, а значит и между прямой,
содержащей ребро, и диагональю.

Остановимся подробнее на применении каждого
способа для изучаемых в школе многогранников.

СПОСОБ I.

Применение первого способа достаточно
ограничено: он хорошо применяется лишь в
некоторых задачах, так как достаточно сложно
определить и обосновать в простейших задачах
точное, а в сложных – ориентировочное
местоположение общего перпендикуляра двух
скрещивающихся прямых. Кроме того, при
нахождении длины этого перпендикуляра в сложных
задачах можно столкнуться с непреодолимыми
трудностями.

Примеры

Задача 1. В прямоугольном параллелепипеде с
размерами a, b, h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю основания.

Рисунок 5

Пусть AHBD.
Так как А₁А перпендикулярна плоскости АВСD ,
то А₁А
AH.

AH перпендикулярна обеим из двух скрещивающихся
прямых, следовательно AH?- расстояние между
прямыми А₁А и BD. В прямоугольном
треугольнике ABD, зная длины катетов AB и AD, находим
высоту AH, используя формулы для вычисления
площади прямоугольного треугольника. Ответ:

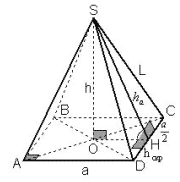
Задача 2. В правильной 4-угольной пирамиде с
боковым ребром L и стороной основания a
найти расстояние между апофемой и стороной
основания, пересекающей боковую грань,
содержащую эту апофему.

Рисунок 6

SHCD как
апофема, ADCD,
так как ABCD – квадрат. Следовательно, DH –
расстояние между прямыми SH и AD. DH равно половине
стороны CD. Ответ:

СПОСОБ II

Применение этого способа также ограничено в
связи с тем, что если можно быстро построить (или
найти уже готовую) проходящую через одну из
скрещивающихся прямых плоскость, параллельную
другой прямой, то затем построение
перпендикуляра из любой точки второй прямой к
этой плоскости (внутри многогранника) вызывает
трудности. Однако в несложных задачах, где
построение (или отыскивание) указанного
перпендикуляра трудностей не вызывает, данный
способ является самым быстрым и легким, и поэтому
доступен.

Примеры

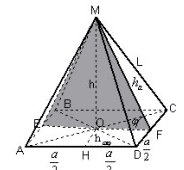
Задача 2. Решение уже указанной выше задачи
данным способом особых трудностей не вызывает.

Рисунок 7

Плоскость EFM параллельна прямой AD, т. к AD || EF.
Прямая MF лежит в этой плоскости, следовательно,
расстояние между прямой AD и плоскостью EFM равно
расстоянию между прямой AD и прямой MF. Проведем OHAD. OHEF, OHMO,
следовательно, OH(EFM),
следовательно, OH – расстояние между прямой AD и
плоскостью EFM, а значит, и расстояние между прямой
AD и прямой MF. Находим OH из треугольника AOD.

Ответ:

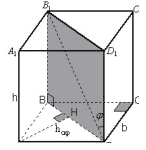
Задача 3. В прямоугольном параллелепипеде с
размерами a,b и h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю параллелепипеда.

Рисунок 8

Прямая AA₁ параллельна плоскости BB₁D₁D,
B₁D принадлежит этой плоскости,
следовательно расстояние от AA₁ до
плоскости BB₁D₁D равно расстоянию между
прямыми AA₁ и B₁D. Проведем AHBD. Также, AH B₁B,
следовательно AH(BB₁D₁D), следовательно AHB₁D, т. е. AH –
искомое расстояние. Находим AH из прямоугольного
треугольника ABD.

Ответ:

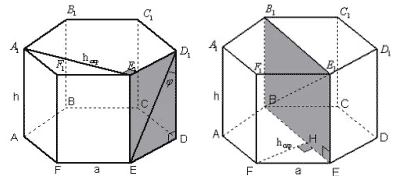
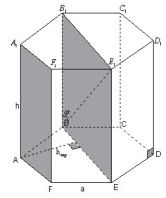
Задача 4. В правильной шестиугольной призме
A:F₁ c высотой h и стороной основания a
найти расстояние между прямыми:

Рисунок 9 Рисунок 10

а) AA₁ и ED₁.

Рассмотрим плоскость E₁EDD₁. A₁E₁EE₁, A₁E₁E₁D₁,
следовательно

A₁E₁ (E₁EDD₁). Также A₁E₁ AA₁.
Следовательно, A₁E₁ является
расстоянием от прямой AA₁ до плоскости E₁EDD₁.
ED₁(E₁EDD₁).,
следовательно AE₁ – расстояние от прямой AA₁
до прямой ED₁. Находим A₁E₁ из
треугольника F₁A₁E₁ по теореме
косинусов. Ответ:

б) AF и диагональю BE₁.

Проведем из точки F прямую FH перпендикулярно BE.
EE₁FH, FHBE, следовательно
FH(BEE₁B₁),
следовательно FH является расстоянием между
прямой AF и (BEE₁B₁), а значит и
расстоянием между прямой AF и диагональю BE₁.
Ответ:

СПОСОБ III

Применение этого способа крайне ограничено,
так как плоскость, параллельную одной из прямых
(способ II) строить легче, чем две параллельные
плоскости, однако способ III можно использовать в
призмах, если скрещивающиеся прямые принадлежат
параллельным граням, а также в тех случаях, когда
в многограннике несложно построить параллельные
сечения, содержащие заданные прямые.

Примеры

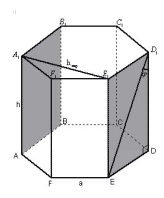
Задача 4.

Рисунок 11

а) Плоскости BAA₁B₁ и DEE₁D₁
параллельны, так как AB || ED и AA₁ || EE₁. ED₁DEE₁D₁,
AA₁(BAA₁B₁),
следовательно, расстояние между прямыми AA₁
и ED₁ равно расстоянию между плоскостями BAA₁B₁
и DEE₁D₁. A₁E₁AA₁, A₁E₁A₁B₁, следовательно, A₁E₁BAA₁B₁.
Аналогично доказываем, что A₁E₁(DEE₁D₁). Т.о., A₁E₁
является расстоянием между плоскостями BAA₁B₁
и DEE₁D₁, а значит, и между прямыми AA₁
и ED₁. Находим A₁E₁ из треугольника
A₁F₁E₁, который является
равнобедренным с углом A₁F₁E₁,
равным .
Ответ:

Рисунок 12

б) Расстояние между AF и диагональю BE₁
находится аналогично.

Ответ:.

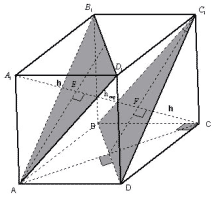
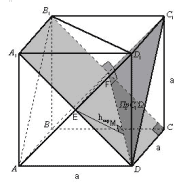
Задача 5. В кубе с ребром а найти
расстояние между двумя непересекающимися
диагоналями двух смежных граней.

Данная задача рассматривается как
классическая в некоторых пособиях, но, как
правило, ее решение дается способом IV, однако
является вполне доступной для решения с помощью
способа III.

Рисунок 13

Некоторую трудность в данной задаче вызывает
доказательство перпендикулярности диагонали A₁C
обеим параллельным плоскостям (AB₁D₁ ||
BC₁D). B₁CBC₁ и BC₁A₁B₁, следовательно,
прямая BC₁ перпендикулярна плоскости A₁B₁C,
и следовательно, BC₁A₁C. Также, A₁CBD.
Следовательно, прямая A₁C перпендикулярна
плоскости BC₁D. Вычислительная же часть
задачи особых трудностей не вызывает, так как h_скр
= EF находится как разность между диагональю куба
и высотами двух одинаковых правильных пирамид A₁AB₁D₁
и CC₁BD.

Ответ:

СПОСОБ IV.

Данный способ имеет достаточно широкое
применение. Для задач средней и повышенной
трудности его можно считать основным. Нет
необходимости применять его только тогда, когда
один из трех предыдущих способов работает проще
и быстрее, так как в таких случаях способ IV может
только усложнить решение задачи, или сделать его
труднодоступным. Данный способ очень выгодно
использовать в случае перпендикулярности
скрещивающихся прямых, так как нет необходимости
построения проекции одной из прямых на “экран”

Примеры.

Задача 5. Все та же “классическая” задача
(с непересекающимися диагоналями двух смежных
граней куба) перестает казаться сложной, как
только находится “экран” – диагональное
сечение куба.

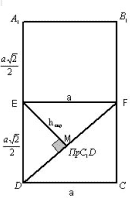
Рисунок 14

Экран:

Рисунок 15

Рассмотрим плоскость A₁B₁CD. C₁F (A₁B₁CD),
т. к. C₁FB₁C
и C₁FA₁B₁.
Тогда проекцией C₁D на “экран” будет
являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием
между двумя непересекающимися диагоналями двух
смежных граней. Находим EM из прямоугольного
треугольника EDF. Ответ:.

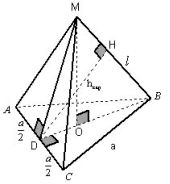
Задача 6. В правильной треугольной пирамиде
найти расстояние и угол между скрещивающимися
прямыми: боковым ребром l и стороной
основания a.

Рисунок 16

В данной и аналогичных ей задачах способ IV
быстрее других способов приводит к решению, так
как построив сечение, играющее роль “экрана”,
перпендикулярно AC (треугольник BDM), видно, что
далее нет необходимости строить проекцию другой
прямой (BM) на этот экран. DH – искомое расстояние. DH
находим из треугольника MDB, используя формулы
площади. Ответ: .

Комментарии преподавателя

1. Тема урока

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых

плоскости, параллельной другой прямой.

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых.

2. Определение скрещивающихся прямых

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

3. Теорема 1 (признак скрещивающихся прямых) и ее доказательство

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Доказательство

Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Рис. 1.

Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость – α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.

4. Возможные случаи расположения прямых

Три случая расположения прямых

1) Прямые a и b пересекаются в некоторой точке С:  (Рис. 2.). Как мы знаем, через две пересекающиеся прямые проходит единственная плоскость.

Рис. 2.

2) Прямые a и b параллельны: a || b (Рис. 3.). Если прямые параллельны, то они лежат в одной плоскости и не пересекаются.

Рис. 3.

Заметим, что и в первом, и во втором случае прямые лежали в одной плоскости.

3) Прямые a и b скрещиваются (Рис. 4.). То есть прямые a и b не лежат в одной плоскости.

Рис. 4.

5. Пример скрещивающихся прямых в треугольной пирамиде

Пример

Дана треугольная пирамида ABCD, АВС – плоскость основания, точка D не лежит в плоскости АВС (Рис. 5.). Почему прямые АВ и DC скрещивающиеся?

Рис. 5.

Прямая DC пересекает плоскость АВС в точке С, не лежащей на прямой АВ, а прямая АВ лежит в плоскости АВС. Значит, по признаку, прямые АВ и DC – скрещивающиеся. То есть противоположные ребра треугольной пирамиды лежат на скрещивающихся прямых.

6. Теорема 2 и ее доказательство

Теорема 2.

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство.

Пусть нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.

Рис. 6.

Проведем через точку А прямую АЕ, параллельную прямой DC (Рис. 6.). По теореме о параллельных прямых, такая прямая существует и единственная. Тогда через две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α. Так как прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости α,  значит, что прямая DC параллельна плоскости α, по признаку параллельности прямой и плоскости. Существование доказано.

Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямаяDC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α – единственная. Теорема доказана.

7. Задача 1

Точка D не лежит в плоскости треугольника АВС, точки M, N, P – середины отрезков DA, DB и DC соответственно, точка K лежит на отрезке BN (Рис. 7.). Выясните взаимное расположение прямых.

Рис. 7.

1) ND и AB.

Прямая ND – это другое обозначение прямой ВD. Прямая ВD и прямая АВ лежат в плоскости АВD и пересекаются.

2) PK и ВС.

Прямые PK и ВС лежат в одной плоскости. Значит, они либо параллельные, либо пересекаются. Проведем среднюю линию NP (N, P – середины отрезков DB и DC соответственно). По свойству средней линии, прямая NPпараллельна прямой ВС. Через точку Р можно провести только одну прямую, параллельную прямой ВС, и это прямая NP. Значит, любая другая прямая, проходящая через точку Р, не параллельна прямой ВС. Значит, PK иВС пересекаются.

3) MN и AB.

В треугольнике ABD точки M и N – середины сторон АD и ВD. Значит, МN – средняя линия. По свойству средней линии, МN параллельна АВ.

4) МР и АС.

В треугольнике ADС точки M и Р – середины сторон АD и СD. Значит, МР – средняя линия. По свойству средней линии, МР параллельна АС.

5) КN и АС.

Прямая КN и прямая ВD – это одна и та же прямая. Прямая АС лежит в плоскости АВС, прямая  ВD пересекает плоскость АВС в точке, не лежащей на прямой АС. Значит, по признаку, прямые ВD и АС – скрещивающиеся. То есть, прямые КN и АС- скрещивающиеся.

6) МD и ВС.

Прямая МD и прямая АD – это одна и та же прямая. Прямая ВС лежит в плоскости АВС, прямая  АD пересекает плоскость АВС в точке, не лежащей на прямой ВС. Значит, по признаку, прямые АD и ВС – скрещивающиеся. То есть, прямые МD и ВС – скрещивающиеся.

8. Задача 2

Докажите, что если АВ и СD скрещиваются, то АD и ВС тоже скрещиваются.

Доказательство

Предположим, что прямые АD и ВС не скрещивающиеся, то есть лежат в одной плоскости. Значит, все точки А, В, С, D лежат в этой плоскости, значит прямые АВ и СD тоже лежат в этой плоскости. Но прямые АВ и СDскрещивающиеся по условию. Получили противоречие. Значит, прямые АD и ВС – скрещивающиеся.

9. Итоги урока

Итак, мы познакомились со скрещивающимися прямыми: дали определение, доказали признак скрещивающихся прямых. Также мы доказали теорему о том, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теперь нам известны все случаи взаимного расположения прямых в пространстве: они могут пересекаться, быть параллельными, быть скрещивающимися.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/parallelnost-pryamyh-i-ploskostej/skreschivayuschiesya-pryamye-provedenie-cherez-odnu-iz-skreschivayuschihsya-pryamyh-ploskosti-parallelnoy-drugoy-pryamoy?seconds=0&chapter_id=210

http://www.metod-kopilka.ru/images/doc/54/49016/hello_html_m1b2a5d9c.png

http://festival.1september.ru/articles/593938/

http://www.proektant.ru/i/content/2014_II/4526_transportnaia_razviazka_02.jpg

Скрещивающиеся прямые

Две прямые в пространстве называются скрещивающимися, если они не пересекаются и не параллельны.

Теорема (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Доказательство. Пусть прямая а лежит в плоскости α, а прямая b пересекает эту плоскость в точке В, не лежащей на прямой а.

Докажем, что прямые а и b скрещивающиеся, т.е. не существует плоскости, в которой они обе лежат. Предположим, что прямые а и b лежат в некоторой плоскости β. Тогда плоскость β проходит через прямую а и точку В, а следовательно, совпадает с плоскостью α (так как через прямую и не лежащую на ней точку проходит единственная плоскость).

Получили, что прямая b лежит в плоскости α, а это противоречит условию теоремы. Таким образом, наше предположение неверно, а значит, прямые а и b – скрещивающиеся.

Теорема доказана.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная второй прямой, и притом только одна.

Доказательство. Пусть а и b – скрещивающиеся прямые. Докажем, что через прямую b проходит плоскость, параллельная прямой а.

Через какую-либо точку B прямой b проведем прямую с, параллельную прямой а.

Пусть α – плоскость, проходящая через прямые b и с. Так как прямая а не лежит в плоскости α и параллельная прямой с, лежащей в этой плоскости, то прямая параллельная плоскости α.

Плоскость α – единственная плоскость, проходящая через прямую b и параллельная прямой а.

Действительно, любая другая плоскость, проходящая через прямую b, пересекается с прямой с, а, следовательно, пересекается и с параллельной ей прямой.

Теорема доказана.

Пример 1. Используя рисунок, укажите прямую, скрещивающуюся с прямой АВ и принадлежащую плоскости АВВ1.

Решение. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Прямая АВ лежит в плоскости АВВ1. Эту плоскость пересекает прямая А1С1, следовательно, прямые АВ и А1С1 скрещиваются.

Ответ: АВ и А1С1

Задание 1. Используя рисунок, укажите прямую, скрещивающуюся с…

1)	прямой В1D1 и принадлежащую плоскости АВС	6)	прямой АС
2)	прямой ВС	7)	прямой СD1 и принадлежащую плоскости АВВ1
3)	прямой CD	8)	прямой А1D и принадлежащую плоскости ВСС1
4)	прямой ВВ1	9)	прямой AB
5)	прямой СВ и принадлежащую плоскости АDD1	10)	прямой АВ

Пример 2. Сколько прямых, содержащих ребра треугольной призмы ABCA1B1C1 скрещиваются с прямой ВС?

Решение. Прямая ВС лежит в плоскостях АВС и ВСС1В1.

Эти плоскости пересекают прямые АА1, А1В1 и А1С1. Следовательно, с прямой ВС скрещивается три прямых, содержащих ребра треугольной призмы.

Ответ: 3

Задание 2. Сколько прямых, содержащих ребра…

1)	куба ABCDA1B1C1D1 скрещиваются с прямой АВ?	4
2)	правильной треугольной призмы АВСА1В1С1, скрещиваются с прямой АВ?	3
3)	треугольной пирамиды ТАВС (Т – вершина пирамиды), скрещиваются с прямой АС?	1
4)	куба ABCDA1B1C1D1 скрещиваются с прямой ВD1?	6
5)	правильной треугольной призмы ABCA1B1C1 скрещиваются с прямой ВВ1?	2
6)	четырехугольной пирамиды ТАВСD (Т – вершина пирамиды), скрещиваются с прямой ВС?	2
7)	правильной треугольной призмы ABCA1B1C1 скрещиваются с прямой АВ1?	3
8)	четырехугольной пирамиды ТАВСD (Т – вершина пирамиды), скрещиваются с прямой АС?	2
9)	прямоугольного параллелепипеда ABCDA1B1C1D1 скрещиваются с прямой ВС?	4
10)	четырехугольной пирамиды ТАВСD (Т – вершина пирамиды), скрещиваются с прямой ТС?	2

Пример 3. DABC – треугольная пирамида. Точка Р лежит на ребре АС, а точка О – на медиане DF грани CDB. Верно ли, что прямые AD и РО параллельны?

Дано: DABC – пирамида. Доказать: AD║PO

Решение: Предположим, что прямые AD и РО параллельны между собой, тогда они лежат в одной плоскости, т.е. точки А, Р, D и О лежат в одной плоскости. Прямая DO пересекает плоскость АВС в точке F, не лежащей на прямой АР. Следовательно, прямые DO и АР являются скрещивающимися, т.е. не существует плоскости, в которой лежат точки А, Р, D и О. Это противоречит предположению параллельности прямых AD и РО, следовательно, прямые AD и РО не являются параллельными. Ответ: AD╫РО

Задание 3. Дан куб ABCDA1B1C1D1. Докажите, что данные прямые скрещиваются…

1)	А1А и ВС
2)	АВ и А1D
3)	АА1 и DВ1
4)	АВ1 и DC
5)	АС и ВD1

Задание 4. Отметьте верные утверждения…

1)	Через точку, не принадлежащую данной прямой, можно провести только одну прямую, параллельную этой прямой.
2)	Через точку, не принадлежащую данной прямой, можно провести только одну прямую, перпендикулярную этой прямой.
3)	Прямые, перпендикулярные одной и той же прямой параллельны.
4)	Прямая, пересекающая одну из двух данных параллельных прямых, пересекает и другую.
5)

Угол между скрещивающимися прямыми

Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми. Этот угол не зависит от того, какие взяты пересекающиеся прямые.

Для нахождения угла между двумя данными скрещивающимися прямыми а и b можно взять на одной из них, например на прямой а, некоторую точку О и провести через нее прямую b1, параллельную прямой b.

Тогда угол между прямыми а и b1 будет равен углу между скрещивающимися прямыми a и b.

Пример 4. Дана правильная треугольная призма АВСА1В1С1. Чему равен угол между прямыми АВ и А1С1?

	Дано: АВСА1В1С1 – призма. Найти: ∠(АВ;А1С1)
Решение: Прямые АВ и А1С1 скрещиваются. Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми. Прямая А1С1||АС, АС пересекается с прямой АВ. Поскольку призма АВСА1В1С1 правильная, то в ее основании лежит равносторонний треугольник с углами в 60О. Следовательно, прямыми АВ и А1С1 равен 60О. Ответ: 60О

Задание 3. Чему равен угол между прямыми…

1)	АВ и В1С1 в кубе ABCDA1B1C1D1?	90
2)	СС1 и АА1 в прямоугольном параллелепипеде ABCDA1B1C1D1?	0
3)	АВ и В1С1 в правильной треугольной призме ABCA1B1C1?	60
4)	АС и В1С1 в кубе ABCDA1B1C1D1?	45
5)	АС и B1D1 в прямоугольном параллелепипеде ABCDA1B1C1D1, если диагонали основания пересекаются под углом в 60о?	60
6)	АВ и CС1 в правильной треугольной призме ABCA1B1C1?	90
7)	АС и В1D1 в кубе ABCDA1B1C1D1?	45
8)	АС и B1D1 в прямоугольном параллелепипеде ABCDA1B1C1D1, если диагонали основания пересекаются под углом в 60о?	30
9)	ВС и АА1 в прямоугольном параллелепипеде ABCDA1B1C1D1?	90
10)	АА1 и CС1 в правильной треугольной призме ABCA1B1C1?	0

Задание 4. Решите задачу…

1)	Прямые ОВ и CD параллельные, а ОА и CD – скрещивающиеся. Найдите угол между прямыми ОА и СD, если ∠АОВ=40О.	40О
2)	Прямые ОВ и CD параллельные, а ОА и CD – скрещивающиеся. Найдите угол между прямыми ОА и СD, если ∠АОВ=135О.	45О
3)	Найдите угол между скрещивающимися прямыми АВ и PQ, если точки Р и Q равноудалены от концов отрезка АВ.	90О

Пример 6. Длина ребра правильного тетраэдра  равна 1. Найдите угол между прямыми  и , где  – середина ребра ,  – середина ребра .

Решение. Пусть  прямая параллельная прямой  и  точка ее пересечения с . Тогда искомый угол между прямыми  и  равен углу .  – средняя линия треугольника .

, .

По теореме косинусов: 

Поскольку  и , получим , откуда .

Ответ: 

Пример 7. Сторона правильной треугольной призмы  равна 8. Высота этой призмы равна 6. Найти угол между прямыми  и .

Решение. Достроим треугольную прямую призму до четырехугольной прямой призмы, в основании которой ромб , составленный из двух равносторонних треугольников.

Полученная призма является прямым параллелепипедом. Поэтому . Значит, искомый угол . Площадь ромба равна произведению квадрата его стороны на синус угла: .

С другой стороны, площадь ромба можно найти как половину произведения длин его диагоналей: , следовательно, .

Из прямоугольного треугольника  по теореме Пифагора находим . Аналогично, .

Из равнобедренного треугольника  получаем .

Ответ: 

Пример 8. Точка  – середина ребра  куба . Найдите угол между прямыми  и .

Решение. Примем ребро куба за единицу. Тогда .

Прямая , значит, искомый угол равен углу . Из прямоугольного треугольника  с прямым углом  имеем , тогда .

Ответ: 

Пример 9. На ребре  куба  отмечена точка  так, что . Найдите угол между прямыми  и .

Решение. Примем ребро куба за . Тогда .

Поскольку , получаем  и .

Проведем через точку  прямую, параллельную . Она пересекает ребро  в точке , причем треугольники  и  равны. Искомый угол равен углу  (или смежному с ним).

В прямоугольном треугольнике  с прямым углом  .

В прямоугольном треугольнике  с прямым углом  .

В треугольнике  . Откуда . Тогда .

Ответ: 

Пример 10. Боковое ребро правильной треугольной пирамиды  равно 10, а косинус угла  при вершине боковой грани равен  . Точка  – середина ребра . Найдите косинус угла между прямыми  и .

Решение. Пусть  – середина .

Поскольку  по теореме о средней линии треугольника, угол  искомый. Найдём стороны треугольника .

По теореме о средней линии треугольника .

По теореме косинусов из треугольника  получаем .

Чтобы найти , найдём сначала сторону основания по теореме косинусов из треугольника : .  как высота в равностороннем треугольнике со стороной 8. Отсюда .

Ответ: 

Пример 11.  – правильная треугольная призма, боковое ребро которой в два раза больше стороны основания. Точки  и  – середины ребер  и . Вычислите косинус угла между прямыми  и .

Решение. В плоскости грани  строим прямую . Тогда угол между скрещивающимися прямыми  и  есть угол между пересекающимися прямыми  и .

Пусть φ. В треугольнике  по теореме косинусов , откуда .

В треугольнике  (,,).

В треугольнике  (,,).

В треугольнике  (,,) . Отсюда .

Ответ: 

Пример 12. Все боковые грани призмы  – квадраты. На ребрах , ,  и  взяты соответственно точки , ,  и  – середины этих ребер. Найдите угол между прямыми  и .

Решение. Через прямую  и точку , взятую на прямой , проведем плоскость, в результате чего получим сечение призмы – четырехугольник .

В плоскости через точку  проведем прямую . Угол между прямыми  и  равен искомому углу.

На прямой  возьмем точку , а на прямой  – точку  и найдем .

Пусть ребро призмы равно .

В прямоугольном треугольнике  , . Тогда .

В прямоугольном треугольнике  , . Тогда .

В прямоугольном треугольнике  , . Тогда .

По теореме косинусов , откуда .

Таким образом, угол  тупой, поэтому искомый угол , значит, , т.е. .

Ответ: 

Пример 13. В правильной шестиугольной пирамиде  стороны основания равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми  и .

Решение. Прямая  параллельна прямой . Следовательно, искомый угол – .

В равнобедренном треугольнике  проведём медиану и высоту .

. Из прямоугольного треугольника  получаем .

Ответ: 

Пример 14. В правильном тетраэдре  найдите угол между высотой тетраэдра  и медианой  боковой грани .

Решение. Пусть и  – средняя линия треугольника . Тогда , значит,  и, следовательно, .

Кроме того, . Пусть длина ребра тетраэдра равна , тогда ; ; ; ; .

Ответ: 

Пример 15. Длины всех ребер правильной четырехугольной пирамиды  равны между собой. Найдите угол между прямыми  и , если отрезок  – высота данной пирамиды, точка  – середина ее бокового ребра .

Решение. Пусть отрезок  – средняя линия треугольника ,параллельная его стороне .

Поскольку  – правильная пирамида, точка  – центр квадрата . Так как  и , то , значит, . Прямые  и  параллельны, следовательно, угол между прямыми  и  равен углу между прямыми  и , то есть острому углу  прямоугольного треугольника .

Пусть длина ребра пирамиды равна , тогда ; ;  и, следовательно, .

Ответ: 

Пример 16. В правильной треугольной призме  все рёбра равны 1. Найдите косинус угла между прямыми  и .

Решение. Поскольку , необходимо найти угол .

По теореме Пифагора . Тогда . Высота  правильного треугольника  равна . По теореме косинусов , откуда .

Ответ: 

Пример 17. В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ=1 см, AD=2 см, АА1=1 см. Найдите угол между прямыми А1F и D1К, где точки F и К – середины ребер В1С1 и AD соответственно.

Дано: ABCDA1B1C1D1 – параллелепипед, АВ=1 см, AD=2 см, АА1=1 см. Найти: ∠(А1F, D1К)

Решение: Рассмотрим плоскость, проходящую через прямую A1F и точку К. Плоскость проходит через прямую А1К, параллельную плоскости грани ВВ1С1С (так как А1К║В1О, где точка О – середина ребра ВС), а следовательно, пересекает эту грань по отрезку, параллельному прямой В1О, т.е. по отрезку FC. Сечение параллелепипеда плоскостью есть четырехугольник КА1FC, который является параллелограммом (так как А1К=FC, А1К║FC). Следовательно, КС║A1F. Отсюда следует, что угол D1KC – искомый. Градусную меру угла D1KC найдем из треугольника D1КС. ΔKDD1=ΔCDD1, (DK=DC, ∠KDD1=∠CDD1=90o, DD1 – общая сторона). ΔKDC=ΔCDD1 (DK=DD1, DC – общая сторона, ∠KDC=∠CDD1=90o). Отсюда следует, что треугольник D1KC – равносторонний. Значит, ∠D1KC=60о. Ответ: 60о

Пример 18. SABC – тетраэдр. Точки F и К – середины его ребер АВ и АС соответственно. Найдите косинус угла между прямыми SF и ВК.

Дано: SABC – тетраэдр, AF=FB, AK=KC. Найти: cos(SF, BK)

Решение: В плоскости SCF через точку О=ВК∩FC проведем прямую OD, параллельную прямой SF. Тогда угол DOK – искомый. Соединим точку D с точкой К и найдем косинус угла DOK треугольника DOK. Для нахождения косинуса угла вычислим длины сторон треугольника DOK и воспользуемся теоремой косинусов. Пусть длина ребра тетраэдра равна а, ∠DOK=х. В треугольнике DKC (CD=CS=a, CK=, ∠KDC=60o) DK2=CK2+CD2-2CK⋅CDcos60o, DK2=a2. В треугольнике SFC OD║SF, OC=FC, следовательно, OD=SF==. В треугольнике DOK (OD=, OK=BK=) DK2=OD2+OK2-2OD⋅OKcosx, a2=a2+a2-2cosx. Отсюда cosх= Ответ:

Задание 5. Решите задачу…

1)	На ребрах AA1 и CD куба ABCDA1B1C1D1 взяты соответственно точки Р и Q – середины этих ребер. Найдите угол между прямой PQ и A1D.	30
2)	На ребрах В1С1, АС и А1В1 прямой призмы АВСА1В1С1, у которой АС=ВС=АА1 и ∠АСВ=90о, взяты соответственно точки D и E – середины ребер В1С1 и АС. Найти угол между прямой DE и АС1.	30
3)	На ребрах B1C1, АС и А1В1 прямой призмы АВСА1В1С1, у которой АС=ВС=АА1 и ∠АСВ=90°, взяты точки Р и Q – середины ребер АС и ВС. Найдите угол, который образует прямая АС1 с прямой PQ.	30
4)	В правильной призме ABCDA1B1C1D1 угол между диагоналями BD1 и B1D равен 90о. Найти угол, который образует прямая B1D с прямой АА1.	45
5)	Сторона основания правильной треугольной призмы равна 2 cм. Найдите косинус угла между прямыми, на которых лежат непересекающиеся диагонали двух смежных боковых граней призмы, если расстояния между этими прямыми равно 2 см.	0
6)	В основании пирамиды SABCD лежит квадрат, а ее боковое ребро SA равно стороне основания и перпендикулярно плоскости основания. На ребре SD взяты точки М1, М2 и М3 – такие, что DM1=M1M2=M2M3=M3S. Найти угол, который образует прямая SD с прямой СМ2.	30
7)	Основанием призмы АВСА1В1С1 является прямоугольный треугольник АВС, у которого АС=ВС. Грань ВСС1В1 перпендикулярна плоскости основания и угол С1СВ=45о, а ВС1=ВС. Найти угол между прямой АС и А1В.	90
8)	На ребрах В1С1, АС и А1В1 прямой призмы АВСА1В1С1, у которой АС=ВС=АА1 и угол АСВ=90о, взяты соответственно точки D, E и F – середины ребер В1С1, АС и А1В. Найти угол между прямой DE и AF.	0
9)	Основанием призмы АВСА1В1С1 является прямоугольный треугольник, у которого АС=ВС. Грань ВСС1В1 перпендикулярна плоскости основания, и ∠С1CB=45°, а ВС1=ВС. Найдите угол, которые образует прямая АС1 с прямой А1В.	90
10)	На диагонали АС квадрата ABCD взяты точки К1, К2 и К3 – такие, что АК1=К1К2=К2К3=К3С. Квадрат ABCD согнут по диагонали АС так, что треугольник BK2D равносторонний. Найдите угол, который образует прямая CD с прямой ВК1.	90
11)	Основанием призмы АВСА1В1С1 является прямоугольный треугольник, у которого АС=ВС. Грань ВСС1В1 перпендикулярна плоскости основания, и ∠C1CB=45°, а ВС1=ВС. Найдите угол, который образует прямая АС1 с прямой А1В.	90
12)	В основании пирамиды SABCD лежит квадрат ABCD. Ребро SB перпендикулярно плоскости основания и SB:AB=1:1. На ребре SC взята точка Р – середина этого ребра. Найти угол, который образует прямая DP с прямой SA.	30
13)	В основании пирамиды SABC лежит прямоугольный треугольник АВС (∠С=90о). Ребро SС перпендикулярно плоскости основания и SC=АС=ВС. На ребрах SB и SС взяты соответственно точки E и F – середины этих ребер. Найти угол между прямыми СЕ и AF.	90
14)	На ребрах А1В1 и АС прямой призмы АВСА1В1С1, у которой АС=ВС=АА1 и угол АСВ=90о, взяты соответственно точки D и Е – середины ребер АВ и ВС. Найти угол между прямыми А1С и BD.	30
15)	В правильной призме ABCDA1B1C1D1 угол между диагоналями BD1 и B1D равен 90о. Найти угол, который образует прямая B1D с прямой А1С1.	90

Пример 19. SАBCD – четырехугольная пирамида, основание которой – параллелограмм ABCD. Точка О – середина ребра SC. Постройте угол между прямыми DO и ВС.

	Дано: SАBCD – четырехугольная пирамида, SO=OC. Построить: ∠(DО, ВC)
Построение: Рассмотрим плоскость α, которая проходит через точку О∈DC и прямую DF. Эта плоскость пересекает ребро SB в точке К (FK║AB). В этой плоскости через точку О проведем прямую, параллельную прямой DF (прямая ОК). Таким образом, угол между скрещивающимися прямыми SO и DF есть угол между пересекающимися прямыми SO и ОК.

Пример 20. ABCDA1B1C1D1 – куб. Постройте угол между прямыми B1D и D1C.

	Дано: ABCDA1B1C1D1 – куб Построить: ∠(B1D, D1C)
Построение: В плоскости α, проходящей через точку D∈B1D и прямую D1C (плоскость грани DD1C1C), проведем прямую DK, параллельную прямой D1С. Тогда угол между скрещивающимися прямыми В1D и D1С есть угол между пересекающимися прямыми В1D и DК.

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми определяется как кратчайшее расстояние между точками этих прямых – оно равно длине их общего перпендикуляра.

Это расстояние равно расстоянию от одной из скрещивающихся прямых до плоскости, которая проходит через другую прямую параллельно первой.

Пример 21. Дан куб ABCDA1B1C1D1. Найдите расстояние между прямыми АВ1 и CD1, если длина ребра куба 4 см.

	Дано: ABCDA1B1C1D1 – куб, АВ=4 см Найти: (АВ1; CD1)
Решение: Расстояние между прямыми CD1 и АВ1 есть расстояние от любой точки прямой CD1 до плоскости АВВ1. Отрезок D1A1 – перпендикуляр, проведенный из точки D1 к плоскости АВВ1: D1A1⊥A1B1, D1A1⊥AA1, значит, D1A1⊥(АВВ1). Следовательно, его длина равна расстоянию между прямыми АВ1 и CD1, т.е. 4 см. Ответ: 4 см

Пример 22. В основании пирамиды МАВС лежит равнобедренный треугольник с прямым углом при вершине С. Высота пирамиды проектируется в точку О – середину ребра АВ, и ∠АМВ=90°. На ребре МА взята точка Р – середина этого ребра, а в грани МВС взята точка Q, в которой пересекаются медианы грани МВС. Найдите расстояние между прямыми АВ и PQ, если ВС=а.

Дано: МАВС – пирамида, ∠АМВ=90°, МР=РА. Найти: ОН

Решение: В плоскости МАВ через точку Р проведем прямую РК||АВ. Построим плоскость β, определяемую прямыми PQ и РК. Так как точка Q – точка пересечения медиан треугольника МВС, то прямая KQ пройдет через вершину С. Таким образом, в сечении пирамиды плоскостью β мы получаем треугольник СКР. Так как прямая АВ||РК, то прямая АВ параллельна плоскости СКР. Найдем расстояние от точки О до плоскости СКР. Для этого через точку О проведем плоскость γ, перпендикулярную прямой РК, лежащей в плоскости СКР. Так как прямая РК||АВ, то плоскость γ перпендикулярна и прямой АВ. Итак, в плоскости МАВ прямая ОМ перпендикулярна прямой АВ и в плоскости ABC прямая ОС перпендикулярна прямой АВ. Тогда плоскость, определяемая пересекающимися прямыми ОМ и ОС – это и есть плоскость γ перпендикулярная прямой АВ, т.е. и прямой РК. Находим линию пересечения плоскостей СКР и γ – прямую CL. Расстояние от точки О до прямой CL равно расстоянию между скрещивающимися прямыми АВ и PQ. Найдем его как высоту прямоугольного треугольника LCO. Если ОН – высота этого треугольника, то OH⋅CL=OC⋅OL, где из прямоугольного треугольника ABC находим ОС=АВ/2=а/2, из прямоугольного треугольника МАВ OL=ОМ/2=а/4, и из прямоугольного треугольника LCO CL==a/4. Таким образом, ОН=ОС⋅OL/CL=a/10. Ответ: a/10

Пример 23. В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ=3, АА1=4. Найдите расстояние между BD1 и AD.

	Дано: АВ=3; АА1=4 Найти: АК
Решение: BD1 и AD скрещиваются. Спроецируем эти прямые на плоскость грани АА1В1В. Получим точку А – проекцию прямой AD и прямую А1В – проекцию прямой BD1. Расстояние между BD1 и AD равно расстоянию от точки А до А1В, т.е. высоте АК прямоугольного треугольника АА1В: =2,4. Ответ: 2,4

Задание 6. Решите задачу…

1)	Ребро куба ABCDAlBlClDl равно 5 см. Найдите расстояния между прямой BlD и прямой D1C.	5
2)	На ребре СС1 правильной призмы ABCDA1B1C1D1 взяты соответственно точки Р1 и Р2, такие, что СР1=Р1Р2=Р2С1. Считая АВ= см, а АА1=3АВ, найдите расстояние между прямыми В1С и DP1.	1
3)	В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=АА1=10 см, AD=20 см. На ребре СС1 взята точка Р такая, что CP:CC1=1:3, а на ребре А1В1 взята точка V – середина этого ребра. Найдите расстояния между прямой В1С1 и прямой PV.	4
4)	На ребрах AB и ВlСl куба ABCDAlBlClDl взяты соответственно точки R и Q — середины этих ребер. Считая ребро куба равным 6 см, найдите расстояния между прямой BlD и прямой QR.	3
5)	Все ребра прямой призмы АВСА1В1С1 равны 2 см. На ребре АА1 взята точка Р — середина этого ребра. Найдите расстояния между прямой АВ1 и прямой СР.	3
6)	На ребре СС1 правильной призмы ABCDA1B1C1D1 взяты соответственно точки Р1 и Р2, такие, что СР1=Р1Р2=Р2С1. Считая АВ= см, а АА1=3АВ. Найдите расстояние между прямыми DC1 и В1Р1.	2
7)	В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=АА1= см, AD=2 см. На ребрах СС1 и AD взяты соответственно точки Р и Q, такие, что CP:CC1=AQ:AD=1:3. Найдите расстояния между прямой В1С1 и прямой PQ.	2
8)	Высота МО правильной пирамиды MABCD равна стороне ее основания и равна 3 см. На ребре МС взяты точки Р1, Р2 и Р3, такие, что СР1=Р1Р2=Р2Р3=Р3М. Найдите расстояние между прямой АС и прямой DP2.	3
9)	На ребре C1D1 куба ABCDA1B1C1D1 взята точка R – середина этого ребра. Ребро куба равно 6 см. Найдите расстояние между прямой B1D1 и прямой DR.	2
10)	На ребрах CD и ВlСl куба ABCDAlBlClDl взяты соответственно точки Р и Q — середины этих ребер. Считая ребро куба равным 2 см, найдите расстояния между прямой BlD и прямой PQ.	1
11)	Сторона основания правильной треугольной призмы равна 3 cм, а косинус угла между прямыми, на которых лежат непересекающиеся диагонали двух смежных боковых граней призмы, равен 1/2. Найдите расстояния между этими прямыми.	2
12)	На ребре DD1 куба ABCDA1B1C1D1 взята точка Q, такая, что DQ:DD1=2:3, а на диагонали А1В грани АВВ1А1 взята точка P —середина А1В. Считая ребро куба равным 2 см, найдите расстояния между прямой DP и прямой C1Q.	4
13)	На ребре СС1 правильной призмы ABCDA1B1C1D1 взяты соответственно точки Р1 и Р2, такие, что СР1=Р1Р2=Р2С1. Считая АВ= см, а АА1=3АВ, найдите расстояние между прямыми В1С и DP2.	2
14)	На ребре DD1 куба ABCDA1B1C1D1 взята точка Q, такая, что DQ:DD1=2:3, а на диагонали А1В грани АВВ1А1 взята точка P —середина А1В. Считая ребро куба равным 3 см, найдите расстояния между прямой DP и прямой С1A1.	6
15)	Высота МО правильной пирамиды MABCD равна стороне ее основания и равна 6 см. На ребре МС взяты точки Р1, Р2 и Р3, такие, что СР1=Р1Р2=Р2Р3=Р3М. Найдите расстояние между прямой АС и прямой DP1.	2
16)	Все ребра прямой призмы АВСА1В1С1 равны 2 см. На ребре СС1 взята точка Q — середина этого ребра. Найдите расстояния между прямой АВ1 и прямой BQ.	6
17)	На ребре АВ куба ABCDA1B1C1D1 взята точка Р – середина этого ребра. Ребро куба равно 4 см. Найдите расстояние между прямой B1D1 и прямой DP.	4
18)	Все ребра прямой призмы АВСА1В1С1 равны  см. Найдите расстояния между прямой АВ1 и прямой ВС.	3
19)	В основании пирамиды SABC лежит треугольник с прямым углом при вершине С и АС= см, ВС=2 см, а боковое ребро SC перпендикулярно плоскости и SC=BC. На ребрах АВ, SB и SC взяты соответственно точки Р, М и D –середины этих ребер. Найдите расстояние между прямыми АМ и РD.	1
20)	На ребре DD1 куба ABCDA1B1C1D1 взята точка Q, такая, что DQ:DD1=2:3, а на диагонали А1В грани АВВ1А1 взята точка P —середина А1В. Считая ребро куба равным  см, найдите расстояния между прямой DP и прямой C1D1.	2
21)	Сторона основания правильной треугольной призмы равна 18 cм, а косинус угла между прямыми, на которых лежат непересекающиеся диагонали двух смежных боковых граней призмы, равен -5/13. Найдите расстояния между этими прямыми.	9