Математика для блондинок
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Страницы
четверг, 14 марта 2013 г.
Куб и угол между прямыми
Сейчас решим задачу про куб и угол между прямыми. Задача звучит так:
Точка Е – середина ребра АА1 куба ABCDA1B1C1D1. Найдите угол между прямыми DE и BD1.
Для начала нужно соорудить конструкцию куба и разукрасить её буквами обозначений. Затем попробуем разобраться, чего надобно этим старцам от математики. Рисуем куб и прямые линии.
Получилось, что одна прямая линия совпадает с диагональю куба, вторая прямая линия проходит через боковую грань куба. Математики такие лини называют скрещивающиеся прямые. Угол между скрещивающимися прямыми определяется (не в смысле математическое определение типа “бла-бла-бла”, а когда конкретное дело делается) как угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым. Это не я такой умный, это у меня книжка умная есть, там и вычитал.
Возьмем ту прямую, которая на боковой грани и проведем параллельную ей прямую линию, проходящую через вершину D1. В этом случае мы получили две пересекающиеся прямые, для которых уже можно определить угол.
| Скрещивающиеся и пересекающиеся прямые |
Для определения угла нам нужны размеры куба. Без этого математика бессильна. Поскольку, по условию задачи, размеры куба нам не заданы, мы можем сами выбрать любой, благо все три размера у куба одинаковы. Примем длину ребра нашего куба за единицу. Получился куб в собственном соку, то есть в собственных единицах измерения. Весь этот математический фокус заключается в том, что угол между заданными нам прямыми совершенно не зависит от размеров куба. И в большом кубе, и в маленьком кубике углы между этими прямыми будут одинаковы.
Дальше всё просто, как в реанимации. Назначаем пациенту, то есть кубу:
1. Две теоремы Пифагора для двухмерного пространства.
2. Одну теорему Пифагора для трехмерного пространства.
3. Одну теорему косинусов.
4. Одну таблицу косинусов.
Теперь разберемся, к каким местам на теле куба всё это нужно прикладывать.
| Два прямоугольных треугольника, диагональ куба, искомый угол в треугольнике |
Рассуждаем от конца к началу. По таблице косинусов мы можем найти значение угла в градусах. Значение косинуса угла можно найти по теореме косинусов, если знать размеры сторон синенького треугольника из рисунка выше. По теореме Пифагора для трехмерного пространства мы можем найти диагональ куба – это одна из сторон треугольника. Две другие стороны треугольника можно найти на гранях куба по обычной (двухмерной) теореме Пифагора. А вот для применения теоремы Пифагора нам необходимы числовые размеры куба. Ведь просто слово “ребро” во вторую степень возвести не возможно. Вот для этого мы и приняли в самом начале размер ребра равным единице.
Мы проутюжили наше решение от начала к концу и от конца к началу. Лично у меня оно где-то по середине и срослось, на теореме Пифагора. Что бы там не утверждали наши современные математики, а математических инструментов мощнее тригонометрии и теоремы Пифагора они так и не создали.
Для полного счастья нам нужно ещё рассмотреть теорему косинусов. Ведь тупо записать её могут многие, а вот применять на практике этот калейдоскоп символов нужно ещё уметь. Посмотрите, как буковки в формулах переливаются! Это и есть первозданная красота математики.
Что такое математическая функция арккосинус? Это очень умное выражение, которым нас пугают математики. А фактически это наша голова и таблица косинусов перед глазами. Или специальная кнопочка на калькуляторе. Только вместо команды “Бобик, фас!” ( косинус – найти число по значению угла), нужно выполнять команду “Фас, покусай Бобика!” (арккосинус – найти значение угла по числовому значению косинуса).
Пусть у нас неизвестный угол будет по кличке “гамма”, а диагональку куба мы обзовем “а”. Отрезок прямой, что расположен на грани куба прямо перед нами, будет именоваться “с”, а на грани слева – “b”. Вот теперь можно погонять циферки и получить числовое решение задачи.
Угол между скрещивающимися прямыми : определение, примеры нахождения
В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.
В трехмерном пространстве имеются скрещивающиеся прямые a и b . Проведем прямые а 1 и b 1 параллельные скрещивающимся a и b . Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b 1 являются пересекающимися прямыми.
Обозначим угол между a 1 и b 1 равным значению α . Построение прямых a 2 и b 2 параллельно скрещивающимися относительно a и b в точке М 2 отличной от М 1 приводит к тому, что значение угла между ними обозначим как α . То есть угол между прямыми a 1 и b 1 равен углу между a 2 и b 2 . В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М 1 и М 2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.
Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат О х у z . Имеется задача, в которой необходимой найти угол α , образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M , что дает понять, через нее проходят прямые a 1 и b 1 , которые параллельны скрещивающимся a и b . Угол α , образованными прямыми a и b , из этого определения получится равным пересекающимся a 1 и b 1 .
Для нахождения искомого угла между a 1 и b 1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a 1 и b 1 .
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) .
Векторы a → и b → имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α = a r c cos a → , b → a → · b → = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 , а a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α = a → , b → a → · b → = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 .
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α = 1 – cos 2 α .
Найти угол между скрещивающимися прямыми a и b , которые заданы уравнениями x 2 = y – 4 0 = z + 1 – 3 и x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R и определяются в системе координат О х у z .
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a → = ( 2 , 0 , – 3 ) является направляющим вектором прямой x 2 = y – 4 0 = z + 1 – 3 . При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b → = ( 1 , – 1 , 4 ) является направляющим вектором для прямой вида x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R .
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 = a r c cos 2 · 1 + 0 · ( – 1 ) + ( – 3 ) · 4 2 2 + 0 2 + ( – 3 ) 2 · 1 2 + ( – 1 ) 2 + 4 2 = = a r c cos 10 13 · 18 = a r c cos 10 3 26
Ответ: угол между скрещивающимися прямыми равен a r c cos 10 3 26 .
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра A D и В С , принадлежащие пирамиде A B C D , с известными вершинами с координатами A ( 0 , 0 , – 1 ) , B ( 5 , 7 , – 5 ) , C ( 3 , 7 , – 5 ) , D ( 1 , 3 , 1 ) .
A D → и B C → являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что A D → = ( 1 – 0 , 3 – 0 , 1 – ( – 1 ) ) ⇔ A D → = ( 1 , 3 , 2 ) B C → = ( 3 – 5 , 7 – 7 , – 5 – ( – 3 ) ) ⇔ B C → = ( – 2 , 0 , – 2 )
Из формулы cos α = a r c cos A D → , B C → A D → · B C → находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α = 1 · ( – 2 ) + 3 · 0 + 2 · ( – 2 ) 1 2 + 3 2 + 2 2 · ( – 2 ) 2 + 0 2 + ( – 2 ) 2 = 6 14 · 8 = 3 2 7
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α = 1 – cos 2 α = 1 – 3 2 7 2 = 19 2 7 .
Ответ: sin α = 19 2 7 , cos α = 3 2 7 .
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
Имеется прямоугольный параллелепипед A B C D A 1 B 1 C 1 D 1 со сторонами А В = 3 , А D = 2 и A A 1 = 7 единиц. Точка E делит прямую А А 1 как 5 : 2 . Определить угол между скрещивающимися прямыми В Е и А 1 С .
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат О х у z . Получаем, что начало координат является совпадающим с вершиной A , а О х совпадает с прямой A D , О у с A B , а О z с А А 1 . Рассмотрим рисунок, приведенный ниже.
Отсюда имеем, что точка B с координатами ( 0 , 3 , 0 ) , E – ( 0 , 0 , 5 ) , A А – ( 0 , 0 , 7 ) , C – ( 2 , 3 , 0 ) . Исходя из координат, мы можем получить координаты векторов B E → и A 1 C → , необходимые для дальнейшего решения задачи. Получаем, что B E → = ( 0 , – 3 , 5 ) , A 1 C → = ( 2 , 3 , – 7 ) .
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α = a r c cos B E → , A 1 C → B E → · A 1 C → = a r c cos 0 · 2 + ( – 3 ) · 3 + 5 · ( – 7 ) 0 2 + ( – 3 ) 2 + 5 2 · 2 2 + 3 2 + ( – 7 ) 2 = = a r c cos 44 34 · 62 = a r c cos 22 527
Угол между прямыми в пространстве
Пусть в пространстве заданы прямые l и m. Через некоторую точку А пространства проведем прямые l1 || l и m1 || m (рис. 138).
Заметим, что точка А может быть выбрана произвольно, в частности она может лежать на одной из данных прямых. Если прямые l и m пересекаются, то за А можно взять точку пересечения этих прямых (l1 = l и m1 = m).
Углом между непараллельными прямыми l и m называется величина наименьшего из смежных углов, образованных пересекающимися прямыми l1 и m1 ( l1 || l , m1 || m). Угол между параллельными прямыми считается равным нулю.
Угол между прямыми l и m обозначается ( widehat <(l;m)>). Из определения следует, что если он измеряется в градусах, то 0° π /2 .
Найти угол между прямыми АВ и DС1.
Прямые АВ и DС1 скрещивающиеся. Так как прямая DC параллельна прямой АВ, то угол между прямыми АВ и DС1, согласно определению, равен (widehatDC>).
Следовательно, (widehat<(AB;DC_1)>) = 45°.
Прямые l и m называются перпендикулярными, если ( widehat <(l;m)>) = π /2. Например, в кубе
(см. рис. 139) прямая A1D1перпендикулярна прямым DC, DC1, СС1 .
Вычисление угла между прямыми.
Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости. Обозначим через φ величину угла между прямыми l1 и l2, а через ψ – величину угла между направляющими векторами а и b этих прямых.
ψ 90° (рис. 206,6), то φ = 180° – ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин) имеем
Пусть прямые заданы своими каноническими уравнениями
Тогда угол φ между прямыми определяется с помощью формулы
Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).
Задача 1. Вычислить угол между прямыми
Направляющие векторы прямых имеют координаты:
По формуле (1) находим
Следовательно, угол между данными прямыми равен 60°.
Задача 2. Вычислить угол между прямыми
За направляющий вектор а первой прямой возьмем векторное произведение нормальных векторов n1 = (3; 0; -12) и n2 = (1; 1; -3) плоскостей, задающих эту прямую. По формуле ( [a; b]=begin i & j & k \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 end ) получаем
$$ a=[n_1; n_2]=begin i & j & k \ 3 & 0 & -12 \ 1 & 1 & -3 end=12i-3i+3k $$
Аналогично находим направляющий вектор второй прямой:
$$ b=begin i & j & k \ 4 & -1 & 1 \ 0 & 1 & 1 end=-2i-4i+4k $$
Но формуле (1) вычисляем косинус искомого угла:
Следовательно, угол между данными прямыми равен 90°.
Задача 3. В треугольной пирамиде МАВС ребра MA, MB и МС взаимно перпендикулярны, (рис. 207);
их длины соответственно равны 4, 3, 6. Точка D – середина [МА]. Найти угол φ между прямыми СА и DB.
Пусть СА и DB – направляющие векторы прямых СА и DB.
Примем точку М за начало координат. По условию зядачи имеем А (4; 0; 0), В(0; 0; 3), С(0; 6; 0), D (2; 0; 0). Поэтому (overrightarrow) = (4; – 6;0), (overrightarrow)= (-2; 0; 3). Воспользуемся формулой (1):
По таблице косинусов находим, что угол между прямыми СА и DB равен приблизительно 72°.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/ugol-mezhdu-skreschivajuschimisja-prjamymi/
http://razdupli.ru/teor/84_ugol-mezhdu-pryamymi-v-prostranstve.php
[/spoiler]
В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.
В трехмерном пространстве имеются скрещивающиеся прямые a и b. Проведем прямые а1 и b1 параллельные скрещивающимся a и b. Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b1 являются пересекающимися прямыми.
Обозначим угол между a1 и b1 равным значению α. Построение прямых a2 и b2 параллельно скрещивающимися относительно a и b в точке М2 отличной от М1 приводит к тому, что значение угла между ними обозначим как α. То есть угол между прямыми a1 и b1 равен углу между a2 и b2. В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М1 и М2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.
Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат Охуz. Имеется задача, в которой необходимой найти угол α, образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M, что дает понять, через нее проходят прямые a1 и b1, которые параллельны скрещивающимся a и b. Угол α , образованными прямыми a и b, из этого определения получится равным пересекающимся a1 и b1.
Для нахождения искомого угла между a1 и b1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a1 и b1.
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a→=(ax, ay, az) и b→=(bx, by, bz).
Векторы a→ и b→ имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α=arccosa→, b→a→·b→=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2, а a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2.
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α=1-cos2 α.
Найти угол между скрещивающимися прямыми a и b, которые заданы уравнениями x2=y-40=z+1-3 и x=1+λy=1-λz=-3+4·λ, λ∈R и определяются в системе координат Охуz.
Решение
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a→=(2, 0, -3) является направляющим вектором прямой x2=y-40=z+1-3. При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b→=(1, -1, 4) является направляющим вектором для прямой вида x=1+λy=1-λz=-3+4·λ, λ∈R.
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2=arccos2·1+0·(-1)+(-3)·422+02+(-3)2·12+(-1)2+42==arccos1013·18=arccos10326
Ответ: угол между скрещивающимися прямыми равен arccos10326.
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра AD и ВС, принадлежащие пирамиде ABCD, с известными вершинами с координатами A(0, 0, -1), B(5, 7, -5), C(3, 7, -5), D(1, 3, 1).
Решение
AD→ и BC→ являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что AD→=(1-0, 3-0, 1-(-1))⇔AD→=(1, 3, 2)BC→=(3-5, 7-7, -5-(-3))⇔BC→=(-2, 0, -2)
Из формулы cos α=arccosAD→, BC→AD→·BC→ находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α=1·(-2)+3·0+2·(-2)12+32+22·(-2)2+02+(-2)2=614·8=327
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α=1-cos2α=1-3272=1927.
Ответ: sin α=1927, cos α=327.
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
Имеется прямоугольный параллелепипед ABCDA1B1C1D1 со сторонами АВ=3, АD=2 и AA1=7 единиц. Точка E делит прямую АА1 как 5:2. Определить угол между скрещивающимися прямыми ВЕ и А1С.
Решение
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат Охуz. Получаем, что начало координат является совпадающим с вершиной A, а Ох совпадает с прямой AD, Оу с AB, а Оz с АА1. Рассмотрим рисунок, приведенный ниже.
Отсюда имеем, что точка B с координатами (0, 3, 0), E – (0, 0, 5), AА – (0, 0, 7), C – (2, 3, 0). Исходя из координат, мы можем получить координаты векторов BE→ и A1C→, необходимые для дальнейшего решения задачи. Получаем, что BE→=(0, -3, 5), A1C→=(2, 3,-7).
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α=arccosBE→, A1C→BE→·A1C→=arccos0·2+(-3)·3+5·(-7)02+(-3)2+52·22+32+(-7)2==arccos4434·62=arccos22527
Ответ: arccos22527.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Начнем разбирать это задание с самых легких задач. Необходимо найти угол между двумя прямыми в кубе.
В кубе много параллельных ребер, поэтому задачи решаются просто. Если прямые скрещивающиеся, то используем определение угла между скрещивающимися прямыми: “Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым”.
В треугольной призме так же можно найти параллельные прямые.
В треугольной призме можно выполнить дополнительные построения, выходящие за пределы многогранника.
Из треугольника КАС легко можно найти угол КАС.
Вот еще случай, когда точка пересечения прямых лежит вне многогранника
Слайд 1Интерактивный метод в рамках ФГОС

Слайд 2ВСЕ ,ЧТО ХОЧЕШЬ, СКАЗАТЬ, СПРОСИ!

Слайд 3Пример модели урока с использованием интерактивного метода обучения
Класс : 10
в.
Тема: «Углы между скрещивающимися
прямыми в кубе».
Тип урока : формирование
умений и навыков.

Слайд 4Цели урока:
Дидактическая: научить находить и вычислять угол между скрещивающимися прямыми
в кубе; вырабатывать пространственное воображение.
Развивающая: активизировать познавательные способности, вырабатывать умение
анализировать и сравнивать.
Воспитательная: прививать аккуратность и трудолюбие, приучать умению выслушивать других и умению общаться.

Слайд 5Повторение-мать учения.
1.Отвечают два-три ученика вслух.
2.Отвечают друг- другу.
Результаты ответа оцениваются учениками.
В повторении задействованы все!!!

Слайд 6Всё, что мы знаем о кубе
Дать определение куба.
Сформулировать основные свойства
куба.
Вычислить длину диагонали грани.
Вычислить длину диагонали куба.

Слайд 7Всё, что мы знаем про угол между двумя прямыми в
пространстве.
Дать определение угла между двумя прямыми в пространстве.
Дать
определение угла между скрещивающимися прямыми.
Дать определение перпендикулярности прямых.
Сформулировать теорему о трёх перпендикулярах.

Слайд 8Ключ к решению задач.
Задача сводится к нахождению угла между
пересекающимися прямыми, соответственно параллельные данным.
Для этого параллельным переносом спроецировать
скрещивающиеся прямые на одну плоскость.
Для установления перпендикулярности скрещивающихся прямых использовать теорему о трёх перпендикулярах.

Слайд 9АНАЛИЗ КОНКРЕТНЫХ СИТУАЦИЙ.
Работа в группах по четыре человека

Слайд 10Ситуация 1
Найти все пары скрещивающихся прямых в кубе. Прямые- рёбра
куба . Найти углы между ними.Ответ:90o.

Слайд 11Ситуация 2
Найти все пары скрещивающихся прямых в кубе. Одна прямая-
ребро куба, другая-диагональ одной из граней. Найти углы между ними.
Ответ:45o.

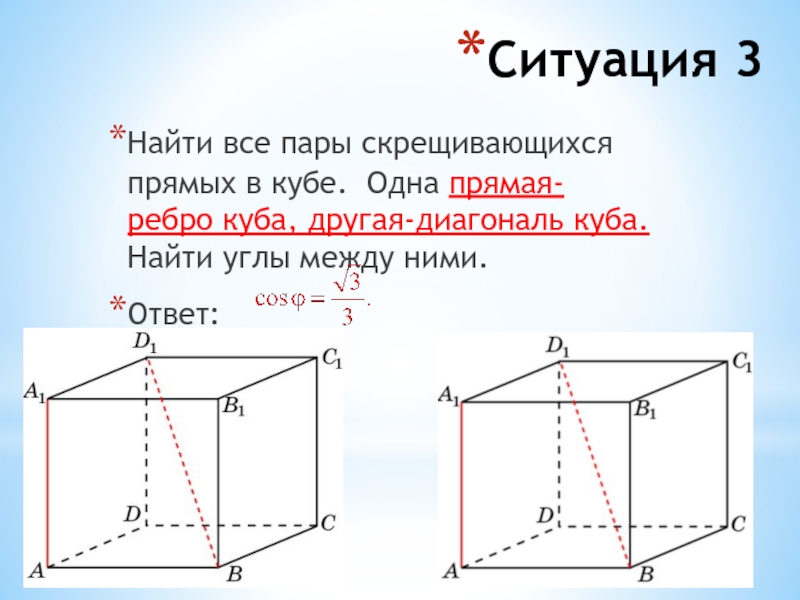
Слайд 12Ситуация 3
Найти все пары скрещивающихся прямых в кубе. Одна прямая-
ребро куба, другая-диагональ куба. Найти углы между ними.
Ответ:
Слайд 13Ситуация 4
Найти все пары скрещивающихся прямых в кубе. Прямые –
диагонали граней куба. Найти углы между ними.
Ответ:60o;90o.

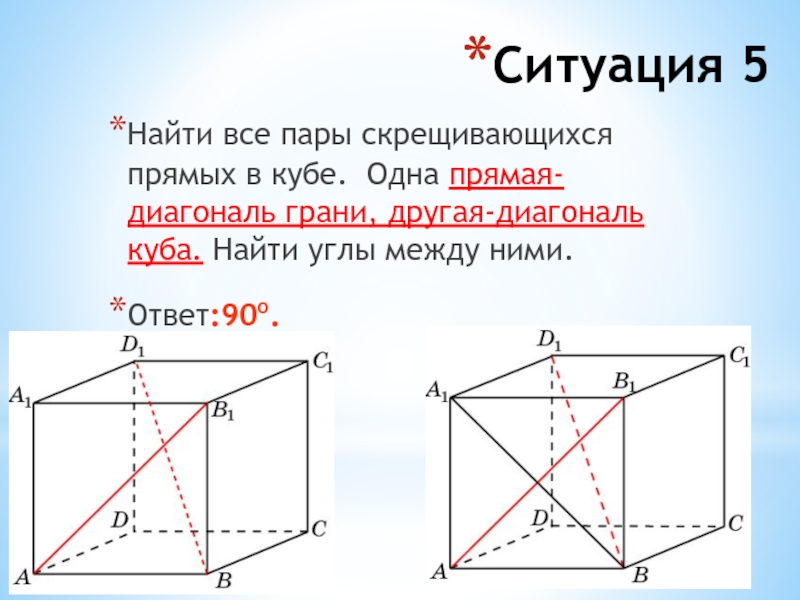
Слайд 14Ситуация 5
Найти все пары скрещивающихся прямых в кубе. Одна прямая-
диагональ грани, другая-диагональ куба. Найти углы между ними.
Ответ:90o.
Слайд 15Домашнее задание.
Чтобы знать путь, надо его пройти.
Письменное оформление решения
разобранных задач.

Рассмотрим
решения стереометрических задач из открытого банка заданий, расподоженного на
сайте Федерального института педагогических измерений (ФИПИ). Задачи на
нахождение углов между скрещивающимися прямыми в кубе.
Перед тем, как мы приступим к решению
первой задачи, вспомним определение угла между скрещивающимися прямыми.
Углом
между скрещивающимися прямыми называется угол
между двумя пересекающимися прямыми, которые соответственно параллельны
заданным скрещивающимся прямым.
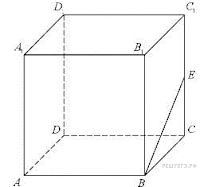
Решение.
По условию, задача верна для любого куба. Для того
чтобы в решении было меньше дробей, предположим, что ребро куба равно 2
единицам. Тогда CE=1 .
Прямая AD параллельна
прямой BC, значит, угол
между прямыми BE и AD равен углу CBE.
Из прямоугольного треугольника CBE с прямым углом С имеем:
tg ÐCBE = CE: CB =1:2 =0,5,
тогда ÐCBE = arctg0,5.
Ответ: arctg0,5.
Перед решением второй задачи напомним теорему
косинусов:
Квадрат стороны
треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними.
Задача 2. На ребре CC1
куба
ABCDA1B1C1D1 отмечена
точка E так, что CE:EC1=1:2. Найдите угол
между прямыми BE и AC1.
Задания для
самостоятельной работы.
1.
На
ребре CC1 куба ABCDA1B1C1D1
отмечена точка E так, что CE:EC1=3:1. Найдите угол между прямыми BE и AC1.
2.
На
ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=2:1. Найдите угол
между прямыми BE и AC1.
3.
На
ребре CC1 куба ABCDA1B1C1D1 отмечена
точка E так, что CE:EC1=2:3. Найдите угол
между прямыми BE и AC1.
4.
На
ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=1:3. Найдите угол
между прямыми BE и AC1.
5.
На
ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=3:2. Найдите угол
между прямыми BE и AC1.
6.
Точка
E — середина
ребра BB1 куба ABCDA1B1C1D1. Найдите угол
между прямыми AE и CA1.
7.
Точка
E — середина
ребра CC1 куба ABCDA1B1C1D1. Найдите
площадь сечения куба плоскостью A1BE, если рёбра
куба равны 2.
8.
Точка
E — середина
ребра DD1 куба ABCDA1B1C1D1. Найдите угол
между прямыми CE и AC1.
9.
Точка
E — середина
ребра BB1 куба ABCDA1B1C1D1. Найдите
площадь сечения куба плоскостью D1AE, если рёбра
куба равны 4.
10.
Точка
E — середина
ребра AA1 куба ABCDA1B1C1D1. Найдите угол
между прямыми DE и BD1.
11.
Точка
E — середина
ребра CC1 куба ABCDA1B1C1D1. Найдите угол
между прямыми BE и B1D.
12.
Точка
E — середина
ребра AA1 куба ABCDA1B1C1D1. Найдите
площадь сечения куба плоскостью C1DE, если рёбра
куба равны 2.
Точка E — середина ребра DD1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью B1CE, если рёбра куба равны 4.




