Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости
1.1. Условие задания
Построить следы плоскости, заданной ∆BCD, и определить расстояние от точки А до заданной плоскости методом прямоугольного треугольника (координаты точек А, В, С и D см. в Таблице 1 раздела Задания);
1.2. Пример выполнения задания № 1
Первое задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам трех точек B, C, D построить горизонтальную и фронтальную проекции плоскости, заданной ∆BCD;
2. Следы прямой, следы плоскости, свойства принадлежности прямой плоскости: построить следы плоскости, заданной ∆BCD;
3. Плоскости общего и частного положения, пересечение прямой и плоскости, перпендикулярность прямой и плоскости, пересечение плоскостей, метод прямоугольного треугольника: определить расстояние от точки А до плоскости ∆BCD.
1.2.1. По известным координатам трех точек B, C, D построим горизонтальную и фронтальную проекции плоскости, заданной ∆BCD (Рисунок 1.1), для чего необходимо построить горизонтальные и фронтальные проекции вершин ∆BCD, а затем одноименные проекции вершин соединить.
Известно, что следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с плоскостью проекций.
У плоскости общего положения 3 следа: горизонтальный, фронтальный и профильный.
Для того чтобы построить следы плоскости, достаточно построить следы (горизонтальный и фронтальный) любых двух прямых, лежащих в этой плоскости, и соединить их между собой. Таким образом, след плоскости (горизонтальный или фронтальный) будет однозначно определен, поскольку через две точки на плоскости (в данном случае этими точками будут следы прямых) можно провести прямую, и при том, только одну.
Основанием для такого построения служит свойство принадлежности прямой плоскости: если прямая принадлежит заданной плоскости, то ее следы лежат на одноименных следах этой плоскости.
Следом прямой называется точка пересечения этой прямой с плоскостью проекций.
Горизонтальный след прямой лежит в горизонтальной плоскости проекций, фронтальный – во фронтальной плоскости проекций.
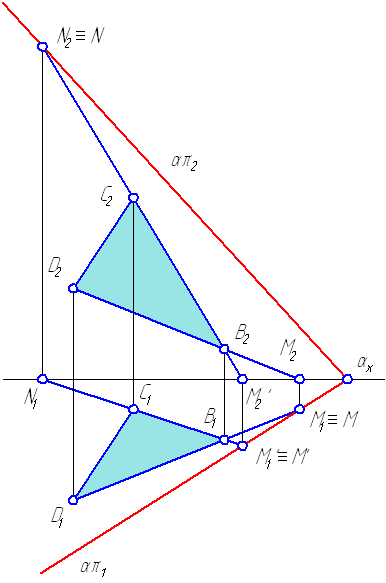
Рассмотрим построение горизонтального следа прямой DB, для чего необходимо:
1. Продолжить фронтальную проекцию прямой DB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
2. Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой DB или ее продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа (Рисунок 1.1), которая совпадает с самим следом М.
Аналогично выполняется построение горизонтального следа отрезка СВ прямой: точка М’.
Чтобы построить фронтальный след отрезка CB прямой, необходимо:
1. Продолжить горизонтальную проекцию прямой CB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
2. Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой CB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Соединив точки M′1 и M1 отрезком прямой, получим горизонтальный след плоскости απ1. Точка αx пересечения απ1 с осью X называется точкой схода следов. Для построения фронтального следа плоскости απ2 необходимо соединить фронтальный след N2 с точкой схода следов αx
Рисунок 1.1 — Построение следов плоскости
Алгоритм решения этой задачи может быть представлен следующим образом:
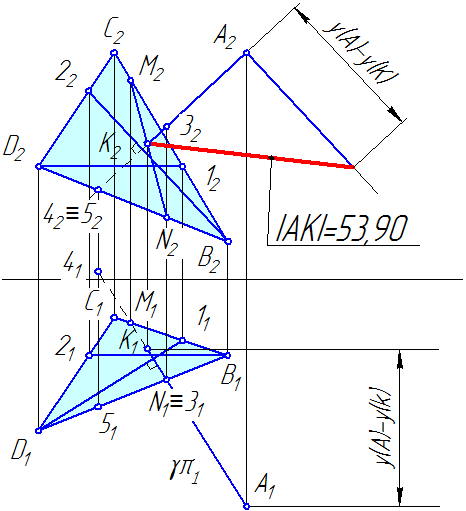
1.2.2. Для решения второй части первого задания необходимо знать, что:
- расстояние от точки А до плоскости ∆BCD определяется длиной перпендикуляра, восстановленного из этой точки на плоскость;
- любая прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- на эпюре проекции прямой, перпендикулярной плоскости, перпендикулярны наклонным проекциям горизонтали и фронтали этой плоскости или одноименным следам плоскости (рис. 1.2) (см. в лекциях Теорему о перпендикуляре к плоскости).
Чтобы найти основание перпендикуляра, необходимо решить задачу на пересечение прямой (в данной задаче такой прямой является перпендикуляр к плоскости) с плоскостью:
1. Заключить перпендикуляр во вспомогательную плоскость, в качестве которой следует взять плоскость частного положения (горизонтально-проецирующую или фронтально-проецирующую, в примере в качестве вспомогательной плоскости взята горизонтально-проецирующая γ, то есть перпендикулярная к π1, ее горизонтальный след γ1 совпадает с горизонтальной проекцией перпендикуляра);
2. Найти линию пересечения заданной плоскости ∆BCD со вспомогательной γ (MN на рис. 1.2);
3. Найти точку пересечения линии пересечения плоскостей MN с перпендикуляром (точка К на рис. 1.2).
4. Для определения истинной величины расстояния от точки А до заданной плоскости ∆BCD следует воспользоваться методом прямоугольного треугольника: истинная величина отрезка есть гипотенуза прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность расстояний от его концов до плоскости проекций, в которой ведётся построение.
5. Определите видимость участков перпендикуляра методом конкурирующих точек. На примере — точки N и 3 для определения видимости на π1, точки 4, 5 — для определения видимости на π2.
Рисунок 1.2 — Построение перпендикуляра к плоскости 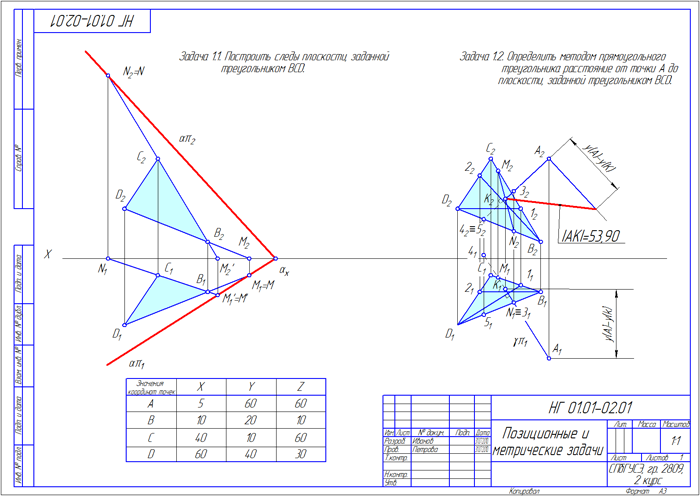
Рисунок 1.3 — Пример оформления контрольного задания №1
Следы плоскости
На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П1, П2, П3 по прямым h0α, f0α и p0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.
Оси координат пл. α пересекает в точках Xα, Yα и Zα. Они называются точками схода следов. При этом Xα = h0α ∩ f0α, Yα = h0α ∩ p0α, Zα = f0α ∩ p0α. Здесь знак ∩ означает пересечение.
На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве.
Алгоритм построения следов плоскости
На рисунке, который представлен ниже, некоторая плоскость α задана проекциями двух пересекающихся прямых a и b. Чтобы найти её следы, необходимо:
- Построить точки Ha и Hb – горизонтальные следы прямых a и b. Провести через них h0α – горизонтальный след пл. α до пересечения его с осью x.
- Построить точки Fa и Fb – фронтальные следы прямых a и b. Провести через них f0α – одноименный след плоскости α.
- Если построения выполнены верно, то прямые h0α и f0α пересекутся между собой в точке Xα, расположенной на оси проекций.
Решение задачи можно сократить. Для этого, построив горизонтальный след плоскости, фронтальный нужно провести через Xα и одну из точек, Fa или Fb. Таким образом, вместо четырех следов прямых a и b будет достаточно найти три.
Начертательная геометрия, решение задачи №1 ОмГУПС
Омский государственный Университет Путей Сообщения
З а д а ч а 1.
По координатам вершин А, B, C построить проекции треугольника. Найти горизонтальный и фронтальный следы плоскости треугольника ABC.
Горизонтальным (фронтальным) следом прямой называют точку пересечения прямой с горизонтальной П1 (фронтальной П2) плоскостью проекции.
Горизонтальным (фронтальным) следом плоскости называют линию пересечения плоскости с одноименной плоскостью проекций.
Следы плоскости проходят через следы прямых, лежащих в этой плоскости, и пересекаются на оси проекций 0х. Так как следы прямых и плоскостей принадлежат плоскостям проекций, то их проекции на эти плоскости совпадают с самими следами, а другие проекции принадлежат осям проекций.
Решение и построения: По заданным координатам для варианта 24 (заочное обучение) строим проекции точек А, B, C в плоскостях проекций П2 и П1 в масштабе М 2:1, соединяем точки получаем проекции треугольника АВС.
Определяем горизонтальный след плоскости треугольника h0 по горизонтальным следам прямых АC и BС, принадлежащих заданной плоскости. Для нахождения горизонтального следа прямой АС продолжаем ее фронтальную проекцию А2С2 до пересечения с осью проекции H2, которая является фронтальной проекцией искомого следа. Проводим из этой точки перпендикуляр к оси проекций (линию связи) до пересечения его с продолжением горизонтальной проекции А1С1, Н1 является горизонтальной проекцией искомого следа, она совпадает с самим следом H.
Аналогичным образом находим фронтальный след H’ прямой BС. Соединив проекции H1 и H’1, найдем горизонтальную проекцию горизонтального следа плоскости h0, и точку схода следов SX на оси проекций.
Фронтальный след заданной плоскости пройдет через точку схода следов SX и фронтальный след любой прямой этой плоскости, например прямой АС. Для нахождения последнего продолжаем проекцию А1С1 до пересечения с осью проекций, F1 является горизонтальной проекцией искомого следа. Фронтальную проекцию F2 определяем по линии связи на продолжении проекции А2С2. Соединив Sх и F2, найдем фронтальный след плоскости f0.
В нашем случае точка схода следов плоскости выходит за пределы чертежа, этом случае можно было найти два фронтальных и два горизонтальных следа прямых заданной плоскости.
В налиции все варианты готовых чертежей для ОмГУПС. Чертежи высылаются, сразу после оплаты на карту Сбербанка, Яндекс.Деньги или Киви кошелек, в формате *.cdw (Компас)+рисунки jpeg в цвете в хорошем разрешении 300dpi. По желанию, могу заполнить штампы. Выполнение карандашом таких чертежей на заказ 5 листов- 1500 руб.
[spoiler title=”источники:”]
http://ngeometry.ru/sledy-ploskosti.html
http://stud55.ru/nachertatelnaya-zadacha1-omgups/
[/spoiler]
Плоскость, как и прямая, и точка, является одним из основополагающих понятий в геометрии.
Плоскость, в зависимости от расположения в пространстве, может быть общего и частного положения.
К плоскостям частного положения относятся:
- параллельные одной из плоскостей проекций;
- проецирующие плоскости, перпендикулярные одной из плоскостей проекций.
Плоскости общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций.
Способы задания плоскостей в пространстве
Плоскость можно задать следующими способами:
- Тремя точками. Три точки пространства однозначно задают одну и только одну плоскость. Так же говорят о задании плоскости треугольником, вершины которого и являются этими тремя точками (рис. 6.1-а).
- Плоскость можно задать прямой и точкой (рис. 6.1-б).
- Двумя пересекающимися прямыми (рис. 6.1-в).
- Двумя параллельными прямыми (рис.6.1-г).
- Плоскость можно задать следами (рис.6.1-д).
Построение следов плоскости
Следом плоскости называется линия пересечения этой плоскости с плоскостью проекций.
Поскольку следом плоскости является прямая, лежащая в плоскости проекций, для ее построения достаточно найти следы двух любых прямых, лежащих в заданной плоскости.
Рассмотрим на примере последовательность построения горизонтального и фронтального следов плоскости.
Задача 6.1.
Построить горизонтальный и фронтальный следы плоскости α, заданной треугольником АВС (рис. 6.2).
Решение:
Выберем в заданной плоскости две прямые и построим их следы. В качестве таких прямых можно взять стороны треугольника – АВ и ВС.
Построим сначала горизонтальные следы этих прямых. На рисунке 6.3 показано построение точек 1 и 2, которые являются горизонтальными следами прямых АВ и ВС соответственно.
Порядок построения следующий:
- Продлим фронтальную проекцию стороны треугольника А2В2 до пересечения с осью х и отметим точку 12.
- Продлим горизонтальную проекцию отрезка А1В1 ( на рисунке показано штриховой линией).
- Спроецируем точку 12 на продолжение прямой А1В1 и получим точку 11.
Итак, мы получили две проекции горизонтального следа прямой АВ – точки 11, 12.
По строим в том же порядке горизонтальный след прямой ВС – точки 22и 21.
Соединим точки 11и 21, продолжим эту прямую до оси х. Получили горизонтальный след плоскости α – прямую αх. (Рис.6.4).
Для построения фронтального следа заданной плоскости, нужно построить фронтальные следы прямых АВ и ВС.
Построим фронтальный след прямой ВС (рис. 6.5). Как видно из рисунка, для этого необходимо продлить проекцию В1С1 до оси х, где получим точку 31; затем надо продлить проекцию В2С2таким образом, чтобы на нее можно было спроецировать точку 31и получить фронтальный след прямой ВС — точку 32.
Выполним построение фронтального следа прямой АВ, аналогично предыдущему построению, как показано на рисунке 6.6. Точка 42 является фронтальным следом прямой АВ.
Для завершения построения фронтального следа плоскости, заданной треугольником АВС, нужно соединить точки 32 и 42. Фронтальный след плоскости проводят до пересечения с осью х. Следы плоскости общего положения всегда имеют общую точку на оси проекций. В данном случае это ось х (рис. 6.7). Задача решена.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
171
Добавлен:
12.03.2015
Размер:
4.24 Mб
Скачать

2. «ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ И ИХ ВЗАИМОРАСПОЛОЖЕНИЕ»
Каждый след плоскости представляет собой прямую, для построения которой нужно знать либо две точки, либо одну точку и направление. Двумя точками, с помощью которых определяется положение следа плоскости, могут быть одноименные следы двух прямых, принадлежащих плоскости. В качестве одной из точек может быть использована точка схода следов на оси проекций.
На рис. 2.1 показано построение следов плоскости, заданной треугольником BCD. Чтобы построить фронтальный след РV плоскости BCD, находим фронтальные следы прямых CD и ВС (точки N и N1) в следующей последовательности:
а) продолжаем горизонтальную проекцию cd стороны треугольника CD до пересечения с осью Ох в точке п;
б) из точки п восстанавливаем перпендикуляр к оси Ох;
в) продолжаем фронтальную проекцию CD (c’d’) до пересечения с перпендикуляром;
г) на пересечении получаем фронтальный след прямой CD – точку N≡п’. Затем аналогично строим фронтальный след прямой ВС –
точку N1≡п1′. Фронтальный след РV плоскости Р будет проходить через
точки N и N1.
Горизонтальный след плоскости РН строится аналогично. Следует отметить, что в данном случае для построения следа РН достаточно иметь горизонтальный след только одной прямой, например, ВD – точку М. Второй точкой, определяющей положение следа РН, будет точка схода следов РХ (точка пере-
Рис. 2.1 сечения ранее построенного следа РV с осью Ох).
2.2. Определение расстояния от точки до плоскости
Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Таким образом поставленная задача сводится к проведению через точку А прямой, перпендикулярной к плоско-
11

сти, нахождению точки встречи этой прямой с плоскостью и определению истинной величины отрезка прямой, заключенного между точкой А и точкой встречи. Как известно, если прямая перпендикулярна плоскости, то ее проекции перпендикулярны одноименным следам или соответствующим проекциям линий уровня этой плоскости (горизонтали и фронтали).
2.2.1. Определение расстояния от точки А до плоскости треугольника BCD
Проведем в плоскости треугольника BCD (рис. 2.2) горизонталь ВI (b1; b′1′) и фро нталь СII (с2; с′2′) и опустим из точки а′ перпендикуляр на
прямую с′2′, а из точки а – перпендикуляр на прямую b1. Основанием перпендикуляра является точка его пересечения с плоскостью BCD.
Для того, чтобы найти точку пересечения перпендикуляра с плоскостью заключаем перпендикуляр в горизонтально проецирующую плоскость R, которая пересекает плоскость треугольника BCD по прямой MN (mn; m‘n’). На пересечении m‘n’ с фронталь-
Рис. 2.2 ной проекцией перпендикуляра находим фронтальную проекцию его осно-
вания – точку k′. Спроецировав точку
k′ на горизонтальную проекцию линии MN (mn), получим точку k. Натуральную величину перпендикуляра АК определим способом прямoугольного треугольника как длину гипотенузы
A0k′треугольника A0 a′k′.
2.2.2 Определение расстояния от точки А до плоскости Р, заданной следами
|
Строим проекции перпендикуля- |
||
|
ра к плоскости. Горизонтальную про- |
||
|
екцию перпендикуляра проводим из |
||
|
точки а перпендикулярно горизон- |
||
|
тальному следу плоскости PH, а |
||
|
фронтальную проекцию из точки а′ |
||
|
перпендикулярно PV (рис. 2.3). Осно- |
||
|
ванием перпендикуляра является точ- |
Рис. 2.3 |
|
|
ка его пересечения с плоскостью P. |
||
12

Чтобы ее найти, заключаем перпендикуляр в горизонтально проецирующую
плоскость T, которая пересекает плоскость Р по прямой MN (mn; m′n’). На пересечении фронтальной проекции прямой с фронтальной проекцией пер-
пендикуляра находим фронтальную проекцию его основания – точку k′.
Спроецировав точку k′ на горизонтальную проекцию линии MN (mn), получим точку k. Натуральную величину перпендикуляра АК определим способом прямoугольного треугольника.
2.3.Построение плоскости S (SH; SV), параллельной плоскости Р
иотстоящей от нее на три масштабные единицы
На натуральной величине перпендикуляра АК (рис. 2.4) откладываем от точки k′ три масштабные единицы (30 мм) – получаем точку 30. Опустив из этой точки перпендикуляр на фронтальную проекцию отрезка а’k′, получим
точку 3′, а затем в проекционной связи точку 3 на горизонтальной проекции перпендикуляра аk.
Рис. 2.4
Проводим через точку (3, 3′) горизонталь искомой плоскости S параллельно произвольной горизонтали плоскости Р. Ее горизонтальная проекция должна проходить через точку 3, параллельно следу РН, а фронтальная проекция – через точку 3′, параллельно оси проекций. Найдя фронтальный след
этой горизонтали N2≡п2‘, проводим следы искомой плоскости: сначала фронтальный след SV через точку N2≡п2‘, параллельно следу РV до пересечения с
13
осью проекций в точке SХ, а затем через эту точку – горизонтальный след SH,
параллельно следу РН.
2.4. Проведение через произвольно взятую точку Е плоскости R, перпендикулярной к заданной прямой
|
Первый способ. При решении |
||||
|
этой задачи |
необходимо |
выполнить |
||
|
требование |
о |
том, чтобы прямая |
||
|
(например, сторона треугольника BD) |
||||
|
была перпендикулярна к двум пересе- |
||||
|
кающимся прямым плоскости (кото- |
||||
|
рую предстоит построить). В соответ- |
||||
|
ствии с теоремой об ортогональной |
||||
|
проекции прямого угла в качестве |
||||
|
двух пересекающихся прямых следует |
||||
|
выбрать прямые уровня – горизонталь |
||||
|
и фронталь, а их соответствующие |
||||
|
проекции построить так, чтобы вы- |
||||
|
полнились требования: h bd, f′ b′d′. |
||||
|
Рис. 2.5 |
||||
|
Именно так |
построена |
плоскость |
||
R(h×f), проведенная через произвольную точку Е (е; е′), на рис. 2.5. Нахож-
дение точки К(k, k′) пересечения стороны BD с плоскостью R показано на рисунке.
Второй способ. Через произвольно взятую точку Е проводим горизонталь: фронтальную проекцию горизонтали параллельно оси проекций Ох, а горизонтальную проекцию – перпендикулярно bс (рис. 2.6). Через фронтальный след гори-
зонтали N≡n′ проводим фронтальный след
плоскости RV перпендикулярно b′с′. Из точки RХ проводим горизонтальный след плоскости RН перпендикулярно bс. Для нахождения точки пересечения прямой ВС с плоскостью R заключаем прямую ВС в горизонтально проецирующую плоскость Т. Находим линию пересечения
|
M1N1 (m1n1, m1′n1′) плоскостей R и Т. От- |
||
|
мечаем точку К (k, k′) на пересечении |
||
|
Рис. 2.6 |
||
|
прямых ВС и M1N1. |
||
14
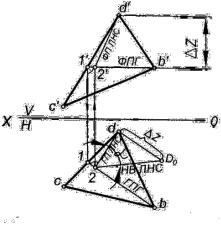
Рис. 2.7
2.5. Определение угла наклона плоскости к горизонтальной плоскости проекций
Для определения угла α наклона плоскости треугольника BCD к горизонтальной плоскости проекций Н используем линию наибольшего наклона (ската) плоскости.
Линиями наибольшего ската называют прямые данной плоскости, перпендикулярные к линиям уровня этой плоскости. Поэтому из точки d проводим горизонтальную проекцию линии наибольшего ската (ГП ЛНС) плоскости BCD под прямым углом к горизонтальной проекции горизонтали – получаем точку 2 (рис. 2.7). Затем строим фронтальную проек-
цию этой точки – 2′. Фронтальная проекция линии наибольшего ската (ФП ЛНС) пройдет через точки d′ и
2′. Натуральную величину линии наибольшего ската DII определим способом прямoугольного треуголь-
ника. Угол α между линией наибольшего ската и ее горизонталь-
ной проекцией определяет наклон плоскости BCD к плоскости Н.
15

3. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
Наиболее простое и точное решение задач удается получить, если заданные геометрические фигуры приведены в определенное частное положение относительно плоскостей проекций. Это достигается следующими способами:
1.оставляя проецируемый объект (фигуру) в заданном полож ении, изменяют положение плоскостей проекций относительно объекта (способ замены плоскостей проекций);
2.оставляя плоскости проекций в заданном положении, из меняют положение проецируемого объекта (фигуры) относительно этих плоскостей (способ вращения).
3.1.Способзаменыплоскостейпроекций
Сущность способа замены плоскостей проекций состоит в том, что заданную систему плоскостей проекций заменяют новой системой так, что геометрические фигуры оказываются в частном положении относительно новой системы плоскостей проекций.
Рис. 3.1
Проследим, как изменятся проекции точки B, если плоскость V заменить на новую плоскость проекций V1 (рис. 3.1, а) . Плоскость V1 проводим перпендикулярно плоскости Н, положение которой остается без изменения. Плоскости Н и V1 пересекутся по прямой 0х1, определяющей новую ось проекций. В новой системе плоскостей проекций вместо проекций b и b’ получим новые проекции b и b1′. Легко убедиться, что расстояние от новой проекции точки b1′ до новой оси 0х1
16
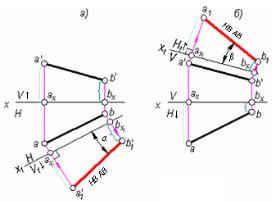
(координата Z) равно расстоянию от заменяемой проекции b’ до заменяемой оси 0х. Чтобы перейти от пространственного чертежа к эпюру, нужно совместить плоскость V1 с плоскостью Н. На эпюре (рис. 3.1, 6) для построения новой проекции b1′ используем неизменность координаты Z точки B. Для этого достаточно из горизонталь ной про-
екции b провести перпендикуляр к новой оси 0х1 и от точки bX1 от-
|
ложить координату Z, определяемую расстоянием b’bx (ZB) в прежней |
|
|
системе. |
горизонтальной плоскости Н новой плоскостью Н1 |
|
Замена |
|
|
(рис. 3.1, в) |
производится аналогично, с той лишь разницей, что т е- |
перь не изменяется фронтальная проекция точки b’, для построения новой горизонтальной проекции b1 необходимо из сохраняемой фронтальной проекции b’ провести линию связи к новой оси 0х1 и отложить от новой оси расстояние, равное расстоянию от заменяемой проекции b до заменяемой оси 0х.
Замена плоскостей проекций может осуществляться только п о- следовательно, нельзя менять обе плоскости сразу.
Рассмотрим на примерах, как производится з амена плоскостей проекций и строятся новые проекции фигур.
Задача 1. Определить длину отрезка прямой АВ общего положе-
ния.
Заменяем плоскость V плоскостью V1, параллельной отрезку АВ (рис. 3.2, а). Проводим новую ось Х1 параллельно ab и на перпендикулярах, проведенных к ней из точек а и b, откладыва-
ем аX1а1′ = аxа’ и bX1b1′ =
bxb’. Получаем новую про-
екцию a1′b1′ = AB и одновременно угол α
наклона прямой к пло с- кости Н.
Если плоскость Н заменим плоскостью H1 параллельной отрезку АВ (рис. 3.2, б), то получим
а1b1 = АВ и угол β накло- Рис. 3.2 на прямой к плоскости V.
Задача 2. Определить
натуральную величину треугольника ABC.
Задача решается последовательной заменой двух плоскостей проек-
ций.
17

Рис. 3.3
Сначала плоскость V заменяем плоскостью V1, перпендикулярной к плоскости треугольника (рис. 3.3). Для этого в плоскости треугольника проводим горизонталь
AD (ad, a’d’) и новую ось
Х1 располагаем перпендикулярно к ad. На новой плоскости проек-ций треугольник спроецируется в прямую b1′а1 ′с1 . На втором этапе плоскость Н заменяем плоскостью Н1,
параллельной плоскости треугольника, располагая ось Х2 параллельно прямой b1′а1 ′с1′. По-строенная проекция a1b1с1 определяет нату-ральную величину и форму треугольника ABC.
Задача 3. Определить расстояние от точки А (а, а’) до плоскости Р, заданной следами PH и PV (рис. 3.4).
Задача решается путем замены одной из плоскостей проекций новой, относительно которой плоскость Р будет проецирующей.
Заменим, например, плоскость V плоскостью V1, перпендикулярной к плоскости Р. Новую ось X1 проводим перпендикулярно к следу РН. Выбираем на следе PV произвольную точку N (п, п’) и находим ее новую проекцию п1 ′,
откладывая nX1n1′ = nxn’ = yN. Через точки PX1 и п1 ′ проводим новый след PV1. По-
строив новую проекцию a1 ′ и опустив из нее перпендикуляр на PV1, определяем расстояние от точки А до плоскости Р, которое равно отрезку a1′k1′. После этого опре-деляем на первона- чаль-ном чертеже положение проекции основания перпендикуляра (k, k′).
Рис.3.4
18

3.2. Способ вращения
Сущность способа вращения состоит в изменении положения объекта, заданного на эпюре, таким образом, чтобы определенные его элементы заняли относительно плоскостей проекций частное положение и проецировались без искажений.
Рассмотрим следующие разновидности способа вращения: вращение вокруг линий уровня и совмещение.
При вращении важно правильно определить его элементы: ось, а также плоскость, центр, радиус и угол вращения.
3.2.1. Вращение вокруг линий уровня
Одним поворотом вокруг горизонтали или фронтали можно расположить плоскую фигуру или плоский угол параллельно одной из плоскостей проекций и тем самым определить их натуральную величину.
На рис. 3.5 показаны построения при вращении точки D вокруг горизонтали до положения, при котором радиус вращения RD = DO становится параллельным плоскости H и проецируется на нее в натуральную величину, т.е. d1o = D1O = DO.
Рис. 3.5
Построения на эпюре сводятся к определению способом прямоугольного треугольника длины радиуса вращения RD и откладыванию ее на перпендикуляре, проведенном из точки d к горизонтали I (i, i′). Точка D (d, d’) перемещается в положение D1 (d1, d1′).
Задача. Определить натуральную величину треугольника ABC
(рис. 3.6).
В плоскости треугольника АВС (аbс, а′b’с’) проводим горизонталь СD (cd, c’d’) и вращаем вокруг нее заданный треугольник до положения, при котором он станет параллельным плоскости Н. Точки С (с, с’) и D (d, d’) неподвижны. Для определения повернутого положения вершины А определяем
19

величину радиуса RA способом прямоугольного треугольника и откладываем ее на перпендикуляре к cd, опущенном из точки а. Получаем точку а1.
Положение точки b1 определяем, проводя прямую а1d до пересечения с перпендикуляром, опущенным из точки b на cd.
Горизонтальная проекция треугольника а1b1c1 по величине равна треугольнику AВС. Новая фронтальная проекция представляет собой прямую, совпадающую с с’d’.
|
3.2.2. Способ совмещения |
|
|
Вращение плоскости вокруг оси, |
|
|
совпадающей с плоскостью проекций, |
|
|
Рис. 3.6 |
т.е. вокруг следа плоскости, является |
|
частным случаем вращения вокруг ли- |
нии уровня плоскости.
Способ совмещения заключается в том, что заданную плоскость Р вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов РН или РV до совмещения с соответствующей плоскостью проекций Н или V.
Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам.
Если плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов, так как другой след, принимаемый за ось вращения, не мен я- ет своего положения.
Как видно из рис. 3.7 , для определения совмещенного следа Pv0 при вращении плоскости Р вокруг следа РH достаточно найти совмещенное положение N0 любой точки N следа РV. На рис. 3.7 показано также совмещение точки А (а, а’), лежащей в плоскости Р, с плоскостью Н при использовании горизонтали.
Задача. Найти натуральную величину треугольника ABC, расположенного в плоскости Р общего положения (рис. 3.8).
20

Рис. 3.7
Плоскость Р совмещаем с плоскостью Н вращением вокруг следа РН.. Используя горизонталь плоскости, на которых лежат вершины треугольника, находим совмещенные положения В0, С0 этих вершин и получаем треугольник А0В0С0, равный заданному.
Рис. 3.8
21
4. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЯМИ
4.1.Общие сведения
Вобщем случае, для того чтобы построить линию пересечения поверхности с плоскостью, нужно найти ряд точек, принадлежащих как поверхности, так и плоскости, а затем эти точки соединить плавной кривой или ломаной линией.
Для нахождения произвольной точки линии пересечения, необходимо: 1. рассечь заданные фигуры вспомогательной плоскостью; 2. найти линии пересечения этой плоскости с поверхностью и с задан-
ной плоскостью; 3. на пересечении найденных линий получить искомые точки (чаще
всего – две).
Последовательно проводя ряд вспомогательных плоскостей, можно найти необходимое число точек.
Вспомогательную плоскость следует выбирать так, чтобы ее линия пересечения с поверхностью проецировалась на плоскости проекций в виде простейших линий – прямой или окружности.
При построении линии пересечения находят, прежде всего, ее характерные (опорные) точки, а затем, по мере необходимости, промежуточные точки.
Характерные точки определяют характер линии пересечения и ее видимость. К ним относятся: экстремальные точки (высшая и низшая, крайняя левая и крайняя правая, ближняя и дальняя); точки, лежащие на проекциях очерка поверхности; точки, лежащие на проекциях осей поверхности.
Среди характерных точек выделяются очевидные точки, которые для своего нахождения не требуют дополнительных построений, а определяются при помощи линий проекционной связи. В некоторых случаях одна и та же точка может выполнять несколько функций.
Промежуточные точки выделяются на заданной линии для более точного графического построения искомой проекции линии.
Если заданная поверхность имеет прямолинейные образующие, то линию пересечения можно найти также следующим образом: нанести на поверхности ряд образующих и найти точки их пересечения с плоскостью, а затем соединить эти точки плавной кривой линией.
При построении сечения гранных поверхностей плоскостью используют два способа: способ граней – определяются стороны многоугольника сечения; способ ребер – определяются вершины многоугольника сечения.
Построение сечений значительно упрощается, если секущая плоскость является проецирующей. В этом случае одна проекция сечения совпадает с проецирующим следом плоскости.
22
Омский государственный Университет Путей Сообщения
З а д а ч а 1.
По координатам вершин А, B, C построить проекции треугольника. Найти горизонтальный и фронтальный следы плоскости треугольника ABC.
Горизонтальным (фронтальным) следом прямой называют точку пересечения прямой с горизонтальной П1 (фронтальной П2) плоскостью проекции.
Горизонтальным (фронтальным) следом плоскости называют линию пересечения плоскости с одноименной плоскостью проекций.
Следы плоскости проходят через следы прямых, лежащих в этой плоскости, и пересекаются на оси проекций 0х. Так как следы прямых и плоскостей принадлежат плоскостям проекций, то их проекции на эти плоскости совпадают с самими следами, а другие проекции принадлежат осям проекций.
Решение и построения: По заданным координатам для варианта 24 (заочное обучение) строим проекции точек А, B, C в плоскостях проекций П2 и П1 в масштабе М 2:1, соединяем точки получаем проекции треугольника АВС.
Определяем горизонтальный след плоскости треугольника h0 по горизонтальным следам прямых АC и BС, принадлежащих заданной плоскости. Для нахождения горизонтального следа прямой АС продолжаем ее фронтальную проекцию А2С2 до пересечения с осью проекции H2, которая является фронтальной проекцией искомого следа. Проводим из этой точки перпендикуляр к оси проекций (линию связи) до пересечения его с продолжением горизонтальной проекции А1С1, Н1 является горизонтальной проекцией искомого следа, она совпадает с самим следом H.
Аналогичным образом находим фронтальный след H’ прямой BС. Соединив проекции H1 и H’1, найдем горизонтальную проекцию горизонтального следа плоскости h0, и точку схода следов SX на оси проекций.
Фронтальный след заданной плоскости пройдет через точку схода следов SX и фронтальный след любой прямой этой плоскости, например прямой АС. Для нахождения последнего продолжаем проекцию А1С1 до пересечения с осью проекций, F1 является горизонтальной проекцией искомого следа. Фронтальную проекцию F2 определяем по линии связи на продолжении проекции А2С2. Соединив Sх и F2, найдем фронтальный след плоскости f0.
В нашем случае точка схода следов плоскости выходит за пределы чертежа, этом случае можно было найти два фронтальных и два горизонтальных следа прямых заданной плоскости.
В налиции все варианты готовых чертежей для ОмГУПС. Чертежи высылаются, сразу после оплаты на карту Сбербанка, Яндекс.Деньги или Киви кошелек, в формате *.cdw (Компас)+рисунки jpeg в цвете в хорошем разрешении 300dpi. По желанию, могу заполнить штампы. Выполнение карандашом таких чертежей на заказ 5 листов- 1500 руб.
http://stud55.ru/category/nachertatelnaya-kupit/omgups
>>>Далее к решению задачи №2 <<<
Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
1.1. Условие задания
Построить следы плоскости, заданной ∆BCD, и определить расстояние от точки А до заданной плоскости методом прямоугольного треугольника (координаты точек А, В, С и D см. в Таблице 1 раздела Задания);
1.2. Пример выполнения задания № 1
Первое задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам трех точек B, C, D построить горизонтальную и фронтальную проекции плоскости, заданной ∆BCD;
2. Следы прямой, следы плоскости, свойства принадлежности прямой плоскости: построить следы плоскости, заданной ∆BCD;
3. Плоскости общего и частного положения, пересечение прямой и плоскости, перпендикулярность прямой и плоскости, пересечение плоскостей, метод прямоугольного треугольника: определить расстояние от точки А до плоскости ∆BCD.
1.2.1. По известным координатам трех точек B, C, D построим горизонтальную и фронтальную проекции плоскости, заданной ∆BCD (Рисунок 1.1), для чего необходимо построить горизонтальные и фронтальные проекции вершин ∆BCD, а затем одноименные проекции вершин соединить.
Известно, что следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с плоскостью проекций.
У плоскости общего положения 3 следа: горизонтальный, фронтальный и профильный.
Для того чтобы построить следы плоскости, достаточно построить следы (горизонтальный и фронтальный) любых двух прямых, лежащих в этой плоскости, и соединить их между собой. Таким образом, след плоскости (горизонтальный или фронтальный) будет однозначно определен, поскольку через две точки на плоскости (в данном случае этими точками будут следы прямых) можно провести прямую, и при том, только одну.
Основанием для такого построения служит свойство принадлежности прямой плоскости: если прямая принадлежит заданной плоскости, то ее следы лежат на одноименных следах этой плоскости.
Следом прямой называется точка пересечения этой прямой с плоскостью проекций.
Горизонтальный след прямой лежит в горизонтальной плоскости проекций, фронтальный – во фронтальной плоскости проекций.
Рассмотрим построение горизонтального следа прямой DB, для чего необходимо:
1. Продолжить фронтальную проекцию прямой DB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
2. Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой DB или ее продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа (Рисунок 1.1), которая совпадает с самим следом М.
Аналогично выполняется построение горизонтального следа отрезка СВ прямой: точка М’.
Чтобы построить фронтальный след отрезка CB прямой, необходимо:
1. Продолжить горизонтальную проекцию прямой CB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
2. Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой CB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Соединив точки M′1 и M1 отрезком прямой, получим горизонтальный след плоскости απ1. Точка αx пересечения απ1 с осью X называется точкой схода следов. Для построения фронтального следа плоскости απ2 необходимо соединить фронтальный след N2 с точкой схода следов αx
Рисунок 1.1 — Построение следов плоскости
Алгоритм решения этой задачи может быть представлен следующим образом:
- (D2B2 ∩ OX) = M2;
- (MM1 ∩ D1B1) = M1 = M;
- (C2B2 ∩ OX) = M′2;
- (M′2M′1 ∩ C1B1) = M′1 = M′;
- (CВ ∩ π2) = N2= N;
- (MM′) ≡ απ1;
- (αxN) ≡ απ2.
1.2.2. Для решения второй части первого задания необходимо знать, что:
- расстояние от точки А до плоскости ∆BCD определяется длиной перпендикуляра, восстановленного из этой точки на плоскость;
- любая прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- на эпюре проекции прямой, перпендикулярной плоскости, перпендикулярны наклонным проекциям горизонтали и фронтали этой плоскости или одноименным следам плоскости (рис. 1.2) (см. в лекциях Теорему о перпендикуляре к плоскости).
Чтобы найти основание перпендикуляра, необходимо решить задачу на пересечение прямой (в данной задаче такой прямой является перпендикуляр к плоскости) с плоскостью:
1. Заключить перпендикуляр во вспомогательную плоскость, в качестве которой следует взять плоскость частного положения (горизонтально-проецирующую или фронтально-проецирующую, в примере в качестве вспомогательной плоскости взята горизонтально-проецирующая γ, то есть перпендикулярная к π1, ее горизонтальный след γ1 совпадает с горизонтальной проекцией перпендикуляра);
2. Найти линию пересечения заданной плоскости ∆BCD со вспомогательной γ (MN на рис. 1.2);
3. Найти точку пересечения линии пересечения плоскостей MN с перпендикуляром (точка К на рис. 1.2).
4. Для определения истинной величины расстояния от точки А до заданной плоскости ∆BCD следует воспользоваться методом прямоугольного треугольника: истинная величина отрезка есть гипотенуза прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность расстояний от его концов до плоскости проекций, в которой ведётся построение.
5. Определите видимость участков перпендикуляра методом конкурирующих точек. На примере — точки N и 3 для определения видимости на π1, точки 4, 5 — для определения видимости на π2.
Рисунок 1.2 — Построение перпендикуляра к плоскости
Рисунок 1.3 — Пример оформления контрольного задания №1
Видеопример выполнения задания №1
1.3. Варианты задания 1
| Вариант | Координаты (x, y, z) точек | |||
|---|---|---|---|---|
| А | В | С | D | |
| 1 | 15; 55; 50 | 10; 35; 5 | 20; 10; 30 | 70; 50; 40 |
| 2 | 80; 65; 50 | 50; 10; 55 | 10; 50; 25 | 75; 25; 0 |
| 3 | 95; 45; 60 | 130; 40; 50 | 40; 5; 25 | 80; 30; 5 |
| 4 | 115; 10; 0 | 130; 40; 40 | 40; 5; 25 | 80; 30; 5 |
| 5 | 55; 5; 60 | 85; 45; 60 | 100; 5; 30 | 50; 25; 10 |
| 6 | 55; 5; 60 | 70; 40; 20 | 30; 30; 35 | 30; 10; 10 |
| 7 | 60; 10; 45 | 80; 45; 5 | 35; 0; 15 | 10; 0; 45 |
| 8 | 5; 0; 0 | 35; 0; 25 | 20; 0; 55 | 40; 40; 0 |
| 9 | 50; 5; 45 | 65; 30; 10 | 30; 25; 55 | 20; 0; 20 |
| 10 | 60; 50; 35 | 40; 30; 0 | 30; 15; 30 | 80; 5; 20 |
| 11 | 65; 35; 15 | 50; 0; 30 | 20; 25; 25 | 5; 0; 10 |
| 12 | 75; 65; 50 | 45; 10; 35 | 60; 20; 10 | 10; 65; 0 |
| 13 | 95; 0; 15 | 85; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 14 | 45; 40; 40 | 80; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 15 | 80; 20; 30 | 55; 30; 60 | 15; 10; 20 | 70; 65; 30 |
| 16 | 75; 35; 35 | 55; 30; 60 | 25; 10; 20 | 70; 65; 30 |
| 17 | 75; 65; 50 | 45; 5; 55 | 5; 45; 10 | 70; 20; 0 |
| 18 | 65; 15; 20 | 40; 5; 60 | 0; 5; 25 | 60; 60; 20 |
| 19 | 70; 20; 10 | 45; 15; 60 | 5; 10; 20 | 60; 65; 10 |
| 20 | 20; 50; 45 | 10; 20; 10 | 55; 50; 10 | 80; 0; 60 |
| 21 | 0; 5; 50 | 50; 50; 40 | 5; 55; 10 | 45; 5; 0 |
| 22 | 55; 50; 65 | 45; 55; 5 | 0; 10; 45 | 70; 0; 40 |
| 23 | 65; 5; 15 | 40; 60; 10 | 0; 20; 5 | 60; 20; 60 |
| 24 | 50; 20; 45 | 45; 60; 30 | 5; 20; 10 | 60; 30; 5 |
| 25 | 55; 15; 40 | 40; 50; 25 | 5; 15; 10 | 50; 40; 10 |
| 26 | 15; 45; 40 | 10; 25; 5 | 20; 10; 30 | 65; 40; 35 |
| 27 | 70; 30; 30 | 55; 30; 60 | 20; 5; 15 | 65; 60; 25 |
| 28 | 90; 0; 15 | 80; 45; 10 | 10; 10; 10 | 50; 10; 45 |
| 29 | 110; 10; 0 | 120; 35; 30 | 35; 5; 20 | 70; 20; 5 |
| 30 | 45; 40; 40 | 80; 45; 10 | 10; 10; 10 | 55; 10; 40 |
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.