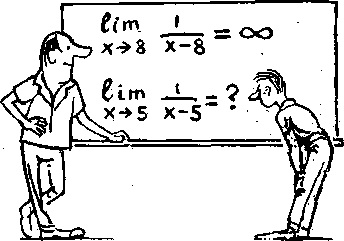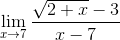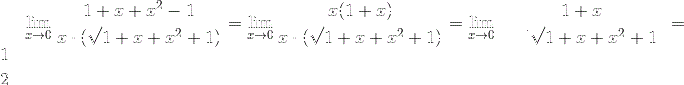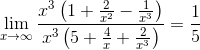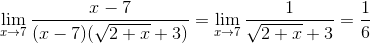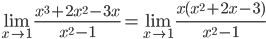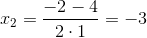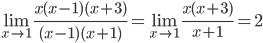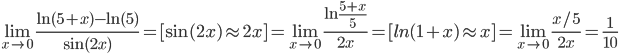Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что “скучная теория” должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание “чайникам” 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать: $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними – это не так страшно как кажется 🙂 |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её 🙂 Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате – это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное – возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: “ноль делить на ноль” или “бесконечность делить на бесконечность” и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность “ноль делить на ноль” нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность “бесконечность делить на бесконечность”, тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
В этой заметке речь пойдет о пределах. С ними сталкиваются в 10-11 классах на уроках физики, когда начинают выводить частоту колебаний математического или физического маятников. В математике с пределами сталкиваются, когда учащихся знакомят с производными и дифференцированием. Поэтому эта одно из самых базовых понятий математического анализа, в котором не должно быть пробелов.
Давайте начнем с простых (условно и относительно) пределов, которые вам могут попасться на первом курсе.
С некоторыми из них практически ничего не нужно делать, а только подставить значение…
А другие становятся легче, если разделить на общий одночлен, который представляет собой старшую степень переменной.
В пределах, имеющих радикалы частенько помогает домножение на “сопряженное” выражение. Также упростит понимание таких действий тот факт, если вы хорошо помните формулы сокращенного умножения, в частности разность квадратов.
Структурировать информацию лучше сразу
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.
Перечислим все основные виды неопределенностей:
1) ноль делить на ноль
2) бесконечность делить на бесконечность
3) ноль умножить на бесконечность
4) бесконечность минус бесконечность
5) единица в степени бесконечность
6) ноль в степени ноль формула
7) бесконечность в степени ноль
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать неопределенности позволяет:
● упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
● использование замечательных пределов;
● применение правила Лопиталя;
● использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только к первому и второму из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности. Если числитель и знаменатель являются бесконечно малыми или бесконечно большими одновременно, то можно посчитать отношениях производных этих функций. При дифференцировании числителя и знаменателя значение предела не меняется.
Иногда приходится применять правило Лопиталя последовательно несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге.Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.
Для раскрытия неопределённостей видов 0^0, 1^∞, ∞^0 пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
Для раскрытия неопределённостей типа ∞/∞ используется следующий алгоритм:
● Выявление старшей степени переменной;
● Деление на эту переменную как числителя, так и знаменателя.Для раскрытия неопределённостей типа 0/0 существует следующий алгоритм:
● Разложение на множители числителя и знаменателя;
● Сокращение дроби.Для раскрытия неопределённостей типа ∞ – ∞ иногда удобно применить следующее преобразование:
● f(x) – g(x) = 1/ (1/f(x) ) – 1/(1/g(x)) = (1/g(x) – 1/f(x))/( (1/g(x)) * (1/f(x)) )
Данный вид неопределённостей может раскрываться с использованием асимптотических разложений уменьшаемого и вычитаемого, при этом бесконечно большие члены одного порядка должны уничтожаться.
При раскрытии неопределённостей также применяются замечательные пределы и их следствия.
Ещё немного примеров для закрепления материала
В пределах могут быть и суммы вместо функций. Подумайте какой подвох в следующем пределе ? Правильно ли получен ноль ?
Вы еще думаете, что пределы – это просто? А как насчет предела с параметром?
Интересная задачка по математике с параметрическим интегралом.
Чему равен предел lim[ I(a) ] при a → 0 если в качестве I(a) выступает интеграл: I(a) = Int( x⁵ ⋅ ( cos(a²x) + sin(5a²x) )^(x/a²) ) dx
в пределах от 2^a до 2^(a+1).
Так как предел считается от параметра, а параметр не зависит от переменной интегрирования, то вполне законно пронести предел внутрь выражения и применить его только к той части, которая представляет наибольшую сложность. Аппроксимация сводит выражение ко второму замечательному пределу. А дальше дело за аккуратными вычислениями интегралов по частям. Придумали другой способ? Напишите в комментариях.
Рассмотрим ещё один сложный предел, для которого вам не помогут табличные бесконечно малые функции в силу их небольшой точности
Интересный предел на базе второго замечательного предела.
Задача: вычислить предел lim(1/n + exp(-1/n))^(n²) при n → ∞
Пределы на базе второго замечательного могут быть очень запутанные. Приведу вам ещё один пример. Что может быть интереснее, чем посидеть зимним вечером за математическим анализом с чашечкой кофе? 🙂
Задание: найти предел
Естественно, интересно решить это аналитически. Потому что вбивать в математические пакеты сможет любой человек. Мы видим, что у нас одна зависящая от x функция возводится в степень другой зависимой от x функции. Уже это должно нам намекнуть “а не второй замечательный предел у нас тут спрятался?”
Конечно же он! Только нужно подойти к нему. Делаем искусственный прием, чтобы отсечь единичку от дроби, а оставшуюся часть заменить на некоторую переменную. Я назвал её t, но можно называть как угодно. Сразу же нужно посмотреть к чему будет стремиться данная переменная, при стремлении x —> 1. Видим, что стремление t происходит в бесконечность, а значит мы уже можем определиться с формой записи второго замечательного предела, под который будем подгонять наши преобразования.
Так как мы пытаемся перейти к t, в степени, в косинусе у нас находится голенькое x, то нам придется выразить его из предшествующей замены переменных. Получается квадратное уравнения, которое дает два корня. Эта неоднозначность не должна вас смущать, так как корень подходит только один, причем положительный для x, т.к. x —> 1 (значит x > 0)
Далее несколько преобразований приводят нас к тому, что у нас получается е в некоторой степени, лимит (предел) которой нам предстоит найти. Но степень оказывается тоже с неопределенностью в знаменателе 0 * infinity. Тогда мы искусственно перебрасываем лишнюю переменную в числитель. Применяем правило Лопиталя-Бернулли (предел отношений функций равен пределу отношения производных этих функций). И у нас получается что-то очень похожее на первый замечательный предел. Но на самом деле уже сюда достаточно подставить t = infinity и получить конечный ответ.
Решение полное будет выглядеть так:
Под вторым замечательным пределам также могут скрывать тригонометрические функции, которые также усложняют жизнь, потому что студенты часто пытаются разрешить их простейшими преобразованиями или разложением в ряд, что не всегда кончается успехом.
Например задание:
Интересный предел. Сложность в том, чтобы вспомнить универсальную тригонометрическую подстановку, затем не побояться её подставить и сделать правильную замену переменных, чтобы выделить второй замечательный предел.
Есть и задачи, где можно применить первый замечательный предел
Очередная интересная задача на нахождение предела. Не особо очевидное применение первого замечательного предела. Конечно же применение правила Бернулли — Лопиталя, возможно, упростило бы нахождение ответа, но разве ценителям математики интересны простые пути? 🙂
На сегодня закончим, ведь тут итак есть над чем задуматься. А с каким самым сложным пределом сталкивались вы на занятиях математикой? Расскажите об этом в комментариях!
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида 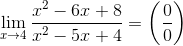
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6. Нахождение пределов, используя свойства второго замечательного предела ,
,
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число “пи” (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел 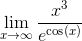
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 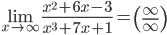
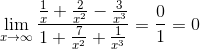
2. 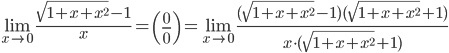
3. 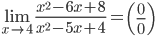
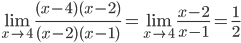
4. 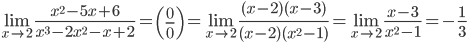
5. 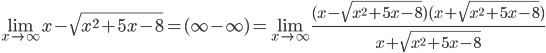
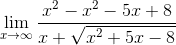
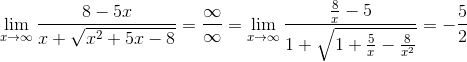
6. 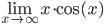
7. 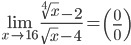
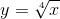
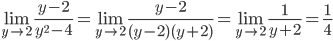
8. 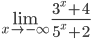
9. 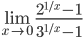
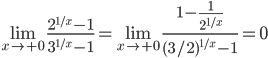
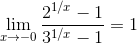
Следовательно, 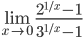
Найти пределы функции, не применяя правило Лопиталя.
а)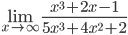
Ответ: 1/5
б) 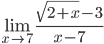
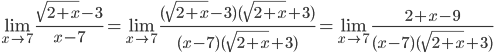
Ответ: 1/6
в) 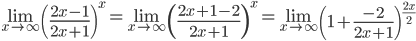
e-2/2 = e-1
Ответ: 1/e
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
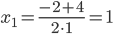
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д) 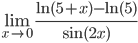
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).