Следы плоскости
На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П1, П2, П3 по прямым h0α, f0α и p0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.
Оси координат пл. α пересекает в точках Xα, Yα и Zα. Они называются точками схода следов. При этом Xα = h0α ∩ f0α, Yα = h0α ∩ p0α, Zα = f0α ∩ p0α. Здесь знак ∩ означает пересечение.
На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве.
Алгоритм построения следов плоскости
На рисунке, который представлен ниже, некоторая плоскость α задана проекциями двух пересекающихся прямых a и b. Чтобы найти её следы, необходимо:
- Построить точки Ha и Hb – горизонтальные следы прямых a и b. Провести через них h0α – горизонтальный след пл. α до пересечения его с осью x.
- Построить точки Fa и Fb – фронтальные следы прямых a и b. Провести через них f0α – одноименный след плоскости α.
- Если построения выполнены верно, то прямые h0α и f0α пересекутся между собой в точке Xα, расположенной на оси проекций.
Решение задачи можно сократить. Для этого, построив горизонтальный след плоскости, фронтальный нужно провести через Xα и одну из точек, Fa или Fb. Таким образом, вместо четырех следов прямых a и b будет достаточно найти три.
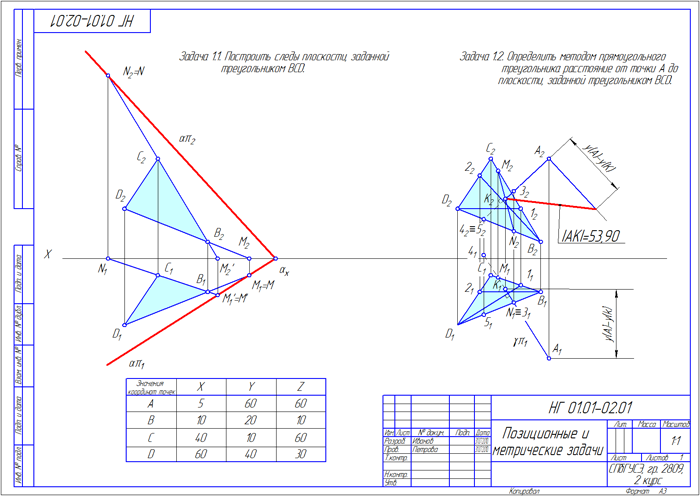
Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
1.1. Условие задания
Построить следы плоскости, заданной ∆BCD, и определить расстояние от точки А до заданной плоскости методом прямоугольного треугольника (координаты точек А, В, С и D см. в Таблице 1 раздела Задания);
1.2. Пример выполнения задания № 1
Первое задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам трех точек B, C, D построить горизонтальную и фронтальную проекции плоскости, заданной ∆BCD;
2. Следы прямой, следы плоскости, свойства принадлежности прямой плоскости: построить следы плоскости, заданной ∆BCD;
3. Плоскости общего и частного положения, пересечение прямой и плоскости, перпендикулярность прямой и плоскости, пересечение плоскостей, метод прямоугольного треугольника: определить расстояние от точки А до плоскости ∆BCD.
1.2.1. По известным координатам трех точек B, C, D построим горизонтальную и фронтальную проекции плоскости, заданной ∆BCD (Рисунок 1.1), для чего необходимо построить горизонтальные и фронтальные проекции вершин ∆BCD, а затем одноименные проекции вершин соединить.
Известно, что следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с плоскостью проекций.
У плоскости общего положения 3 следа: горизонтальный, фронтальный и профильный.
Для того чтобы построить следы плоскости, достаточно построить следы (горизонтальный и фронтальный) любых двух прямых, лежащих в этой плоскости, и соединить их между собой. Таким образом, след плоскости (горизонтальный или фронтальный) будет однозначно определен, поскольку через две точки на плоскости (в данном случае этими точками будут следы прямых) можно провести прямую, и при том, только одну.
Основанием для такого построения служит свойство принадлежности прямой плоскости: если прямая принадлежит заданной плоскости, то ее следы лежат на одноименных следах этой плоскости.
Следом прямой называется точка пересечения этой прямой с плоскостью проекций.
Горизонтальный след прямой лежит в горизонтальной плоскости проекций, фронтальный – во фронтальной плоскости проекций.
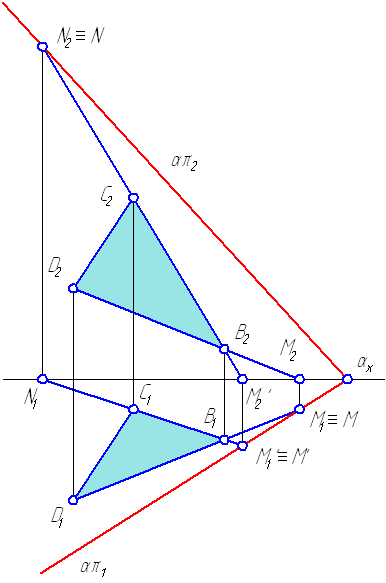
Рассмотрим построение горизонтального следа прямой DB, для чего необходимо:
1. Продолжить фронтальную проекцию прямой DB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
2. Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой DB или ее продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа (Рисунок 1.1), которая совпадает с самим следом М.
Аналогично выполняется построение горизонтального следа отрезка СВ прямой: точка М’.
Чтобы построить фронтальный след отрезка CB прямой, необходимо:
1. Продолжить горизонтальную проекцию прямой CB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
2. Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой CB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Соединив точки M′1 и M1 отрезком прямой, получим горизонтальный след плоскости απ1. Точка αx пересечения απ1 с осью X называется точкой схода следов. Для построения фронтального следа плоскости απ2 необходимо соединить фронтальный след N2 с точкой схода следов αx
Рисунок 1.1 — Построение следов плоскости
Алгоритм решения этой задачи может быть представлен следующим образом:
- (D2B2 ∩ OX) = M2;
- (MM1 ∩ D1B1) = M1 = M;
- (C2B2 ∩ OX) = M′2;
- (M′2M′1 ∩ C1B1) = M′1 = M′;
- (CВ ∩ π2) = N2= N;
- (MM′) ≡ απ1;
- (αxN) ≡ απ2.
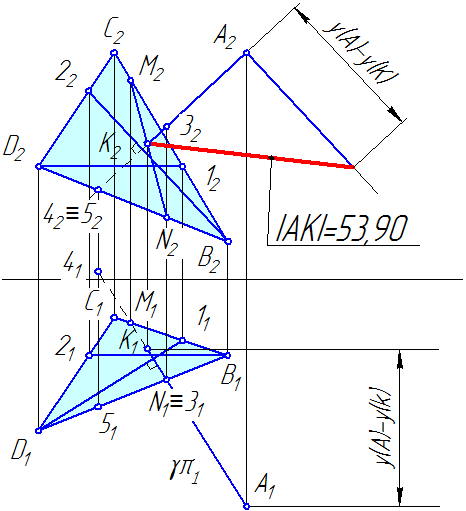
1.2.2. Для решения второй части первого задания необходимо знать, что:
- расстояние от точки А до плоскости ∆BCD определяется длиной перпендикуляра, восстановленного из этой точки на плоскость;
- любая прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- на эпюре проекции прямой, перпендикулярной плоскости, перпендикулярны наклонным проекциям горизонтали и фронтали этой плоскости или одноименным следам плоскости (рис. 1.2) (см. в лекциях Теорему о перпендикуляре к плоскости).
Чтобы найти основание перпендикуляра, необходимо решить задачу на пересечение прямой (в данной задаче такой прямой является перпендикуляр к плоскости) с плоскостью:
1. Заключить перпендикуляр во вспомогательную плоскость, в качестве которой следует взять плоскость частного положения (горизонтально-проецирующую или фронтально-проецирующую, в примере в качестве вспомогательной плоскости взята горизонтально-проецирующая γ, то есть перпендикулярная к π1, ее горизонтальный след γ1 совпадает с горизонтальной проекцией перпендикуляра);
2. Найти линию пересечения заданной плоскости ∆BCD со вспомогательной γ (MN на рис. 1.2);
3. Найти точку пересечения линии пересечения плоскостей MN с перпендикуляром (точка К на рис. 1.2).
4. Для определения истинной величины расстояния от точки А до заданной плоскости ∆BCD следует воспользоваться методом прямоугольного треугольника: истинная величина отрезка есть гипотенуза прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность расстояний от его концов до плоскости проекций, в которой ведётся построение.
5. Определите видимость участков перпендикуляра методом конкурирующих точек. На примере — точки N и 3 для определения видимости на π1, точки 4, 5 — для определения видимости на π2.
Рисунок 1.2 — Построение перпендикуляра к плоскости
Рисунок 1.3 — Пример оформления контрольного задания №1
Видеопример выполнения задания №1
1.3. Варианты задания 1
| Вариант | Координаты (x, y, z) точек | |||
|---|---|---|---|---|
| А | В | С | D | |
| 1 | 15; 55; 50 | 10; 35; 5 | 20; 10; 30 | 70; 50; 40 |
| 2 | 80; 65; 50 | 50; 10; 55 | 10; 50; 25 | 75; 25; 0 |
| 3 | 95; 45; 60 | 130; 40; 50 | 40; 5; 25 | 80; 30; 5 |
| 4 | 115; 10; 0 | 130; 40; 40 | 40; 5; 25 | 80; 30; 5 |
| 5 | 55; 5; 60 | 85; 45; 60 | 100; 5; 30 | 50; 25; 10 |
| 6 | 55; 5; 60 | 70; 40; 20 | 30; 30; 35 | 30; 10; 10 |
| 7 | 60; 10; 45 | 80; 45; 5 | 35; 0; 15 | 10; 0; 45 |
| 8 | 5; 0; 0 | 35; 0; 25 | 20; 0; 55 | 40; 40; 0 |
| 9 | 50; 5; 45 | 65; 30; 10 | 30; 25; 55 | 20; 0; 20 |
| 10 | 60; 50; 35 | 40; 30; 0 | 30; 15; 30 | 80; 5; 20 |
| 11 | 65; 35; 15 | 50; 0; 30 | 20; 25; 25 | 5; 0; 10 |
| 12 | 75; 65; 50 | 45; 10; 35 | 60; 20; 10 | 10; 65; 0 |
| 13 | 95; 0; 15 | 85; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 14 | 45; 40; 40 | 80; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 15 | 80; 20; 30 | 55; 30; 60 | 15; 10; 20 | 70; 65; 30 |
| 16 | 75; 35; 35 | 55; 30; 60 | 25; 10; 20 | 70; 65; 30 |
| 17 | 75; 65; 50 | 45; 5; 55 | 5; 45; 10 | 70; 20; 0 |
| 18 | 65; 15; 20 | 40; 5; 60 | 0; 5; 25 | 60; 60; 20 |
| 19 | 70; 20; 10 | 45; 15; 60 | 5; 10; 20 | 60; 65; 10 |
| 20 | 20; 50; 45 | 10; 20; 10 | 55; 50; 10 | 80; 0; 60 |
| 21 | 0; 5; 50 | 50; 50; 40 | 5; 55; 10 | 45; 5; 0 |
| 22 | 55; 50; 65 | 45; 55; 5 | 0; 10; 45 | 70; 0; 40 |
| 23 | 65; 5; 15 | 40; 60; 10 | 0; 20; 5 | 60; 20; 60 |
| 24 | 50; 20; 45 | 45; 60; 30 | 5; 20; 10 | 60; 30; 5 |
| 25 | 55; 15; 40 | 40; 50; 25 | 5; 15; 10 | 50; 40; 10 |
| 26 | 15; 45; 40 | 10; 25; 5 | 20; 10; 30 | 65; 40; 35 |
| 27 | 70; 30; 30 | 55; 30; 60 | 20; 5; 15 | 65; 60; 25 |
| 28 | 90; 0; 15 | 80; 45; 10 | 10; 10; 10 | 50; 10; 45 |
| 29 | 110; 10; 0 | 120; 35; 30 | 35; 5; 20 | 70; 20; 5 |
| 30 | 45; 40; 40 | 80; 45; 10 | 10; 10; 10 | 55; 10; 40 |
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
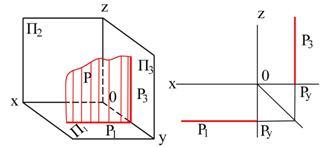
Положение плоскости
в пространстве может быть определено
ее следами. Следами плоскости называются
прямые линии, по которым данная плоскость
пересекается с плоскостями проекций.
В общем случае
плоскость имеет три следа – горизонтальный,
фронтальный и профильный.
На рис. 3.1. и в таблице
3.1. п.6 они обозначены соответственно
P1, P2,
P3 (буквой Р обозначена
заданная плоскость, а индексы 1, 2, 3
означают, с какой из плоскостей проекций
пересекается плоскость Р).
В точках Px,
Py,
Pz,
лежащих на осях координат, следы плоскости
пересекаются. Эти точки называются
точками схода следов плоскости.
Следы плоскости
всегда можно построить, если положение
плоскости в пространстве задано одним
из перечисленных выше способов.
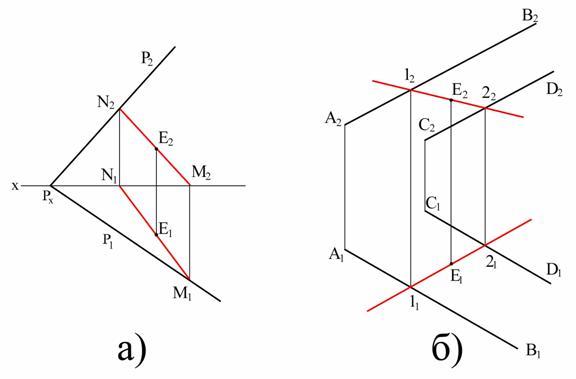
Если прямая АВ
(рис.3.1. а и б) лежит в плоскости Р, то она
пересечет плоскость П1 в точке М1
расположенной на линии Р1, т.е.
горизонтальный след прямой, лежащей в
плоскости, расположен на горизонтальном
следе плоскости.
Рис.
3.1.
Плоскость П2
прямая АВ пересечет в точке N,
расположенной на линии Р2.
Иными словами, следы
прямой, лежащей в плоскости, расположены
на одноименных следах плоскости.
Отсюда следует, что
следы плоскости должны проходить
через одноименные следы прямых, лежащих
в плоскости.
Чтобы построить
след плоскости, необходимо определить
следы двух прямых, лежащих в плоскости.
На рис. 3.1. плоскость
задана двумя пересекающимися прямыми
АВ и СD. Чтобы построить
горизонтальный след плоскости необходимо
найти горизонтальный след прямой АВ –
точку М и прямой СD – точку
М1. Горизонтальный след плоскости
будет проходить через точки М и М1.
Фронтальный след
плоскости Р2 строится аналогично.
Следует отметить, что для построения
следа Р2 достаточно иметь фронтальный
след только одной прямой, так как второй
точкой, определяющей положение следа
Р2 будет точка Рх схода
следов (точка пересечения ранее
построенного следа Р1 с осью х).
3.3 Принадлежность прямой и точки заданной плоскости
Прямая принадлежит
плоскости, если две её точки принадлежат
этой плоскости. Прямая MN
(рис.3.2,а) расположена в плоскости Р,
заданной следами, поскольку две точки
прямой М и N(горизонтальный
и фронтальный её следы) принадлежат
плоскости, т.е. расположены на её следах.
Прямая 1-2 (рис.3.2, б) принадлежит плоскости,
заданной параллельными прямыми, поскольку
имеет с ней две общие точки.
Рис.
3.2
Точка принадлежит
плоскости, если она расположена на
прямой, принадлежащей данной плоскости.
Для того, чтобы построить в плоскости
точку (рис. 3.2), необходимо провести в
плоскости прямую, принадлежащую
плоскости, а затем задать на ней точку
Е, которая принадлежит прямой и,
следовательно, и плоскости.
3.4 Плоскости общего и частного положения
Различают частные
и общие случаи расположения плоскости
в пространстве относительно плоскостей
проекций.
Плоскость общего
положения. Плоскость, произвольно
расположенная по отношению к плоскостям
проекций, называется плоскостью общего
положения (рис. 3.1).
Проекции элементов,
которыми задана такая плоскость (точки,
прямые, следы плоскости, плоские фигуры),
составляют случайные углы с линиями
связи и осями проекций комплексного
чертежа, т.е. располагаются произвольно
и ни в одной проекции на вырождаются в
более простой геометрический образ.
Плоскости,
перпендикулярные одной или двум
плоскостям проекций называются
плоскостями частного положения.
Плоскость,
перпендикулярная к плоскости проекций
называется проецирующей плоскостью.
Проецирующая плоскость, перпендикулярная
к горизонтальной плоскости проекций
называется горизонтально-проецирующей,
к фронтальной – фронтально-проецирующей,
к профильной – профильно-проецирующей.
В прямоугольных
проекциях плоскость, перпендикулярная
к плоскости проекций, параллельна
направлению проецирования и поэтому
является проецирующей. Её проекция
на этой плоскости вырождается в прямую;
проекция на другую плоскость является
неограниченным полем точек.
Горизонтально-проецирующая
плоскость. Фронтальной проекцией
плоскости РП1
является неограниченное поле точек
(табл. 3.2, п.1), горизонтальной – прямая
Р1. Горизонтальная проекция любой
линии (точки, фигуры), лежащей в
горизонтально-проецирующей плоскости,
располагается на выродившейся в прямую
горизонтальной проекции этой плоскости.
Фронтально-проецирующая
плоскость. Горизонтальная проекция
плоскости РП2
представляет собой неограниченное поле
точек (табл. 3.2, п.2), фронтальная проекция
Р2 вырождается в прямую. Фронтальная
проекция любой точки, линии или фигуры,
лежащих во фронтально-проецирующей
плоскости, располагаются на выродившейся
в прямую фронтальной проекции этой
плоскости.
Профильно-проецирующая
плоскость. Профильная проекция
плоскости РП3,
вырождается в прямую (табл. 3.2., п.3).
Проекциями на плоскость П1 и П2
являются неограниченные поля точек.
Профильная проекция любой линии (точки,
фигуры), лежащей в профильно-проецирующей
плоскости, располагается на выродившейся
в прямую профильной проекции этой
плоскости. Из рисунков в таблице 3.2.
видно, что один след проецирующей
плоскости (так называемый след-проекция)
совпадает с выродившейся в прямую
проекцией плоскости, а другой-
перпендикулярен к оси проекций.
Задание на комплексном
чертеже проецирующих плоскостей следами
изображено в таблице 3.2. и не нуждается
в пояснениях (сопоставьте изображения
каждой проецирующей плоскости в таблице).
Заметим, что угол
между следом-проекцией и осью проекции
равен углу наклона проецирующей плоскости
к плоскости проекций.
На комплексном
чертеже проецирующие плоскости чаще
изображаются не следами, а своей
проекцией, выродившейся в прямую. Вторая
проекция, представляющая поле точек,
безгранична и обычно не изображается
и не обозначается.
Таблица
3.2 Положение плоскости относительно
плоскости проекций.
|
№ |
Положение |
Наглядное |
Эпюр |
Положение |
|
1 |
Перпендикулярна |
|
Р1 – Р3 |
|
|
2 |
Перпендикулярна |
|
Р1 – Р2 Р3 |
|
|
3 |
Перпендикулярна |
|
Р1 и Р2 Р3 |
|
|
4 |
Параллельна |
|
Р1 – Р2 Р3 |
|
|
5 |
Параллельна |
|
Р1 – Р2 Р3 |
|
|
6 |
Параллельна |
|
Р1 и Р2 Р3 |
Плоскость, параллельная
плоскости проекций называется плоскостью
уровня. Такая плоскость перпендикулярна
к двум другим плоскостям проекций и,
следовательно, по отношению к ним
является проецирующей и проецируется
на них в прямую линию. Плоскость,
параллельная горизонтальной плоскости
проекций называется горизонтальной,
параллельная фронтальной – фронтальной
и параллельная профильной – профильной
плоскостью уровня.
В таблице 3.2. п. 4, 5,
6 изображены плоскости параллельные
плоскостям проекций – плоскости уровня.
Здесь же даны изображения этих плоскостей
на комплексном чертеже.
Плоскости уровня
не имеют следа на параллельной себе
плоскости проекций и проецируются на
неё в неограниченные поля точек (эти
проекции на комплексном чертеже не
обозначаются и не ограничиваются).
Итак, положение
плоскостей уровня подчинено общему
правилу: если плоскость параллельна
плоскости проекций, то на эту плоскость
она проецируется в поле точек. Её проекция
на другой плоскости – прямая,
перпендикулярная к линии связи.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.7. Следы плоскости
Следом плоскости α называется линия пересечения этой плоскости с плоскостью проекций.
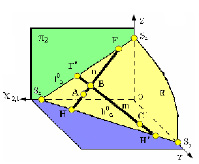
На рис. 2.19. изображена плоскость общего положения α(m∩n), образованная двумя пересекающимися прямыми, проходящими через точки А и В, расположенными в первом октанте.
Для построения следов плоскости на комплексном чертеже, необходимо помнить, что след плоскости – это линия, значит необходимо найти две точки, через которые пройдет эта линия, т. е. след плоскости. При построении плоскости за такие точки можно принять следы любых прямых линий, принадлежащих этой плоскости.
На рис. 2.19 в горизонтальной плоскости проекций π1 её горизонтальный след h0α проходит через горизонтальные следы Н и Н’ прямых m и n, а во фронтальной плоскости проекций π2 – фронтальный след плоскости f0α проходит через фронтальные следы прямых F и F’.
Рис. 2.19. Пример изображения следов плоскости α в пространстве
Для нахождения следов плоскости нужно применить правило построения следов прямых линий, который был рассмотрен выше (§2.4). Для построения горизонтального следа плоскости необходимо построить два горизонтальных следа прямых, принадлежащих плоскости, а для построения фронтального следа плоскости – два горизонтальных следа прямых, принадлежащих плоскости α(m∩n).
В системе двух плоскостей проекций π1 и π2 плоскость в общем случае имеет два следа: горизонтальный ha0 и фронтальный fa0, которые являются пересечением плоскости α соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.19, 2.20).
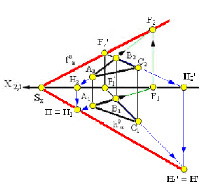
Рис. 2.20. Пример изображения следов плоскости и их алгоритм построения на комплексном чертеже
Точки пересечения плоскости α с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно Sx, Sy, Sz (рис. 2.16). На рис. 2.20. приведен комплексный чертеж плоскости треугольника АВС и разобран пример построения двух следов этой плоскости – горизонтального ha0 и фронтального fa0. Для этого выполнено построение горизонтальных следов прямых АВ и ВС, принадлежащих плоскости треугольника. Эти следы обозначены буквами Н и Н’. Решение на рисунке выполнено синими линиями со стрелками. Аналогичное построение выполнено и для фронтального следа линиями зелёного цвета. Порядок построения следов ясен из рисунка.
Вопросы для самоконтроля
1. Когда точка принадлежит какой либо плоскости проекций?
2. Как может быть задана прямая на комплексном чертеже?
3. Какие основные свойства прямой общего положения?
4. Какие частные положения относительно плоскостей проекций может занимать прямая линия?
5. Когда прямая линия может принадлежать плоскости проекций?
6. Какие прямые являются проецирующими?
7. Что называется следом прямой?
8. Как определяются на комплексном чертеже следы прямой линии?
9. Как на комплексном чертеже может быть задана плоскость?
10. Какие плоскости являются проецирующими?
11. Какие плоскости являются плоскостями уровня?
12. Какие плоскости являются плоскостями частного положения?
13. Что называется следом плоскости и как он определяется?
[1] То́чка – абстрактный объект в пространстве, не имеющий никаких измеримых характеристик (нульмерный объект).
Плоскость, как и прямая, и точка, является одним из основополагающих понятий в геометрии.
Плоскость, в зависимости от расположения в пространстве, может быть общего и частного положения.
К плоскостям частного положения относятся:
- параллельные одной из плоскостей проекций;
- проецирующие плоскости, перпендикулярные одной из плоскостей проекций.
Плоскости общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций.
Способы задания плоскостей в пространстве
Плоскость можно задать следующими способами:
- Тремя точками. Три точки пространства однозначно задают одну и только одну плоскость. Так же говорят о задании плоскости треугольником, вершины которого и являются этими тремя точками (рис. 6.1-а).
- Плоскость можно задать прямой и точкой (рис. 6.1-б).
- Двумя пересекающимися прямыми (рис. 6.1-в).
- Двумя параллельными прямыми (рис.6.1-г).
- Плоскость можно задать следами (рис.6.1-д).
Построение следов плоскости
Следом плоскости называется линия пересечения этой плоскости с плоскостью проекций.
Поскольку следом плоскости является прямая, лежащая в плоскости проекций, для ее построения достаточно найти следы двух любых прямых, лежащих в заданной плоскости.
Рассмотрим на примере последовательность построения горизонтального и фронтального следов плоскости.
Задача 6.1.
Построить горизонтальный и фронтальный следы плоскости α, заданной треугольником АВС (рис. 6.2).
Решение:
Выберем в заданной плоскости две прямые и построим их следы. В качестве таких прямых можно взять стороны треугольника – АВ и ВС.
Построим сначала горизонтальные следы этих прямых. На рисунке 6.3 показано построение точек 1 и 2, которые являются горизонтальными следами прямых АВ и ВС соответственно.
Порядок построения следующий:
- Продлим фронтальную проекцию стороны треугольника А2В2 до пересечения с осью х и отметим точку 12.
- Продлим горизонтальную проекцию отрезка А1В1 ( на рисунке показано штриховой линией).
- Спроецируем точку 12 на продолжение прямой А1В1 и получим точку 11.
Итак, мы получили две проекции горизонтального следа прямой АВ – точки 11, 12.
По строим в том же порядке горизонтальный след прямой ВС – точки 22и 21.
Соединим точки 11и 21, продолжим эту прямую до оси х. Получили горизонтальный след плоскости α – прямую αх. (Рис.6.4).
Для построения фронтального следа заданной плоскости, нужно построить фронтальные следы прямых АВ и ВС.
Построим фронтальный след прямой ВС (рис. 6.5). Как видно из рисунка, для этого необходимо продлить проекцию В1С1 до оси х, где получим точку 31; затем надо продлить проекцию В2С2таким образом, чтобы на нее можно было спроецировать точку 31и получить фронтальный след прямой ВС — точку 32.
Выполним построение фронтального следа прямой АВ, аналогично предыдущему построению, как показано на рисунке 6.6. Точка 42 является фронтальным следом прямой АВ.
Для завершения построения фронтального следа плоскости, заданной треугольником АВС, нужно соединить точки 32 и 42. Фронтальный след плоскости проводят до пересечения с осью х. Следы плоскости общего положения всегда имеют общую точку на оси проекций. В данном случае это ось х (рис. 6.7). Задача решена.