- Главная
- Найти слово по буквам в квадрате
Филворд – это задание головоломка для детей по поиску слов среди букв. Упражнение развивает внимание и пространственную ориентацию, а также словарный запас ребенка…
Филворды или венгерский кроссворд – разновидность словесных кроссвордов, в которых уже написаны слова. Перед каждым заданием есть список слов которые необходимо найти среди букв…
Здесь вы можете скачать задания для детей “Найти слово по буквам в квадрате”, с помощью которых обучение чтению можно сделать еще более эффективным. Ребенок должен найти в квадратах, среди беспорядочно разбросанных букв, названия овощей и ягод, которые он увидит на картинках.
Найти слово по заданным буквам – это одновременно и полезное развивающее занятие для ребенка, и интересная игра, в которой необходимо среди букв найти заданные слова, изображенные на картинках.
Найти слово по буквам “Девчонки” – это полезная и интересная игра для деток, которые учатся чтению. Такие игры особенно положительно влияют на развитие внимания малышей. В первом задании, чтобы узнать как зовут девочек, ребенку нужно найти их имена среди хаотично расположенных букв в квадрате; во втором: узнать, на каком уроке сидят ученицы. Слова в задании могут располагаться и по-горизонтали, и по-вертикали, и по-диагонали.
Найти слова – Игра по составлению слов из букв – это упражнение развивает внимание, а также стимулирует умение ребенка находить слова среди хаотично расположенных букв в таблице.
| Квадрат из слов | |
|---|---|
| Модельный элемент | SATOR |

Квадрат из слов — головоломка со словами, в которой надо написать друг под другом слова (обычно подразумевается, что это нарицательные существительные в начальной форме, как в кроссворде), чтобы они образовали квадрат, в котором во всех столбцах сверху вниз читаются слова. В столбцах могут стоять те же слова, что и в соответствующих им по номерам строках (такой квадрат называют полумагическим), а могут читаться и другие слова. Найти вручную квадрат 5×5 из десяти различных слов (полный или магический квадрат) очень трудно.
История[править | править код]
Самым древним квадратом слов, вероятно, является латинский палиндром квадрат SATOR. До 1990−х гг. такие квадраты находили вручную, что было сопряжено с большими трудностями. Было известно лишь несколько квадратов слов размером 2×2, 3×3, 4×4 и 5×5. Самые большие квадраты слов в любом языке имеют размер 11×11 и были построены на латыни.[1]
Публикации[править | править код]
В журнале «Наука и жизнь»[2] под рубрикой «Психологический практикум» по письму Сергея Мельникова была опубликована статья «Квадраты из слов», в которой говорилось:
В журнале «Наука и жизнь» неоднократно публиковались задачи, в которых требовалось заполнить словами квадратные матрицы 2×2, 3×3, 4×4, 5×5 так, чтобы по вертикали и горизонтали слова не повторялись (см., например, № 1, 1975 г.; № 6, 1977 г.).
В журнале «Интеллектуальные игры»[3], который издавался в Челябинске, член редколлегии и известный специалист в области интеллектуальных игр Олег Степанов привёл два квадрата из слов, второй из которых (из десяти слов) был составлен М. Эскиным:
|
|
Первым, кто применил в этом деле компьютер, видимо, был Сергей Мельников, который получил несколько сотен квадратов из слов 5×5 и нашёл два квадрата из слов 6×6. Впоследствии, воспользовавшись более полным словарём существительных, он нашёл несколько десятков квадратов из слов 6×6, но ни квадрата 7×7, ни 8×8 найти не удалось.
Использование в головоломках[править | править код]
Квадраты из слов используются в качестве кроссвордов, в этом случае в их сетке нет пустых клеток. Ещё в них оставляют лишь верхнее горизонтальное и левое вертикальное слово или некоторые буквы заменяют точками и предлагают восстановить все слова.
Примечания[править | править код]
- ↑ Эрик Тентарелли. Большие квадраты слов на латыни (англ.). Word Ways (2020). Дата обращения: 23 декабря 2020. Архивировано 26 марта 2021 года.
- ↑ Сергей Мельников. Квадраты из слов // Наука и жизнь. — 1996. — Вып. 7. — С. 45.
- ↑ Олег Степанов. Опять квадратные слова // Интеллектуальные игры. — 1992. — Вып. 5. — С. 10.
Ссылки[править | править код]
- Статья Сергея Мельникова «Головоломки со словами: „Квадраты из слов“» Архивная копия от 25 июня 2012 на Wayback Machine

47
Мы сразу откажемся от глобальной задачи – составить вообще все возможные квадраты, поскольку труд окажется непосильным. Мы предоставим пользователю возможность самому выбрать первое слово для квадрата, а все остальные будет подбирать наша программа.
Нетрудно догадаться, что нам потребуется словарь, из которого мы и будем выбирать слова для квадрата. Все слова в квадрате имеют равную длину, поэтому вполне разумно воспользоваться фракционным словарем.
Большая часть полей нашей программы как раз и будет задействована при загрузке словаря и хранении списка подходящих слов. Другие поля понадобятся нам для работы с магическим квадратом – для хранения порядка
квадрата, слова пользователя и массива слов в квадрате:
//ПРОГРАММА ДЛЯ СОСТАВЛЕНИЯ //СЛОВЕСНЫХ МАГИЧЕСКИХ КВАДРАТОВ //порядок квадрата:
int N = 0;
Random rand = new Random();
//словарь: rvDict dict;
//магический квадрат: string[] mq;
//число подходящих слов:
//int nLex;
//число найденных магических квадратов: int nVar;
//список подходящих слов:
List<string> lex= new List<string>(); //=true, если слово использовано: List<bool> flg= new List<bool>();
Словарь по умолчанию лучше загрузить сразу же при запуске приложения, чтобы не заставлять пользователя делать это самостоятельно. А затем он может выбрать любой словарь из папки с программой или загрузить собственный.
public frmWS()
{
InitializeComponent(); //загружаем словарь:
dict = new rvDict(“frc.txt”); dict.CreateBeginWord();
}

48
В текстовое поле txtWord1 пользователь должен впечатать первое слово для квадрата. Мы должны разумно ограничить его длину. Действительно, квадрат из одной буквы составить можно и без помощи компьютера, а для квадрата из семибуквенных слов практически невозможно наугад выбрать первое слово.
После нажатия на кнопку btnGen мы переходим в метод btnGen_Click, где по длине слова легко определяем порядок квадрата и создаём новый строковый массив для него. Первое слово нам уже известно, поэтому мы тут же записываем его в квадрат:
//СОСТАВЛЯЕМ МАГИЧЕСКИЙ КВАДРАТ
private void btnGen_Click(object sender, EventArgs e)
{
//первое слово:
string word1 = txtWord1.Text.ToUpper();
//Длина слова:
N = word1.Length;
//если слово отсутствует, выбираем случайно из словаря: if (word1 == “”)
{
N = (int)udLength.Value;
int id= rand.Next(dict.beginWord[N], dict.beginWord[N]+dict.numWord[N]);
word1 = (string)dict.list[id]; txtWord1.Text = word1.ToUpper();
}
else if (N < 2 || N > 6)
{
MessageBox.Show(“В слове должно быть от двух до шести букв!”);
return;
}
//создаем массив для слов: mq = new string[N + 1]; mq[1] = word1; flg.Clear();
//составляем список подходящих слов:
//nLex = 0;
string letters = word1.Substring(1, N – 1); lex.Clear();
//длина всех слов должна быть равна порядку квадрата n: for (int i = dict.beginWord[N]; i < dict.beginWord[N] +
dict.numWord[N]; ++i)
{
//не включаем в список первое слово:
49
if ((string)dict.list[i] == word1) continue;
//слово должно начинаться с буквы в letters: char ch = ((string)dict.list[i])[0];
//если нашли слово,
if (letters.IndexOf(ch) >= 0)
{
//добавляем его в список: lex.Add((string)dict.list[i]);
//слово не использовано: flg.Add(false);
}
}
//пока не нашли ни одного квадрата: nVar = 0;
//составляем квадрат, начиная со второго слова: recGenerate(2);
lstRes.Items.Add(“”);
lstRes.Items.Add(“Найдены все решения: ” + nVar.ToString()); lstRes.Items.Add(“”);
lstRes.TopIndex = lstRes.Items.Count – 27;
}
Так как словарь dict довольно большой, а нам придётся перебирать все слова заданной длины, то лучше сразу об этом призадуматься и постараться уменьшить перебор. Это очень просто! Первое слово квадрата даёт нам начальные буквы всех остальных слов. Это легко понять, если посмотреть, как составлен магический квадрат Sator. Нам известна длина слов и их начальные буквы, поэтому мы составляем словарик lex, в который включаем только те слова, которые могут быть поставлены в квадрат. Он, безусловно, будет значительно короче общего списка слов. Также мы не забываем заполнить список флажков «фальшивыми» значениями, которые отмечают еще неиспользованные слова.
Иногда первое слово не приходит в голову или его нужно выбрать слу-
чайно. Поэтому мы установим на форме компонент udLength, в котором
удобно задавать длину слов (или порядок квадрата). Но тут может воз-
никнуть непреднамеренная коллизия со словом в поле txtWord1, по-
скольку программа будет теряться в догадках, выбирать ли ей слово слу-
чайно или брать то, которое ввёл пользователь. Чтобы рассеять её со-
мнения, следует очистить поле txtWord1, дважды кликнув на нём:
private void txtWord1_MouseDoubleClick(object sender, MouseEven-
tArgs e)
{
txtWord1.Text = “”;

50
}
Вот теперь программа поймёт вас правильно и выберет слово случайно.
И вот у нас всё готово для составления магического квадрата, и мы отправляемся прямиком в рекурсивный метод recGenerate.
Конечно, метод должен быть именно рекурсивным, поскольку действия при составлении квадрата практически полностью повторяются для каждого нового слова: ставим второе слово с учётом первого, затем ставим третье слово с учётом первых двух, и так далее, пока квадрат не будет построен или мы не убедимся, что его построить нельзя.
Единственная трудность здесь – в организации проверки слов из списка: годятся ли они для квадрата или нет.
Опять обратимся к магическому квадрату Sator. В нашем случае первое слово уже стоит в квадрате:
SATOR
A….
T….
O….
R….
Хорошо видно, что второе слово оно должно начинаться с буквы А (второе слово – вторая буква в исходном слове), а все остальные четыре буквы могут быть любыми.
Ставим второе слово:
SATOR
AREPO
TE…
OP…
RO…
Третье слово должно начинаться с букв TE – а это третья буква первого слова и третья буква второго слова.
51
Если решение ещё не пришло вам в голову, то продолжайте составлять квадрат. Рано или поздно вы найдёте простой алгоритм для составления подстроки shablon, с которой и должно начинаться очередное слово:
//создаём шаблон для слова num: string shablon = “”;
for (j = 1; j < num; ++j)
shablon += mq[j].Substring(num – 1, 1);
Остальное, как говорится, дело техники, и рекурсивный метод готов:
//Рекурсивный метод составления магических квадратов void recGenerate(int num)
{
int j = 0;
//создаем шаблон для слова num: string shablon = “”;
for (j = 1; j < num; ++j)
shablon += mq[j].Substring(num – 1, 1);
//перебираем все слова в списке lex: foreach (string s in lex)
{
//оно должно начинаться с букв shablon: if (s.StartsWith(shablon))
{
//нашли подходящее слово–> //ставим его в квадрат: mq[num] = s;
flg[j] = true;
if (num < N) recGenerate(num + 1); else writeVar();
++j; }//if
flg[j] = false; }//for
} //recGenerate
Найденные магические квадраты мы печатаем в списке lstRes:
//ПЕЧАТАЕМ МАГИЧЕСКИЙ КВАДРАТ void writeVar()
{
//нашли еще один магический квадрат: nVar++;
lstRes.Items.Add(“”); lstRes.Items.Add(“Вариант: ” + nVar.ToString());
for (int i = 1; i <= N; ++i) lstRes.Items.Add(mq[i]); //прокручиваем список вниз:
52
lstRes.TopIndex = lstRes.Items.Count – 27; lstRes.Invalidate(); Application.DoEvents();
}
Ну вот и пришло время позабавиться!
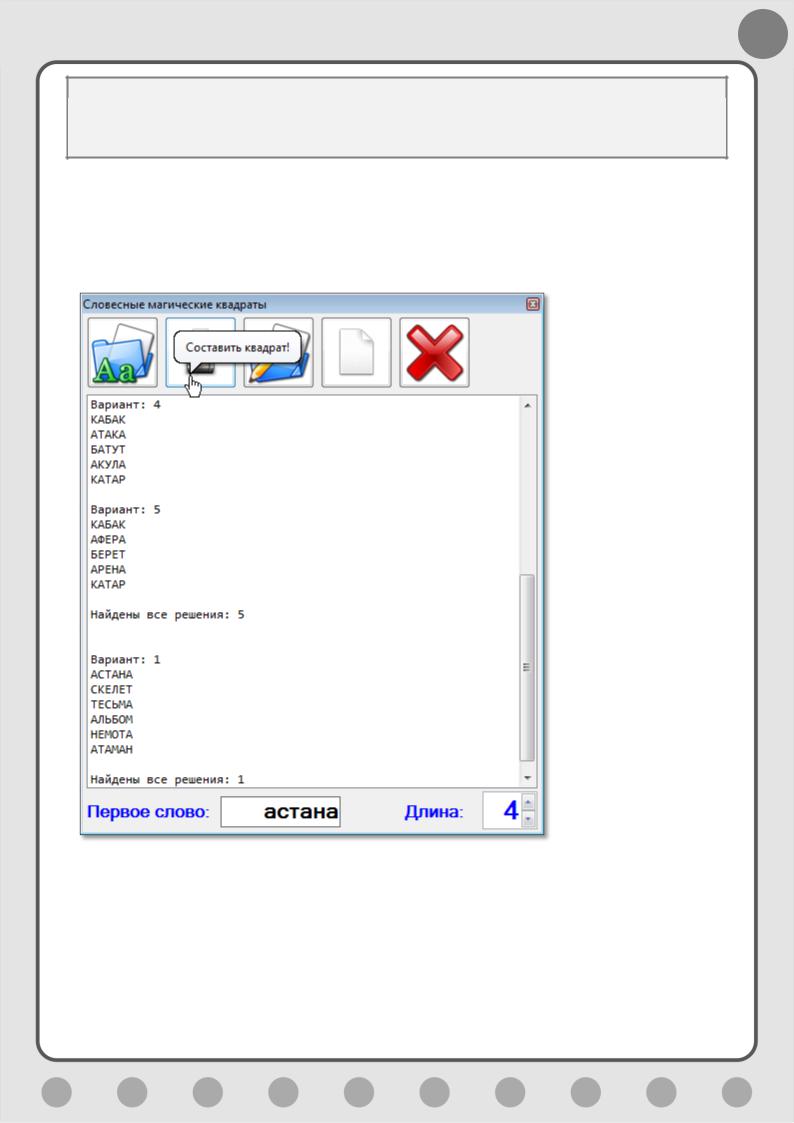
Запускаем программу и вводим слова из 2-6 букв. Результат получаем мгновенно (Рис. 6.6).
Рис. 6.6. Магическое производство налажено!
Так мы можем составить сколько угодно магических квадратов!
Если вам наскучит словарь по умолчанию, вы в любой подходящий момент можете загрузить другой, нажав кнопку btnLoadDict:
53
//ЗАГРУЖАЕМ СЛОВАРЬ ПО ВЫБОРУ
private void btnLoadDict_Click(object sender, EventArgs e)
{
dict = new rvDict();
dict.Load();
//фракционируем список:
//dict.Fract();
dict.CreateBeginWord();
}
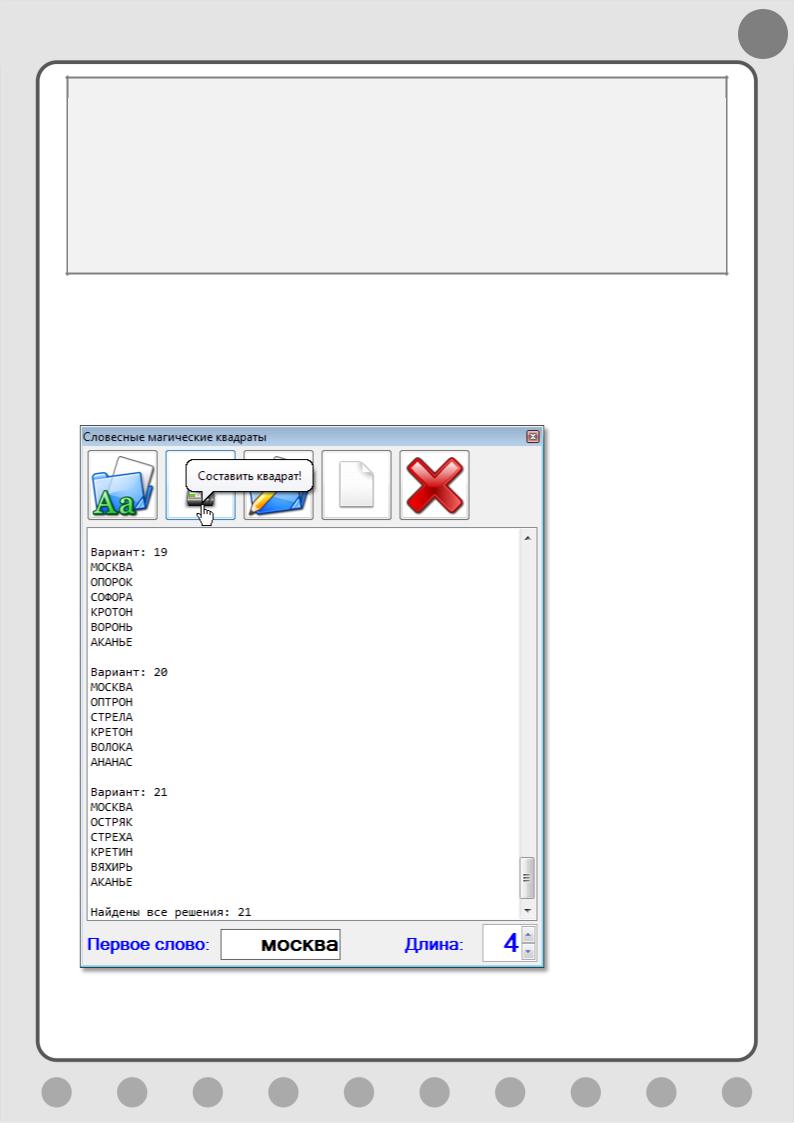
Для составления больших магических квадратов нужен и солидный словарь. Например, с файлом SSSRLfrc.txt я нашёл 21 решение для ведущего слова МОСКВА (Рис. 6.7), тогда как словарь по умолчанию не находит вообще ни одного!
Рис. 6.7. Москва – как много в этом!..
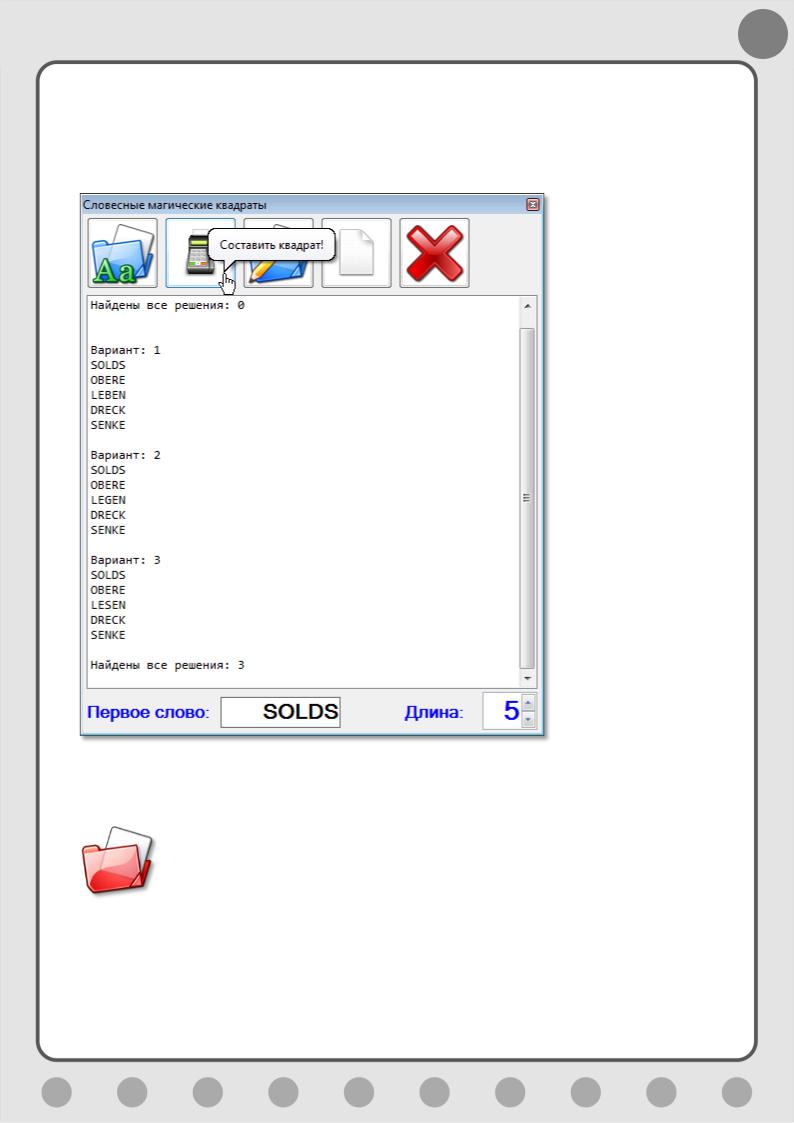
54
А с иностранными словарями, например DeutschUnicodeFRC.txt, вы можете составлять магические квадраты на чуждых вам языках, даже не зная ни одного иностранного слова (Рис. 6.8)!
Рис. 6.8. Шпрехен Зи дойч?
Исходный код программы находится в папке WordSquares.
55
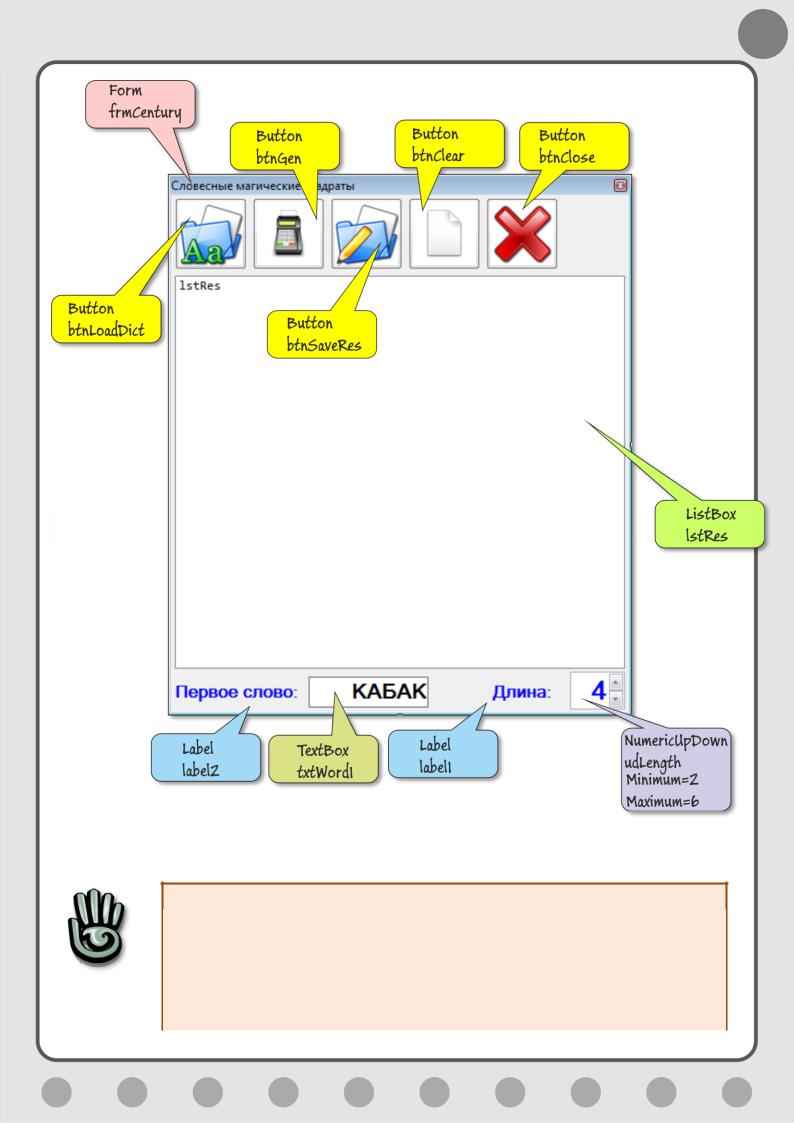
Примерный интерфейс приложения
1. Хотя наш алгоритм работает достаточно быстро, но при поиске всех квадратов заданного размера он будет неуклюже составлять список подходящих слов для каждого нового начального слова. Лучше один раз и навсегда запомнить индексы начала не только слов заданной длины, но и каждой буквы в отдельности. Тогда при необходимости вы сразу выйдете на нужную часть списка. Для
56
хранения начальных индексов годится структура данных Dictionary<>, а вот для индексов начала и конца слов, а также флажка их использования придётся завести структуру.
Ещё одна возможность оптимизации – записывать слова в сетку не последовательно, а выбирать такую начальную букву, на которую имеется меньше всего подходящих слов. Например, если первое слово ПАРОЛЬ, то нет никакого смысла перебирать начальные слова, поскольку на мягкий знак слов нет вообще.
2. В нынешнее время словесные квадраты утратили свою магическую силу и используются исключительно как головоломки.
В простейшем варианте – это обычный кроссворд (Рис. 6.9). Иногда такие задания встречаются в головоломных журналах, но магические квадраты здесь сильно уступают своим потомкам: они маленькие по размерам и все слова в сетке повторяются дважды, что не очень хорошо действует на умных людей. Совсем маленькие квадраты и вовсе неинтересны, а большие трудно составлять, поэтому в них неизбежно попадают редкие слова.
Рис. 6.9. Магический кроссворд
1.Вот тебе проблема!
2.Приятный запах денег.
3.Главный герой третьей главы.
4.Жидкий ароматизированный крахмал для машинной и ручной стирки.
5.Традиционное блюдо грузинской кухни.
6.Потеря тонуса мышц.
57
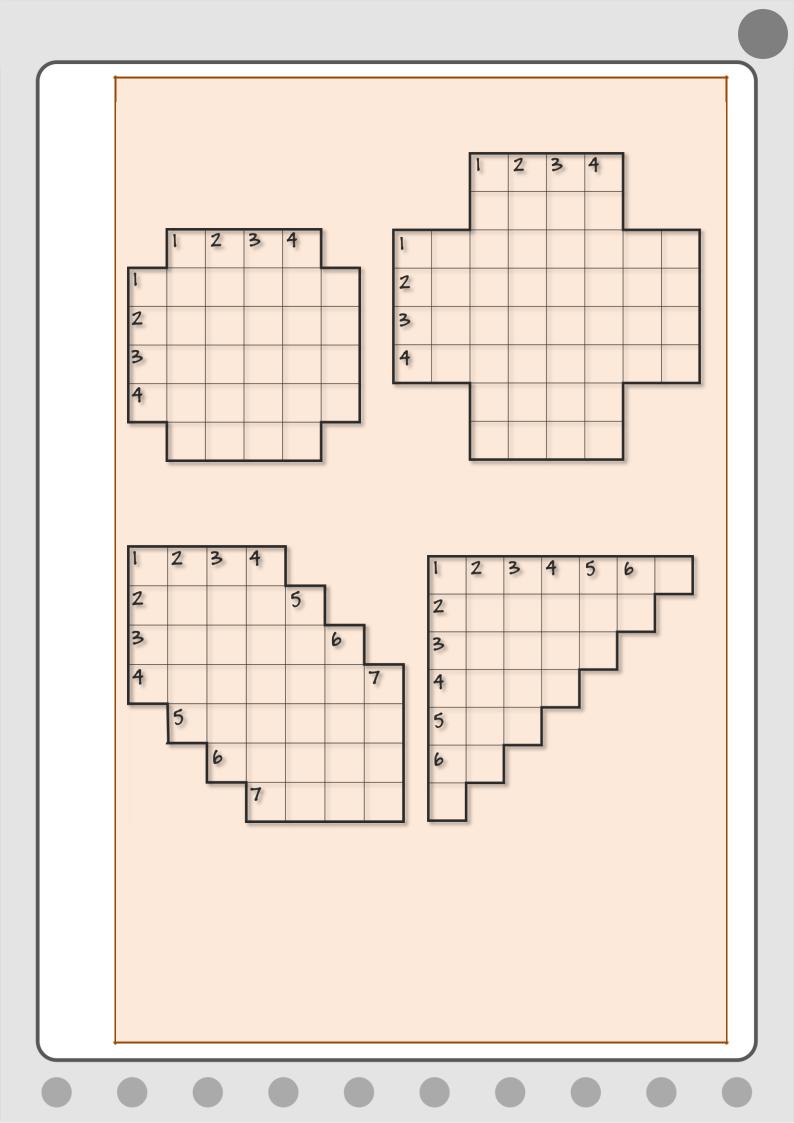
Некоторое разнообразие привносят новые формы сетки, отличные от квадратной (Рис. 6.10):
Магические кресты
Магическая лестница Магический треугольник
Рис. 6.10. Магические фигуры
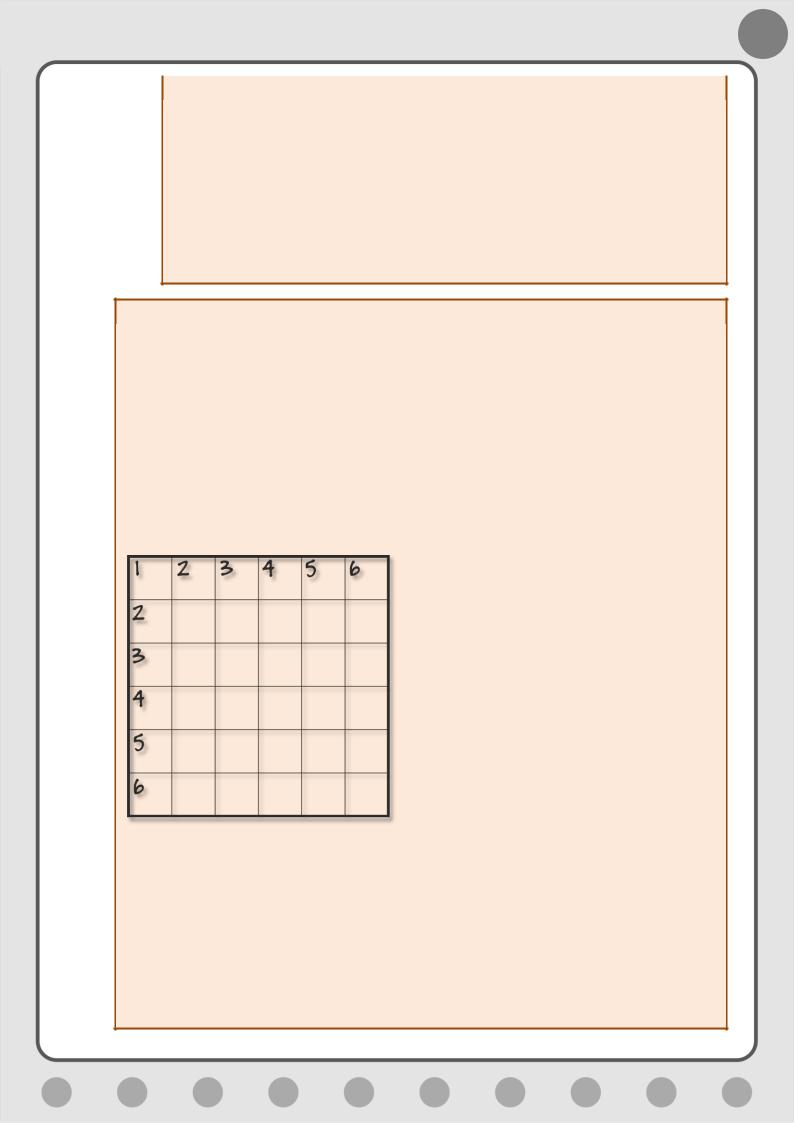
Другой тип заданий скорее логический и напоминает знаменитые пазлы. Нужно правильно расставить слова в пустом квадрате (Рис. 6.11).
58
Рис. 6.11. Магический пазл
И наконец, самая популярная головоломка из этой серии. Первое слово
записано в квадрат (Рис. 6.12).
Рис. 6.12. Магическая сетка
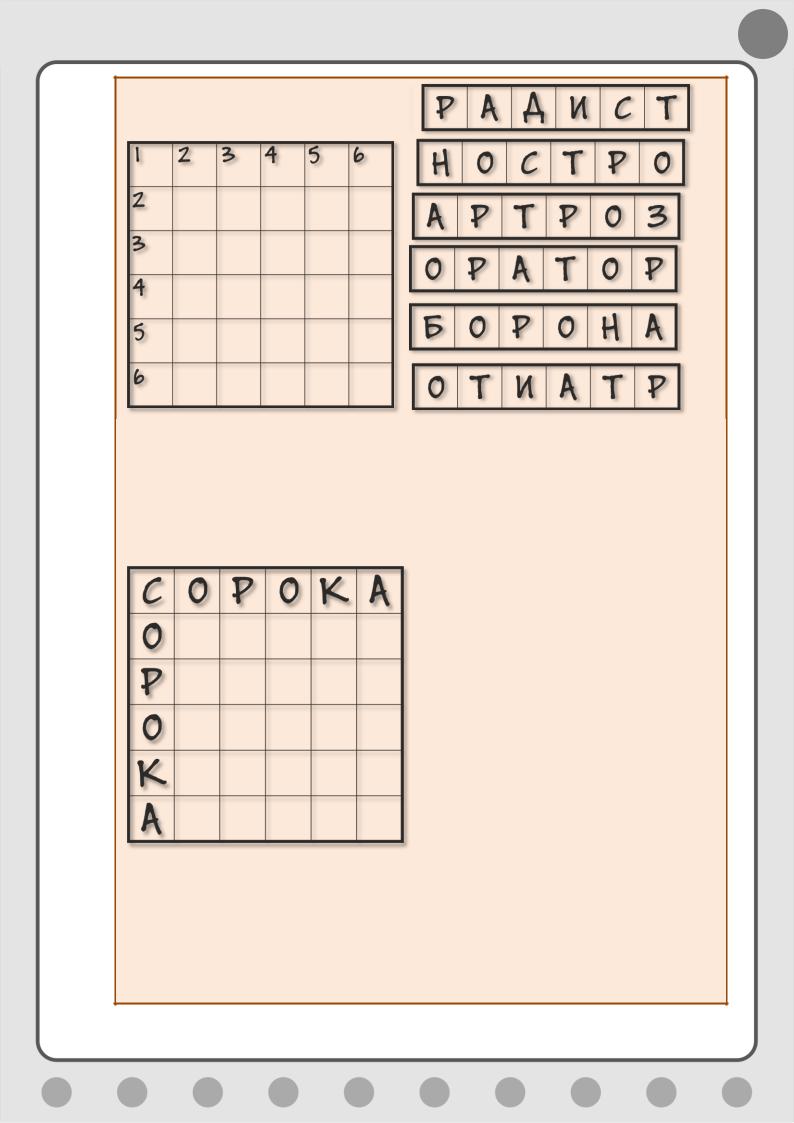
Сетка сопровождается таблицей, в которой указаны буквы и их число – для тех слов, которые нужно найти (Рис. 6.13).

59
Рис. 6.13. Магическая статистика
Последняя строка этой таблицы оставлена пустой, чтобы отгадчик мог отмечать вышедшие буквы. По этим данным нужно «вычислить» все слова и заполнить сетку.
Эта задача также логическая, но предполагает и знание слов. Легко догадаться, что табличная буква, присутствующая в единственном числе, должна стоять на главной нисходящей диагонали квадрата, а остальные буквы располагаются симметрично относительно этой диагонали.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Квадрат из слов
- Квадрат из слов — головоломка со словами, в которой надо написать друг под другом слова (обычно подразумевается, что это нарицательные существительные в начальной форме, как в кроссворде), чтобы они образовали квадрат, в котором во всех столбцах сверху вниз читаются слова. В столбцах могут стоять те же слова, что и в соответствующих им по номерам строках (такой квадрат называют полумагическим), а могут читаться и другие слова. Найти вручную квадрат 5×5 из десяти различных слов (полный или магический квадрат) очень трудно.
Источник: Википедия
Связанные понятия
Метагра́ммы (от др.-греч. μετά — «между», γράμμα — «буква») — разновидность шарад, загадок, в которых зашифрованы различные слова, состоящие из одного и того же числа букв. Разгадав одно из слов метаграммы, нужно заменить в нём одну или несколько букв так, чтобы получилось новое слово по смыслу загадки. Также существуют головоломки, целью которых является последовательным изменением по одной букве перейти от одного загаданного слова к другому в заданное число шагов.
Амбигра́мма (от лат. ambi — «двойной» и др.-греч. γράμμα — «буква») — каллиграфический узор, позволяющий совместить два различных прочтения из одного и того же набора линий.
Гре́ко-лати́нский квадра́т, или э́йлеров квадра́т, — квадрат N×N в каждой клетке которого стоят 2 числа от 1 до N так, что выполняются следующие условия…
Одной из разновидностей мудрой литореи является тайнопись «в квадратах». В рукописях XVII века преимущественно грамматического содержания в виде ключа к «риторскому письму» помещались таблицы из сорока квадратов, в каждом из которых изображались две разные буквы алфавита. Причём одни буквы были окрашены киноварью (красные), а другие просто чернильные (см. рис. 1). Кроме того, в квадратах вместе с буквами приводились некоторые грамматико-орфографические термины, поясняющие смысл и характер употребления…
Подробнее: Письмо в квадратах
Чайнворд (англ. chain — цепь, англ. word — слово) — вид кроссвордов, в которых, как следует из названия, пересечение слов представляет собой линию (то есть цепь). Поэтому второе распространенное название — линейный кроссворд.
Подробнее: Линейный кроссворд
Головоломка по поиску слов (от англ. Word search — «поиск слова») — головоломка, представляющая собой прямоугольную таблицу из букв, в которой ищутся слова — вертикально, горизонтально и по диагонали, в прямом и обратном порядке. В некоторых вариантах сразу дан список спрятанных слов, в других он отсутствует — напротив, загадано слово, которое образуется из букв, не вошедших ни в одно слово данной головоломки. Зачастую головоломки посвящены какой-то теме и используются при обучении новым словам и…
Танграм (кит.七巧板, пиньинь qī qiǎo bǎn, букв. «семь дощечек мастерства») — головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма…
Японская головоломка (также японский кроссворд, японское рисование, нонограмма) — головоломка, в которой, в отличие от обычных кроссвордов, зашифрованы не слова, а изображения.
Теоре́ма о бесконе́чных обезья́нах (в одном из многочисленных вариантов формулировки) утверждает, что абстрактная обезьяна, ударяя случайным образом по клавишам пишущей машинки в течение неограниченно долгого времени, рано или поздно напечатает любой наперёд заданный текст.
Шрифт Брайля (фр. Braille) — рельефно-точечный тактильный шрифт, предназначенный для письма и чтения незрячими и плохо видящим людям. Разработан в 1824 году французом Луи Брайлем (фр. Louis Braille), сыном сапожника. Луи в возрасте трёх лет поранился в мастерской отца шорным ножом; из-за начавшегося воспаления глаза мальчик потерял зрение. В возрасте 15 лет Луи создал свой рельефно-точечный шрифт как альтернативу рельефно-линейному шрифту Валентина Гаюи, вдохновившись простотой «ночного шрифта» капитана…
Многото́чие (…) — знак препинания в виде нескольких (в русском языке трёх) поставленных рядом точек. Служит для обозначения прерванности речи, незаконченности высказывания или пропуска в тексте.
Судо́ку (яп. 数独 су:доку, произношение ) — головоломка с числами. Иногда судоку называют магическим квадратом, что в общем-то неверно, так как судоку является латинским квадратом 9-го порядка. Судоку активно публикуют газеты и журналы разных стран мира, сборники судоку издаются большими тиражами. Решение судоку — популярный вид досуга.
Математическая шутка — фраза или небольшой текст юмористического содержания, который опирается на аспекты математики или стереотипы о математике. Юмор может определяться игрой слов или двойным смыслом математического термина. Эти шутки часто непонятны для тех, кто не обладает математическим складом ума. Относится к научному юмору.
Бо́ггл (англ. Boggle) — настольная игра, в которую играют обычно два человека, составляя слова из имеющихся у них букв и записывая их на бумаге.
Япо́нская пунктуа́ция (яп. 約物 якумоно) — знаки препинания и правила их использования в японском языке.
У́стный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т. п.) и приспособлений (ручка, карандаш, бумага и т. п.).
Скрэббл (англ. Scrabble — «рыться в поисках чего-либо») — настольная игра, в которой от двух до четырёх играющих соревнуются в образовании слов с использованием буквенных деревянных плиток на доске, разбитой на 225 квадратов. В русскоязычной среде известна также под названиями «Эрудит» или «Словодел». На русском языке игра впервые описана в журнале «Наука и жизнь» (1968, № 7) под названием «Крестословица».
Данная статья — часть обзора История математики. Современная математика изучает абстрактные структуры совершенно различной природы (множества, высказывания, логические языки, функции), но её основным объектом изучения изначально были понятия натурального числа и геометрической фигуры, возникшие из практической деятельности человека.
Подробнее: Возникновение математики
Кроссво́рд (англ. Crossword — пересечение слов) — головоломка, представляющая собой переплетение рядов клеточек, которые заполняются словами по заданным значениям.Обычно значения слов задаются описательно под этой фигурой, сначала значения слов, которые должны получиться по горизонтали, затем — по вертикали.
Папирус Ахмеса был обнаружен в 1858 году в Фивах и часто называется папирусом Ринда (Райнда) по имени его первого владельца.
Пантограмма, омограмма, равнобуквица, равнорифмица, заикалочка (термин Г. Лукомникова) — произведение комбинаторной поэзии, в котором буквенный состав стихотворных строк попарно идентичен, а различно лишь расположение словоразделов. В некоторых источниках также ошибочно называется гетерограммой несмотря на то, что этот термин был ранее закреплён за другой формой комбинаторной поэзии. Пантограмму также квалифицируют как визуальную панторифму: в отличие от собственно панторифмы, в пантограмме могут…
Шифр нигилистов — это метод шифрования, используемый движением российских нигилистов для борьбы против царского режима в 1880-х годах.Оригинальный алгоритм был, скорее, базовым шифром, но потом появились модификации, которые обеспечивают лучшую безопасность. Одним из шифров, принадлежащих Нигилистической семье шифров, является шифр ВИК.
«Нау́ка уме́ет мно́го ги́тик» — крылатая фраза, поговорка, изначально предназначенная для демонстрации фокуса с двадцатью игральными картами. Первое документально подтвержденное употребление фразы относится к 1891 году. Иногда слово «умеет» ошибочно заменяют на «имеет». Рассматривая это выражение как псевдовысказывание, Б. Ю. Норман подчёркивает его мнемоническую функцию…
Шифр Бэкона (или «двухлитерный шифр») — метод сокрытия секретного сообщения, придуманный Фрэнсисом Бэконом в начале XVII века. Он разрабатывал шифры, которые бы позволяли передавать секретные сообщения в обычных текстах так, чтобы никто не знал об этих сообщениях. Шифр базируется на двоичном кодировании алфавита символами «A» и «B», которым можно сопоставить «0» и «1». Затем секретное послание «прячется» в открытом тексте, с помощью одного из способов сокрытия сообщений.
Нурикабе (яп. ぬりかべ) — это логическая головоломка, разработанная компанией Nikoli и опубликованная в 1991 году. Перед игроком ставится задача в рисовании «островов», разделённых «рекой», и при этом заданные числа задают размеры рассматриваемых островов.
Гексамино — шестиклеточное полимино, то есть плоская фигура, состоящая из шести равных квадратов, соединённых сторонами. С фигурами гексамино, как со всеми полимино, связано много задач занимательной математики.
Пазигра́фия Маймье́ — система письменного языка для международного общения, изобретённая Жозефом де Маймье и изложенная в его книге «Pasigraphie ou Premiers éléments du nouvel art-science, d’écrire et d’imprimer en une langue, de manière à être lu et entendu dans toute autre langue sans traduction…» (Париж, 1797). Под руководством Маймье были организованы пазиграфические курсы при Бюро пазиграфии, которое открылось в Париже для поддержки проекта Маймье, однако широкого распространения в мире этот…
Шахматная нотация (от лат. notatio — записывание, обозначение) — система условных обозначений, применяемых для записи шахматной партии или положения фигур на шахматной доске.
Коса́я черта́, или косая, — символ в виде тонкой прямой линии с наклоном вправо (то есть вперёд при направлении письма слева направо).
Мнемо́ника (др.-греч. μνημονικόν — искусство запоминания), мнемоте́хника — совокупность специальных приёмов и способов, облегчающих запоминание нужной информации и увеличивающих объём памяти путём образования ассоциаций (связей): замена абстрактных объектов и фактов на понятия и представления, имеющие визуальное, аудиальное или кинестетическое представление, связывание объектов с уже имеющейся информацией в памяти различных типов модификации для упрощения запоминания.
Ри́мские ци́фры — цифры, использовавшиеся древними римлянами в их непозиционной системе счисления.
О́белюс, обел (÷) (лат. obelus — от греч. ὀβελός, тот же корень, что и обелиск) — небуквенный символ, внешне напоминающий объединение знаков минуса и двоеточия.
Книжный шифр — вид шифра, в котором каждый элемент открытого текста (каждая буква или слово) заменяется на указатель (например, номер страницы, строки и столбца) аналогичного элемента в дополнительном тексте-ключе.
Ноль (нуль, от лат. nullus — никакой) — название первой (по порядку) цифры в стандартных системах исчисления, а также математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех левее стоящих цифр на разряд (например, в десятичной системе счисления, умножает на десять). Сравните, например, числа 410 и 4010; 416 и 4016 (нижний индекс означает основание системы…
«Гло́кая ку́здра ште́ко будлану́ла бо́кра и курдя́чит бокрёнка» — искусственная фраза на основе русского языка, в которой все корневые морфемы заменены на бессмысленные сочетания звуков.
Дешифровка ронго-ронго, письменности острова Пасхи, обнаруженной в конце XIX века, до сих пор не осуществлена. Аналогично другим недешифрованным письменностям, существует множество гипотез относительно ронго-ронго, в том числе фантастических. Известно содержание только части одной таблички, имеющей отношение к лунному календарю, но даже эту часть пока не удалось расшифровать. Дешифровке препятствуют три обстоятельства: малое количество сохранившихся текстов (содержащих в сумме не более 15 000 знаков…
Марсиа́нский язы́к (также «марсианское письмо»:225, кит. трад. 火星文, пиньинь: huǒxīng wén, палл.: хосин вэнь) — условное название способа кодирования китайской письменности, применяемого в интернете с начала 2000-х годов, изначально — как игровой приём, а впоследствии также как способ избежания цензурных запретов.
«Говорящая доска» или «уиджа» (англ. Ouija board) — доска для спиритических сеансов вызова душ умерших с нанесёнными на неё буквами алфавита, цифрами от 1 до 9 и нулём, словами «да» и «нет» и со специальной планшеткой-указателем.
Китайская стена (яп. スリザーリンク) — это логическая головоломка, разработанная компанией Nikoli и опубликованная в 1989 году. Цель игры — нарисовать по правилам головоломки на предоставленном игровом поле единый непересекающийся замкнутый контур.
Палиндро́м (от др.-греч. πάλιν — «назад, снова» и др.-греч. δρóμος — «бег, движение»), пе́ревертень — число, буквосочетание, слово или текст, одинаково читающееся в обоих направлениях. Например, число 101; слова «топот» в русском языке и фин. saippuakivikauppias (продавец мыла; торговец щёлоком) — самое длинное слово-палиндром в мире; текст «а роза упала на лапу Азора» и пр.
Ифку́иль (ифк. Iţkuîl), также Ыфкуил или Илакш — искусственный язык философского направления. Обладает крайней сложностью грамматики и огромным набором фонем, что делает язык весьма трудным для изучения.
Данная статья — часть обзора История математики.Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э.
Подробнее: Математика в Древнем Египте
Липограмма (от др.-греч. λειπογράμματος, «пренебрегать буквой») — литературный приём, заключающийся в написании текста без использования в словах какой-то одной буквы.
Словослияние (или словостяжение) — способ словообразования, разновидность такого способа, как «сокращение».
Языкова́я игра́ (нем. Sprachspiel) — термин Людвига Витгенштейна, введённый им в «Философских исследованиях» 1945 года для описания языка как системы конвенциональных правил, в которых участвует говорящий. Понятие языковой игры подразумевает плюрализм значений. Концепция языковой игры приходит на смену концепции метаязыка.В отечественном языкознании термин вошёл в широкий научный обиход после публикации одноимённой работы Е. А. Земской, М. В. Китайгородской и Н. Н. Розановой, хотя сами лингвистические…
Шифр Виженера (фр. Chiffre de Vigenère) — метод полиалфавитного шифрования буквенного текста с использованием ключевого слова.Этот метод является простой формой многоалфавитной замены. Шифр Виженера изобретался многократно. Впервые этот метод описал Джовани Баттиста Беллазо (итал. Giovan Battista Bellaso) в книге La cifra del. Sig. Giovan Battista Bellasо в 1553 году, однако в XIX веке получил имя Блеза Виженера, французского дипломата. Метод прост для понимания и реализации, он является недоступным…
История арифметики охватывает период от возникновения счёта до формального определения чисел и арифметических операций над ними с помощью системы аксиом. Арифметика — наука о числах, их свойствах и отношениях — является одной из основных математических наук. Она тесно связана с алгеброй и теорией чисел.
Бруски Женая — Люка — это счётный прибор, изобретенный французским инженером Анри Женаем и математиком Эдуардом Люка…
Метод Каси́ски (Метод Кази́ского) — метод криптоанализа полиалфавитных шифров, таких как шифр Виженера. Основан на факте того, что повторяющиеся части открытого текста, зашифрованные одним и тем же ключевым словом, приводят к идентичным сегментам шифрованного текста. Разработан независимо криптоаналитиками Фридрихом Касиски и Чарльзом Бэббиджем.
