Сложение рациональных чисел происходит по правилам сложения дробей. В этой теме рассмотрим подробно как складывать положительные и отрицательные рациональные числа, а также рациональные числа с одинаковыми и разными знаменателями.
Тема. Сложение рациональных чисел с одинаковыми знаменателями.
Определение:
Сумма дробей с одинаковыми положительными знаменателями, есть дробь с тем же знаменателем и суммой их числителей.
Правила сложения рациональных чисел.
- Если у дробей одинаковый знаменатель, записываем его в знаменатель итоговой дроби.
- Числители складываем по правилам сложения и результат записываем в числитель итоговой дроби.
- Если требуется итоговую дробь сокращаем и преобразовываем.
Пример:
Выполните сложение рациональных чисел с одинаковыми знаменателями: а) (frac{-3}{4}+frac{1}{4}) б) (frac{-6}{13}+frac{-2}{13}) в) (frac{17}{47}+frac{12}{47}) г) (frac{32}{15}+frac{-12}{15})
Решение:
а) Так как знаменатели у дробей одинаковые, записываем знаменатель тот же. Числители складываем по правилу сложения целых чисел. Итоговую дробь (frac{-2}{4}) сокращаем на 2.
(begin{align}frac{-3}{4}+frac{1}{4}=frac{-3+1}{4}=frac{-2}{4}=-frac{2}{4}=-frac{1}{2}\\ end{align})
б) (begin{align}frac{-6}{13}+frac{-2}{13}=frac{-6+(-2)}{13}=frac{-8}{13}=-frac{8}{13}\\ end{align})
в) (begin{align}frac{17}{47}+frac{12}{47}=frac{17+12}{47}=frac{29}{47}\\ end{align})
г) (begin{align}frac{32}{15}+frac{-12}{15}=frac{32+(-12)}{15}=frac{20}{15}=frac{4 times 5}{3 times 5}=frac{4}{3}=1frac{1}{3}\\ end{align})
Урок. Сложение рациональных чисел с разными знаменателями.
Определение:
Чтобы сложить две дроби с разными знаменателями необходимо сначала найти общий знаменатель, а потом сложить их числители.
Формула сложение рациональных чисел с разными знаменателями:
(begin{align}
&bf frac{a}{b}+frac{c}{d}=frac{a times d + c times b}{b times d} \\
end{align})
Алгоритм действия при сложении рациональных чисел с разными знаменателями.
- Найти общий знаменатель. (Как находить общий знаменатель можете узнать, нажав на ссылку)
- Найти сумму дробей по правилам сложения рациональных чисел с одинаковыми знаменателями.
Пример:
Выполните сложение рациональных чисел с разными знаменателями: а) (frac{-4}{7}+frac{5}{8}) б) (frac{-3}{11}+frac{-7}{22}) в) (frac{11}{15}+frac{9}{25}) г) (frac{8}{3}+frac{-1}{13})
Решение:
а) Дроби (frac{-4}{7}+frac{5}{8}) имеют разные знаменатели, поэтому нужно найти общий знаменатель. Общий знаменатель будет равен 56, поэтому первую дробь (frac{-4}{7}) умножаем на 8, а вторую дробь (frac{5}{8}) на 7
(begin{align}frac{-4}{7}+frac{5}{8}=frac{-4 times 8 + 5 times 7}{7 times 8}=frac{-32+35}{56}=frac{3}{56}\\
end{align})
б) Так как у дробей разные знаменатели, находим общий знаменатель. Общий знаменатель равен 22.
(begin{align}frac{-3}{11}+frac{-7}{22}=frac{-3 times 2 + (-7)}{11 times 2}=frac{-6 + (-7)}{22}=frac{-13}{22}=-frac{13}{22}\\
end{align})
в) У дробей (frac{11}{15}) и (frac{9}{25}) разные знаменатели. Находим общий знаменатель, он равен 75. Первую дробь умножаем на 5, а вторую дробь умножаем на 3.
(begin{align}frac{11}{15}+frac{9}{25}=frac{11 times 5}{15 times 5} + frac{9 times 3}{25 times 3}=frac{55}{75}+frac{27}{75}=frac{55+27}{75}=frac{82}{75}=1frac{7}{75}\\
end{align})
г) Общий знаменатель этих дробей (frac{8}{3}) и (frac{-1}{13}) равен 39.
(begin{align}frac{8}{3}+frac{-1}{13}=frac{8 times 13 + (-1) times 3}{3 times 13}=frac{104+(-3)}{39}=frac{101}{39}=2frac{23}{39}\\
end{align})
Сложение противоположных рациональных чисел.
Правило сложения противоположных рациональных чисел.
Результатом сложения противоположных рациональных чисел будет нуль.
Пример:
Выполните сложение дробей (frac{-5}{18}+frac{5}{18}) .
Решение:
(begin{align}frac{-5}{18}+frac{5}{18}=frac{-5+5}{18}=frac{0}{18}=0\\
end{align})
Сложение положительных рациональных чисел.
Сложение положительных рациональных чисел сводится к сложение обыкновенных дробей. Может быть два варианта:
- Если у положительных рациональных чисел разные знаменатели, то ищем общий знаменатель.
- Если у положительных рациональных чисел одинаковые знаменатели, то переходим к сложению числителей, а знаменатель переписываем.
Примеры:
Выполните сложение положительных рациональных дробей: а) (frac{4}{15}+frac{7}{15}) б) (frac{3}{8}+frac{5}{12}).
Решение:
а) (begin{align}frac{4}{15}+frac{7}{15}=frac{4+7}{15}=frac{11}{15}\\
end{align})
б) У дробей разные знаменатели нужно найти общий знаменатель. Общий знаменатель равен 24.
(begin{align}frac{3}{8}+frac{5}{12}=frac{3 times 3}{8 times 3}+frac{5 times 2}{12 times 2}=frac{9}{24}+frac{10}{24}=frac{9+10}{24}=frac{19}{24}\\
end{align})
Сложение отрицательных рациональных чисел.
Складываем отрицательные рациональные числа по этим правилам:
- Если знаменатели разные, то приводим к общему знаменателю.
- Если знаменатели одинаковые складываем числители по правилу сложения отрицательных целых чисел.
Пример:
Сложите отрицательные рациональные числа: а) (-frac{13}{19}+(-frac{1}{19})) б) (-frac{1}{49}+(-frac{5}{14})).
Решение:
а) (begin{align}-frac{13}{19}+(-frac{1}{19})=frac{-13+(-1)}{19}=frac{-14}{19}=-frac{14}{19}\\
end{align})
б) Для начала найдем общий знаменатель. Общий знаменатель у дробей равен 98.
(begin{align}-frac{1}{49}+(-frac{5}{14})=-frac{1 times 2}{49 times 2}+(-frac{5 times 7}{14 times 7})=-frac{2}{98}+(-frac{35}{98})=-frac{-2+(-35)}{98}=frac{-37}{98}=-frac{37}{98}\\
end{align})
Сложение рациональных чисел с разными знаками, примеры.
Правило:
- Если у дробей разные знаменатели, нужно привести их к общему знаменателю.
- Если у дробей одинаковые знаменатели, нужно в итоговую дробь переписать знаменатель, а числители сложить по правилам сложения целых чисел с разными знаками.
Пример:
Выполните сложение рациональных чисел с разными знаками: а) (-frac{2}{5}+frac{1}{5}) б) (frac{1}{27}+(-frac{5}{9}))
Решение:
а) У дробей общий знаменатель, переходим к сложению числителей. Определим какой знак будет в результате. Для этого посмотри модуль какого числа больше |-2|=2 и |1|=1. Получаем 2>1, то есть модуль отрицательного числа больше модуля положительного, поэтому в ответе будет стоять знак минус. Если сказать проще, у нас два минуса и один плюс. Минусов больше поэтому в результате поставим знак минус.
(begin{align}-frac{2}{5}+frac{1}{5}=frac{-2+1}{5}=frac{-1}{5}=-frac{1}{5}\\
end{align})
б) Сначала приведем к общему знаменателю, он равен 27, а потом сложим числители. Определим знак ответа. Найдем модули чисел |-15|=15 и |1|=1. Модуль отрицательного числа больше положительного 15>1, поэтому в ответе будет знак минус.
(begin{align}frac{1}{27}+(-frac{5}{9})=frac{1}{27}+(-frac{5 times 3}{9 times 3})=frac{1}{27}+(-frac{15}{27})=frac{1+(-15)}{27}=-frac{14}{27}\\
end{align})
Представим
себе такую историю…
–
Паша, помоги мне, пожалуйста, – попросил у друга Саша.
–
Давай помогу, – сказал Паша.
–
Вчера на улице было мороза.
Утром мне старший брат сказал, что сегодня намного теплее, так как температура
стала выше на ,
– начал Саша. – Но я не могу понять, какая сегодня погода.
–
Что же здесь непонятного? – удивился Паша. – Надо к прибавить
6.
Но как сложить отрицательное и положительное числа, я не знаю.
–
Вот и я не знаю, – сказал Саша.
–
Может, спросим у Мудряша? – предложил другу Паша.
–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и
выполним устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Разберёмся, как сложить отрицательное
число и положительное число. Для этого мы начертим
координатную прямую. Отметим на ней начало отсчёта и единичный отрезок. Вы
сказали, что вчера было мороза.
Отметим точку А ()
на координатной прямой. Сегодня температура повысилась на ,
а значит, на нашей координатной прямой мы переместимся на 6
единичных отрезков вправо и окажемся в точке В (2). Тогда мы с вами
можем записать, что .
–
А если бы, например, температура понизилась на ,
то нам надо было бы к прибавить
.
Как бы мы это сделали? – спросил у Мудряша Саша.
–
В этом случае мы бы переместились на 3
единичных отрезка влево и оказались в точке С (),
– ответил Мудряш. – То есть можно записать так: .
Запомните!
Если к числу а прибавить положительное число b,
то точка с координатой a
переместится по координатной прямой на b
единичных
отрезков вправо.
Если
к числу a прибавить отрицательное
число b, то точка с координатой a
переместится
по координатной прямой на минус b
единичных отрезков влево.
–
Давайте вычислим суммы: ;
;
, –
предложил мальчишкам Мудряш. – Снова воспользуемся координатной прямой. Итак,
сложим и
5.
Сначала отметим точку с координатой на
координатной прямой. Затем переместимся на 5
единичных отрезков вправо и окажемся в точке с координатой .
То есть .
Теперь
к прибавим
6,5.
Для этого из точки с координатой переместимся
на 6,5
единичных отрезков вправо и окажемся в точке с координатой 3,5.
То есть .
И
в последнем примере мы сложим 4 и .
Отметим точку с координатой 4 и, так как прибавляем
отрицательное число ,
переместимся на 7 единичных отрезков влево
и окажемся в точке с координатой .
Запишем это так: .
–
В каждом из рассмотренных примеров мы находили сумму чисел с разными знаками, –
заметили мальчишки.
–
И обратите внимание, что в каждом примере знак суммы такой же, что и у
слагаемого, модуль которого больше. Так, в первом примере .
И сумма имеет знак «».
Во втором примере .
Сумма – положительное число. И в третьем примере .
Сумма со знаком «»,
– объяснил Мудряш.
–
Понятно, как определять знак суммы, – сказали Саша и Паша. – Но можно ли найти
её значение без помощи координатной прямой?
–
Конечно, можно, – ответил Мудряш. – Давайте сформулируем правило сложения двух
чисел с разными знаками. Запомните! Чтобы сложить два числа с разными
знаками, надо: 1) найти модули слагаемых; 2) из большего модуля вычесть меньший модуль; 2) перед
полученным числом поставить знак слагаемого с большим
модулем.
Давайте
ещё раз решим наши примеры, но уже с помощью правила.
Первый
пример: .
;
.
Значение модуля отрицательного слагаемого у нас больше значения модуля
положительного слагаемого. А значит, сумма у нас будет со знаком «».
Найдём теперь: .
Следующий
пример: .
;
.
Модуль положительного слагаемого больше модуля отрицательного слагаемого.
–
А значит, сумма у нас будет со знаком «»,
– подсказали ребята. – Теперь из большего
модуля вычтем меньший и получим: .
–
Верно, – сказал Мудряш. – При этом знак «»
ставить совсем не обязательно. И последний пример: .
;
.
–
Здесь сумма будет со знаком «»,
так как ,
– продолжили мальчики. – Найдём разность: .
–
Молодцы! – похвалил Сашу и Пашу Мудряш и предложил. – Давайте мы с вами решим
ещё несколько примеров: ;
;
.
–
Нам надо будет снова вычислить сумму. Мы это уже умеем делать, – обрадовался
Саша.
–
Посмотри внимательнее, – сказал Паша. – В каждом примере оба слагаемых
отрицательные числа. А мы пока не умеем их складывать.
–
Ребята, чтобы решить эти примеры, мы с вами снова воспользуемся координатной
прямой. Начертим её. Отметим начало отсчёта и
выберем единичный отрезок. В первом примере нам надо к прибавить
.
Отметим точку с координатой .
Затем переместимся на 2 единичных отрезка влево и
окажемся в точке с координатой .
То есть .
Чтобы
вычислить сумму ,
отметим точку с координатой .
Переместимся 4,5 единичных отрезка влево и окажемся в
точке с координатой .
То есть .
И
вычислим последнюю сумму .
–
Для этого отметим точку с координатой ,
– продолжили ребята. – Потом переместимся влево на 2,5 единичных
отрезка и окажемся в точке с координатой .
Получим: .
А
может, как и для чисел с разными знаками, есть правило сложения отрицательных
чисел?
–
Такое правило есть, – сказал Мудряш. – Сформулируем его. Чтобы сложить два
отрицательных числа, надо: 1) найти модули слагаемых; 2) сложить модули
слагаемых; 3) перед полученным числом поставить знак «».
Решим
с помощью этого правила рассмотренные выше примеры. Итак, первый пример: .
;
.
Запишем сумму модулей и поставим перед ней знак
«»:
. Выполним
сложение в скобках и получим .
Второй
пример: .
;
.
Запишем сумму модулей и поставим перед ней знак
«»:
. Выполним
сложение в скобках и получим .
И
последний пример: .
;
.
Запишем сумму модулей и перед ней поставим
знак «»:
.
Сложим числа в скобках и получим .
–
Интересно, а чему равна сумма двух противоположных чисел? – задал вопрос
Мудряшу Паша.
–
Это хороший вопрос! – сказал Мудряш. – Снова воспользуемся координатной прямой,
чтобы найти, например, сумму и
5.
Отметим точку с координатой .
Теперь переместимся на 5 единичных отрезков
вправо и окажемся в точке с координатой 0.
То есть сумма и
5
равна 0.
Давайте
ещё вычислим сумму 3,5 и .
Отметим на координатной прямой точку с координатой 3,5.
Затем переместимся на 3,5 единичных отрезка влево
и окажемся в точке с 0. А значит, сумма 3,5
и равна
0.
–
То есть при сложении двух противоположных чисел всегда получаем 0?
– спросили мальчишки.
–
Всё верно, – сказал Мудряш. – Запомните! Сумма двух противоположных
чисел равна нулю. Для любого рационального числа a
верно равенство: .
Давайте
для закрепления новых знаний выполним несколько заданий.
Задание
первое: выполните сложение:
а)
;
б) ;
в) ;
г) .
Решение: заметим,
что в каждом из примеров нам надо сложить два числа с разными знаками. А
значит, мы с вами будет пользоваться правилом сложения двух чисел с разными
знаками. В первом примере нам надо вычислить сумму и
53.
;
. Значение
модуля положительного слагаемого у нас больше значения модуля отрицательного слагаемого.
Поэтому сумма у нас будет положительной. Из большего
модуля вычтем меньший модуль, то есть из ,
и получим 11.
Во
втором примере мы вычислим сумму и
.
;
.
Значение модуля отрицательного слагаемого у нас больше значения модуля положительного
слагаемого. А значит, сумма у нас будет со знаком «».
Запишем разность большего и меньшего модулей со знаком «»,
то есть .
Выполним вычитание в скобках и получим в результате .
В
следующем примере нам надо найти сумму и
.
Найдём модуль каждой дроби: ;
.
Чтобы сравнить значения модулей, приведём дробь
к
знаменателю 6: .
.
Сумма будет положительной, так как модуль положительной дроби больше, чем
модуль отрицательной дроби. Отнимаем от
:
.
Сокращаем дробь на
3
и получаем .
И
в последнем примере нам надо найти сумму противоположных чисел и
.
Мы с вами знаем, что сумма двух противоположных чисел равна 0.
А значит, .
Второе
задание: выполните сложение:
а)
;
б) ;
в) ;
г) .
Решение: в
этом задании мы будем складывать отрицательные числа. Для этого мы
воспользуемся правилом сложения двух отрицательных чисел.
В
первом примере надо найти сумму и
.
Сначала найдём модули слагаемых. ;
. Запишем
сумму модулей и перед ней поставим знак «»:
.
Выполним вычисления и получим .
Во
втором примере надо найти сумму и
.
;
.
Запишем сумму модулей и перед ней поставим
знак «»:
.
Выполним вычисления и получим .
В
следующем примере нам надо найти сумму двух отрицательных десятичных дробей и
.
;
. Запишем
сумму модулей и поставим перед ней знак «»:
Выполним
вычисления и получим .
И
последний пример .
;
.
Перед суммой модулей дробей поставим знак «»:
. И,
выполнив вычисления, получим .
Сложение рациональных чисел – это сложение целых и дробных положительных и отрицательных чисел.
1. Числа с одинаковыми знаками складывают. Числа с разными знаками вычитают.
2. Чтобы сложить два отрицательных числа, надо поставить знак минус и сложить их модули.
Например: (-7-10=-(7+10)=-17; -15+(-11))(=-15-11=-(15+11)=-26).
3. Если два числа имеют разные знаки, то ставят знак того слагаемого, модуль которого больше, и от большего по модулю числа вычитают меньшее.
Например: (-7+9=9-7=2; 5-12=-(12-5))(=-7; 20+(-15)=20-15=5).
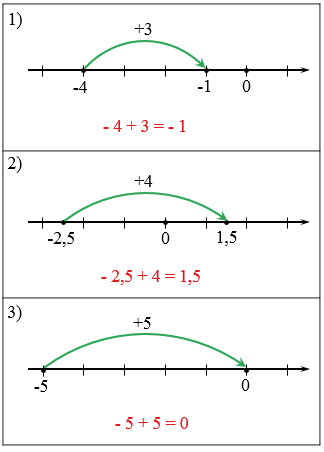
Чтобы прибавить к числу а положительное число b, достаточно продвинуться от а вправо на b единиц:
Ответ: (-5+4=-1).
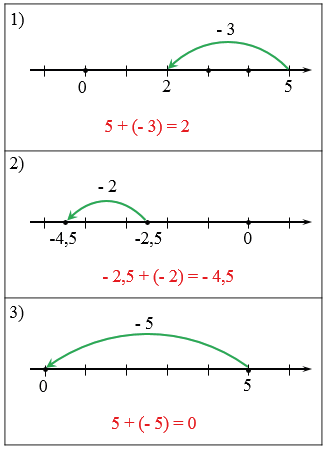
Чтобы прибавить к числу а отрицательное число b, достаточно продвинуться от а влево на (–b) единиц:
Ответ: (-4+(-3)=-7).
4. Сумма противоположных чисел равна нулю.
Например: (-8+8=0; 10,5+(-10,5))(=10,5-10,5=0).
Выполним сложение чисел с разными знаками с помощью координатной прямой.
1) Требуется к числу –4 прибавить число 6. Отметим число –4 точкой на координатной прямой. Число 6 – положительное, значит от точки с координатой –4 нам нужно идти вправо на 6 единичных отрезков. Мы оказались справа от начала отсчета (от нуля) на 2 единичных отрезка.
-
Вычислите.
(-7+(-frac34+0,5))
-
Решите уравнение.
(x+32frac5{12}=30frac16)
-
Вычислите.
(-0,8+0,5+(-0,75)+0,32)
-
Выполните сложение.
(-8,1+(-10,9)+(-1,9)+(-4,1))
-
Выполните сложение.
(-16frac23+(-8,75)+(-2frac5{12}))
-
Найдите значение выражения ((a+b)+(-14,5)), при (a=-28,7), (b=-3,8).
-
Вычислите.
(big(-1frac25+(-3,6)big)+big(-2frac56+(-frac23)big))
-
Найдите значение выражения.
(-3frac23+0,9+(-frac25)+6,7+(-frac8{15}))
Действия с рациональными числами
- Сложение
- Вычитание
- Умножение
- Деление
Сложение
При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.
Пример 1. Найти сумму рациональных чисел 2,5 и 3,2.
Решение: Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:
2,5 + 3,2 = 5,7.
Пример 2. Найти сумму отрицательных чисел (-2,5) и (-3,2).
Решение: Сначала надо сложить модули слагаемых:
2,5 + 3,2 = 5,7.
Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:
(-2,5) + (-3,2) = -5,7.
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4,7) + (+12) = 7,3, так как 12 – 4,7 = 7,3;
9 + (-15) = -6, так как 15 – 9 = 6.
Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю.
Примеры:
125 + (-125) = 0;
-34 + (+34) = 0.
Вычитание
Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.
Примеры:
(+10) – (+3,4) = (+10) + (-3,4) = 6,6;
(+10) – (-3,4) = (+10) + (+3,4) = 13,4;
(-10) – (-3,4) = (-10) + (+3,4) = -6,6;
(-10) – (+3,4) = (-10) + (-3,4) = -13,4.
Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение
При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.
Примеры:
3 · 5 = 15;
3 · (-5) = -15;
-3 · 5 = -15;
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | – | = | – |
| – | · | + | = | – |
| – | · | – | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 · (-1) = 1,5;
2,5 · (-1) = -2,5.
Деление
При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3;
15 : (-5) = -3;
-15 : 5 = -3;
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | – | = | – |
| – | : | + | = | – |
| – | : | – | = | + |
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 : (-1) = 1,5;
2,5 : (-1) = -2,5.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Рациональные числа
- Сложение рациональных чисел
Примеры:
Примеры:
Обратите внимание: любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.
На основе примеров 



Чтобы сложить два числа с разными знаками, надо:
1) найти модули слагаемых;
2) из большего модуля вычесть меньший модуль;
3) перед полученным числом поставить знак слагаемого с большим модулем.
На основе примера 


Чтобы сложить два отрицательных числа, надо:
1) найти модули слагаемых;
2) сложить модули слагаемых;
3) перед полученным числом поставить знак “
На основе примера 

Также справедливо следующее правило:
Примеры:
1) 5 + 0 = 0 + 5 = 5;
2) 


Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Модуль числа
Рациональные числа
Сравнение рациональных чисел
Вычитание рациональных чисел
Умножение рациональных чисел
Деление рациональных чисел
Свойства действий с рациональными числами
Раскрытие скобок
Решение уравнений
Рациональные числа
Правило встречается в следующих упражнениях:
6 класс
Номер 1099,
Мерзляк, Полонский, Якир, Учебник
Номер 1151,
Мерзляк, Полонский, Якир, Учебник
Номер 1345,
Мерзляк, Полонский, Якир, Учебник
Задание 1061,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1073,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1139,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1257,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1488,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1491,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 7,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 42,
Мерзляк, Полонский, Якир, Учебник
Номер 328,
Мерзляк, Полонский, Якир, Учебник
Номер 371,
Мерзляк, Полонский, Якир, Учебник
Номер 396,
Мерзляк, Полонский, Якир, Учебник
Номер 404,
Мерзляк, Полонский, Якир, Учебник
Номер 538,
Мерзляк, Полонский, Якир, Учебник
Номер 582,
Мерзляк, Полонский, Якир, Учебник
Номер 688,
Мерзляк, Полонский, Якир, Учебник
Номер 959,
Мерзляк, Полонский, Якир, Учебник
Номер 1068,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 71,
Мерзляк, Полонский, Якир, Учебник
Номер 72,
Мерзляк, Полонский, Якир, Учебник
Номер 86,
Мерзляк, Полонский, Якир, Учебник
Номер 122,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 195,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 217,
Мерзляк, Полонский, Якир, Учебник
Номер 276,
Мерзляк, Полонский, Якир, Учебник
Номер 389,
Мерзляк, Полонский, Якир, Учебник