Мы разобрались, что вообще из себя представляет степень числа в математике. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. как возвести число в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя – как его находить и как его возвести в степень. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с такого проверочного действия, как формулирование базовых определений.
Возвести число в степень – это вычисление значения степени некоторого числа.
То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0,5 в пятую степень”, это следует понимать как “вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Что собой представляет такое вычисление? Это можно написать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Вычислите значение 3272
Как будем решать
Данную запись можно перевести или переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость посчитать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи 
.
От основания степени это не зависит.
Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими математическими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно будет возводиться в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем знакомые примеры задач.
Выполните возведение 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби. Сколько получим? Цифра (или сумма) будет равна восьмидесяти восьми: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат (квадратный показатель) в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: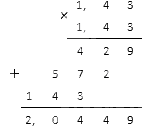 
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай – возведение числа в минус первую (минусовую) степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени (в кубе или кубический) из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадратик: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и рассчитать, как указано выше.
Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная и большая работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную – значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считается на компе (компьютере) или онлайн из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Возведение степени в степень
Как степень возвести в степень? Рассмотрим пример.
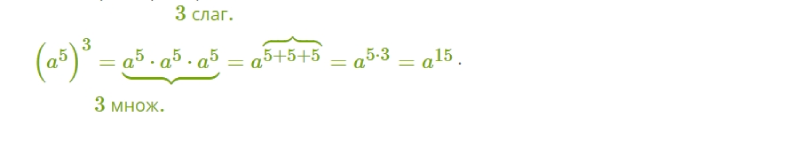Если степень возвести в степень, то показатели перемножатся, а основание не меняется: (aᵑ)ᵐ = aᵑ*ᵐ.
Здесь а – это любое число, а n и m – натуральные числа. Вот такой пример вы можете использовать, чтобы получить степень в степени.
Все примеры воззведения в степень можно найти в интернете в удобных таблицах.
Приветствую Вас!
Предлагаю разобрать выражения, содержащие степени как положительные, так и отрицательные, дробные, сложные.
Начнем сначала. Для решения степенных выражений существует несколько правил, и они не меняются на протяжении всей математики. Как бы что не выглядело, в любом случае:
- при умножении степени складываются,
- при делении – вычитаются,
- при возведении степени в степень – перемножаются.
Именно такие определения дает основная масса населения. Но, в данной интерпретации отсутствует главная мысль: основание должно быть одинаковое(!), т.е. то число, которое возводится в степень. Оттуда и ошибки по типу: 2^4×3^3=6^7.
Поэтому, прежде чем выполнять какие-либо действия со степенями, нужно обратить внимание на основания. Если они разные, никаких действий со степенями совершать нельзя. Для начала требуется сделать основания одинаковыми, говоря простым языком. Например:
Это, конечно, самые элементарные примеры, но на них строятся более сложные. Бывает так, что в одном выражении находятся разные основания. В этом случае, если это возможно, нужно получить одинаковые, и выполнить действия:
Теперь об отрицательных степенях. Если какое-либо число стоит в отрицательной степени, то, по сути, это дробное число. Дроби и минуса неудобны, поэтому от них, по возможности, лучше избавиться. Это не всегда возможно, но когда-то мы и могём. Вот один из экзаменационных примеров:
Безусловно, можно высчитать степени и в таком виде как они даны, т.е. -11+4-(-3)=-4. Но это не совсем удобно, и как показывает практика, некоторые ребятишки в 9ом классе не знают как сосчитывать отрицательные числа. Поэтому давайте уберем минуса:
Из примера видно, что число в отрицательной степени из числителя перешло в знаменатель, и наоборот. Это произошло из правил умножения/деления дробных выражений. Помним, что минус в степени показывает, что число дробное. Теперь совокупим несколько приемов. Допустим, такой пример:
Запишем его для удобства в виде дроби, пустив по боку две точечки, и проведем нужные манипуляции:
И не надо ничего мудрить. Всё очень просто. Ну и апогей экзаменационных выражений выглядит примерно так:
Здесь мы сталкиваемся со сложными степенями. И, сложные они не потому, что трудные, а потому, что сложенные. А в каком случае степени складываются? Правильно, при умножении чисел с одинаковыми основаниями. Воспользуемся всё теми же правилами и разложим сложное на простое в обратном направлении и применим вышеуказанные действа:
Благодарю за внимание..
Как вычислить большую степень?
Онлайн калькулятор разложения Шенкса (задача дискретного логарифмирования) выдал подобные результаты.
2^(1⋅24) ≡ 265(mod541)
2^(2⋅24) ≡ 436(mod541)
.
Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.
Какие подходы задействованы для вычисления:
а) большой степени
б) откуда взялось деление с остатком?
в) не понял суть знака «тождественно равно» (вики прочитал, но разницы от обычного знака равенства не уяснил)
- Вопрос задан более трёх лет назад
- 5101 просмотр
- Вконтакте
Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак «тождественное равенство» используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.
Дискретное логарифмирование — формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.
Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b — произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) — неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.
Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат — 1, 1, 1, 1, 75, 75*215 mod 541 = 436.
Как посчитать число в большой степени
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Возведение в степень – это вычисление значения степени некоторого числа.
То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0 , 5 в пятую степень”, это следует понимать как “вычислите значение степени ( 0 , 5 ) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите – 2 в степень 4 .
Решение
Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи .
От основания степени это не зависит.
Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
5 0 = 1 , ( – 2 , 56 ) 0 = 1 2 3 0 = 1
0 0 – не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Возведите 2 в степень – 3 .
Решение
Используя определение выше, запишем: 2 – 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8
Возведите 1 , 43 в степень – 2 .
Решение
Переформулируем: 1 , 43 – 2 = 1 ( 1 , 43 ) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло ( 1 , 43 ) – 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: ( 1 , 43 ) – 2 = 10000 20449
Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .
Пример: 3 − 1 = 1 / 3
9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Вычислите 8 – 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2
После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь – 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную – значения не имеет: 0 – 4 3 .
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 21 , 174367 .
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Онлайн калькулятор разложения Шенкса (задача дискретного логарифмирования) выдал подобные результаты.
2^(1⋅24) ≡ 265(mod541)
2^(2⋅24) ≡ 436(mod541)
.
Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.
Какие подходы задействованы для вычисления:
а) большой степени
б) откуда взялось деление с остатком?
в) не понял суть знака “тождественно равно” (вики прочитал, но разницы от обычного знака равенства не уяснил)
- Вопрос задан более года назад
- 602 просмотра
Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак “тождественное равенство” используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.
Дискретное логарифмирование – формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.
Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b – произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) – неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.
Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат – 1, 1, 1, 1, 75, 75*215 mod 541 = 436.
Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.
Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».
Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.
Как возвести число в степень.
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:
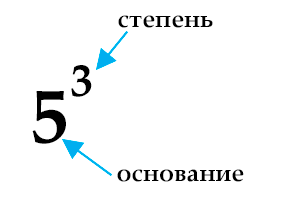
Возведение в степень
А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.
5 3 = 5 x 5 x 5 = 125
Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.
Как возводить в отрицательную степень.
При возведении в отрицательную степень необходимо использовать простое правило:
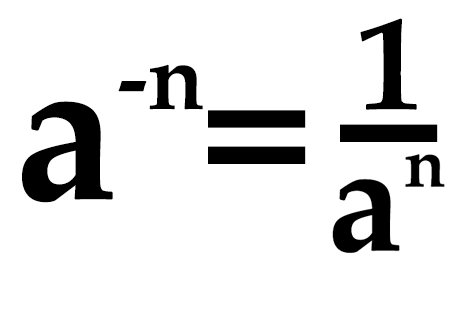
как возводить в отрицательную степень
Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
2 -3
Возвести в степень (по модулю) + большие числа
Алгоритм быстрого возведения в степень онлайн с решением по модулю и без модуля. Функциональность поддерживает работу с большими числами.
Использование:
alt=»✔» />Заполняем необходимые данные целыми числами, отвечая на вопросы формы.
alt=»✔» />Жмем кнопку вычислить и получаем результат.
alt=»ℹ» />Галочка «по модулю» позволяет указать модуль, по которому необходимо возводить в степень.
alt=»ℹ» />Галочка «с решением» позволяет получить этапы вычисления: каким образом число возводилось в степень.
Ограничения калькулятора:
Максимальное число, которое можно возвести в степень — 1 000 000. Максимальная степень, в которую можно возвести — 5000. Модуль может быть довольно-таки большим, до 100 символов в числе. [1; 10e100)
Алгоритм быстрого возведения в степень (по модулю).
Одним из основных действий арифметики вычетов, возникающих, например, в криптографии, является вычисление а х (mod m), то есть нахождение такого у, что
где a, x, m — натуральные числа. Далее считаем, что a < m. Запись у = b (mod m) означает, что у ≡ b (mod m) и 0 ≤ у < m, т.е, y — наименьший неотрицательный вычет по модулю m, лежащий в том классе, что и b.
Если вычислять «в лоб», т.е. последовательно находить (приводим формулы по модулю):
то нужно выполнить (x — 1) умножение в кольце Zm, Если n — количество разрядов в двоичной записи х, то число умножений не меньше, чем 2 n-1.
Лемма 1: Пусть x, m, a ∈ N. Пусть x = (x0x1 … xn-1)2 т.е.
Определим целые аj по реккурентным формулам
Алгоритм (быстрого возведения в степень). Даны натуральные a, m и x = (xn-1xn-2 … x0)2. Нужно вычислить y = a x (mod m),
1. Вычисляем aj (0 ≤ j ≤ n — 1) по формулам (2),
Лемма 2. Пусть n — число разрядов в двоичной записи x. Тогда, приведенный выше алгоритм требует выполнения не более, чем, 2(n -1) умножений в кольце Zm
Пример 1. Возведем число 2 50 без модуля.
5010 = 1100102 , считаем длину в двоичной записи n = 6. Следовательно, нам надо посчитать a1 … a6 по формулам 2 из теории.
a1 = 2; a2 = 2 2 = 4, a3 = 4 2 = 16, a4 = 16 2 = 256, a5 = 256 2 = 65536, a6 = 65536 2 = 4294967296
x1 = 0, x2 = 1, x3 = 0, x4 = 0, x5 = 1, x6 = 1 — двоичная запись в обратном порядке (от младших разрядов к старшим).
Перемножаем ai-ые по второй формуле пункта 2. Другими словами, перемножаем между собой те ai-ые, у которых на соответствующей позиции в двоичной записи степени стоят единицы — это a2, a5 и a6;
2 50 = 4 * 65536 * 4294967296 = 1125899906842624
Пример 2. Возведем число 2 50 по модулю 100. Все аналогично, только считаем ai-ые и произведения ai-ых по модулю 100.
5010 = 1100102 , считаем длину в двоичной записи n = 6. Следовательно, нам надо посчитать a1 … a6 по формулам 2 из теории.
a1 = 2; a2 = 2 2 = 4, a3 = 4 2 = 16, a4 = 16 2 = 56, a5 = 56 2 = 36, a6 = 36 2 = 96 по модулю 100
x1 = 0, x2 = 1, x3 = 0, x4 = 0, x5 = 1, x6 = 1 — двоичная запись в обратном порядке (от младших разрядов к старшим).
Перемножаем ai-ые по второй формуле пункта 2. Другими словами, перемножаем между собой те ai-ые, у которых на соответствующей позиции в двоичной записи степени стоят единицы — это a2, a5 и a6;
2 50 = 4 * 36 * 96 = 24 по модулю 100.
Заметили неточность в работе калькулятора? Убедительная просьба сообщить об этом в комментариях или через форму обратной связи. Заранее Вас благодарим.
Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
При умножении степеней с одинаковыми основаниями основание остаётся без изменений,
а показатели степеней складываются.
am · an = am + n, где
«a» — любое
число, а «m», «n» — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
Примеры.
- Упростить выражение.
b · b2 · b3 · b4 · b5 =
b 1 + 2 + 3 + 4 + 5 = b15 - Представить в виде степени.
615 · 36 = 615 · 62 = 615 · 62 =
617 - Представить в виде степени.
(0,8)3 · (0,8)12 = (0,8)3 + 12 = (0,8)15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями. Оно не относится к их сложению.
Нельзя заменять сумму
(33 + 32) на 35. Это понятно, если
посчитать
(33 + 32) = (27 + 9) = 36 , а
35 = 243
Свойство № 2
Частное степеней
Запомните!
При делении степеней с одинаковыми основаниями основание остаётся без изменений,
а из показателя степени делимого вычитают показатель степени делителя.
=
am − n, где
«a» — любое
число, не равное нулю, а «m», «n» — любые
натуральные числа такие, что «m > n».
Примеры.
- Записать частное в виде степени
(2b)5 : (2b)3 = (2b)5 − 3 = (2b)2 - Вычислить.
=
113 − 2 · 4 2 − 1 = 11 · 4 = 44 - Пример. Решить уравнение. Используем свойство частного степеней.
38 : t = 34t = 38 : 34
t = 38 − 4
t = 34
Ответ: t = 34 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
45m + 6 · 4m + 2 : 44m + 3 =
45m + 6 + m + 2 : 44m + 3 =
46m + 8 − 4m − 3 = 42m + 5 - Пример. Найти значение выражения, используя свойства степени.
=
==
=
=
211 − 5 = 2 6 = 64
Важно!
Обратите внимание, что в свойстве 2 речь шла только
о делении степеней с одинаковыми основаниями.
Нельзя заменять разность
(43 −42) на 41. Это понятно, если посчитать
(43 −42) = (64 − 16) = 48, а
41 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степень
Запомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней
перемножаются.
(an)m = an · m, где
«a» — любое
число, а «m», «n» — любые натуральные числа.
- Пример.
(a4)6 = a4 · 6 = a24 - Пример. Представить 320 в виде степени с основанием
32.По свойству возведения степени в степень известно, что при возведении
в степень показатели перемножаются, значит: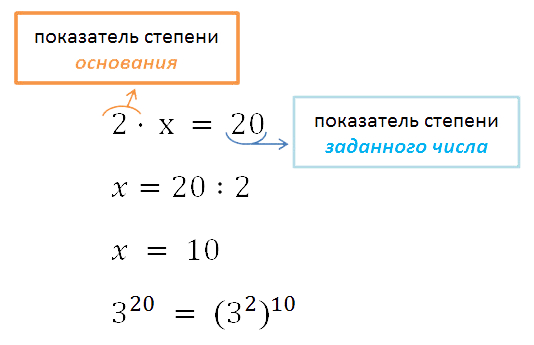
Свойства 4
Степень произведения
Запомните!
При возведении в степень произведения каждый из множителей
возводится в степень. Затем полученные результаты перемножаются.
(a · b)n = an · bn, где
«a», «b» — любые рациональные
числа; «n» — любое натуральное число.
- Пример 1.
(6 · a2 · b3 · c )2 =
62 · a2 · 2 · b3 · 2
· с 1 · 2 = 36 a4 · b6
· с 2
- Пример 2.
(−x2 · y)6 =( (−1)6 · x2 · 6 · y1 · 6) =
x12 · y6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней,
применяют и в обратном порядке.
(an · bn)=
(a · b) n
То есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
24 · 54 = (2 · 5)4 =
104 = 10 000 - Пример. Вычислить.
0,516 · 216 = (0,5 · 2)16 =
1
В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.
Например,
45 · 32 = 43 ·
42 · 32 = 43 · (4 · 3)2 =
64 · 122 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
421 · (−0,25)20 = 4 · 4 20 ·
(−0,25) 20 = 4 · (4 · (−0,25))20 = 4 · (−1)20 =
4 · 1 = 4
Свойства 5
Степень частного (дроби)
Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель,
и первый результат разделить на второй.
(a : b)n = an : bn, где
«a», «b» — любые рациональные
числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5 : 3)12 = 512 : 312
Напоминаем, что частное можно представить в виде дроби. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
24 апреля 2023 в 13:57
София Елизарьева
Профиль
Благодарили: 0
Сообщений: 2
София Елизарьева
Профиль
Благодарили: 0
Сообщений: 2
ЛяяялДляля
0
Спасибо
Ответить
24 апреля 2023 в 13:57
София Елизарьева
Профиль
Благодарили: 0
Сообщений: 2
София Елизарьева
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
( 2+2+2+2+2+2+2+2=16 )
Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: (displaystyle 2cdot 8=16).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, (displaystyle 2cdot 8=16) считается легче и быстрее, чем (displaystyle 2+2+2+2+2+2+2+2=16).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Круто, да?
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.
И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Далее, почему говорят «степень числа с натуральным показателем»?
Ты уже наверное, догадался: потому что показатель степени – это натуральное число. Да, но что такое натуральное число? Элементарно! Натуральные это те числа, которые используются в счете при перечислении предметов: один, два, три… Мы же когда считаем предметы не говорим: «минус пять», «минус шесть», «минус семь». Мы так же не говорим: «одна третья», или «ноль целых, пять десятых». Это не натуральные числа. А какие это числа как ты думаешь?
Числа типа «минус пять», «минус шесть», «минус семь» относятся к целым числам.
Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным (то есть взятые со знаком минус), и число ( displaystyle 0) . Ноль понять легко – это когда ничего нет.
А что означают отрицательные («минусовые») числа? А вот их придумали в первую очередь для обозначения долгов: если у тебя баланс на телефоне ( displaystyle -100) рублей, это значит, что ты должен оператору ( displaystyle 100) рублей.
Всякие дроби — это рациональные числа. Как они возникли, как думаешь? Очень просто. Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т.п. И они придумали рациональные числа… Интересно, правда ведь?
Есть еще иррациональные числа. Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число ( displaystyle 3,141592…).
Итак…
Откуда взялись, например, первые два свойства? Сейчас покажу.
1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})
Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?
По определению:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }leftarrow )
Сколько здесь множителей всего?
Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.
Итак, в правой части этого выражения получается такое произведение:
( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})
Но по определению это степень числа ( displaystyle a) с показателем ( displaystyle n+m) , то есть: ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.
Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .
Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}})
Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .
Решение:
Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания!
Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:
( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}})
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нельзя написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}).
Начнем с показателя, равного ( displaystyle 0) .
Любое число в нулевой степени равно единице:
( displaystyle {{a}^{0}}=1, ane 0)
Как всегда, зададимся вопросом: почему это так?
Рассмотрим какую-нибудь степень с основанием ( displaystyle 3). Возьмем, например ( displaystyle {{3}^{5}}), и домножим на ( displaystyle {{3}^{0}}):
( displaystyle {{3}^{5}}cdot {{3}^{0}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+0}}={{3}^{5}})
Итак, мы умножили число ( displaystyle {{3}^{5}}) на ( displaystyle {{3}^{0}}) и получили то же, что и было – ( displaystyle {{3}^{5}}). А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на ( displaystyle 1) . Значит ( displaystyle {{3}^{0}}=1) .
Можем проделать то же самое уже с произвольным числом ( displaystyle a):
( displaystyle {{a}^{n}}cdot {{a}^{0}}underset{по правилу умножения}{mathop{=}},{{a}^{n+0}}={{a}^{n}}={{a}^{n}}cdot 1text{ }Rightarrow text{ }{{a}^{0}}=1)
Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И здесь оно тоже есть – это число ( displaystyle 0) (в качестве основания).
С одной стороны, ( displaystyle 0) в любой степени должен равняться ( displaystyle 0) – сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, ( displaystyle {{0}^{0}}) , как и любое число в нулевой степени, должен равняться ( displaystyle 1) . Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень.
То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Поехали дальше. Кроме натуральных чисел и числа ( displaystyle 0) к целым относятся отрицательные числа.
Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:
( displaystyle {{3}^{5}}cdot {{3}^{-5}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+left( -5 right)}}={{3}^{5-5}}={{3}^{0}}=1)
Отсюда уже несложно выразить искомое ( displaystyle {{3}^{-5}}) :
( displaystyle {{3}^{5}}cdot {{3}^{-5}}=1text{ }Rightarrow text{ }{{3}^{-5}}=frac{1}{{{3}^{5}}})
Теперь распространим полученное правило на произвольную степень:
( displaystyle {{a}^{n}}cdot {{a}^{-n}}={{a}^{n+left( -n right)}}={{a}^{0}}=1text{ }Rightarrow text{ }{{a}^{-n}}=frac{1}{{{a}^{n}}})
Итак, сформулируем правило:
Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: ( displaystyle ane 0) (т.к. на ( displaystyle 0) делить нельзя).
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)
Подведем итоги:
I. Выражение ( {{0}^{k}}) не определено в случае ( kle 0) . Если ( k>0) , то ( {{0}^{k}}=0) .
II. Любое число в нулевой степени равно единице: ( displaystyle {{a}^{0}}=1, ane 0) .
III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: ( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0).
( displaystyle {{6}^{-1}}=frac{1}{6})
( displaystyle {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})
Чтобы понять, что такое «дробная степень», рассмотрим дробь ( displaystyle frac{1}{n}) :
пусть ( displaystyle {{3}^{frac{1}{n}}}=x) .
Возведем обе части уравнения в степень ( displaystyle n) :
( displaystyle {{left( {{3}^{frac{1}{n}}} right)}^{n}}={{x}^{n}})
Теперь вспомним правило про «степень в степени»:
( displaystyle {{x}^{n}}={{left( {{3}^{frac{1}{n}}} right)}^{n}}={{3}^{frac{1}{n}cdot n}}={{3}^{1}}=3)
Какое число надо возвести в степень ( displaystyle n) , чтобы получить ( displaystyle 3) ?
Эта формулировка – определение корня ( displaystyle n) -ой степени.
Напомню: корнем ( displaystyle n) -ой степени числа ( displaystyle a) (( displaystyle sqrt[n]{a}) ) называется число, которое при возведении в степень ( displaystyle n) равно ( displaystyle a) .
То есть, корень ( displaystyle n) -ой степени – это операция, обратная возведению в ( displaystyle n) степень: ( displaystyle sqrt[n]{a}=btext{ }Leftrightarrow text{ }a={{b}^{n}}) .
Получается, что ( displaystyle x={{3}^{frac{1}{n}}}=sqrt[n]{3}) . Очевидно, этот частный случай можно расширить: ( displaystyle {{a}^{frac{1}{n}}}=sqrt[n]{a}) .
Теперь добавляем числитель: что такое ( displaystyle {{a}^{frac{m}{n}}}) ? Ответ легко получить с помощью правила «степень в степени»:
( displaystyle {{a}^{frac{m}{n}}}={{a}^{frac{1}{n}cdot m}}={{left( {{a}^{frac{1}{n}}} right)}^{m}}={{left( sqrt[n]{a} right)}^{m}}) или ( displaystyle sqrt[n]{{{a}^{m}}}) .
Но может ли основание ( displaystyle a) быть любым числом? Ведь корень можно извлекать не из всех чисел.
Например, можно ли посчитать число ( displaystyle sqrt[4]{-16}) ? То есть, какое число нужно возвести в ( displaystyle 4) степень, чтобы получить ( displaystyle -16) ?
Никакое!
Вспоминаем правило: любое число, возведенное в четную степень – число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!
А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение ( displaystyle {{left( -1 right)}^{frac{1}{2}}}) не имеет смысла.
А что насчет выражения ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) ?
Его уже вроде бы можно посчитать: это ( displaystyle sqrt[3]{-1}=-1) .
Но тут возникает проблема.
Число ( displaystyle frac{1}{3}) можно представить в виде дргих, сократимых дробей, например, ( displaystyle frac{2}{6}) или ( displaystyle frac{4}{12}) .
И получается, что ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) существует, но ( displaystyle {{left( -1 right)}^{frac{2}{6}}}) не существует, а ведь это просто две разные записи одного и того же числа.
Или другой пример: раз ( displaystyle sqrt[3]{-8}=-2) , то можно записать ( displaystyle {{left( -8 right)}^{frac{1}{3}}}=-2) . Но стоит нам по-другому записать показатель, и снова получим неприятность: ( displaystyle {{left( -8 right)}^{frac{1}{3}}}={{left( -8 right)}^{frac{2}{6}}}=sqrt[6]{{{left( -8 right)}^{2}}}=sqrt[6]{64}=2) (то есть, получили совсем другой результат!).
Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем.
Итак, если:
- ( a>0);
- ( m) – натуральное число;
- ( n) – целое число;
Тогда:
( {{a}^{frac{n}{m}}}=sqrt[m]{a^n})
Примеры:
( {{a}^{frac{1}{2}}}=sqrt{a})
( {{a}^{frac{1}{5}}}=sqrt[5]{a})
( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{a^3}})
( displaystyle frac{{{5}^{-frac{1}{2}}}cdot {{left( {{5}^{frac{5}{6}}} right)}^{frac{3}{10}}}cdot {{3}^{-frac{5}{4}}}}{{{3}^{-frac{3}{2}}}}={{5}^{-frac{1}{2}}}cdot {{5}^{frac{5}{6}cdot frac{3}{10}}}cdot {{3}^{left( -frac{5}{4}+frac{3}{2} right)}}=)
( displaystyle={{5}^{left( -frac{1}{2}+frac{1}{4} right)}}cdot {{3}^{frac{1}{4}}}={{5}^{-frac{1}{4}}}cdot {{3}^{frac{1}{4}}}={{left( frac{3}{5} right)}^{frac{1}{4}}}=sqrt[4]{frac{3}{5}})
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
( displaystyle frac{sqrt[9]{6}cdot sqrt[18]{6}}{sqrt[6]{6}}=frac{{{6}^{frac{1}{9}}}cdot {{6}^{frac{1}{18}}}}{{{6}^{frac{1}{6}}}}={{6}^{frac{1}{9}+frac{1}{18}-frac{1}{6}}}={{6}^{frac{2+1-3}{18}}}={{6}^{0}}=1)
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем – это число, несколько раз умноженное само на себя; число в нулевой степени – это как-бы число, умноженное само на себя ( 0) раз, то есть его еще не начали умножать, значит, само число еще даже не появилось – поэтому результатом является только некая «заготовка числа», а именно число ( 1) ; степень с целым отрицательным показателем – это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель – это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)
Например: ( {{3}^{sqrt{2}}}cdot {{3}^{1-sqrt{2}}}={{3}^{sqrt{2}+1-sqrt{2}}}=3)
Или: ( frac{{{2}^{3sqrt{3}}}}{{{8}^{sqrt{3}-1}}}=frac{{{2}^{3sqrt{3}}}}{{{2}^{3left( sqrt{3}-1 right)}}}={{2}^{3sqrt{3}-3sqrt{3}+3}}=8)
И еще: ( {{left( {{5}^{sqrt[3]{4}}} right)}^{sqrt[3]{2}}}={{5}^{sqrt[3]{8}}}={{5}^{2}}=25).
Определение степени
Степенью называется выражение вида: ( {{a}^{b}}), где ( a) – основание степени и ( b) – показатель степени.
Степень с натуральным показателем {n = 1, 2, 3,…}
- ( {{a}^{1}}=a)
- ( {{a}^{2}}=acdot a)
- ( {{a}^{3}}=acdot acdot a)
Возвести число в натуральную степень n — значит умножить число само на себя ( n) раз:
- ( {{a}^{n}}=underbrace{acdot acdot acdot …a}_{n})
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
( {{a}^{n}}={{a}^{n}}, n>0)
Возведение в нулевую степень:
( {{a}^{0}}=1, ane 0) . ( {{0}^{0}}) – выражение неопределенное, т.к., с одной стороны, ( 0) в любой степени – это ( 0) , а с другой – любое число в ( 0) -ой степени – это ( 1) .
Если показателем степени является целое отрицательное число:
( {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0) (т.к. на ( 0) делить нельзя).
Еще раз о нулях: выражение ( {{0}^{k}}) не определено в случае ( kle 0). Если ( k>0) , то ( {{0}^{k}}=0) .
Примеры:
( {{6}^{-1}}=frac{1}{6})
( {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})
Степень с рациональным показателем
Если,
- ( a>0);
- ( m) – натуральное число;
- ( n) – целое число;
Тогда:
- ( {{a}^{frac{n}{m}}}=sqrt[m]{{{a}^{n}}})
Примеры:
( {{a}^{frac{1}{2}}}=sqrt{a})
( {{a}^{frac{1}{5}}}=sqrt[5]{a})
( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{{{a}^{3}}}})
Свойства степеней
| Произведение степеней | ( {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) ( {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}) |
| Деление степеней | ( frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}) ( frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}}) |
| Возведение степени в степень | ( {{left( {{a}^{m}} right)}^{n}}={{a}^{mcdot n}}) |
Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.
Доказательства свойств степени
1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})
Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?
По определению:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}})
Сколько здесь множителей всего? Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.
Итак, в правой части этого выражения получается такое произведение:
( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})
Но по определению это степень числа ( displaystyle mathbf{a}) с показателем ( displaystyle mathbf{n}+mathbf{m}), то есть:
( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.
Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .
Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}}) .
Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .
Решение: Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:
( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}}) .
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нелья написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}) .
2. ( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}})
Так же, как и с предыдущим свойством, обратимся к определению степени:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}) .
Перегруппируем это произведение так:
( displaystyle {{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}=underbrace{left( acdot b right)cdot left( acdot b right)cdot …cdot left( acdot b right)}_{ntext{ множителей}}).
Получается, что выражение ( displaystyle acdot b) умножается само на себя ( displaystyle n) раз, то есть, согласно определению, это и есть ( displaystyle n) -я степень числа ( displaystyle acdot b) :
( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}), ч.т.д.
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: ( displaystyle {{2}^{4}}+{{3}^{4}}ne {{left( 2+3 right)}^{4}}) !
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+{{b}^{2}}) ? Но это неверно, ведь ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}) .
3. ( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}})
И снова используем определение степени:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}})
Здесь, очевидно, можем сократить. Но с одной оговоркой: чтобы степень получилась натуральная, нам придется предположить, что ( displaystyle n>m) (то есть, в числителе множителей должно быть больше, чем в знаменателе). Тогда ( displaystyle m) множителей числителя сокращаются со всеми ( displaystyle m) множителями знаменателя. Таким образом множители остаются только в числителе, причем в количестве ( displaystyle n-m) штук:
( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}}=frac{underbrace{acdot acdot …cdot a}_{n-mtext{ множителей}}}{1}={{a}^{n-m}}) , ч.т.д.
4. ( displaystyle frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}})
Все как обычно – записываем определение степеней ( displaystyle {{a}^{n}}) и ( displaystyle {{b}^{n}}) , делим их друг на друга, разбиваем на пары ( displaystyle frac{a}{b}) и получаем:
( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{b}^{n}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}}=underbrace{frac{a}{b}cdot frac{a}{b}cdot …cdot frac{a}{b}}_{ntext{ множителей}}={{left( frac{a}{b} right)}^{n}}) , ч.т.д.
Прежде чем разобрать последнее правило, решим несколько примеров.
