Содержание:
- Координаты вектора
- Длина (модуль) вектора
- Угол между векторами
- Разложение вектора по ортам координатных осей
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других
прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать
все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме – координаты вектора.
Пример
Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы векторы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$
Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Пример
Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$
Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$
Пример
Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$
Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Длина (модуль) вектора
Теоретический материал по теме – длина вектора.
Пример
Задание. Найти длину вектора $overline{a}=(-4 ; 3)$
Решение. Используя формулу, получаем:
$|overline{a}|=sqrt{(-4)^{2}+3^{2}}=sqrt{16+9}=sqrt{25}=5$
Пример
Задание. Найти длину вектора $overline{a}=(1 ; 0 ;-4)$
Решение. Используя формулу, получаем:
$|overline{a}|=sqrt{1^{2}+0^{2}+(-4)^{2}}=sqrt{1+0+16}=sqrt{17}$
Угол между векторами
Теоретический материал по теме – угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов $(overline{a} ; overline{b})=2$,
а их длины $|overline{a}|=2,|overline{b}|=2$.
Найти угол между векторами $overline{a}$ и
$overline{b}$.
Решение. Косинус искомого угла:
$$cos (bar{a}, bar{b})=frac{(bar{a} ; bar{b})}{|bar{a}| cdot|bar{b}|}=frac{2}{2 cdot 2}=frac{1}{2} Rightarrow(bar{a}, bar{b})=60^{circ}$$
Пример
Задание. Найти угол между векторами $overline{a}=(1 ; sqrt{3})$ и
$overline{b}=(1 ; 0)$
Решение. Косинус искомого угла
$$cos (bar{a}, bar{b})=frac{1 cdot 1+sqrt{3} cdot 0}{sqrt{1^{2}+(sqrt{3})^{2}} cdot sqrt{1^{2}+0^{2}}}=frac{1}{2}$$
$$(bar{a}, bar{b})=arccos frac{1}{2}=60^{circ}$$
Пример
Задание. Найти угол между векторами $overline{a}=(1 ; 3)$
и $overline{b}=(2 ; 1)$
Решение. Косинус искомого угла:
$$cos (bar{a}, bar{b})=frac{1 cdot 2+3 cdot 1}{sqrt{1^{2}+3^{2}} cdot sqrt{2^{2}+1^{2}}}=frac{5}{sqrt{10} cdot sqrt{5}}=sqrt{frac{1}{2}}=frac{sqrt{2}}{2}$$
$$(bar{a}, bar{b})=arccos frac{sqrt{2}}{2}=45^{circ}$$
Разложение вектора по ортам координатных осей
Теоретический материал по теме – разложение вектора по ортам.
Пример
Задание. Зная разложения вектора $overline{a}$
по базисной системе векторов: $overline{a}=3 overline{i}-overline{k}$, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $overline{a}=3 overline{i}-0 cdot overline{j}-overline{k}$,
получаем, что $overline{a}=(3 ; 0 ;-1)$
Пример
Задание. Вектор $overline{a}$ задан
своими координатами: $overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора – это коэффициенты при ортах координатных осей в разложении вектора
по базисной системе векторов, поэтому искомое разложение:
$overline{a}=2 overline{i}-overline{j}+5 overline{k}$
Скалярное произведение векторов
Теоретический материал по теме – скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов $overline{a}$ и
$overline{b}$ , если их длины соответственно равны 2 и 3,
а угол между ними 60°.
Решение. Так как из условия $|overline{a}|=2$,
$|overline{b}|=3$, а 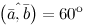 , то
, то
$overline{a} cdot overline{b}=(overline{a}, overline{b})=2 cdot 3 cdot cos 60^{circ}=6 cdot frac{1}{2}=3$
Пример
Задание. Найти скалярное произведение векторов $overline{a}=(3 ;-1)$ и
$overline{b}=(-2 ; 7)$
Решение. Скалярное произведение
$overline{a} overline{b}=3 cdot(-2)+(-1) cdot 7=-6-7=-13$
Векторное произведение векторов
Теоретический материал по теме – векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов $overline{a}=(6 ; 7 ; 10)$ и
$overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$overline{a} times overline{b}=left| begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {6} & {7} & {10} \ {8} & {5} & {9}end{array}right|=overline{i} left| begin{array}{cc}{7} & {10} \ {5} & {9}end{array}right|-overline{j} left| begin{array}{cc}{6} & {10} \ {8} & {9}end{array}right|+overline{k} left| begin{array}{cc}{6} & {7} \ {8} & {5}end{array}right|=$
$=overline{i}(7 cdot 9-5 cdot 10)-overline{j}(6 cdot 9-8 cdot 10)+overline{k}(6 cdot 5-8 cdot 7)=$
$=13 overline{i}+26 overline{j}-26 overline{k}=(13 ; 26 ;-26)$
Смешанное произведение векторов
Теоретический материал по теме – смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной на векторах $overline{a}=(2 ; 3 ; 5)$,
$overline{b}=(1 ; 4 ; 4)$,
$overline{c}=(3 ; 5 ; 7)$
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель,
по строкам которого запишем координаты векторов $overline{a}$,
$overline{b}$ и $overline{c}$:
$(overline{a}, overline{b}, overline{c})=left| begin{array}{lll}{2} & {3} & {5} \ {1} & {4} & {4} \ {3} & {5} & {7}end{array}right|=2 cdot 4 cdot 7+1 cdot 5 cdot 5+3 cdot 4 cdot 3-$
$-3 cdot 4 cdot 5-5 cdot 4 cdot 2-1 cdot 3 cdot 7=-4$
$$V_{пир}=frac{1}{6}|(overline{a}, overline{b}, overline{c})|=frac{1}{6} cdot 4=frac{2}{3}$$
Читать первую тему – операции над векторами,
раздела векторы.
Содержание:
- Векторы
- Действия над векторами
- Умножение вектора на число
- Скалярное произведение векторов
- Векторное произведение
- Смешенное произведение векторов
- Разложение вектора по базису
- Действия над векторами, заданными своими координатами
- Проекция вектора на ось
- Проекции вектора на оси координат
- Направляющие косинусы вектора
- Разложение вектора по ортам
- Действия над векторами, заданными в координатной форме
- Вектор – основные определения
- Операции над векторами и их свойства
- Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
- Координаты вектора
- Скалярное произведение векторов и его свойства
- Векторы и их решение
- Собственные числа и собственные векторы
- Векторная алгебра
- Векторы: основные определения, линейные операции
- Линейные операции над векторами
- Умножения вектора на скаляр
- Основные свойства проекции вектора на ось
- Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
- Скалярное, векторное, смешанное произведения векторов
- Векторное произведение двух векторов
- Смешанное произведение векторов, заданных в координатной форме
- Простейшие задачи аналитической геометрии
- Задача об определении площади треугольника
- Задача о деление отрезка в заданном отношении
Векторы
В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.

Векторы обозначают малыми латинскими буквами с чертой сверху  , или двумя большими латинскими буквами, которые обозначают его начало и конец, например
, или двумя большими латинскими буквами, которые обозначают его начало и конец, например  . Длина (модуль) вектора — это длина отрезка, который отвечает данному вектору и обозначается
. Длина (модуль) вектора — это длина отрезка, который отвечает данному вектору и обозначается  В зависимости от соотношения длин и направлений различают следующие виды векторов:
В зависимости от соотношения длин и направлений различают следующие виды векторов:


Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов  называют вектор
называют вектор  , который соединяет начало вектора
, который соединяет начало вектора  с концом вектора
с концом вектора  , при условии, что вектор
, при условии, что вектор  отложен от конца вектора
отложен от конца вектора  . Такой способ сложения векторов называют правилом треугольника.
. Такой способ сложения векторов называют правилом треугольника.

Учитывая, что  , то найти сумму векторов
, то найти сумму векторов  можно также по так называемым “правилом параллелограмма” (рис. 3)
можно также по так называемым “правилом параллелограмма” (рис. 3)

Вычитание векторов сводится к сложению противоположного вектора

Запишем основные свойства действий сложения векторов:

Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:

Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является  (рис. 5).
(рис. 5).

Умножение вектора на число
Произведением вектора  на число
на число  называют вектор
называют вектор  , для которого выполняются условия:
, для которого выполняются условия:
а)  ;
;
б)  , причём
, причём  сонаправленные если
сонаправленные если  противоположно направленные, если
противоположно направленные, если  . Отсюда, очевидно, что необходимым и достаточным условием коллинеарности векторов является соотношение
. Отсюда, очевидно, что необходимым и достаточным условием коллинеарности векторов является соотношение  .
.
Запишем основные свойства действий умножения вектора на число:

Скалярное произведение векторов
Скалярным произведением  или
или  векторов
векторов  и
и  называют выражение
называют выражение  , где
, где  угол, который образуют векторы. Отметим, что углом между векторами считают угол между их направлениями. Если хотя бы один из векторов равен
угол, который образуют векторы. Отметим, что углом между векторами считают угол между их направлениями. Если хотя бы один из векторов равен  , то их скалярное произведение считают равным нулю.
, то их скалярное произведение считают равным нулю.
Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если  . Но
. Но  , следовательно,
, следовательно,

Наоборот, если  и согласно определениям
и согласно определениям
 .
.
Например, скалярное произведение  будет равным
будет равным

Запишем основные свойства действий скалярного умножения векторов:

Векторное произведение
Векторным произведением  двух векторов
двух векторов  и
и  называется вектор
называется вектор  , который удовлетворяет условия:
, который удовлетворяет условия:
1) модуль вектора  равен произведению модулей векторов
равен произведению модулей векторов  и
и  на синус угла между ними
на синус угла между ними

2) вектор  перпендикулярный к плоскости, которая определяется векторами
перпендикулярный к плоскости, которая определяется векторами  и
и  (рис. 5).
(рис. 5).
3) вектор  направленный так, что кратчайший поворот вектора
направленный так, что кратчайший поворот вектора  к вектору
к вектору  видно с конца вектора
видно с конца вектора  таким, что происходит против движения стрелки (то есть вектора
таким, что происходит против движения стрелки (то есть вектора  ,
,  и образуют правую упорядоченную тройку, или правый руль).
и образуют правую упорядоченную тройку, или правый руль).

Модуль векторного произведения равен площади параллелограмма, построенного на векторах  и
и  . Векторное произведение выражается формулой
. Векторное произведение выражается формулой  , где
, где  площадь параллелограмма построенного на векторах
площадь параллелограмма построенного на векторах  и
и  ,
,  единичный вектор направления
единичный вектор направления  .
.
Приведём основные свойства векторного произведения:
1) векторное произведение  равно нулю, если векторы
равно нулю, если векторы  и
и  коллинеарные, или один из них нулевой;
коллинеарные, или один из них нулевой;
2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный:  (векторное произведение не имеет свойств перестановки);
(векторное произведение не имеет свойств перестановки);
3)  (распределительный закон);
(распределительный закон);
4)  (соединительный закон).
(соединительный закон).
Физическое содержание векторного произведения такое. Если  сила, а
сила, а  радиус-вектор точки её приложения, которая имеет начало в точке
радиус-вектор точки её приложения, которая имеет начало в точке  , то моментом силы
, то моментом силы  относительно точки
относительно точки  является вектор, который равен векторному произведению
является вектор, который равен векторному произведению  на
на  , то есть
, то есть  .
.
Смешенное произведение векторов
Смешенным произведением векторов  называют скалярное произведение вектора
называют скалярное произведение вектора  на вектор
на вектор  . Смешенное произведение обозначают (
. Смешенное произведение обозначают ( ), поэтому по определению имеем
), поэтому по определению имеем

Как результат скалярного произведения векторов  и
и  смешенное произведение является скалярной величиной (числом). Геометрически смешенное произведение — это объём параллелепипеда, построенного на эти векторах, взятый со знаком плюс, если векторы
смешенное произведение является скалярной величиной (числом). Геометрически смешенное произведение — это объём параллелепипеда, построенного на эти векторах, взятый со знаком плюс, если векторы  образуют правую тройку, и со знаком минус, когда эта тройка левая (рис. 7).
образуют правую тройку, и со знаком минус, когда эта тройка левая (рис. 7).

Действительно,  , где
, где  угол между векторами
угол между векторами  угол между векторами
угол между векторами  и
и  .
.
Объём V параллелепипеда, построенного на векторах  равный произведению площади основы S на высоту h.
равный произведению площади основы S на высоту h.

Однако, знак смешенного произведения совпадает со знаком  , то есть он положительный, когда угол
, то есть он положительный, когда угол  острый (
острый ( образуют правую тройку векторов) и отрицательный, когда угол
образуют правую тройку векторов) и отрицательный, когда угол  тупой (
тупой ( образуют левую тройку векторов). Поэтому:
образуют левую тройку векторов). Поэтому:

Из геометрического содержания смешенного произведения выходит, что
1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);
2) 
Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов  имеем
имеем

Пример 1.
Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство: 
Решение.
Пусть  медиана треугольника АВС. По свойствам медиан треугольника
медиана треугольника АВС. По свойствам медиан треугольника  Применив к векторам
Применив к векторам  и
и  формулу вычитания векторов
формулу вычитания векторов

тогда

Пример 2.
У прямоугольного параллелепипеда рёбра  , имеют длину 2, 3, 5. Вычислить длины отрезков
, имеют длину 2, 3, 5. Вычислить длины отрезков  и
и  и угол между прямыми
и угол между прямыми  и
и  .
.
Решение.
Пусть  единичные вектора направленные вдоль рёбер, которые рассматриваются. Тогда
единичные вектора направленные вдоль рёбер, которые рассматриваются. Тогда  (поскольку параллелепипед прямоугольный).
(поскольку параллелепипед прямоугольный).
рис. 9.
Далее,

Этим закончен “перевод” условия задачи на “язык” векторов.
Теперь произведём вычисления с векторами:

Наконец “переводим” полученные вектора равенства снова на “геометрический язык”. Поскольку  аналогично
аналогично  .
.
Далее поскольку  , где
, где  угол между данными векторами то
угол между данными векторами то  , отсюда получаем
, отсюда получаем  . Теперь с помощью тригонометрических таблиц находим значения угла
. Теперь с помощью тригонометрических таблиц находим значения угла  .
.
Разложение вектора по базису
Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта.
Теорема. Любой вектор  на плоскости можно разложить по двум неколлинеарным векторам
на плоскости можно разложить по двум неколлинеарным векторам  и
и  , то есть представить в виде:
, то есть представить в виде:  .
.
Доказательство.

Пусть векторы  компланарные и векторы
компланарные и векторы  и
и  неколлинеарные. От точки О отложим все три вектора и на продолжении векторов
неколлинеарные. От точки О отложим все три вектора и на продолжении векторов  и
и  построим параллелограмм ONCM так, чтобы вектор
построим параллелограмм ONCM так, чтобы вектор  был его диагональю.
был его диагональю.
Тогда по правилу параллелограмма  .
.
Но  , как коллинеарные векторы. Следовательно, вектор
, как коллинеарные векторы. Следовательно, вектор .
.
Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают  .
.
Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта. Для четырёх некомпланарных векторов справедлива следующая теорема.
Теорема. Любой вектор  в пространстве можно разложить по трём некомпланарным векторам
в пространстве можно разложить по трём некомпланарным векторам  ,
,  и
и  , то есть представить в виде:
, то есть представить в виде:  .
.
Доказательство.
От точки О отложим векторы  и на продолжении векторов
и на продолжении векторов  построим параллелограмм
построим параллелограмм 

в котором вектор  является диагональю. Как видим
является диагональю. Как видим

Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают  . Если базисные вектора взаимно перпендикулярны (их обозначают
. Если базисные вектора взаимно перпендикулярны (их обозначают  ), то вместе с точкой отсчёта они образуют декартовую систему координат, а координаты вектора в таком базисе называют декартовыми координатами. В декартовой системе координат разложение вектора будет иметь вид
), то вместе с точкой отсчёта они образуют декартовую систему координат, а координаты вектора в таком базисе называют декартовыми координатами. В декартовой системе координат разложение вектора будет иметь вид  . Если началом вектора
. Если началом вектора  является точка
является точка  , а концом — точка
, а концом — точка  , то координаты вектора
, то координаты вектора  вычисляют как разность соответствующих координат точек А и В,
вычисляют как разность соответствующих координат точек А и В,

Отсюда легко установить длину вектора как расстояние между двумя точками:

Действия над векторами, заданными своими координатами
1. При сложении двух, или более векторов их соответствующие координаты складываются:

Действительно:

2. При вычитании векторов соответствующие координаты вычитаются:

Доказательство аналогично предыдущему.
3. При умножении вектора на число все координаты умножаются на это число.
Правда, для вектора  и числа
и числа  имеем:
имеем:

4. Скалярное произведение двух векторов  равно сумме произведений соответствующих координат:
равно сумме произведений соответствующих координат:
Правда:

Поскольку  выполняется
выполняется  Следовательно, мы можем записать
Следовательно, мы можем записать

5. Векторное произведение векторов  заданных своими координатами вычисляется так:
заданных своими координатами вычисляется так:

6. Смешенное произведение трёх векторов  равняется:
равняется:

Пример 1.
Зная координаты векторов  , найти координаты векторов
, найти координаты векторов  .
.
Решение:

Ответ:  .
.
Пример 2.
Зная координаты векторов  вычислить координаты вектора
вычислить координаты вектора  .
.
Решение.

Ответ:  .
.
Пример 3.
Зная координаты векторов  вычислить:
вычислить:
а) скалярное произведение векторов 
б) векторное произведение векторов 
в) смешенное произведение векторов  .
.
Решение.

Ответ: 
На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов

1. Угол между векторами.

2. Условие перпендикулярности двух векторов:

(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).
3. Условие коллинеарности двух векторов:  (векторы коллинеарные тогда и только тогда, когда соответствующие их координаты пропорциональны).
(векторы коллинеарные тогда и только тогда, когда соответствующие их координаты пропорциональны).
4. Условие компланарности трёх векторов.

(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).
5. Деление отрезка АВ в заданном отношении.
Если точка  делит отрезок АВ в отношении
делит отрезок АВ в отношении  , то координаты точки М находят по формуле:
, то координаты точки М находят по формуле:

Если точка М делит отрезок АВ на пополам то  , и координаты точки находят согласно формуле:
, и координаты точки находят согласно формуле:

Действия над векторами (теория)
а) Произведение вектора на число.
Определение 1. Произведением вектора  на число λ называется вектор
на число λ называется вектор  ,
,
который имеет длину  и направление его совпадает с направлением вектора
и направление его совпадает с направлением вектора  если λ > 0, и противоположно ему, если λ < 0 (рис.12).
если λ > 0, и противоположно ему, если λ < 0 (рис.12).

Рис. 12.
Условие  (2.6)
(2.6)
является условием коллинеарности двух векторов.
б) Сложение векторов.
Определение 2. Суммой двух векторов  и
и  называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец совпадает с концом вектора
, а конец совпадает с концом вектора  , при условии, что начало вектора
, при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  (правило треугольника) (рис.13).
(правило треугольника) (рис.13).

Рис. 13.
Понятно, что вектор  в этом случае является диагональю параллелограмма, построенного на векторах
в этом случае является диагональю параллелограмма, построенного на векторах  и
и  (правило параллелограмма) (рис.13).
(правило параллелограмма) (рис.13).
Для векторной суммы справедливый переместительный закон

Легко убедиться, что для векторной суммы имеет место соединительный
закон  .
.
Исходя из определения 2, легко находим сумму, например, четырех векторов  (рис. 14).
(рис. 14).

Рис. 14.
Вектор  соединяет начало первого вектора
соединяет начало первого вектора  с концом вектора
с концом вектора  (правило многоугольника).
(правило многоугольника).
в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.
Определение. Разностью  называется вектор
называется вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  (рис. 15), т.е.
(рис. 15), т.е. 

Рис. 15.
Как видно из рис. 15, одна диагональ  является суммой
является суммой  , а вторая диагональ
, а вторая диагональ  является разностью векторов
является разностью векторов  и
и  .
.
Дадим еще одно определение разности векторов.
Определение. Разностью двух векторов  и
и  , которые имеют общее начало, называется вектор
, которые имеют общее начало, называется вектор  , который соединяет концы этих векторов и направлен в сторону уменьшаемого.
, который соединяет концы этих векторов и направлен в сторону уменьшаемого.
Проекция вектора на ось
Пусть имеем произвольную ось l на плоскости и некоторый вектор  (рис. 16).
(рис. 16).

Рис. 16.
Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A1 и B1, которые называются проекциями точек A и B.
Величина A1B1 называется проекцией вектора  на ось l и обозначается
на ось l и обозначается  , то есть
, то есть  .
.
Определение 1. Проекцией вектора  на ось l называется величина отрезка A1B1, взята со знаком плюс, если направление отрезка A1B1 совпадает с направлением оси l, и с знаком минус, если направления противоположные.
на ось l называется величина отрезка A1B1, взята со знаком плюс, если направление отрезка A1B1 совпадает с направлением оси l, и с знаком минус, если направления противоположные.
Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок BB1 в точке C. Вектор  образует с осью l угол φ. Величина отрезка AC равна величине отрезка A1B1, а тогда из Δ ABC находим
образует с осью l угол φ. Величина отрезка AC равна величине отрезка A1B1, а тогда из Δ ABC находим
 или
или  (2.7)
(2.7)
Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.
Если угол φ острый, то проекция  — положительное число, а если угол φ тупой, то проекция
— положительное число, а если угол φ тупой, то проекция  — отрицательное число.
— отрицательное число.
Свойства проекций.
1. Если векторы  и
и  равны, то величины их проекций на одну и ту же ось l также равны, то есть:
равны, то величины их проекций на одну и ту же ось l также равны, то есть:  .
.
2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:

3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:

4. Если вектор  умножен на любое число λ, то величина проекции вектора
умножен на любое число λ, то величина проекции вектора  на ось l также умножится на число λ, то есть:
на ось l также умножится на число λ, то есть:

Проекции вектора на оси координат
Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор  .
.
Пусть 

Проекции x, y, z вектора  на координатные оси называют координатами вектора и записывают
на координатные оси называют координатами вектора и записывают  .
.
Если заданы две точки A (x1; y1; z1) и B (x2; y2; z2), то координаты вектора  находятся по формулам
находятся по формулам
x = x2 – x1, y = y2 – y1, z = z2 – z1 .

Рис. 17
Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A1 и B1 (рис.17). Точки A1 и B1 имеют на оси Ox координаты x1 и x2 , но  на основе формулы (2.1), а потому
на основе формулы (2.1), а потому
x = x2 – x1 . Аналогично доказывается, что y = y2 – y1, z = z2 – z1 .
Направляющие косинусы вектора
Пусть имеем вектор  и будем считать, что он выходит из начала координат и не находится ни в одной координатной плоскости.
и будем считать, что он выходит из начала координат и не находится ни в одной координатной плоскости.

Рис. 18
Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор  с осями координат. Величины cos α, cos β, cos γ называются направляющими косинусами вектора
с осями координат. Величины cos α, cos β, cos γ называются направляющими косинусами вектора  . Координаты вектора
. Координаты вектора  .
.
Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому
 или
или 
 (2.8)
(2.8)
Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим

Отсюда для направляющих косинусов получаем
 (2.9)
(2.9)
Для направляющих косинусов справедливо равенство  (это вытекает из (2.9)).
(это вытекает из (2.9)).
Разложение вектора по ортам
Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .

Рис. 19.
Обозначим орты осей координат Ox, Oy, Oz соответственно через  , причем
, причем

Спроецируем вектор  на координатные оси (через точку M проведем плоскости, перпендикулярные координатным осям). Проекциями точки M на координатные оси будут соответственно точки А, В, С (рис.19).
на координатные оси (через точку M проведем плоскости, перпендикулярные координатным осям). Проекциями точки M на координатные оси будут соответственно точки А, В, С (рис.19).
Из прямоугольника ODMC видно, что вектор  , но из прямоугольника AOBD получаем, что вектор
, но из прямоугольника AOBD получаем, что вектор  .
.
Тогда
 (2.10)
(2.10)
Вектор  , который соединяет точку O с точкой M (x, y, z) называется радиусом-вектором этой точки.
, который соединяет точку O с точкой M (x, y, z) называется радиусом-вектором этой точки.
Векторы  называются составными или компонентами вектора
называются составными или компонентами вектора  , а их величины OA = x, OB = y, OC = z координатами этого вектора. Компоненты вектора
, а их величины OA = x, OB = y, OC = z координатами этого вектора. Компоненты вектора  выразим через его координаты и единичные векторы
выразим через его координаты и единичные векторы  , а именно
, а именно  .
.
Подставляя эти значения в равенство (2.10), учитывая, что  , получим
, получим
 (2.11)
(2.11)
Слагаемые  являются составными или компонентами вектора
являются составными или компонентами вектора  .
.
Тройка векторов  называется координатным базисом, а разложение (2.11) называется разложением вектора по базису
называется координатным базисом, а разложение (2.11) называется разложением вектора по базису  . Это основная формула векторной алгебры.
. Это основная формула векторной алгебры.
Пример 1. Построить вектор  .
.

Рис. 20.
Решение. Компоненты вектора  являются
являются  и
и  , и им
, и им
соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).
Действия над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.
Правило 1. При сложении векторов их одноименные координаты складываются
Пусть имеем векторы  и
и  . Найдем
. Найдем  . Запишем разложение векторов
. Запишем разложение векторов  и
и  . Тогда
. Тогда  .
.
Сложив эти равенства, получим
 .
.
Итак, координаты вектора  будут
будут 
Правило 2. Чтобы отнять от вектора  вектор
вектор  нужно вычесть из координат вектора
нужно вычесть из координат вектора  соответствующие координаты вектора
соответствующие координаты вектора  , то есть
, то есть

Правило 3. Чтобы умножить вектор  на число λ, нужно каждую из его координат умножить на это число. То есть, если
на число λ, нужно каждую из его координат умножить на это число. То есть, если
 то
то  .
.
Пример 1. Найти вектор  , если
, если 
Решение. Выполним действия последовательно и найдем

 .
.
Значит, 
Вектор – основные определения
Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Так же как и на плоскости, векторы обозначаются  и т. п. и на чертеже изображаются стрелкой.
и т. п. и на чертеже изображаются стрелкой.
Определение 2. Длиной (или модулем) вектора  называется длина отрезка
называется длина отрезка  а направление, определяемое лучом
а направление, определяемое лучом  называется направлением вектора
называется направлением вектора 
Длина вектора  обозначается
обозначается  длина вектора
длина вектора  обозначается
обозначается 
Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора: 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение 3. Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если ненулевые векторы  и
и  лежат на параллельных прямых (следовательно, в одной плоскости), причём лучи
лежат на параллельных прямых (следовательно, в одной плоскости), причём лучи  лежат в одной полуплоскости, границей которой является прямая
лежат в одной полуплоскости, границей которой является прямая  то векторы
то векторы  и
и  называются сонаправленными в случае же, когда эти векторы принадлежат одной прямой, они называются сонаправленными, если один из лучей
называются сонаправленными в случае же, когда эти векторы принадлежат одной прямой, они называются сонаправленными, если один из лучей  или
или  целиком содержится в другом. Нулевой вектор будем считать сонаправленным с любым вектором в пространстве.
целиком содержится в другом. Нулевой вектор будем считать сонаправленным с любым вектором в пространстве.
Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными:  (векторы
(векторы  и
и  сонаправлены),
сонаправлены),  (векторы
(векторы  и
и  противоположно направлены).
противоположно направлены).
Определение 4. Векторы  и
и  называются равными, если
называются равными, если  и
и  (т.е. если векторы сонаправлены и их длины равны).
(т.е. если векторы сонаправлены и их длины равны).
Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
Возможно вам будут полезны данные страницы:
Операции над векторами и их свойства
Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.
Пусть даны два вектора  и
и  В силу теоремы 1 от произвольной точки
В силу теоремы 1 от произвольной точки  пространства можно отложить вектор
пространства можно отложить вектор  а от точки
а от точки  — вектор
— вектор  Тогда вектор
Тогда вектор  называется по определению суммой векторов
называется по определению суммой векторов  и
и  а описанное правило построения суммы двух векторов — правилом треугольника (рис. 1).
а описанное правило построения суммы двух векторов — правилом треугольника (рис. 1).
Теорема 2. Сумма  векторов
векторов  и
и  не зависит от выбора точки
не зависит от выбора точки  от которой при сложении откладывается вектор
от которой при сложении откладывается вектор  (Докажите эту теорему самостоятельно.)
(Докажите эту теорему самостоятельно.)
Правило треугольника можно сформулировать и так: для любых трёх точек  пространства выполняется равенство
пространства выполняется равенство

Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма:  где
где  — вектор, модуль которого_равен длине диагонали параллелограмма, построенного на векторах
— вектор, модуль которого_равен длине диагонали параллелограмма, построенного на векторах  причём вектор
причём вектор  откладывают от той же точки, что и векторы
откладывают от той же точки, что и векторы  (рис. 2).
(рис. 2).
Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:
1) 
2)  — коммутативность (переместительный закон);
— коммутативность (переместительный закон);
3)  — ассоциативность (сочетательный закон).
— ассоциативность (сочетательный закон).
Здесь  — произвольные векторы в пространстве.
— произвольные векторы в пространстве.
Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору  обозначается
обозначается 
Определение 6. Разностью двух векторов  и
и  называется вектор
называется вектор  такой, что его сумма с вектором
такой, что его сумма с вектором  равна вектору
равна вектору 
Разность векторов  и
и  обозначается
обозначается  Таким образом, по определению
Таким образом, по определению  если
если 
Разность векторов  и
и  можно найти по формуле
можно найти по формуле  (рис. 3) (докажите эту формулу самостоятельно).
(рис. 3) (докажите эту формулу самостоятельно).  Замечание. Так же как и на плоскости, для сложения нескольких векторов в пространстве можно использовать правило многоугольника (рис. 4), только в последнем случае этот многоугольник будет пространственным (т.е. не все векторы, его составляющие, лежат в одной плоскости).
Замечание. Так же как и на плоскости, для сложения нескольких векторов в пространстве можно использовать правило многоугольника (рис. 4), только в последнем случае этот многоугольник будет пространственным (т.е. не все векторы, его составляющие, лежат в одной плоскости).

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.
Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.
Определение 7. Произведением ненулевого вектора  на действительное число
на действительное число  называется вектор
называется вектор  длина которого равна произведению длины вектора
длина которого равна произведению длины вектора  на модуль числа
на модуль числа  причём вектор
причём вектор  сонаправлен с вектором
сонаправлен с вектором  при
при  и противоположно направлен вектору
и противоположно направлен вектору  при
при 
Таким образом, по определению,  если
если  причём
причём  при
при  Ясно, что векторы
Ясно, что векторы  коллинеарны. Если же
коллинеарны. Если же  или
или  то
то 
Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:
-
 — ассоциативность (сочетательный закон);
— ассоциативность (сочетательный закон); -
 —дистрибутивность относительно сложения векторов (1-й распределительный закон);
—дистрибутивность относительно сложения векторов (1-й распределительный закон); -
 — дистрибутивность относительно сложения чисел (2-й распределительный закон).
— дистрибутивность относительно сложения чисел (2-й распределительный закон).
Здесь  и
и  — произвольные векторы,
— произвольные векторы,  — произвольные действительные числа.
— произвольные действительные числа.
Справедлива также и лемма о коллинеарных векторах: если векторы  и
и  коллинеарны и
коллинеарны и  то существует такое действительное число
то существует такое действительное число 
что  (ясно, что
(ясно, что  если
если 
Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
Теорема 3. Пусть  где
где  — некоторое действительное число, отличное от -1, тогда точки
— некоторое действительное число, отличное от -1, тогда точки 
 принадлежат одной прямой. Для произвольной точки
принадлежат одной прямой. Для произвольной точки  пространства справедливо равенство:
пространства справедливо равенство:

Доказательство
1. Из равенства  следует, что векторы
следует, что векторы  коллинеарны, и так как
коллинеарны, и так как  — общая точка прямых
— общая точка прямых  и
и  эти прямые совпадают, поэтому точки
эти прямые совпадают, поэтому точки  принадлежат одной прямой.
принадлежат одной прямой.
2. Пусть  — произвольная точка пространства. Тогда
— произвольная точка пространства. Тогда  и поскольку
и поскольку 
 откуда
откуда  Поделив обе части последнего равенства на
Поделив обе части последнего равенства на  приходим к формуле (1). Теорема доказана.
приходим к формуле (1). Теорема доказана.
З. Компланарные и некомпланарные векторы
Следующее понятие уже не имеет аналога в планиметрии.
Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.
Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.
Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.
Теорема 4. Векторы  из которых никакие два не коллинеарны, являются компланарными в том и только том случае, если существуют такие действительные числа
из которых никакие два не коллинеарны, являются компланарными в том и только том случае, если существуют такие действительные числа  и
и  что
что
 (иными словами, векторы
(иными словами, векторы  являются компланарными в том и только том случае, если один из них можно выразить через два других, или, как говорят, разложить по двум другим).
являются компланарными в том и только том случае, если один из них можно выразить через два других, или, как говорят, разложить по двум другим).
Доказательство
1. Пусть векторы  компланарны. Докажем, что для них имеет место равенство (5). Отложим от произвольной
компланарны. Докажем, что для них имеет место равенство (5). Отложим от произвольной
точки  векторы
векторы 
 Векторы
Векторы  лежат в одной плоскости (см. замечание). Проведём через точку
лежат в одной плоскости (см. замечание). Проведём через точку  прямую
прямую  до пересечения с прямой
до пересечения с прямой  в точке
в точке  и прямую
и прямую  до пересечения с прямой
до пересечения с прямой  в точке
в точке  (см. рис. 8). Так как векторы
(см. рис. 8). Так как векторы  коллинеарны, по лемме о коллинеарных векторах (см. §1.2) существуют такие действительные числа
коллинеарны, по лемме о коллинеарных векторах (см. §1.2) существуют такие действительные числа  и
и  что
что 
 Но по правилу параллелограмма
Но по правилу параллелограмма  откуда
откуда  Обратно, пусть выполнено равенство (5).
Обратно, пусть выполнено равенство (5).
Докажем, что векторы  компланарны. Векторы
компланарны. Векторы  при откладывании от одной точки определяют некоторую плоскость. Согласно правилу параллелограмма и равенству (5) вектор
при откладывании от одной точки определяют некоторую плоскость. Согласно правилу параллелограмма и равенству (5) вектор  принадлежит той же плоскости, откуда следует, что векторы
принадлежит той же плоскости, откуда следует, что векторы 
 и
и  а значит, и векторы
а значит, и векторы  компланарны. Теорема доказана.
компланарны. Теорема доказана.
Отложим от произвольной точки  пространства векторы
пространства векторы 
 где
где  — три данных некомпланарных вектора, и рассмотрим параллелепипед
— три данных некомпланарных вектора, и рассмотрим параллелепипед  построенный на векторах
построенный на векторах  (рис. 9). Тогда сумму векторов
(рис. 9). Тогда сумму векторов  можно найти следующим образом:
можно найти следующим образом: 
 Это правило сложения трёх некомпланарных векторов называется правилом параллелепипеда.
Это правило сложения трёх некомпланарных векторов называется правилом параллелепипеда.
Если векторы  не являются компланарными и для вектора
не являются компланарными и для вектора  имеет место равенство
имеет место равенство  где
где  — некоторые действительные числа, то говорят, что вектор
— некоторые действительные числа, то говорят, что вектор  разложен по трём некомпланарным векторам
разложен по трём некомпланарным векторам
 а числа
а числа  называются коэффициентами разложения.
называются коэффициентами разложения.
Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.
Теорема 5. Любой вектор  пространства можно разложить по трём данным некомпланарным векторам
пространства можно разложить по трём данным некомпланарным векторам  причём коэффициенты разложения определятся единственным образом. Доказательство. 1. Если векторы
причём коэффициенты разложения определятся единственным образом. Доказательство. 1. Если векторы  и
и  коллинеарны, то
коллинеарны, то 
 и теорема доказана.
и теорема доказана.
2. Пусть векторы  и
и  не коллинеарны. Отложим от произвольной точки
не коллинеарны. Отложим от произвольной точки  пространства векторы
пространства векторы 
 (рис. 10). Проведём через точку
(рис. 10). Проведём через точку  прямую
прямую  до пересечения с плоскостью
до пересечения с плоскостью  в точке
в точке  Через точку
Через точку  в плоскости
в плоскости  проведём прямую
проведём прямую  до пересечения с прямой
до пересечения с прямой  в точке
в точке  (в частности, если
(в частности, если  то точка
то точка  совпадает с точкой
совпадает с точкой  Согласно правилу многоугольника
Согласно правилу многоугольника  но векторы
но векторы 
 по построению коллинеарны, поэтому в силу леммы о коллинеарных векторах
по построению коллинеарны, поэтому в силу леммы о коллинеарных векторах 
 где
где  — некоторые действительные числа Таким образом, учитывая, что
— некоторые действительные числа Таким образом, учитывая, что  приходим к равенству
приходим к равенству 

3. Докажем теперь, что разложение вектора  по данным векторам
по данным векторам  единственно. Допустим, что это не так, т.е. существует ещё одно разложение
единственно. Допустим, что это не так, т.е. существует ещё одно разложение  в котором хотя бы один коэффициент не равен соответствующему коэффициенту в полученном нами разложении. Пусть, например,
в котором хотя бы один коэффициент не равен соответствующему коэффициенту в полученном нами разложении. Пусть, например,  Вычтем последнее равенство из предпоследнего.
Вычтем последнее равенство из предпоследнего.
Тогда
отсюда
– т. е. векторы
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
по данным векторам
единственно. Теорема доказана.
Итак, любой вектор  пространства можно разложить по трём данным некомпланарным векторам
пространства можно разложить по трём данным некомпланарным векторам  причём единственным образом. Заданную тройку некомпланарных векторов
причём единственным образом. Заданную тройку некомпланарных векторов  называют базисом, сами векторы
называют базисом, сами векторы  — базисными векторами, а разложение вектора
— базисными векторами, а разложение вектора  по векторам
по векторам  называют разложением по данному базису
называют разложением по данному базису 
Координаты вектора
Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора  отложенных от некоторой точки
отложенных от некоторой точки  пространства, таких, что
пространства, таких, что  (например, их можно направить по рёбрам единичного куба). Эти векторы, очевидно, не являются компланарными. Поэтому, в силу теоремы 5, любой вектор
(например, их можно направить по рёбрам единичного куба). Эти векторы, очевидно, не являются компланарными. Поэтому, в силу теоремы 5, любой вектор  можно разложить_по векторам
можно разложить_по векторам  причём единственным образом:
причём единственным образом:  Введём прямоугольную систему координат с началом в точке
Введём прямоугольную систему координат с началом в точке  так, чтобы направления осей
так, чтобы направления осей  совпали_с направлениями векторов
совпали_с направлениями векторов  соответственно. Тогда векторы
соответственно. Тогда векторы  называются единичными векторами осей координат, а числа
называются единичными векторами осей координат, а числа  — координатами вектора
— координатами вектора  в системе координат
в системе координат  (обозначения:
(обозначения: 
Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:
- Два вектора равны в том и только том случае, если равны их координаты.
- Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов
 получаем
получаем 
- При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора
 и действительного числа
и действительного числа  получаем
получаем 
Докажем, например, свойство 2. Так как 
 то, согласно свойствам сложения векторов и умножения вектора на число,
то, согласно свойствам сложения векторов и умножения вектора на число,  т. е. вектор
т. е. вектор  имеет координаты
имеет координаты  что и требовалось доказать. Остальные свойства доказываются аналогично.
что и требовалось доказать. Остальные свойства доказываются аналогично.
Скалярное произведение векторов и его свойства
Определение скалярного произведения векторов  и
и  в пространстве ничем не отличается от аналогичного определения для векторов на плоскости.
в пространстве ничем не отличается от аналогичного определения для векторов на плоскости.
Определение 11. Скалярным произведением векторов  называется произведение длин этих векторов на косинус угла между ними (обозначение:
называется произведение длин этих векторов на косинус угла между ними (обозначение:  Таким образом, по определению,
Таким образом, по определению,

Теорема 8. Два ненулевых вектора  взаимно перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, т. е.
взаимно перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, т. е.

Доказательство этой теоремы вытекает из формулы (9).
Определение 12. Скалярным квадратом вектора  называется скалярное произведение
называется скалярное произведение  Скалярный квадрат обозначается
Скалярный квадрат обозначается  т.е. по определению
т.е. по определению 
Так как  то
то

Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.
Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись: 
Если векторы  и
и  заданы своими координатами:
заданы своими координатами: 
 то скалярное произведение может быть выражено через их координаты.
то скалярное произведение может быть выражено через их координаты.
Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.

Доказательство. Отложим от произвольной точки  пространства векторы
пространства векторы  При этом, как мы знаем, соответствующие координаты векторов
При этом, как мы знаем, соответствующие координаты векторов  и
и  а также
а также  и
и  будут равны, а угол
будут равны, а угол  По теореме косинусов для треугольника
По теореме косинусов для треугольника  получим
получим

итак как  имеем
имеем 
 откуда
откуда  Но
Но

поэтому

Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.
Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.
Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.
Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.
Примеры с решением
Задача 1.
Основанием четырёхугольной пирамиды  является параллелограмм
является параллелограмм  Точки
Точки  и
и  — середины рёбер
— середины рёбер  и
и  соответственно. Найдите разложение векторов
соответственно. Найдите разложение векторов  по векторам
по векторам 
Решение (см. рис. 14).
1.  но
но  поэтому
поэтому 
2. Так как  — середина
— середина  но
но 
 (см. следствие 1 теоремы 3), поэтому
(см. следствие 1 теоремы 3), поэтому 

Ответ: 
Заметим, что в разложении вектора  по векторам
по векторам  коэффициент разложения при векторе
коэффициент разложения при векторе  равен нулю, а это означает, в силу теоремы 4, что векторы
равен нулю, а это означает, в силу теоремы 4, что векторы  компланарны. Если заранее «увидеть», что
компланарны. Если заранее «увидеть», что  где
где  — середина
— середина  (отсюда
(отсюда  то разложение вектора
то разложение вектора  можно было бы найти проще. Но векторный метод тем и хорош, что, даже не обладая развитым пространственным воображением, а лишь зная основные определения и теоремы, можно получить правильный ответ (пусть и не всегда самым оптимальным путём)!
можно было бы найти проще. Но векторный метод тем и хорош, что, даже не обладая развитым пространственным воображением, а лишь зная основные определения и теоремы, можно получить правильный ответ (пусть и не всегда самым оптимальным путём)!
Задача 2.
Пусть  — точка пересечения медиан треугольника
— точка пересечения медиан треугольника  — произвольная точка пространства. Найдите разложение вектора
— произвольная точка пространства. Найдите разложение вектора  по векторам
по векторам 
Решение (см. рис. 15). Пусть  — середина ребра
— середина ребра  Так как
Так как  — точка пересечения медиан треугольника
— точка пересечения медиан треугольника  точки
точки  принадлежат одной прямой, причём, в силу теоремы о точке пересечения медиан треугольника,
принадлежат одной прямой, причём, в силу теоремы о точке пересечения медиан треугольника,  Согласно следствию I теоремы 3
Согласно следствию I теоремы 3  Тогда
Тогда 

Ответ: 
Векторы и их решение
Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка.
Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого.
Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора  называется абсолютной величиной или модулем вектора и обозначается
называется абсолютной величиной или модулем вектора и обозначается 
Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом.
Чтобы найти сумму двух векторов  и
и  совместим начало вектора
совместим начало вектора  с концом вектора
с концом вектора  .
.
Суммой  векторов
векторов  и
и  называется вектор, начало которого сходится с началом вектора
называется вектор, начало которого сходится с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  (рис. 1.1).
(рис. 1.1).
 Правило треугольника
Правило треугольника
 Правило параллелограмма
Правило параллелограмма

Для складывания векторов имеют место такие законы:
1) переставной (коммутативный)

2) связующий

3) для каждого вектора  существует противоположный
существует противоположный  такой, что
такой, что

4)
5) для некоторых двух векторов  и
и  выполняются неравенства:
выполняются неравенства:

Если вектор  образует угол
образует угол  с осью
с осью  (рис. 1.2), то проекцию вектора
(рис. 1.2), то проекцию вектора  на ость называется величина
на ость называется величина

Пусть вектор имеет начало в точке  а конец – в точке
а конец – в точке  Тогда величины
Тогда величины 
 являются проекциями вектора
являются проекциями вектора  на оси
на оси  Проекции вектора однозначно определяют вектор. Потому имеет место равенство
Проекции вектора однозначно определяют вектор. Потому имеет место равенство

Если вектор  то проекция суммы векторов
то проекция суммы векторов

Произведением вектора  на число
на число  называется вектор
называется вектор  длина которого равна
длина которого равна  Умножение вектора на число имеет свойство ассоциативности и дистрибутивности, то есть для произвольных чисел
Умножение вектора на число имеет свойство ассоциативности и дистрибутивности, то есть для произвольных чисел  и векторов
и векторов  и
и  справедливы равенства:
справедливы равенства:

Любой вектор  можно записать в виде
можно записать в виде
где  – единичные векторы,
– единичные векторы, 
 называются компонентами вектора
называются компонентами вектора  (рис. 1.3) .
(рис. 1.3) .


Пример 1.73
Даны два вектора:  и
и 
Найти вектор 
Решение 
Признаком колинеарности двух векторов  и
и  является пропорциональность их координат:
является пропорциональность их координат:

Скалярным произведением двух векторов  и
и  называется число
называется число  которое равно произведению их модулей на косинус угла между ними:
которое равно произведению их модулей на косинус угла между ними:

Скалярное произведение можно записать в таком виде:

Если векторы  и
и  заданы своими координатами, то их скалярное произведение вычисляется по формуле:
заданы своими координатами, то их скалярное произведение вычисляется по формуле:

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами  и
и  :
:

Отсюда получается условие перпендикулярности двух векторов: если  и
и  или в координатной форме:
или в координатной форме:

Среди свойств скалярного произведения отметим так:

Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  который имеет такие свойства:
который имеет такие свойства:
1) длина вектора  равна произведению длин сомножителей на синус угла между ними:
равна произведению длин сомножителей на синус угла между ними: 
2) вектор  перпендикулярный к векторам
перпендикулярный к векторам  и
и 
3) из конца вектора  кратчайший поворот от
кратчайший поворот от  к
к  является таким, что происходит против часовой стрелки (рис. 1.4).
является таким, что происходит против часовой стрелки (рис. 1.4).

Заметим, что  а модуль векторного произведения равен плоскости параллелограмма, построенного на векторах
а модуль векторного произведения равен плоскости параллелограмма, построенного на векторах  и
и  , если у них общее начало.
, если у них общее начало.
В координатной форме векторное произведение векторов  и
и  можно записать в виде:
можно записать в виде:

Смешанным или скалярно – векторным произведением трех векторов  называется векторное произведение векторов
называется векторное произведение векторов  и
и  , скалярно умноженный на вектор
, скалярно умноженный на вектор  то есть
то есть 
Если векторы  – компланарны, то есть расположены в одной плоскости или на параллельных плоскостях, то их смешанное произведение равно нулю.
– компланарны, то есть расположены в одной плоскости или на параллельных плоскостях, то их смешанное произведение равно нулю.
Если известные координаты сомножителей 
 то смешанное произведение вычисляется по формуле:
то смешанное произведение вычисляется по формуле:

Если три ненулевых  разложены в одной плоскости (компланарны), то из смешанное произведение
разложены в одной плоскости (компланарны), то из смешанное произведение 
Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид:

Решение примеров:
Пример 1.74
Заданы координатами точек 
 и
и  Найти:
Найти:
1) вектор  если
если 
2) угол между векторами  и
и 
3) координаты вектора 
4) объем пирамиды с вершинами в точках 
Решение
1) По формуле (1.14) находим

тогда 
2) Косинус угла между векторами  и
и  вычислим по формуле (1.20):
вычислим по формуле (1.20):

Поскольку косинус угла отрицательный, то угол  тупой.
тупой.
3) Координаты векторного произведения находим по формуле (1.22):


4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды:

Тогда объем пирамиды

Собственные числа и собственные векторы
Вектор – столбец  называется собственным вектором квадратной матрицы
называется собственным вектором квадратной матрицы 
 – ого порядка, что соответствует собственному значению
– ого порядка, что соответствует собственному значению  если он удовлетворяют матричному уравнению
если он удовлетворяют матричному уравнению  или
или 

Тут  – единичная матрица
– единичная матрица  – ого порядка, а
– ого порядка, а  – нулевой вектор – столбец. При условии, что
– нулевой вектор – столбец. При условии, что  получим характеристическое уравнение для определения собственных значений
получим характеристическое уравнение для определения собственных значений 

Координаты собственного вектора  что соответствуют собственному значению
что соответствуют собственному значению  является решением системы уравнений:
является решением системы уравнений:

Собственный вектор обозначаются с точностью к постоянному множителю.
Решение примеров:
Пример 1.90.
Обозначить собственные определения и собственные векторы матрицы

Решение. Характеристические уравнения данной матрицы имеет вид (1.24):
 или
или 
отсюда получается, что матрица  имеет два собственных значения
имеет два собственных значения  и
и  Собственный вектор
Собственный вектор  что соответствует
что соответствует  обозначаются с системой уравнений вида (1.25)
обозначаются с системой уравнений вида (1.25)
 или
или 
которое приводится к одному уравнению 
Возьмем  получим решение в виде
получим решение в виде 
Следует, первый собственный вектор является

Второй вектор  что соответствует собственному значению
что соответствует собственному значению  определяется из системы уравнений вида (1.25)
определяется из системы уравнений вида (1.25)

Эта система уравнений так же приводится к одному уравнению  положив
положив  запишем ее решение в виде
запишем ее решение в виде  Следует, второй собственный вектор:
Следует, второй собственный вектор:

Таким образом, матрица  имеет два разных определения
имеет два разных определения  и
и  и два собственных вектора, равных
и два собственных вектора, равных  и
и  (с точностью к постоянному множителю).
(с точностью к постоянному множителю).
Пример 1.91
Найти собственные векторы и собственные значения матрицы

Решение. Характеристическое уравнение

Раскрыв определитель получим:

Корень  – кратный, показатель кратности
– кратный, показатель кратности  корень
корень  – простой,
– простой, 
Система уравнений для определения собственных векторов имеет вид:

Последовательно подставим  и
и  в записанную систему:
в записанную систему:


Фундаментальная система уравнений получается, если свободным переменным  последовательно дать значения
последовательно дать значения 

Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению  имеет вид:
имеет вид:



Фундаментальная система решений получается, если взять 

Векторная алгебра
Понятие «вектор» (от лат. vector – носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем  -мерных векторов: они предполагают геометрическую интерпретацию, потому что принадлежат к векторным линейных пространств размерности
-мерных векторов: они предполагают геометрическую интерпретацию, потому что принадлежат к векторным линейных пространств размерности 
Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия – математическая наука, объектом изучения которой являются геометрические фигуры, а предметом – установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.
Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) – французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.
После изучения данной темы вы сможете:
● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.
Векторы: основные определения, линейные операции
Выберем на произвольной прямой (в  или в
или в  ) отрезок
) отрезок  и укажем, которую из точек
и укажем, которую из точек  или
или  считать начальной (началом отрезка), а какую – конечной (концом отрезка). Конец отрезка обозначают стрелке и говорят, что на отрезке задано направление. Отрезок
считать начальной (началом отрезка), а какую – конечной (концом отрезка). Конец отрезка обозначают стрелке и говорят, что на отрезке задано направление. Отрезок  с заданным на нем направлением, или коротко – направленный отрезок, называется вектором. Вектор обозначается символом
с заданным на нем направлением, или коротко – направленный отрезок, называется вектором. Вектор обозначается символом  или строчными буквами латинского
или строчными буквами латинского
алфавита с чертой:  и др. (Рис. 6.1).
и др. (Рис. 6.1).

Рис. 6.1
В применимых задачах естественных наук существенным является обстоятельство – где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.
Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы
Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов: 
Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).
Единичным вектором  называется вектор, длина которого равна единице.
называется вектор, длина которого равна единице.
Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.
Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору  , обозначают символом
, обозначают символом  .
.
Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.
Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.
Линейные операции над векторами
Будем считать, что векторы  принадлежат одни плоскости. Осуществляя параллельный перенос одного из векторов
принадлежат одни плоскости. Осуществляя параллельный перенос одного из векторов  , совместим начало вектора
, совместим начало вектора  с концом вектора
с концом вектора  (или наоборот) и по отрезками, соответствующие векторам, как по двум сторонам, построим треугольник (рис. 6.2 а).
(или наоборот) и по отрезками, соответствующие векторам, как по двум сторонам, построим треугольник (рис. 6.2 а).
1. Суммой векторов  называется вектор
называется вектор  , который определяется третьей стороной треугольника, с началом в начале вектора
, который определяется третьей стороной треугольника, с началом в начале вектора  . Порядок построения суммы двух векторов по этому определению называют правилом треугольника.
. Порядок построения суммы двух векторов по этому определению называют правилом треугольника.
Параллельный перенос можно осуществить и так, что объединятся начала векторов  и
и  , тогда на векторах как на сторонах построим параллелограмм (рис. 6.2 б), и придем к известному из школьного курса алгебры правилу параллелограмма.
, тогда на векторах как на сторонах построим параллелограмм (рис. 6.2 б), и придем к известному из школьного курса алгебры правилу параллелограмма.

Рис. 6.2
Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):


Рис. 6.3
Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:

2) соединительная, или ассоциативная:

3) 
4) 
Разницу  можно рассматривать как сумму вектора
можно рассматривать как сумму вектора  с вектором, противоположным вектору
с вектором, противоположным вектору 

Умножения вектора на скаляр
Пусть  – некоторое действительное число
– некоторое действительное число  . Произведением вектора
. Произведением вектора  со скаляром
со скаляром  называется вектор
называется вектор  , модуль которого равен произведению модулей
, модуль которого равен произведению модулей  , а направление
, а направление  совпадает с направлением
совпадает с направлением  , если
, если  , или противоположно направлению
, или противоположно направлению  , если
, если  (рис. 6.4):
(рис. 6.4):


Рис. 6.4
При вектор
вектор  превращается в ноль-вектор
превращается в ноль-вектор  .
.
Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:
 где
где 
2) соединительный, или ассоциативный закон:
 где
где 
3) распределительный или дистрибутивный закон:
 где
где 
4) 
5) 
Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора  и
и  коллинеарны тогда и только тогда, когда каждый из них является произведением другого из скаляром:
коллинеарны тогда и только тогда, когда каждый из них является произведением другого из скаляром:

Известно, что три ненулевые векторы  и
и  компланарны тогда и только тогда, когда один из них является линейной комбинацией двух других:
компланарны тогда и только тогда, когда один из них является линейной комбинацией двух других:
 компланарны
компланарны 
Рассмотрим понятие, имеет очень важное значение в теории векторов – проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление – отрицательным).
Компонентой вектора  относительно оси
относительно оси  называют вектор, начало которого является проекцией начала вектора
называют вектор, начало которого является проекцией начала вектора  на ось
на ось  , а конец – проекцией конца вектора
, а конец – проекцией конца вектора  на ось
на ось  (рис. 6.5).
(рис. 6.5).

Рис. 6.5
Проекцией вектора  на ось
на ось  называют скаляр, равный длине компоненты вектора
называют скаляр, равный длине компоненты вектора  относительно оси
относительно оси  со знаком
со знаком  , если направление компоненты совпадает с направлением оси
, если направление компоненты совпадает с направлением оси  , или со знаком
, или со знаком  , если ее направление противоположно направлению оси:
, если ее направление противоположно направлению оси:

Основные свойства проекции вектора на ось
1. Проекция вектора на ось  равна произведению длины вектора
равна произведению длины вектора  с косинусом угла между вектором и осью:
с косинусом угла между вектором и осью:

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:

Это свойство обобщается на любое конечное число векторов.
3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:

Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
Пусть в трехмерном векторном пространстве  задана прямоугольная декартова система координат
задана прямоугольная декартова система координат  , что определяется тремя взаимно перпендикулярными числовыми осями – осями, на которых указано масштаб (единицу длины) – с общей точкой
, что определяется тремя взаимно перпендикулярными числовыми осями – осями, на которых указано масштаб (единицу длины) – с общей точкой  – началом координат (рис. 6.6).
– началом координат (рис. 6.6).

Рис. 6.6
Выберем в пространстве произвольную точку  и соединим ее отрезком прямой с началом координат
и соединим ее отрезком прямой с началом координат  . Вектор
. Вектор  , началом которого является начало координат
, началом которого является начало координат  , а концом данная точка
, а концом данная точка  , называется радиусом-вектором точки
, называется радиусом-вектором точки  . Отметим, что радиусы-векторы точек пространства являются связанными векторами.
. Отметим, что радиусы-векторы точек пространства являются связанными векторами.
Под декартовыми прямоугольными координатами точки  понимают проекции ее радиус-вектора
понимают проекции ее радиус-вектора  на оси
на оси 

Точка  с координатами
с координатами  обозначается через
обозначается через  . Вектор
. Вектор  каждой точки пространства (кроме точки
каждой точки пространства (кроме точки  ) определяет прямоугольный параллелепипед с диагональю, что является отрезком, на котором построено вектор
) определяет прямоугольный параллелепипед с диагональю, что является отрезком, на котором построено вектор  (рис. 6.6).
(рис. 6.6).
Измерениями параллелепипеда есть модули координат точки  . Длина диагонали параллелепипеда определяется по формуле:
. Длина диагонали параллелепипеда определяется по формуле:

Углы  , которые образованы радиусом-вектором
, которые образованы радиусом-вектором  с координатными осями
с координатными осями  называются его направляющими углами.
называются его направляющими углами.

откуда:

Косинусы направляющих углов называются направляющими косинусами радиус-вектора  . С (6.4) получаем свойства:
. С (6.4) получаем свойства:
1) направляющие косинусы являются координатами единичного радиус-вектора: 
2) сумма квадратов направляющих косинусов вектора  равна единице:
равна единице: 
Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало  , дает радиус вектор определенной точки.
, дает радиус вектор определенной точки.
Координатами любого вектора  в пространстве называются его проекции на оси координат. Они обозначаются символами
в пространстве называются его проекции на оси координат. Они обозначаются символами  и пишут:
и пишут:  или
или  , где согласно определению координат:
, где согласно определению координат:

Задача вектора тройкой его координат  , называют координатной формой задачи.
, называют координатной формой задачи.
Для единичных векторов  , расположенных соответственно на осям
, расположенных соответственно на осям  , имеем:
, имеем:

Длина произвольного вектора  и его направляющие косинусы вычисляются по формулам:
и его направляющие косинусы вычисляются по формулам:

Найти длину и направляющие косинусы вектора 

По формулам (6.5) имеем:

Установим связь между координатами вектора – числами – и его компонентами – векторами – с помощью единичных векторов  (рис. 6.7).
(рис. 6.7).

Рис. 6.7
Компонентами вектора  относительно координатных осей являются векторы
относительно координатных осей являются векторы 
 (рис. 6.7). Согласно операции сложения векторов по правилу многоугольника получаем:
(рис. 6.7). Согласно операции сложения векторов по правилу многоугольника получаем:

Следовательно, любой вектор  в трехмерном пространстве является суммой трех его компонент относительно координатных осей:
в трехмерном пространстве является суммой трех его компонент относительно координатных осей:

Изображение вектора с  в виде суммы произведений координат с единичными векторами (ортами) называют алгебраической формой задания вектора.
в виде суммы произведений координат с единичными векторами (ортами) называют алгебраической формой задания вектора.
Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с  :
:  и
и  , их соответствующие по номеру координаты прилагаются (вычитаются):
, их соответствующие по номеру координаты прилагаются (вычитаются):

Действительно, по свойствам ассоциативности и дистрибутивности имеем:

2. При умножении вектора  на скаляр
на скаляр  все его координаты умножаются на этот скаляр:
все его координаты умножаются на этот скаляр:

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:

Скалярное, векторное, смешанное произведения векторов
Скалярным произведением двух векторов  и
и  называется число (скаляр), равное произведению их модулей с косинус угла между ними
называется число (скаляр), равное произведению их модулей с косинус угла между ними  и обозначается
и обозначается  :
:

Вместо  часто пишут
часто пишут  или используют обозначения
или используют обозначения  . Название этой операции согласуется с ее сути, а именно: скалярное произведение является скаляром, то есть числом.
. Название этой операции согласуется с ее сути, а именно: скалярное произведение является скаляром, то есть числом.
Для определения угла  между векторами
между векторами  и
и  совмещают их начала и рассматривают угол между двумя лучами
совмещают их начала и рассматривают угол между двумя лучами  и
и  (рис. 6.8). Если угол
(рис. 6.8). Если угол  острый, то
острый, то  , если тупой, то
, если тупой, то  .
.
Основные свойства скалярного произведения векторов вытекают из его определения (6.7).
1. Скалярное произведение  ненулевых векторов равно нулю тогда и только тогда, когда векторы взаимно перпендикулярны (ортогональные):
ненулевых векторов равно нулю тогда и только тогда, когда векторы взаимно перпендикулярны (ортогональные):

2. Скалярный квадрат вектора равен квадрату его модуля, то есть

3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:


4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:

Доказательство этого свойства основывается на определении (6.3).
Скалярное произведение векторов  и
и  , заданных в координатной форме. Пусть имеем два вектора
, заданных в координатной форме. Пусть имеем два вектора 
1. Вычислим скалярные произведения единичных векторов  По свойству
По свойству  Для других пар на основании свойства 1 имеем:
Для других пар на основании свойства 1 имеем: 
2. Находим произведение  , подавая векторы в алгебраической форме (6.6) и используя распределительный закон:
, подавая векторы в алгебраической форме (6.6) и используя распределительный закон:

Раскрываем скобки и получаем:

Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения  -мерных векторов.
-мерных векторов.
Как следствие из (6.12) при  получаем формулу (6.5) модуля вектора через его координаты:
получаем формулу (6.5) модуля вектора через его координаты:

Определим угол между двумя ненулевыми векторами  и
и  , заданные в координатной форме. Воспользуемся определением скалярного произведения (6.7) и соотношения (6.5). В результате получаем:
, заданные в координатной форме. Воспользуемся определением скалярного произведения (6.7) и соотношения (6.5). В результате получаем:

Следовательно, косинус угла между двумя векторами определяется формулой:

Отсюда 
В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме:

Критерием коллинеарности векторов  и
и  , заданных в координатной форме является пропорциональность их координат:
, заданных в координатной форме является пропорциональность их координат:

Векторное произведение двух векторов
Пусть  и
и  – векторы пространства
– векторы пространства 
 , определяющие некоторую плоскость
, определяющие некоторую плоскость  . Вектор
. Вектор  называется векторным произведением векторов
называется векторным произведением векторов  и
и  , если вектор
, если вектор  удовлетворяет условиям:
удовлетворяет условиям:
1) модуль его численно равен площади параллелограмма, построенного на векторах  и
и  как на сторонах;
как на сторонах;
2) он перпендикулярный плоскости параллелограмма  и направленный так, что поворот вектора
и направленный так, что поворот вектора  до совмещения с вектором
до совмещения с вектором  кратчайшим путем наблюдается с конца вектора
кратчайшим путем наблюдается с конца вектора  против часовой стрелки (рис. 6.9).
против часовой стрелки (рис. 6.9).

Рис. 6.9
Векторное произведение обозначается символами:  , или
, или 
Следовательно,

где  наименьший из углов
наименьший из углов  что соответствует совмещению
что соответствует совмещению  с
с  поворотом вектора
поворотом вектора  против часовой стрелки.
против часовой стрелки.
Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы  и
и  коллинеарны:
коллинеарны:

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.
2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:

Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.
3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:

где 
Векторное произведение векторов  и
и  , заданных в координатной форме. Пусть имеем два ненулевые векторы:
, заданных в координатной форме. Пусть имеем два ненулевые векторы: 
1. Определяем векторные произведения ортов  (рис. 6.10).
(рис. 6.10).
Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:

Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:


Рис. 6.10
Рассмотрим, например, произведение  . Совмещение
. Совмещение  с
с  кратчайшим путем (указано дугой со стрелкой на рис. 6.10) происходит против часовой стрелки, если смотреть с конца вектора
кратчайшим путем (указано дугой со стрелкой на рис. 6.10) происходит против часовой стрелки, если смотреть с конца вектора  , следовательно,
, следовательно,  . Тогда по свойству
. Тогда по свойству 
2. Находим произведение  , подавая векторы в алгебраической форме и используя арифметические свойства (6.18) и соотношения (6.19):
, подавая векторы в алгебраической форме и используя арифметические свойства (6.18) и соотношения (6.19):

Множители при  это вскрытые определители 2-го порядка, поэтому
это вскрытые определители 2-го порядка, поэтому 
Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора  как векторного произведения векторов
как векторного произведения векторов  и
и  .
.
Если символы  в соотношении (6.20) считать элементами первой строки определителя 3-го порядка, то окончательно получим представление
в соотношении (6.20) считать элементами первой строки определителя 3-го порядка, то окончательно получим представление  в виде определителя:
в виде определителя:

Найдем векторное произведение векторов  и
и 

Модуль векторного произведения  определяет площадь параллелограмма, построенного на векторах
определяет площадь параллелограмма, построенного на векторах  и
и 
Смешанным произведением трех векторов  и
и  называется векторное произведение двух из них, умножен скалярно на третий вектор, то есть
называется векторное произведение двух из них, умножен скалярно на третий вектор, то есть  и т. д.
и т. д.
Смешанное произведение можно обозначать тройкой векторов  , в которой первые два элемента считают связанными векторным произведением, а результат векторного произведения умножают на третий вектор скалярно, то есть
, в которой первые два элемента считают связанными векторным произведением, а результат векторного произведения умножают на третий вектор скалярно, то есть  – это все равно, что
– это все равно, что  . Понятно, что результатом смешанного произведения является скаляр, поскольку векторное произведение
. Понятно, что результатом смешанного произведения является скаляр, поскольку векторное произведение  является вектором (обозначим его через
является вектором (обозначим его через  ), а произведение
), а произведение  дает скаляр.
дает скаляр.
Геометрическая интерпретация смешанного произведения. Пусть  и
и  – некомпланарные векторы. Построим на этих векторах как на ребрах параллелепипед (рис. 6.11).
– некомпланарные векторы. Построим на этих векторах как на ребрах параллелепипед (рис. 6.11).

Рис. 6.11
Вектор  по длине численно равна площади параллелограмма, построенного на векторах
по длине численно равна площади параллелограмма, построенного на векторах  и
и  как на сторонах. Этот параллелограмм является основой параллелепипеда, построенного на векторах
как на сторонах. Этот параллелограмм является основой параллелепипеда, построенного на векторах  и
и  . Вектор
. Вектор  является перпендикулярным плоскости параллелограмма.
является перпендикулярным плоскости параллелограмма.
Согласно (6.11) скалярное произведение  можно представить как произведение модуля
можно представить как произведение модуля  и проекции вектора
и проекции вектора  на ось, определяется вектором
на ось, определяется вектором  :
:

где  , причем
, причем  является положительным числом, если угол между векторами
является положительным числом, если угол между векторами  и
и  острый, и отрицательным, если этот угол тупой. По модулю эта проекция равна высоте параллелепипеда
острый, и отрицательным, если этот угол тупой. По модулю эта проекция равна высоте параллелепипеда  .
.
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда  , построенного на векторах как на ребрах:
, построенного на векторах как на ребрах:

Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три – компланарны, и наоборот.
Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:
 компланарны
компланарны 
Свяжем с изображенными на плоскости векторами  круг (рис. 6.12). Перечисление векторов, начиная с любого, против часовой стрелки назовем положительным, или циклическим, перестановкой векторов, в противном случае – отрицательной перестановкой.
круг (рис. 6.12). Перечисление векторов, начиная с любого, против часовой стрелки назовем положительным, или циклическим, перестановкой векторов, в противном случае – отрицательной перестановкой.
2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:

Смешанное произведение векторов, заданных в координатной форме
Пусть имеем три ненулевые векторы  По определению смешанного произведения и представлением векторного и скалярного произведений в координатной форме имеем:
По определению смешанного произведения и представлением векторного и скалярного произведений в координатной форме имеем:

Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:

Векторы  компланарны тогда и только тогда, когда определитель 3-го порядка, элементами строк которого являются координаты этих векторов равен нулю (свойство 1):
компланарны тогда и только тогда, когда определитель 3-го порядка, элементами строк которого являются координаты этих векторов равен нулю (свойство 1):
 компланарны
компланарны 
С помощью смешанного произведения векторов легко определить, относятся ли четыре точки  одной плоскости. Для этого следует проверить выполнение условия компланарности трех векторов с общим началом в одной из точек.
одной плоскости. Для этого следует проверить выполнение условия компланарности трех векторов с общим началом в одной из точек.
Простейшие задачи аналитической геометрии
Задача об определении длины отрезка. Найти длину отрезка  , если известны координаты его концов:
, если известны координаты его концов:  . Эту задачу можно рассматривать как задачу о нахождении расстояния между двумя точками.
. Эту задачу можно рассматривать как задачу о нахождении расстояния между двумя точками.
1. Введем в рассмотрение вектор  с началом
с началом  и концом
и концом  и радиусы-векторы
и радиусы-векторы 
 (рис. 6.13).
(рис. 6.13).
2. Определим координаты вектора  как разности векторов
как разности векторов  и
и  :
: 
3. Находим модуль вектора  , который и равна длине отрезка
, который и равна длине отрезка  :
:

Задача об определении площади треугольника
Найдем площадь треугольника, заданного координатами вершин: 

По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник  , принадлежащей плоскости
, принадлежащей плоскости  :
:  и
и  .
.
1. Введем в рассмотрение векторы:

и найдем их векторное произведение 
По соотношению (6.20) имеем:

2. Вычислим модуль вектора  , численно равна площади параллелограмма
, численно равна площади параллелограмма  , построенного на векторах
, построенного на векторах  как на сторонах (рис. 6.14):
как на сторонах (рис. 6.14):

Тогда для площади треугольника  имеем:
имеем:

Знак  или
или  берется в зависимости от того, каким будет определитель – положительным или отрицательным.
берется в зависимости от того, каким будет определитель – положительным или отрицательным.
Если треугольник принадлежит не плоскости  , а любой другой плоскости в пространстве, то его площадь тоже можно найти по формуле:
, а любой другой плоскости в пространстве, то его площадь тоже можно найти по формуле:

Найдем площадь треугольника с вершинами 


Введем в рассмотрение векторы:  и
и 
 и определим их векторное произведение:
и определим их векторное произведение:

Тогда
 (кв. ед.)
(кв. ед.)
Задача о деление отрезка в заданном отношении
Пусть в пространстве заданы две точки  . Проведем через них произвольную прямую
. Проведем через них произвольную прямую  и установим на этой прямой положительное направление, согласно которому определим направление на отрезке
и установим на этой прямой положительное направление, согласно которому определим направление на отрезке  (рис. 6.15). На прямой
(рис. 6.15). На прямой  возьмем точку
возьмем точку  , которая может принадлежать отрезку
, которая может принадлежать отрезку  , или его продолжению. При этом, если точка
, или его продолжению. При этом, если точка  принадлежит отрезку
принадлежит отрезку  (рис. 6.15 а), говорится, что она осуществляет внутреннее деление отрезка на части, если не принадлежит (рис. 6.15 б) – то внешний.
(рис. 6.15 а), говорится, что она осуществляет внутреннее деление отрезка на части, если не принадлежит (рис. 6.15 б) – то внешний.

Рис. 6.15
Число  , которое определяется формулой
, которое определяется формулой

называется отношением, в котором точка  разделяет направленный отрезок
разделяет направленный отрезок  . Если
. Если  , то
, то  осуществляет внутреннее (внешнее) деление отрезка на части.
осуществляет внутреннее (внешнее) деление отрезка на части.
Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки  , что разделяет отрезок
, что разделяет отрезок  в отношении
в отношении  , если отрезок
, если отрезок  задан координатами начала
задан координатами начала  и конца –
и конца – 
Пусть точкам  соответствуют радиусы-векторы
соответствуют радиусы-векторы  (рис. 6.16). Из определения (6.29) следует, что векторы
(рис. 6.16). Из определения (6.29) следует, что векторы  и
и  коллинеарны, то есть
коллинеарны, то есть  . Следовательно,
. Следовательно, 
С этого векторного равенства найдем вектор 

или в координатах:

Отсюда, если отрезок разделить на две равные части точкой  то координаты точки
то координаты точки  могут быть найдены следующим образом:
могут быть найдены следующим образом:

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин  вычисляются по формулам:
вычисляются по формулам:



Лекции:
- Объем конуса
- Разложение на множители
- Деление многочлена на многочлен
- Правила дифференцирования
- Теорема Пифагора
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций
Знакомимся с вектором
Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
 Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве
Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
 Аналитическое представление вектора: данные можно перевести в числа
Аналитическое представление вектора: данные можно перевести в числа
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
 Математическое представление вектора: данные можно перевести в числа или график
Математическое представление вектора: данные можно перевести в числа или график
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
 Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат
Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
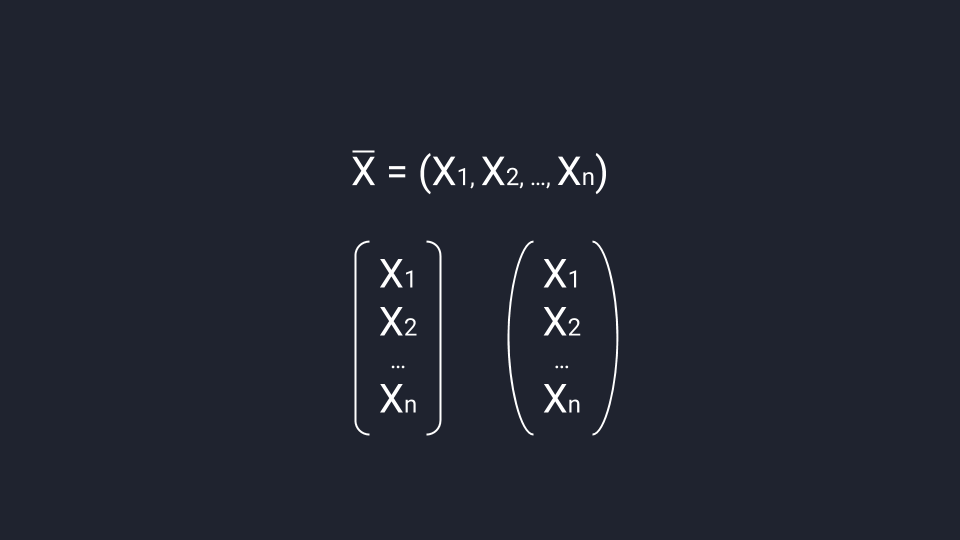 Способы записи вектора
Способы записи вектора
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
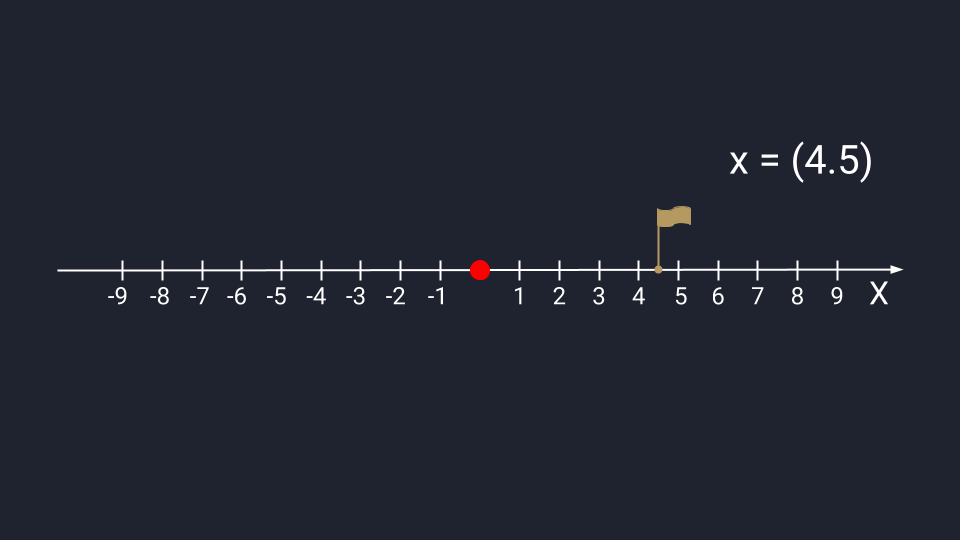 Графическое представление скаляра. Записывается в круглых скобках
Графическое представление скаляра. Записывается в круглых скобках
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
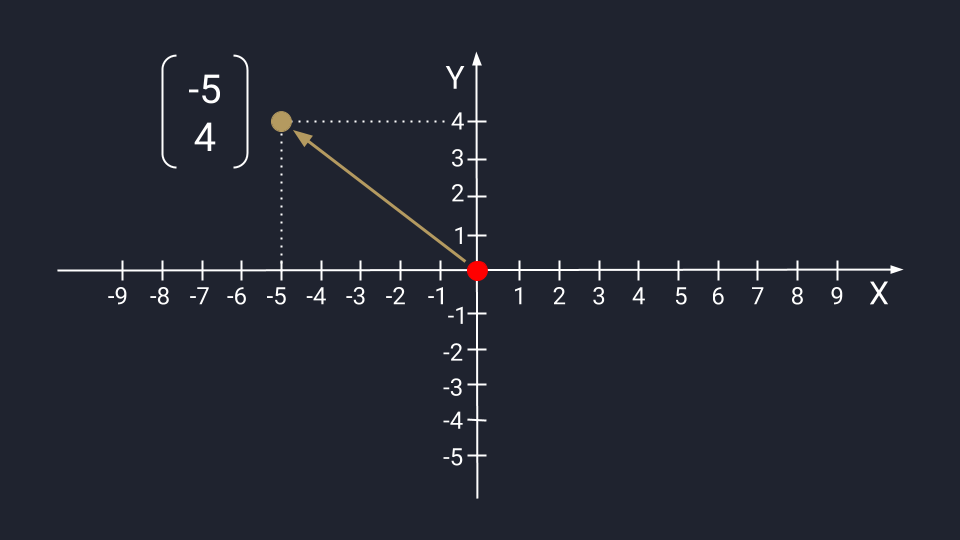 Графическое представление числового вектора в двух измерениях
Графическое представление числового вектора в двух измерениях
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
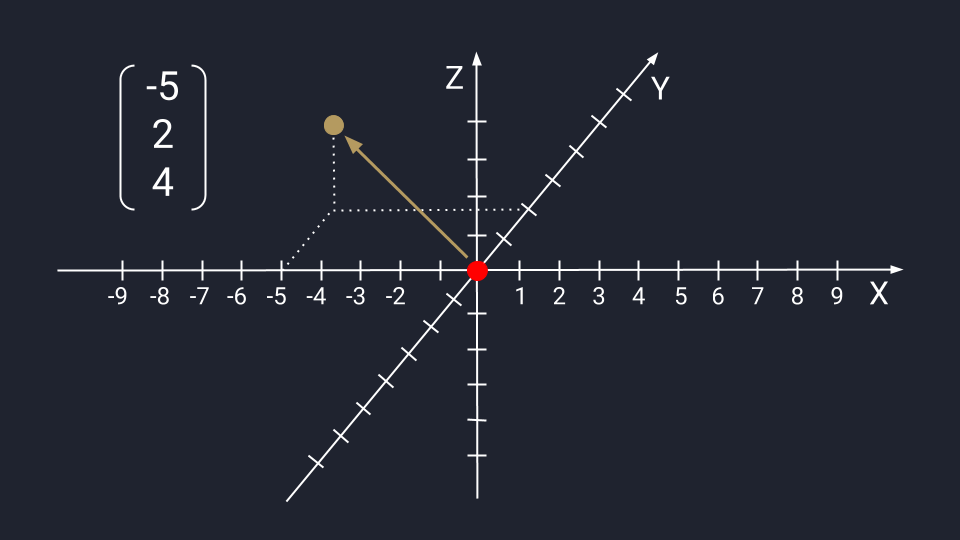 Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4
Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
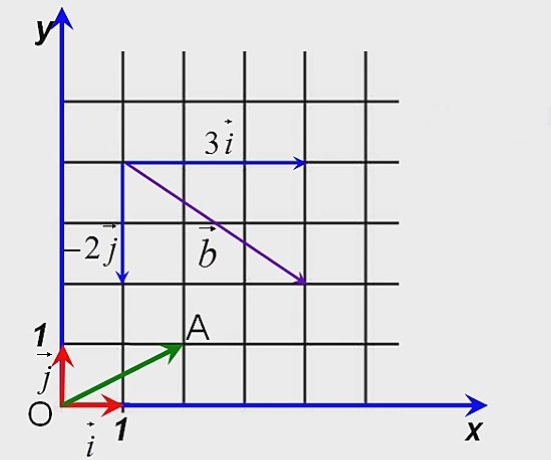
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; – 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
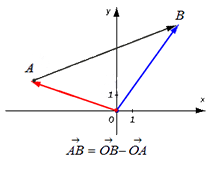
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → – O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → – O A → = x b – x a , y b – y a .
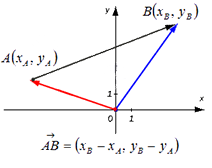
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , – 3 ) , B ( – 4 , – 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , – 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( – 4 – 2 , – 1 – ( – 3 ) ) = ( – 6 , 2 ) .
Ответ: O A → = ( 2 , – 3 ) , A B → = ( – 6 , – 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , – 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b – 3 , y b – 5 , z b – 7 ) .
По условию известно, что A B → = ( 2 , 0 , – 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b – 3 = 2 y b – 5 = 0 z b – 7 = – 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Большая теория по векторам
И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь ((L)).
А некоторые имеют и число, и направление — например, перемещение ((vec)).
И сейчас ты узнаешь, почему это настолько важно.
Векторы — коротко о главном
Решать задачи с векторами — легко!
Векторы и… Колумб
В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.
Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.
Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?
О направлении
Направление – одна из важнейших характеристик движения.
Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.
Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.
Так вот, «просто числа» — это скалярные величины (их также называют скалярами).
А «числа с направлением» — это векторные величины (их иногда называют векторы).
В физике существует множество скалярных и векторных величин.
Что такое скалярная величина?
Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)
Это, например, время, длина, масса, температура (продолжи сам!)
Что такое векторная величина?
Векторная величина – это величина, которая определяется и значением, и направлением.
В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.
Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):
![]()
Как обозначаются векторы?
Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: (vec)
Значение вектора – это модуль вектора, то есть его длина.
Обозначить это можно двумя способами: (left| <vec> right|) или (S)
Операции над векторами
Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.
Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!
Умножение вектора на число
Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.
(Если направление противоположно, обозначаем так: (vecuparrow downarrow vec))
Рассмотрим на примере, используя клетку для точности построений:
![]()
Если вектор умножить на ноль, он станет нулевым.
Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:
Рассмотрим некоторые свойства нулевого вектора.
Если он нулевой, то его длина равна нулю! Логично, не правда ли?
А это значит, что его начало совпадает с концом, это просто какая-то точка.
Нулевой вектор – вектор, начало которого совпадает с концом.
Нулевой вектор принято считать сонаправленным любому вектору.
Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:
А если к любому вектору прибавит нулевой, ничего не изменится:
Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.
![]()
Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.
Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.
![]()
Две прямые параллельны: (qparallel p)
Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:
Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:
Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:
(vecuparrow downarrow vec)
Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.
Параллельный перенос векторов
Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.
Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство – параллельный перенос.
![]()
Сложение векторов по правилу треугольника
Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:
![]()
Наша цель – найти такой вектор, который будет являться суммой двух данных:
Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:
![]()
Теперь достроим до треугольника.
Но как узнать направление нужного нам вектора?
Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:
![]()
Это называется правилом треугольника.
Больше двух слагаемых векторов. Сложение по правилу многоугольника
Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?
Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:
![]()
Это называется правилом многоугольника.
Вычитание векторов через сложение
Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:
Тогда нам лишь остается найти сумму с обратным вектором:
![]()
А сделать это очень легко по правилу треугольника:
![]()
Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.
Вычитание векторов через треугольник
Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.
Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:
![]()
![]()
Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.
Универсальное правило параллелограмма
Есть еще один способ сложения и вычитания векторов.
Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.
![]()
Ничего не напоминает?
Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.
В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:
![]()
Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:
![]()
Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.
![]()
Скалярное произведение векторов
Еще одной важной операцией является произведение векторов. Рассмотрим скалярное произведение. Его результатом является скаляр.
Уравнение очень простое: произведение длин этих векторов на косинус угла между ними.
![]()
Векторное произведение векторов
Векторное произведение векторов пригодится нам в электродинамике.
Его формула лишь немного отличается от предыдущей:
В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!
После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:
![]()
Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.
![]()
Об этом мы поговорим подробнее, когда будем изучать электродинамику.
Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.
Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.
Проекции векторов
Что такое проекция вектора и с чем ее едят?
Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.
Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.
Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.
Проекция вектора – словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.
Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.
Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.
Именно поэтому необходимо научиться работать с проекциями и осями.
Построение проекции. Определение знака
Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.
![]()
Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х0) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.
Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, – большое заблуждение.
Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:
![]()
Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.
В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:
Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:
![]()
Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:
![]()
Рассмотрим еще один интересный случай.
Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!
![]()
Анализ углов
Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!
Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось. Получим угол между вектором и осью.
Если угол острый, проекция положительна:
![]()
Если угол тупой, проекция отрицательна:
![]()
Обрати особое внимание на то, какой именно угол является углом между вектором и осью!
Частные случаи проекции
Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.
Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180 О ). Это зависит от направления.
При этом длина проекции совпадает с длиной вектора! Смотри!
Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:
![]()
Если вектор направлен в другую сторону, проекция отрицательна:
![]()
Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.
Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.
Что? Почему раньше не сказал? А… Ну…
Хватит вопросов! Вот тебе пример:
![]()
(vec) направлен противоположно оси. Его проекция отрицательна.
Еще один частный случай – работа с обратными векторами.
Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:
![]()
Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.
Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.
Прямоугольные треугольники равны по углу и гипотенузе. Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:
![]()
Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:
Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.
Проекции обратных векторов равны по модулю и противоположны по знаку.
Давайте еще раз уточним.
Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).
Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.
Проекция вектора бывает отрицательной. Это зависит от направления вектора.
Способы нахождения проекций и векторов с помощью тригонометрии
Зная угол между вектором и осью, можно не прибегать к координатам. Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.
Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.
Рассмотрим вектор и его проекции на оси:
![]()
Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:
![]()
Тогда обозначим прямой угол и угол между вектором и осью:
![]()
Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.
Из этих уравнений легко выражаются проекции.
А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:
Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.
Действия над проекциями векторов. Решение задач
Умение применять свои знания на практике невероятно важны. Это касается не только физики.
Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.
Сложение проекций. Доказательство главного свойства
Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:
![]()
Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:
![]()
Давай посчитаем проекции векторов и проекцию вектора их суммы:
![]()
Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!
Намного важнее уметь доказывать гипотезы в общем виде.
Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!
Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:
![]()
Затем запишем, чему равна сумма этих векторов.
![]()
![]()
![]()
Мы доказали нашу гипотезу.
Но что насчет разности?
Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!
Проекция суммы векторов равна сумме проекций векторов.
Проекция разности векторов равна разности проекций векторов.
Или можно записать так:
Простейшие задачи на нахождение проекций
Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.
Давай научимся с ними работать.
Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.
![]()
Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.
В первом случае вектор направлен против оси Х.
Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.
Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!
![]()
Рассмотрим второй вектор.
Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.
Убедимся в этом.
На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:
![]()
Рассмотрим (vec). Заметим, что он является обратным для (vec): их длины равны, а направления противоположны.
Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:
![]()
Поступаем с (vec) так же, как поступали с первым вектором.
Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.
Проведя перпендикуляры, считаем проекцию на ось Y:
![]()
С (vec) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:
![]()
Задачи на нахождение вектора и его угла с осью
С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.
Давай попробуем это сделать.
Даны проекции вектора на две оси. Для начала нарисуем оси:
![]()
Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.
С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?
![]()
Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.
Проекция на ось Y положительна. Вектор смотрит в ту же сторону, что и ось.
Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:
![]()
Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:
![]()
Обозначим угол (alpha ), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?
Рассмотрим смежный ему угол (beta ). Его найти гораздо проще, а в сумме они дадут 180 градусов.
Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла (beta ) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.
Вычитанием угла (beta ) из 180 градусов найдем угол (alpha ):
![]()
![]()
Главный метод работы с осями и проекциями в решении физических задач
В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.
Поэтому важно научиться искать проекции вектора и связывать их с ней.
Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):
![]()
Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.
Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.
Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.
Сделаем это для данного рисунка:
![]()
Мы видим, что остальные векторы расположены к осям под каким-то углом.
Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:
![]()
Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:
![]()
Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.
Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:
![]()
Переходим к векторам, которые расположены под углом.
Выглядит страшно, но это не так!
Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.
![]()
Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).
Обозначим, что является проекцией. Это катет:
![]()
Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.
Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.
Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…
Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:
![]()
Значит, проекцию на ось Х можно найти через косинус.
Не забываем смотреть на направления векторов!
Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.
![]()
Значит, проекцию на ось Х можно найти через косинус.
Не забываем смотреть на направления векторов!
Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.
Заключение
Итак, теперь мы знаем о векторах очень много! Мы выяснили, зачем они нужны и как с ними работать, а еще разобрали их роль в решении различных задач. Теперь векторы — наша прочная опора.
Именно из таких знаний складывается порой нечто более сложное и комплексное, что-то, что безусловно нам однажды поможет.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie_kordinat_vectora/
[/spoiler]
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами 
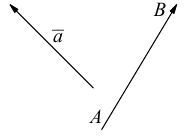
Длина отрезка, изображающего вектор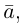 называется его длиной и обозначается через
называется его длиной и обозначается через 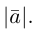 Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение
Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение 
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
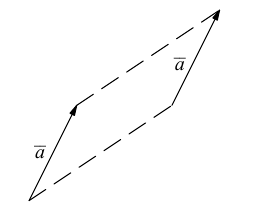
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора  называются коллинеарными (обозначение
называются коллинеарными (обозначение  ), если отрезки их изображающие параллельны.
), если отрезки их изображающие параллельны.
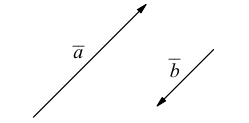
Аналогично, векторы а и b называются ортогональными (обозначение 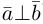 ), если соответствующие отрезки перпендикулярны.
), если соответствующие отрезки перпендикулярны.
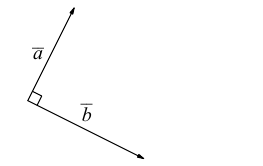
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 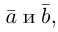 приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами
приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами 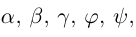 … или через
… или через 
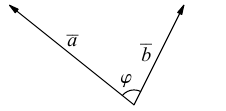
Два ненулевых вектора 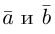 мы будем считать одинаково направленными, если
мы будем считать одинаково направленными, если 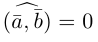 и противоположно направленными, если
и противоположно направленными, если 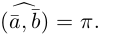
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 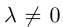 на вектор
на вектор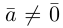 называется вектор
называется вектор 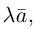 длина которого равна
длина которого равна 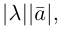 а направление его совпадает с направлением вектора
а направление его совпадает с направлением вектора 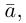 если
если 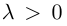 и имеет противоположное с ним направление, если
и имеет противоположное с ним направление, если 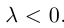 Если
Если  или
или 
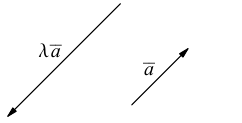
В частности, вектор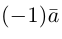 обозначается через
обозначается через 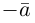 и называется вектором, противоположным вектору
и называется вектором, противоположным вектору 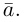
Если 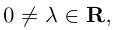 то произведение
то произведение 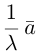 мы будем иногда записывать в виде
мы будем иногда записывать в виде 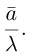
Из приведенного определения сразу же следует, что коллинеарные векторы  линейно связаны, т. е. существует константа
линейно связаны, т. е. существует константа 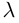 такая,что
такая,что 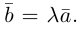 В качестве такой константы следует
В качестве такой константы следует
взять число 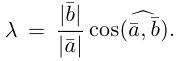 Если
Если 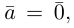 то
то 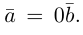 В частности, если
В частности, если 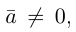 то вектором единичной длины с направлением данного вектора является вектор
то вектором единичной длины с направлением данного вектора является вектор 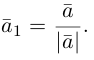
b) Сложение векторов.
Суммой двух векторов  называется вектор
называется вектор 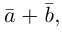 который находится по правилу треугольника
который находится по правилу треугольника
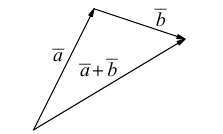
или по равносильному ему правилу параллелограмма
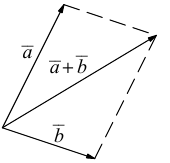
Вектор 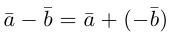 называется разностью векторов
называется разностью векторов 
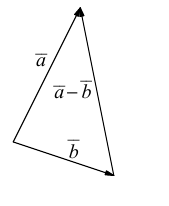
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 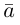 на вектор
на вектор 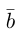 называется число
называется число
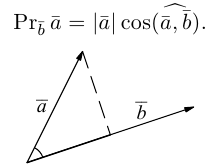
Геометрически очевидны следующие свойства проекции:
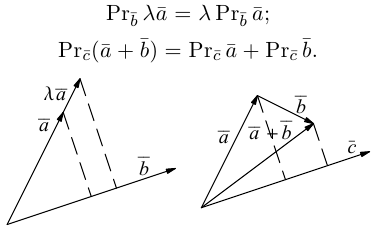
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
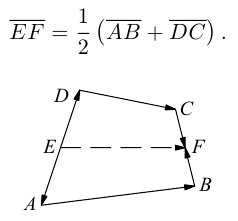
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
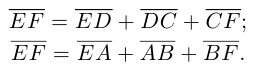
Сложив данные равенства и учитывая, что 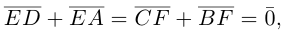 будем иметь:
будем иметь:
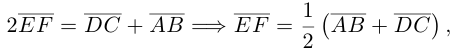
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 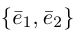 — базис на плоскости,
— базис на плоскости, 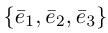 — базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора
— базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора 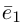 к вектору
к вектору 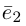 совершается против часовой стрелки, если наблюдение ведется со стороны вектора
совершается против часовой стрелки, если наблюдение ведется со стороны вектора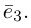 Сформулируем теперь фундаментальное свойство базиса.
Сформулируем теперь фундаментальное свойство базиса.
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 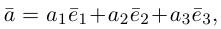 где действительные числа
где действительные числа 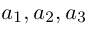 – координаты вектора
– координаты вектора 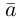 в базисе
в базисе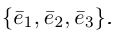
Приведем геометрическое доказательство этого утверждения.
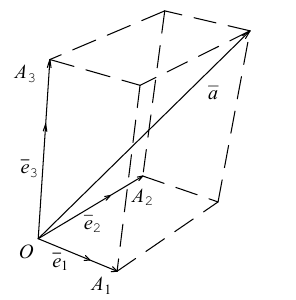
Вектор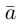 можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов
можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов 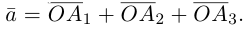 В виду коллинеарности векторов
В виду коллинеарности векторов 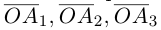 соответствующим базисным векторам, мы можем записать, что
соответствующим базисным векторам, мы можем записать, что 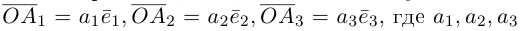 — некоторые действительные числа. Отсюда и следует искомое разложение.
— некоторые действительные числа. Отсюда и следует искомое разложение.
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 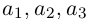 коротко записывается как
коротко записывается как 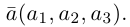
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 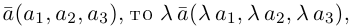 если
если 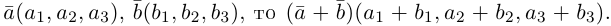 Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
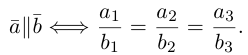
Рассмотрим теперь ортонормированный базис 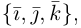 т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе
т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе 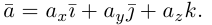
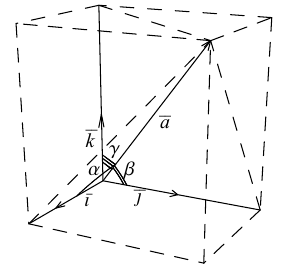
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
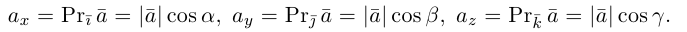
Величины 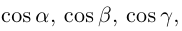 т. е. косинусы углов, которые образует данный вектор с ортами
т. е. косинусы углов, которые образует данный вектор с ортами  к соответственно, называются направляющими косинусами вектора
к соответственно, называются направляющими косинусами вектора  Единичный вектор
Единичный вектор 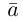 имеет координаты
имеет координаты 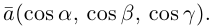
Очевидно также, что
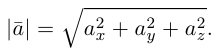
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта  ось
ось 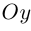 (ординат) — вдоль орта
(ординат) — вдоль орта 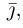 наконец, ось
наконец, ось 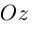 (аппликат) направим вдоль орта
(аппликат) направим вдоль орта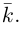

В выбранной системе координат координаты радиуса-вектора 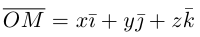 мы будем называть координатами точки М и записывать
мы будем называть координатами точки М и записывать 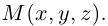
Если известны координаты начальной 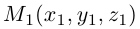 и конечной
и конечной 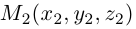 точек вектора, то из равенства
точек вектора, то из равенства 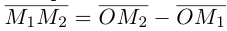 слезет, что его координаты равны
слезет, что его координаты равны
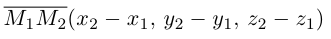 и, значит, расстояние между точками
и, значит, расстояние между точками  вычисляется по формуле
вычисляется по формуле
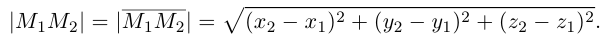
Найдем теперь координаты точки М, делящей отрезок с концами в точках 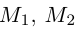 в данном
в данном
отношении 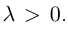 Так как
Так как 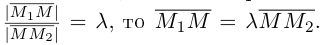 Отсюда, переходя к координатам получим:
Отсюда, переходя к координатам получим:
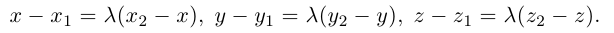
Следовательно, координаты искомой точки вычисляются по формулам:
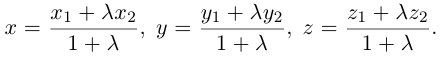
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
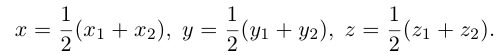
Пример №2
Треугольник задан координатами своих вершин 
 Найти координаты точки пересечения его медиан. Решение.
Найти координаты точки пересечения его медиан. Решение.
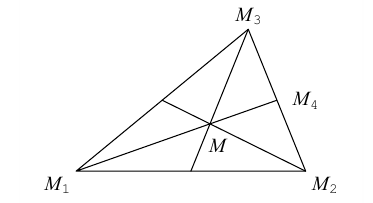
Пусть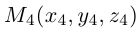 – середина отрезка
– середина отрезка  – точка пересечения медиан. Тогда
– точка пересечения медиан. Тогда
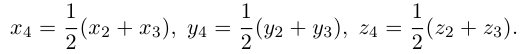
По известному свойству точки пересечения медиан 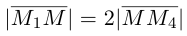 и потому
и потому
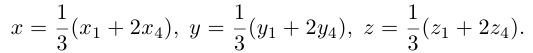
Подставив сюда найденные координаты точки  ползучим:
ползучим:
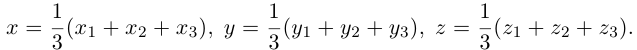
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 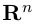 называется упорядоченная совокупность n векторов
называется упорядоченная совокупность n векторов

обладающая тем свойством, что любой вектор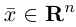 единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа
единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа 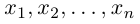 (координаты вектора
(координаты вектора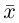 в базисе (1)) такие, что
в базисе (1)) такие, что

В качестве базиса в 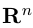 мы можем взять, например, векторы
мы можем взять, например, векторы
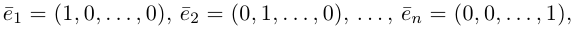
так как, очевидно, любой вектор 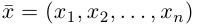 однозначно представляется в виде (2).
однозначно представляется в виде (2).
Скалярное произведение векторов
Определение: Скалярным произведением векторов 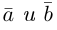 называется число
называется число
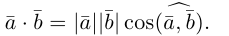
Из этого определения сразу же следует, что
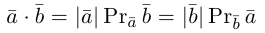
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
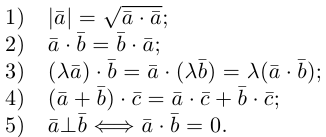
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 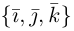 векторы
векторы 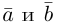 имеют координаты
имеют координаты 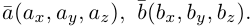 Заметив, что по свойствам 1) и 5) скалярного произведения
Заметив, что по свойствам 1) и 5) скалярного произведения
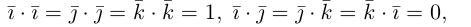
перемножим векторы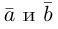 скалярно, используя свойства 2) – 4):
скалярно, используя свойства 2) – 4):
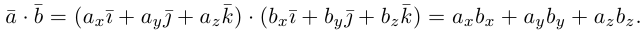
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 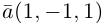 на две ортогональные составляющие, одна из которых коллинеарна вектору
на две ортогональные составляющие, одна из которых коллинеарна вектору 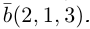
Решение.
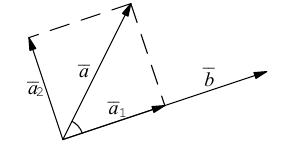
Из чертежа следует, что 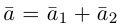 – искомое разложение. Найдем векторы
– искомое разложение. Найдем векторы 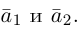 Составляющая
Составляющая 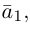 коллинеарная вектору
коллинеарная вектору 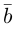 равна, очевидно, вектору проекции
равна, очевидно, вектору проекции 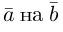 и, следовательно,
и, следовательно,
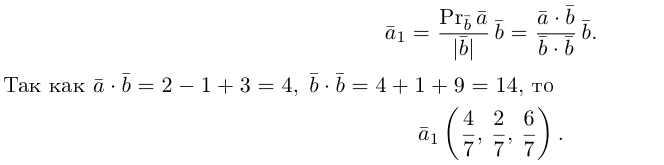
Тогда вторая ортогональная составляющая вектора  равна
равна
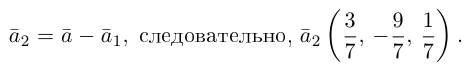
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы  материальная тотп<а переместилась по прямой из положения В в положение С.
материальная тотп<а переместилась по прямой из положения В в положение С.
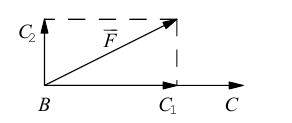
Найдем работу этой силы. Для этого разложим вектор силы  на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения
на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения  Тогда
Тогда
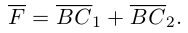
Составляющая 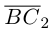 работы не совершает, следовательно, работа силы
работы не совершает, следовательно, работа силы 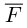 равна работе составляющей
равна работе составляющей 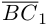 и, таким образом,
и, таким образом,
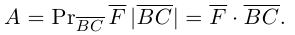
Окончательно, работа силы , под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
, под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
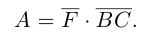
Замечание. Скалярным произведением векторов  n-мерного пространства
n-мерного пространства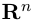 называется число
называется число 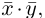 равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
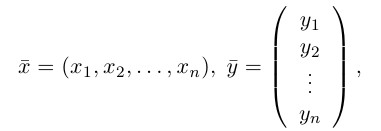
то
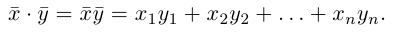
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 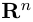 обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
Длиной вектора 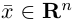 называется число
называется число
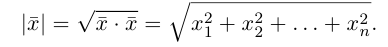
Векторы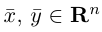 называются ортогональными, если
называются ортогональными, если 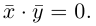 Векторы
Векторы
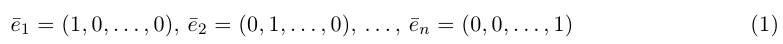
составляют ортонормированный базис пространства  , так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
, так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
Любой вектор  мы можем рассматривать как точку
мы можем рассматривать как точку
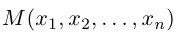
n-мерного пространства с координатами 
Взяв еще одну точку 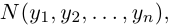 соответствующую вектору
соответствующую вектору 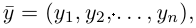 мы под расстоянием между точками М и N будем понимать длину вектора
мы под расстоянием между точками М и N будем понимать длину вектора  т. е. число
т. е. число
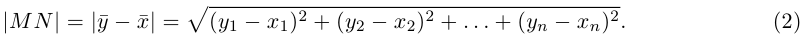
Таким образом переопределенное пространство 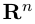 с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов  называется вектор
называется вектор  такой, что
такой, что
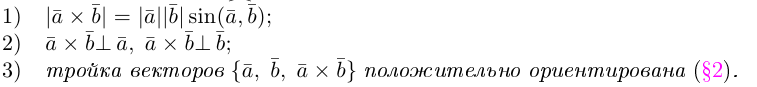
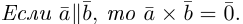
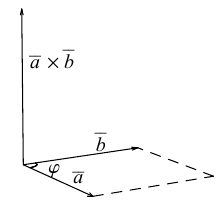
Из этого определения следует, что площадь параллелограмма, построенного на векторах  и
и  равна длине векторного произведения
равна длине векторного произведения  , т. е.
, т. е.
Сформулируем основные свойства векторного произведения.
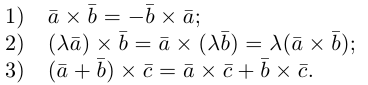
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 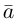 и
и 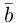 в ортонормированном базисе
в ортонормированном базисе 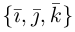 имеют координаты
имеют координаты 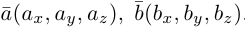 Учитывая, tito по определению векторного произведения
Учитывая, tito по определению векторного произведения
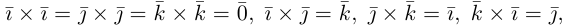
раскроем скобки в векторном произведении 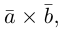 принимая во внимание свойства 1) – 3):
принимая во внимание свойства 1) – 3): 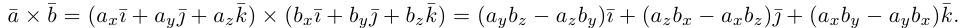
Полученный вектор мы можем записать в виде следующего символического определителя.
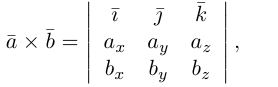
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 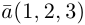 , ортогональную плоскости векторов
, ортогональную плоскости векторов 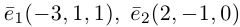 .
.
Решение.
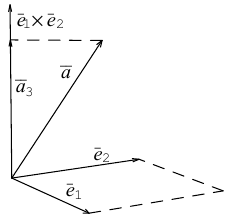
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 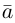 на векторное произведение
на векторное произведение и, следовательно.
и, следовательно.
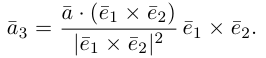
Переходим к вычислениям:
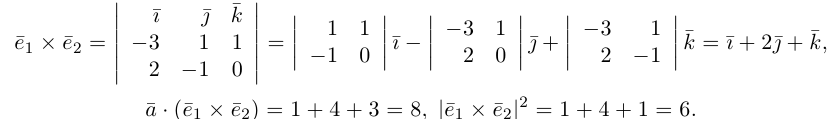
Тогда 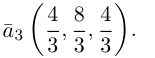
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
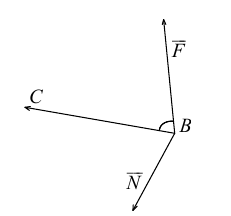
Итак, пусть сила 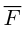 приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
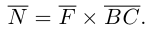
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов  называется число
называется число
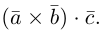
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
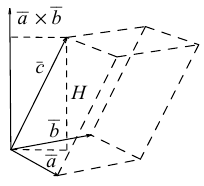
По определению смешанного произведения
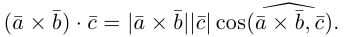
Поскольку 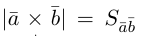 – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах 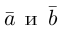 (§4)
(§4)
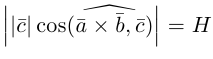 -высота параллелепипеда построенного на векторах
-высота параллелепипеда построенного на векторах  то
то
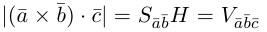
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 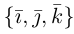 , т.е.
, т.е. 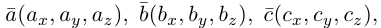 то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
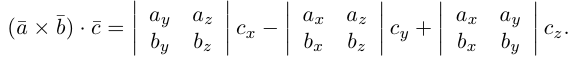
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
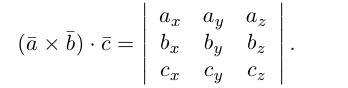
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
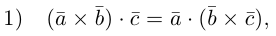
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 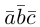 . которым мы и будем пользоваться в дальнейшем.
. которым мы и будем пользоваться в дальнейшем.
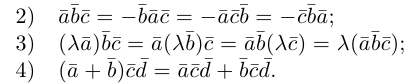
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 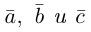 компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 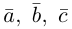 компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение
компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение 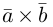 ортогонально вектору с и, следовательно,
ортогонально вектору с и, следовательно, 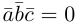 . Аналогично проверяется достаточность условия теоремы.
. Аналогично проверяется достаточность условия теоремы.
Следствие. Три вектора 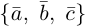 образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
Заметим, кроме того, что, если 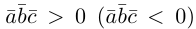 , то угол между векторами
, то угол между векторами 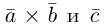 -острый (тупой) и, следовательно, базис
-острый (тупой) и, следовательно, базис 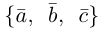 является положительно (отрицательно) ориентированным.
является положительно (отрицательно) ориентированным.
Пример №5
Доказать, что пять точек
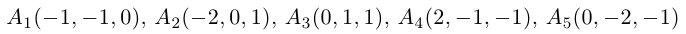
расположены в одной плоскости.
Решение. Рассмотрим векторы 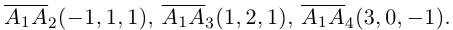 Так как
Так как
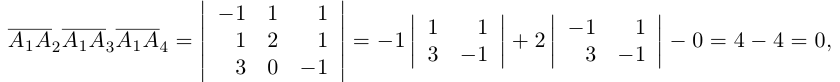
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки  находятся в одной плоскости
находятся в одной плоскости  Аналогично покажем, что и точки
Аналогично покажем, что и точки 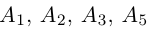 также принадлежат одной плоскости
также принадлежат одной плоскости  . Действительно,
. Действительно, 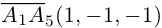
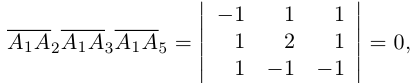
так как первая и третья строки в определителе пропорциональны. Плоскости  имеют три общие точки
имеют три общие точки  , следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
, следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
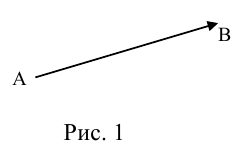 А – начало, В – конец вектора
А – начало, В – конец вектора 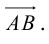
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 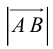 – расстояние между его началом и концом.
– расстояние между его началом и концом.
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
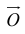 – нулевой вектор: его направление не определено, а длина
– нулевой вектор: его направление не определено, а длина 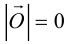 .
.
Определение: Векторы  называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 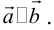
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 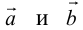 совмещаются в одной точке, и
совмещаются в одной точке, и 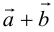 – диагональ параллелограмма, построенного на
– диагональ параллелограмма, построенного на 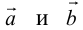 .
.
б) Правило треугольника (рис. 3): начало 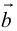 совмещается с концом
совмещается с концом 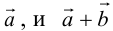 направлен от начала
направлен от начала 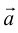 к концу
к концу 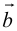 .
.
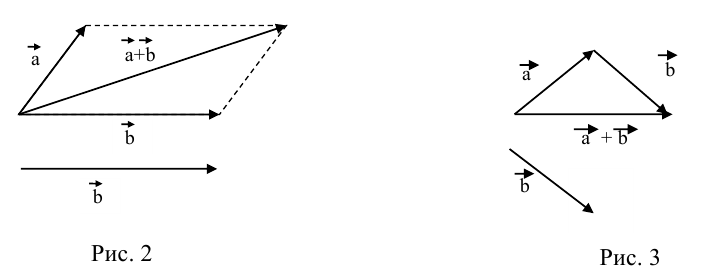
в) Правило сложения нескольких векторов (рис. 4).
Вектор  замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и
замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и  направлен от начала
направлен от начала  к концу
к концу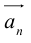 .
.
Умножение на число
Определение: Произведением вектора  на число
на число  называется вектор
называется вектор 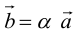 , aудовлетворяющий условиям:
, aудовлетворяющий условиям:
а) 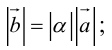
б) 
в)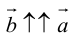 , если
, если 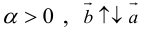 ,a если
,a если  , если
, если  .
.
Произведение 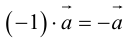 называется вектором, противоположным вектору
называется вектором, противоположным вектору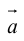 . Очевидно,
. Очевидно, 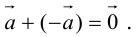 .
.
Определение: Разностью 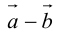 называется сумма вектора
называется сумма вектора 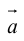 и вектора, противоположного
и вектора, противоположного 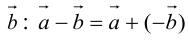 (рис. 5).
(рис. 5).

Начала  совмещаются в одной точке, и
совмещаются в одной точке, и 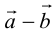 направлен от конца
направлен от конца  к концу
к концу  .
.
Свойства линейных операций
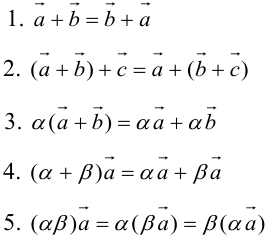
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: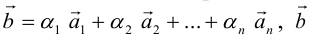 – линейная комбинация векторов
– линейная комбинация векторов  с коэффициентами
с коэффициентами 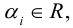
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 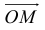 как линейную комбинацию
как линейную комбинацию
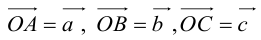 (рис. 6).
(рис. 6).
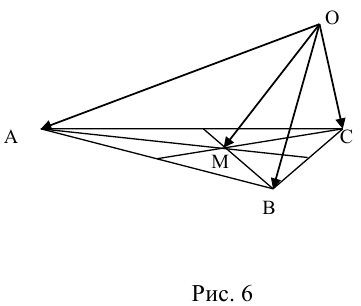
 . Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что
. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что 
По правилу треугольника  , то есть
, то есть 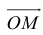 – линейная комбинация
– линейная комбинация 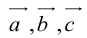 с коэффициентами
с коэффициентами 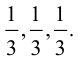
Теорема: Пусть 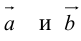 – неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
– неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
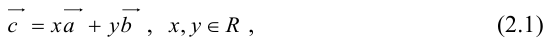
где коэффициенты (2.1) определяются единственным образом.
Представление вектора  в виде (2.1) называется разложением его по двум неколлинеарным векторам.
в виде (2.1) называется разложением его по двум неколлинеарным векторам.
Доказательство:
- Пусть среди
 есть два коллинеарных, например:
есть два коллинеарных, например: 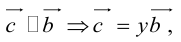
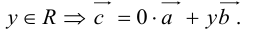
- Пусть среди
 коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с  , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат  (рис. 7).
(рис. 7).
Тогда c 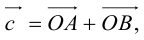 но
но 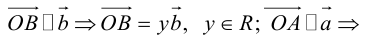
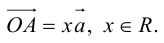 Поэтому
Поэтому 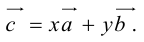
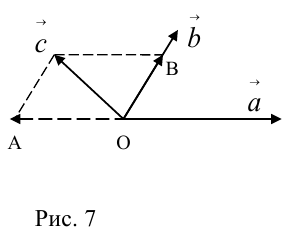
Докажем единственность разложения. Предположим, что 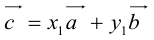 и
и 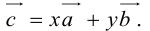 Тогда, вычитая одно равенство из другого, получим:
Тогда, вычитая одно равенство из другого, получим: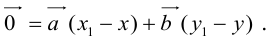
Если 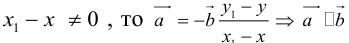 , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Теорема: Пусть 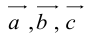 – некомпланарные векторы. Тогда любой вектор
– некомпланарные векторы. Тогда любой вектор  может быть представлен в виде
может быть представлен в виде
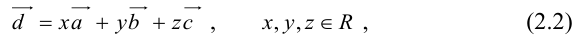
причем единственным образом.
Представление вектора 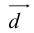 в виде (2.2) называется разложением его по трем некомпланарным.
в виде (2.2) называется разложением его по трем некомпланарным.
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 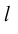 называется единичный вектор
называется единичный вектор 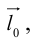
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 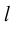 называется основание
называется основание 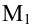 перпендикуляра, опущенного из М на
перпендикуляра, опущенного из М на 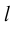 .
.
Определение: Ортогональной проекцией вектора 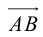 на ось
на ось  называется длина отрезка
называется длина отрезка  этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора
этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора  совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
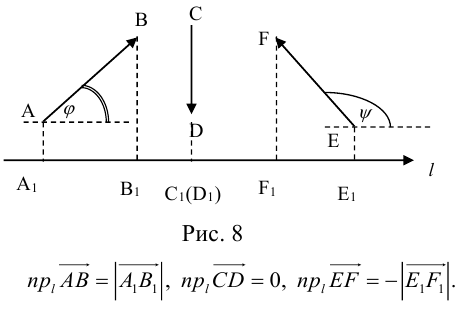
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
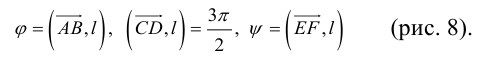
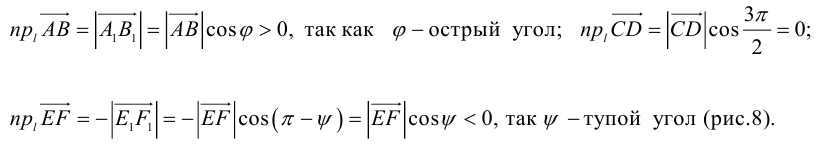
Очевидно, проекцию вектора на ось можно найти по формуле
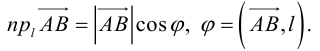
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
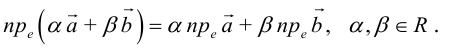
В частности, проекция суммы векторов равна сумме их проекций:
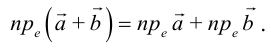
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 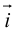 – орт оси ОХ,
– орт оси ОХ, 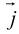 – орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
– орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).

Аналогично в пространственной системе OXYZ 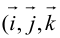 – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
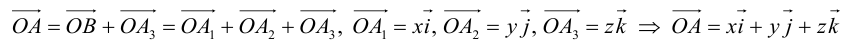
– разложение  по ортам координатных осей (единственно по теореме 2).
по ортам координатных осей (единственно по теореме 2).
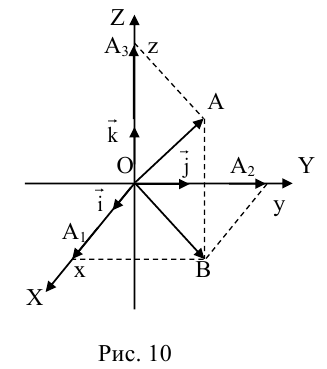
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором  можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
Определение: Координатами вектора  в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 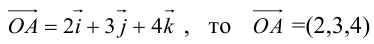 и наоборот, если
и наоборот, если
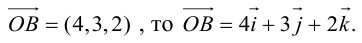
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
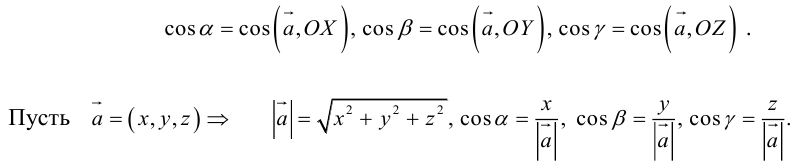
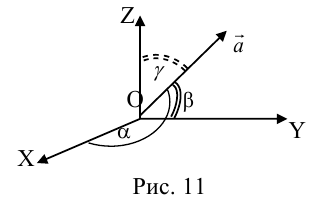
Из этих формул очевидно следует основное свойство направляющих косинусов:
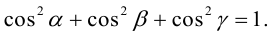
Если известны длина  и направляющие косинусы вектора, то его координаты вычисляются по формулам:
и направляющие косинусы вектора, то его координаты вычисляются по формулам:
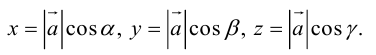
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
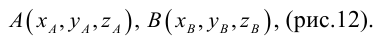
Тогда
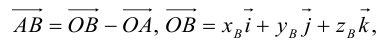
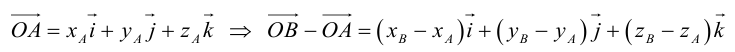 (см. свойства линейных операций над векторами). Таким образом,
(см. свойства линейных операций над векторами). Таким образом,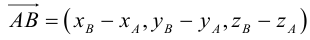 , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
, то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
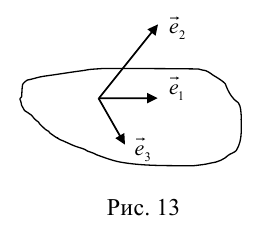
Если  – базис, то
– базис, то  – другой базис, так как изменился порядок следования векторов.
– другой базис, так как изменился порядок следования векторов.
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать 
Из теоремы 2 следует, что всякий вектор  может быть разложен по базису
может быть разложен по базису 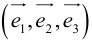 , то есть представлен в виде:
, то есть представлен в виде: 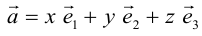 . Числа x,y,z называются координатами
. Числа x,y,z называются координатами  в базисе
в базисе 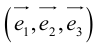 .
.
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 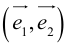 – базис, то представление вектора в виде
– базис, то представление вектора в виде 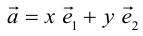 называется разложением
называется разложением 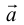 по базису
по базису и x, y – координаты
и x, y – координаты  в этом базисе.
в этом базисе.
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 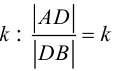 (рис. 14).
(рис. 14).
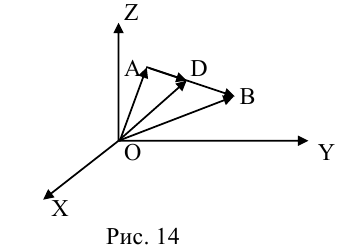
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
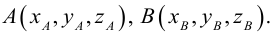
Обозначим
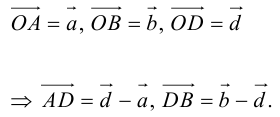
Так как  (лежат на одной прямой) и
(лежат на одной прямой) и 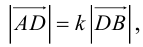 то
то
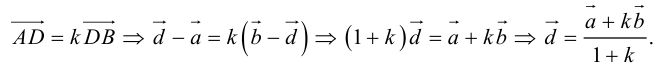
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
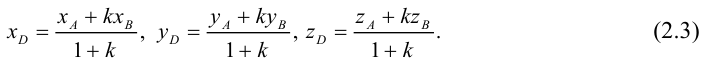
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
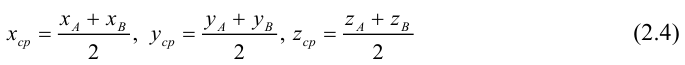
ЗАМЕЧАНИЕ 2. Если k < 0,  , то точка D лежит за пределами AB : так как
, то точка D лежит за пределами AB : так как 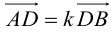 , то при
, то при 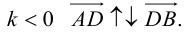
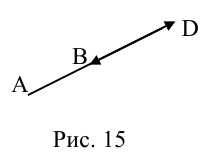
В этом случае 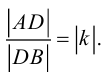
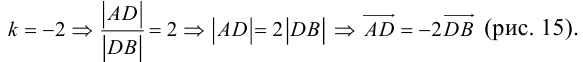
Скалярное произведение векторов
Определение: Скалярным произведением векторов 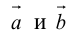 называется скаляр (число), равный
называется скаляр (число), равный 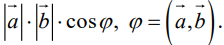
Скалярное произведение обозначается так: 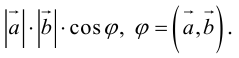 или
или 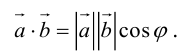
Так как 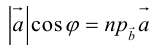 (рис. 16) или
(рис. 16) или 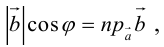 то
то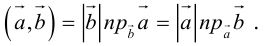
Свойства скалярного произведения
1.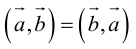 – очевидно из определения.
– очевидно из определения.
2.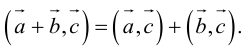
Доказательство:
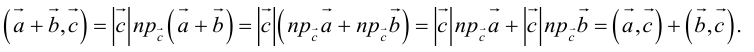
3.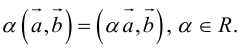
Доказательство:
а) 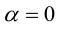 – очевидно.
– очевидно.
б) 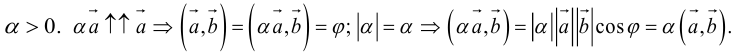
в) 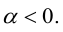 В этом случае
В этом случае
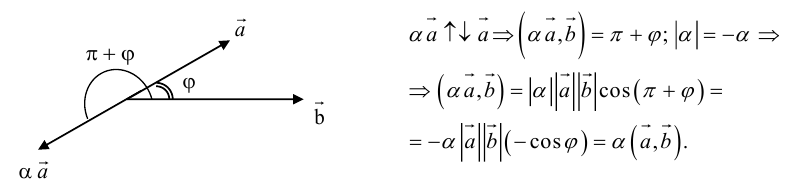
4.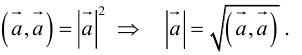
Отсюда следует, что 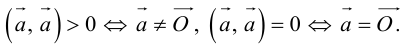
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.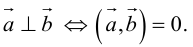
Доказательство:
а) пусть 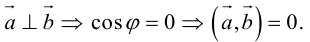
б) пусть 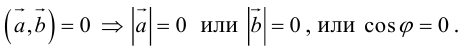
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 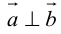 . В третьем случае
. В третьем случае 
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов 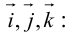
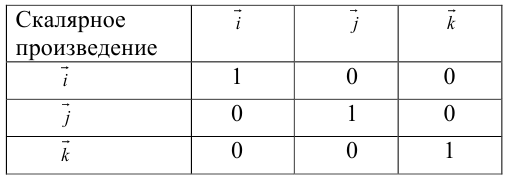
Пусть в некоторой пдск 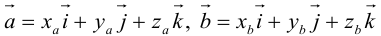 . Найдем скалярное произведение этих векторов:
. Найдем скалярное произведение этих векторов:
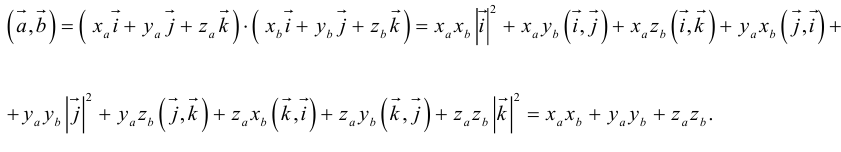
Таким образом, 
Пример №8
Найти, при каком значении x векторы 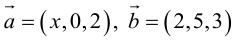 перпендикулярны.
перпендикулярны.
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 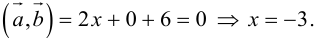
Пример №9
Найти угол между биссектрисой AD и медианой  если
если 
Так как 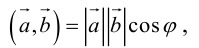
то 
Найдем координаты векторов 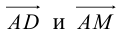 . Точка M – середина BC , поэтому по формулам (2.4)
. Точка M – середина BC , поэтому по формулам (2.4)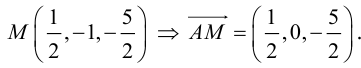
По теореме о биссектрисе внутреннего угла треугольника 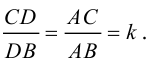
Чтобы найти k , вычислим длины AC и AB :
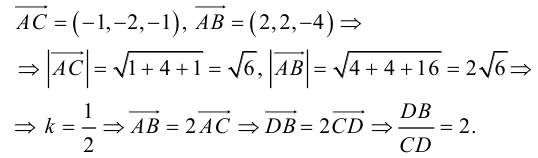
Разделим отрезок CB в данном отношении по формулам (2.3):
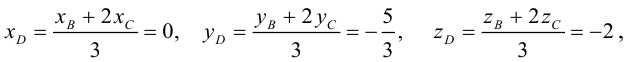
отсюда 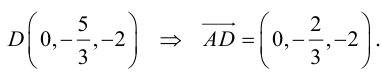
Заметим, что 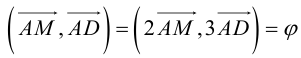 . Это замечание позволит нам не иметь дело с дробями, так как
. Это замечание позволит нам не иметь дело с дробями, так как
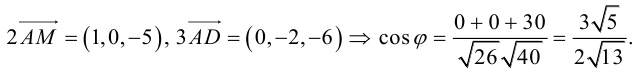
Пример №10
Найти 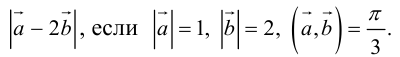
Воспользуемся свойствами 1–4 скалярного произведения:
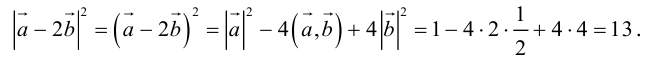
Отсюда 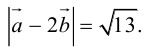
ЗАМЕЧАНИЕ. Так как работа силы  по перемещению материальной точки вдоль вектора
по перемещению материальной точки вдоль вектора 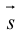 вычисляется по формуле
вычисляется по формуле 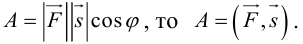
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов  , имеющих общее начало, называется правой (левой), если
, имеющих общее начало, называется правой (левой), если  конца третьего вектора c вращение первого вектора
конца третьего вектора c вращение первого вектора  ко второму вектору
ко второму вектору  по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
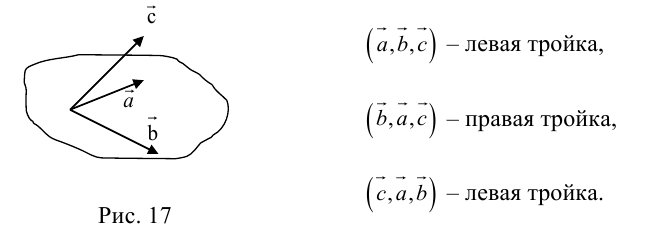
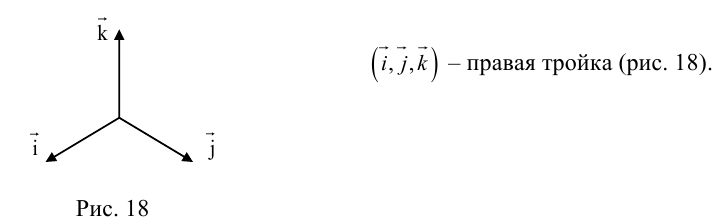
Определение: Векторным произведением вектора 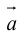 на вектор
на вектор 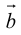 называется вектор
называется вектор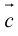 , удовлетворяющий условиям:
, удовлетворяющий условиям:
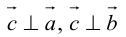 (
(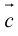 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 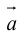 и
и 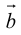 ).
). - Направление
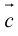 таково, что тройка
таково, что тройка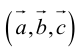 – правая.
– правая. 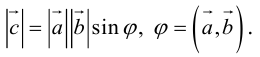
Векторное произведение обозначается так: 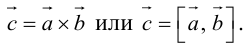
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
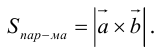
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
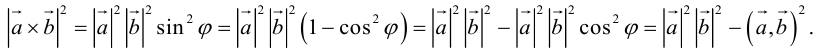
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
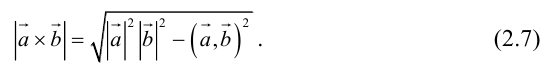
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7): 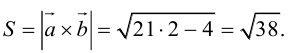
ЗАМЕЧАНИЕ 2. Направление вектора  можно также (кроме п.2) определить по правилу винта: направление вектора
можно также (кроме п.2) определить по правилу винта: направление вектора  совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора
совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора  ко второму вектору
ко второму вектору 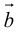 по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).
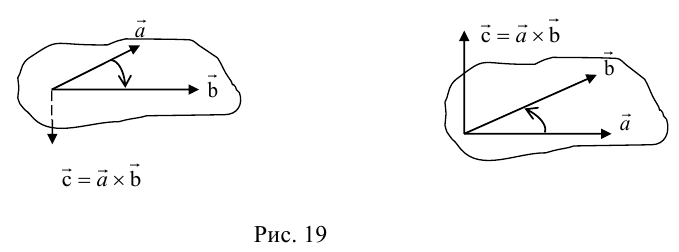
Свойства векторного произведения
1.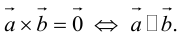
Доказательство:
а)пусть 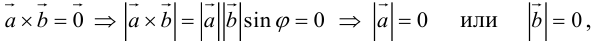 или
или 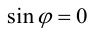 . В первом и втором случаях один из сомножителей – нулевой вектор.
. В первом и втором случаях один из сомножителей – нулевой вектор.
Его направление не определено, поэтому можно считать, что 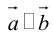 . Если
. Если 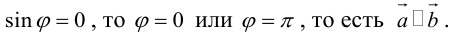
б)пусть 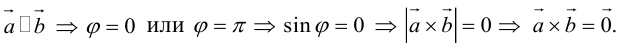
2. 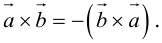
Доказательство: По определению направления векторов 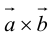 и
и 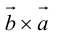 противоположны, а модули равны, значит, векторы отличаются лишь знаком.
противоположны, а модули равны, значит, векторы отличаются лишь знаком.
3.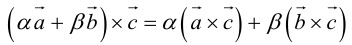 – свойство линейности векторного произведения по первому сомножителю (без доказательства).
– свойство линейности векторного произведения по первому сомножителю (без доказательства).
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 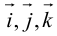 : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
: векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
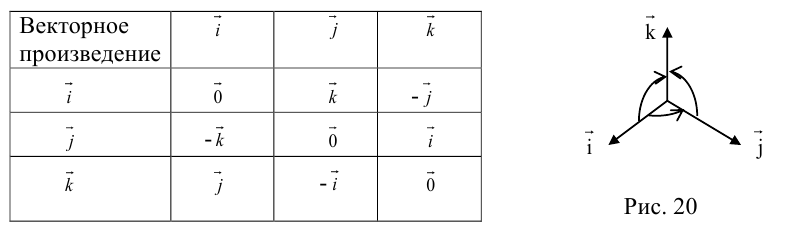
Пусть в некоторой пдск 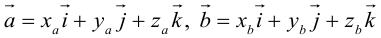 . Найдем векторное произведение этих векторов:
. Найдем векторное произведение этих векторов:
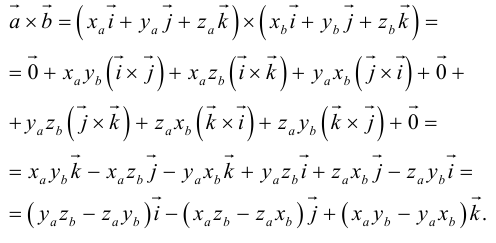
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
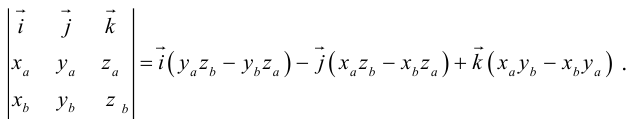
Таким образом,
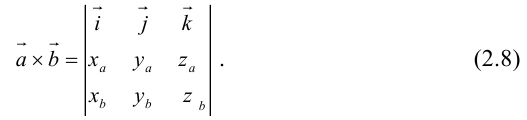
Пример №12
Вычислить векторное произведение векторов 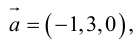
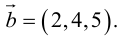
По формуле (2.8): 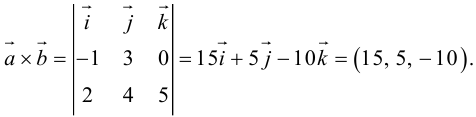
Заметим, что площадь треугольника, построенного на векторах  , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что
, можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что 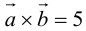
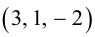
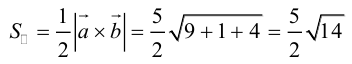
или
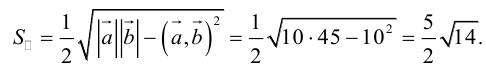
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 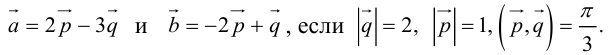
Так как 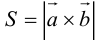 , то вычислим векторное произведение, используя его свойства:
, то вычислим векторное произведение, используя его свойства: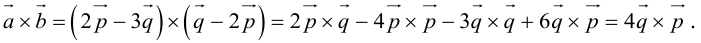
Отсюда 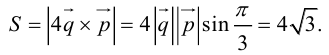
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов  называется число
называется число  – скалярное произведение a на векторное произведение
– скалярное произведение a на векторное произведение 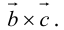
Смешанное произведение обозначается так: 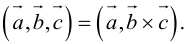
Пусть в некоторой пдск 
Обозначим
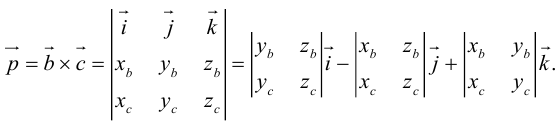
Тогда
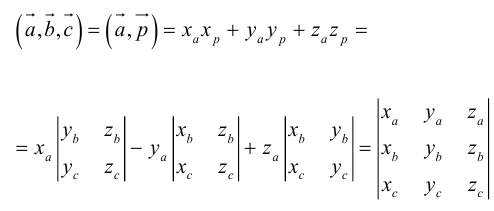
по 7 свойству определителей.
Таким образом,
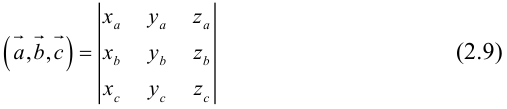
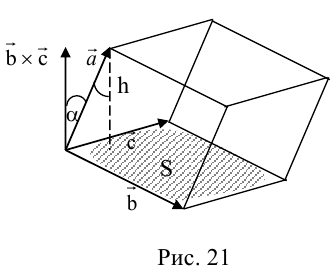
По определению скалярного произведения 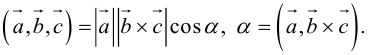
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
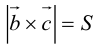 – площадь параллелограмма,
– площадь параллелограмма,
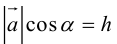 – высота параллелепипеда,
– высота параллелепипеда,
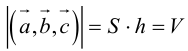 – объем параллелепипеда.
– объем параллелепипеда.
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 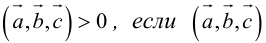 – правая тройка, и
– правая тройка, и 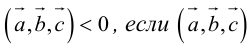 – левая тройка.
– левая тройка.
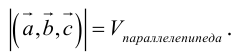
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения:  компланарны
компланарны
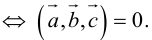
Доказательство: а) 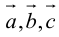 компланарны
компланарны 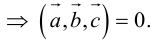
Если 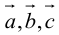 компланарны, то на них нельзя построить параллелепипед, а потому
компланарны, то на них нельзя построить параллелепипед, а потому 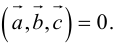
б)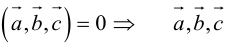 компланарны.
компланарны.
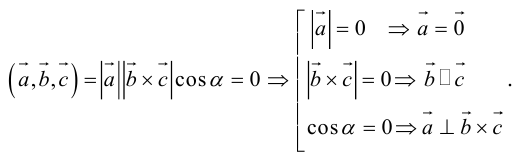
Во всех трех случаях 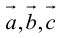 компланарны: в частности, если
компланарны: в частности, если 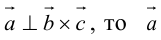 параллелен плоскости векторов
параллелен плоскости векторов 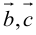 , что означает их компланарность.
, что означает их компланарность.
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
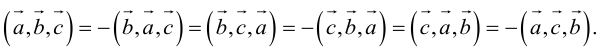
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами: 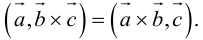
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим: 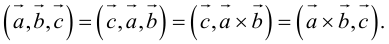
4. Смешанное произведение линейно по каждому из трех сомножителей.
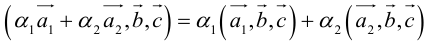 – линейность по первому сомножителю.
– линейность по первому сомножителю.
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
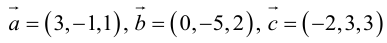 , и его высоту, перпендикулярную плоскости векторов
, и его высоту, перпендикулярную плоскости векторов  .
.
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 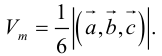
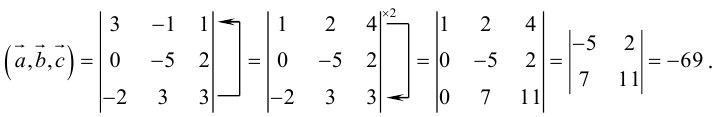
Отсюда 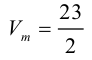 (заметим, что
(заметим, что  – левая тройка, так как смешанное произведение отрицательно).
– левая тройка, так как смешанное произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
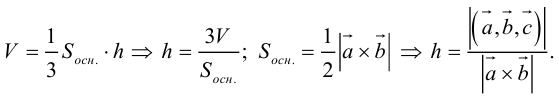
По формуле (2.7) 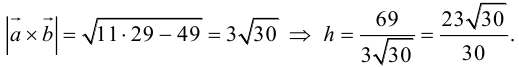
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми?
Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора. Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.
Вычисление координат векторов
Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:
- Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):

- Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
- Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).
На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.
Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:
![]()
Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.
Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.
- Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем: A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
- Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения: A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
- A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
- Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.
Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.
Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!
Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:
Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.
Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A: AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).
- Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем: AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).
- Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B: BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).
Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)
Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!
Вычисление направляющих векторов для прямых
Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.
Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую…
Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:
Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.
Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.
Теперь разберемся с прямой BD1. На ней также есть две точки: B = (1; 0; 0) и D1 = (0; 1; 1). Получаем направляющий вектор BD1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).
Ответ: AC = (1; 1; 0); BD1 = (− 1; 1; 1)
Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.
Для начала разберемся с прямой AB1. Тут все просто: у нас есть точки A = (0; 0; 0) и B1 = (1; 0; 1). Получаем направляющий вектор AB1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).
Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:
![]()
Ответ: AB1 = (1; 0; 1);
![]()
Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца.
К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.
Вычисление нормальных векторов для плоскостей
Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.
Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.
Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).
Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:
Задача. В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.
- Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем: A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;
- Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения: A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
- A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
- Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B: B = − 1 − A − C = − 1 + 1 + 1 = 1.
- Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).
Задача. В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.
- Подставим вместо x, y и z координаты точки A1 = (0; 0; 1).
- Имеем: A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;
- Аналогично, для точки C = (1; 1; 0) получим уравнение: A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;
- Положим B = 1.
- Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0,
- Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).
Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.
Координаты середины отрезка
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.
Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1).
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.
Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т.е. точка L — это середина отрезка A1C1. Но A1 = (0; 0; 1), C1 = (1; 1; 1).
Ответ: L = (0,5; 0,5; 1)
Источник: https://www.berdov.com/ege/solid_geometry/method/
Координаты вектора на плоскости
Координаты вектора на плоскости
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы:

Векторы и ортогональны. Ортогональны = Перпендикулярны. Вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность. Обозначение: ортогональность векторов записывают привычным значком перпендикулярности.
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.
Любой вектор плоскости единственным образом выражается в виде:, где – числа, которые называются координатами вектора в данном базисе. А само выражение называется разложением вектора по базису .

Простейшие задачи аналитической геометрии.Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть. Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии.
Как найти вектор по двум точкам?
Координаты точек – это обычные координаты в прямоугольной системе координат. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис.
Как найти длину отрезка?
Отрезок – это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Как найти длину вектора?
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? Округление целесообразно проводить до 2-3-х знаков после запятой.
Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка равна длине вектора . Так же очевидно, что длина вектора будет такой же.
Источник: https://infourok.ru/koordinati-vektora-na-ploskosti-teoreticheskaya-podborka-1306882.html
Метод координат. Координаты вектора
Итак, построим прямоугольную систему координат. От точки О начала координат отложим единичные векторы и . Т.е. векторы длины, которых равны единице.
Причём, направление вектора совпадает с направлением оси , а направление вектора совпадает с направлением оси.
Векторы называются координатными векторами. Коэффициенты разложения вектора по координатным векторам называют координатами вектора в данной системе координат. Напомним, что координаты вектора записывают в фигурных скобках через точку с запятой.
- Если векторы равны, то их разложения по векторам и также будут равны, а значит, равны будут и коэффициенты разложения.
Вспомним ещё один особенный случай — противоположные векторы. Их разложения противоположны. Координатами вектора являются числа 8 и –1. Значит, чтобы переместиться из точки О на вектор , сначала нужно переместиться на вектор , а затем на вектор . Соединив точку О с конечной точкой, получим вектор .
Далее изобразим вектор . Для этого из точки О переместимся на вектор . Тем самым получим искомый вектор.
Чтобы из точки О переместиться на вектор , сначала переместимся на вектор , а затем на вектор . Проведём вектор из точки О в конечную точку. Так мы получили вектор .
Теперь давайте вспомним правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
- Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
- Каждая координата разности двух векторов равна разности соответствующих координат данных векторов.
- Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Радиус-вектором точки называют вектор, начало которого совпадает с точкой начала координат, а конец — с данной точкой.
Пользуясь этим утверждением, выразим координаты вектора через координаты его начала и конца. Пусть точка А имеет координаты , а точка В имеет координаты .
- Каждая координата вектора равна разности соответствующих координат его конца и начала.
- Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Источник: https://videouroki.net/video/49-mietod-koordinat-koordinaty-viektora.html
Как найти вектор по двум точкам?
Из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Координаты точек – это обычные координаты в прямоугольной системе координат. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости .
- Правило сложения векторов. Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты.
Аналогичное правило справедливо для суммы любого количества векторов, например, найдём сумму трёх векторов. Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы , то их суммой является вектор .
- Правило умножения вектора на число. Для того чтобы вектор умножить на число , необходимо каждую координату данного вектора умножить на число. Для пространственного вектора правило такое же.
Источник: https://poisk-ru.ru/s61557t1.html
Нахождение координат вектора через координаты точек. Как найти вектор по двум точкам
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i→ должно совпадать с осью Ox, а направление вектора j→ с осью Oy. Векторы i→ и j→ называют координатными векторами.
Координатные векторы не коллинеарны. Поэтому любой вектор p→ можно разложить по векторам p→=xi→+yj→. Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p→ по координатным векторам называются координатами вектора p→ в данной системе координат.
Координаты вектора записываются в фигурных скобках p→x; y. На рисунке вектор OA→ имеет координаты 2; 1, а вектор b→ имеет координаты 3;-2. Нулевой вектор представляется в виде 0→0; 0.
Если векторы a→ и b→ равны, то и y1=y2. Запишем это так: a→=x1i→+y1j→=b→=x2i→+y2j→, значит x1=x2, y1=y2 . Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на Oxy заданы координаты точек начала и конца AB→: Axa, ya, Bxb, yb. Найти координаты заданного вектора.
Изобразим координатную ось. Из формулы сложения векторов имеем OA→+AB→=OB→, где O – начало координат. Отсюда следует, что AB→=OB→-OA→.
OA→ и OB→ – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения OA→=xa, ya, OB→=xb, yb.
По правилу операций над векторами найдем AB→=OB→-OA→=xb-xa, yb-ya.
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек. Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Пример 1
Найти координаты OA→ и AB→ при значении координат точек A(2,-3), B(-4,-1).
Решение
Для начала определяется радиус-вектор точки A. OA→=(2,-3). Чтобы найти AB→, нужно вычесть значение координат точек начала из координат точек конца. Получаем: AB→=(-4-2,-1-(-3))=(-6, 2).
Ответ: OA→=(2,-3), AB→=(-6,-2).
Пример 2
Задано трехмерное пространство с точкой A=(3, 5, 7), AB→=(2, 0,-2). Найти координаты конца AB→.
Решение
- Подставляем координаты точки A: AB→=(xb-3, yb-5, zb-7).
- По условию известно, что AB→=(2, 0,-2).
- Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: xb-3=2yb-5=0zb-7=-2
- Отсюда следует, что координаты точки B AB→равны: xb=5yb=5zb=5
Ответ: B(5, 5, 5).
Источник: https://Zaochnik.com/spravochnik/matematika/vektory/Nahozhdenie_kordinat_vectora/

