Как найти случайное число в математике

И так, человеку крайне сложно получить случайное число, тем более если нужно сгенерировать более 1 000, а то и 1 000 000 чисел. Поэтому мы придумали алгоритмы генерации чисел. Случайное число можно получить 2-мя видами либо с помощью физики, либо математике.

Но есть одна проблема, любой алгоритм можно предугадать и он начнет зацикливаться, так в 1983г на шоу “Поймай свою удачу”, водитель грузовика Майкл Ларсон он выиграл просто блять сумасшедшие деньги просчитав алгоритм случайных числе этой передачи. После этого случая появился сайт random.org, который генерирует по настоящему рандомное число.

Давайте разберем, как он их получает. Получает этот сайт благодаря матушки природы, да-да наша природа которую мы порой блять недооцениваем, потому-что только матушка природа способна получить хаос который мы не можем предугадать, точнее можем, но это будет пиздец как не скоро, т.к. надо будет рассчитать движение каждого атома во вселенной. Сайт random.org генерирует свои основываясь на данных атмосферных шумов.

Окей, нахуя я тут распинался и рассказывал про этот сайт рандом орг?

Благодаря природе, наш цифровой мир находиться под защитой. Случайные коды которые приходят при платежах ваших банков, основаны на подобных алгоритмах, то есть ни один хакер в мире не сможет предугадать код и спиздить ваши 300р на последний дошик, в военной промышленности тоже эта хрень используется, поэтому, что вы сейчас прочитали, не так уж и не нужно.

Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite

Сегодня сложная тема, но мы объясним её просто и понятно. Разговор пойдёт про алгоритмы и немного про математику. 

Методы Монте-Карло — это набор методов в математике для изучения случайных процессов. Случайных — это когда что-то в них происходит непредсказуемым образом, например:

Смысл методов Монте-Карло в том, чтобы использовать данные случайных событий, чтобы на их основе получить более-менее точные результаты каких-то других вычислений. Они не будут идеально и математически точными, но их уже будет достаточно, чтобы с ними полноценно работать. Иногда это проще и быстрее, чем считать всё по точным формулам.

Пример такого вычисления — построение маршрута в навигаторе. В исходном виде это задача коммивояжёра, которая требует колоссальных вычислительных ресурсов. Но благодаря приближённым методам с ней справится даже не самый мощный телефон. Один из таких методов — метод Монте-Карло.

В чём идея метода

Если совсем примитивно, то работает так: 

Вместо того чтобы строить сложную математическую модель, мы берём простую формулу и пуляем в неё случайные числа. Считаем результат по каждому числу и получаем результат с нужной нам точностью. Чем больше случайных чисел — тем точнее результат. 

Вот то же самое немного подробнее:

Чем больше будет случайных чисел — тем точнее результат. 

Плюс этого метода в том, что нам не нужно запрягать весь математический аппарат для решения задачи — достаточно подставлять числа в формулу и смотреть, получилось верное значение или нет.

Как найти число пи методом Монте-Карло

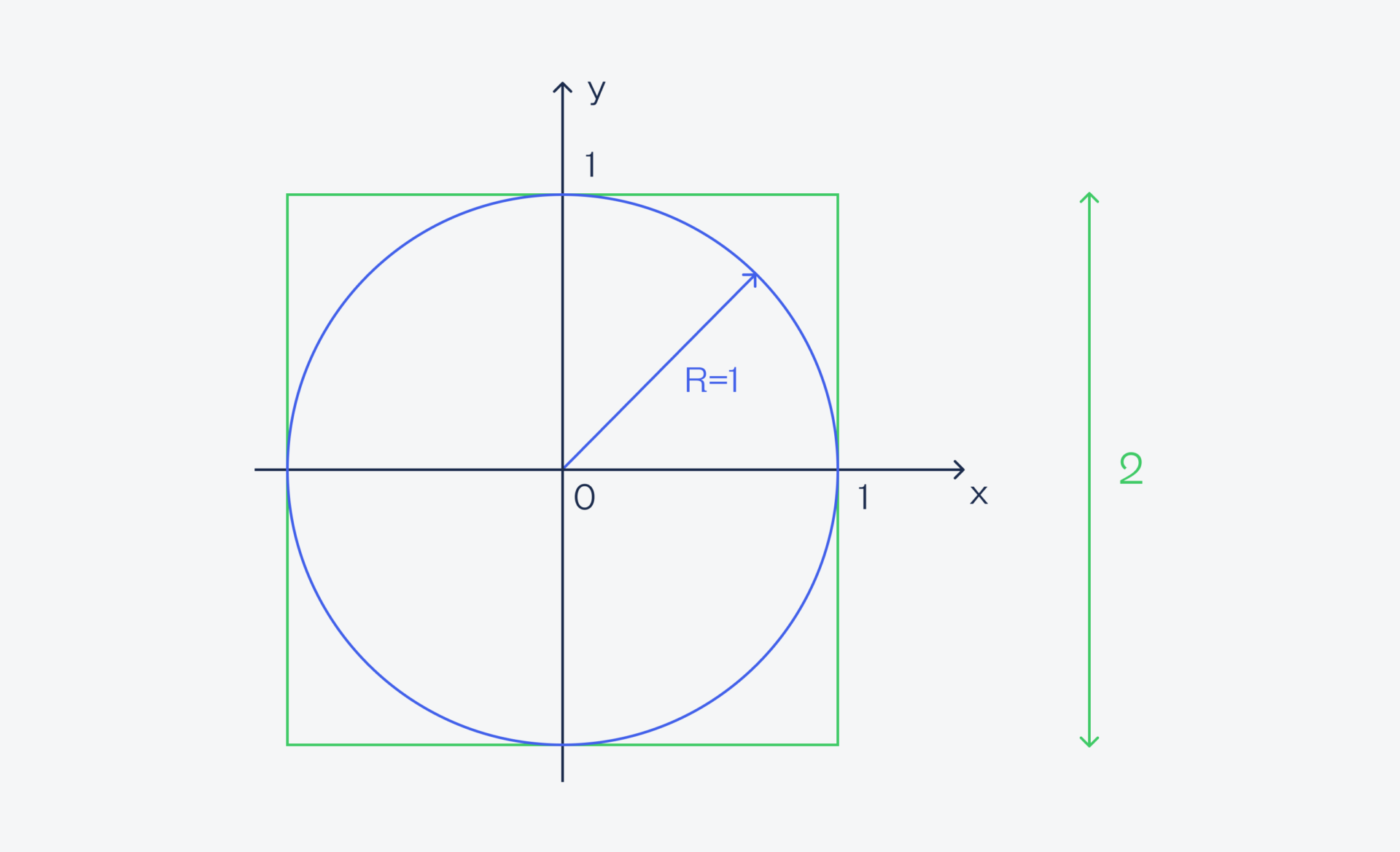
Для примера покажем классическое использование метода Монте-Карло — найдём число пи. Для этого нам понадобится круг, вписанный в квадрат, причём у круга радиус будет равен 1. Это значит, что сторона квадрата равна 2 — это диаметр (или два радиуса) круга:

В этот квадрат мы будем случайным образом кидать песчинки и смотреть, попадут они в круг или нет (но останутся в границах квадрата). Исходя из этого набора данных мы можем посчитать отношение всех песчинок, которые попали в круг, ко всем песчинкам.

Теперь смотрим на формулы: 

Если мы разделим площадь круга на площадь квадрата, то получим π / 4. Но мы ещё не можем по условию посчитать площадь круга, потому что мы не знаем число π. Вместо этого мы можем разделить количество одних песчинок на другие — в этом и суть метода Монте-Карло. 

Это соотношение даст нам результат — π / 4. Получается, что если мы умножим этот результат на 4, то получим число π, причём чем больше песчинок мы кинем, тем точнее будет результат.

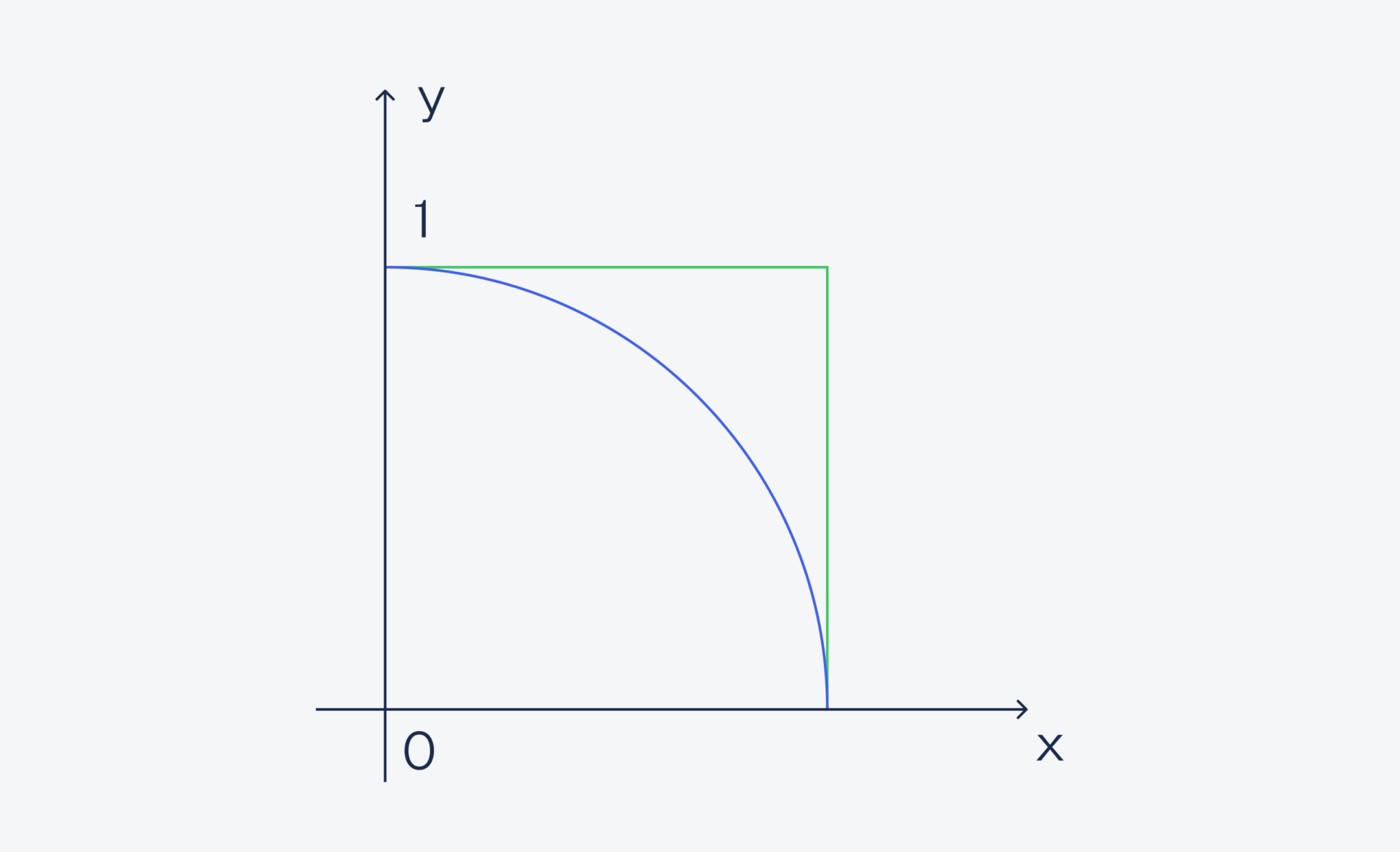
Кидать песчинки будем так: в качестве координат попадания X и Y будем брать случайные числа от 0 до 1. Это значит, что все числа попадут только в один квадрант — правый верхний:

Но так как в этом квадранте ровно четверть круга и ровно четверть квадрата, то соотношение промахов и попаданий будет таким же, как если бы мы бросали песчинки в целый круг и целый квадрат.

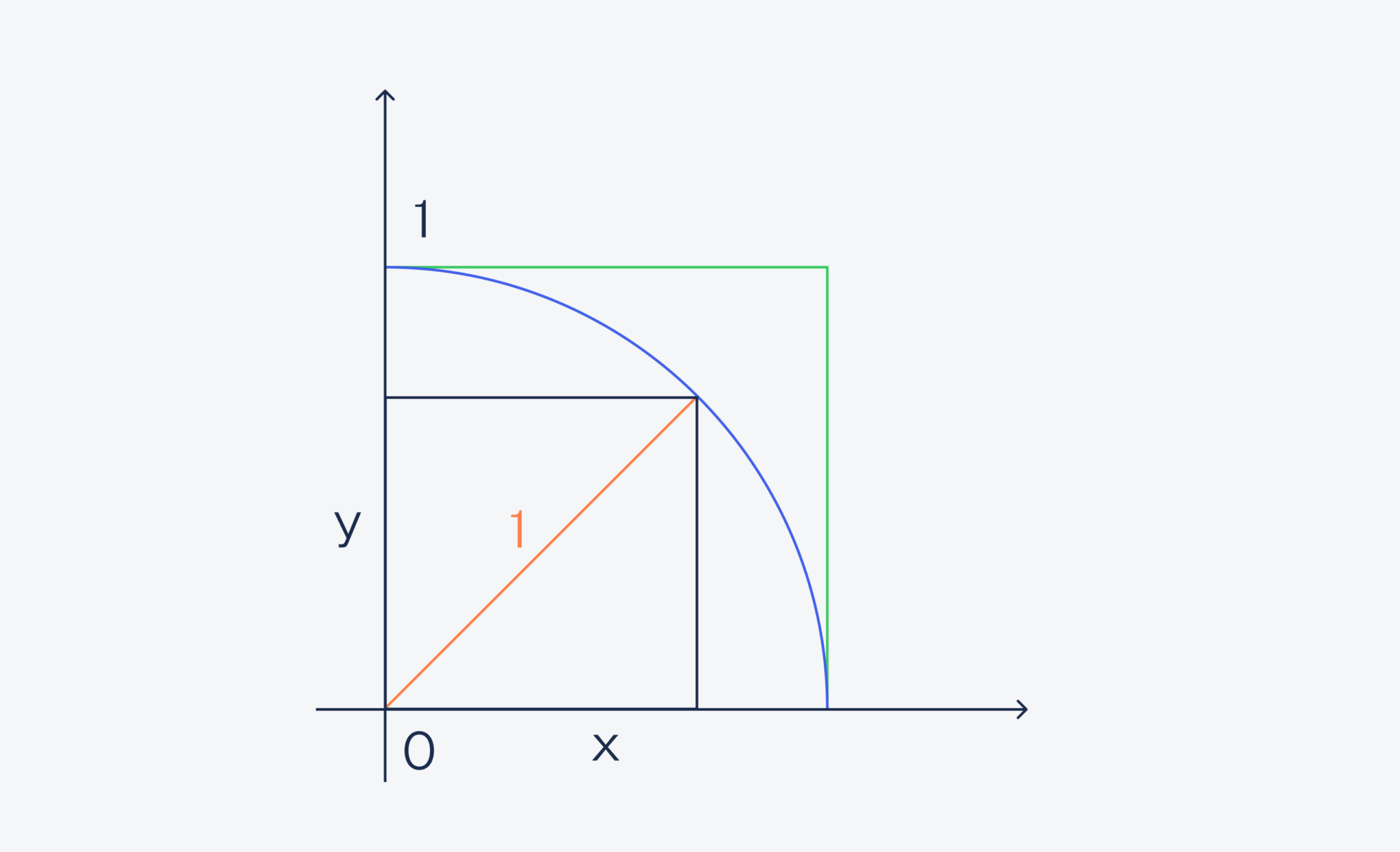
Чтобы проверить, попадает ли песчинка в круг, используем формулу длины гипотенузы: x² + Y² = 1 (так как гипотенуза — это радиус окружности):

Если длина гипотенузы меньше единицы — точка попадает в круг. В итоге мы посчитаем и общее количество точек, и точек, которые попали в круг. Потом мы разделим одно на другое, умножим результат на 4 и получим приближённое значение числа π.

Программируем поиск числа пи по методу Монте-Карло

Алгоритм на языке Python, читайте комментарии, чтобы лучше разобраться в происходящем:

# подключаем модуль случайных чисел
import random
 
# функция, которая посчитает число пи
def count_pi(n):
	# общее количество бросков
    i = 0
	# сколько из них попало в круг
    count = 0
    # пока мы не дошли до финального броска
    while i < n:
        # случайным образом получаем координаты x и y
        x = random.random()
        y = random.random()
        # проверяем, попали мы в круг или нет
        if (pow(x, 2) + pow(y, 2)) < 1:
			# если попали — увеличиваем счётчик на 1
            count += 1
		# в любом случае увеличиваем общий счётчик
        i += 1
    # считаем и возвращаем число пи
    return 4 * (count / n)
 
# запускаем функцию
pi = count_pi(1000000)
# выводим результат
print(pi)

Где ещё используется метод Монте-Карло

На методах Монте-Карло основано много полезного:

Без них изучать современный мир и совершать новые открытия было бы сложнее.

Что дальше

В следующей части поговорим про отжиг — интересное применение метода Монте-Карло, который имитирует физические процессы. Благодаря отжигу мы можем обучать нейросети и решать сложные комбинаторные задачи.

Краеугольный камень псевдослучайности: с чего начинается поиск чисел

(с)

Случайные числа постоянно генерируются каждой машиной, которая может обмениваться данными. И даже если она не обменивается данными, каждый компьютер нуждается в случайности для распределения программ в памяти. При этом, конечно, компьютер, как детерминированная система, не может создавать истинные случайные числа.

Когда речь заходит о генераторах случайных (или псевдослучайных) чисел, рассказ всегда строится вокруг поиска истинной случайности. Пока серьезные математики десятилетиями ведут дискуссии о том, что считать случайностью, в практическом отношении мы давно научились использовать «правильную» энтропию. Впрочем, «шум» — это лишь вершина айсберга.

С чего начать, если мы хотим распутать клубок самых сильных алгоритмов PRNG и TRNG? На самом деле, с какими бы алгоритмами вы не имели дело, все сводится к трем китам: seed, таблица предопределенных констант и математические формулы.

Каким бы ни был seed, еще есть алгоритмы, участвующие в генераторах истинных случайных чисел, и такие алгоритмы никогда не бывают случайными.

Что такое случайность

Первое подходящее определение случайной последовательности дал в 1966 году шведский статистик Пер Мартин-Лёф, ученик одного из крупнейших математиков XX века Андрея Колмогорова. Ранее исследователи пытались определить случайную последовательность как последовательность, которая проходила все тесты на случайность.

Основная идея Мартина-Лёфа заключалась в том, чтобы использовать теорию вычислимости для формального определения понятия теста случайности. Это контрастирует с идеей случайности в вероятности; в этой теории ни один конкретный элемент пространства выборки не может быть назван случайным.

«Случайная последовательность» в представлениях Мартина-Лёфа должна быть типичной, т.е. не должна обладать индивидуальными отличительными особенностями.

Было показано, что случайность Мартина-Лёфа допускает много эквивалентных характеристик, каждая из которых удовлетворяет нашему интуитивному представлению о свойствах, которые должны иметь случайные последовательности:

• несжимаемость;
• прохождение статистических тестов для случайности;
• сложность создания прогнозов.

Существование множественных определений рандомизации Мартина-Лёфа и устойчивость этих определений при разных моделях вычислений свидетельствуют о том, что случайность Мартина-Лёфа является фундаментальным свойством математики.

Seed: основа псевдослучайных алгоритмов

Первые алгоритмы формирования случайных чисел выполняли ряд основных арифметических действий: умножить, разделить, добавить, вычесть, взять средние числа и т.д. Сегодня такие мощные алгоритмы, как Fortuna и Yarrow (используется в FreeBSD, AIX, Mac OS X, NetBSD) выглядят как генераторы случайных чисел для параноиков. Fortuna, например, это криптографический генератор, в котором для защиты от дискредитации после выполнения каждого запроса на случайные данные в размере 220 байт генерируются еще 256 бит псевдослучайных данных и используются в качестве нового ключа шифрования — старый ключ при этом каждый раз уничтожается.

Прошли годы, прежде чем простейшие алгоритмы эволюционировали до криптографически стойких генераторов псевдослучайных чисел. Частично этот процесс можно проследить на примере работы одной математической функции в языке С.

Функция rand () является простейшей из функций генерации случайных чисел в C.

#include <stdio.h>
#include <stdlib.h>

int main()
{
int r,a,b;

     puts("100 Random Numbers");
     for(a=0;a<20;a++)
     {
         for(b=0;b<5;b++)
         {
             r=rand();
             printf("%dt",r);
          }
          putchar('n');
      }
      return(0);
}

В этом примере рандома используется вложенный цикл для отображения 100 случайных значений. Функция rand () хороша при создании множества случайных значений, но они являются предсказуемыми. Чтобы сделать вывод менее предсказуемым, вам нужно добавить seed в генератор случайных чисел — это делается с помощью функции srand ().

Seed — это стартовое число, точка, с которой начинается последовательность псевдослучайных чисел. Генератор псевдослучайных чисел использует единственное начальное значение, откуда и следует его псевдослучайность. Генератор истинных случайных чисел всегда имеет в начале высококачественную случайную величину, предоставленную различными источниками энтропии.

#include <stdio.h>
#include <stdlib.h>

int main()
{
    unsigned seed;
    int r,a,b;

    printf("Input a random number seed: ");
    scanf("%u",&seed);
    srand(seed);
    for(a=0;a<20;a++)
    {
        for(b=0;b<5;b++)
        {
            r=rand();
            printf("%dt",r);
         }
         putchar('n');
     }  
     return(0);
}

srand() принимает число и ставит его в качестве отправной точки. Если seed не выставить, то при каждом запуске программы мы будем получать одинаковые случайные числа.

Вот пример простой формулы случайного числа из «классики» — книги «Язык программирования C» Кернигана и Ричи, первое издание которой вышло аж в 1978 году:

int rand() { random_seed = random_seed * 1103515245 +12345;  
return (unsigned int)(random_seed / 65536) % 32768; }

Эта формула предполагает существование переменной, называемой random_seed, изначально заданной некоторым числом. Переменная random_seed умножается на 1 103 535 245, а затем 12 345 добавляется к результату; random_seed затем заменяется этим новым значением. Это на самом деле довольно хороший генератор псевдослучайных чисел. Если вы используете его для создания случайных чисел от 0 до 9, то первые 20 значений, которые он вернет при seed = 10, будут такими:

44607423505664567674

Если у вас есть 10 000 значений от 0 до 9, то распределение будет следующим:

0 — 10151 — 10242 — 10483 — 9964 — 9885 — 10016 — 9967 — 10068 — 9659 — 961

Любая формула псевдослучайных чисел зависит от начального значения. Если вы предоставите функции rand() seed 10 на одном компьютере, и посмотрите на поток чисел, которые она производит, то результат будет идентичен «случайной последовательности», созданной на любом другом компьютере с seed 10.

К сожалению, у генератора случайных чисел есть и другая слабость: вы всегда можете предсказать, что будет дальше, основываясь на том, что было раньше. Чтобы получить следующее число в последовательности, мы должны всегда помнить последнее внутреннее состояние генератора — так называемый state. Без state мы будем снова делать одну и ту же математическую операцию с одинаковыми числами, чтобы получить тот же ответ.

Как сделать seed уникальным для каждого случая? Самое очевидное решение — добавить в вычисления текущее системное время. Сделать это можно с помощью функции time().

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
    int r,a,b;

    srand((unsigned)time(NULL));
    for(a=0;a<20;a++)
    {
        for(b=0;b<5;b++)
        {
            r=rand();
            printf("%dt",r);
         }
         putchar('n');
     }
     return(0);
}

Функция time() возвращает информацию о текущем времени суток, значение, которое постоянно изменяется. При этом метод typecasting гарантирует, что значение, возвращаемое функцией time(), является целым числом.

Итак, в результате добавления «случайного» системного времени функция rand() генерирует значения, которые являются более случайными, чем мы получили в первом примере.

Однако в этом случае seed можно угадать, зная системное время или время запуска приложения. Как правило, для приложений, где случайные числа являются абсолютно критичными, лучше всего найти альтернативное решение.

В .net framework есть функция System.Security.Cryptography.RandomNumberGenerator, где в расчетах учитываются следующие факторы:

• ID текущего процесса;
• текущий ID потока;
• количество отсчетов с момента загрузки;
• текущее время;
• различные высокоточные счетчики производительности процессора;
• MD4-хэш среды пользователя (имя пользователя, имя компьютера и т.д.).

Но опять же, все эти числа не случайны.

Лучшее, что вы можете сделать с детерминированными генераторами псевдослучайных чисел — добавить энтропию физических явлений.

Период (цикл) генератора

Одними из наиболее часто используемых методов генерации псевдослучайных чисел являются различные модификации линейного конгруэнтного метода, схема которого была предложена Дерриком Лемером еще в 1949 году:

X_n+1 = (aX_n + c) mod m, где m — модуль, a — множитель, c — приращение, mod — операция взятия остатка от деления. Причем m > 0, 0 < a ≤ m, 0 < c ≤ m, также задается начальное значение X₀: 0 < X₀ ≤ m.

Линейный конгруэнтный метод дает нам повторяющиеся последовательности — конгруэнтная последовательность всегда образует «петли». Этот цикл (период), повторяющийся бесконечное число раз — свойство всех последовательностей вида X_n+1 = f(n).

В языке С линейно-конгруэнтный метод реализован в уже знакомой вам функции rand():

#define RAND_MAX 32767 
unsigned long next=1; 
int rand(void) 
{ next=next*1103515245+12345; 
return((unsigned int)(next/65536)%RAND_MAX);} 
void srand(unsigned int seed) 
{ next=seed; } 

Что вообще такое цикл с точки зрения случайных чисел? Период — это количество чисел, которое генерируется до того, как они вернутся в той же последовательности. Для примера число периодов в шифре А5 в среднем составляет 2²³, а сложность атаки 240, что позволяет взломать его на любом персональном компьютере.

Рассмотрим случай, когда seed равен 1, а период — 100 (на языке Haskell):

random i = (j, ans)
    where j   = 7 * i  `mod` 101
          ans = (j — 1) `mod` 10 + 1 — just the ones place, but 0 means 10

В результате мы получим следующий ответ:

random 1 —> ( 7, 7)
random 7 —> (49, 9)
random 49 —> (40, 10)
random 40 —> (78, 8)
random 78 —> (41, 1)
random 41 —> (85, 5)
random 85 —> (90, 10)
random 90 —> (24, 4)
random 24 —> (67, 7)
random 67 —> (65, 5)
random 65 —> (51, 1)

Это лишь пример и подобную структуру в реальной жизни не используют. В Haskell, если вы хотите построить случайную последовательность, можно воспользоваться следующим кодом:

random :: StdGen —> (Int, StdGen)

Выбор случайного Int дает вам обратно Int и новый StdGen, который вы можете использовать для получения более псевдослучайных чисел. Многие языки программирования, включая Haskell, имеют генераторы случайных чисел, которые автоматически запоминают свое состояние (в Haskell это randomIO).

Чем больше величина периода, тем выше надежность создания хороших случайных значений, однако даже с миллиардами циклов крайне важно использовать надежный seed. Реальные генераторы случайных чисел обычно используют атмосферный шум (поставьте сюда любое физическое явление — от движения мыши пользователя до радиоактивного распада), но мы можем и схитрить программным методом, добавив в seed асинхронные потоки различного мусора, будь то длины интервалов между последними heartbeat потоками или временем ожидания mutual exclusion (а лучше добавить все вместе).

Истинная случайность бит

Итак, получив seed с примесью данных от реальных физических явлений (либо максимально усложнив жизнь будущему взломщику самым большим набором потоков программного мусора, который только сможем придумать), установив state для защиты от ошибки повтора значений и добавив криптографических алгоритмов (или сложных математических задач), мы получим некоторый набор данных, который будем считать случайной последовательностью. Что дальше?

Дальше мы возвращаемся к самому началу, к одному из фундаментальных требований — тестам.

Национальный институт стандартов и технологий США вложил в «Пакет статистических тестов для случайных и псевдослучайных генераторов чисел для криптографических приложений» 15 базовых проверок. Ими можно и ограничиться, но этот пакет вовсе не является «вершиной» проверки случайности.

Одни из самых строгих статистических тестов предложил профессор Джордж Марсалья из Университета штата Флорида. «Тесты diehard» включают 17 различных проверок, некоторые из них требуют очень длинных последовательностей: минимум 268 мегабайт.

Случайность можно проверить с помощью библиотеки TestU01, представленной Пьером Л’Экуйе и Ричардом Симардом из Монреальского университета, включающей классические тесты и некоторые оригинальные, а также посредством общедоступной библиотеки SPRNG.

Еще один полезный сервис для количественного измерения случайности.

Случайные числа — искусственно полученная последовательность реализаций случайной величины с заданным законом распределения.

Применение случайных чисел[править | править код]

Случайные числа используются при исследовании и оптимизации сложных стохастических систем методом статистического моделирования (см. метод Монте-Карло) с помощью компьютеров.

Способы получения[править | править код]

Известны три способа получения случайных чисел:

1. с помощью таблиц случайных чисел;
2. с помощью специальных устройств — генераторов случайных чисел;
3. путем замены случайных чисел последовательности так называемых псевдослучайных чисел.

Случайные числа, используемые для моделирования некоторой случайной системы, должны удовлетворять двум основным требованиям:

1. с достаточной точностью воспроизводить поведение моделируемой случайной величины с заданным распределением;
2. требовать минимальное количество компьютерных операций для формирования одного случайного числа.

Любая последовательность случайных чисел лишь приблизительно воспроизводит поведение моделируемой случайной величины. Точность такого приближения можно определять проводя статистическую оценку последовательности случайных чисел достаточно большого объема, используя известные статистические критерии, например критерий χ².

См. также[править | править код]

• Случайное простое число
• Случайная величина
• Генератор псевдослучайных чисел

Литература[править | править код]

• Енциклопедія кібернетики, Костіна Н. И., т. 2, ст. 377. (укр.)