Как найти случайную погрешность физика

Случайные погрешности в лабораторных работах по физике можно оценивать только с использованием калькулятора

О теории случайных погрешностей

Теория случайных погрешностей была создана К.Ф.Гауссом в первой половине XIX в. в связи с его занятиями астрономией и геодезией.

Напомним, что случайные погрешности δ_i = x_i – a проявляются при проведении серии измерений одной и той же физической величины в неизменных условиях одним и тем же методом.

Одним из фундаментальных положений теории Гаусса является “принцип арифметической середины”. В соответствии с этим принципом за истинное значение величины а принимается среднее значение

при n → ∞, если метод не сопровождается систематическими погрешностями.

Для случайных погрешностей характерны следующие свойства:

1. Положительные и отрицательные случайные погрешности встречаются с одинаковой вероятностью, т. е. одинаково часто.
2. Среднее арифметическое из алгебраической суммы случайных погрешностей при неограниченном возрастании числа наблюдений стремится к нулю, т. е.

   

3. Малые по абсолютной величине случайные погрешности встречаются с большей вероятностью, чем большие.

Основная идея теории Гаусса может быть выражена следующим образом

Возможные конкретные значения случайной погрешности, как и сам результат измерения, предсказать невозможно. Однако после того как экспериментатор определил измеряемый параметр и метод его измерения, сразу “возник” объективный закон, неизвестный исследователю. Этот закон определяет совокупность случайных погрешностей, которые возникают в процессе измерений.

Всегда можно эмпирически (на конкретных опытах) выявить закон распределения случайных погрешностей, который обычно выражается в виде так называемой функции распределения f(δ). Этот закон позволяет определить вероятность, с которой погрешность может оказаться в интервале от δ₁ до δ₂. Вероятность эта равна площади заштрихованной криволинейной трапеции, представленной на графике функции распределения.

Гауссу удалось определить универсальный закон распределения, которому подчиняется огромный класс случайных погрешностей измерений самых разных величин различными методами.

Этот закон носит название нормального закона распределения. Конечно, существуют измерения, погрешность которых не распределена по нормальному закону. Однако всегда можно определить степень их отклонения от нормального закона.

Функция распределения φ(δ), открытая Гауссом, имеет следующие свойства:

1) Функция δ(φ) четная, т. е. δ-(φ-)δ(φ), и в силу этого симметрична относительно оси координат.

2) Функция δ(φ) имеет максимум при значениях случайной погрешности, равных нулю.

3) Функция δ(φ) имеет две точки перегиба, расположенные симметрично относительно оси координат. Координаты точек перегиба равны ±σ.

4) Касательные к кривой δ(φ) в точках перегиба отсекают на оси абcцисс отрезки, равные ±2σ.

5) Максимальное значение функции δ(φ) равно

6) Площадь под всей кривой δ(φ) стремится к 1. Площадь криволинейной трапеции, ограниченной прямыми, проходящими через точки δ_1,2 = ±σ, составляет 0,68 от всей площади; если прямые проходят через точки δ_3,4 = ±2σ, то площадь составляет 0,95; площадь криволинейной трапеции, ограниченной прямыми δ_5,6 = ±3σ, равна 0,99.

Параметр σ, определяющий все фундаментальные свойства нормального закона, называется средним квадратическим отклонением. Этот параметр может быть определен после получения достаточно большой серии результатов измерений x₁, х₂, х₃, …, х_n. Тогда

Важность параметра σ состоит в том, что он позволяет определить границы случайных погрешностей. Действительно, вероятность получения случайных погрешностей, превосходящих по абсолютной величине 3σ, равна 1%.

При обычной организации измерений не представляется возможности провести не только бесконечно большое число измерений, но и провести просто большое их число.

Специальные исследования показали, что такая граница может быть определена при небольшом числе опытов в серии.

В такой серии из k измерений находят так называемую среднюю квадратичную погрешность

Затем Δх_кв увеличивают в S раз.

Число S называется коэффициентом Стьюдента (коэффициент был предложен в 1908 г. английским математиком В. С. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент – студент). Коэффициент Стьюдента позволяет определить границу случайной погрешности серии: Δх_случ = S Δх_кв.

Таблица коэффициентов S для различного числа опытов в серии

Погрешность среднего арифметического

После проведения серии равноточных измерений и нахождения х_ср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [х_ср ± 3σ], если в серии достаточно много измерений, и имеет вид [х_ср ± S Δх_кв] при небольшом числе опытов. Это означает, что 3σ (или S Δх_кв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σ_х или ΔS_кв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около х_ср, чем [x_cp ± 3σ_х].

Понять, почему должно быть именно так, помогут следующие рассуждения

Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение х_ср. Таких средних значений получается N: х_ср1, х_ср2, …, x_cpN. Для этой совокупности средних определяется среднее квадратичное отклонение

Величина σ_{х ср} характеризует предельное распределение средних значений, это и есть величина, которая позволяет найти интервал, в котором находится истинное значение измеряемой в опыте величины [х_ср ± 3σ_{х ср}]. На практике такая процедура никогда не реализуется не только потому, что это очень трудоемко, но и потому, что теория погрешностей позволяет по результатам одной серии определить погрешность среднего. Это делается на основе фундаментального результата теории погрешностей:

стандартное отклонение среднего σ_{х ср} в  раз меньше стандартного отклонения каждого опыта серии σ_х, т.е.

Итак, если в серии с достаточно большим числом опытов определено х_ср, то граница случайной погрешности среднего равна

Если в серии небольшое число опытов, то граница случайной погрешности среднего находится по формуле:

Все расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел “Статистические расчеты”), следуя методическим рекомендациям, приведенным ниже.

Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей

1. Включаем калькулятор, клавиша [ON]
2. Нажимаем клавишу [SHIFT](SETUP)
3. Входим в режим статистики. Нажимаем клавишу [2]
4. Выбираем режим 1-Variable. Нажимаем клавишу [1]
5. Заполняем таблицу
6. Нажимаем клавишу [OPTN]
7. Выбираем режим 1-Variable. Нажимаем клавишу [3]
8. На дисплее получаем ряд характеристик
   8.1. Первая сверху – значение среднего значения
   8.2. Вторая снизу – случайная погрешность каждого опыта серии σ_х
9. Вычисляем погрешность среднего
   
10. Находим границу случайной погрешности среднего
    

Пример

Измерялась скорость тела, брошенного горизонтально. В десяти опытах были получены следующие значения дальности полета L (в мм): 250, 245, 250, 262, 245, 248, 262, 260, 260, 248. Дальность полета тела измерялась линейкой с основной погрешностью Δ₁ = 1мм. Высота, с которой брошено тело, в опыте равнялась Н = 1 м и измерялась мерной лентой с основной погрешностью Δ₂ = 1 см и ценой деления С₂ =1 см.

Решение

Сначала определим среднее значение дальности полета тела и вычислим его начальную скорость. Для этого сведем все данные в таблицу и проведем их первичную обработку.

Так как

Легко определить среднее значение скорости по результатам серии опытов:

Граница относительной погрешности измерения скорости:

В этой формуле ΔL – граница абсолютной погрешности измерения дальности полета, Δg – погрешность округления g, ΔН – погрешность прямого однократного измерения высоты.

ΔН = 1 см + 0,5 см = 1,5 см

ΔL складывается из погрешности линейки Δ₁ и случайной погрешности ΔL_случ.:

ΔL = Δ₁ + ΔL_случ.

Так как ΔL_кв = 7мм, то при оценке ΔL_случ. нет смысла учитывать погрешность линейки Δ₁ = 1мм.

Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для ε_v следует вместо ∆L подставить его границу ∆L = S ∆L_кв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).

Имеем:

Первое слагаемое в этой сумме равно 0,09; слагаемое в скобках (0,01 + 0,0075) = 0,0175. Следовательно, ε_v = 0,09. Граница абсолютной погрешности каждого опыта серии не превосходит

ε_v = ε₀ = 0,565 ∙ 0,09 = 0,05 м/с

Это значит, если на данной установке провести еще один опыт, то гарантировать можно, что значение скорости, рассчитанное по его результатам, будет принадлежать интервалу [(0,56 – 0,05)м/с; (0,56 + 0,05)м/с].

Найдем границу случайной погрешности среднего значения скорости тела, брошенного горизонтально. Для этого в формулу для ε_v следует вместо ∆L подставить границу случайной погрешности среднего:

Таким образом,

Относительная погрешность среднего равна

0,027 + 0,01 + 0,0075

Последним слагаемым в этой сумме можно пренебречь. Итак, ср = 0,04 = 4%. Мы видим, что погрешность среднего в два раза меньше погрешности каждого опыта. Граница абсолютной погрешности среднего равна:

Таким образом, из серии 10 опытов по измерению скорости можно сделать вывод о том, что в любой другой такой серии из 10 опытов на данной установке среднее значение скорости будет находиться в интервале [(0,56 – 0,02)м/с; (0,56 + 0,02)м/с]. Этому же интервалу принадлежит неизвестное значение скорости, которое получится, если проделать серию с очень большим числом опытов, т. е. такое значение, которое можно назвать истинным значением.

Вычисление случайных погрешностей при измерениях

Пусть при измерениях
систематические погрешности пренебрежимо
малы. Рассмотрим случай, когда измерение
проведено большое число раз (n→∞).

Как показывает
опыт, отклонение результатов измерений
от их среднего значения в большую или
меньшую сторону одинаковы. Результаты
измерений с малым отклонением от среднего
значения наблюдается значительно чаще,
чем с большими отклонениями.

Расположим все
численные значения результатов измерений
в ряд в порядке их возрастания и разделим
этот ряд на равные интервалы.
Пусть–
число измерений с результатом, попавшим
в интервал [].
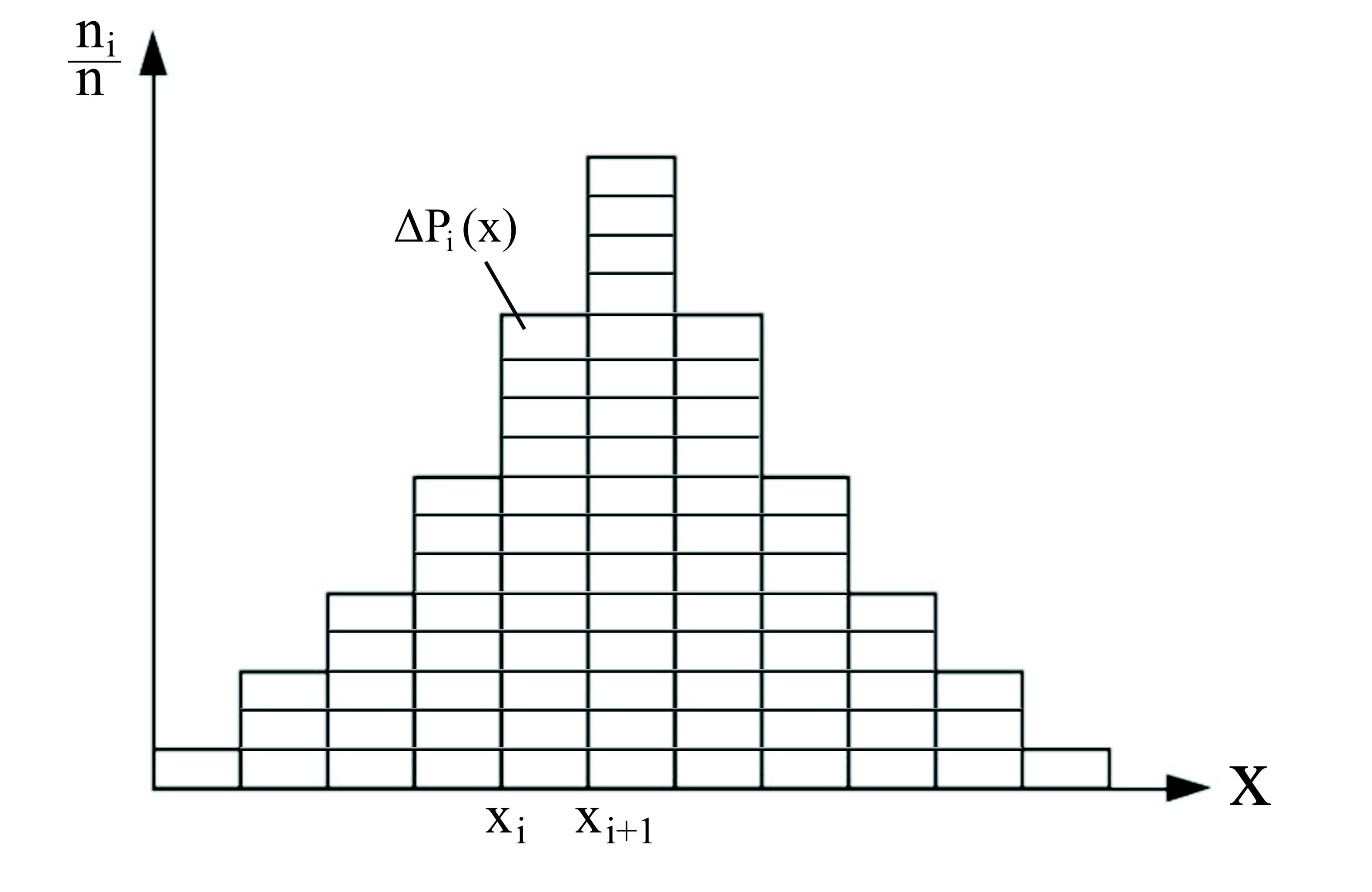
Величинаесть вероятность ΔP_i(х)
получения результата со значением в
интервале [].

Графически
представим
,
соответствующее каждому интервалу []
(рис.1). Изображенная на рис.1 ступенчатая
кривая называется гистограммой. Допустим,
что измерительный прибор обладает
чрезвычайно высокой чувствительностью.
Тогда ширину интервала можно сделать
бесконечно малой величинойdx.
Ступенчатая кривая в этом случае
заменяется кривой, представляемой
функцией φ(х) (рис.2). Функцию φ(х) принято
называть функцией плотности распределения.
Её смысл состоит в том, что произведение
φ(х)dx
есть вероятность dP(x)
получения результатов со значением в
интервале от х до х+dх.
Графически значение вероятности
представляется в виде площади
заштрихованного прямоугольника.
Аналитически функция плотности
распределения записывается следующим
образом:

.
(5)

Представленную в
виде (5) функцию φ(х) называют функцией
Гаусса, а соответствующее распределение
результатов измерений Гауссовым или
нормальным.

рис.1

Параметры
иσ
имеют следующий смысл (рис.2).

–среднее значение
результатов измерений. При
=функция Гаусса достигает максимального
значения. Если число измерений бесконечно
велико, торавно истинному значению измеряемой
величины.

σ
– характеризует степень разброса
результатов измерения от их среднего
значения. Параметр σ
вычисляется по формуле:

.
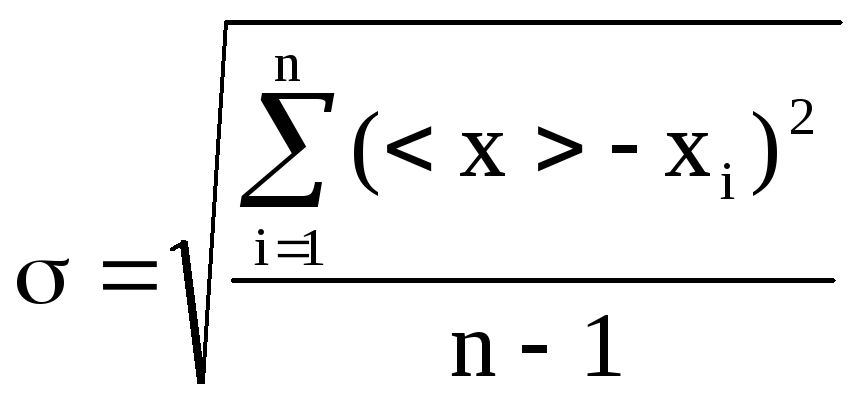
(6)

Этот параметр
представляет собой среднеквадратичную
погрешность. Величину σ²
в теории
вероятностей называют дисперсией
функции φ(х).

Чем выше точность
измерений, тем ближе располагаются
результаты измерений к истинному
значению измеряемой величины, и,
следовательно, меньше σ.

Вид функции φ(х),
очевидно, не зависит от числа измерений.

В теории вероятностей
показано, что 68% всех измерений дадут
результат, который располагается в
интервале
,
95% – в интервале []
и 99,7% в интервале [].

рис.2

Таким образом, с
вероятностью (надёжностью) 68% величина
отклонения результата измерения от
среднего значения лежит в интервале
[],
с вероятностью (надёжностью) 95% – в
интервале []
и с вероятностью (надежностью) 99,7% – в
интервале [].

Интервал,
соответствующий той или иной вероятности
отклонения от среднего значения,
называется доверительным.

В реальных
экспериментах число измерений, очевидно,
не может быть бесконечно большим, поэтому
маловероятно, чтобы
совпало с истинным значением измеряемой
величины.
В связи с этим важно оценить на основе
теории вероятностей величину возможного
отклоненияот.

Расчеты показывают,
что при числе измерений более 20 с
вероятностью 68%
попадает в доверительный интервал [],
с вероятностью 95% – в интервале[],
с вероятностью 99,7% – в интервале [].

Величина
,
определяющая границы доверительного
интервала, называется стандартным
отклонением или просто – стандартом.

Стандарт
вычисляется по формуле:

.
(7)

С
учетом формулы (6), выражение (7) приобретает
следующий вид:

.
(8)

Чем больше число
измерений n,
тем ближе Х располагается к
.
Если число измерений не велико меньше
15, то вместо распределения Гаусса
используют распределение Стьюдента,
которое приводит к увеличению ширины
доверительного интервала возможного
отклонения Х отвt_n,p
раз.

Сомножитель t_n,p
называется коэффициентом Стьюдента.
Индексы Р и n
указывают, с какой надежностью и какому
числу измерений соответствует коэффициент
Стьюдента. Величина коэффициента
Стьюдента для данного числа измерений
и заданной надежности определяется по
таблице 1.

Таблица
1

Коэффициент
Стьюдента.

Число измерений n	Надежность Р,%
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,999
2 3 4 5 6 7 8 9 10 15 20 40 60 120 ∞	1,00 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,69 0,69 0,68 0,68 0,68 0,67	1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,87 0,86 0,85 0,85 0,85 0,84	2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,0	3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,3 1,3 1,3 1,3 1,3 1,3	6,3 2,9 2,1 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,7 1,7 1,7 1,7 1,6	12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,1 2,1 2,0 2,0 2,0 2,0	31,8 7,0 4,5 3,7 3,4 3,1 3,0 2,9 2,8 2,6 2,5 2,4 2,4 2,4 2,3	36,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,1 3,9 3,6 3,5 3,4 3,3

Например, при
заданной надежности 95% и числе измерений
n=20
коэффициент Стьюдента t_20,95=2,1
(доверительный интервал
)
при числе измеренийn=4,
t_4,95=3,2
(доверительный интервал
).
То есть, при увеличении числа измерений
с 4 до 20 возможное отклонениеотX
уменьшается в 1,524 раза.

Таким образом,
чтобы рассчитать абсолютную случайную
погрешность необходимо:

1. Провести несколько
   измерений.

2. Найти средний
   арифметический результат измерений.

3. Вычислить по
   формуле (8) стандартное отклонение.

4. По таблице найти
   для заданной надежности коэффициент
   Стьюдента. Величина t_n,p
   S_m
   есть абсолютная погрешность
   в определении Х.

5. Результат записать
   в виде Х=(с надежностью Р).

Ниже приводится
пример расчета абсолютной случайной
погрешности

№	Хi	Хi – <X>	(Хi – <X>)2
1 2 3 4 5 6	20,2 19,6 19,9 20,4 20,2 20,3	-0.1 +0.5 +0.2 -0.3 -0.1 -0.2	0.01 0.25 0.04 0.09 0.01 0.04
∑	120,6		0,44

По формуле (2)
находим среднее значение измеряемой
величины
(без указания размерности физической
величины)

.

По
формуле (8) вычисляем величину стандартного
отклонения

.

Коэффициент
Стьюдента, определенный для n=6,
и Р=95%, t_6,95=2,6
окончательный результат:

Х=20,1±2,6·0,121=20,1±0,315
(с Р=95%).

Вычисляем
относительную погрешность:

.

При записи
окончательного результата измерений
нужно иметь в виду, что погрешность
должна содержать только одну значащую
цифру (отличную от нуля). Две значащие
цифры в погрешности записываются лишь
в том случае, если предпоследняя цифра
1. Большее число значащих цифр записывать
бесполезно, поскольку они будут не
достоверны. В записи среднего значения
измеряемой величины последняя цифра
должна принадлежать тому же разряду,
что и последняя цифра в записи погрешности.

Примеры:

Х=531±2;

Х=(243±5)·10²;

Х=232,567±0,003.

При проведении
нескольких измерений может получится
один и тот же результат. Это возможно в
том случае, если чувствительность
измерительного прибора низкая. Когда
измерение производится прибором с
низкой чувствительностью достаточно
и однократного измерения. Не имеет
смысла, например, многократно измерять
длину стола рулеткой с сантиметровыми
делениями. Результат измерения в этом
случае будет один и тот же. Погрешность
при проведении однократного измерения
определяется ценой наименьшего деления
прибора. Она называется приборной
погрешностью. Её значение
вычисляется по следующей формуле:

,
(10)

где γ – цена деления
прибора;

t_∞,p
– коэффициент Стьюдента, соответствующий
бесконечно большому числу измерений.

С учетом приборной
погрешности, абсолютная погрешность с
заданной надежностью определяется по
формуле:

,
(11)

где
.

С учетом формул
(8) и (10), (11) записывается так:

.
(12)

В литературе для
сокращения записи величину погрешности
иногда не указывают. Предполагается,
что величина погрешности составляет
половину единицы последней значащей
цифры. Так, например, величина радиуса
Земли записана в виде
м.
Это означает, что в качестве погрешности
следует взять величину, равную ±м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В статье представлен метод расчета случайной погрешности прямого измерения. К прямым измерениям относят нахождение величины из опытных данных с помощью прибора. К прямым измерениям можно отнести измерение длины линейкой, времени секундомером, объема цилиндром и так далее.

1. Измерим n раз некоторую величину X при одинаковых условиях. В результате получим набор значений X1, X2, X3,…,Xn.

2. Далее вычислим среднее арифметическое значение величины X по формуле:

Для увеличения точности измерений необходимо увеличить количество измерений. При многократном увеличении числа измерений среднее арифметическое значение измеряемой величины будет стремиться к её истинному значению. То есть следует учитывать, что при конечном числе они будут равны друг другу лишь приближенно. Поэтому необходимо определять степень этого приближения, чтобы данное количество было достаточным для оценки результата.

3. Найдем среднее квадратичное отклонение среднего арифметического:

При этом значение случайной погрешности в случае небольшого числа измерений можно представить в виде

где t – это коэффициент Стьюдента, зависящий от доверительной вероятности и числа измерений . Значения коэффициента Стьюдента для доверительной вероятности приведены в таблице.

Таблица 1

Значения коэффициента Стьюдента.

Случайная погрешность – это ошибка в измерениях, которая носит неконтролируемый характер и очень труднопредсказуема. Так происходит из-за того, что существует огромное количество параметров, находящихся вне контроля экспериментатора, которые влияют на итоговые показатели. Случайные погрешности с абсолютной точностью вычислить невозможно. Они вызваны не сразу очевидными источниками и требуют много времени на выяснение причины их возникновения.

Как определить наличие случайной погрешности

Непредсказуемые ошибки присутствует не во всех измерениях. Но для того чтобы полностью исключить ее возможное влияние на результаты измерений, необходимо повторить эту процедуру несколько раз. Если итог не меняется от эксперимента к эксперименту либо изменяется, но на определенное относительное число – величина этой случайной погрешности равна нулю, и о ней можно не думать. И, наоборот, если полученный результат измерений каждый раз другой (близкий к какому-то среднему значению, но отличный), и отличия носят неопределенный характер, следовательно, на него влияет непредсказуемая ошибка.

Пример возникновения

Случайная составляющая погрешности возникает вследствие действия различных факторов. Например, при измерении сопротивления проводника, необходимо собрать электрическую цепь, состоящую из вольтметра, амперметра и источника тока, которым служит выпрямитель, подключенный в осветительную сеть. Первым делом нужно измерить напряжение, записав показания с вольтметра. Затем перенести взгляд на амперметр, чтобы зафиксировать его данные о силе тока. После использовать формулу, где R = U / I.

Но может случиться так, что в момент снятия показаний с вольтметра в соседней комнате включили кондиционер. Это довольно мощный прибор. В результате этого напряжение сети немного уменьшилось. Если бы не пришлось отводить взгляд на амперметр, можно было заметить, что показания вольтметра изменились. Поэтому данные первого прибора уже не соответствуют записанным ранее значениям. Из-за непредсказуемого включения кондиционера в соседней комнате получается результат уже со случайной погрешностью. Сквозняки, трения в осях измерительных приборов – потенциальные источники ошибок в измерениях.

Как проявляется

Допустим, необходимо рассчитать сопротивление круглого проводника. Для этого нужно знать его длину и диаметр. Помимо этого, учитывается удельное сопротивление материала, из которого он изготовлен. При измерении длины проводника случайная погрешность себя проявлять не будет. Ведь этот параметр всегда один и тот же. Но вот при измерении диаметра штангенциркулем или микрометром окажется, что данные разняться. Так происходит потому, что идеально круглый проводник невозможно изготовить в принципе. Поэтому, если измерить диаметр в нескольких местах изделия, то он может оказаться разным вследствие действия непредсказуемых факторов в момент его изготовления. Это случайная погрешность.

Иногда она также называется статистической погрешностью, поскольку эту величину можно уменьшить, увеличив количество экспериментов при одинаковых условиях их проведения.

Природа возникновения

В отличие от систематической ошибки, простое усреднение нескольких итоговых показателей одной и той же величины компенсирует случайные погрешности результатов измерений. Природа их возникновения определяется очень редко, и поэтому никогда не фиксируется, как постоянная величина. Случайная погрешность – это отсутствие каких-либо природных закономерностей. Например, она не пропорциональна измеряемой величине или никогда не остается постоянной при проведении нескольких измерений.

Может существовать ряд возможных источников случайных ошибок в экспериментах, и он полностью зависит от типа эксперимента и используемых приборов.

Например, биолог, изучающий размножение конкретного штамма бактерии, может столкнуться с непредсказуемой ошибкой из-за небольшого изменения температуры или освещения в помещении. Однако когда эксперимент будет повторяться в течение определенного периода времени, он избавится от этих различий в результатах путем их усреднения.

Формула случайной погрешности

Допустим, нужно определить какую-то физическую величину x. Чтобы исключить случайную погрешность необходимо провести несколько измерений, итогом которых будет серия результатов N количества измерений – x_1, x_2,…, x_n.

Чтобы обработать эти данные следует:

1. За результат измерений х₀ принять среднее арифметическое х̅. Иными словами, х₀ = (x₁ + x₂ +… + x_n) / N_.
2. Найти стандартное отклонение. Обозначается оно греческой буквой σ и вычисляется следующим образом: σ = √((х₁ – х̅ )² + (х₂-х̅ )² + … + (х_n – х̅ )² / N – 1). Физический смысл σ состоит в том, что если провести еще одно измерение (N+1), то оно с вероятностью 997 шансов из 1000 ляжет в интервал х̅ -3σ < х_n+1 < с + 3σ.
3. Найти границу абсолютной погрешности среднего арифметического х̅. Находится она по следующей формуле: Δх = 3σ / √N.
4. Ответ: х = х̅ + (-Δх).

Относительная погрешность будет равна ε = Δх /х̅.

Пример вычисления

Формулы расчета случайной погрешности достаточно громоздкие, поэтому, чтобы не запутаться в вычислениях, лучше использовать табличный способ.

Пример:

При измерении длины l, были получены следующие значения: 250 см, 245 см, 262 см, 248 см, 260 см. Количество измерений N = 5.

N п/п	l, см	I ср. арифм., см	|l-l ср. арифм.|	(l-l ср. арифм.)2	σ, см	Δ l, см
1	250	253,0	3	9	7,55	10,13
2	245	8	64
3	262	9	81
4	248	5	25
5	260	7	49
	Σ = 1265			Σ = 228

Относительная погрешность равна ε = 10,13 см / 253,0 см = 0,0400 см.

Ответ: l = (253 + (-10)) см, ε = 4 %.

Практическая польза высокой точности измерений

Следует учитывать, что достоверность результатов тем выше, чем большее количество измерений проводится. Чтобы повысить точность в 10 раз, необходимо провести в 100 раз больше измерений. Это достаточно трудоемкое занятие. Однако оно может привести к очень важным результатам. Иногда приходится иметь дело со слабыми сигналами.

Например, в астрономических наблюдениях. Допустим, необходимо изучить звезду, блеск которой изменяется периодически. Но это небесное тело настолько далеко, что шум электронной аппаратуры или датчиков, принимающих излучения, может быть во много раз больше, чем сигнал, который необходимо обработать. Что же делать? Оказывается, если проводить миллионы измерений, то возможно среди этого шума выделить необходимый сигнал с очень большой достоверностью. Однако для этого потребуется совершать огромное количество измерений. Такая методика используется, чтобы различать слабые сигналы, которые едва заметны на фоне различных шумов.

Причина, по которой случайные погрешности могут быть решены путем усреднения, заключается в том, что они имеют нулевое ожидаемое значение. Они действительно непредсказуемы и разбросаны по среднему значению. Исходя из этого, среднее арифметическое ошибок ожидается равным нулю.

Случайная погрешность присутствуют в большинстве экспериментов. Поэтому исследователь должен быть подготовлен к ним. В отличие от систематических, случайные погрешности не предсказуемы. Это затрудняет их обнаружение, но от них легче избавиться, поскольку они являются статистическими и удаляются математическим методом, таким как усреднение.