Случайные погрешности в лабораторных работах по физике можно оценивать только с использованием калькулятора
О теории случайных погрешностей
Теория случайных погрешностей была создана К.Ф.Гауссом в первой половине XIX в. в связи с его занятиями астрономией и геодезией.
Напомним, что случайные погрешности δi = xi – a проявляются при проведении серии измерений одной и той же физической величины в неизменных условиях одним и тем же методом.
Одним из фундаментальных положений теории Гаусса является “принцип арифметической середины”. В соответствии с этим принципом за истинное значение величины а принимается среднее значение
![]()
при n → ∞, если метод не сопровождается систематическими погрешностями.
Для случайных погрешностей характерны следующие свойства:
- Положительные и отрицательные случайные погрешности встречаются с одинаковой вероятностью, т. е. одинаково часто.
- Среднее арифметическое из алгебраической суммы случайных погрешностей при неограниченном возрастании числа наблюдений стремится к нулю, т. е.

- Малые по абсолютной величине случайные погрешности встречаются с большей вероятностью, чем большие.
Основная идея теории Гаусса может быть выражена следующим образом
Возможные конкретные значения случайной погрешности, как и сам результат измерения, предсказать невозможно. Однако после того как экспериментатор определил измеряемый параметр и метод его измерения, сразу “возник” объективный закон, неизвестный исследователю. Этот закон определяет совокупность случайных погрешностей, которые возникают в процессе измерений.
Всегда можно эмпирически (на конкретных опытах) выявить закон распределения случайных погрешностей, который обычно выражается в виде так называемой функции распределения f(δ). Этот закон позволяет определить вероятность, с которой погрешность может оказаться в интервале от δ1 до δ2. Вероятность эта равна площади заштрихованной криволинейной трапеции, представленной на графике функции распределения.

Гауссу удалось определить универсальный закон распределения, которому подчиняется огромный класс случайных погрешностей измерений самых разных величин различными методами.
Этот закон носит название нормального закона распределения. Конечно, существуют измерения, погрешность которых не распределена по нормальному закону. Однако всегда можно определить степень их отклонения от нормального закона.
Функция распределения φ(δ), открытая Гауссом, имеет следующие свойства:

1) Функция δ(φ) четная, т. е. δ-(φ-)δ(φ), и в силу этого симметрична относительно оси координат.
2) Функция δ(φ) имеет максимум при значениях случайной погрешности, равных нулю.
3) Функция δ(φ) имеет две точки перегиба, расположенные симметрично относительно оси координат. Координаты точек перегиба равны ±σ.
4) Касательные к кривой δ(φ) в точках перегиба отсекают на оси абcцисс отрезки, равные ±2σ.
5) Максимальное значение функции δ(φ) равно
![]()
6) Площадь под всей кривой δ(φ) стремится к 1. Площадь криволинейной трапеции, ограниченной прямыми, проходящими через точки δ1,2 = ±σ, составляет 0,68 от всей площади; если прямые проходят через точки δ3,4 = ±2σ, то площадь составляет 0,95; площадь криволинейной трапеции, ограниченной прямыми δ5,6 = ±3σ, равна 0,99.
Параметр σ, определяющий все фундаментальные свойства нормального закона, называется средним квадратическим отклонением. Этот параметр может быть определен после получения достаточно большой серии результатов измерений x1, х2, х3, …, хn. Тогда

Важность параметра σ состоит в том, что он позволяет определить границы случайных погрешностей. Действительно, вероятность получения случайных погрешностей, превосходящих по абсолютной величине 3σ, равна 1%.
При обычной организации измерений не представляется возможности провести не только бесконечно большое число измерений, но и провести просто большое их число.
Специальные исследования показали, что такая граница может быть определена при небольшом числе опытов в серии.
В такой серии из k измерений находят так называемую среднюю квадратичную погрешность

Затем Δхкв увеличивают в S раз.
Число S называется коэффициентом Стьюдента (коэффициент был предложен в 1908 г. английским математиком В. С. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент – студент). Коэффициент Стьюдента позволяет определить границу случайной погрешности серии: Δхслуч = S Δхкв.
Таблица коэффициентов S для различного числа опытов в серии

Погрешность среднего арифметического
После проведения серии равноточных измерений и нахождения хср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [хср ± 3σ], если в серии достаточно много измерений, и имеет вид [хср ± S Δхкв] при небольшом числе опытов. Это означает, что 3σ (или S Δхкв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σх или ΔSкв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около хср, чем [xcp ± 3σх].
Понять, почему должно быть именно так, помогут следующие рассуждения
Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение хср. Таких средних значений получается N: хср1, хср2, …, xcpN. Для этой совокупности средних определяется среднее квадратичное отклонение
![]()
Величина σх ср характеризует предельное распределение средних значений, это и есть величина, которая позволяет найти интервал, в котором находится истинное значение измеряемой в опыте величины [хср ± 3σх ср]. На практике такая процедура никогда не реализуется не только потому, что это очень трудоемко, но и потому, что теория погрешностей позволяет по результатам одной серии определить погрешность среднего. Это делается на основе фундаментального результата теории погрешностей:
стандартное отклонение среднего σх ср в ![]() раз меньше стандартного отклонения каждого опыта серии σх, т.е.
раз меньше стандартного отклонения каждого опыта серии σх, т.е.
![]()
Итак, если в серии с достаточно большим числом опытов определено хср, то граница случайной погрешности среднего равна
![]()
Если в серии небольшое число опытов, то граница случайной погрешности среднего находится по формуле:

Все расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел “Статистические расчеты”), следуя методическим рекомендациям, приведенным ниже.
Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей
- Включаем калькулятор, клавиша [ON]
- Нажимаем клавишу [SHIFT](SETUP)
- Входим в режим статистики. Нажимаем клавишу [2]
- Выбираем режим 1-Variable. Нажимаем клавишу [1]
- Заполняем таблицу
- Нажимаем клавишу [OPTN]
- Выбираем режим 1-Variable. Нажимаем клавишу [3]
- На дисплее получаем ряд характеристик
8.1. Первая сверху – значение среднего значения
8.2. Вторая снизу – случайная погрешность каждого опыта серии σх - Вычисляем погрешность среднего

- Находим границу случайной погрешности среднего

Пример
Измерялась скорость тела, брошенного горизонтально. В десяти опытах были получены следующие значения дальности полета L (в мм): 250, 245, 250, 262, 245, 248, 262, 260, 260, 248. Дальность полета тела измерялась линейкой с основной погрешностью Δ1 = 1мм. Высота, с которой брошено тело, в опыте равнялась Н = 1 м и измерялась мерной лентой с основной погрешностью Δ2 = 1 см и ценой деления С2 =1 см.

Решение
Сначала определим среднее значение дальности полета тела и вычислим его начальную скорость. Для этого сведем все данные в таблицу и проведем их первичную обработку.

Так как

Легко определить среднее значение скорости по результатам серии опытов:
![]()
Граница относительной погрешности измерения скорости:

В этой формуле ΔL – граница абсолютной погрешности измерения дальности полета, Δg – погрешность округления g, ΔН – погрешность прямого однократного измерения высоты.
ΔН = 1 см + 0,5 см = 1,5 см
ΔL складывается из погрешности линейки Δ1 и случайной погрешности ΔLслуч.:
ΔL = Δ1 + ΔLслуч.
Так как ΔLкв = 7мм, то при оценке ΔLслуч. нет смысла учитывать погрешность линейки Δ1 = 1мм.
Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для εv следует вместо ∆L подставить его границу ∆L = S ∆Lкв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).
Имеем:
![]()
Первое слагаемое в этой сумме равно 0,09; слагаемое в скобках (0,01 + 0,0075) = 0,0175. Следовательно, εv = 0,09. Граница абсолютной погрешности каждого опыта серии не превосходит
εv = ε0 = 0,565 ∙ 0,09 = 0,05 м/с
Это значит, если на данной установке провести еще один опыт, то гарантировать можно, что значение скорости, рассчитанное по его результатам, будет принадлежать интервалу [(0,56 – 0,05)м/с; (0,56 + 0,05)м/с].
Найдем границу случайной погрешности среднего значения скорости тела, брошенного горизонтально. Для этого в формулу для εv следует вместо ∆L подставить границу случайной погрешности среднего:
![]()
Таким образом,
![]()
Относительная погрешность среднего равна
0,027 + 0,01 + 0,0075
Последним слагаемым в этой сумме можно пренебречь. Итак, ср = 0,04 = 4%. Мы видим, что погрешность среднего в два раза меньше погрешности каждого опыта. Граница абсолютной погрешности среднего равна:
![]()
Таким образом, из серии 10 опытов по измерению скорости можно сделать вывод о том, что в любой другой такой серии из 10 опытов на данной установке среднее значение скорости будет находиться в интервале [(0,56 – 0,02)м/с; (0,56 + 0,02)м/с]. Этому же интервалу принадлежит неизвестное значение скорости, которое получится, если проделать серию с очень большим числом опытов, т. е. такое значение, которое можно назвать истинным значением.
4.1.
Основные
свойства случайных величин.
Пусть Хi
– некоторая случайная величина,
принимающая непрерывный ряд значений
(Х1,
Х2,
Х3,
…,Хn),
которые подчиняются определенному
закону распределения.
Функция
Y
=f (Xi),
характеризующая вероятность попадания
случайной величины Хi
в единичный интервал (Х=1),
называется плотностью вероятности.
Вероятность
того, что случайная величина Хi
попадает в интервал [X,
(X
dX)],
будет равна
![]()
Вероятность
того, что случайная величина обнаруживается
в интервале значений [X,
(X
dX)],
равна
![]() .
.
Вероятность
того, что случайная величина обнаруживается
в интервале значений от -
до +,
равна 1, т.е. такое событие будет
достоверным, а сама функция f(X)
– нормируемой.
![]()
4.2.
Функция
распределения случайных величин и ее
свойства.
Всякое
соотношение, устанавливающее связь
между возможными значениями, называется
законом распределения случайных величин.
Одним из наиболее распространенных
является нормальный закон распределения
(НЗР) Гаусса, для которого характерно
то, что среднее арифметическое значение
измеряемой величины является наиболее
вероятным; другими словами, среднее
арифметическое значение <X>
является наилучшим приближением к
истинному значению.
Закон
Гаусса имеет вид:
 (8)
(8)
где
<X>
– среднее арифметическое значение,
определяемое по формуле (6);
– средняя квадратичная погрешность,
определяемая по формуле:
 ,
,
(9)
г

Рис.4
де Xi
– результат i – измерения; (Хi
– <X>) – абсолютная погрешность
отдельного измерения.
На
рис.4 графически представлена зависимость
f(Х). Как показали исследования, кривая
распределения Гаусса симметрична
относительно прямой Х = <X>, т.е.
отклонения случайных величин Xi
вправо и влево от <X> равновероятны
(встречаются одинаково часто).
При
Х = <X> плотность вероятности принимает
максимальное значение, равное
![]() (10)
(10)
При
Х0
и Х
кривая распределения асимптотически
приближается к оси абсцисс (f(Х)0).
Средняя
квадратичная погрешность (9) подбирается
так, что при проведении большого числа
серий измерений погрешность в 2/3 (67%)
случаев меньше ,
а в 1/3 (33%) случаев она больше .
Другими словами, если провести не одну,
а например 10 серий по 10 опытов в каждой,
то следует ожидать, что 67-70 случаях из
ста (10х10) измерений среднее значение
будет отличаться от истинного меньше,
чем на
(Х
< ),
а в остальных 33-30% случаях Х
> .
На
рис.4 заштрихованная область составляет
около 67% от всей площади под кривой, т.е.
наиболее часто встречаются случайные
величины Хi
в интервале [(<X>-);
(<X>+)].
4.3.
Доверительная
надежность и доверительный интервал.
Вероятность
того, что истинное значение содержится
в интервале от (Х-)
до (Х+),
называется доверительной
вероятностью
(или надежностью). Графически эта
надежность определяется как площадь
под кривой распределения (рис.4) в
интервале [(X-);
(X+)].
Сам интервал значений случайных величин
от (X-)
до (X+)
называется доверительным
интервалом.
Погрешность,
определяемая с надежностью
0,67, называется стандартной среднеквадратичной
погрешностью ст.
Формула (9) позволяет хорошо оценивать
величину стандартной погрешности, когда
число опытов n
5. Целесообразность оценки погрешности
с помощью формулы (9) объясняется тем,
что ст
является одним из параметров в формуле
Гаусса (8). Поэтому всегда можно рассчитать
вероятность того, что результат измерения
будет отличаться от <X>
не более, чем на ст.
Таким
образом, для характеристики случайной
погрешности измерений следует указывать
не только случайную погрешность, но и
надежность .
Результат измерений в этом случае
представляют в виде: X
= <X>
ст,
(с надежностью
0,67), где ст
определяет абсолютную погрешность
данной серии измерений. Это справедливо
при малом числе опытов (n
= 35).
От
величины стандартной средней квадратичной
погрешности зависит форма кривой
распределения: чем меньше ст,
тем выше максимум функции распределения
и тем более круто поднимается кривая
f(X).
4.4.
Критерий
определения грубой погрешности в
физическом эксперименте. Как
уже указывалось, погрешность ,
определяемая формулой (9), подбирается
так, что вероятность того, что результат
измерения отличается от истинного не
более, чем на
= ст,
равна 0,67. При этом Х
ст,
т.е. отношение
= Х/ст
= 1, а доверительная надежность
= 0,67.
В
табл.3 приведены значения доверительной
вероятности
при некоторых значениях отношений
(
= Х/ст).
Анализ этой таблицы показывает:
вероятность того, что измеренная величина
отличается от истинного на ст,
растет с увеличением абсолютной
погрешности Х.
Из
табл.3 видно, что при
= 1 (Х
= ст)
надежность =0,67.
Это означает, что в 67% случаев Х
< ст,
а в остальных 33% случаев Х
> ст.
Если
= 2 (Х
= 2ст),
то вероятность того, что результаты
измерений будут отличаться от истинного
не более, чем на 2ст,
равна 0,95, т.е. 95% случайных погрешностей
меньше 2ст,
а 5% – больше 2ст.
При
= 3 (Х
= 3ст)
надежность
= 0,997.
Таблица
3
|
|
0,9 |
1,0 |
1,5 |
1,7 |
2,0 |
2,5 |
3,0 |
|
|
0,63 |
0,67 |
0,87 |
0,91 |
0,95 |
0,988 |
0,997 |
Условились
считать, что если результат измерения
Хi
отличается от среднего значения <X>
больше, чем на 3ст,
то его отбрасывают как промах. Если Х
< 3ст,
результат оставляют в ряду измеренных.
Чаще всего при оценке погрешности
измерений в физическом практикуме
достаточной надежностью можно считать
= 0,95.
4.5.
Формула
для расчета случайной погрешности
(формула Стьюдента). Данные,
приведенные в табл.3, справедливы только
для большого числа опытов (n
> 30). Для оценки доверительной вероятности
в случае малого числа опытов (n
30) вместо параметра
вводят параметр t,n,
зависящий от числа опытов n
и надежности .
Этот коэффициент называют коэффициентом
Стьюдента. Он связан со средней
квадратичной погрешностью соотношением:
![]() (11)
(11)
Для
данного числа опытов (n
= const)
и выбранной надежности (
= const)
коэффициент Стьюдента имеет вполне
определенное значение.
Значение
t,n
приведены в табл.4. Сравнивая табл.3 и
табл.4, можно убедиться, что с увеличением
числа опытов значение коэффициента
Стьюдента t,n
уменьшается, приближаясь к значению
(при заданном ).
При
данном числе опытов (n = const) с ростом
надежности
коэффициент Стьюдента растет. Вообще
говоря, надежность выбирают произвольно,
в зависимости от значимости проводимых
измерений. Но можно договориться,
например, при проведении физического
практикума всегда выбирать
= 0,95.
Таблица
4
|
n |
Надежность |
||||||
|
0,63 |
0,70 |
0.80 |
0, |
0,95 |
0,98 |
0,99 |
|
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
7 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,4 |
|
12 |
0,87 |
1,1 |
1,4 |
1,8 |
2,2 |
2,7 |
3,1 |
|
15 |
0,87 |
1,1 |
1,3 |
1,8 |
2,2 |
2,7 |
3,0 |
|
25 |
0,86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,6 |
3,0 |
Анализ
табл.4 показывает, что с ростом числа
опытов (при заданной надежности )
коэффициент Стьюдента уменьшается, а,
следовательно, уменьшается и абсолютная
погрешность. Выразим Х
из формулы (11), получим выражение для
расчета случайной погрешности.
![]() (12)
(12)
Подставив
в последнее соотношение выражение для
средней квадратичной погрешности (9),
получим формулу расчета случайной
абсолютной погрешности в общем виде.
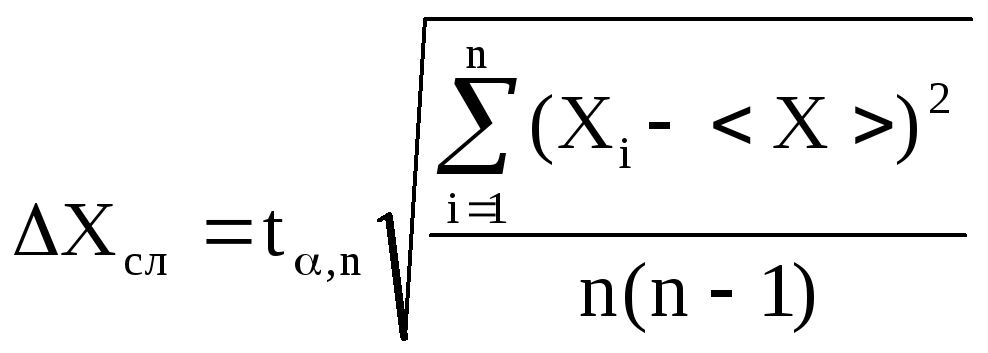 (13)
(13)
Оценив
случайную погрешность по формуле (13) и
сравнив ее с инструментальной (приборной)
погрешностью, студент должен решить,
что принять за абсолютную погрешность
эксперимента: либо Хпр,
либо Хсл,
либо искать полную погрешность по
формуле (7).
4.6.
Методика
обработки случайных величин, полученных
в физическом эксперименте.
Пусть в результате эксперимента по
измерению некоторой величины получен
статистический ряд значений (Х1,
Х2,
Х3,…,Хi,
…,Хn).
Чтобы наглядно представить, как часто
появляются те или иные значения Хi,
необходимо построить диаграмму
распределения случайных величин, которая
называется гистограммой. Для этого
статистический ряд значений записывают
в упорядоченном виде (по мере возрастания
или убывания элементов).

Рис.5
Далее весь диапазон значений от
Хmax
до Xmin
разбивают на К одинаковых интервалов
шириной Х’=(
Хmax
– Xmin)/К.
Затем подсчитывают число m попаданий
случайных величин в каждый из полученных
интервалов. По оси абсцисс откладывают
значения Хi,
а по оси ординат – число m
попаданий случайных величин статистического
ряда в каждый из интервалов и строят
прямоугольники с основанием Х’
и высотой m.
В результате такого построения получается
ступенчатая диаграмма, называемая
гистограммой (рис.5).
Как
показывает опыт, максимальное число
попаданий (заштрихованная область на
рис.5) приходится на интервал в окрестности
точки Х=<X>:
[<X>-Х’/2,
<X>+Х’/2].
Если
увеличивать число опытов (n)
и число интервалов, на которое разбивается
статистический ряд (К),
то в пределе Х’0
и вместо ступенчатой гистограммы
получится плавная кривая распределения
случайных величин (пунктирная линия на
рис.5).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) – это истинное значение, а (triangle a) – погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? 
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
И снова о погрешностях
Окончание. См. № 15/07
Д.А.ИВАШКИНА,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
И снова о погрешностях
4. Учёт случайных погрешностей при
прямых измерениях
Если, проведя одно и то же измерение
несколько раз, вы видите, что результат остаётся
одним и тем же, то случайные погрешности
эксперимента малы, их не следует учитывать. Но
если при повторении измерения получаются разные
значения, то следует взять среднее значение из
серии измерений:
![]()
где n – число измерений. Как
узнать, какова погрешность результата? Логично, и
ученики сами обычно предлагают это, определить
среднее отклонение результата от среднего
значения. Полученная величина носит название средней
арифметической ошибки: ![]() Она показывает, на сколько в
Она показывает, на сколько в
среднем каждое измеренное значение отклоняется
от среднего значения. Но эта величина слабо
зависит от количества проведённых измерений. В
чём же тогда смысл многократных измерений?
Для среднеквадратичной погрешности,
которая определяется немного сложнее:
![]()
есть простое правило: средняя
квадратичная погрешность среднего
арифметического равна средней квадратичной
погрешности отдельного результата, делённой на
корень квадратный из числа измерений: ![]() Из формулы ясно,
Из формулы ясно,
что с увеличением числа измерений случайная
погрешность среднего значения уменьшается.
Поэтому необходимо проводить столько измерений,
чтобы случайная погрешность стала меньше
значения систематической погрешности данного
измерения.
К сожалению, в лабораторных работах и
при любых других экспериментах в школе провести
достаточное количество измерений невозможно в
силу нехватки времени. Как поступать, может
решить сам учитель. На мой взгляд, для нахождения
средней арифметической погрешности среднего
значения можно использовать формулу,
аналогичную формуле для средней квадратичной
ошибки: ![]()
Хотя эта формула и неверна, она
помогает понять смысл проведения большого числа
измерений. Использоваться же она будет всего в
нескольких работах, и, следовательно, нет нужды
специально обучать нахождению погрешности
среднего значения. Зато, получив в этих работах
случайную погрешность меньше погрешности
систематической, ученик запомнит, что каждое
измерение следует производить несколько раз при
малейшем подозрении, что в данном эксперименте
имеется случайная погрешность. Как правило, уже
при пяти измерениях достигается необходимая
малость случайной погрешности по сравнению с
систематической.
5. Определение погрешности
результата косвенных измерений
К определению погрешности результата
косвенных измерений учащиеся готовы, на мой
взгляд, уже к 8-му классу. В зависимости от уровня
класса впервые метод границ [1, 12] можно
применить или в работе по сравнению количеств
теплоты при смешивании воды, или при нахождении
сопротивления проводника. Поясню на примерах.
-
Допустим, при нагревании холодной
воды в процессе смешивания мы имеем следующие
результаты измерений:
– температура холодной воды t1
= (16,0 ± 1,5) °С;
– температура смеси t = (43,0 ± 1,5) °С;
– объём холодной воды V1 = (80
± 2) мл = (80 ± 2) • 10–6 м3.
Получаем количество теплоты,
полученное холодной водой:
Q = 4190 Дж/(кг • °С) • 1000 кг/м3
• 80 • 10–6 м3 ![]() (43 – 16) °С = 9050,4 Дж.
(43 – 16) °С = 9050,4 Дж.
(1)
Возникает вопрос: а какова погрешность
полученного значения? Другими словами, на
сколько мы можем ошибиться, если точные значения
не равны измеренным, а лежат где-то в интервале,
даваемом погрешностью? Например, начальная
температура воды может быть равна 16,5 °С, 17,0 °С и
т.д. Тогда вычисленное количество теплоты будет
меньше. Логично посмотреть, на сколько мы можем
ошибиться по максимуму. Максимальное количество
теплоты получится, если взять для всех
сомножителей максимальные значения, т.е. верхние
границы интервалов значений с погрешностью, для
уменьшаемого взять верхнюю границу значения, а
для вычитаемого – нижнюю:
Qв = 4190 Дж/(кг • °С) • 1000
кг/м3 • 82 • 10–6 м3 ![]() (44,5 – 14,5)°С = 10 307,4 Дж.
(44,5 – 14,5)°С = 10 307,4 Дж.
Аналогично вычисляем нижнюю границу
значения количества теплоты:
Qн = 4190 Дж/(кг • °С) • 1000
кг/м3 • 78 • 10–6 м3 ![]() (41,5 – 17,5) °С = 7843,68
(41,5 – 17,5) °С = 7843,68
Дж.
В данных пределах и лежит искомое
значение. Чтобы сравнивать методом интервалов
это значение с количеством теплоты, отданным
горячей водой, надо округлить значения верхней и
нижней границ. Лучше это сделать, оценив
абсолютную погрешность найденного значения
количества теплоты.
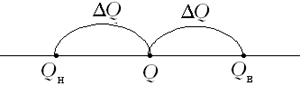
Рис. 2
Из рис. 2 видно, что
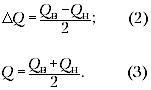
Найденное выше значение (1) близко к (3),
поэтому его не стоит находить ещё раз. А вот для
погрешности найдём с помощью (2):
![]() (две
(две
значащие цифры, т.к. первая «1»). Поэтому
количество теплоты, полученное холодной водой,
можно округлить: Qполуч = 9000 Дж ±
1200 Дж (т.е. между 7800 Дж и 10 200 Дж). Если количество
теплоты, отданное горячей водой, лежит между 8500
Дж и 11 500 Дж (Qотдан = 10 000 Дж ± 1500 Дж), то
можно видеть, что эти количества теплоты
совпадают в пределах погрешности эксперимента
(рис. 3).
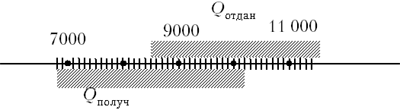
Рис.3
-
Определение сопротивления резистора.
Пусть измеренные значения напряжения и силы тока
следующие:
– U = 2,60 В ± 0,15 В (инструментальная
погрешность 0,15 В; погрешность отсчёта может быть
взята равной 0,05 В, т.е. в 3 раза меньше
инструментальной, поэтому ею можно пренебречь);
– I = 1,2 А ± 0,1 А (инструментальная
погрешность 0,05 А, погрешность отсчёта 0,05 А).
Тогда для сопротивления получаем:
![]()
Но на самом резисторе написано: «2 ± 0,1 ![]() ». Получается, что
». Получается, что
мы неверно определили сопротивление? Рассчитаем
погрешность нашего определения значения
сопротивления:
Uв = 2,75 В; Uн = 2,45 В; Iв
= 1,3 А, Iн = 1,1 А;
![]()
Полученное экспериментально значение
сопротивления R = (2,2 ± 0,3) Ом совпадает в
пределах погрешности со значением R = (2,0 ± 0,1)
Ом, указанным на резисторе.
С помощью метода границ можно вывести
и формулы для погрешности при обобщении темы
«Определение погрешности косвенных измерений»,
но уже в 9-м классе.
Определение погрешности разности. Пусть
А = В – С. Рассчитаем погрешность А в
общем виде:
Ав = Вв – Сн
= (В + ![]() В)
В)
– (С – ![]() С)
С)
= (В – С) + (![]() В
В
+ ![]() С);
С);
Ан = Вн – Св
= (В – ![]() В)
В)
– (С + ![]() С)
С)
= (В – С) – (![]() В
В
+ ![]() С);
С);
![]()
Полученное очень важно: в некоторых
работах в формулах для вычисления результата
встречается разность двух близких по значению
величин, что приводит к большой относительной
погрешности результата.
-
В cтарой работе «Определение модуля
Юнга резины» [11] удлинение резинового жгута
находилось как разность его результирующей и
начальной длин. Если условия опыта таковы, что
эта разность мала, например, составляет 1,5 см, то
относительная погрешность определения разности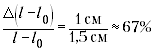 (погрешность
(погрешность
отсчёта взята гораздо меньше инструментальной
погрешности). Ясно, что такое измерение
использовать для определения модуля Юнга
нежелательно, – может получиться погрешность
больше 100%. Лучше увеличить нагрузку на жгут.
Аналогичная проблема возникает в работе
«Измерение ЭДС и внутреннего сопротивления
источника» [2] (одно сопротивление должно быть в
несколько раз больше другого) и др.
Определение погрешности частного
двух величин. Пусть ![]() Рассчитаем погрешность в общем виде:
Рассчитаем погрешность в общем виде:
![]()
Такую формулу трудно запоминать.
Поэтому найдём относительную погрешность
величины А:
![]()
Итак, относительная погрешность
частного равна сумме относительных погрешностей
величин, входящих в него. Такая же формула
получается и для относительной погрешности
произведения.
Важным я считаю не сам процесс расчёта
погрешности. Эти формулы дают мощный инструмент
для оценки обоснованности проведения
эксперимента. При их использовании легко
объяснить, при измерении какой из величин
следует увеличить точность, чтобы получить
лучший результат.
Рассмотрим формулу для нахождения
модуля Юнга: 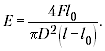
Если воспользоваться для расчёта погрешности
результата методом границ, то неясным останется,
какая из величин в формуле вносит наибольшую
погрешность.
Для нахождения относительной
погрешности результата лучше воспользоваться
формулой:
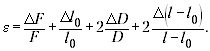
При подстановке значений оказывается,
что слагаемое 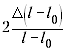
даёт максимальный вклад в сумму, а остальные
слагаемые в несколько раз меньше, так что ими
можно пренебречь. Если l – l0 будет
невелико, то значение относительной погрешности
окажется очень большим, порой выше 100%. Какой
вывод сделают в таком случае ученики?
Такая ситуация – пример того, как
применение упрощённого способа вычисления
погрешностей может привести к большим ошибкам.
Конечно же, этот эксперимент совершенно
обоснован, с помощью него можно найти модуль
Юнга. Только следует выбрать те измерения, где l
– l0 достаточно велико, и не забыть
пренебречь малыми слагаемыми при расчёте
погрешности.
6. Определение коэффициента
прямой пропорциональности
В лабораторных работах нередко
встречается ситуация, когда необходимо по
графику определить коэффициент
пропорциональности в зависимости одной величины
от другой. И здесь в учебниках встречаются две
ситуации.
В работе «Определение модуля Юнга» [13]
после нахождения модуля Юнга для измерений с
тремя различными нагрузками учащимся
предлагается найти среднее арифметическое трёх
полученных значений. Такой подход ошибочен, т.к.
каждое значение получено с различными
систематическими погрешностями, т.е. с разной
степенью точности. Нельзя суммировать эти
значения «с одинаковым весом». При подобных
вычислениях в теории ошибок находится сумма этих
значений с разными коэффициентами.
Далее, в работе «Измерение жёсткости
пружины» [7] в аналогичной ситуации совершенно
справедливо отмечено, что, поскольку жёсткость
пружины в каждом из опытов получена при разных
условиях, среднее арифметическое этих значений
находить нельзя. И предлагается найти среднее
значение коэффициента жёсткости по графику как
коэффициент пропорциональности. Однако,
поскольку учащиеся не могут найти погрешность
найденного таким образом коэффициента
пропорциональности, предлагается взять в
качестве этой погрешности погрешность
наихудшего результата. Я считаю, что такой подход
не оправдан. Зачем брать погрешность самого
ненадёжного результата, если сам способ
нахождения коэффициента жёсткости из графика
применяется для того, чтобы определить этот
коэффициент наиболее точно? Думаю, авторы просто
не хотели заострять внимание на этом вопросе.
На мой взгляд, для определения
коэффициента пропорциональности по графику
можно предложить несколько вариантов.
Вариант 1. Самый простой, а потому
пригодный для младших классов. Отмечаем на
графике экспериментальные значения с указанием
погрешности. Обращаем внимание учащихся на то,
что если бы мы не нанесли погрешности на графики,
то провести прямую было бы затруднительно. В 7-м
классе достаточно просто отметить тот факт, что
зависимость между двумя величинами прямо
пропорциональна. Но если всё-таки необходимо
найти значение коэффициента пропорциональности,
можно обойтись без расчёта погрешности, отметив
только, что этот способ (многократные измерения
при различных условиях и построение графика)
используется именно для того, чтобы уменьшить
погрешность результата.
Вариант 2. Чертим прямую, находим
экспериментальную точку, которая лежит ближе
всего к прямой, и именно эту точку и считаем самой
точной. Остаётся вычислить результат для неё по
обычным формулам, рассчитав также и погрешность.
Вариант 3. Самый логичный. Пробуем
провести через точки вместе с их погрешностями
две прямые: с наибольшим и с наименьшим наклоном.
Значения коэффициентов для них и будут верхней и
нижней границами для результата. Зная границы,
рассчитываем среднее значение коэффициента и
погрешность. Данная погрешность неявно будет
содержать в себе как систематическую
погрешность экспериментально измеренных
величин, так и случайную погрешность определения
среднего, но уже с учётом точности каждого
результата. Этот вариант годится для
использования в экспериментах, когда
коэффициент должен быть оценён достаточно точно.
Но он достаточно сложен, поэтому не стоит его
использовать во всех случаях.
Вариант 4. Использование
встроенных программ в калькуляторах или готовых
компьютерных программ для вычисления
коэффициентов по методу наименьших квадратов.
Этот способ пригоден для практикума в старших
классах и/или в классах физматпрофиля. К
сожалению, в такие программы, как правило,
встроен метод наименьших квадратов, не
учитывающий погрешностей экспериментальных
точек. Применение имеет смысл в случаях, когда
погрешности всех точек практически одинаковы
или когда доминирующей является случайная
погрешность. Она и будет учтена.
Какой из этих вариантов выбрать, может
решать сам учитель. К счастью, таких работ
довольно мало. Продемонстрируем все эти варианты
на примере.
-
Возьмём данные эксперимента по
зависимости пути от времени равномерного
движения (машинка из конструктора с
электрическим приводом):
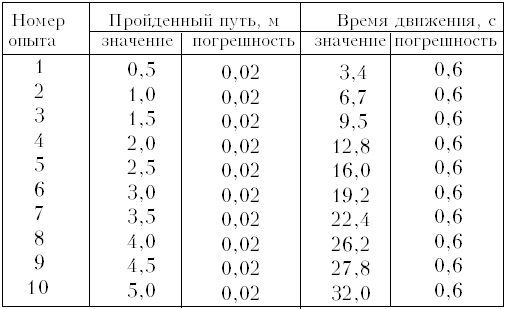
Действуя так, как описано в варианте 1,
строим график (рис. 4).
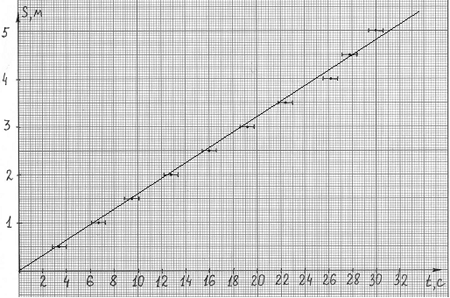
Рис. 4
Так как точек на графике много, можно с
уверенностью утверждать, что 8-я и 10-я точки
являются «выбросами», т.е. измерены небрежно.
Учитывая погрешность эксперимента, можно
провести прямую практически единственным
способом: соответствующая скорость 0,16 м/с. Если
воспользоваться методом наименьших квадратов
(например, встроенной функцией ЛИНЕЙН в
программе MicrosoftExcel), то для коэффициента мы
получим значение 0,158 ± 0,002 м/с (вариант 4).
Для варианта 2 подходит 3-я точка.
Скорость, вычисленная по данным для этой точки,
0,158 м/с. Рассчитаем погрешность: ![]() Так как относительная
Так как относительная
погрешность пути мала по сравнению с
относительной погрешностью времени,
пренебрегаем ею. Абсолютная погрешность
результата: ![]() 0,063
0,063
• 0,158 = 0,010 м/с. То есть скорость, вычисленная в
варианте 2: (0,158 ± 0,010) м/с.
Из приведённого примера видно, что
значения коэффициента пропорциональности
получаются очень близкими. В этом примере
погрешности отдельных измерений были достаточно
малы, а точек, наоборот, было много. Рассмотрим
пример, когда погрешности, напротив, велики, а
количество опытов в силу объективных причин
мало.
-
Найдём плотности пластмассы путём
измерения массы и объёмов тел.
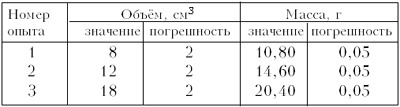
В случае варианта 1 прямую проводим
так, чтобы количество точек над и под прямой было
одинаково (рис. 5), т.е. в данном случае – одна
сверху, одна снизу (прямая 1). Плотность в
этом случае равна 1,23 г/см3.
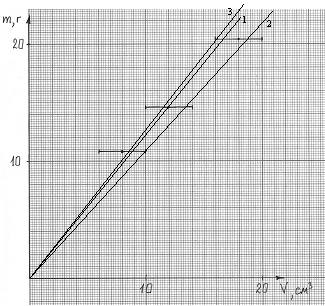
Рис. 5
В случае варианта 2 пригодна 2-я точка.
Для неё значение плотности (1,2 ± 0,2) г/см3.
Вариант 3: проведём прямые 2 и 3.
Для прямой 2 коэффициент пропорциональности
1,09 г/см3 является нижней границей
искомого значения плотности, а для прямой 3
(1,27 г/см3) – верхней. Полусумма этих
значений есть значение плотности (1,18 г/см3),
а полуразность – значение погрешности (0,09 г/см3).
Вариант 4 в данном случае менее
пригоден, т.к. не учитывает больших значений
погрешностей при измерении объёма с помощью
мерного цилиндра, но и в этом варианте плотность
(1,18 ± 0,05) г/см3.
Следует заметить, что в двух последних
примерах на графиках были обозначены только
погрешности вдоль горизонтальной оси, т.к.
погрешности значений второй переменной были
очень малы.
Послесловие
Научиться обрабатывать результаты
экспериментов учащиеся могут, лишь обрабатывая
результаты экспериментов. Это означает, что
помимо стандартного набора лабораторных работ
необходимо проводить много фронтальных и
демонстрационных экспериментов с обработкой
результатов. Это большая работа, и я хочу
пожелать успехов всем учителям, кто вступит на
этот путь или уже стоит на нём.
Литература
1. Анофрикова С.В., Стефанова Г.П.
Практическая методика преподавания физики.
Часть первая. – Астрахань: Издательство
Астраханского ГПИ, 1995.
2. Физика: Под ред. А.А.Пинского: Учебник
для 10 кл. школ и классов с угл. изучением физики. –
М.: Просвещение, 2002.
3. Попова О.Н. Обучение учащихся
выявлению устойчивых связей и отношений между
физическими величинами: Методическое пособие
для учителей физики. – Элиста: Элистинский лицей,
1998.
4. Анофрикова С.В. Азбука
учительской деятельности, иллюстрированная
примерами деятельности учителя физики. Ч. 1.
Разработка уроков. – М.: МПГУ, 2001.
5. Пёрышкин А.В. Физика-8. – М.:
Дрофа, 2004.
6. Громов С.В., Родина Н.А. Физика-8.
– М.: Просвещение, 2000.
7. Кикоин И.К., Кикоин А.К. Физика-10.
Механика. – М.: Просвещение, 2001.
8. Фронтальные лабораторные занятия по
физике в 7–11 классах общеобразовательных
учреждений. Книга для учителя: Под ред. В.А.Бурова,
Г.Г.Никифорова. – М.: Просвещение, Учебная
литература, 1996.
9. Зайдель А.Н. Элементарные оценки
ошибок измерений. – Л.: Наука, 1967.
10. Хорозов С.А. Работа над
ошибками: В кн. «Энциклопедия для детей», т. 16
«Физика», ч. 1 «Биография физики. Путешествие в
глубь материи. Механистическая картина мира». –
М.: Аванта+, 2000.
11. Мякишев Г.Я., Буховцев Б.Б., Сотский
Н.Н. Физика-10. – М.: Просвещение, 2004.
12. Кирик Л.А. Физика-9: Методические
материалы. – М.: Илекса, 2003.
13. Шахмаев Н.М., Шахмаев С.Н., Шодиев
Д.Ш. Физика-10. – М.: Просвещение, 1994.
